下载文档原格式
明渠恒定非均匀流水面线的简化速算法摘要：目前对于非均匀流的水面线计算，仅为数值模拟法，或逐段试算法，方法复杂。
本文通过建立明渠非均匀流水深沿程变化微分方程[1]，对方程简化并无量纲化后并积分，求解出水面线方程，形式简单可行。
关键词：明渠；非均匀流；临界水深；无量纲化。
一基本方程建立能量守恒方程，形式如下[1]：（1）取底坡i，并忽略沿程水头损失dhj，经简化得：。
流速换为形式，根据流量守恒定律，q可作为常数提到微分号外。
代入上式，得到：（2），其中其中ids为渠底高差。
沿程水头损失dhf采用形式。
简化计，采用朗道提出的抛物线型的明渠流速分布公式[2]，当z=时，。
代入（2）式，化简得：（3）对（3）式进行无量纲化，均除以临界水深，令为，则（3）式转化为：（4）。
代入边界条件s=0，，积分得（5），特别的，当边界水位为临界水深时，h0=hk，方程将简化为（6）。
二、算例1. 某矩形输水明渠，因上下游渠道底坡不同产生非均匀流，流量Q=4.7m3/s，B=1.5m，上游底坡0.003，对应的正常水深h0=1.236m；下游底坡0.03，对应的正常水深h0=0.518m；控制断面为里程500米处，水位Z=100m。
采用上述方法，求得水面线如图（水流趋于均匀流后水深将为正常水深而不再变化）。
2.仍采用上述条件，调整上游底坡为0.03，下游底坡为0.003，求得水面线如图3（水流趋于均匀流后水深将为正常水深而不再变化），按壅水曲线特征，图3中拐点处实际将发生水跃。
三结语（1）对能量守恒方程进行简化，得到明渠非均匀流水深沿程分布的无量纲简化式，形式工整、简单。
（2）采用此法对非均匀流的水面线计算，与实际较吻合。
（3）对于下游为缓坡的渠道，实际情况下，在临界水深附近将出现水跃，但方程并不能反映水跃发生时所产生的涡旋。
参考文献：[1] 吴持恭.水力学第三版（上册）.高等教育出版社，2003[2] 朗道.流体力学。
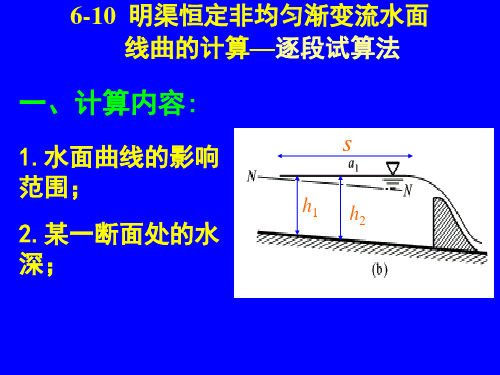
明渠恒定非均匀渐变流水面曲线的定性分析6.1 棱柱体明渠水深沿程变化的微分方程由前面我们知道断面比能0s E E Z =-，方程两边同时对流程l 求导，得：0s dE dZ dE dl dl dl=- 而 dE J dl =-，0dZ i dl=- 所以()s dE J i i J dl =---=- （4-28） 式（4-28）即为断面比能沿流程的变化规律。
又断面比能随水深的变化规律：21s dE Fr dh=- （4-29） 由式（4-28）和式（4-29）可得：21dh i J dl Fr-=- (4-30） 式（4-30）就是棱柱体明渠水深沿程变化的微分方程，利用式(4-30)，可定性分析棱柱体渠道水面线的沿程变化。
当0dh dl >时，表明水深沿程增加，水流作减速流动，水面曲线为壅水曲线；当0dh dl<时，水深沿程减小，水流作加速流动，水面曲线为降水曲线。
6.2水面线的分类6.2.1 明渠的底坡从式(4-30)可以看出，水深沿流程的变化率dh dl，与渠道的底坡i 有关，明渠的底坡不同，可以产生不同型式的水面线。
为了便于分析，需要根据底坡对水面线进行分类。
明渠的底坡分为：正坡(i >0)，平坡(i ＝0)和逆坡(i <0)。
正坡渠道又分为缓坡(k i i <)，陡坡（k i i >）和临界坡(k i i =)。
如图4-13所示。
图4-136.2.2 N －N 线和K －K 线N －N 线：渠道正常水深0h 的连线；K －K 线：渠道临界水深k h 的连线；各种底坡类型上的N －N 线和K －K 线如图4-13所示。
只有在正坡(i >0)渠道上才有可能产生均匀流，所以在平坡 (i ＝0)和逆坡(i <0)渠道上不存在N －N 线。
Ｎ－Ｎ线和K －K 线的相对位置可由正常水深和临界水深的关系确定。
缓坡k h h >0，N －N 线位于K －K 线之上；陡坡k h h <0，N －N 线位于K －K 线之下；临界坡k h h =0，N －N 线与K －K 线重合。
