水力学-第五章 明渠均匀流
- 格式:pptx
- 大小:1.54 MB
- 文档页数:48

明渠均匀流基本公式明渠均匀流是水力学中一个非常重要的概念,它有着一系列的基本公式,这些公式对于我们理解和解决水流问题起着关键作用。
咱先来说说啥是明渠均匀流。
想象一下,一条直直的渠道,水在里面稳稳地流着,速度不变,水深不变,水面线也是平平的,这就是明渠均匀流啦。
明渠均匀流的基本公式里,有一个很关键的,就是谢才公式:$V = C\sqrt{RJ}$ 。
这里的 V 代表流速,C 是谢才系数,R 是水力半径,J 是水力坡度。
那这个水力半径是啥呢?简单说,就是过水断面面积除以湿周。
比如说,一个矩形的渠道,宽是 b,水深是 h,那水力半径 R 就等于 bh / (b + 2h) 。
我记得有一次去郊外考察,看到一条灌溉用的渠道。
那渠道看起来普普通通,但仔细一观察,就能发现其中的门道。
水流很平稳,水深基本一致,这明显就是明渠均匀流的典型特征。
我就拿工具测了测渠道的宽度、水深,还算了算水力半径。
当时旁边有个农民大哥好奇地看着我,问我在干啥。
我就跟他解释,说这是在研究水流,通过这些计算能知道水的流速,对灌溉效率有很大影响。
大哥听了,似懂非懂地点点头,说:“原来这还有这么多学问呢!”再来说说谢才系数 C 。
它的取值跟渠道的粗糙程度有关。
渠道表面越粗糙,C 值就越小,水流阻力就越大。
水力坡度 J 呢,其实就是单位长度渠道上的水头损失。
如果渠道是水平的,那 J 就等于零。
在实际应用中,明渠均匀流的基本公式能帮我们解决很多问题。
比如设计排水渠道的尺寸,计算水流的输送能力等等。
总之,明渠均匀流基本公式虽然看起来有点复杂,但只要咱耐心琢磨,结合实际情况去理解和运用,就能在水力学的世界里游刃有余啦!。



1、明渠均匀流计算公式: Q=Aν=AC Ri C=n 1R y (一般计算公式)C=n 1R 61(称曼宁公式) 2、渡槽进口尺寸(明渠均匀流)z :渡槽进口的水位降(进出口水位差)ε:渡槽进口侧向收缩系数,一般ε=0.8~0.9b :渡槽的宽度(米)h :渡槽的过水深度(米)φ:流速系数φ=0.8~0.953、倒虹吸计算公式: Q=mA z g 2(m 3/秒)4、跌水计算公式:5、流量计算公式:Q=Aν式中Q ——通过某一断面的流量,m 3/s ;ν——通过该断面的流速,m /hA ——过水断面的面积,m 2。
6、溢洪道计算1)进口不设闸门的正流式开敞溢洪道(1)淹没出流:Q =εσMBH 23=侧向收缩系数×淹没系数×流量系数×溢洪道堰顶泄流长度×溢洪水深23(2)实用堰出流:Q=εMBH 23=侧向收缩系数×流量系数×溢洪道堰顶泄流长度×溢洪水深232)进口装有闸门控制的溢洪道(1)开敞式溢洪道。
Q =εσMBH 23=侧向收缩系数×淹没系数×流量系数×溢洪道堰顶泄流长度×溢洪水深23(2)孔口自由出流计算公式为 Q=MωH=堰顶闸门自由式孔流的流量系数×闸孔过水断面面积×H 其中:ω=be7、放水涵管(洞)出流计算1)、无压管流 Q=μA 02gH=流量系数×放水孔口断面面积×02gH2)、有压管流Q =μA 02gH=流量系数×放水孔口断面面积×02gH8、测流堰的流量计算——薄壁堰测流的计算1)三角形薄壁测流堰,其中θ=90°,即自由出流:Q =1.4H 25或Q =1.343H 2.47(2-15)淹没出流:Q =(1.4H 25)σ(2-16)淹没系数:σ=2)13.0(756.0--Hh n +0.145(2-17) 2)梯形薄壁测流堰,其中θ应满足tanθ=41,以及b >3H ,即 自由出流:Q =0.42b g 2H 23=1.86bH 23(2-18)淹没出流:Q =(1.86bH 23)σ(2-19)淹没系数:σ=2(23.1)Hh n --0.127(2-20) 9、水力发电出力计算N=9.81HQη式中N ——发电机出力,kW ;H ——发电毛水头,m ,为水库上游水位与发电尾水位之差,即H=Z 上-Z 下; Q ——发电流量,m 3/s ;η——发电的综合效率系数(包括发电输水管的水头损失因素和发电机组效率系数),小型水库发电一般为0.6—0.7。





明渠恒定均匀流和非均匀流概述1.1 明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响,因此在水力学中把明渠分为以下类型。
(1) 棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道,称为棱柱形渠道,否则为非棱柱形渠道。
前者的过水断面面积A 仅随水深h 变化,即A =f (h );后者的过水断面面积不仅随水深变化,而且还随着各断面的沿程位置而变化。
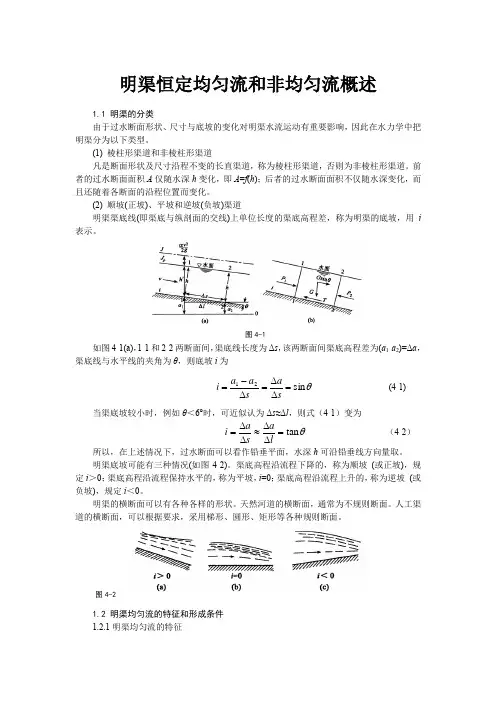
(2) 顺坡(正坡)、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差,称为明渠的底坡,用i 表示。
图4-1如图4-1(a),1-1和2-2两断面间,渠底线长度为Δs ,该两断面间渠底高程差为(a 1-a 2)=Δa ,渠底线与水平线的夹角为θ,则底坡i 为θsin 21=∆∆=∆-=sa s a a i (4-1) 当渠底坡较小时,例如θ<6°时,可近似认为Δs ≈Δl ,则式(4-1)变为 θtan =∆∆≈∆∆=la s a i (4-2) 所以,在上述情况下,过水断面可以看作铅垂平面,水深h 可沿铅垂线方向量取。
明渠底坡可能有三种情况(如图4-2)。
渠底高程沿流程下降的,称为顺坡 (或正坡),规定i >0;渠底高程沿流程保持水平的,称为平坡,i =0;渠底高程沿流程上升的,称为逆坡 (或负坡),规定i <0。
明渠的横断面可以有各种各样的形状。
天然河道的横断面,通常为不规则断面。
人工渠道的横断面,可以根据要求,采用梯形、圆形、矩形等各种规则断面。
图4-21.2 明渠均匀流的特征和形成条件1.2.1明渠均匀流的特征明渠均匀流有下列特性:(1) 过水断面的形状和尺寸、流速分布、水深,沿流程都不变;(2) 总水头线、测压管水头线(在明渠水流中,就是水面线)和渠底线三者为相互平行的直线(图4-1a),因而它们的坡度相等,即J=J p=i(4-3)1.2.2明渠均匀流的形成条件对明渠恒定均匀流,图4-1(b),取1-1、2-2断面之间的水体作为研究对象,分析这块水体上的受力,并沿流向写动力平衡方程为P1-P2+G sinθ-T=0式中P1和P2为1-1和2-2过水断面的动水压力,G为Δs流段水体重量,T为边壁(包括岸壁和渠底)阻力。
明渠均匀流计算公式明渠均匀流是水力学中的一个重要概念,咱们今天就来好好聊聊它的计算公式。
先给大家举个小例子,就说咱们村头那条灌溉渠吧。
每到灌溉的时候,水就顺着渠道哗哗地流。
如果这水流的速度、水深啥的在整个渠道里都差不多,那这就是明渠均匀流啦。
明渠均匀流的计算公式有好几个,其中最常用的就是谢才公式。
这个公式是这样的:V = C * √(RJ) 。
这里的 V 表示流速,C 是谢才系数,R 是水力半径,J 是水力坡度。
咱先来说说这水力半径 R 。
它等于过水断面面积 A 除以湿周 X 。
比如说一个矩形的渠道,宽是 b ,水深是 h ,那过水断面面积 A 就是b * h ,湿周 X 就是 b + 2h ,算出来的 R 就是 (b * h) / (b + 2h) 。
再讲讲水力坡度 J 。
简单说就是渠道底坡的坡度。
要是渠道底坡没有啥变化,那这 J 就等于底坡的坡度 i 。
谢才系数 C 呢,它的计算有点复杂,一般可以用曼宁公式来算:C= (1 / n) * R^(1/6) 。
这里的 n 是糙率,反映渠道壁面的粗糙程度。
糙率越大,水流受到的阻力就越大,速度就越慢。
就像我之前去参观一个水利工程,看到他们设计的渠道。
工作人员拿着各种仪器测量数据,然后就在那算啊算的。
我凑过去看,他们就是在根据这些公式来确定渠道的尺寸和水流速度,以保证水能顺利地流到需要灌溉的地方,还不浪费水资源。
实际应用这些公式的时候,可得仔细啦。
比如说测量数据得准确,一点小误差可能就会导致结果大不同。
还有就是要根据具体情况选择合适的公式和参数。
总之,明渠均匀流的计算公式虽然看起来有点复杂,但只要咱们搞清楚每个参数的含义,多结合实际情况练习练习,就一定能掌握好,让水流乖乖地按照我们的想法流动,为生产生活服务。
希望今天讲的这些能对大家理解明渠均匀流的计算公式有点帮助,大家加油学,以后说不定还能自己设计渠道呢!。
第五章 明渠恒定均匀流第一节 概 述一.明渠水流1、明渠定义:人工渠道、天然河道、未充满水流的管道统称为明渠。
2、明渠水流是指在明渠中流动,具有显露在大气中的自由表面,水面上各点的压强都等于大气压强。
故明渠水流又称为无压流。
明渠水流的运动是在重力作用下形成的。
在流动过程中,自由水面不受固体边界的约束(这一点与管流不同),因此,在明渠中如有干扰出现,例如底坡的改变、断面尺寸的改变、粗糙系数的变化等,都会引起自由水面的位置随之升降,即水面随时空变化,这就导致了运动要素发生变化,使得明渠水流呈现出比较多的变化。
在一定流量下,由于上下游控制条件的不同,同一明渠中的水流可以形成各种不同形式的水面线。
正因为明渠水流的上边界不固定,故解决明渠水流的流动问题远比解决有压流复杂得多。
明渠水流可以是恒定流或非恒定流,也可以是均匀流或非均匀流,非均匀流也有急变流和渐变流之分。
本章首先学习恒定均匀流。
明渠恒定均匀流是一种典型的水流,其有关的理论知识是分析和研究明渠水流各种现象的基础,也是渠道断面设计的重要依据。
对明渠水流而言,当然也有层流和紊流之分,但绝大多数水流(渗流除外)为紊流,并且接近或属于紊流阻力平方区。
因此,本章及以后各章的讨论将只限于此种情况。
二、渠槽的断面形式(一)按横断面的形状分类渠道的横断面形状有很多种。
人工修建的明渠,为便于施工和管理,一般为规则断面,常见的有梯形断面、矩形断面、U 型断面等,具体的断面形式还与当地地形及筑渠材料有关。
天然河道 一般为无规则,不对称,分为主槽与滩地。
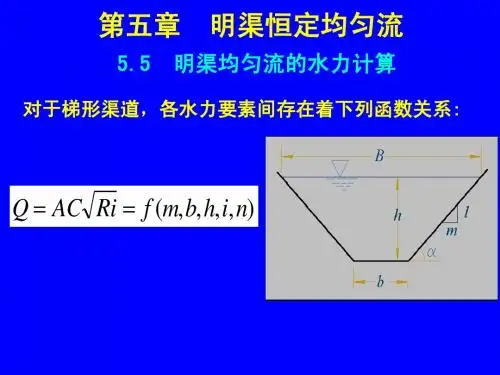
在今后的分析计算中,常用的是渠道的过水断面的几何要素,主要包括:过水断面面积A 、湿周χ、水力半径R 、水面宽度B 。
对梯形断面而言,其过水断面几何要素计算公式如下:2)()h m h mh b A +=+=β(h m m h b )12(1222++=++=βχχAR = h m mh b B )2(2+=+=β式中,b 为底宽;m 为边坡系数;h 为水深;β为宽深比,定义为h b =β(二)按横断面形状尺寸沿流程是否变化分类棱柱体明渠是指断面形状尺寸沿流程不变的长直明渠。