2015年高考数学真题分类汇编专题05平面向量理

平面向量1.【2015高考新课标1，理7】设D 为ABC ∆所在平面内一点3BC CD =u u u r u u u r，则（ ）（A ）1433AD AB AC =-+u u u r u u ur u u u r (B)1433AD AB AC =-u u u r u u u r u u u r（C ）4133AD AB AC =+u u u u u r u u u r u u u r (D)4133AD AB AC =-u u u u u u u ru u u r u u u r【答案】A【解析】由题知11()33AD AC CD AC BC AC AC AB =+=+=+-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r =1433AB AC -+u u ur u u u r ，故选A.2.【2015高考山东，理4】已知菱形ABCD 的边长为a ，60ABC ∠=o,则BD CD ⋅=u u u r u u u r （ ）（A ）232a -（B ）234a - （C ） 234a 错误!未找到引用源。

（D ）232a 错误!未找到引用源。

【答案】D【解析】因为()BD CD BD BA BA BC BA ⋅=⋅=+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r ()22223cos 602BA BC BA a a a +⋅=+=o u u u r u u u r u u u r .故选D.3.【2015高考陕西，理7】对任意向量,a b r r，下列关系式中不恒成立的是（ ）A ．||||||a b a b ⋅≤r r r rB ．||||||||a b a b -≤-r r r rC ．22()||a b a b +=+r r r r D ．22()()a b a b a b +-=-r r r r r r【答案】B【解析】因为cos ,a b a b a b a b ⋅=≤r r r r r r r r ，所以选项A 正确；当a r 与b r方向相反时，a b a b -≤-r r r r 不成立，所以选项B 错误；向量的平方等于向量的模的平方，所以选项C 正确；()()22a b a b a b +-=-r r r r r r ，所以选项D 正确．故选B ．4.【2015高考四川，理7】设四边形ABCD 为平行四边形，6AB =u u u r ，4AD =u u u r .若点M ，N 满足3BM MC =u u u u r u u u u r ，2DN NC =u u u r u u u r ，则AM NM ⋅=u u u u r u u u u r（ ）（A ）20 （B ）15 （C ）9 （D ）6 【答案】C【解析】311,443AM AB AD NM CM CN AD AB =+=-=-+u u u u r u u u ru u u r u u u u r u u u u r u u u r u u ur u u u r ，所以 221111(43)(43)(169)(1636916)94124848AM NM AB AD AB AD AB AD =+-=-=⨯-⨯=u u u u r u u u u r u u u r u u u r u u u r u u u r u u u r u u u r g g ，选C.5.【2015高考重庆，理6】若非零向量a ，b 满足|a ||b |，且（a -b ）⊥（3a +2b ），则a 与b 的夹角为 （ ） A.4πB.2πC.34πD.π【答案】A6.【2015高考安徽，理8】C ∆AB 是边长为2的等边三角形，已知向量a r ，b r 满足2a AB =u u u r r，C 2a b A =+u u u r rr ，则下列结论正确的是（ ）（A ）1b =r （B ）a b ⊥r r （C ）1a b ⋅=r r （D ）()4C a b +⊥B u u u r rr【答案】D【解析】如图，由题意，(2)2BC AC AB a b a b =-=+-=u u u r u u u r u u u r r r r r ，则||2b =r ，故A 错误；|2|2||2a a ==r r ，所以||1a =r，又22(2)4||222cos 602AB AC a a b a ab ⋅=⋅+=+=⨯=ou u u r u u u r r r r r r r ，所以1a b ⋅=-r r ，故,B C 错误；设,B C 中点为D ，则2AB AC AD +=u u u r u u u r u u u r ，且AD BC ⊥u u u r u u u r ，而22(2)4AD a a b a b =++=+u u u r r r r r r，所以()4C a b +⊥B u u u r rr ，故选D.7.【2015高考福建，理9】已知1,,AB AC AB AC t t⊥==u u u r u u u r u u u r u u u r，若P 点是ABC ∆ 所在平面内一点，且4AB ACAP AB AC=+u u u r u u u ru u u r u u u r u u u r ，则PB PC ⋅u u u r u u u r 的最大值等于（ ）A ．13B ．15C ．19D ．21【答案】A【解析】以A 为坐标原点，建立平面直角坐标系，如图所示，则1(,0)B t，(0,)C t ，1AP =u u u r （，0)+4(0,1)=(1,4)，即1P （，4)，所以11PB t-u u u r =（，-4)，1PC -u u u r =（，t-4)，因此PB PC ⋅u u u r u u u rxy BCAP11416t t =--+117(4)t t =-+，因为114244t t t t +≥⋅=，所以PB PC ⋅u u u r u u u r 的最大值等于13，当14t t=，即12t =时取等号． 8.【2015高考北京，理13】在ABC △中，点M ，N 满足2AM MC =u u u u r u u u u r ，BN NC =u u u r u u u r ．若MN xAB y AC =+u u u u r u u u r u u u r，则x = ；y = ．【答案】11,26-9.【2015高考湖北，理11】已知向量OA AB ⊥u u u r u u u r ，||3OA =u u u r，则OA OB •=u u u r u u u r .【答案】9【解析】因为OA AB ⊥u u u r u u u r ，||3OA =u u u r，所以OA OB •=u u u r u u u r 93||||)(222===•+=+•OA OB OA OA AB OA OA .10.【2015高考天津，理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠=o,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==u u u r u u u r u u u r u u u r 则AE AF ⋅u u u r u u u r的最小值为 .【答案】2918【解析】因为1,9DF DC λ=u u u r u u ur 12DC AB =u u u r u u u r ，119199918CF DF DC DC DC DC AB λλλλλ--=-=-==u u u r u u u r u u u r u u u r u u u r u u u r u u u r ，AE AB BE AB BC λ=+=+u u u r u u u r u u u r u u u r u u u r ，19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ，()221919191181818AE AF AB BC AB BC AB BC AB BCλλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r 19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒211721172929218921818λλλλ=++≥⋅+= 当且仅当2192λλ=即23λ=时AE AF ⋅u u u r u u u r 的最小值为2918. BAD C E11.【2015高考浙江，理15】已知12,e e r r 是空间单位向量，1212e e ⋅=r r ，若空间向量b r 满足1252,2b e b e ⋅=⋅=r r r r ，且对于任意,x y R ∈，12010200()()1(,)b xe ye b x e y e x y R -+≥-+=∈r u r u u r r u r u u r u u u u r ，则0x = ，0y = ，b =r．【答案】1，2，22.12.【2015高考新课标2，理13】设向量a r ，b r 不平行，向量a b λ+r r 与2a b +r r 平行，则实数λ=_________．【答案】12【解析】因为向量a b λ+r r 与2a b +r r 平行，所以2a b k a b λ+=+r r r r （），则12,k k λ=⎧⎨=⎩，所以12λ=．13.【2015江苏高考，14】设向量a k (cos ,sin cos )(0,1,2,,12)666k k k k πππ=+=L ，则11k =∑(a k g a k+1)的值为【答案】93 【解析】 a k g a k+1(1)(1)(1)(cos ,sin cos )(cos ,sin cos )666666k k k k k k ππππππ+++=+⋅+ (1)(1)(1)coscos (sin cos )(sin cos )666666k k k k k k ππππππ+++=++⋅+(1)(1)(1)(1)(1)(coscos sin sin )(sin cos cos sin )cos cos 6666666666k k k k k k k k k k ππππππππππ+++++=++++22(1)3231cos sincos cos sin cos cos sin66662626266k k k k k k k ππππππππππ+++=++=++- 3231sin (1cos )sin 264343k k k ππππ+=+++-3321(21)sin cos4626k k πππ++=++ 因为21(21)sin cos 626k k πππ++，的周期皆为6，一个周期的和皆为零， 因此11k =∑(a k g a k+1)3312934=⨯=. 14.【2015江苏高考，6】已知向量a =)1,2(，b=)2,1(-, 若m a +n b =)8,9(-(R n m ∈,), 则n m -的值为______. 【答案】3-【解析】由题意得：29,282,5, 3.m n m n m n m n +=-=-⇒==-=-15.【2015高考湖南，理8】已知点A ，B ，C 在圆221x y +=上运动，且AB BC ⊥，若点P 的坐标为(2,0)，则PA PB PC ++u u u r u u u r u u u r的最大值为（ ）A.6B.7C.8D.9 【答案】B.。

第五章 平面向量
1.【2015高考新课标1，文2】已知点，向量，则向量( )
（A） （B） （C） （D）
2.【2015高考广东，文9】在平面直角坐标系中，已知四边形是平行四
边形，，，则（ ）
A． B． C． D．
3.【2015高考重庆，文7】已知非零向量满足则的夹角为（ ）
(A) (B) (C) (D)
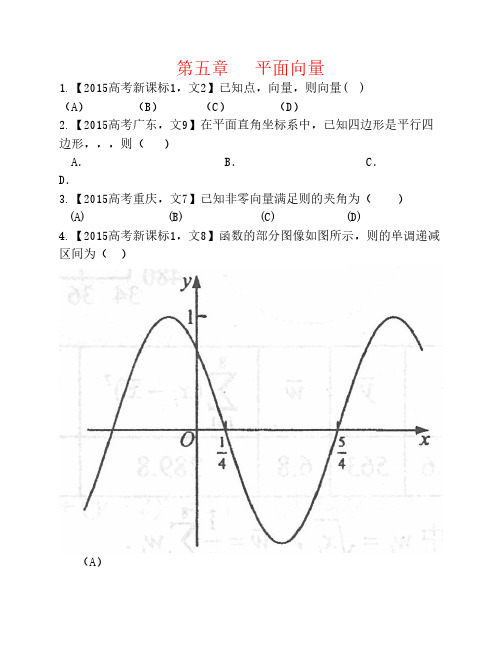
4.【2015高考新课标1，文8】函数的部分图像如图所示，则的单调递减
区间为（ ）
（A）
（B）
（C）
（D）
5.【2015高考福建，文7】设，，．若，则实数的值等于（ ）
A． B． C． D．
6.【2015高考北京，文6】设，是非零向量，“”是“”的（ ）
A．充分而不必要条件 B．必要而不充
分条件
C．充分必要条件 D．既不充分也
不必要条件
7.【2015高考陕西，文8】对任意向量，下列关系式中不恒成立的是（ ）
A． B． C． D．
8.【2015高考湖北，文11】.已知向量，，则_________．
9.【2015高考安徽，文15】是边长为2的等边三角形，已知向量满
足，，则下列结论中正确的是 .（写出所有正确结论得序号）
①为单位向量；②为单位向量；③；④；⑤。

10. 【2015高考山东，文13】 过点作圆
的两条切线，切点分别为，则
= .
11.【2015高考天津，文13】在等腰梯形ABCD中,已知, 点E和点F分别在
线段BC和CD上,且 则的值为 ．
12.【2015高考浙江，文13】已知，是平面单位向量，且．若平面向量满足，则 ．。

2015年全国各地高考数学试题及解答分类大全（平面向量）一、选择题：1.（2015安徽理）C ∆AB 是边长为2的等边三角形，已知向量a ，b 满足2a AB = ，C 2a b A =+，则下列结论正确的是（）（A）1b = （B）a b⊥ （C）1a b ⋅= （D）()4Ca b +⊥B2、（2015北京文）设a ，b是非零向量，“a b a b ⋅= ”是“//a b ”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【答案】A 【解析】试题分析：||||cos ,a b a b a b ∙=∙<> ，由已知得cos ,1a b <>= ，即,0a b <>= ，//a b .而当//a b时，,a b <> 还可能是π，此时||||a b a b ∙=- ，故“a b a b ⋅= ”是“//a b”的充分而不必要条件.考点：充分必要条件、向量共线.3．（2015福建文）设(1,2)a = ，(1,1)b = ，c a kb =+ ．若b c ⊥，则实数k 的值等于（）A．32-B．53-C．53D．32【答案】A考点：平面向量数量积．4．（2015福建理）已知1,,AB AC AB AC t t⊥==，若P 点是ABC ∆所在平面内一点，且4AB AC AP AB AC=+ ，则PB PC ⋅的最大值等于（）A．13B．15C．19D．21【答案】A考点：1、平面向量数量积；2、基本不等式．5.（2015广东文）在平面直角坐标系x y O 中，已知四边形CD AB 是平行四边形，()1,2AB =-，()D 2,1A =，则D C A ⋅A = （）A ．2B ．3C ．4D ．5【答案】D 【解析】试题分析：因为四边形CD AB 是平行四边形，所以()()()C D 1,22,13,1A =AB +A =-+=-，所以()D C 23115A ⋅A =⨯+⨯-=，故选D．考点：1、平面向量的加法运算；2、平面向量数量积的坐标运算．6、(2015湖南文)已知点A,B,C 在圆221x y +=上运动，且AB ⊥BC，若点P 的坐标为（2，0），则PA PB PC ++的最大值为（）A、6B、7C、8D、9【答案】B【解析】试题分析：由题根据所给条件不难得到该圆221x y +=是一AC 位直径的圆，然后根据所给条件结合向量的几何关系不难得到24PA PB PC PO PB PB ++++==，易知当B 为（-1，0）时取得最大值.由题意，AC 为直径，所以24PA PB PC PO PB PB ++++== ,已知B 为（-1，0）时，4PB+取得最大值7，故选B.考点：直线与圆的位置关系、平面向量的运算性质7.(2015湖南理)已知点A ，B ，C 在圆221x y +=上运动，且AB BC ⊥，若点P 的坐标为(2,0)，则PA PB PC ++的最大值为（）A.6B.7C.8D.9【答案】B.【考点定位】1.圆的性质；2.平面向量的坐标运算及其几何意义.【名师点睛】本题主要考查向量的坐标运算，向量的几何意义以及点到圆上点的距离的最值问题，属于中档题，结合转化思想和数形结合思想求解最值，关键是把向量的模的最值问题转化为点与圆上点的距离的最值问题，即圆221x y +=上的动点到点)0,6(距离的最大值.8、(2015全国新课标Ⅰ卷文)已知点(0,1),(3,2)A B ，向量(4,3)AC =--，则向量BC = ()（A）(7,4)--（B）(7,4)（C）(1,4)-（D）(1,4)9.(2015全国新课标Ⅰ卷理)设D 为ABC 所在平面内一点3BC CD =，则（）（A ）1433AD AB AC =-+(B)1433AD AB AC=-（C ）4133AD AB AC=+ (D)4133AD AB AC =-【答案】A【解析】试题分析：由题知11()33AD AC CD AC BC AC AC AB =+=+=+-= =1433AB AC -+，故选A.考点：平面向量运算10.(2015全国新课标Ⅱ卷文)已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a （）A ．1-B ．0C ．1D ．2【答案】C【解析】试题分析：由题意可得22=a ,3,⋅=-a b 所以()222431+⋅=+⋅=-=a b a a a b .故选C.考点：向量数量积.11.(2015山东理)已知菱形ABCD 的边长为a ，60ABC ∠=,则BD CD ⋅=（）（A）232a -（B）234a -（C）234a （D）232a【答案】D【考点定位】平面向量的线性运算与数量积.【名师点睛】本题考查了平面向量的基础知识，重点考查学生对平面向量的线性运算和数量积的理解与掌握，属基础题，要注意结合图形的性质，灵活运用向量的运算解决问题.12.(2015陕西文、理)对任意向量,a b，下列关系式中不恒成立的是（）A ．||||||a b a b ∙≤B ．||||||||a b a b -≤- C ．22()||a b a b +=+ D ．22()()a b a b a b +-=- 【答案】B考点：1.向量的模；2.数量积.13.(2015四川理)设四边形ABCD 为平行四边形，6AB = ，4AD = .若点M，N 满足3BM MC =，2DN NC = ，则AM NM ⋅= （）（A）20（B）15（C）9（D）6【答案】C【考点定位】平面向量.【名师点睛】涉及图形的向量运算问题，一般应选两个向量作为基底，选基底的原则是这两个向量有尽量多的已知元素.本题中，由于6AB = ，4AD = 故可选,AB AD作为基底.14、(2015四川文)设向量a ＝(2，4)与向量b ＝(x ，6)共线，则实数x ＝()(A )2(B )3(C )4(D )6【答案】B【考点定位】本题考查平面向量的坐标表示，向量共线的性质，考查基本的运算能力.【名师点睛】平面向量的共线、垂直以及夹角问题，我们通常有两条解决通道：一是几何法，可以结合正余弦定理来处理.二是代数法，特别是非零向量的平行与垂直，一般都直接根据坐标之间的关系，两个非零向量平行时，对应坐标成比例(坐标中有0时单独讨论)；两个向量垂直时，对应坐标乘积之和等于0，即通常所采用的“数量积”等于0.属于简单题.15．(2015重庆理)若非零向量a ，b 满足|a |=3|b |，且（a -b ）⊥（3a +2b ），则a 与b 的夹角为（）A、4πB、2πC、34πD、π【答案】A【考点定位】向量的夹角.16.(2015重庆文)已知非零向量,a b 满足||=4||(+)b a a a b ⊥，且2则a b 与的夹角为（）(A)3π(B)2π(C)32π(D)65π【答案】C考点：向量的数量积运算及向量的夹角.二、填空题：1.（2015安徽文）ABC ∆是边长为2的等边三角形，已知向量b a 、满足a AB 2=→，b a AC+=→2，则下列结论中正确的是.（写出所有正确结论得序号）①a为单位向量；②b 为单位向量；③b a ⊥；④→BC b // ；⑤→⊥+BC b a )4( 。

2015年高考数学理一轮复习精品资料【新课标版】预测卷第五章 平面向量 第四节 平面向量的应用一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的。

）1.【2013-2014学年广东省云浮市云浮中学高一5月】如图所示，向量OA a OB b OC c === ，A 、B 、C 在一条直线上，且 3 AC BC =，则（ ）.A 、1322c a b =-+ B 、31 22c a b =-C 、 2 b a c +-=D 、 2 b a c +=2. 【2013-2014学年广东省云浮市云浮中学高一5月】如图所示，D 是ABC ∆的边AB 上的中点，记BC a =，BA c =，则向量CD =（ ）．A ．12a c --B ．12a c -+ C ．12a c - D ．12a c +【答案】B【解析】1111()()2222CD CA CB BA BC BC BA BC a b =+=--=-=-+． 3.【2014届四川绵阳高中高三第二次诊断性考试】已知△ABC 的外接圆的圆心为O ，半径为1，若345OA OB OC ++=0，则△AOC 的面积为( )A ．25 B ．12 C ．310 D ．654.【2014年高考数学人教版评估检测】如图所示,非零向量=a,=b,且BC ⊥OA,C 为垂足,若=λa(λ≠0),则λ=( )5. 【2013-2014学年辽宁省抚顺市六校联合体高一下学期期末】已知)0,3(-A ，)2,0(B ，O 为坐标原点，点C 在∠AOB 内，且45=∠AOC ，设(1),()OC OA OB R λλλ=+-∈，则λ的值为（ ）A.51 B.31C.52D.32【答案】C.6. 【2014届浙江省绍兴市第一中学高三上学期期中考试】已知1e 和2e 是平面上的两个单位向量，且121e e +≤，12,OP me OQ ne ==，若O 为坐标原点，,m n 均为正常数，则()2OP OQ +的最大值为( )A ．22m n mn +-B ．22m n mn ++C ．2()m n + D ．2()m n -7.【2014年高考数学（理）二轮复习】如图，在直角梯形ABCD 中，AD ⊥AB ，AB ∥DC ，AD ＝DC ＝1，AB ＝2，动点P 在以点C 为圆心，且与直线BD 相切的圆上或圆内移动，设AP ＝λAD ＋μAB (λ，μ∈R)，则λ＋μ的取值范围是 ( )．A ．(1,2)B ． (0,3)C ．[1,2]D ．[1,2)【答案】C【解析】以A为原点，AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系，则B(2,0)，D(0,1)，8.【2014届四川绵阳高中高三第二次诊断性考试】已知O是锐角△ABC的外心，若OC=xOA yOB+(x，y ∈R)，则（）A．x+y≤-2 B．-2≤x+y<-1 C．x+y<-1 D．-1<x+y<09.【2014届山西省太原市太原五中高三12月月考】△ABC的外接圆的圆心为O，半径为2，且OA AB AC++=，则向量CA在CB方向上的投影为( )A．3 C．．-310.【2014届浙江省建人高复高三上学期第二次月考】在ABC ∆中，2,2AB BC A π==∠=，如果不等式BA tBC AC -≥恒成立，则实数t 的取值范围是（ ） A.[)1,+∞ B.1,12⎡⎤⎢⎥⎣⎦ C.[)1,1,2⎛⎤-∞+∞ ⎥⎝⎦D.(][),01,-∞+∞11.【2014届天津市蓟县高三上学期期中考试】如图A 是单位圆与x 轴的交点，点P 在单位圆上，(0)AOP θθπ∠=<<,OQ OA OP =+,四边形OAQP 的面积为S ,当OA OP S ⋅+取得最大值时θ的值和最大值分别为( )A.6π3π，1 C.4π2π12.【改编自2013年辽宁五校联考】设函数()f x 的定义域为D ，如果存在正实数k ，使对任意x D ∈，都有x k D ∈＋，且()()f x k f x >＋恒成立，则称函数()f x 为D 上的“k 型增函数”．已知()f x 是定义在R 上的奇函数，且当0x >时，()||2f x x a a ＝－－，若()f x 为R 上的“2 013型增函数”，则实数a 的取值范围是（ ） A. 671,2⎛⎫-∞ ⎪⎝⎭ B. (),300-∞ C. (300,)+∞ D. 671,2⎛⎫+∞ ⎪⎝⎭【答案】D二、填空题（本大题共4小题，每小题5分，共20分。

5.2平面向量的数量积及平面向量的应用考点一平面向量的数量积1.(2015课标Ⅱ,4,5分)向量a=(1,-1),b=(-1,2),则(2a+b)·a=()A.-1B.0C.1D.2答案C2.(2015北京,6,5分)设a,b是非零向量.“a·b=|a||b|”是“a∥b”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案A3.(2015重庆,7,5分)已知非零向量a,b满足|b|=4|a|,且a⊥(2a+b),则a与b的夹角为()A.π3B.π2C.2π3D.5π6答案C10.(2015浙江,13,4分)已知e1,e2是平面单位向量,且e1·e2=12.若平面向量b满足b·e1=b·e2=1,则|b|=.答案23311.(2015天津,13,5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°.点E和F分别在线段BC和DC上,且BE=23BC,DF=16DC,则AE·AF的值为.答案291812.(2015湖北,11,5分)已知向量OA⊥AB,|OA|=3,则OA·OB=.答案9考点二向量的应用3.(2015安徽,15,5分)△ABC是边长为2的等边三角形,已知向量a,b满足AB=2a,AC=2a+b,则下列结论中正确的是.(写出所有正确结论的编号) ①a为单位向量;②b为单位向量;③a⊥b;④b∥BC;⑤(4a+b)⊥BC.答案①④⑤。

数 学F 单元 平面向量F1 平面向量的概念及其线性运算 2．F1[2015·四川卷] 设向量a ＝(2,4)与向量b ＝(x ,6)共线,则实数x ＝( ) A ．2 B ．3 C ．4 D ．62．B [解析] 由向量a ,b 共线,得2×6－4x ＝0,解得x ＝3,选B.2．F1、F2[2015·全国卷Ⅰ] 已知点A (0,1),B (3,2),向量AC →＝(－4,－3),则向量BC →＝( ) A ．(－7,－4) B ．(7,4) C ．(－1,4) D ．(1,4)2．A [解析] AB →＝(3,1),BC →＝AC →－AB →＝(－4,－3)－(3,1)＝(－7,－4)．2．F1[2015·四川卷] 设向量a ＝(2,4)与向量b ＝(x ,6)共线,则实数x ＝( ) A ．2 B ．3 C ．4 D ．62．B [解析] 由向量a ,b 共线,得2×6－4x ＝0,解得x ＝3,选B.F2 平面向量基本定理及向量坐标运算 6．F2[2015·江苏卷] 已知向量a ＝(2,1),b ＝(1,－2),若m a ＋n b ＝(9,－8)(m ,n ∈R ),则m －n 的值为________．6．－3 [解析] 因为m a ＋n b ＝(2m ＋n ,m －2n )＝(9,－8),所以⎩⎪⎨⎪⎧2m ＋n ＝9，m －2n ＝－8，解得⎩⎪⎨⎪⎧m ＝2，n ＝5，故m －n ＝－3.2．F1、F2[2015·全国卷Ⅰ] 已知点A (0,1),B (3,2),向量AC →＝(－4,－3),则向量BC →＝( ) A ．(－7,－4) B ．(7,4) C ．(－1,4) D ．(1,4)2．A [解析] AB →＝(3,1),BC →＝AC →－AB →＝(－4,－3)－(3,1)＝(－7,－4)．4．F2、F3[2015·全国卷Ⅱ] 向量a ＝(1,－1),b ＝(－1,2),则(2a ＋b )·a ＝( ) A ．－1 B ．0 C ．1 D ．24．C [解析] 2a ＋b ＝2(1,－1)＋(－1,2)＝(1,0),所以(2a ＋b )·a ＝(1,0)·(1,－1)＝1. 9．F2、F4[2015·湖南卷] 已知点A ,B ,C 在圆x 2＋y 2＝1上运动,且AB ⊥BC ,若点P 的坐标为(2,0),则|P A →＋PB →＋PC →|的最大值为( )A ．6B ．7C ．8D ．99．B [解析] 方法一：因为A ,B ,C 均在单位圆上,且AB ⊥BC ,所以A ,C 为直径的端点,故P A →＋PC →＝2PO →＝(－4,0),|P A →＋PB →＋PC →|＝|2PO →＋PB →|≤2|PO →|＋|PB →|,又|PB →|≤|PO →|＋1＝3,所以|P A →＋PB →＋PC →|≤4＋3＝7,故最大值为7,选B.方法二：因为A ,B ,C 均在单位圆上,且AB ⊥BC ,所以A ,C 为直径的端点,令A (cos x ,sin x ),B (cos (x ＋α),sin (x ＋α)),C (－cos x ,－sin x ),0<α<π,则P A →＋PB →＋PC →＝(cos(x ＋α)－6,sin(x ＋α)), |P A →＋PB →＋PC →|＝[cos （x ＋α）－6]2＋sin 2（x ＋α）＝37－12cos （x ＋α）≤7,故选B. F3 平面向量的数量积及应用 4．F2、F3[2015·全国卷Ⅱ] 向量a ＝(1,－1),b ＝(－1,2),则(2a ＋b )·a ＝( ) A ．－1 B ．0 C ．1 D ．24．C [解析] 2a ＋b ＝2(1,－1)＋(－1,2)＝(1,0),所以(2a ＋b )·a ＝(1,0)·(1,－1)＝1. 6．A2,F3[2015·北京卷] 设a ,b 是非零向量．“a·b ＝|a||b|”是“a ∥b ”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 6．A [解析] 根据数量积的定义,a ·b ＝||a ·||b cos θ,由a ·b ＝||a ·||b 可得cos θ＝1,根据向量所成角的范围得到θ＝0,所以a ∥b ；若a ∥b ,可得向量a 与向量b 共线,即所成的角为0或π,所以a ·b ＝±||a ·||b ,故选A. 13．H4、F3[2015·山东卷] 过点P (1,3)作圆x 2＋y 2＝1的两条切线,切点分别为A ,B ,则P A →·PB →＝________．13.32 [解析] 如图所示,|P A |＝|PB |＝3,|OP |＝2,|OA |＝1,且P A ⊥OA ,∴∠APO ＝π6,即∠APB ＝π3,∴P A →·PB →＝|P A →||PB →|cos ∠APB ＝3×3×cos π3＝32.8．F3[2015·陕西卷] 对任意平面向量a ,b ,下列关系式中不恒成立．．．．的是( ) A ．|a ·b|≤|a||b| B ．|a －b|≤||a|－|b|| C ．(a ＋b )2＝|a ＋b|2 D ．(a ＋b )·(a －b )＝a 2－b 2 8．B [解析] 根据数量积的定义知a·b ＝|a||b|cos 〈a ,b 〉,所以|a·b|＝||a||b|cos 〈a ,b 〉|≤|a||b |,选项A 中的关系式一定成立；如果选项B 中的关系式成立,则|a －b|2≤||a|－|b||2,可得a·b ≥|a||b|,此式只可能在a ,b 共线且同向时成立；根据向量的运算法则可知,选项C,D 中的关系式是恒成立的．20．F3,H5,H8[2015·四川卷] 如图1-3,椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率是22,点P (0,1)在短轴CD 上,且PC →·PD →＝－1.(1)求椭圆E 的方程．(2)设O 为坐标原点,过点P 的动直线与椭圆交于A ,B 两点．是否存在常数λ,使得OA →·OB →＋λP A →·PB →为定值？若存在,求λ的值；若不存在,请说明理由．图1-320．解：(1)由已知,点C ,D 的坐标分别为(0,－b ),(0,b )． 又点P 的坐标为(0,1),且PC →·PD →＝－1,于是⎩⎪⎨⎪⎧1－b 2＝－1，c a ＝22，a 2－b 2＝c 2，解得a ＝2,b ＝2.所以椭圆E 的方程为x 24＋y 22＝1.(2)当直线AB 的斜率存在时,设直线AB 的方程为y ＝kx ＋1,A ,B 的坐标分别为(x 1,y 1),(x 2,y 2)．联立⎩⎪⎨⎪⎧x 24＋y 22＝1，y ＝kx ＋1，得(2k 2＋1)x 2＋4kx －2＝0.其判别式Δ＝(4k )2＋8(2k 2＋1)>0, 所以x 1＋x 2＝－4k 2k 2＋1,x 1x 2＝－22k 2＋1.从而OA →·OB →＋λP A →·PB →＝x 1x 2＋y 1y 2＋λ[x 1x 2＋(y 1－1)(y 2－1)] ＝(1＋λ)(1＋k 2)x 1x 2＋k (x 1＋x 2)＋1 ＝（－2λ－4）k 2＋（－2λ－1）2k 2＋1＝－λ－12k 2＋1－λ－2.所以,当λ＝1时,－λ－12k 2＋1－λ－2＝－3.此时,OA →·OB →＋λP A →·PB →＝－3为定值． 当直线AB 斜率不存在时,直线AB 即为直线CD .此时,OA →·OB →＋λP A →·PB →＝OC →·OD →＋PC →·PD →＝－2－1＝－3. 故存在常数λ＝1,使得OA →·OB →＋λP A →·PB →为定值－3.13．F3[2015·浙江卷] 已知e 1,e 2是平面单位向量,且e 1·e 2＝12.若平面向量b 满足b ·e 1＝b ·e 2＝1,则|b |＝________．13.233 [解析] 令b ＝x e 1＋y e 2(x ,y ∈R ),b ·e 1＝x e 1·e 1＋y e 2·e 1＝x ＋12y ＝1,b ·e 2＝x e 1·e 2＋y e 2·e 2＝12x ＋y ＝1,解得x ＝y ＝23,则b ＝23(e 1＋e 2),所以b 2＝49(e 1＋e 2)2＝49(e 21＋2e 1·e 2＋e 22)＝43,故|b |＝2 33. 7．F3[2015·重庆卷] 已知非零向量a ,b 满足|b|＝4|a|,且a ⊥(2a ＋b ),则a 与b 的夹角为( )A.π3B.π2C.2π3D.5π67．C [解析] 由已知得a ·(2a ＋b )＝2a 2＋a ·b ＝0,即a ·b ＝－2a 2,所以cos 〈a ,b 〉＝a ·b|a ||b |＝－2a 24a 2＝－12,所以〈a ,b 〉＝2π3. 9．F3[2015·广东卷] 在平面直角坐标系xOy 中,已知四边形ABCD 是平行四边形,AB →＝(1,－2),AD →＝(2,1),则AD →·AC →＝( )A ．5B ．4C ．3D ．29．A [解析] 因为四边形ABCD 是平行四边形,所以AC →＝AB →＋AD →＝(1,－2)＋(2,1)＝(3,－1),所以AD →·AC →＝2×3＋1×(－1)＝5,故选A.11．F3[2015·湖北卷] 已知向量OA →⊥AB →,|OA →|＝3,则OA →·OB →＝________． 11．9 [解析] 根据题意作出图形,如图所示．设向量OA →,OB →的夹角为θ,则OA →·OB →＝||OA →||OB→cos θ.因为OA →⊥AB →,所以||OB →cos θ＝||OA →,所以OA →·OB →＝||OA →2＝9. 14．C7、F3[2015·江苏卷] 设向量a k ＝⎝⎛⎭⎫cos k π6，sin k π6＋cos k π6(k ＝0,1,2,…,12),则k ＝011(a k ·a k ＋1)的值为________．14．93 [解析] 因为a k ·a k ＋1＝cosk π6cos （k ＋1）π6＋⎝⎛⎭⎫sin k π6＋cos k π6⎣⎡⎦⎤sin （k ＋1）π6＋cos （k ＋1）π6＝2cosk π6cos （k ＋1）π6＋sin k π6sin （k ＋1）π6＋sin k π6cos （k ＋1）π6＋cos k π6sin （k ＋1）π6＝cos k π6cos （k ＋1）π6＋cos π6＋sin （2k ＋1）π6＝12cos （2k ＋1）π6＋sin （2k ＋1）π6＋334,所以k ＝011(a k ·a k ＋1)＝12×334＋12k ＝011c os （2k ＋1）π6＋k ＝011s in （2k ＋1）π6＝9 3.F4 单元综合7．F4[2015·福建卷] 设a ＝(1,2),b ＝(1,1),c ＝a ＋k b .若b ⊥c ,则实数k 的值等于( )A ．－32B ．－53 C.53 D.327．A [解析] c ＝(1,2)＋k (1,1)＝(1＋k ,2＋k ),因为b ⊥c ,所以b ·c ＝1×(1＋k )＋1×(2＋k )＝3＋2k ＝0,所以k ＝－32.9．F2、F4[2015·湖南卷] 已知点A ,B ,C 在圆x 2＋y 2＝1上运动,且AB ⊥BC ,若点P 的坐标为(2,0),则|P A →＋PB →＋PC →|的最大值为( )A ．6B ．7C ．8D ．99．B [解析] 方法一：因为A ,B ,C 均在单位圆上,且AB ⊥BC ,所以A ,C 为直径的端点,故P A →＋PC →＝2PO →＝(－4,0),|P A →＋PB →＋PC →|＝|2PO →＋PB →|≤2|PO →|＋|PB →|,又|PB →|≤|PO →|＋1＝3,所以|P A →＋PB →＋PC →|≤4＋3＝7,故最大值为7,选B.方法二：因为A ,B ,C 均在单位圆上,且AB ⊥BC ,所以A ,C 为直径的端点,令A (cos x ,sin x ),B (cos (x ＋α),sin (x ＋α)),C (－cos x ,－sin x ),0<α<π,则P A →＋PB →＋PC →＝(cos(x ＋α)－6,sin(x ＋α)), |P A →＋PB →＋PC →|＝[cos （x ＋α）－6]2＋sin 2（x ＋α）＝37－12cos （x ＋α）≤7,故选B. 13．F4[2015·天津卷] 在等腰梯形ABCD 中,已知AB ∥DC ,AB ＝2,BC ＝1,∠ABC ＝60°.点E 和F 分别在线段BC 和DC 上,且BE →＝23BC →,DF →＝16DC →,则AE →·AF →的值为________．13.2918 [解析] 根据题意,AE →·AF →＝(AB →＋BE →)·(AD →＋DF →)＝AB →＋23BC →·AD →＋16DC →＝AB →·AD →＋16AB →·DC →＋23BC →·AD →＋19BC →·DC →＝1＋13＋13－118＝2918. 15．F4[2015·安徽卷] △ABC 是边长为2的等边三角形,已知向量a ,b 满足AB →＝2a ,AC →＝2a ＋b ,则下列结论中正确的是________．(写出所有正确结论的编号)①a 为单位向量；②b 为单位向量；③a ⊥b ；④b ∥BC →；⑤(4a ＋b )⊥BC →.15．①④⑤ [解析] 由AB →＝2a ,AC →＝2a ＋b ,得a ＝12AB →,b ＝AC →－2a ＝BC →,④正确；|a |＝12|AB→|＝1,①正确；|b |＝|BC →|＝2,②错误；且a 与b 的夹角为120°,故a ·b ＝1×2×cos 120°＝－1,③错误；(4a ＋b )·b ＝4a ·b ＋b 2＝－4＋4＝0,⑤正确．10．[2015·泉州五校联考] 在直角梯形ABCD 中,AB ∥DC ,AD ⊥AB ,AD ＝DC ＝2,AB ＝3,点M 是梯形ABCD 内(包括边界)的一个动点,点N 是CD 边的中点,则AM →·AN →的最大值是________．10．6 [解析] 以A 为原点,分别以AB →,AD →所在的方向为x 轴、y 轴的正方向,建立平面直角坐标系,可得A (0,0),B (3,0),C (2,2),D (0,2),N (1,2),则直线BC 的方程为y ＝－2x ＋6.由题易知,当AM →·AN →取得最大值时,点M 在线段BC 上,故设M (λ,－2λ＋6)(2≤λ≤3),可得AM →＝(λ,－2λ＋6),AN →＝(1,2),∴AM →·AN →＝λ＋2×(－2λ＋6)＝12－3λ.∵2≤λ≤3,∴当λ＝2时,AM →·AN →取得最大值6.7．[2015·丽水一模] 已知P 是边长为2的正方形ABCD 内的点,若△P AB ,△PBC 的面积均不大于1,则AP →·BP →的取值范围是( )A ．(－1,2)B ．(－1,1)C ．0,12 D.12,327．B [解析]以A 为坐标原点,AB 所在直线为x 轴,建立直角坐标系(如图所示),则B (2,0),C (2,2)．设P (x ,y ),0<x <2,0<y <2.由△P AB ,△PBC 的面积均不大于1,得0<y ≤1,1≤x <2,则AP →·BP →＝x (x －2)＋y 2＝(x －1)2＋y 2－1.又(x －1)2＋y 2表示平面区域0<y ≤1,1≤x <2内的点P (x ,y )与点(1,0)间的距离的平方,所以AP →·BP →的取值范围是(－1,1)． 9．[2015·辽宁师大附中模拟] 已知a ,b 是单位向量,且a·b ＝0.若向量c 满足|c －a －b|＝1,则|c|的取值范围是________．9．[2－1,2＋1] [解析] 由a ,b 是单位向量,且a·b ＝0,可设a ＝(1,0),b ＝(0,1),c ＝(x ,y )． ∵向量c 满足|c －a －b|＝1,∴（x －1）2＋（y －1）2＝1,即(x －1)2＋(y －1)2＝1.该方程表示圆心为(1,1),半径为1的圆,∴2－1≤|c |＝x 2＋y 2≤2＋1,∴|c |的取值范围是[2－1,2＋1]．4．[2015·湛江调研] 在平面直角坐标系中,O 为坐标原点,设向量OA →＝a ,OB →＝b ,其中a ＝(3,1),b ＝(1,3)．若OC →＝λOA →＋μOB →,且0≤λ≤μ≤1,则点C 所有可能的位置区域用阴影表示正确的是( )4．D [解析] 当λ＝μ＝1时,OC →＝λa ＋μb ＝a ＋b ＝(4,4),故可以排除C.当λ＝μ＝0时,OC→＝λa ＋μb ＝(0,0),故可以排除 B.当μ＝13,λ＝12时,OC →＝λa ＋μb ＝12a ＋13b ＝116,32,故可以排除A.故选D.。

第五章 平面向量考点1 平面向量的概念及坐标运算1.(2015·新课标全国Ⅰ，7)设D 为△ABC 所在平面内一点，BC →＝3CD →，则( ) A.AD →＝－13AB →＋43AC → B.AD →＝13AB →－43AC → C.AD →＝43AB →＋13AC → D.AD →＝43AB →－13AC →1.A [∵BC →＝3CD →，∴AC →－AB →＝3(AD →－AC →)，即4AC →－AB →＝3AD →， ∴AD →＝－13AB →＋43AC →.]2.(2015·湖南，8)已知点A ，B ，C 在圆x 2＋y 2＝1上运动，且AB ⊥BC .若点P 的坐标为(2,0)，则|PA →＋PB →＋PC →|的最大值为( ) A.6 B.7 C.8 D.92.B [由A ,B ,C 在圆x 2＋y 2＝1上,且AB ⊥BC ,∴AC 为圆直径,故PA →＋PC →＝2PO →＝(－4，0),设B (x ，y )，则x 2＋y 2＝1且x ∈[-1,1]，PB →＝(x －2，y )，所以PA →＋PB →＋PC →＝(x -6，y ).故|PA →＋PB →＋PC →|＝－12x ＋37，∴x ＝－1时有最大值49＝7，故选B.]3.(2014·福建，8)在下列向量组中，可以把向量a ＝(3,2)表示出来的是( ) A.e 1＝(0,0)，e 2＝(1,2) B.e 1＝(－1,2)，e 2＝(5，－2) C.e 1＝(3,5)，e 2＝(6,10) D.e 1＝(2，－3)，e 2＝(－2,3)3.B [法一 若e 1＝(0，0)，e 2＝(1，2)，则e 1∥e 2，而a 不能由e 1，e 2表示，排除A ；若e 1＝(－1，2)，e 2＝(5，－2)，因为－15≠2－2，所以e 1，e 2不共线，根据共面向量的基本定理，可以把向量a ＝(3，2)表示出来，故选B.法二 因为a ＝(3，2)，若e 1＝(0，0)，e 2＝(1，2)，不存在实数λ，μ，使得a ＝λe 1＋μe 2，排除A ；若e 1＝(－1，2)，e 2＝(5，－2)，设存在实数λ，μ，使得a ＝λe 1＋μe 2，则(3，2)＝(－λ＋5μ，2λ－2μ)，所以⎩⎪⎨⎪⎧3＝－λ＋5μ，2＝2λ－2μ，解得⎩⎪⎨⎪⎧λ＝2，μ＝1.所以a ＝2e 1＋e 2，故选B.]4.(2014·安徽，10)在平面直角坐标系xOy 中，已知向量a ，b ，|a |＝|b |＝1，a ·b ＝0，点Q 满足OQ →＝2(a ＋b ).曲线C ＝{P |OP →＝a cos θ＋b cos θ，0≤θ<2π}，区域Ω＝{P |0<r ≤|PQ →|≤R ，r <R }.若C ∩Ω为两段分离的曲线，则( )A.1<r <R <3B.1<r <3≤RC.r ≤1<R <3D.1<r <3<R4.A [由已知可设OA →＝a ＝(1，0)，OB →＝b ＝(0，1)，P (x ，y )，则OQ →＝(2，2)，曲线C ＝{P |OP →＝(cos θ，sin θ)，0≤θ<2π}，即C ：x 2＋y 2＝1，区域Ω＝{P |0<r ≤|PQ →|≤R ，r <R }表示圆P 1：(x －2)2＋(y －2)2＝r 2与圆P 2：(x －2)2＋(y －2)2＝R 2所形成的圆环，如图所示，要使C ∩Ω为两段分离的曲线，只有1<r <R <3.]5.（2017•浙江,15）已知向量 、 满足| |=1，| |=2，则| + |+| ﹣ |的最小值是________，最大值是________． 5. 4；记∠AOB=α，则0≤α≤π，如图，由余弦定理可得：| + |=，| ﹣ |=，则x 2+y 2=10（x 、y≥1），其图象为一段圆弧MN ，如图，令z=x+y ，则y=﹣x+z ，则直线y=﹣x+z 过M 、N 时z 最小为z min =1+3=3+1=4，当直线y=﹣x+z 与圆弧MN 相切时z 最大，由平面几何知识易知z max 即为原点到切线的距离的倍，也就是圆弧MN 所在圆的半径的倍，所以z max =×=．综上所述，| + |+| ﹣ |的最小值是4，最大值是 ．故答案为：4、．6.（2017•江苏,12）如图，在同一个平面内，向量，，的模分别为1，1，， 与的夹角为α，且tanα=7，与的夹角为45°．若=m+n（m ，n ∈R ），则m+n=________．6. 3 如图所示，建立直角坐标系．A （1，0）．由与的夹角为α，且tanα=7．∴cosα= ，sinα= ．∴C ．cos （α+45°）=（cosα﹣sinα）= ．sin （α+45°）= （sinα+cosα）= ．∴B．∵ =m +n （m ，n ∈R ），∴=m ﹣n ，=0+n ，解得n=，m=．则m+n=3．故答案为：3．7.(2016·全国Ⅰ，13)设向量a ＝(m ，1)，b ＝(1，2)，且|a ＋b |2＝|a |2＋|b |2，则m ＝________. 7.－2[由|a ＋b |2＝|a |2＋|b |2，得a ⊥b ，所以m ×1＋1×2＝0，得m ＝－2.]8.(2015·新课标全国Ⅱ，13)设向量a ，b 不平行，向量λa ＋b 与a ＋2b 平行，则实数λ＝____________.8.12[∵向量a ，b 不平行，∴a ＋2b ≠0，又向量λa ＋b 与a ＋2b 平行，则存在唯一的实数μ，使λa ＋b ＝μ(a ＋2b )成立，即λa ＋b ＝μa ＋2μb ，则得⎩⎪⎨⎪⎧λ＝μ，1＝2μ，解得λ＝μ＝12.]9.(2015·北京，13)在△ABC 中，点M ，N 满足AM →＝2MC →，BN →＝NC →.若MN →＝xAB →＋yAC →，则x ＝________；y ＝________.9.12 －16 [MN →＝MC →＋CN →＝13AC →＋12CB →＝13AC →＋12(AB →－AC →)＝12AB →－16AC →，∴x ＝12，y ＝－16.]10.(2015·江苏，6)已知向量a ＝(2,1)，b ＝(1，－2)，若m a ＋n b ＝(9，－8)(m ，n ∈R )，则m －n 的值为________.10.－3 [∵a ＝(2,1),b ＝(1,-2),∴m a ＋n b ＝(2m ＋n ,m －2n )＝(9,-8)，即⎩⎪⎨⎪⎧2m ＋n ＝9，m －2n ＝－8，解得⎩⎪⎨⎪⎧m ＝2，n ＝5，故m －n ＝2－5＝－3.]11.(2014·新课标全国Ⅰ，15)已知A ，B ，C 为圆O 上的三点，若AO →＝12(AB →＋AC →)，则AB →与AC→的夹角为________.11.90°[由AO →＝12(AB →＋AC →)可知O 为BC 的中点，即BC 为圆O 的直径，又因为直径所对的圆周角为直角，所以∠BAC ＝90°，所以AB →与AC →的夹角为90.]12.(2014·湖南，16)在平面直角坐标系中，O 为原点，A (－1，0)，B (0，3)，C (3,0)，动点D 满足|CD →|＝1，则|OA →＋OB →＋OD →|的最大值是________.12.1＋7 [设D (x ，y )，由|CD →|＝1，得(x －3)2＋y 2＝1，向量OA →＋OB →＋OD →＝(x －1，y ＋3)，故|OA →＋OB →＋OD →|＝（x －1）2＋（y ＋3）2的最大值为圆(x －3)2＋y 2＝1上的动点到点(1，－3)距离的最大值，其最大值为圆(x －3)2＋y 2＝1的圆心(3，0)到点(1，－3)的距离加上圆的半径，即（3－1）2＋（0＋3）2＋1＝1＋7.]考点2 平面向量的数量积及其应用1.（2017•北京,6）设 ， 为非零向量，则“存在负数λ，使得 =λ ”是 • ＜0”的（ ）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件1. A ， 为非零向量，存在负数λ，使得 =λ ，则向量 ， 共线且方向相反，可得 • ＜0．反之不成立，非零向量 ， 的夹角为钝角，满足 • ＜0，而 =λ 不成立．∴ ， 为非零向量，则“存在负数λ，使得 =λ ”是 • ＜0”的充分不必要条件．故选A ．2.（2017•新课标Ⅲ,12）在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若=λ+μ，则λ+μ的最大值为（ ）A.3B.2C.D.22. A 如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，则A（0，0），B（1，0），D（0，2），C（1，2），∵动点P在以点C为圆心且与BD相切的圆上，设圆的半径为r，∵BC=2，CD=1，∴BD= = ,∴BC•CD= BD•r，∴r= ，∴圆的方程为（x﹣1）2+（y﹣2）2= ，设点P的坐标为（cosθ+1，sinθ+2），∵=λ +μ ，∴（cosθ+1，sinθ﹣2）=λ（1，0）+μ（0，2）=（λ，2μ），∴cosθ+1=λ，sinθ+2=2μ，∴λ+μ= cosθ+sinθ+2=sin（θ+φ）+2，其中tanφ=2，∵﹣1≤sin（θ+φ）≤1，∴1≤λ+μ≤3，故λ+μ的最大值为3，故选A.3.（2017•浙江,10）如图，已知平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD 交于点O，记I1= •，I2= •，I3= •，则（）A.I1＜I2＜I3B.I1＜I3＜I2C.I3＜I1＜I2D.I2＜I1＜I33. C ∵AB⊥BC，AB=BC=AD=2，CD=3，∴AC=2 ，∴∠AOB=∠COD＞90°，由图象知OA＜OC，OB＜OD，∴0＞•＞•，•＞0，即I3＜I1＜I2，故选C．4.（2017•新课标Ⅱ,12）已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则•（+ ）的最小值是（）A.﹣2B.﹣C.﹣D.﹣14. B 建立如图所示的坐标系，以BC 中点为坐标原点，则A （0， ），B （﹣1，0），C（1，0），设P （x ，y ），则=（﹣x ，﹣y ），=（﹣1﹣x ，﹣y ），=（1﹣x ，﹣y ），则 •（ + ）=2x 2﹣2y+2y 2=2[x 2+（y ﹣）2﹣]∴当x=0，y=时，取得最小值2×（﹣ ）=﹣ ，故选B.5.(2016·四川，10)在平面内，定点A ，B ，C ，D 满足|DA →|＝|DB →|＝|DC →|，DA →·DB →＝DB →·DC →＝DC →·DA →＝－2，动点P ，M 满足|AP →|＝1，PM →＝MC →，则|BM →|2的最大值是( ) A.434 B.494 C.37＋634 D.37＋23345.B[由题意,|DA →|＝|DB →|＝|DC →|,所以D 到A ,B ,C 三点的距离相等,D 是△ABC 的外心； DA →·DB →＝DB →·DC →＝DC →·DA →＝-2⇒DA →·DB →－DB →·DC →＝DB →·(DA →－DC →)＝DB →·CA →＝0,所以DB ⊥AC ， 同理可得，DA ⊥BC ，DC ⊥AB ，从而D 是△ABC 的垂心，∴△ABC 的外心与垂心重合，因此△ABC 是正三角形，且D 是△ABC 的中心. DA →·DB →＝|DA →||DB →|cos ∠ADB ＝|DA →||DB →|×⎝ ⎛⎭⎪⎫－12＝－2⇒|DA →|＝2，所以正三角形ABC 的边长为23；我们以A 为原点建立直角坐标系,B ,C ,D 三点坐标分别为B (3,－3)，C (3,3)，D (2,0)，由|AP →|＝1,设P 点的坐标为(cos θ，sin θ)，其中θ∈[0，2π)，而PM →＝MC →，即M 是PC 的中点，可以写出M 的坐标为M ⎝⎛⎭⎪⎫3＋cos θ2，3＋sin θ2 则|BM →|2＝⎝ ⎛⎭⎪⎫cos θ－322＋⎝ ⎛⎭⎪⎫33＋sin θ22＝37＋12sin ⎝ ⎛⎭⎪⎫θ－π64≤37＋124＝494，当θ＝23π时，||2取得最大值494.故选B.6.(2016·山东，8)已知非零向量m ，n 满足4|m |＝3|n |，cos 〈m ，n 〉＝13.若n ⊥(t m ＋n )，则实数t 的值为( )A.4B.－4C.94D.－946.B[∵n ⊥(t m ＋n )，∴n ·(t m ＋n )＝0，即t ·m ·n ＋n 2＝0，∴t |m ||n |cos 〈m ，n 〉＋|n |2＝0，由已知得t ×34|n |2×13＋|n |2＝0，解得t ＝－4，故选B.]7.(2016·全国Ⅲ，3)已知向量BA →＝⎝ ⎛⎭⎪⎫12，32，BC →＝⎝ ⎛⎭⎪⎫32，12，则∠ABC ＝( )A.30°B.45°C.60°D.120°7.A [|BA →|＝1，|BC →|＝1，cos ∠ABC ＝BA →·BC →|BA →|·|BC →|＝32.]8.(2016·全国Ⅱ，3)已知向量a ＝(1，m )，b ＝(3，－2)，且(a ＋b )⊥b ，则m ＝( ) A.－8 B.－6 C.6 D.88.D[由题知a ＋b ＝(4，m －2)，因为(a ＋b )⊥b ，所以(a ＋b )·b ＝0， 即4×3＋(－2)×(m －2)＝0，解之得m ＝8，故选D.]9.(2015·山东，4)已知菱形ABCD 的边长为a ，∠ABC ＝60° ，则BD →·CD →＝( ) A.－32a 2B.－34a 2C.34a 2D.32a29.D [如图所示，由题意，得BC ＝a ，CD ＝a ，∠BCD ＝120°.BD 2＝BC 2＋CD 2－2BC ·CD ·cos 120°＝a 2＋a 2－2a ·a ×⎝ ⎛⎭⎪⎫－12＝3a 2，∴BD ＝3a .∴BD →·CD →＝|BD →|·|CD →|cos 30°＝3a 2×32＝32a 2.]10.(2015·安徽，8)△ABC 是边长为2的等边三角形，已知向量a ，b 满足AB →＝2a ，AC →＝2a ＋b ，则下列结论正确的是( )A.|b |＝1B.a ⊥bC.a ·b ＝1D.(4a ＋b )⊥BC →10.D [由于△ABC 是边长为2的等边三角形；∴(AB →＋AC →)·(AB →－AC →)＝0，即(AB →＋AC →)·CB →＝0，∴(4a ＋b )⊥CB →，即(4a ＋b )⊥BC →，故选D.]11.(2015·四川，7)设四边形ABCD 为平行四边形，|AB →|＝6，|AD →|＝4，若点M ，N 满足BM →＝3MC →，DN →＝2NC →，则AM →·NM →＝( ) A.20 B. 15 C.9 D.611.C[AM →＝AB →＋34AD →，NM →＝CM →－CN →＝－14AD →＋13AB →∴AM →·NM →＝14(4AB →＋3AD →)·112(4AB →－3AD →)＝148(16AB →2－9AD →2)＝148(16×62－9×42)＝9，选C.]12.(2015·福建，9)已知AB →⊥AC →，|AB →|＝1t，|AC →|＝t ，若点P 是△ABC 所在平面内的一点，且AP →＝AB →|AB →|＋4AC →|AC →|，则PB →·PC →的最大值等于( )A.13B.15C.19D.2112.A [建立如图所示坐标系，则B⎝ ⎛⎭⎪⎫1t ，0，C (0，t )，AB →＝⎝ ⎛⎭⎪⎫1t ，0，AC →＝(0，t )，AP →＝AB →|AB →|＋4AC →|AC →|＝t ⎝ ⎛⎭⎪⎫1t ，0＋4t (0，t )＝(1，4)，∴P (1，4)，PB →·PC→＝⎝ ⎛⎭⎪⎫1t－1，－4·(－1，t －4)＝17－⎝ ⎛⎭⎪⎫1t＋4t ≤17－21t·4t ＝13，故选A.]13.(2015·重庆，6)若非零向量a ，b 满足|a |＝223|b |，且(a －b )⊥(3a ＋2b )，则a 与b的夹角为( )A.π4B.π2C.3π4D.π 13.A [由题意(a －b )·(3a ＋2b )＝3a 2－a·b －2b 2＝0，即3|a |2－|a |·|b |cos θ－2|b |2＝0，所以3×⎝ ⎛⎭⎪⎫2232－223cos θ－2＝0，cos θ＝22，θ＝π4，选A.]14.(2015·陕西，7)对任意向量a ，b ，下列关系式中不恒成立的是( )A.|a ·b |≤|a ||b |B.|a －b |≤||a |－|b ||C.(a ＋b )2＝|a ＋b |2D.(a ＋b )(a －b )＝a 2－b214.B [对于A ，由|a ·b |＝||a ||b |cos<a ,b >|≤|a ||b |恒成立；对于B ，当a ，b 均为非零向量且方向相反时不成立；对于C 、D 容易判断恒成立.故选B.]15.(2014·新课标全国Ⅱ，3)设向量a ，b 满足|a ＋b |＝10，|a －b |＝6，则a ·b ＝( ) A.1 B.2 C.3 D.515.A [由向量的数量积运算可知,∵|a ＋b |＝10,∴(a ＋b )2＝10,∴a 2+b 2+2a ·b ＝10,① 同理a 2＋b 2－2a ·b ＝6，② ① －②得4a ·b ＝4，∴a ·b ＝1.]16.(2014·大纲全国，4)若向量a 、b 满足：|a |＝1，(a ＋b )⊥a ，(2a ＋b )⊥b ，则|b |＝( ) A.2 B. 2 C.1 D.2216.B [由题意得⎩⎪⎨⎪⎧（a ＋b ）·a ＝a 2＋a ·b ＝0，（2a ＋b ）·b ＝2a ·b ＋b 2＝0⇒-2a 2+b 2＝0,即－2|a |2＋|b |2＝0,又|a |＝1，∴|b |＝ 2.故选B.]17.(2014·天津，8)已知菱形ABCD 的边长为2，∠BAD ＝120°，点E ，F 分别在边BC ，DC 上，BE ＝λBC ，DF ＝μDC .若AE →·AF →＝1，CE →·CF →＝－23，则λ＋μ＝( )A.12B.23C.56D.71217.C [如图所示,以菱形ABCD 的两条对角线所在直线为坐标轴,建立平面直角坐标系xOy ,不妨设A (0，－1),B (－3，0),C (0，1),D (3，0),由题意得CE →＝(1－λ)·CB →＝(3λ－3，λ－1)，CF →＝(1－μ)CD →＝(3－3μ，μ－1).因为CE →·CF →＝-23，所以3(λ-1)·(1-μ)＋(λ-1)(μ-1)＝－23，即(λ-1)(μ-1)＝13.因为AE →＝AC →＋CE →＝(3λ－3，λ＋1).AF →＝AC →＋CF →＝(3－3μ，μ＋1)，又AE →·AF →＝1，所以(λ＋1)(μ＋1)＝2.由⎩⎪⎨⎪⎧（λ－1）（μ－1）＝13.（λ＋1）（μ＋1）＝2，整理得λ＋μ＝56.选C.]18.（2017•新课标Ⅰ,13）已知向量 ， 的夹角为60°，| |=2，| |=1，则| +2 |=________． 18. ∵向量 ， 的夹角为60°，且| |=2，| |=1，∴=+4 • +4=22+4×2×1×cos60°+4×12=12，∴| +2 |=2 ．故答案为：2．19.（2017•山东,12）已知 ，是互相垂直的单位向量，若﹣与 +λ的夹角为60°，则实数λ的值是________．19. ， 是互相垂直的单位向量，∴| |=||=1，且 • =0； 又 ﹣ 与 +λ 的夹角为60°，∴（﹣）•（ +λ）=| ﹣|×|+λ|×cos60°，即 +（ ﹣1） •﹣λ= ××，化简得﹣λ=×× ，即 ﹣λ= ，解得λ= ．故答案为：． 20.（2017·天津,13）在△ABC 中，∠A=60°，AB=3，AC=2．若 =2，=λ﹣ （λ∈R ），且 =﹣4，则λ的值为________．20.如图所示，△ABC 中，∠A=60°，AB=3，AC=2，=2 ， ∴ = += += + （ ﹣ ）= + ， 又 =λ﹣ （λ∈R ）， ∴ =（ + ）•（λ ﹣ ） =（ λ﹣ ）•﹣+λ=（ λ﹣ ）×3×2×cos60°﹣ ×32+ λ×22=﹣4，∴λ=1，解得λ= ．故答案为：．21.(2016·浙江，15)已知向量a ，b ，|a |＝1，|b |＝2.若对任意单位向量e ，均有|a ·e |＋|b ·e |≤6，则a ·b 的最大值是________.21.12 [由已知可得：6≥|a ·e |＋|b ·e |≥|a ·e ＋b ·e |＝|(a ＋b )·e | 由于上式对任意单位向量e 都成立.∴6≥|a ＋b |成立.∴6≥(a ＋b )2＝a 2＋b 2＋2a ·b ＝12＋22＋2a ·b .即6≥5＋2a ·b ，∴a ·b ≤12.]22.(2015·天津，14)在等腰梯形ABCD 中，已知AB ∥DC ，AB ＝2，BC ＝1，∠ABC ＝60°，动点E 和F 分别在线段BC 和DC 上，且BE →＝λBC →，DF →＝19λDC →，则|AE →|·|AF →|的最小值为________.22.2918 [在梯形ABCD 中，AB ＝2，BC ＝1，∠ABC ＝60°，可得DC ＝1，AE →＝AB →＋λBC →，AF →＝AD →＋19λDC →，∴AE →·AF →＝(AB →＋λBC →)·(AD →＋19λDC →)＝AB →·AD →＋AB →·19λDC →＋λBC →·AD →＋λBC →·19λDC →＝2×1×cos 60°＋2×19λ＋λ×1×cos 60°＋λ19λ×cos 120°＝29λ＋λ2＋1718≥229λ·λ2＋1718＝2918，当且仅当29λ＝λ2，即λ＝23时，取得最小值为2918.]23.(2015·浙江，15)已知e 1,e 2是空间单位向量,e 1·e 2＝12，若空间向量b 满足b ·e 1＝2，b ·e 2＝52，且对于任意x ，y ∈R ，|b －(x e 1＋ye 2)|≥|b －(x 0e 1＋y 0e 2)|＝1(x 0，y 0∈R )，则x 0＝________，y 0＝________，|b |＝________.23.1 2 2 2 [∵e 1·e 2＝|e 1|·|e 2|cos 〈e 1，e 2〉＝12，∴〈e 1，e 2〉＝π3.不妨设e 1＝⎝ ⎛⎭⎪⎫12，32，0，e 2＝(1，0，0)，b ＝(m ，n ，t ). 由题意知⎩⎪⎨⎪⎧b ·e 1＝12m ＋32n ＝2，b ·e 2＝m ＝52，解得n ＝32，m ＝52，∴b ＝⎝ ⎛⎭⎪⎫52，32，t .∵b －(x e 1＋y e 2)＝⎝ ⎛⎭⎪⎫52－12x －y ，32－32x ，t ，∴|b －(x e 1＋y e 2)|2＝⎝ ⎛⎭⎪⎫52－x 2－y 2＋⎝ ⎛⎭⎪⎫32－32x 2＋t 2＝x 2＋xy ＋y 2－4x －5y ＋t 2＋7＝⎝ ⎛⎭⎪⎫x ＋y －422＋34(y －2)2＋t 2.由题意知，当x ＝x 0＝1，y ＝y 0＝2时，⎝⎛⎭⎪⎫x ＋y －422＋34(y －2)2＋t 2取到最小值.此时t 2＝1，故|b |＝⎝ ⎛⎭⎪⎫522＋⎝ ⎛⎭⎪⎫322＋t 2＝2 2.] 24.（2017•江苏,16）已知向量 =（cosx ，sinx ）， =（3，﹣ ），x ∈[0，π]．（Ⅰ）若 ∥ ，求x 的值； （Ⅱ）记f （x ）=，求f （x ）的最大值和最小值以及对应的x 的值．24.（Ⅰ）∵ =（cosx ，sinx ）， =（3，﹣）， ∥ ，∴﹣ cosx+3sinx=0， ∴tanx=，∵x ∈[0，π]， ∴x=，（Ⅱ）f （x ）= =3cosx ﹣ sinx=2 （ cosx ﹣ sinx ）=2 cos （x+ ），∵x ∈[0，π]，∴x+ ∈[ ， ]，∴﹣1≤cos（x+ ）≤ ，当x=0时，f （x ）有最大值，最大值3，当x= 时，f （x ）有最小值，最大值﹣225.(2015·广东，16)在平面直角坐标系xOy 中,已知向量m ＝⎝⎛⎭⎪⎫22，－22,n ＝(sin x ，cosx )，x ∈⎝⎛⎭⎪⎫0，π2.(1)若m ⊥n ，求tan x 的值. (2)若m 与n 的夹角为π3，求x 的值.25.解 (1)因为m ＝⎝ ⎛⎭⎪⎫22，－22，n ＝(sin x ，cos x )，m ⊥n .所以m ·n ＝0，即22sin x －22cos x ＝0，所以sin x ＝cos x ，所以tan x ＝1. (2)因为|m |＝|n |＝1,所以m ·n ＝cos π3＝12，即22sin x －22cos x ＝12，所以sin ⎝ ⎛⎭⎪⎫x －π4＝12， 因为0<x <π2，所以－π4<x －π4<π4，所以x －π4＝π6，即x ＝5π12.26.(2014·北京，10)已知向量a ，b 满足|a |＝1，b ＝(2,1)，且λa ＋b ＝0(λ∈R )，则|λ|＝________.26. 5 [∵|a |＝1，∴可令a ＝(cos θ，sin θ)，∵λa ＋b ＝0，∴⎩⎪⎨⎪⎧λcos θ＋2＝0，λsin θ＋1＝0，即⎩⎪⎨⎪⎧cos θ＝－2λ，sin θ＝－1λ，由sin 2θ＋cos 2θ＝1得λ2＝5，得|λ|＝5.]27.(2014·江西，14)已知单位向量e 1与e 2的夹角为α，且cos α＝13，向量a ＝3e 1－2e 2与b ＝3e 1－e 2的夹角为β，则cos β＝________. 27.223[因为a 2＝(3e 1-2e 2)2＝9-2×3×2×cos α＋4＝9,所以|a |＝3,b 2＝(3e 1-e 2)2＝9-2×3×1×cos α＋1＝8，所以|b |＝22，a ·b ＝(3e 1－2e 2)·(3e 1－e 2)＝9e 21－9e 1·e 2＋2e 22＝9－9×1×1×13＋2＝8，所以cos β＝a ·b |a |·|b |＝83×22＝223.]28.(2014·湖北，11)设向量a ＝(3,3)，b ＝(1，－1).若(a ＋λb )⊥(a －λb )，则实数λ＝________.28.±3 [(a ＋λb )⊥(a －λb )⇒(a ＋λb )·(a －λb )＝a 2－λ2b 2＝0⇒18－2λ2＝0⇒λ＝±3.]29.(2014·江苏，12)如图，在平行四边形ABCD 中，已知AB ＝8，AD ＝5，CP →＝3PD →，AP →·BP →＝2，则AB →·AD →的值是________.29.22 [因为AP →＝AD →＋DP →＝AD →＋14AB →，BP →＝BC →＋CP →＝AD →－34AB →，所以AP →·BP →＝(AD →＋14AB →)·(AD→－34AB →)＝|AD →|2－316|AB →|2－12AD →·AB →＝2，将AB ＝8，AD ＝5代入解得AB →·AD →＝22.]。

A.考点7 平面向量的概念及其运算【1】（A ，新课标I ，文2）已知点(0,1),(3,2)A B ，向量(4,3)AC =--，则向量BC =A 。

(7,4)--B 。

(7,4) C.(1,4)- D.(1,4)【2】（A ，新课标I,理7)设D 为ABC ∆所在平面内一点，3BC CD =，则A 。

1433AD AB AC =-+ B 。

1433AD AB AC =- C 。

4133AD AB AC =+ D 。

4133AD AB AC =- 【3】（A ，新课标Ⅱ，文4)向量(1,1)=-a ，b (1,2)=-，则(2)+⋅a b a =A.1-B.0 C 。

1 D.2【4】(A ，重庆，文7）已知非零向量,a b 满足||b 4||a =，且(2)a a b ⊥+，则a b 与的夹角为(A ）3π (B ）2π （C ）32π (D)56π 【5】（A,四川，文2）设向量)4,2(=a 与向量)6,(x b =共线，则实数=xA 。

2B 。

3C 。

4 D.6【6】（A ，广东，文9)在平面直角坐标系xoy 中,已知四边形ABCD 是平行四边形，()1,2AB =-，()2,1AD =，则AD AC ⋅=A.5B.4 C 。

3 D 。

2【7】（A ，山东，文4理3）要得到函数sin(4)3y x π=-的图象，只需要将函数sin 4y x =的图象A.向左平移12π个单位 B 。

向右平移12π个单位 C 。

向左平移3π个单位 D.向右平移3π个单位 【8】（A,山东，理4)已知菱形ABCD 的边长为a ,60ABC ︒∠=，则BD CD ⋅＝ A 。

232a - B.234a - C.234a D.232a【9】（A ，福建，文7）设(1,2)a =,(1,1)b =，c a kb =+．若b c ⊥，则实数k 的值等于A ．32-B ．53-C ．53D ．32【10】（B ，重庆，理6)若非零向量b a ,,满足||322||b a =且),23()(b a b a +⊥-，则a 与b 的夹角为A 。

专题五 平面向量1.【2015高考新课标1，理7】设D 为ABC ∆所在平面内一点3BC CD =，则（ ）（A ）1433AD AB AC =-+(B)1433AD AB AC =-（C ）4133AD AB AC =+ (D)4133AD AB AC =-【答案】A【博雅解析】由题知11()33AD AC CD AC BC AC AC AB =+=+=+-= =1433AB AC -+，故选A.【考点定位】平面向量的线性运算【名师点睛】本题以三角形为载体考查了平面向量的加法、减法及实数与向量的积的法则与运算性质，是基础题，解答本题的关键是结合图形会利用向量加法将向量AD表示为AC CD + ，再用已知条件和向量减法将CD 用,AB AC表示出来.2.【2015高考山东，理4】已知菱形ABCD 的边长为a ，60ABC ∠=,则BD CD ⋅=（ ）（A ）232a - （B ）234a - （C ） 234a （D ） 232a 【答案】D【博雅解析】因为()BD CD BD BA BA BC BA ⋅=⋅=+⋅ ()22223cos 602BA BC BA a a a +⋅=+=故选D.【考点定位】平面向量的线性运算与数量积.【名师点睛】本题考查了平面向量的基础知识，重点考查学生对平面向量的线性运算和数量积的理解与掌握，属基础题，要注意结合图形的性质，灵活运用向量的运算解决问题.3.【2015高考陕西，理7】对任意向量,a b，下列关系式中不恒成立的是（ ） A ．||||||a b a b ⋅≤B ．||||||||a b a b -≤-C ．22()||a b a b +=+ D ．22()()a b a b a b +-=-【答案】B【博雅解析】因为cos ,a b a b a b a b ⋅=≤ ，所以选项A 正确；当a 与b方向相反时，a b a b -≤-不成立，所以选项B 错误；向量的平方等于向量的模的平方，所以选项C 正确；()()22a b a b a b +-=- ，所以选项D 正确．故选B ．【考点定位】1、向量的模；2、向量的数量积．【名师点晴】本题主要考查的是向量的模和向量的数量积，属于容易题．解题时一定要抓住重要字眼“不”，否则很容易出现错误．解本题需要掌握的知识点是向量的模和向量的数量积，即cos ,a b a b a b ⋅=，22a a = ．4.【2015高考四川，理7】设四边形ABCD 为平行四边形，6AB = ，4AD =.若点M ，N 满足3BM MC = ，2DN NC = ，则AM NM ⋅=（ ）（A ）20 （B ）15 （C ）9 （D ）6 【答案】C 【博雅解析】311,443AM AB AD NM CM CN AD AB =+=-=-+，所以221111(43)(43)(169)(1636916)94124848AM NM AB AD AB AD AB AD =+-=-=⨯-⨯= ，选C.【考点定位】平面向量.【名师点睛】涉及图形的向量运算问题，一般应选两个向量作为基底，选基底的原则是这两个向量有尽量多的已知元素.本题中，由于6AB = ，4AD = 故可选,AB AD作为基底.5.【2015高考重庆，理6】若非零向量a ，b 满足|a ||b |，且（a -b ）⊥（3a +2b ），则a 与b 的夹角为 （ ） A 、4πB 、2π C 、34π D 、π 【答案】A【考点定位】向量的夹角.【名师点晴】本题考查两向量的夹角，涉及到向量的模，向量的垂直，向量的数量积等知识，体现了数学问题的综合性，考查学生运算求解能力，综合运用能力.6.【2015高考安徽，理8】C ∆AB 是边长为2的等边三角形，已知向量a ，b 满足2a AB = ，C 2a b A =+，则下列结论正确的是（ ）（A ）1b = （B ）a b ⊥ （C ）1a b ⋅= （D ）()4C a b +⊥B【答案】D【博雅解析】如图，由题意，(2)2BC AC AB a b a b =-=+-= ，则||2b = ，故A 错误；|2|2||2a a == ，所以||1a =，又22(2)4||222cos 602AB AC a a b a ab ⋅=⋅+=+=⨯=，所以1a b ⋅=- ，故,B C 错误；设,B C 中点为D ，则2AB AC AD += ，且AD BC ⊥ ，而22(2)4AD a a b a b =++=+，所以()4C a b +⊥B，故选D.【考点定位】1.平面向量的线性运算；2.平面向量的数量积.【名师点睛】平面向量问题中，向量的线性运算和数量积是高频考点.当出现线性运算问题时，注意两个向量的差OA OB BA -= ，这是一个易错点，两个向量的和2OA OB OD +=（D 点是AB 的中点）.另外，要选好基底向量，如本题就要灵活使用向量,AB AC，当涉及到向量数量积时，要记熟向量数量积的公式、坐标公式、几何意义等.7.【2015高考福建，理9】已知1,,AB AC AB AC t t⊥==，若P 点是ABC ∆ 所在平面内一点，且4AB ACAP AB AC=+，则PB PC ⋅ 的最大值等于（ ）A ．13B ．15C ．19D ．21 【答案】A【博雅解析】以A 为坐标原点，建立平面直角坐标系，如图所示，则1(,0)B t，(0,)C t ，1AP =（，0)+4(0,1)=(1,4)，即1P （，4)，所以11PB t- =（，-4)，1PC - =（，t-4)，因此PB PC ⋅11416t t =--+117(4)t t=-+，因为144t t +≥=，所以PB PC ⋅ 的最大值等于13，当14t t =，即12t =时取等号．【考点】1、平面向量数量积；2、基本不等式．【名师点睛】本题考查平面向量线性运算和数量积运算，通过构建直角坐标系，使得向量运算完全代数化，实现了数形的紧密结合，同时将数量积的最大值问题转化为函数的最大值问题，本题容易出错的地方是对AB AB的理解不到位，从而导致解题失败． 8.【2015高考湖北，理11】已知向量OA AB ⊥ ，||3OA =，则OA OB ∙= .【答案】9【博雅解析】因为OA AB ⊥ ，||3OA =，所以OA OB ∙= 93||||)(222===∙+=+∙OA OB OA OA AB OA OA .【考点定位】 平面向量的加法法则，向量垂直，向量的模与数量积.【名师点睛】平面向量是新教材新增内容，而且由于向量的双重“身份”是研究一些数学问题的工具.这类问题难度不大，以考查基础知识为主.9.【2015高考天津，理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠=,动点E和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ== 则AE AF ⋅ 的最小值为 . 【答案】2918【博雅解析】因为1,9DF DC λ= 12DC AB= ，119199918CF DF DC DC DC DC AB λλλλλ--=-=-== ，AE AB BE AB BC λ=+=+ ，19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+ ，()221919191181818AE AF AB BC AB BC AB BC AB BC λλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥+= 当且仅当2192λλ=即23λ=时AE AF ⋅ 的最小值为2918.BAD C EF【考点定位】向量的几何运算、向量的数量积与基本不等式.【名师点睛】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ，体现了数形结合的基本思想，再运用向量数量积的定义计算AE AF ⋅，体现了数学定义的运用，再利用基本不等式求最小值，体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现.11.【2015高考新课标2，理13】设向量a ，b 不平行，向量a b λ+ 与2a b +平行，则实数λ=_________．【答案】12【博雅解析】因为向量a b λ+ 与2a b + 平行，所以2a b k a b λ+=+ （），则12,k k λ=⎧⎨=⎩，所以12λ=．【考点定位】向量共线．【名师点睛】本题考查向量共线，明确平面向量共线定理，利用待定系数法得参数的关系是解题关键，属于基础题．12.【2015江苏高考，14】设向量a k (cos ,sin cos )(0,1,2,,12)666k k k k πππ=+= ，则11k =∑(a k a k+1)的值为【答案】【博雅解析】 a k a k+1(1)(1)(1)(cos ,sin cos )(cos ,sin cos )666666k k k k k k ππππππ+++=+⋅+ (1)(1)(1)coscos (sin cos )(sin cos )666666k k k k k k ππππππ+++=++⋅+(1)(1)(1)(1)(1)(coscos sin sin )(sin cos cos sin )cos cos 6666666666k k k k k k k k k k ππππππππππ+++++=++++22(1)21cos sincos cos sin cos sin666666266k k k k k k k ππππππππππ+++=++=-21sin cos )sin 6343k k k ππππ+=+++-21(21)sin cos626k k πππ++=+ 因为21(21)sin cos 626k k πππ++，的周期皆为6，一个周期的和皆为零， 因此11k =∑(a k a k+1)12==.【考点定位】向量数量积，三角函数性质【名师点晴】向量数量积在本题中仅是一个表示，实质是三角函数化简求和，首先根据角之间的差别与联系，对通项进行重新搭配，对不可搭配的项再一次展开，重新配角搭配，这样将通项化为一次式，利用三角函数周期性进行求和.作为压轴题，主要考查学生基础题型的识别与综合应用.13.【2015江苏高考，6】已知向量a =)1,2(，b=)2,1(-, 若m a +n b =)8,9(-(R n m ∈,), 则n m -的值为______. 【答案】3-【博雅解析】由题意得：29,282,5, 3.m n m n m n m n +=-=-⇒==-=- 【考点定位】向量相等【名师点晴】明确两向量相等的充要条件，它们的对应坐标相等.其实质为平面向量基本定理应用. 向量共线的充要条件的坐标表示：若1122()()a x y b x y ==，，，，则a b ∥⇔12210x y x y =-.向量垂直的充要条件的坐标表示：若1122()()a x y b x y ==，，，，则a b ⊥⇔1212+0x x y y =.14.【2015高考湖南，理8】已知点A ，B ，C 在圆221x y +=上运动，且AB BC ⊥，若点P 的坐标为(2,0)，则PA PB PC ++的最大值为（ ）A.6B.7C.8D.9 【答案】B. 【博雅解析】【考点定位】1.圆的性质；2.平面向量的坐标运算及其几何意义.【名师点睛】本题主要考查向量的坐标运算，向量的几何意义以及点到圆上点的距离的最值问题，属于中 档题，结合转化思想和数形结合思想求解最值，关键是把向量的模的最值问题转化为点与圆上点的距离的 最值问题，即圆221x y +=上的动点到点)0,6(距离的最大值.。