第3-3章管理数据表-副本
- 格式:pdf
- 大小:3.30 MB
- 文档页数:23
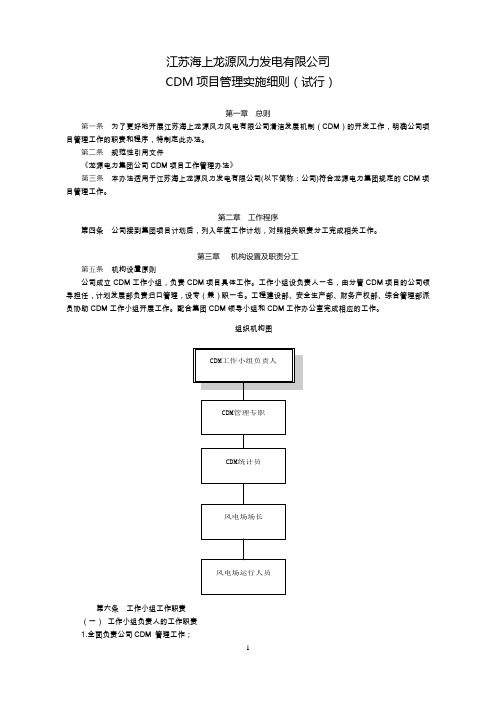
江苏海上龙源风力发电有限公司CDM项目管理实施细则(试行)第一章总则第一条为了更好地开展江苏海上龙源风力风电有限公司清洁发展机制(CDM)的开发工作,明确公司项目管理工作的职责和程序,特制定此办法。
第二条规范性引用文件《龙源电力集团公司CDM项目工作管理办法》第三条本办法适用于江苏海上龙源风力发电有限公司(以下简称:公司)符合龙源电力集团规定的CDM项目管理工作。
第二章工作程序第四条公司接到集团项目计划后,列入年度工作计划,对照相关职责分工完成相关工作。
第三章机构设置及职责分工第五条机构设置原则公司成立CDM工作小组,负责CDM项目具体工作。
工作小组设负责人一名,由分管CDM项目的公司领导担任,计划发展部负责归口管理,设专(兼)职一名。
工程建设部、安全生产部、财务产权部、综合管理部派员协助CDM工作小组开展工作。
配合集团CDM领导小组和CDM工作办公室完成相应的工作。
组织机构图第六条工作小组工作职责(一)工作小组负责人的工作职责1.全面负责公司CDM 管理工作;2.指导工作小组成员开展工作;3.及时向公司总经理汇报CDM项目的开发进度。
(二)工作小组专(兼)职的工作职责1.做出详细的《信息管理记录》,配合DOE和咨询公司完成审定和审查。
2.收集项目主机合同、财务审计报告、竣工报告、并网协议、售电协议、电表校核机构资质证明、关口表主副表和备用线路电表的校核报告等核查所需资料。
3.收集每月的售购电发票、电网公司出具的《电量结算单》、由电网公司打印并盖章的关口表主表和副表的遥测度数表,保存其原件和备用件。
4.按照组织结构图协调相关部门安排工作人员。
5.当关口表异常时依据售电协议中的应急处理方案与电网公司协调确定最终计量数据、与电表校核机构的沟通和协调。
6.组织相关人员参加CDM项目的各类学习培训工作。
7.由于工作或者其它原因需更换CDM工作人员时,以书面报告说明更换理由以及新的CDM工作人员姓名,并做好新老CDM工作人员工作的交接。

3.3.3 最大值与最小值一、填空题1.给出下列四个命题:①若函数f (x )在[a ,b ]上有最大值,则这个最大值一定是[a ,b ]上的极大值; ②若函数f (x )在[a ,b ]上有最小值,则这个最小值一定是[a ,b ]上的极小值; ③若函数f (x )在[a ,b ]上有最值,则最值一定在x =a 或x =b 处取得; ④若函数f (x )在(a ,b )内连续,则f (x )在(a ,b )内必有最大值与最小值. 其中真命题共有________个.2.函数f (x )=x (1-x 2)在[0,1]上的最大值为______.3.已知函数f (x )=ax 3+c ,且f ′(1)=6,函数在[1,2]上的最大值为20,则c =________.4.若函数f (x )、g (x )在区间[a ,b ]上可导,且f ′(x )>g ′(x ),f (a )=g (a ),则在区间[a ,b ]上有f (x )与g (x )的大小关系为____________.5.已知函数y =-x 2-2x +3在[a,2]上的最大值为154,则a =________.6.函数f (x )=ln x -x 在(0,e]上的最大值为________.7.函数f (x )=12e x (sin x +cos x )在区间⎣⎢⎡⎦⎥⎤0,π2上的值域为________.8.若函数f (x )=x 3-3x -a 在区间[0,3]上的最大值、最小值分别为M 、N ,则M -N 的值为________.二、解答题9.求下列各函数的最值.(1)f (x )=12x +sin x ,x ∈[0,2π];(2)f (x )=x 3-3x 2+6x -2,x ∈[-1,1].10.已知f (x )=x 3-x 2-x +3,x ∈[-1,2],f (x )-m <0恒成立,求实数m 的取值范围.能力提升11.设函数f (x )=12x 2e x.(1)求f (x )的单调区间;(2)若当x ∈[-2,2]时,不等式f (x )>m 恒成立,求实数m 的取值范围.12.若f (x )=ax 3-6ax 2+b ,x ∈[-1,2]的最大值为3,最小值是-29,求a 、b 的值.1.求闭区间上函数的最值也可直接求出端点函数值和导数为零时x对应的函数值,通过比较大小确定函数的最值.2.在求解与最值有关的函数综合问题时,要发挥导数的解题功能,同时也要注意对字母的分类讨论;而有关恒成立问题,一般是转化为求函数的最值问题.3.可以利用导数的实际意义,建立函数模型,解决实际生活中的最大值最小值问题.3.3.3 最大值与最小值知识梳理1.f(x)≤f(x0) 定义域上3.(1)极值作业设计1.0解析因为函数的最值可以在区间[a,b]的两端取得,也可以在内部取得,当最值在端点处取得时,其最值就一定不是极值,故命题①与②不真.由于最值可以在区间内部取得,故命题③也不真.对于命题④,我们只要考虑在(a,b)内的单调函数,它在(a,b)内必定无最值(也无极值),因此命题④也不真.综上所述,四个命题均不真.2.23 9解析∵f(x)=x-x3,∴f′(x)=1-3x2,令f′(x)=0,得x=±33,∵f(0)=0,f(1)=0,f ⎝⎛⎭⎪⎫33=239,f ⎝ ⎛⎭⎪⎫-33=-239. ∴f (x )max =239.3.4解析 ∵f ′(x )=3ax 2,∴f ′(1)=3a =6,∴a =2.当x ∈[1,2]时,f ′(x )=6x 2>0,即f (x )在[1,2]上是增函数,∴f (x )max =f (2)=2×23+c =20,∴c =4.4.f (x )≥g (x )解析 ∵f ′(x )>g ′(x ),∴f (x )-g (x )单调递增. ∵x ≥a ,∴f (x )-g (x )≥f (a )-g (a ), 即f (x )-g (x )≥0.5.-12解析 y ′=-2x -2,令y ′=0,得x =-1.当a ≤-1时,最大值为f (-1)=4,不合题意.当-1<a <2时,f (x )在[a,2]上单调递减,最大值为f (a )=-a 2-2a +3=154,解得a =-12或a =-32(舍去).6.-1解析 f ′(x )=1x -1=1-xx,令f ′(x )>0得0<x <1,令f ′(x )<0得x <0或x >1,∴f (x )在(0,1]上是增函数,在(1,e]上是减函数.∴当x =1时,f (x )有最大值f (1)=-1.7. 211,22e π⎡⎤⎢⎥⎣⎦解析 ∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴f ′(x )=e xcos x ≥0,∴f (0)≤f (x )≤f ⎝ ⎛⎭⎪⎫π2.即12≤f (x )≤122e π.8.20解析 f ′(x )=3x 2-3,令f ′(x )=0, 得x =1,(x =-1舍去).∵f (0)=-a ,f (1)=-2-a ,f (3)=18-a . ∴M =18-a ,N =-2-a .∴M -N =20.9.解 (1)f ′(x )=12+cos x .令f ′(x )=0,又∵0≤x ≤2π,∴x =2π3或x =4π3.∴f ⎝ ⎛⎭⎪⎫2π3=π3+32,f ⎝ ⎛⎭⎪⎫4π3=2π3-32,又∵f (0)=0,f (2π)=π.∴当x =0时,f (x )有最小值f (0)=0, 当x =2π时,f (x )有最大值f (2π)=π.(2)f ′(x )=3x 2-6x +6=3(x 2-2x +2)=3(x -1)2+3,∵f ′(x )在[-1,1]内恒大于0, ∴f (x )在[-1,1]上为增函数. 故x =-1时,f (x )最小值=-12; x =1时,f (x )最大值=2.即f (x )在[-1,1]上的最小值为-12,最大值为2.10.解 由f (x )-m <0,即m >f (x )恒成立, 知m >f (x )max ,f ′(x )=3x 2-2x -1,令f ′(x )=0,解得x =-13或x =1.因为f (-13)=8627,f (1)=2,f (-1)=2,f (2)=5. 所以f (x )的最大值为5,故m 的取值范围为(5,+∞).11.解 (1)f ′(x )=x e x+12x 2e x =e x2x (x +2).由ex 2x (x +2)>0,解得x >0或x <-2, ∴(-∞,-2),(0,+∞)为f (x )的增区间, 由ex 2x (x +2)<0,得-2<x <0, ∴(-2,0)为f (x )的减区间.∴f (x )的单调增区间为(-∞,-2),(0,+∞); 单调减区间为(-2,0).(2)令f ′(x )=0,得x =0或x =-2,∵f (-2)=2e 2,f (2)=2e 2,f (0)=0,∴f (x )∈[0,2e 2],又∵f (x )>m 恒成立,∴m <0. 故m 的取值范围为(-∞,0).12.解 ∵f (x )=ax 3-6ax 2+b ,∴f ′(x )=3ax 2-12ax .令f ′(x )=0,解得x =0或4. ∵4D ∈/[-1,2],故舍去,∴f (x )取最大值,最小值的点在x =-1、0、2上取得,f (-1)=-7a +b ,f (0)=b , f (2)=-16a +b .当a >0时,最大值为b =3, 最小值为-16a +b =-29,解得⎩⎪⎨⎪⎧a =2,b =3,当a <0时,最大值为-16a +b =3,b =-29,解得⎩⎪⎨⎪⎧a =-2b =-29,综上所述:⎩⎪⎨⎪⎧a =2b =3或⎩⎪⎨⎪⎧a =-2b =-29.§3.4 导数在实际生活中的应用一、填空题1.随着人们生活水平的提高,汽车的拥有量越来越多,据有关统计数据显示,从上午6 点到9点,车辆通过某一路段的用时y (分钟)与车辆进入该路段的时刻t 之间的关系可近似表示为y =-18t 3-34t2+36t -6294.则在这段时间内,通过该路段用时最多的时刻是________.2.若底面为等边三角形的直棱柱的体积为V ,则其表面积最小时,底面边长为________.3.要做一个圆锥形的漏斗,其母线长为20 cm ,要使其体积最大,则高为________ cm.4.某厂生产某种产品x 件的总成本:C (x )=1 200+275x 3,又产品单价的平方与产品件数x 成反比,生产100件这样的产品的单价为50元,总利润最大时,产量应定为________件. 5.如图所示,一窗户的上部是半圆,下部是矩形,如果窗户面积一定,窗户周长最小时,x 与h 的比为________.6.某公司生产某种产品,固定成本为20 000元,每生产一件产品成本增加100元,已知总收益R 与年产量x 的关系式为R =⎩⎪⎨⎪⎧400x -12x 2 x ,x 则总利润最大时,每年生产的产品件数是________.7.某公司租地建仓库,每月土地占用费y 1与仓库到车站的距离成反比,而每月库存货物的运费y 2与到车站的距离成正比,如果在距离车站10千米处建仓库,这两项费用y 1和y 2分别为2万元和8万元.那么,要使这两项费用之和最小,仓库应建在离车站________千米处.8.做一个无盖的圆柱形水桶,若需使其体积是27π,且用料最省,则圆柱的底面半径为________.二、解答题9.某地建一座桥,两端的桥墩已建好,这两墩相距m 米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元,距离为x 米的相邻两墩之间的桥面工程费用为(2+x )x 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其它因素.记余下工程的费用为y 万元. (1)试写出y 关于x 的函数关系式;(2)当m =640米时,需新建多少个桥墩才能使y 最小?10.某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值x (单位:元,0≤x ≤30)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成x 的函数; (2)如何定价才能使一个星期的商品销售利润最大?能力提升11.某单位用2 160万元购得一块空地,计划在该块地上建造一栋至少10层、每层2 000平方米的楼房.经测算,如果将楼房建为x (x ≥10)层,则每平方米的平均建筑费用为560+48x (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用建筑总面积)12.已知某商品生产成本C 与产量q 的函数关系式为C =100+4q ,价格p 与产量q 的函数关系式为p=25-18q ,求产量q 为何值时,利润L 最大.利用导数解决生活中的优化问题的一般步骤.(1)分析实际问题中各变量之间的关系,建立实际问题的数学模型,写出实际问题中变量之间的函数关系y =f (x );(2)求函数的导数f ′(x ),解方程f ′(x )=0;(3)比较函数在区间端点和f ′(x )=0的点的函数值的大小,最大(小)者为最大(小)值;(4)写出答案.§3.4 导数在实际生活中的应用作业设计 1.8解析 由题意知,所求的量为当y 为最大值时的自变量t 的取值,y ′=-38t 2-32t +36,令y ′=0,得3t 2+12t -36×8=0, ∴t 1=8,t 2=-12(舍).当t ∈(6,8)时.y ′>0,t ∈(8,9)时,y ′<0, 所以t =8时,y 有最大值.2.34V解析 设底面边长为a ,直三棱柱高为h .体积V =34a 2h ,所以h =4V3a 2, 表面积S =2·34a 2+3a ·4V 3a2=32a 2+43Va , S ′=3a -43V a2,由S ′=0,得a =34V . 当a =34V 时,表面积最小. 3.2033解析 设高为x cm ,则底面半径为202-x 2cm ,体积V =π3x ·(202-x 2) (0<x <20),V ′=π3(400-3x 2),由V ′=0,得x =2033或x =-2033(舍去).当x ∈⎝ ⎛⎭⎪⎫0,2033时,V ′>0,当x ∈⎝ ⎛⎭⎪⎫2033,20时,V ′<0,所以当x =2033时,V 取最大值. 4.25解析 设产品单价为a 元,又产品单价的平方与产品件数x 成反比,即a 2x =k ,由题知k =250 000,则a 2x =250 000,所以a =500x .总利润y =500x -275x 3-1 200 (x >0),y ′=250x -225x 2,由y ′=0,得x =25,x ∈(0,25)时,y ′>0,x ∈(25,+∞)时,y ′<0,所以x =25时,y 取最大值.5.1∶1解析 设窗户面积为S ,周长为L ,则S =π2x 2+2hx ,h =S 2x -π4x ,所以窗户周长L =πx +2x +2h =π2x +2x +S x ,L ′=π2+2-Sx 2.由L ′=0,得x =2S π+4,x ∈⎝⎛⎭⎪⎫0, 2S π+4时,L ′<0, x ∈⎝⎛⎭⎪⎫2S π+4,+∞时,L ′>0, 所以当x =2Sπ+4时,L 取最小值, 此时h x =2S -πx 24x 2=2S 4x 2-π4=π+44-π4=1. 6.300解析 设总成本为C ,则C =20 000+100x , 所以总利润 P =R -C =⎩⎪⎨⎪⎧300x -x 22-20 000 x ,60 000-100x xP ′=⎩⎪⎨⎪⎧300-xx ≤400,-x令P ′=0,得x =300,易知当x =300时,总利润最大. 7.5解析 依题意可设每月土地占用费y 1=k 1x,每月库存货物的运费y 2=k 2x ,其中x 是仓库到车站的距离.于是由2=k 110,得k 1=20;由8=10k 2,得k 2=45.因此两项费用之和为y =20x +4x 5,y ′=-20x 2+45,令y ′=-20x 2+45=0得x =5(x =-5舍去),经验证,此点即为最小值点.故当仓库建在离车站5千米处时,两项费用之和最小. 8.3解析 设半径为r ,则高h =27ππr 2=27r2.∴水桶的全面积S (r )=πr 2+2πr ·27r2=πr 2+54πr.S ′(r )=2πr -54πr 2,令S ′(r )=0,得r =3.∴当r =3时,S (r )最小.9.解 (1)设需新建n 个桥墩,则(n +1)x =m ,即n =m x-1 (0<x <m ),所以y =f (x )=256n +(n +1)(2+x )x=256⎝ ⎛⎭⎪⎫m x -1+mx (2+x )x=256m x+m x +2m -256 (0<x <m ).(2)由 (1)知,f ′(x )=-256m x 2+12m 12x-=m2x2(32x-512). 令f ′(x )=0,得32x=512,所以x =64.当0<x <64时,f ′(x )<0,f (x )在区间(0,64)内为减函数;当64<x <640时,f ′(x )>0,f (x )在区间(64,640)内为增函数,所以f (x )在x =64处取得最小值,此时n =m x -1=64064-1=9.故需新建9个桥墩才能使y 最小.10.解 (1)设商品降低x 元时,多卖出的商品件数为kx 2,若记商品在一个星期的销售利润为f (x ),则依题意有f (x )=(30-x -9)·(432+kx 2)=(21-x )·(432+kx 2),又由已知条件24=k ·22,于是有k =6,所以f (x )=-6x 3+126x 2-432x +9 072,x ∈[0,30].(2)根据(1),有f ′(x )=-18x 2+252x -432 =-18(x -2)(x -12).当x 变化时,f (x )与f ′(x )的变化情况如下表:故x =12时,f (x )达到极大值.因为f (0)=9 072,f (12)=11 664,所以定价为30-12=18(元)能使一个星期的商品销售利润最大.11.解 设楼房每平方米的平均综合费用为f (x )元,则f (x )=(560+48x )+2 160×10 0002 000x=560+48x +10 800x(x ≥10,x ∈N *),f ′(x )=48-10 800x,令f ′(x )=0得x =15. 当x >15时,f ′(x )>0;当0<x <15时,f ′(x )<0. 因此,当x =15时,f (x )取最小值f (15)=2 000.所以为了使楼房每平方米的平均综合费用最少,该楼房应建为15层.12.解 收入R =q ·p =q ⎝⎛⎭⎪⎫25-18q =25q -18q 2. 利润L =R -C =⎝⎛⎭⎪⎫25q -18q 2-(100+4q ) =-18q 2+21q -100 (0<q <200),L ′=-14q +21,11令L ′=0,即-14q +21=0,解得q =84. 因为当0<q <84时,L ′>0;当84<q <200时,L ′<0,所以当q =84时,L 取得最大值. 所以产量q 为84时,利润L 最大.。


408考研计算机网络——第三章数据链路层第3章数据链路层结点:主机、路由器链路:网络中两个结点之间的物理通道,传输介质有双绞线、光纤和微波。
分为有线、无线链路数据链路:网络中两个结点之间的逻辑通道,把实现控制数据传输协议的硬件和软件加到链路上就构成数据链路帧:链路层的协议数据单元,封装网络层数据报功能:为网络层提供服务、链路管理、组帧、流量控制、差错控制3.1 数据链路层的功能数据链路层在物理层提供服务的基础上向网络层提供服务,其最基本的服务是将源自网络层来的数据可靠地传输到相邻节点的目标机网络层。
其主要作用是加强物理层传输原始比特流的功能,将物理层提供的可能出错的物理连接改造成为逻辑上无差错的数据链路,使之对网络层表现为一条无差错的链路·为网络层提供服务无确认无连接服务有确认无连接服务有确认面向连接服务·链路管理即连接的建立、维持、释放(用于面向连接的服务)·组帧(帧定界、帧同步、透明传输)封装成帧:在一段数据的前后部分添加首部和尾部,这样就构成了一个帧。
接收端在收到物理层上交的比特流后,根据首部和尾部的标记,从收到的比特流中识别帧的开始和结束首部和尾部包含许多的控制信息,他们的一个重要作用:帧定界(确定帧的界限)帧同步:接收方应当能从接收到的二进制比特流中区分出帧的起始和终止。
最大传送单元MTU:帧的数据部分的长度上限透明传输:当所传数据中的比特组合恰巧与某一个控制信息完全一样时,采取适当的措施,使收方不会将这样的数据误认为是某种控制信息。
保证数据链路层的传输是透明的组帧的四种方法:字符计数法、字符(节)填充法、零比特填充法、违规编码法·流量控制限制发送方的数据流量,使其发送速率不超过接收方的接受能力✳对于数据链路层:控制的是相邻两结点之间数据链路上的流量对于传输层:控制源端到目的端之间的流量·差错控制位错:循环冗余校验CRC差错控制:自动重传请求ARQ帧错:定时器、编号机制*三个基本问题:封装成帧、透明传输、差错检测3.2 组帧·字符计数法帧首部使用一个计数字段(第一个字节,八位)来标明帧内字符数。

中图版(2019)必修1《第三章数据处理与应用》2022年单元测试卷1. 下列关于数据备份的说法不正确的是( )A. 备份的副本应存储在与源文件同一路径下B. 备份文件有助于避免文件的永久丢失C. 可以用备份的文件恢复丢失的数据D. 为了确保文件不会丢失,可以随时手动备份或者设置自动备份2. 百度公司根据某时段在某区域内“感冒症状”、“治疗”等关键词的搜索量急剧增长,成功预测了甲流的爆发时间、地域。
主要体现了大数据分析理念中的( )A. 在数据规模上强调相对数据而不是绝对数据B. 在分析方法上更注重相关分析而不是因果分析C. 在数据基础上倾向于全体数据而不是抽样数据D. 在分析效果上更追求效率而不是绝对精确3. 下列不属于数据采集是( )A. 系统日志B. 网络爬虫C. 问卷调查D. 数据可视化4. 小明无意间发现了小红记录在笔记本上的邮箱密码,他登录小红邮箱后阅读了小红的各种邮件。
为此小红对邮箱设置进行了调整,现需要用手机接收“动态密码”并输入后才能登录邮箱。
请问小红的做法是属于以下哪种信息系统的安全防范方法?( )A. 身份认证B. 访问控制C. 数据加密D. 修补漏洞5. 下列关于数据安全的说法,不正确的是( )A. 自然灾害也有可能对数据造成损坏B. 数据加密有助于提高数据的安全性C. 数据校验主要是为了保证数据的完整性D. 数据安全只要做好防护上的安全即可6. 因疫情防控需要,学校要求学生家长及时上报体温、行程等数据,汇总后上报上级防控部门,采集上述数据最为高效的方法是( )A. 填写在线收集表B. 填写纸质表格C. 发送电子邮件D. 打电话上报7. 数据分析报告是项目的展示,也是数据分析结论的有效承载形式。
在数据分析报告中,首先需要明确数据分析的,阐述目前及通过分析希望解决的问题;其次需要描述数据来源和数据分析的、和;最后需要重点呈现数据分析的、和。
A. 正确B. 错误8. 数据分析应用对象主要有分析、分析和分析。

第3章 中文Excel 操作Excel 是Windows 下的一个应用程序,是一种功能强大,使用灵活方便,高效率的电子制表软件。
本章将介绍有关Excel 的一般基础知识和制表作图方法。
3.1 Excel 工作窗口单击“开始”按钮,将鼠标指向“程序”,在弹出的菜单中指向“Microsoft Excel ”选项,则进入Excel 中文版的界面,如图3-1所示。
“标题栏”说明当前所编辑的工作簿的工作簿的名字。
“菜单栏”中汇集了各种命令,用来对数据、工作表等进行操作。
“工具栏”由一些工具按钮组成,可快速方便地执行相关的命令。
“单元格名称栏”用于显示当前处于活动的单元格位置。
“公式编辑栏”用来编辑一些简单的公式。
“工作表区”显示所建立的电子表格和电子图表的内容。
“单元格”是整个工作表最基本的编辑单位。
“滚动条”包括垂直滚动条和水平滚动条,由滚动方块和几个滚动按钮组成,利用它可以使文档上下或左右移动,以查看工作表中未曾显示出的内容。
“状态栏”用来显示当前正在执行的命令或操作的提示。
3.2 工作簿的操作用来储存并处理工作数据的文件叫工作表簿。
每一个工作簿可以拥有许多不同的工作表,在Excel 中,在一个工作簿中最多可建立255个工作表。
3.2.1 新建工作簿启动Microsoft Excel 时,系统将打开一个新的工作簿。
任何时候,要建立一个新的工作簿,可以通过下面的操作步骤来实现:(1) 单击工具栏上的“新建”按钮,或者选择“文件”菜单中的“新建”命令,弹出“新建”对话框,单击“常用”选项卡。
(2) 选择“工作簿”图标。
(3) 单击“确定”按钮,建立一个工作簿。
(4) 选择定位A1单元格,输入“图书销售表”作为标题,输入后的内容将同时显示在单元格和编辑栏中。
单元格名称栏 公式编辑栏 工作表区 单元格 工具栏 垂直滚动条 水平滚动条 状态栏(5)单击A3单元格,输入“地区”,然后移动键盘上的方向键,再各单元格输入相应得内容。