九年级数学双休作业(1)12.9.7

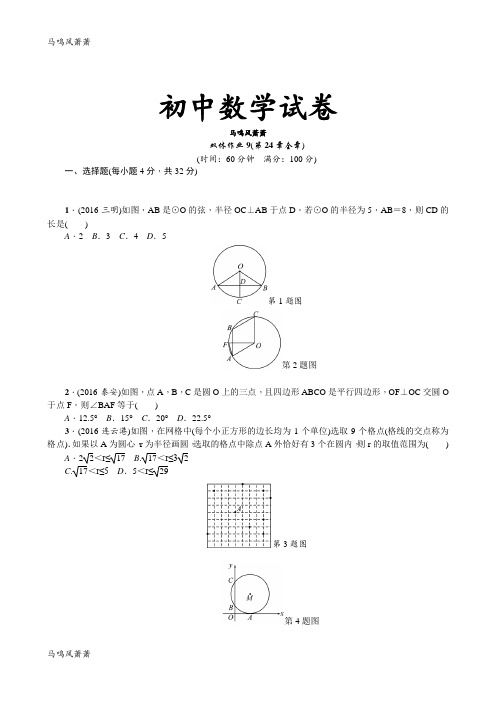
初中数学试卷 马鸣风萧萧双休作业9(第24章全章)(时间：60分钟 满分：100分)一、选择题(每小题4分，共32分)1．(2016·三明)如图，AB 是⊙O 的弦，半径OC ⊥AB 于点D ，若⊙O 的半径为5，AB ＝8，则CD 的长是( )A ．2B ．3C ．4D ．5第1题图第2题图2．(2016·泰安)如图，点A ，B ，C 是圆O 上的三点，且四边形ABCO 是平行四边形，OF ⊥OC 交圆O 于点F ，则∠BAF 等于( )A ．12.5°B ．15°C ．20°D ．22.5°3．(2016·连云港)如图，在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点)．如果以A 为圆心，r 为半径画圆，选取的格点中除点A 外恰好有3个在圆内，则r 的取值范围为( )A ．22＜r≤17B .17＜r≤3 2C .17＜r≤5D ．5＜r≤29第3题图第4题图4．(2016·潍坊)如图，在平面直角坐标系中，⊙M 与x 轴相切于点A(8，0)，与y 轴分别交于点B(0，4)和点C(0，16)，则圆心M 到坐标原点O 的距离是( )A ．10B ．8 2C ．413D ．2415．(2016·山西)如图，在▱ABCD 中，AB 为⊙O 的直径，⊙O 与DC 相切于点E ，与AD 相交于点F ，已知AB ＝12，∠C ＝60°，则FE ︵的长为( )A .π3B .π2C ．πD ．2π第5题图第6题图6．如图，扇形AOB 是直角扇形，以OA ，OB 为直径在扇形内作半圆，M ，N 分别表示两个阴影部分的面积，那么M ，N 的大小关系是( )A ．M ＞NB ．M ＝NC ．M ＜ND ．无法确定7．(2016·泸州)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是( ) A .38 B .34 C .24 D .288．如图，AB 是半圆O 的直径，点C ，D ，E 是半圆弧上的点，且弦AC ＝CD ＝2，弦DE ＝EB ＝2，则直径AB 的长是( )A ．2 5B ．2 2C ．3 2D ．4 2二、填空题(每小题4分，共32分)9．在平面直角坐标系中，O 为坐标原点，则直线y ＝x ＋2与以O 点为圆心，1为半径的圆的位置关系为________．10．已知圆锥的底面半径为10 cm ，它的展开图扇形的半径为30 cm ，则这个扇形圆心角的度数是________．11．(2016·泰安)如图，半径为3的⊙O 与Rt △AOB 的斜边AB 切于点D ，交OB 于点C ，连接CD 交直线OA 于点E ，若∠B ＝30°，则线段AE 的长为________．12．(2016·咸宁)如图，点E 是△ABC 的内心，AE 的延长线和△ABC 的外接圆相交于点D ，连接BD ，BE ，CE ，若∠CBD ＝32°，则∠BEC 的度数为________．第11题图第12题图第13题图13．(2016·广东)如图，把一个圆锥沿母线OA 剪开，展开后得到扇形AOC ，已知圆锥的高h 为12 cm ，OA ＝13 cm ，则扇形AOC 中AC ︵的长是________cm (计算结果保留π)．14．如图，在△ABC 中，∠B ＝30°，∠A ＝15°，BC ＝12，以A 为圆心作圆和直线BC 相切，则⊙A 的半径为________．第14题图第15题图第16题图15．(2016·德州)如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M 与圆心O 重合，则图中阴影部分的面积是________．16．如图，从一块半径是1 m 的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A ，B ，C 在⊙O 上)，将剪下的扇形围成一个圆锥，则这个圆锥的底面圆的半径是________m .三、解答题(共36分)17．(8分)(2016·资阳)如图，在⊙O 中，点C 是直径AB 延长线上一点，过点C 作⊙O 的切线，切点为D ，连接BD.(1)求证：∠A ＝∠BDC ；(2)若CM 平分∠ACD ，且分别交AD ，BD 于点M ，N ，当DM ＝1时，求MN 的长．18．(8分)如图，△ABC中，∠C＝90°，⊙I为△ABC的内切圆，点O为△ABC的外心，BC＝6，AC ＝8.(1)求⊙I的半径；(2)求OI的长．19．(10分)如图，在△ABC中，BA＝BC，以AB为直径的⊙O分别交AC，BC于点D，E，BC的延长线与⊙O的切线AF交于点F.(1)求证：∠ABC＝2∠CAF；(2)若AC＝210，CE∶EB＝1∶4，求CE的长．20．(10分)(2016·云南)如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为点E，F是AE与⊙O的交点，AC平分∠BAE.(1)求证：DE是⊙O的切线；(2)若AE＝6，∠D＝30°，求图中阴影部分的面积．。

江苏省泰兴市黄桥镇九年级数学下学期双休日作业（9）（无答案）编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省泰兴市黄桥镇九年级数学下学期双休日作业（9）（无答案））的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省泰兴市黄桥镇九年级数学下学期双休日作业（9）（无答案）的全部内容。

九年级数学双休日作业（9）一个▲的为中档题,两个▲▲的为提高题,无标志的是基础题一．选择题（本大题共有6题,每小题3分,共18分)1．﹣3的相反数是（）A．3 B．﹣3 C．D．﹣2.实数﹣π,﹣3.14，0，四个数中，最小的是（）A．﹣πB．﹣3.14 C．D．03．要反映我市某一周每天的最高气温的变化趋势，宜采用（）A．条形统计图B．扇形统计图C．折线统计图D．频数分布统计图4．如图，在物理实验课上，小明用弹簧秤将铁块A从完全置身水槽外，到匀速向下放入盛有水的水槽中，直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y（单位:N）与铁块下降的高度x（单位：cm）之间的函数关系的大致图象是( ）A B C D5．如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB,AC,BC的中点，则DC和EF的大小关系是（）A．DC＞EF B．DC＜EF C．DC=EF D．无法比较6．抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示：x…﹣2﹣1012…y…04664…从上表可知,下列说法中，错误的是 （ ) A ．抛物线于x 轴的一个交点坐标为（﹣2,0） B ．抛物线与y 轴的交点坐标为（0，6） C ．抛物线的对称轴是直线x=0D ．抛物线在对称轴左侧部分是上升的二．填空题（本大题共10小题，每小题3分,共30分) 7.若式子有意义，则x 的取值范围为_______________8。

2017年秋九年级数学上册双休作业1（无答案）（新版）北师大版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017年秋九年级数学上册双休作业1（无答案）（新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017年秋九年级数学上册双休作业1（无答案）（新版）北师大版的全部内容。

双休作业1（1.1~1.2)（时间：60分钟满分：100分）一、选择题（每小题4分，共32分)1．菱形具有而平行四边形不具有的性质是（）A．两组对边分别平行B．两组对角分别相等C．对角线互相平分D．对角线互相垂直2．如图，已知某广场菱形花坛ABCD的周长是24 m，∠BAD＝60°,则花坛对角线AC的长等于( ）A．6错误!m B．6 m C．3错误!m D．3 m第2题图第4题图3．若顺次连接四边形的各边中点所得的四边形是菱形，则该四边形一定是（）A．矩形B．对角线相等的四边形C．菱形D．对角线垂直的四边形4．如图,已知菱形ABCD与△ABE,点D在BE上，AB＝17，BD＝16，AE＝25，则DE＝( ）A．8 B．9 C．11 D．125．如图,菱形ABCD的边长为4，过点A,C作对角线AC的垂线，分别交CB和AD的延长线于点E，F,AE＝3，则四边形AECF的周长为( ）A．22 B．18 C．14 D．11，第5题图) ，第6题图)6．如图，在矩形ABCD中,点E在AD上,且EF⊥EC,EF＝EC,DE＝2,矩形的周长为16，则AE的长是（)A．3 B．4 C．5 D．77．如图，在矩形ABCD中，AE平分∠BAD交BC于E，∠CAE＝15°，则下列结论：①△ODC是等边三角形；②BC＝2AB；③∠AOE＝135°；④S△AOE＝S△COE，其中正确的结论的个数是（) A．1 B．2 C．3 D．4第7题图第8题图8．如图，在矩形ABCD中，点E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG 交CD于点F.若AB＝6,BC＝4错误!，则FD的长为（）A．2 B．4 C。

九年级数学双休日作业（12.5-12.6）一．选择题1．关于x 的方程ax 2﹣3x+1=0是一元二次方程，则（ ）A ．a ＞0 B.a ≥0 C ．a ≠0 D.a=12．在Rt △ABC 中，∠C=90°，AC=12，BC=5，则sinA 的值是（ ）A ． B. C. D ． 3．某商店购进一种商品，单价为30元．试销中发现这种商品每天的销售量P （件）与每件的销售价x （元）满足关系：P=100﹣2x ．若商店在试销期间每天销售这种商品获得200元的利润，根据题意，下面所列方程正确的是（ ）A ．（x ﹣30）（100﹣2x ）=200B ．x （100﹣2x ）=200C ．（30﹣x ）（100﹣2x ）=200D ．（x ﹣30）（2x ﹣100）=2004．如图，AB 是⊙O 的直径，⊙O 交BC 的中点于D ，DE ⊥AC 于E ，连接AD ，则下列结论：①AD ⊥BC ；②∠EDA=∠B ；③OA=AC ；④DE 是⊙O 的切线，正确的个数是（ ）A ．1 个B ．2个C ．3 个D ．4个5．若点M （﹣2，y 1），N （﹣1，y 2），P （8，y 3）在抛物线2132y x =-+上，则下列结论正确的是（ ）A ． y 1＜y 2＜y 3B ． y 2＜y 1＜y 3C ． y 3＜y 1＜y 2D ． y 1＜y 3＜y 26．如图，在平面直角坐标系xOy 中，直线AB 过点A （﹣3，0），B （0，3），⊙O 的半径为1（O 为坐标原点），点P 在直线AB 上，过点P 作⊙O 的一条切线PQ ，Q 为切点，则切线长PQ 的最小值为（ ）A ．B ． 2C ． 3D ．二、填空题7．已知x=﹣1是方程x 2+mx ﹣5=0的一个根，则方程的另一根为．8．在Rt △ABC 中，∠C=90°，AB=6，cosB=，则AC 的长为．9．已知圆锥的底面半径为，侧面积为π15，则这个圆锥的侧面展开图的圆心角的度数是．10．若锐角满足2sin(－15°)－1＝0，则tan ＝．11.若实数a 、b 、c 满足9a ﹣3b+c=0，则方程ax 2+bx+c=0必有一个根是．12.如图，A 、B 、C 是⊙上的三个点，∠ABC=130°，则∠AOC 的度数是．13．如图，在▱ABCD 中，E 在AB 上，CE 、BD 交于F ，若AE ：BE=4：3，且BF=2，则DF=..14．已知等边三角形ABC 的高为4，在这个三角形内有一点P ，若点P 到AB 的距离是1，点P 到AC 的距离是2，则点P 到BC 的距离是．15.把二次函数y =错误！未找到引用源。

江苏省丹阳市第三中学 九年级数学上学期双休日作业双休日作业（1 班级 姓名 备课组长： 一、选择题 1.计算2(3)-的结果是………………………………………………………………（ ）B.3-C.3± 2.若二次根式1x -有意义，则x 的取值范围为……………………………………（ ）A.1x ≠B.0>xC.1>xD.1x ≥3.用两块完全相同的直角三角形拼下列图形：①平行四边形（不包含菱形、矩形、正方形）；②矩形；③菱形；④正方形；⑤等腰三角形；⑥等边三角形.一定能拼成的图形是…（ ）A.①④⑤B.①②⑤C.①②③D. ②⑤⑥4.若菱形两条对角线的长分别为6和8，则这个菱形的周长为……………………（ ）.16 C5.如图，已知四边形ABCD 是平行四边形，下列结论中不正确的是………………（ ）A.当AB=BC 时，它是菱形B.当AC⊥BD 时，它是菱形C.当∠ABC=90°时，它是矩形D.当AC=BD 时，它是正方形6.下列各式一定是二次根式的是…………………………………………………… ( )A 7-B x 2C 22y x +D 367..下列二次根式中，最简二次根式的是……………………………………………（ ）A.12+aB.21 C.12 D.b a 2 8.下列计算正确的是…………………………………………………………………( )A.532=+B. 2333=-C. 23222=+D.224=-9.下列方程为一元二次方程的是 …………………………………………………( )A.0233122=--x x B. 0522=+-y x C. 02=++c bx ax D.07142=+-xx 10一个直角三角形的面积为24,两条直角边的和为14,则斜边长为………………( )A. 372B. 10C. 382D. 14二、填空题11．8×2＝ .12.将方程1242-=x x 化成一般形式为 ， 其二次项系数是 ，一次项是 ．A C13.当x 时, 是二次根式1-x . 14.点A(-2,b)与点B(a,1)关于原点对称,则a+b= . 15．当c =__________时，（填一个符合要求的数即可）关于x 的方程2280x x c ++=有实数根．16．已知三角形的两边长为4和5，第三边的长是方程2560x x -+=的一个根，则这个三角形的周长是_________________.17．如图，在等腰梯形ABCD 中，AC ⊥BD ，AC ＝6cm ，则等腰梯形ABCD 的面积为 cm 2.18．已知一元二次方程x 2－6x+5－k=0•的根的判别式等于4，则这个方程的根为_______19．毛毛的作业本上有以下4题：①325+=；②3223-=；③632a a =；④33431163116=⋅=，其中毛毛做错的题有 （填写序号）. 20.数a 在数轴上的位置如图所示，化简：()2|1|2a a -+-= .三、解答题21．计算或化简： （1）4821319125+- （2）22)8321464(÷+-（3）)23)(13(2)23()13(22+--++- （4）8)63(322+-+22．解下列方程：(1) （2x ＋1）2＝3（2x ＋1） (2) 0142=+-x x （配方法）-1012a（3）0152=-+a a （4）x x x 32)1)(1(=-+23已知关于x 的方程()0214122=⎪⎭⎫ ⎝⎛-++-k x k x （1） 求证：无论k 取什么实数值，这个方程总有实数根（2） 当等腰三角形ABC 一边长a =4，另两边长b ，c 恰好是这个方程的两根，求△ABC 的周长。

初中数学试卷灿若寒星整理制作双休作业7(第四章全章) (时间：60分钟 满分：100分)一、选择题(每小题4分，共32分) 1．如图，在▱ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF ∶EC 等于( ) A ．3∶2 B ．3∶1 C ．1∶1 D ．1∶3第1题图第2题图2．如图，△ABC 中，∠C ＝90°，四边形DEFC 是正方形，AC ＝4 cm ，BC ＝3 cm ，则正方形的面积为( )A .127 cm 2B ．3 cm 2C ．4 cm 2D .14449cm 2 3．如图，身高为1.6 m 的吴格婷想测量学校旗杆的高度，当她站在C 处时，她头顶端的影子正好与旗杆顶端的影子重合，并测得AC ＝2.0 m ，BC ＝8.0 m ，则旗杆的高度是( ) A ．6.4 m B ．7.0 m C ．8.0 m D ．9.0 m第3题图第4题图4．如图，点A ，B ，C ，D 的坐标分别是(1，7)，(1，1)，(4，1)，(6，1)，以点C ，D ，E 为顶点的三角形与△ABC 相似，则点E 的坐标不可能是( ) A ．(6，0) B ．(6，3) C ．(6，5) D ．(4，2)5．如图，以点O 为位似中心，将△ABC 放大得到△DEF.若AD ＝OA ，则△ABC 与△DEF 的面积之比为( )A ．1∶2B ．1∶4C ．1∶5D ．1∶6第5题图第6题图6．如图，△OAB 与△OCD 是以点O 为位似中心的位似图形，相似比为1∶2，∠OCD ＝90°，CO ＝CD.若B(1，0)，则点C 的坐标为( )A ．(1，2)B ．(1，1)C ．(2，2)D ．(2，1)7．将边长分别为2，3，5的三个正方形按如图方式排列，则图中阴影部分的面积为( ) A .214 B .154 C .72D ．3第7题图第8题图8．(2016·泸州)如图，矩形ABCD 的边长AD ＝3，AB ＝2，E 为AB 的中点，点F 在边BC 上，且BF ＝2FC ，AF 分别与DE ，DB 相交于点M ，N ，则MN 的长为( ) A .225 B .9220 C .324 D .425 二、填空题(每小题4分，共24分)9．如果x 2＝y 3＝z4≠0，那么x ＋2y ＋3z 3x ＋2y －2z的值是______．10．两个相似三角形的面积比为9∶25，其中一个三角形的周长为36，则另一个三角形的周长为________．11．如图，D ，E 是AB 的三等分点，DF ∥EG ∥BC ，则图中三部分面积S 1∶S 2∶S 3＝________．第11题图第12题图12．如图，一束光线从点A(3，3)出发，经过y 轴上的C 点反射后经过点B(1，0)，则光线从A 点到B 点经过的路线长是_________．13．如图，正方形ABCD 和正方形OEFG 中，点A 和点F 的坐标分别为(3，2)，(－1，－1)，则两个正方形的位似中心的坐标是________．第13题图第14题图14．如图，在△ABC 中，BC ＝6，E ，F 分别是AB ，AC 的中点，动点P 在射线EF 上，BP 交CE 于点D ，∠CBP 的平分线交CE 于点Q ，当CQ ＝13CE 时，EP ＋BP ＝________．三、解答题(共44分)15．(8分)如图，△ABC 与△A′B′C′是位似图形，点A ，B ，A ′，B ′，O 共线，点O 为位似中心．(1)AC 与A′C′平行吗？为什么？(2)若AB ＝2A′B′，OC ′＝5，求CC′的长．16．(11分)如图，在矩形ABCD 中，CD ＝23，CF ⊥BD 分别交BD ，AD 于点E ，F ，连接BF.(1)求证：△DEC ∽△FDC ；(2)当F 为AD 的中点时，求BC 的长度．17．(11分)如图，M，N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞．工程人员为了计算工程量，必须计算M，N两点之间的直线距离，选择测量点A，B，C，点B，C分别在AM，AN上，现测得AM＝1千米，AN＝1.8千米，AB＝54米，BC＝45米，AC＝30米，求M，N两点之间的直线距离．18．(14分)如图，在矩形ABCD中，AB＝12 cm，BC＝8 cm，点E，F，G分别从A，B，C 三点同时出发，沿矩形的边按逆时针方向移动，点E，G的速度为2 cm/s，点F的速度为4 cm/s，当点F追上点G(即点F与点G重合)时，三个点随之停止移动．设移动开始后第t s时，△EFG的面积为S(cm2)．(1)当t＝1 s时，S的值是多少？(2)若点F在矩形的边BC上移动，当t为何值时，以点E，B，F为顶点的三角形与以点F，C，G为顶点的三角形相似？请说明理由．双休作业7(第四章全章)1．D 2.D 3.C 4.B 5.B 6．B 7.B 8.B点拨：如图，过点F 作FH ⊥AD 于点H ，交ED 于点O ，则FH ＝AB ＝2.∵BF ＝2FC ，BC ＝AD ＝3，∴BF ＝AH ＝2，FC ＝HD ＝1，∴AF ＝FH 2＋AH 2＝22＋22＝22，∵OH ∥AE ，∴HO AE ＝DH AD ＝13，∴OH ＝13AE ＝13，∴OF ＝FH －OH ＝2－13＝53，∵AE ∥FO ，∴△AME ∽FMO ，∴AM FM ＝AE FO ＝153＝35，∴AM ＝38AF ＝324.∵AD ∥BF ，∴△AND ∽△FNB ，∴AN FN ＝AD BF ＝32，∴AN ＝35AF ＝625，∴MN ＝AN －AM ＝625－324＝9220，故选B . 9.5 10.1085或6011.1∶3∶5 12.5 13.(1，0)或(－5，－2) 14.12 15.(1)AC ∥A′C′，理由如下：∵△ABC 与△A′B′C′是位似图形，∴△ABC ∽△A ′B ′C ′.∴∠A ＝∠C′A′B′.∴AC ∥A ′C ′.(2)∵△ABC ∽△A ′B ′C ′，∴AB A′B′＝AC A′C′.∵AB ＝2A′B′，∴AC A′C′＝21.又∵△ABC 与△A′B′C′是位似图形，∴OC O′C′＝AC A′C′＝21.∵OC′＝5，∴OC ＝10，CC ′＝OC －OC′＝10－5＝5.16．(1)∵∠DEC ＝∠FDC ＝90°，∠DCE ＝∠FCD ，∴△DEC ∽△FDC.(2)∵F 为AD 的中点，AD ∥BC ，∴FE ∶EC ＝FD ∶BC ＝1∶2，∴FE ∶FC ＝1∶3，设EF ＝x ，则FC ＝3x ，∵△DEC ∽△FDC ，∴CE CD ＝CDFC ，可得6x 2＝12，解得x ＝2，则CF ＝32，在Rt △CFD 中，DF ＝FC 2－CD 2＝6，∴BC ＝2DF ＝2 6. 17.连接MN ，图略．在△ABC 与△ANM 中，∠A ＝∠A ，AC AB ＝3054＝59，AM AN ＝11.8＝59，∴△ABC ∽△ANM ，∴AC BC ＝AM MN ，即3045＝1MN ，解得MN＝1.5.故M ，N 两点之间的直线距离是1.5千米． 18.(1)当t ＝1 s 时，S ＝S梯形EBCG－S △EBF－S △FCG ＝12×(10＋2)×8－12×10×4－12×4×2＝24(cm 2)．(2)当点F 在边BC 上移动时，F 与B ，E 能构成三角形且F 与C ，G 能构成三角形，则0<t<2，有AE ＝CG ＝2t ，EB ＝12－2t ，BF ＝4t ，FC ＝8－4t.在△EBF 和△FCG 中，∠B ＝∠C ＝90°，①若EB FC ＝BFCG ，即12－2t 8－4t ＝4t 2t ，解得t ＝23，又t ＝23满足0<t<2，所以当t ＝23时，△EBF ∽△FCG ；②若EB GC ＝BF CF ，即12－2t 2t ＝4t8－4t ，解得t ＝32，又t ＝32满足0<t<2，所以当t ＝32时，△EBF ∽△GCF.综上所述，当t ＝23或t ＝32时，以点E ，B ，F 为顶点的三角形与以点F ，C ，G 为顶点的三角形相似．。

初中数学试卷 马鸣风萧萧双休作业9(第24章全章)(时间：60分钟 满分：100分)一、选择题(每小题4分，共32分)1．(2016·三明)如图，AB 是⊙O 的弦，半径OC ⊥AB 于点D ，若⊙O 的半径为5，AB ＝8，则CD 的长是( )A ．2B ．3C ．4D ．5第1题图第2题图2．(2016·泰安)如图，点A ，B ，C 是圆O 上的三点，且四边形ABCO 是平行四边形，OF ⊥OC 交圆O 于点F ，则∠BAF 等于( )A ．12.5°B ．15°C ．20°D ．22.5°3．(2016·连云港)如图，在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点)．如果以A 为圆心，r 为半径画圆，选取的格点中除点A 外恰好有3个在圆内，则r 的取值范围为( )A ．22＜r≤17B .17＜r≤3 2C .17＜r≤5D ．5＜r≤29第3题图第4题图4．(2016·潍坊)如图，在平面直角坐标系中，⊙M 与x 轴相切于点A(8，0)，与y 轴分别交于点B(0，4)和点C(0，16)，则圆心M 到坐标原点O 的距离是( )A ．10B ．8 2C ．413D ．2415．(2016·山西)如图，在▱ABCD 中，AB 为⊙O 的直径，⊙O 与DC 相切于点E ，与AD 相交于点F ，已知AB ＝12，∠C ＝60°，则FE ︵的长为( )A .π3B .π2C ．πD ．2π第5题图第6题图6．如图，扇形AOB 是直角扇形，以OA ，OB 为直径在扇形内作半圆，M ，N 分别表示两个阴影部分的面积，那么M ，N 的大小关系是( )A ．M ＞NB ．M ＝NC ．M ＜ND ．无法确定7．(2016·泸州)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是( ) A .38 B .34 C .24 D .288．如图，AB 是半圆O 的直径，点C ，D ，E 是半圆弧上的点，且弦AC ＝CD ＝2，弦DE ＝EB ＝2，则直径AB 的长是( )A ．2 5B ．2 2C ．3 2D ．4 2二、填空题(每小题4分，共32分)9．在平面直角坐标系中，O 为坐标原点，则直线y ＝x ＋2与以O 点为圆心，1为半径的圆的位置关系为________．10．已知圆锥的底面半径为10 cm ，它的展开图扇形的半径为30 cm ，则这个扇形圆心角的度数是________．11．(2016·泰安)如图，半径为3的⊙O 与Rt △AOB 的斜边AB 切于点D ，交OB 于点C ，连接CD 交直线OA 于点E ，若∠B ＝30°，则线段AE 的长为________．12．(2016·咸宁)如图，点E 是△ABC 的内心，AE 的延长线和△ABC 的外接圆相交于点D ，连接BD ，BE ，CE ，若∠CBD ＝32°，则∠BEC 的度数为________．第11题图第12题图第13题图13．(2016·广东)如图，把一个圆锥沿母线OA 剪开，展开后得到扇形AOC ，已知圆锥的高h 为12 cm ，OA ＝13 cm ，则扇形AOC 中AC ︵的长是________cm (计算结果保留π)．14．如图，在△ABC 中，∠B ＝30°，∠A ＝15°，BC ＝12，以A 为圆心作圆和直线BC 相切，则⊙A 的半径为________．第14题图第15题图第16题图15．(2016·德州)如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M 与圆心O 重合，则图中阴影部分的面积是________．16．如图，从一块半径是1 m 的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A ，B ，C 在⊙O 上)，将剪下的扇形围成一个圆锥，则这个圆锥的底面圆的半径是________m .三、解答题(共36分)17．(8分)(2016·资阳)如图，在⊙O 中，点C 是直径AB 延长线上一点，过点C 作⊙O 的切线，切点为D ，连接BD.(1)求证：∠A ＝∠BDC ；(2)若CM 平分∠ACD ，且分别交AD ，BD 于点M ，N ，当DM ＝1时，求MN 的长．18．(8分)如图，△ABC中，∠C＝90°，⊙I为△ABC的内切圆，点O为△ABC的外心，BC＝6，AC ＝8.(1)求⊙I的半径；(2)求OI的长．19．(10分)如图，在△ABC中，BA＝BC，以AB为直径的⊙O分别交AC，BC于点D，E，BC的延长线与⊙O的切线AF交于点F.(1)求证：∠ABC＝2∠CAF；(2)若AC＝210，CE∶EB＝1∶4，求CE的长．20．(10分)(2016·云南)如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为点E，F是AE与⊙O的交点，AC平分∠BAE.(1)求证：DE是⊙O的切线；(2)若AE＝6，∠D＝30°，求图中阴影部分的面积．。