普通年金的终值与现值
- 格式:docx
- 大小:67.34 KB
- 文档页数:3





六、年金终值和年金现值的计算(一)年金的含义年金是指一定时期内每次等额收付的系列款项。
通常记作A 。
具有两个特点:一是金额相等;二是时间间隔相等。
也可以理解为年金是指等额、定期的系列收支。
在现实工作中年金应用很广泛。
例如,分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款、每年相同的销售收入等,都属于年金收付形式。
老师手写板:①②年、月、半年、2年1年 2年 3年1年 1年 1年(二)年金的种类年金按其每次收付款项发生的时点不同,可以分为四种:普通年金(后付年金):从第一期开始每期期末收款、付款的年金。
预付年金(先付年金、即付年金):从第一期开始每期期初收款、付款的年金。
与普通年金的区别仅在于付款时间的不同。
递延年金:从第二期或第二期以后开始每期期末收付的年金。
永续年金:无限期的普通年金。
注意:各种类型年金之间的关系(1)普通年金和即付年金区别:普通年金的款项收付发生在每期期末,即付年金的款项收付发生在每期期初。
联系:第一期均出现款项收付。
【例题1·单选题】2007年1月1日,甲公司租用一层写字楼作为办公场所,租赁期限3年,每年12月31日支付租金10万元,共支付3年。
该租金有年金的特点,属于( )。
(2010年考试真题)A .普通年金B .即付年金C .递延年金D .永续年金【答案】A【解析】每年年末发生等额年金的是普通年金。
(2)递延年金和永续年金二者都是在普通年金的基础上发展演变起来的,它们都是普通年金的特殊形式。
它们与普通年金的共同点有:它们都是每期期末发生的。
区别在于递延年金前面有一个递延期,也就是前面几期没有现金流,永续年金没有终点。
在年金的四种类型中,最基本的是普通年金,其他类型的年金都可以看成是普通年金的转化形式。
【提示】1.这里的年金收付间隔的时间不一定是1年,可以是半年、一个季度或者一个月等。
A A A A A A A A A A 300万 200万 100万2.这里年金收付的起止时间可以是从任何时点开始,如一年的间隔期,不一定是从1月1日至12月31日,可以是从当年7月1日至次年6月30日。

终值和现值1.年金终值和年金现值(1)年金现值(普通年金现值)普通年金现值是指将在一定时期内按相同时间间隔在每期期末收付的相等金额折算到第一期期初的现值之和。
根据复利现值的方法计算年金现值的公式为:P A=A(1+i)-1+A(1+i)-2+A(1+i)-3+···+A(1+i)-n=A式中称为“年金现值系数”记做(P/A,i,n)【例题】某投资项目于2017年年初完工,假定当年投产,从投产之日起每年末可获得收益100000元。
按年利率5%计算,预期5年收益的现值是多少元?(P/A,5%,5)=4.3295【答案】P A=A×(P/A,i,n)=100000×(P/A,5%,5)=100000×4.3295=432950(元)。
【例题·单选题】2017年1月1日,某企业的投资项目正式投入运营,从运营之日起,该企业每年年末可从该项目中获得收益200000元,预计收益期为4年。
假设年利率6%,已知(P/A,6%,4)=3.4651。
不考虑其他因素,2017年1月1日该项目预期4年总收益的现值为()元。
(2018年)A.693020B.200000C.2772080D.800000【答案】A【解析】P A=200000×(P/A,6%,4)=200000×3.4651=693020(元)。
【例题·单选题】下列各项中,属于普通年金形式的是()。
(2018年)A.企业在某中学设立奖励基金,用于每年发放等额奖学金B.企业租房2年,每个月初向出租方支付等额房租C.企业生产线使用年限为5年,从年初投产之日起每年年末获得等额现金收益D.企业设立一项公益基金,连续10年于每年年初投入等额奖金【答案】C【解析】普通年金是年金的最基本形式,它是指从第一期起,在一定时期内每期期末等额收付的系列款项,又称为后付年金,即选项C正确。
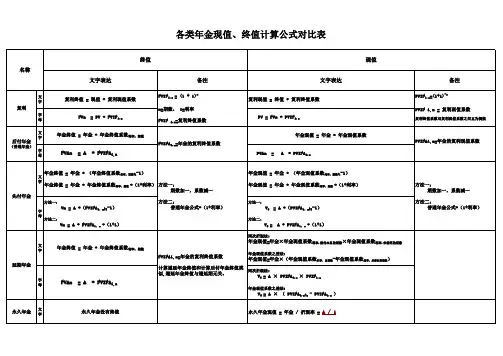


普通年金是指在一定的时期内,按照固定的时间间隔(如每年、每月等)支付相等金额的一系列现金流。
普通年金的计算可以涉及到终值、现
值以及年金的计算。
一、普通年金的终值计算
普通年金的终值是指当一系列相等金额的现金流经过一定期限后的总
金额。
普通年金的终值计算公式如下:
FV=PMT*[(1+r)^n-1]/r
其中,FV表示普通年金的终值,PMT表示每期支付的金额,r表示利率,n表示期数。
例如,假设每年支付1000元,年利率为5%,支付期限为10年,则
普通年金的终值可以通过以下公式进行计算:
二、普通年金的现值计算
普通年金的现值是指在未来一系列相等金额的现金流到达之前,所需
投资金额。
普通年金的现值计算公式如下:
PV=PMT*[1-(1+r)^(-n)]/r
其中,PV表示普通年金的现值,PMT表示每期支付的金额,r表示利率,n表示期数。
例如,假设每年需要支付1000元,年利率为5%,支付期限为10年,则普通年金的现值可以通过以下公式进行计算:
所以,支付每年1000元的普通年金在10年内的现值约为7721.74元。
三、普通年金的年金计算
普通年金的年金是指在特定的期限内以相等间隔时间支付的一系列现金流的总和。
普通年金的年金计算公式如下:
PMT=PV*(r/(1-(1+r)^(-n)))
其中,PMT表示每期支付的金额,PV表示普通年金的现值,r表示利率,n表示期数。
综上所述,普通年金的终值、现值及年金可以通过相应的计算公式得出。
这些公式可以帮助我们在处理普通年金相关问题时进行精确计算,以便做出合理的决策。


普通年⾦终值和现值。
年⾦是指⼀系列稳定有规律的,持续⼀段固定时期的现⾦收付活动。
例如,分期付款赊购、分期偿还贷款、发放养⽼⾦、分期⽀付⼯程款、每年相同的销售收⼊等,都属于年⾦收付形式。
普通年⾦⼜称后付年⾦,是指各期期末收付的年⾦。
如图13—1所⽰。
横线代表时间的延续,上边为各期顺序号;竖线表⽰⽀付时刻,下端数字表⽰⽀付的⾦额。
(1)普通年⾦终值。
普通年⾦终值是指⼀定时期内每期期末等额的系列收付款项的复利终值之和。
设:A——年⾦;i——利息率;n——计息期数;FA——年⾦终值。
×(1+10%) +100×(1+10%)+100=100×1.464+100×1.331+100×1.210+100×1.100=610.5(元)如果年⾦的期数很多,⽤上述⽅法计算年⾦显然很繁琐。
由于每年⽀付额相等,年⾦终值系数⼜是有规律的,所以可简化计算⽅法,按复利计算的普通年⾦终值为:(2)偿债基⾦。
偿债基⾦是指为使年⾦终值达到既定⾦额每年应⽀付的年⾦数额。
[例13—4】拟在5年后还清610.5元,假设银⾏帝款利率为10%,从现在起每年存⼈银⾏⼀笔等额款项,每年需要存⼈多少元?根据普通年⾦计算公式:上式中的⽯茄是普通年⾦终值系数的倒数,称为偿债基⾦系数,可表⽰为(A/S,i,n)。
偿债基⾦系数可根据普通年⾦终值系数求倒数确定。
(3)普通年⾦现值。
普通年⾦现值,是⼀定时期内每期期末等额的系列收付款项的现值之和。
如果是⼀项投资,普通年⾦现值也可以这样理解。
即为了在今后每年取得相等⾦额的款项,现在需要投⼊的⾦额。
设年⾦现值为PA。
[例13—5】某⼈为了在3年内每年取出100元,设银⾏存款利率为10%,那么,他现在应当存⼈多少钱?这个问题可以表述为:请计算i=lO%,n=3,A=100元的普通年⾦现值是多少?如图13—2所⽰:PA=100×O.9091+100×O.8264+100×0.7513=100×2.4868=248.68(元)类似于普通年⾦终值,如果年⾦的期数很多,⽤上述⽅法计算显然很繁琐。
普通年金是指在一定时间周期内,每年末等额支付一定金额的现金流,通常用于计算投资或贷款的终值、现值以及每年应付的等额金额。
首先,我们来计算普通年金的终值。
假设年金金额为A,投资期限为
n年,年利率为r。
根据复利的概念,年金的终值可以通过每年付款的终
值之和来计算。
每年付款的终值可以用复利公式:
FV=A(1+r)^n-1/r
其中FV表示终值。
然后,我们来计算普通年金的现值。
假设年金金额为A,投资期限为
n年,年利率为r。
根据现值的概念,普通年金的现值可以通过每年付款
的现值之和来计算。
每年付款的现值可以用现值公式:
PV=A(1-(1+r)^-n)/r
其中PV表示现值。
最后,我们来计算每年应付的等额金额。
假设年金的终值为FV,投
资期限为n年,年利率为r。
根据年金终值公式,可以得到每年应付的等
额金额:
A=FV*r/(1-(1+r)^-n)
通过以上三个公式,我们可以计算普通年金的终值、现值以及每年应
付的等额金额。
举个例子,假设我们要计算一个年金的终值、现值以及每年应付的等
额金额。
假设年金金额为1000,投资期限为10年,年利率为5%。
首先,我们来计算年金的终值:
然后,我们来计算年金的现值:
PV=1000(1-(1+0.05)^-10)/0.05≈7724.78
最后,我们来计算每年应付的等额金额:
以上就是普通年金终值、现值以及年金的计算方法。
通过这些计算,我们可以更好地理解年金的概念,并应用于实际的投资和贷款中。
终值和现值公式
现值计算公式:P/A=1/i - 1/ [i(1+i)^n],(i表示报酬率,n表示期数,P表示现值,A表示年金)。
终值计算公式:(P/F,i,n)=(1+i)^(-n),(i表示报酬率,n表示期数,P表示现值,F表示年金)。
年金终值计算公式:F=A*(F/A,i,n)=A*(1+i)n-1/i,
其中(F/A,i,n)称作“年金终值系数”、可查普通年金终值系数表。
终值是现在的一笔钱或一系列支付款项按给定的利息率计算所得到的在某个未来时间点的价值。
终值和现值的计算公式区别
复利终值=P×(F/P,i,n),(F/P,i,n)为复利终值系数
复利现值=F×(P/F,i,n),(P/F,i,n)为复利现值系数
普通年金终值=A×(F/A,i,n),(F/A,i,n)为普通年金终值系数
普通年金现值=A×(P/A,i,n),(P/A,i,n)为普通年金现值系数
预付年金终值=A×(F/A,i,n)×(1+i)
预付年金现值=A×(P/A,i,n)×(1+i)
递延年金终值=A×(F/A,i,n)
递延年金现值=A×(P/A,i,n)×(P/F,i,m)=A×(P/A,i,m+n)-A×(P/A,i,m),递延期m(第一次有收支的前一期),连续收支期n
永续年金终值:没有
永续年金现值=A/i
终值是现在的一笔钱或一系列支付款项按给定的利息率计算所得到的在未来某个时间点的价值。
现值是未来的一笔钱或一系列支付款项按给定的利息率计算所得到的现在的价值。