运筹学上机习题(2012)

线性规划问题练习题练习一：一贸易公司专门经营某种杂粮的批发业务。

公司现有库容5000担的仓库。

1月1日，公司拥有库存1000担杂粮，并有资金20000元，估计第一季度杂粮价格如表所示。

如买进的杂粮当月到货，但需到下月才能卖出，且规定“货到付款”。

公司希望本季末库存2000担，问应采取什么样的买进卖出的策略使3个月总的获利最大？练习二、某农场有100hm2（公顷）土地及15000元资金可用于发展生产。

农场劳动力情况为秋冬季3500人日，春夏季4000人日，如劳动力本身用不了时可外出干活，春夏季收入为2.1元/人日，秋冬季收入为1.8元/人日。

该农场种植三种作物：大豆、玉米小麦，并饲养奶牛和鸡。

种作物时不需要专门投资，而饲养动物时没有奶牛投资400元，每只鸡投资3元。

养奶牛时没头需拨出1.5 hm2中饲草，并占用人工秋冬季为100人日，春夏季为50人日，年净收入400元/每头奶牛。

养鸡时不占用土地，需人工为每只鸡秋冬需0.6人日，春夏为0.3人日，年净收入为2元/每只鸡。

农场现有鸡舍允许最多样3000只鸡，牛栏允许最多养32头奶牛。

三作物每年需要的人工及收入如表所1、某公司有三项工作需分别招收技工和力工来完成。

第一项工作可由一个技工单独完成，或由一个技工和两个力工组成的小组来完成。

第二项工作可由一个技工或一个力工单独去完成。

第三项工作可由5个力工组成的小组完成，或由一个技工领着三个力工来完成。

已知技工和力工每周工资分别为100元和80元，他们每周都工作48小时，但他们没人实际的有效工作时间分别为42和36h。

为完成这三项工作任务，该公司需要每周总有效工作时间为：第一项工作1000h。

第二项工作20000h，第三项工作30000h。

能招收到的工人数为技工不超过400人，力工不超过800人。

试建立模型，确定招收技工和力工各多少人。

使总的工资支出为最少2、旭日公司签订了5种产品（i=1，…5）下一年度1~6月份的交货合同。

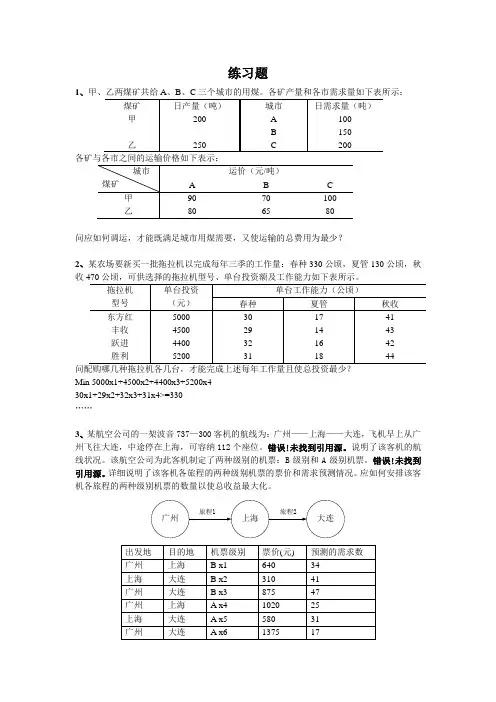
练习题1、各矿与各市之间的运输价格如下表示：问应如何调运，才能既满足城市用煤需要，又使运输的总费用为最少？2、某农场要新买一批拖拉机以完成每年三季的工作量：春种330公顷，夏管130公顷，秋收470公顷，可供选择的拖拉机型号、单台投资额及工作能力如下表所示。

Min 5000x1+4500x2+4400x3+5200x430x1+29x2+32x3+31x4>=330……3、某航空公司的一架波音737—300客机的航线为：广州——上海——大连，飞机早上从广州飞往大连，中途停在上海，可容纳112个座位。

错误！未找到引用源。

说明了该客机的航线状况。

该航空公司为此客机制定了两种级别的机票：B级别和A级别机票。

错误！未找到引用源。

详细说明了该客机各旅程的两种级别机票的票价和需求预测情况。

应如何安排该客机各旅程的两种级别机票的数量以使总收益最大化。

MaxX1+X3+X4+X6<=122;4、有A1，A2，A3三个水泥厂，每天要把生产的水泥运往B1，B2两地。

各厂的产量、各地的需求量（销量）以及各厂地间的运价见下表。

问如何设计调运方案才能使总运费最少？56、设有三个化肥厂（A、B、C）供应四个地区（Ⅰ、Ⅱ、Ⅲ、Ⅳ）的农用化肥。

假定等量的花费在这些地区的使用效果相同。

各化肥厂年产量，各地区需要量及从各化肥厂到各地区运送单位化肥的运价表如下表所示。

试求出总的运费最节省的化肥调拨方案。

若规定每人专门负责一个语种的翻译工作，那么，试回答下列问题：（1）应如何指派，使总的翻译效率最高？（2）若甲不懂德文，乙不懂日文，其他数字不变，则应如何指派？8、某市六个新建单位之间的交通线路的长度（公里）如下表所示。

其中单位A距市煤气供应网最近，为1.5公里。

应如何铺设煤气管道使其总长最短。

9、在下面的网络中，试求：①各点到点t的最短路；②点s到各点的最短路。

-2410、求出下图所示的网络的最大流。

11、试确定关键路径和总工期。

实验报告运筹学A（二）学号：201134010209 姓名：欧阳文娟专业：物流工程指导教师：叶鸿二零一三年四月实验一：最小树、最短路与最大流问题（一）实验目的：掌握WinQSB软件求最小树、最短路与最大流问题（二）内容和要求：用WinQSB软件完成下三例1. 最小树问题——求下图的最小生成树和最大生成树：6V1 V26 6 2 2V6 7 V7 3 V38 3 4 3V5 1 V42. 最短路问题——如图所示网络，各线段上的数字代表相应两节点间的距离，请求出从节点1 到节点10之间的最短距离。

网络图3. 最大流问题——某单位招收懂俄、英、日、德、法文的翻译各一人，有5人应聘。

已知乙懂俄文，甲、乙、丙、丁懂英文，甲、丙、丁懂日文，乙、戊懂德文，戊懂法文，问这5个人是否都能得到聘书？最多几个得到招聘，招聘后每人从事哪一方面翻译任务？（三）操作步骤：最小树、最短路和最大流问题的运算程序是Network Modeling。

最小树（1）选择Minimal Spanning Tree，输入节点数。

两点间的权数只输入一次（上三角）。

（2）点击菜单栏Solve and Analyze，输出表最小树结果；点击菜单栏Results →Graphic Solution,，显示最小部分树形，生成如下运行结果最短路问题（2）选择Shortest Path Problem，如果是有向图就按弧的方向输数据，本例是无向图，每一条边必须输入两次，无向边变为两条方向相反的弧（2）点击Solve and Analyze后系统提示用户选择图的起点和终点，点击Result →Graphic Solution，显示最短路线图，生成如下运行结果。

可知，节点1到节点10之间的最短距离29，途经为V1→V2→V5→V9→V10。

最大流问题（1）选择Maximal Flow Problem。

输入节点数，输入弧容量即可。

（2）点击Solve and Analyze后系统提示用户选择图的起点和终点;点击Result→Graphic Solution，显示各点的流量图。

1、B2、B3、A4、C5、D6对7对8 错9 对10 对11 标准化（用对偶单纯型法解）MAX Z=-5X1 -2X2 -4X3ST-3X1-X2-2X3+X4 = -4-6X1-3X2-5X3 +X5 = -10X1…X5>=0B (-4，-10) 含负数，不是最优解确定进基MIN()=MIN(Zi/x5)=2/3 所以进基X2单纯型表迭代B (-2/3，10/3) 含负数，不是最优解再迭代一次确定离基变量MIN (X4,X2)=MIN(-2/3,-10/3)=-2/3 所以X4 为离基确定进基MIN()=MIN(Zi/x5)=2/3 所以进基X1单纯型表迭代先X2行除以A11=-1每行-AI1*X1Z’=-26/3 所以Z=26/3 X=(2/3,10/3,0,0,0)对偶问题MAX W=4Y1+10Y2ST3Y1+6Y2<5Y1+3Y2<=2Y1+5Y2<=4Y1,Y2>=0最优解就是松弛变量Y1=2 Y2=4/312题表作业法此题是产销平衡问题检验σ不能小于0A11 =4-4+3-2=1A24=9-3+4-11=-1 24不通过,不是最优解检验31，没有标记的格子A31=8-5+6-11+4-3+2=1检验22，没有标记的格子A22=10-3+4-11+6-5=1最小的σ24=-1，需要变换对奇数转角变量减去A14 ,对偶数转角变量加上A14,本身不变于是运费为2×8+2×3+4×12+5×14+6×8+11×4。

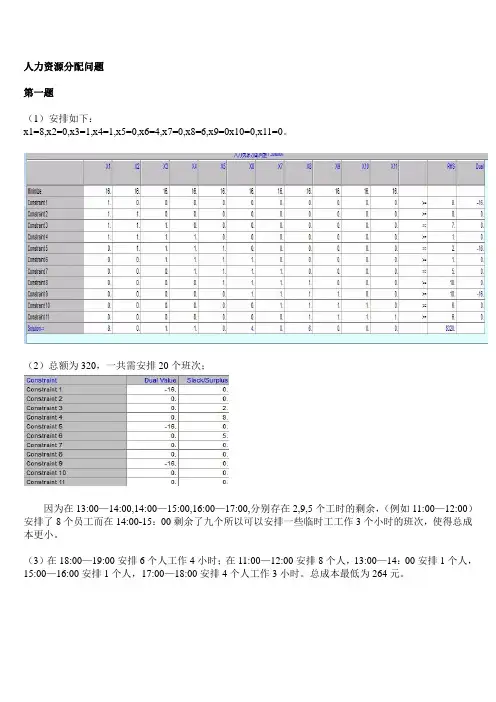
人力资源分配问题第一题（1）安排如下：x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0x10=0,x11=0。

（2）总额为320，一共需安排20个班次；因为在13:00—14:00,14:00—15:00,16:00—17:00,分别存在2,9,5个工时的剩余，（例如11:00—12:00）安排了8个员工而在14:00-15：00剩余了九个所以可以安排一些临时工工作3个小时的班次，使得总成本更小。

（3）在18:00—19:00安排6个人工作4小时；在11:00—12:00安排8个人，13:00—14：00安排1个人，15:00—16:00安排1个人，17:00—18:00安排4个人工作3小时。

总成本最低为264元。

生产计划优化问题第二题产品1在A1生产数量为1200单位，在A2上生产数量为230单位，在B1上不生产，B2上生产数量为858单位，B3上生产数量为571单位；产品2在A1上不生产，在A2上生产数量为500单位，在B1上生产数量为500单位；产品3在A2上生产数量为324单位，在B2上生产数量为324单位。

最大利润为2293.29元。

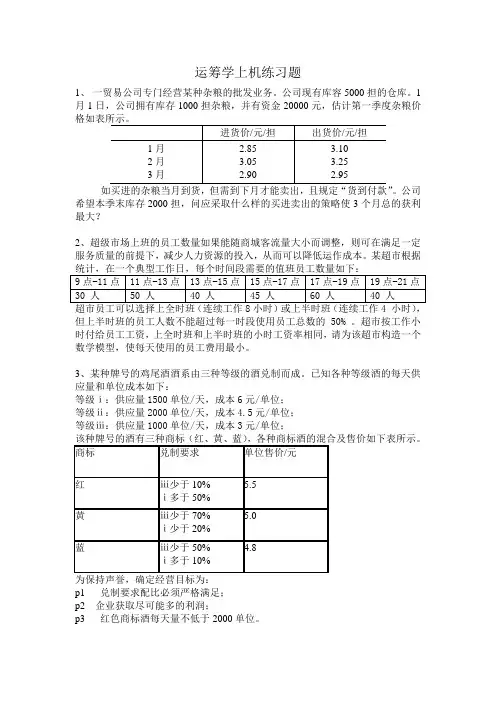
第三题设Xi为产品i最佳生产量。

（1）最优生产方案唯一，为X1=1000、X2=1000、X3=1000、X4=1000、X5=1000、X6=55625、X7=1000. （2）如上图所示，产品5的单价价格为0-30时，现行生产方案保持最优。

（3）由于环织机工的影子价格为300，且剩余变量值为零，而其他几种资源的影子价格为0，剩余变量均大于0，所以应优先增加环织工时这种资源的限额，能增加3.33工时，单位费用应低于其影子价格300才是合算的。

（4）因为产品2对偶价格= -3.2<0 ，950>933.33，3.2*（1000-950）=160；所以当产品2的最低销量从1000减少到950时，总利润增加160元。

运筹学上机练习题1、一贸易公司专门经营某种杂粮的批发业务。

公司现有库容5000担的仓库。

1月1日，公司拥有库存1000担杂粮，并有资金20000元，估计第一季度杂粮价。

公司希望本季末库存2000担，问应采取什么样的买进卖出的策略使3个月总的获利最大？2、超级市场上班的员工数量如果能随商城客流量大小而调整，则可在满足一定服务质量的前提下，减少人力资源的投入，从而可以降低运作成本。

某超市根据但上半时班的员工人数不能超过每一时段使用员工总数的50% 。

超市按工作小时付给员工工资，上全时班和上半时班的小时工资率相同，请为该超市构造一个数学模型，使每天使用的员工费用最小。

3、某种牌号的鸡尾酒酒系由三种等级的酒兑制而成。

已知各种等级酒的每天供应量和单位成本如下：等级ⅰ：供应量1500单位/天，成本6元/单位；等级ⅱ：供应量2000单位/天，成本4.5元/单位；等级ⅲ：供应量1000单位/天，成本3元/单位；p1 兑制要求配比必须严格满足；p2 企业获取尽可能多的利润；p3 红色商标酒每天量不低于2000单位。

4、某快餐店坐落在一个旅游景点中，这个旅游景点远离市区，平时游客不多，而在每个星期六游客猛增，快餐店主要为旅客提供低价位的快餐服务，该快餐店雇佣了两名正式员工，正式员工每天工作8个小时，其余工作由临时工来担任，临时工每天工作4个小时，在星期六，该快餐店从上午营业到下午10点关门，根据游客就餐情况，在星期六每个营业小时所需职工数（包括正式工和临时工）作4小时；另一名正式职工13点开始上班，工作4小时后，休息1个小时，而后再工作4个小时，又知零时工每小时的工资为4元。

在满足对职工需求的条件下，如何安排临时工的班次，使得临时工的成本最小？5、某化工厂生产两种用于轮船上的粘合剂A和B。

这两种粘合剂的强度不同，所需的加工时间也不同，生产1升的A需要20分钟，生产1升的B需要25分钟。

这两种粘合剂都以一种树脂为原料，1升树脂可以制造1升A或者1升B。

运筹学上机实验指导书目录绪论运筹学上机实验软件简介第一章运筹学上机实验指导§1.1 中小型线性规划模型的计算机求解§1.2 大型线性规划模型的编程计算机求解§1.3线性规划的灵敏度分析§1.4运输问题数学模型的计算机求解§1.5目标规划数学模型的计算机求解§1.6整数规划数学模型的计算机求解§1.7 指派问题的计算机求解§1.8最短路问题的计算机求解§1.9最大流问题的计算机求解第二章LINGO软件基础及应用§2.1 原始集(primitive set)和派生集(derived set)与集的定义§2.2 LINGO中的函数与目标函数和约束条件的表示§2.3 LINGO中的数据§2.4 LINDO简介第三章运筹学上机实验及要求实验一.中小型线性规划模型的求解与Lingo软件的初步使用实验二.中小型运输问题数学模型的Lingo软件求解。

实验三.大型线性规划模型的编程求解。

实验四.运输问题数学模型的Lingo编程求解。

实验五.分支定界法上机实验实验六.整数规划、0-1规划和指派问题的计算机求解实验七：最短路问题的计算机求解实验八:最大流问题的计算机求解绪论运筹学是研究资源最优规划和使用的数量化的管理科学，它是广泛利用现有的科学技术和计算机技术，特别是应用数学方法和数学模型，研究和解决生产、经营和经济管理活动中的各种优化决策问题。

运筹学通常是从实际问题出发，根据决策问题的特征，建立适当的数学模型，研究和分析模型的性质和特点，设计解决模型的方法或算法来解决实际问题，是一门应用性很强的科学技术。

运筹学的思想、内容和研究方法广泛应用于工程管理、工商企业管理、物流和供应链管理、交通运输规划与管理等各行各业，也是现代管理科学和经济学等许多学科研究的重要基础。

在解决生产、经营和管理活动中的实际决策问题时，一般都是建立变量多、约束多的大型复杂的运筹学模型，通常都只能通过计算机软件才能求解，因此，学习运筹学的计算机求解和进行上机实验，就是运筹学教学的重要组成部分。

运筹学一、名词解释（每个5分，共20分）运筹学：运筹学主要运用数学方法研究各种系统的优化途径及方案。

为决策者提供科学的决策依据可行解：在线性规划问题的一般模型中，满足约束条件的一组12,,.........n x x x 值称为此线性规划问题的可行解 最优解：在线性规划问题的一般模型中，使目标函数f 达到最优值的可行解称为线性规划问题的最优解。

运输问题：将一批物资从若干仓库运往若干目的地，通过组织运输，使花费的费用最少，这类问题就是运输问题 二、填空题（每题3分，8题共24分）1. 运筹学的主要研究对象是各种有组织系统的管理问题及生产 经营活动，其主要研究方法是量化和模型化方法。

2. 线性规划试题中，如果在约束条件中出现等式约束，我们通常用增加 人工变量 的方法来产生初始可行基。

3. 线性规划问题的所有可行解构成的集合是___凸集_______,它们有有限个____顶点____,线性规划问题的每个基可行解对应可行域的______顶点_____,若线性规划问题有最优解，必在______顶点________得到。

4. 线性规划问题MaxZ=C X ；A X =b ，X ≥0（A 为k x l 的矩阵，且l >k ）的基的最多个数为_Clk__，基的可行解的最多个数为__Clk___. 5．线性规划模型有三种参数，其名称分别为价值系数、__技术系数_和_限定系数__。

6. 在风险型决策问题中，我们一般采用___来反映每个人对待风险的态度。

7．目标规划总是求目标函数的 最小 信，且目标函数中没有线性规划中的价值系数，而是在各偏差变量前加上级别不同的 优先因子(或权重) 。

8. “如果线性规划的原问题存在可行解，则其对偶问题一定存在可行解”，这句话对还是错？ 错的 三．选择题（每题4分，9题共36分） 1、最早运用运筹学理论的是（ A ）A 二次世界大战期间，英国军事部门将运筹学运用到军事战略部署B 美国最早将运筹学运用到农业和人口规划问题上C 二次世界大战期间，英国政府将运筹学运用到政府制定计划D 50年代，运筹学运用到研究人口，能源，粮食，第三世界经济发展等问题上 2、下列哪些不是运筹学的研究范围（ D ）A 质量控制B 动态规划C 排队论D 系统设计3、使用人工变量法求解极大化线性规划问题时，当所有的检验数0j σ≤在基变量中仍含有非零的人工变量，表明该线性规划问题 ( D ) A ．有唯一的最优解 B ．有无穷多最优解 C ．为无界解 D ．无可行解4、关于线性规划的原问题和对偶问题，下列说法正确的是 ( B ) A ．若原问题为元界解，则对偶问题也为无界解B ．若原问题无可行解，其对偶问题具有无界解或无可行解 c ．若原问题存在可行解，其对偶问题必存在可行解 D ．若原问题存在可行解，其对偶问题无可行解5、在产销平衡运输问题中，设产地为m 个，销地为n 个，那么基可行解中非零变量的个数（ A ） A. 不能大于(m+n-1)； B. 不能小于(m+n-1)； C. 等于(m+n-1)； D. 不确定。

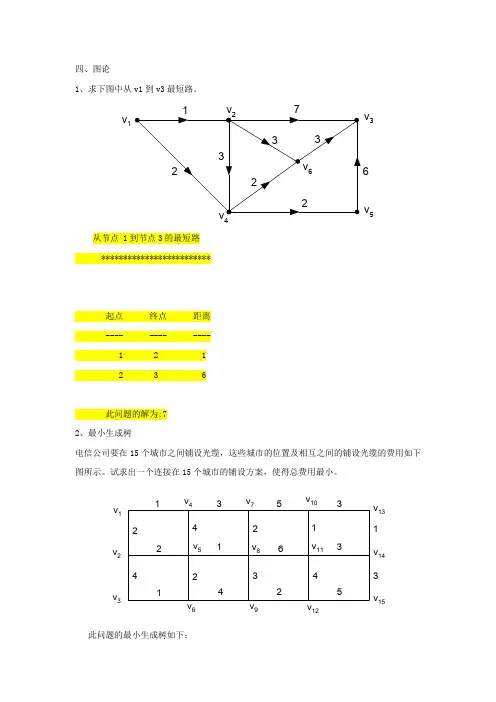
四、图论1、求下图中从v1到v3最短路。

v 1v 3v 546从节点 1到节点3的最短路 *************************起点 终点 距离 ---- ---- ---- 1 2 1 2 3 6此问题的解为:7 2、最小生成树电信公司要在15个城市之间铺设光缆，这些城市的位置及相互之间的铺设光缆的费用如下图所示。

试求出一个连接在15个城市的铺设方案，使得总费用最小。

v 1v 2v 3v 4v 5v 6v 7v 8v 9v 10v 11v 12v 13v 14v 152241131456422323135134此问题的最小生成树如下：*************************起点终点距离---- ---- ----1 4 11 2 22 5 25 8 15 6 26 3 18 7 28 9 39 12 212 11 411 10 110 13 313 14 114 15 3此问题的解为:283、最短路问题例. 求下图中从v1到各点的最短路，并指出有哪些点是不可达到的。

vv7v8v4从节点 1到节点2的最短路*************************起点终点距离---- ---- ---- 1 2 4此问题的解为:41到3没有路1到4没有路从节点 1到节点5的最短路*************************起点终点距离 ---- ---- ---- 1 5 1此问题的解为:1从节点 1到节点6的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 6此问题的解为:7从节点 1到节点7的最短路*************************起点终点距离 ---- ---- ---- 1 7 3此问题的解为:3从节点 1到节点8的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 66 8 3此问题的解为:104、最短路问题有6个村庄，各村庄的距离如下图所示。

2012年9月份考试运筹学第一次作业一、单项选择题（本大题共100分，共40 小题，每小题 2.5 分）1. 一个无(C )、但允许多重边的图称为多重图。

A. 边B. 弧C. 环D. 路2. 运筹学是一门( C )。

A. 决策科学B. 数学科学C. 应用科学D. 逻辑科学3. 基可行解对应的基，称为(B)。

A. 最优基B. 可行基C. 最优可行基D. 极值基4. 运筹学用(D.)来描述问题。

A. 拓补语言B. 计算机语言C. 机器语言D. 数学语言5. 隐枚举法是省去若干目标函数不占优势的(A )的一种检验过程。

A. 基本可行解B. 最优解C. 基本解D. 可行解6. 对偶问题与原问题研究出自(D )目的。

A. 不同B. 相似C. 相反D. 同一7. 资源价格大于影子价格时，应该( A )该资源。

A. 买入B. 卖出C. 保持现状D. 借贷出8. 敏感性分析假定(D)不变，分析参数的波动对最优解有什么影响。

A. 可行基B. 基本基C. 非可行基D. 最优基9. 从系统工程或管理信息预测决辅助系统的角度来看，管理科学与(C)就其功能而言是等同或近似的。

A. 统计学B. 计算机辅助科学C. 运筹学D. 人工智能科学10. 闭回路的特点不包括( D )。

A. 每个顶点都是直角B. 每行或每列有且仅有两个顶点C. 每个顶点的连线都是水平的或是垂直的D. 起点终点可以不同11. 运输问题分布m*n矩阵表的横向约束为(A)。

A. 供给约束B. 需求约束C. 以上两者都有可能D. 超额约束12. 动态规划综合了( D)和“最优化原理”。

A. 一次决策方法B. 二次决策方法C. 系统决策方法D. 分级决策方法13. 线性规划问题不包括(C)。

A. 资源优化配置B. 复杂系统结构性调整C. 混沌系统分析D. 宏、微观经济系统优化14. 运输问题分布m*n矩阵表的纵向约束为(B)。

A. 供给约束B. 需求约束C. 以上两者都有可D. 超额约束15. 路的第一个点和最后一个点相同，称为(C )。