当前位置：文档之家 › 信号与系统作业作业1第二章答案

信号与系统作业作业1第二章答案

  • 格式：doc
  • 大小：261.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

信号与系统课后题解第二章

信号与系统课后题解第二章

⑺
对⑺式求一阶导，有：
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中，有：
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ，则有：
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为：
由联立方程可得 故系统的零输入响应为：
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
（2）由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )

信号与系统 陈后金 第二版 课后习题答案(完整版)

信号与系统 陈后金 第二版 课后习题答案(完整版)

（1） f (t) = 3sin 2t + 6 sinπ t
（2） f (t) = (a sin t) 2
（8）
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解：（1）因为 sin 2t 的周期为π ，而 sin πt 的周期为 2 。
显然，使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示，绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
（3） f (5 − 3t) （7） f ′(t) 解：（3）将 f (t) 表示成如下的数学表达式
（5） f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
（7）方法 1：几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变，所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理，在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号（方向向下，因为是负跳变），而在 0 < t < 2 的区间内有 f ′(t) = −0.5 （由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》（陈后金等编）作业参考解答
（2）显然，该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )

信号与系统 于敏慧(第二版)第二周作业答案

信号与系统 于敏慧(第二版)第二周作业答案

y0(t)
1
t
0
2
4
(6) x(t) = dx0 (t) , h(t) = dh0 (t) 。
dt
dt
x(t) * h(t) = dx0 (t) * dh0 (t) = d 2 y0 (t)
dt dt
dt 2
x(t) ∗ h(t) = 0.5δ(t) − 0.5δ(t − 2)
2.10 求 y[n] = x1[n]* x2[n]* x3[n] 。 其 中 x1[n] = (0.5)n u[n] ， x2[n] = u[n + 3] 和
（2）利用（1）的结果，求系统的逆系统的单位样值（脉冲）响应。
（3）利用（2）的结果，结合卷积性质，求一信号 x[n]，使之满足
x[n]* h[n] = 2n (u[n] − u[n − 4])
解：（1） h[n] − Ah[n −1] = δ [n]，其中 h[n] = (1 )n u[n] ， 2
（通项： an = a1q n−1 ）
n
∑ 此题： a1 = 1, q = 2 ； x[n]* h[n] = 2nu[n]*u[n] = ( 2k )u[n] = (2n+1 −1)u[n] k =0
2.6 计算图 2-45（b）与（c）所示信号 x(n)与 h(n)的卷积和,注意：N＝4。 解：（b）利用脉冲信号δ(n)的卷积性质以及卷积的延时性质计算：
k =−∞
+ 3] =
u[n + 3] 0.5k
k =0
；
= 2(1 − 0.5n+4 )u[n + 3]
（2） x1[n]* x2[n]* x3[n] = 2(1 − 0.5n+4 )u[n + 3]* (δ [n] − δ [n −1]) ； = 2(1 − 0.5n+4 )u[n + 3] − 2(1 − 0.5n+3 )u[n + 2]

信号与系统作业任务作业任务1(第二章)答案解析

信号与系统作业任务作业任务1(第二章)答案解析

第二章作业答案2 - 已知描述某LTI 连续系统的微分方程和系统的初始状态如下, 此系统的零输入响应(1)y (t) 3y(t) 2y(t) 2e(t) e(t)y(0 ) 2，y(0 ) 1解：y (0 ) y(0 ) 1。

解:23 2 0( 1)( 2) 0所以, 其特征根为：i2, 21所以, 零输入响应可设为：y zi (t)C 1e 2tC 2e ty(° ) C i C 22C 1 1又因为y (0 ) 2C iC 21C 2 3所以,y zi (t) 3e t e 2tt根据微分方程, 可知 特征方程为:t 0试求(2)y (t) 5y (t) 6y(t) e(t) 2e(t)根据微分方程，可知特征方程为:(2)( 3) 0所以，其特征根为：i 2 , 2 3所以，零输入响应可设为：y zi(t) C1e 2t C2e 3t t 0”y(0 ) C i C2 1 C1 4又因为y (0 ) 2C i 3C2 1 C2 3所以，y zi (t) 4e 2t 3e 3t t 0某LTI连续系统的微分方程为y (t) 3y(t) 2y(t) e (t)3e(t) 已知y(0 ) 1，y(0 ) 2，试求:(1)系统的零输入响应y zi(t)；(2)输入e(t) (t)时，系统的零状态响应y zs(t)和全响应y(t)解：(1 )根据微分方程，可知特征方程为：2 3 2 0 ( 1)( 2) 0所以，其特征根为： 1 2, 2 1所以，零输入响应可设为：y zi (t) C1e 2t C2e t t 0y(0 ) C i C 2 1 y (0 ) 2C i C 2 2所以，yd)4e ' 3e 2t t 0C i 3C 2 4(2) 可设零状态响应为:y zs (t) C xi e 2t C x2e t p其中p 为特解，由激励信号和系统方程确定。

因为e(t) (t)所以，p 为常数，根据系统方程可知，p 于是，零状态响应可设为为：y zs (t)C xi e” C x2e t 3 232。

信号与系统第一章习题及作业(1,2)

信号与系统第一章习题及作业(1,2)
m=0
(2)（余弦序列是否为周期信号，取决于2л/Ω0是正整 （余弦序列是否为周期信号，取决于 Ω 有理数还是无理数。） 数、有理数还是无理数。） 因此， 因此， 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7； 所以基波周期为N=7； N=7
因为2л/Ω =16л 为无理数， (4) 因为 Ω0=16л,为无理数，则此信号不是周期 信号． 信号． (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统？为什么？ 、判断是否为线性系统？为什么？
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的？非时变的？因果的？ 试确定系统是否为线性的？非时变的？因果的？
解：积分系统是线性的，因此系统是线性系统。 积分系统是线性的，因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )

信号与系统(杨晓非)1,2,3章习题答案

信号与系统(杨晓非)1,2,3章习题答案
(5)f (t ) sin(t )2 为周期信号，周期为 ( s ). 6 8 (6) f (k ) ( ) 7 8 2 2 7 8 4 7 f (k )为周期序列，N 7. 1.3. (1) f (t ) 6 6e j (2) f (t ) 2 2e






e (e e lim (2 j ) 2 0
j 2t

2 t
j 2t
)
1 dt ( ) lim e2t (e j 4t e j 4t 2)dt 4 0

1 ( ) lim [e (2 j 4)t e (2 j 4)t ]dt 4 0


2
4s
6s 3 T ' mT1 12 s T 5 12 60 s f (t )为周期信号，周期为60s.
(3) f (t ) 3e t sin(3t ) 3e t Im[e j (3t ) ] 3e t cos(3t ) 2 (4) f (t ) je( j100t 2) e 2 e( j100t 2) e 2e Re[ f (t )] e 2 cos(100t ) 2
0 0
10
10
(7) sin ( 5) d sin 5 (t 5)
0 t
t
(8) ( 2 1) ( ) d ( 2 1)2 ( ) d 2 (t ) 2
10 1 (9) (2t 2 t 5) (t )dt [2t 2 t 5] 10 4 t t t 1 4
(2)显然f (t ) | cos(2t ) | 为周期信号 (3) f (t ) 3e j (2t 45 )为周期信号

《信号与系统》第二章作业题答案

《信号与系统》第二章作业题答案

第二章 连续时间系统的时域分析1．与()t δ相等的表达式为：A ．1()4t δ B ．2(2)t δ C ．(2)t δ D ．1(2)2t δ解：由()t δ函数的性质1()()t t δαδα=可得，选B2．()j tet dt ωδ∞--∞'=⎰。

解：运用性质0()()()(0)t f t t dt f t f δ∞=-∞'''=-≡-⎰，得到()()j tet dt j j ωδωω∞--∞'=--=⎰。

3．两个线性时不变系统的级联，其总的输入-输出关系与它们在级联中的次序没有关系。

（正确）解：以冲击响应为例。

因为级联时，系统总的冲击响应等于各子系统冲击响应的卷积，而卷积与顺序没有关系，所以冲击响应与子系统顺序没有关系。

4．若()()()y t x t h t =*，则()()()y t x t h t -=-*-。

（错误）解：由()()()y t x h t d τττ∞-∞=-⎰，得()()()y t x h t d τττ∞-∞-=--⎰。

而()()()()()x t h t x h t d y t τττ∞-∞-*-=--+≠-⎰5．已知(21)f t -+波形如图所示，试画出()f t 的波形。

解：根据1反2展36．用图解法求图中信号的卷积()()()t f t f t f 21*=。

（03北邮A,8分）解：当10t -<时，即1t <时，由图1所示，12()()*()0f t f t f t ==图1当1020t t ->⎧⎨-<⎩时，即12t <<时，由图2所示，11201()()*()sin()[cos()1]t f t f t f t d t πττππ-===+⎰图2当1220t t -<⎧⎨->⎩时，即23t <<时，由图3所示，11222()()*()sin()cos()t t f t f t f t d t πττππ--===⎰图3当1222t t ->⎧⎨-<⎩时，即34t <<时，由图4所示，21221()()*()sin()[cos()1]t f t f t f t d t πττππ-===-⎰图4当4t >时，如图5所示，12()()*()0f t f t f t ==图57．如图所示系统由几个子系统组成，各子系统的冲激响应为)()(1t u t h =，)1()(2-=t t h δ，)()(3t t h δ-=，试求此系统的冲激响应)(t h ；若以()()t u e t e t -=作为激励信号，用时域卷积法求系统的零状态响应。

信号与系统课后答案(第二版)+曾禹村+第二章作业参考答案

信号与系统课后答案(第二版)+曾禹村+第二章作业参考答案

i1(t) = i2 (t) + i3 (t) , i2 (t) R2 − L 有 8i2 `(t) + 3i2 (t) = 2e`(t) ˆ ˆ 由 h`(t) + 3h(t) = 2δ (t)
0
h
(−1) t 3
T
t
t 3E − τ E (t) = ∫ δ (τ )dτ − ∫ e 8 u(τ )dτ −∞ 4 −∞ 32
x(t)
1
2 t
yx(t)
1 2 3 4 t
0
1
0
Qh(0) = 0, t ≤ 0, 有 0 ≤ t <1 , h(t) + h(t −1) + h(t − 2) = h(t) = t 时 1≤ t < 2时 h(t) + h(t −1) + h(t − 2) = h(t) + h(t −1) =1 , h(t) =1− h(t −1) =1− (t −1) = 2 −t 2 ≤ t < 3 , h(t) + h(t −1) + h(t − 2) =1 时 h(t) =1− h(t −1) − h(t − 2) =1− (2 − (t −1)) − (t − 2) = 0 3 ≤ t < 4时 h(t) = 4 − t − h(t −1) − h(t − 2) =4 −t − 0 − (2 − (t − 2)) = 0 , t, 0 ≤ t < 1 ∴h(t) = 2 − t, 1 ≤ t ≤ 2 0, t < 0,2 < t
解: (e) 特征方程为 λ2+4λ+4=0 得 λ1=-2， λ2=-2。 则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 3 t+ c2e-2 t)u(t) h`(t)= (c1+ c2)δ(t)+(-3c1e- 3 t-2c2e- 2t)u(t) h``(t)= (c1+ c2)δ`(t)+(-3c1-2c2) δ(t)+ (9c1e- 3 t+4c2e- 2t)u(t) 将x(t)= δ(t), y(t)=h(t)代入原方程得：

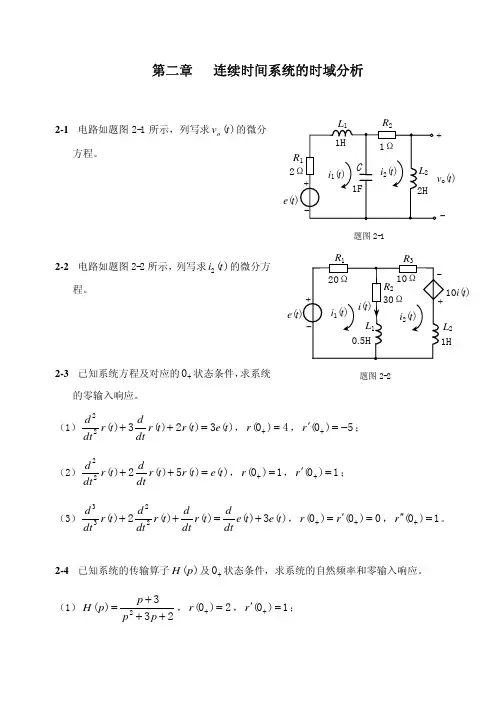
信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布

信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布

2-16 已知 f1 (t ) =
画出下列各卷积的波形。 （1） s1 (t ) = f1 (t ) ∗ f 2 (t ) ； （2） s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ； （3） s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示，列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示， 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) ， 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统，其初始状态一定，当输入 e1 (t ) = δ (t ) 时，其全响应
r1 (t ) = −3e − tU (t ) ； 当 输 入 e2 (t ) = U (t ) 时 ， 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ，其中 f1 (t ) = sgn(t − 1) ， f 2 (t ) = e 2-15 求下列卷积 （1） f1 (t ) = e

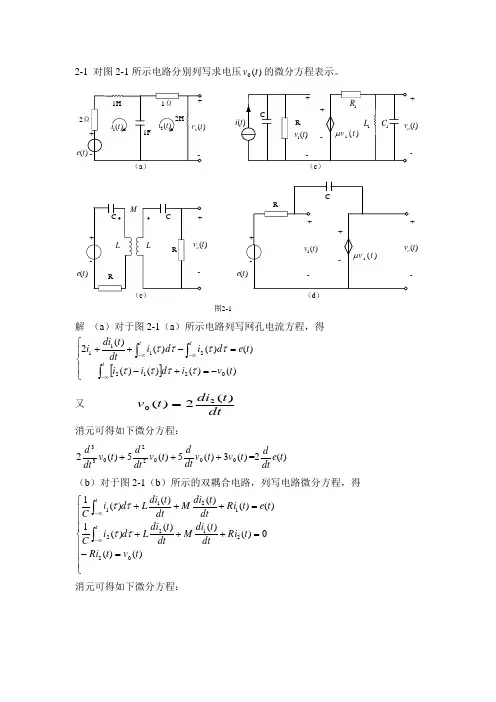
信号与系统课后习题与解答第二章

信号与系统课后习题与解答第二章

2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。

2(t ei )(t +-(e )(e )(t +-图2-1解 （a ）对于图2-1（a ）所示电路列写网孔电流方程，得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程：)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d（b ）对于图2-1（b ）所示的双耦合电路，列写电路微分方程，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程：)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- （c ）对于图2-1（c ）所示电路列写电路方程，得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程：)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ （d ）对图2-1（d ）所示电路列写电路方程，电流)(t i 如图2-2所示，得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程：(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。

信号与系统课后答案 第2章 习题解

信号与系统课后答案 第2章 习题解

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应（1）0)(2)(3)(22=++t y t y dt d t y dt d ；给定：2)0(,3)0(==--y dt dy ； （2）0)(4)(22=+t y t y dt d ；给定：1)0(,1)0(==--y dtd y ；（3）0)(2)(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dt dy ； （4）0)()(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy ； （5）0)()(2)(2233=++t y dt d t y dt d t y dt d ；给定：2)0(,1)0(,1)0(22===---y dt d y dt d y 。

（6）0)(4)(22=+t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy 。

解：（1）微分方程的特征方程为：2320λλ++=，解得特征根：121, 2.λλ=-=- 因此该方程的齐次解为：2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.（2）微分方程的特征方程为：240λ+=，解得特征根：1,22i λ=±.因此该方程的齐次解为：()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.（3）微分方程的特征方程为：2220λλ++=，解得特征根:1,21i λ=-± 因此该方程的齐次解为：()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.（4）微分方程的特征方程为：2210λλ++=，解得二重根:1,21λ=-.因此该方程的齐次解为：()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.（5）微分方程的特征方程为：3220λλλ++=，解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为：()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.（6）微分方程的特征方程为：240λλ+=，解得特征根:120,4λλ==-. 因此该方程的齐次解为：4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号，求系统的零状态响应。

2信号与系统-每章课后答案第二章作业PPT课件

2信号与系统-每章课后答案第二章作业PPT课件

21.11.2020
7
2.7 写出下列信பைடு நூலகம்的波形图。
(a)f(t)u(4t2)
( b ) f( t ) ( t 2 ) 3 ( t 2 ) 2 ( t )
(c) f (t) (34t) 1 (t - 3)
-4 4
1(t - 3)
44
21.11.2020
8
2.8 设 f (t) 在 t 0 及 t 8 时 f(t)， 0 ， f(0 )且 4 ；已知 f(t)f(2t) 的波形如图所示，试确定 f (t) 的波形。
请对以下连续时间系统确定哪些性质成立、哪些不成立，
并陈述你的理由。下列中 y(t) 和 x (t ) 分别记作系统的输出和
输入。
（a）y(t) dx(t) dt
时不变、线性、因果、 稳定
（ b） y(t)co3t)sx((t) 时变、线性、因果、稳 定
（c）y(t) 2t x()d
（d）y(t) x(t ) 3
的波形。
21.11.2020
6
2.6 写出信号 f1(t) 和 f2 (t) 的表达式。
f1(t)u(t)u(t2) f 2 ( t ) - u ( t 1 ) ( t 1 ) u ( t 1 ) ( t 1 ) u ( t 1 ) 2 u ( t 1 ) u ( t 2 )
- 0(t)3(t)d t-3
（3）4(t-5)(t)dt4(t5 )22(t)d t4(-1 -)4
-3
2
-3
（ 4）(t2t2)(2t)dt(t2t2)1(t)d t121
-
-
2
2
（5）t (t2)(t2)dt4t (t2)d t4u(t2)

信号与系统第二章答案

信号与系统第二章答案
令
f (n ) x (n ) y ( n) ，欲使 f (n ) 是周期的，必须有 N 0 kN1 mN 2
(h)
(i)
(j)
x (n ) 2 cos( n / 4) sin( n / 8) 2 sin( n / 2 / 6) x (t ) 2 cos(3t / 4) ，周期信号， T
2 3
。
解：(a)
(b)
x (n ) cos(8 n / 7 2) ，周期信号， Q 0 x (t ) e j ( t 1) ，周期信号， T 2 。
(c)
(a)
h (t 3)
(b)
h (1 2t )
(3) 根据图 P2.1(a) 和(b) 所示的
x (t ) 和 h (t ) ，画出下列各信号的波形图，并加以标注。
(b)
(a)
x(t )h(t )
x(1 t )h(t 1)
(c)
t x (2 )h (t 4) 2
图 P2.1 解：(1) 各信号波形如下图所示：

(d)
x (n ) e j (n / 8 )
(e)
x (n ) (n 3m ) (n 1 3m)
m 0
(f)
x (t ) cos 2 t u (t ) x (t ) Ev cos 2 t u (t )
(g)
x (n ) cos( n / 4) cos( n / 4) x (t ) Ev cos(2 t / 4) u (t )
(b) 不正确。设
x (n ) g (n ) h (n ) ，其中 g ( n) sin
n ，对所有 n ， 4

信号与系统课后习题答案汇总

信号与系统课后习题答案汇总

可编辑第一章习题参考解答1.1 绘出下列函数波形草图。

(1) ||3)(t e t x -= (2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t t x επ= (5) )]4()([4cos )(--=-t t t e t x t εεπ (7) t t t t x 2cos )]2()([)(πδδ--= (9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dt d t x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=t d t x ττδ)1()((14) )()(n n n x --=ε 1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。

(1) ||3)(t e t x -=解 能量有限信号。

信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。

信号能量为：(3) t t x π2sin )(=解 功率有限信号。

周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。

(4) n n x 4sin )(π=解 功率有限信号。

n 4sinπ是周期序列，周期为8。

(5) )(2sin )(t t t x επ= 解 功率有限信号。

由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。

如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。

(6) )(4sin )(n n n x επ=解 功率有限信号。

由题(4)知，在),(∞-∞区间上n 4sinπ的功率为1/2，因此)(4sin n n επ在),(∞-∞区间上的功率为1/4。

信号与系统第二版课后答案

信号与系统第二版课后答案
所以阶跃响应
4-4如题图4-4所示是一个实际的信号加工系统，试写出系统的频率特性H(j)。
题4-4图
解由图可知输出
取上式的傅氏变换，得
故频率特性
4-5设信号f(t)为包含0 ~m分量的频带有限信号，试确定f( 3t)的奈奎斯特采样频率。
解由尺度特性，有
即f( 3t)的带宽比f(t)增加了3倍，即=3m。从而最低的抽样频率s=6m。故采样周期和采样频率分别为
解设T为系统的运算子，则可以表示为：
不失一般性，设f(t) =f1(t) +f2(t)，则
；
故有
显然
即不满足可加性，故为非线性时不变系统。
1-6判断下列方程所表示的系统的性质。
(1) (2)
(3) (4)
解(1)线性；(2)线性时不变；(3)线性时变；(4)非线性时不变。
1-7试证明方程 所描述的系统为线性系统。式中a为常量。
读者也可以用图形扫描法计算之。结果见点，则
f1(t) *f2(t) =f1(t) *[(t)+(t2)+(t+ 2)]
=f1(t)+f1(t2)+f1(t+ 2)
结果见图p2-10(b)所示。
图p2-10
2-11试求下列卷积。
(a)
(b)
解(a)因为 ，故
试证明：
(1)
(2)利用(1)的结果，证明阶跃响应
证（1）因为
y(t)=f(t)h(t)
由微分性质，有
y(t)=f(t)h(t)
再由积分性质，有
（2）因为
s(t)=(t)h(t)
由（1）的结果，得
3-1求题3-1图所示周期信号的三角形式的傅里叶级数表示式。

[信号与系统作业解答]第二章

[信号与系统作业解答]第二章
rzi(t) 3rzi(t) 2rzi(t) 0 rzi(0 ) rzi(0 ) 2 rzi(0 ) rzi(0 ) 1
特征方程为 2 3 2 0 ，特征根为 1
1和 2
2。
所以rzi(t) C1e t C2e 2t, t 0
将 rzi(0 ) r (0 ) 2 和rzi(0 ) r(0 ) 1代入可求得
g(t) 1 e 12t cos 3 t 2
1 e 12t sin 3 t u(t)
3
2
由于系统的冲激响应h(t) h(t) e 12t cos 3 t
2
d g(t) ，所以系统的冲激响应为 dt
1 e 12t sin 3 t u(t)
3
2
3）系统的冲激响应满足方程
d dt
h(t)
2h(t)
(t) 3 (t)
电容两端电压不会发生跳变，vc(0 ) vc(0 ) 10V ，所以i(0 ) 0 ；
因此，电阻两端无电压，电感两端电压变成 10V，所以i (0 ) 10 。
（2）换路后系统的微分方程为
i (t) i (t) i(t) e (t) e(t) 20u(t)
t 0 时间内描述系统的微分方程为
i (t) i (t) i(t) 20 (t)
e(t) (1) 0 (2)
整理得：
2vo(t) 5vo(t) 5vo(t) 3vo(t) 2e (t)
2-4 已知系统相应的齐次方程及其对应的 0+状态条件，求系统的零输入响应。
1）
d2 dt 2
r(t)
2
d dt
r(t
)
2r(t)
0 ，给定r(0 )
1 ，r (0 )
2

信号与系统课后习题参考答案

信号与系统课后习题参考答案

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号？题图1-11-2试写出题1-1图中信号得函数表达式。

1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。

题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。

⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。

1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。

题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。

试做出当输⼊为时,响应得波形图。

题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。

题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。

⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。

第⼆章习题2-1试计算下列各对信号得卷积积分:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。

题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。

题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。

已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。

2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。

信号与系统课后答案

信号与系统课后答案

与奇分量的波形，相应如图题 1.12 中所示。
1-13 已知信号 f(t)的偶分量 fe(t)的波形如图题 1-13(a)所示， 信号 f(t+1)×U(-t-1)的波形如图题 1-13(b) 所示。求 f(t)的奇分量 fo(t)，并画出 fo(t)的波形。
解 因
f (t ) = f e (t ) + f 0 (t )
∫
t
−∞
δ (τ )dτ ，故根据现行系统的积分性有
y (t ) = ∫ h(τ (dτ = ∫ [δ (τ ) − δ (τ − 1) − δ (τ − 2) + δ (τ − 3)]dτ = u (t ) − u (t − 1) − u (t − 2) + u (t − 3)
1-2 已知各信号的波形如图题 1-2 所示，试写出它们各自的函数式。
解： f 1 (t ) = t[u (t ) − u (t − 1)] + u (t − 1)
f 2 (t ) = −(t − 1)[u (t ) − u(t − 1)]
f 3 (t ) = (t − 2)[u(t − 2) − u(t − 3)]
y 2 (t ) 的波形如图题 1.17(c)所示.
1-18 图题 1-18(a)所示为线性时不变系统，已知 h1(t)=δ(t)-δ(t-1), h2(t)=δ(t-2)-δ(t-3)。（1）求响 应 h(t)； （2） 求当 f(t)=U(t)时的响应 y(t)（见图题 1-18(b))。
解（1） h(t ) = h1 (t ) − h2 (t ) = δ (t ) − δ (t − 1) − δ (t − 2) + δ (t − 3) (2) 因 f (t ) = u (t ) =

信号与系统课后答案2

信号与系统课后答案2

A1e −2t
+
2 A2e−8t
故有
uc (0+ ) = A1 + A2 = 6
i(0+ )
=
1 2
A1
+
2 A2
=
0
联解得 A1-=8,A2=-2。故得
uc (t) = 8e−2t − 2e−8t V t ≥ 0
又得
i(t) = −C duc = 4e−2t − 4e−8t A t ≥ 0 dt
1 1
+
p u2 (t)
=
0
即
1 3
p
+ 1u1 (t )
− u2 (t)
=
pf
(t)
( ) − u1(t) + p2 + p +1 u2 (t) = 0
联解得
u2 (t) =
p2
3 + 4p + 4
f (t) =
H ( p) f (t)
故得转移算子为
H（p) =
u2 (t) f (t)
=
p2
3 + 4p + 4
f1(t −1) − f1(t − 2) + f1(t − 3)
y2(t)的波形如图题 2.10(d)所示 2-11．
d f (t)
试证明线性时不变系统的微分性质与积分性质，即若激励 f(t)产生的响应为 y(t)，则激励 dt
产生
∫ ∫ d
的响应为 dt
y(t)
（微分性质），激励
t −∞
f (τ )dτ
故得
3 3
进一步又可求得 uc(t)为
uc
(t )

2014北航《信号与系统》在线作业一答案

2014北航《信号与系统》在线作业一答案

6. 已知f(t)，为求f(t0-at) 则下列运算错误的是（其中 t0， a 为正数） ________。
A. f(-at)左移t0
B. f(-at)右移t0
C. f(at)左移t0
D. f(at)右移t0
正确答案：ACD
7. 偶周期信号的傅氏级数中只有________。
A. 直流项
B. H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应
C. H(z)在单位圆上的高阶极点或单位圆外的极点，其所对应的响应序列都是递增的。即当k→∞时，响应均趋于∞
D. H(z)的零点在单位圆内所对应的响应序列为衰减的。即当k→∞时，响应均趋于0
正确答案：ABC
2. 符合帕什瓦尔定理的描述是 ________。
B. 余弦分量
C. 奇次谐波分量
D. 偶次谐波分量
正确答案：ABD
5. 若f(t)为实信号，下列说法中正确的是 ________。
A. 该信号的幅度谱为偶对称
B. 该信号的相位谱为奇对称
C. 该信号的频谱为实偶信号
D. 该信号的频谱的实部为偶函数，虚部为奇函数
正确答案：ABD
A. 错误
B. 正确
正确答案：A
9. 一个系统的零状态响应就等于它的自由响应。
A. 错误
B. 正确
正确答案：A
10. 奇函数加上直流后，傅氏级数中仍含有正弦分量。
A. 错误
B. 正确
正确答案：B
A. 错误
B. 正确
正确答案：B
2. 单位阶跃响应的拉氏变换称为系统函数。
A. 错误
B. 正确
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章 作业答案
2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下，试求此系统的零输入响应。

(１))()(2)(2)(3)(t e t e t y t y t y +'=+'+'' 2)0(=-y ，1)0(-='-y
解:
根据微分方程,可知特征方程为:
0)2)(1(0232=++⇒=++λλλλ
所以，其特征根为： 1,
221-=-=λλ
所以,零输入响应可设为:0)(221≥+=--t e C e C t y t
t
zi
又因为 ⎩⎨⎧=-=⇒⎩⎨
⎧-=--='=+=--31
12)0(2)0(2
1
2121C C C C y C C y 所以,03)(2≥-=--t e e t y t
t
zi
(2))(2)()(6)(5)(t e t e t y t y t y -'=+'+'' ﻩ1)0()0(=='--y y 。

解:
根据微分方程，可知特征方程为：
0)3)(2(0652=++⇒=++λλλλ
所以，其特征根为： 3,
221-=-=λλ
所以,零输入响应可设为:0)(3221≥+=--t e C e
C t y t
t
zi
又因为 ⎩⎨⎧-==⇒⎩⎨
⎧=--='=+=--3
4
132)0(1)0(21
2121C C C C y C C y 所以,034)(32≥-=--t e
e t y t
t zi
2–２ 某L ＴI 连续系统的微分方程为)(3)()(2)(3)(t e t e t y t y t y +'=+'+'' 已知1)0(=-y ,2)0(='-y ,试求： （1） 系统的零输入响应)(t y zi ;
（2） 输入)()(t t e ε=时，系统的零状态响应)(t y zs 和全响应)(t y 。

解：
（1）根据微分方程,可知特征方程为：
0)2)(1(0232=++⇒=++λλλλ
所以，其特征根为: 1,
221-=-=λλ
所以，零输入响应可设为：0)(221≥+=--t e C e C t y t
t
zi
又因为 ⎩⎨⎧=-=⇒⎩⎨
⎧=--='=+=--43
22)0(1)0(2
12121C C C C y C C y
所以,034)(2≥-=--t e e
t y t
t
zi ﻩ
（2) 可设零状态响应为:0)(221>++=--t p
e C e
C t y t x t
x zs
其中p 为特解，由激励信号和系统方程确定。

因为)()(t t e ε= 所以，p 为常数,根据系统方程可知，23=p 。

于是，零状态响应可设为为：02
3)(221>++=--t e C e C t y t x t x zs
将上式代入原方程中,比较方程两边的系数，可得到
⎪⎩⎪⎨⎧-==
2
2121C C 所以,02322
1)(2>+-=
--t e e t y t t
zs
全响应为 )()()(t y t y t y zs zi +=
0)
23221
()34()(22>+-+-=----t e e e e t y t t t t zs
0)
232
5
2()(2>+-=--t e e t y t t zs
２–3 试求下列各ＬＴI 系统的冲激响应和阶跃响应。

（１）)(2)()(3)(4)(t e t e t y t y t y +'=+'+'' 解：
根据 在激励信号为)(t δ的条件下,求解系统的零状态响应可得
()
)(2
1)(3t e e t h t t
ε⋅+=
-- 因为，单位阶跃响应⎰-
⋅=t
d h t g 0)()(ττ
所以，()
⎰
-⋅+=--t
d e e t g 032
1)(τττ
0),1(6
1
)1(216
12
16030>-+-=
--=-----
-
t e e e e t t t t ττ
0,6
121326>--=
--t e e t
t
(２）)(2)(2)()(2)(3)("t e t e t e t y t y t y +'+''=+'+ 解:
可先求系统 )()(2)(3)("t e t y t y t y =+'+ 的冲激励响应)(0t h ，
则，原系统的冲激响应为)(2)(2)()(0'0"0
t h t h t h t h ++=。

因为)()(2)(3)("t e t y t y t y =+'+的特征根为:1,221-=-=λλ 所以,可设冲激响应为:)()()(2210t e C e C t h t t ε⋅+=-- 将)(0t h 代入系统方程,并确定待定系数后,可得:
)()()(20t e e t h t t ε⋅-=--ﻩ
因为，)(2)(2)()(0'
0"0
t h t h t h t h ++= 又因为，)()2()(2'0
t e e t h t t ε⋅-=--,)()4()()(2"0t e e t t h t t εδ⋅--=-- 所
以,[]
)()(2)()2(2)()4()()(222t e e t e e t e e t t h t t t t t t εεεδ⋅-⋅+⋅-⋅+⋅--=------
)()2()(2t e e t t t εδ⋅--=--
因为,单位阶跃响应⎰-
⋅=t
d h t g 0)()(ττ
所以,[]
⎰-
⋅--=--t
t t d t e e t t g 02)()(2)()(τεδ
()
)(212t e e t t ε⋅-+=--
2–4 各信号的波形如题2–4图所示，试计算下列卷积,并画出其波形。

(1）)()(21t f t f *
（2))()(31t f t f *
(3))()(24t f t f *ﻩ（４）)()(34t f t f *
题２–4 图
解:
根据 )()()(00t t f t t t f -=-*δ,可方便地得到此题的卷积结果。

（１)
(2）
(3）
(4）
2–5 已知某LTI 连续系统的冲激响应)(t h 和各激励信号)(t e 的波形如题2–5图所示，试求此系统对激励信号的零状态响应。

题2–５图
解:
因为，)()()(t h t e t y zs *=
所以,[][])2()()2()()(--*--=t t t t t y zs εεεε
)2()2()2()()()2()()(-*-+-*-*--*=t t t t t t t t εεεεεεεε )4()4()2()2(2)(--+---=t t t t t t εεε
2–６ 题2–6图所示系统是由几个子系统组合而成的,各子系统的冲激响应分别为
)()(1t t h ε=，)1()(2-=t t h δ，)1()(3-=t t h ε
试求总系统的冲激响应)(t h 并画出其波形。

题2–6图
解： 根据系统框图,可得： [])()()()()(1321t h t h t h t h t h **+=
[])()1()1()(t t t t εεδε*-*--= [])()2()(t t t εεε*--=
)2()2()(-⋅--=t t t t εε
此系统的单位冲激响应的波形为:
2–7 题2–7图所示系统是由几个子系统组合而成,各子系统的冲激响应分别为
)1()(1-=t t h δ,)3()1()(2---=t t t h εε
试求总系统的冲激响应)(t h 并画出其波形。

题2–7图
解:根据系统框图,可得:
[])()()()()()(2111t h t h t h t h t t h **++=δ
[][])3()1()1()1()1()(---*-*-+-+=t t t t t t εεδδδδ [][])3()1()2()1()(---*-+-+=t t t t t εεδδδ
[][][])5()3()4()2()3()1(---+---+---=t t t t t t εεεεεε
)5()4()2()1(-----+-=t t t t εεεε 此系统的单位冲激响应的波形为:。