某工程的温度应力计算

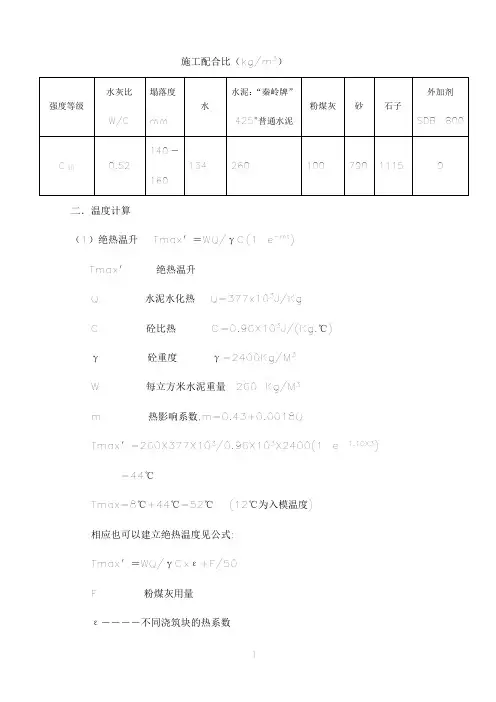
施工配合比（kg/m3）二．温度计算（1）绝热温升Tmax′＝WQ/γC(1-e-mt) Tmax′---绝热温升Q-----水泥水化热Q=377x103J/KgC-----砼比热C=0.96X103J/(Kg.℃)γ-----砼重度γ=2400Kg/M3W-----每立方米水泥重量260 Kg/M3m-----热影响系数,m=0.43+0.0018QTmax′=260X377X103/0.96X103X2400(1-e-1.10X3) =44℃Tmax=8℃+44℃=52℃(12℃为入模温度)相应也可以建立绝热温度见公式:Tmax′＝WQ/γCxε+F/50F-----粉煤灰用量ε――――不同浇筑块的热系数Tmax′＝260X377X103/Tmax=8+55=63℃取Tmax＝63℃三. 温应力计算1.将砼的收缩随时间的进程换算成当量温度计算：Ty(t)= εy(t)/αα=1x10-5砼线膨胀系数εy(t)=ε0M1M2M3······M10(1-e0.01t)Ty(t)------当量温度εy(t)----任意时间的收缩(mm/mm)M1-----水泥品种为普通水泥,取1.0M2-----水泥细度为4000孔，取1.35M3-----骨料为石灰石，取1.00M4-----水灰比为0.52,取1.64M5-----水泥浆量为0.2,取1.00M6------自然养护30天，取0.93M7------环境相对湿度为50%,取0.54M8------水里半径倒数为0.4,取1.2M9------机械振捣，取1.00M10------含筋率为8%,取0.9ε0--ε∞---最终收缩，在标准状态下ε0=3.24X10-4εy(30)=1.01x10-4Ty(30)=10.1℃εy(27)=0.92 x10-4Ty(27)=9.2℃εy(24)=0.83 x10-4Ty(24)=8.3℃εy(21)=0.73 x10-4 Ty(21)=7.3℃εy(18)=0.64 x10-4Ty(18)=6.4℃εy(15)=0.54 x10-4Ty(15)=5.4℃εy(12)=0.439 x10-4 Ty(12)=4.39℃εy(9)=0.335 x10-4 Ty(9)=3.35℃εy(6)=0.226 x10-4 Ty(6)=2.26℃εy(3)=0.114 x10-4 Ty(3)=1.14℃计算中心温度当量温差:△T6=2.26-1.14=1.12℃△T9=3.35-2.26=1.09℃△T12=4.39-3.35=1.04℃△T15=5.4-4.39=1.01℃△T18=6.4-5.4=1.0℃△T21=7.3-6.4=0.9℃△T24=8.3-7.3=1.0℃△T27=9.2-8.3=0.9℃△T30=10.1-9.2=0.9℃2.计算中心温度砼基础施工时处于散热条件，考虑上下表面及侧面的散热条件,当体积厚达3m时,,散热影响系数取0.97；当中心浇筑完第四天后，水化热达峰值。

混凝土温度应力计算方法混凝土浇筑后18d左右，水化热量值基本达到最大，所以计算此时温差和收缩差引起的温度应力。

1、混凝土收缩变形值计算Σy(t)=Σy0(1－e-0.01t)×M1×M2×M3×······×M10式中：Σy(t)——各龄期混凝土的收缩变形值Σy0——标准状态下混凝土最终收缩量，取值3.24×10-4 e——常数，为2.718t——从混凝土浇筑后至计算时的天数M 1、M2、M3······M10——考虑各种非标准条件的修正值，按《简明施工计算手册》表5-55取用，M1=1.0、M2=1.35、M3=1.0、M4=1.41、M5=1.0、M6=0.93，M7=0.77，M 8=1.4、M9=1.0，M10=0.9Σy(18)=3.24×10-4(1－2.718-0.01×18)×1×1.35×1×1.42×1×0.93×0.77×1.4×1×0.9=0.93×10-42、混凝土收缩当量温差计算Ty(t)=- Σy(t)/α式中：Ty(t)——各龄期混凝土收缩当量温差(℃)，负号表示降温。

Σy(t)——各龄期混凝土的收缩变形值α——混凝土的线膨胀系数，取1.0×10-5Ty(t)=-0.93×10-4/1.0×10-5=-9.3℃3、混凝土的最大综合温度差△T=T2＋2/3Tmax＋Ty(t)－Tn式中：△T ——混凝土的最大综合温度差（℃）T2——混凝土拌合经运输至浇筑完成时的温度（℃）Tmax——混凝土最高温开值（℃）Ty(t)——各龄期混凝土收缩当量温度（℃）Tn ——混凝土浇筑后达到稳定时的气温，取55℃△T=35.95+2/3×78.3+(-9.3)－35=43.85℃4、混凝土弹性模量计算E(t)=Ee(1－e-0.09t)式中：E(t)——混凝土从浇筑后至计算时的弹性模量（N/mm2）Ee——混凝土的最终弹性模量（N/mm2），可近视取28d的弹性模量。

一、温差效应理论1，局部温差不对整体结构产生影响，只考虑整体温差。

2，出现温差时梁板等水平构件变形受到竖向构件的约束而产生应力，同时竖向构件会受到相应的水平剪力。

3，使用阶段由于外围有幕墙，屋顶有保温，首层室外楼板也有覆土或其他面层，且室内有空调，常年的温度较为稳定，可不考虑使用阶段的温差效应，只考虑施工阶段的温差效应。

二、温差取值对于温差T1-T2，即施工阶段基准温度T1-施工后保温围护前的最低或最高温度T2：1，施工阶段最低或最高温度（T2）选取：A，对地下室构件，即使地下水位较高，回填土也会在地下室施工完成不久后封闭，温度变化对结构影响很小很缓慢，可考虑地区季节性平均温度变化（地下结构一般从设置后浇带、尽早回填等措施来降低温差的影响，一般不需要计算）。

B，对地上结构，可以认为完全暴露在室外。

可能达到的最低和最高温度可取当地最近十年的历史最低、最高气温（一般参考荷载规范里的基本气温数据，比如青岛地区为-9/33度）。

2，施工阶段基准温度（T1）选取：结构在后浇带合拢前各部分面积较小，温度效应可以忽略不计。

因此后浇带浇注时的温度作为温差效应里的基准温度T1。

当工程进展顺利，地上各层结构的合拢时间可以精确到季节甚至月份时候，这里的基准温度可取当季或当月的近十年平均气温。

当施工进度无法掌握时，基准温度可取近十年月平均气温值T1=（0.0+2.4+6.4+11.9+17.0+20.9+24.4+25.2+22.1+16.9+9.2+3.5）/12=13.3。

因此一般适当控制后浇带合拢温度时，基准温度T1可按15度进行计算：降温温差T1-T2=15-（-9）=24℃；当计算地上结构升温温差时，升温温差T1-T2=15-33=18℃。

只有当地上结构一层顶合拢日期距屋面合拢的日期超过一年时，最大负温差和最大正温差才会共存在一个工程中，因正温差主要产生压应力，所以温度效应仍是按最大负温差来控制。

探讨：对于有后浇带的工程，在满足至少两个月的条件下是否可将后浇带浇注时间限定在温度较低的月份，至少避开最高的月份夜间浇筑，这样计算最大负温差时的基准温度（T1）会降低，相应最大负温差也会减小。

温度应力计算第四节温度应力计算一、温度对结构的影响1 温度影响（1）年温差影响指气温随季节发生周期性变化时对结构物所引起的作用。

假定温度沿结构截面高度方向以均值变化。

则12t t t -=?12t t t -=?该温差对结构的影响表现为：对无水平约束的结构，只引起结构纵向均匀伸缩；对有水平约束的结构，不仅引起结构纵向均匀伸缩，还将引起结构内温度次内力；（2）局部温差影响指日照温差或混凝土水化热等影响。

A ：混凝土水化热主要在施工过程中发生的。

混凝土水化热处理不好，易导致混凝土早期裂缝。

在大体积混凝土施工时，混凝土水化热的问题很突出，必须采取措施控制过高的温度。

如埋入水管散热等。

B ：日照温差是在结构运营期间发生的。

日照温差是通过各种不同的传热方式在结构内部形成瞬时的温度场。

桥梁结构为空间结构，所以温度场是三维方向和时间的函数，即：),,,(t z y x f T i =该类三维温度场问题较为复杂。

在桥梁分析计算中常采用简化近似方法解决。

假定桥梁沿长度方向的温度变化为一致，则简化为二维温度场，即：),,(t z x f T i = 进一步假定截面沿横向或竖向的温度变化也为一致，则可简化为一维温度场。

如只考虑竖向温度变化的一维温度场为：),(t z f T i =我国桥梁设计规范对结构沿梁高方向的温度场规定了有如下几种型式：2 温度梯度f（z，t）（1）线性温度变化梁截面变形服从平截面假定。

对静定结构，只引起结构变形，不产生温度次内力；对超静定结构，不但引起结构变形，而且产生温度次内力；（2）非线性温度变化梁在挠曲变形时，截面上的纵向纤维因温差的伸缩受到约束，从而产。

生约束温度应力，称为温度自应力σ0s对静定结构，只产生截面的温度自应力；对超静定结构，不但产生截面的温度自应力，而且产生温度次应力；二、基本结构上温度自应力计算1 计算简图23 ε和χ的计算三、连续梁温度次内力及温度次应力计算采用结构力学中的力法求解。

工程的温度应力计算温度应力是指由于温度变化引起的物体内部的应力。

在工程领域中，温度应力的计算对于材料的选择、结构设计和工程的安全性评估都具有重要意义。

本文将介绍温度应力的计算方法以及常见的应用案例。

温度应力的计算方法主要有两种：线性热弹性法和非线性热塑性法。

线性热弹性法是一种基于线性弹性理论的计算方法，适用于温度变化幅度较小、材料线性弹性行为较好的情况。

该方法的基本步骤如下：1.确定温度应变：根据温度变化情况和材料的线膨胀系数，计算出温度应变。

2.确定材料的弹性模量：根据材料的力学特性和温度，选择适当的弹性模量。

3.计算温度应力：根据线性弹性理论，利用得到的温度应变和弹性模量，计算出温度应力。

非线性热塑性法是一种基于材料的非线性力学行为的计算方法，适用于温度变化幅度较大、材料非线性行为较明显的情况。

该方法的基本步骤如下：1.确定温度应变：根据温度变化情况和材料的热膨胀系数，计算出温度应变。

2.确定材料的本构关系：根据材料的热塑性行为，选择适当的本构关系。

3.进行有限元分析：利用有限元分析软件，建立模型并进行计算。

4.计算温度应力：根据模型的计算结果，得到温度应力。

温度应力的计算在工程中有许多应用案例。

以下是一些常见的案例：1.管道的热应力计算：管道在运行过程中由于温度变化会产生应力，如果应力超过材料的强度极限，就会导致管道的破裂。

因此，计算管道的热应力是管道工程设计的重要环节。

2.钢结构的温度应力计算：钢结构在夏季高温和冬季低温的环境中，由于温度变化会产生应力，如果应力过大，就会引起结构的变形和破坏。

因此，计算钢结构的温度应力是钢结构工程设计的重要内容。

3.复合材料的热应力计算：复合材料由于材料的组分不同，在温度变化时会产生不同的热应力。

对于复合材料的设计，需要计算不同温度下的热应力，以保证材料的安全性。

4.太阳能电池板的温度应力计算：太阳能电池板在太阳光的照射下会发生温度变化，如果温度应力过大，就会影响电池板的性能和寿命。

宁波LNG冷能空分项目大体积混凝土浇筑体施工阶段温度应力与收缩应力的计算一、混凝土温度的计算①混凝土浇筑温度:Tj =Tc+(Tq-Tc)×(A1+A2+A3+……+An)式中：Tc—混凝土拌合温度（℃），按多次测量资料，在没有冷却措施的条件下，有日照时混凝土拌合温度比当时温度高5-7 ℃，无日照时混凝土拌合温度比当时温度高2-3 ℃，我们按3 ℃计；、Tq—混凝土浇筑时的室外温度（考虑夏季最不利情况以30 ℃计）；A 1、A2、A3……An—温度损失系数，A1—混凝土装、卸，每次A=0.032(装车、出料二次)；A2—混凝土运输时，A=θt查表得6 m3滚动式搅拌车运输θ=0.0042，运输时间t约30分钟，A=0.0042×30=0.126；A3—浇捣过程中A=0.003t, 浇捣时间t约240min, A=0.003×240=0.72；T j =33+(Tq-Tc)×(A1+A2+A3)=33+(30-33)×(0.032×2+0.126+0.72) =33+（-3）×0.91=30.27 ℃二、混凝土绝热温升计算T(t)=W×Q×（1-e-mt）/（C×r）式中：T(t)—在t龄期时混凝土的绝热温升（℃）；W—每m3混凝土的水泥用量（kg/m3），取420kg/m3；Q—每公斤水泥28天的累计水化热(KJ/kg), 采用425号普通硅酸盐水泥Q =375kJ/kg(建筑施工手册 P614表10-81)；C—混凝土比热0.97 KJ/(kg·K) ；r—混凝土容重2400 kg/m3；e—常数，2.71828；m—与水泥品种、浇筑时温度有关，可查建筑施工手册 P614表10-82；t—混凝土龄期（d）。

T3= W×Q×（1-e-mt）/（C×r）=420×375×（1- 2.718-0.406×3）/ (0.97×2400)=47.63（℃）T6= W×Q×（1-e-mt）/（C×r）=420×375×（1- 2.718-0.406×6）/ (0.97×2400)=60.89（℃）T9= W×Q×（1-e-mt）/（C×r）=420×375×（1- 2.718-0.406×9）/ (0.97×2400)=58.35（℃）T 12 = W ×Q ×（1-e -mt ）/（C ×r ）=420×375×（1- 2.718-0.406×12）/ (0.97×2400)=51.35（℃）混凝土最高绝热温升T h =W ×Q/（C ×r ）=340×375/(0.97×2400)=54.77（℃）计算结果如下表三、混凝土内部中心温度计算 T 1(t)=T j + Th ·ξ(t)式中：T 1(t)—t 龄期混凝土中心计算温度；T j —混凝土浇筑温度（℃）；ξ—不同浇筑块厚度的温降系数，查建筑施工手册P 614表10-83得，对2.5m 厚混凝土3天时ξ=0.65，6天时ξ=0.62，9天时ξ=0.57，12天时ξ=0.48；T 1(3)= T j +T h ×ξ(3)= 30+47.63×0.65=60.9（℃） T 1(6)= T j +T h ×ξ(6)= 30+60.89×0.62=66.55（℃） T 1(9)= T j +T h ×ξ(9)= 30+58.35×0.57=63.26（℃） T 1(12)= T j +T h ×ξ(12)= 30+51.35×0.48=54.65（℃）从混凝土温度计算得知,砼第6天左右内部温度最高，则验算第6天砼温差。

大体积混凝土温度应力实用计算方法及控制
工程实例
大体积混凝土的温度应力主要由于混凝土内部温度梯度不均匀所
引起，温度应力大小与混凝土的水泥含量、骨料类型、孔隙结构以及
环境温度等因素有关。

计算温度应力可采用以下公式：σ=αEΔT+(1-ν)αmΔT，其中，σ为温度应力，α为混凝土的线膨胀系数，E为混凝土的弹性模量，
ν为混凝土的泊松比，αm为混凝土的平均线膨胀系数，ΔT为混凝土内部温度差。

控制大体积混凝土的温度应力，可采取以下措施：
1. 使用高性能混凝土材料，降低混凝土线膨胀系数；
2. 对混凝土的成分、配合比等进行优化设计，降低混凝土内部温度梯度；
3. 控制施工环境的温度和湿度，提高混凝土的早期强度和抗裂性能；
4. 采用降温措施，如水帘喷淋、冷却剂等，降低混凝土的温度。

实际工程中，可通过对混凝土施工过程进行监控和管控，以及采
用温度预应力技术等措施，有效控制大体积混凝土的温度应力。

例如，在某大型桥梁工程中，采用了温度预应力技术，并通过建立温度控制
模型对施工过程进行精细化监控，成功地控制了混凝土的温度应力，
确保了施工质量和结构安全。

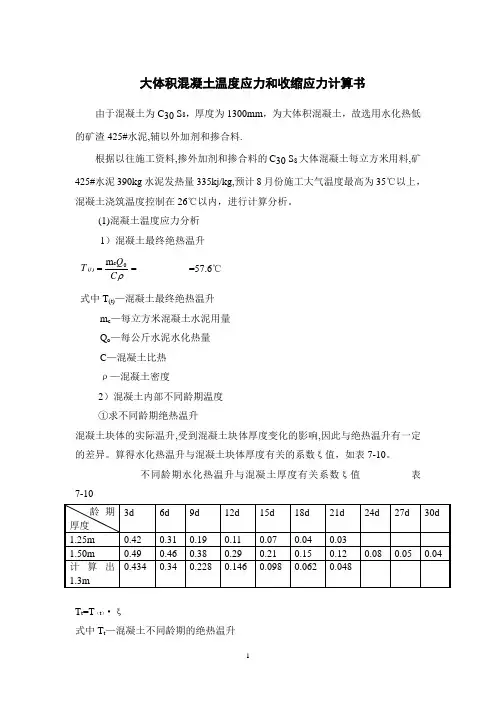
大体积混凝土温度应力和收缩应力计算书由于混凝土为C 30 S 8，厚度为1300mm ，为大体积混凝土，故选用水化热低的矿渣425#水泥,辅以外加剂和掺合料.根据以往施工资料,掺外加剂和掺合料的C 30 S 8大体混凝土每立方米用料,矿425#水泥390kg 水泥发热量335kj/kg,预计8月份施工大气温度最高为35℃以上，混凝土浇筑温度控制在26℃以内，进行计算分析。

(1)混凝土温度应力分析 1）混凝土最终绝热温升 ==ρC Q T t 0c )(m =57.6℃式中T (t)—混凝土最终绝热温升m c —每立方米混凝土水泥用量 Q o —每公斤水泥水化热量 C —混凝土比热 ρ—混凝土密度2）混凝土内部不同龄期温度 ①求不同龄期绝热温升混凝土块体的实际温升,受到混凝土块体厚度变化的影响,因此与绝热温升有一定的差异。

算得水化热温升与混凝土块体厚度有关的系数ξ值，如表7-10。

不同龄期水化热温升与混凝土厚度有关系数ξ值 表7-10T t =T （t ）·ξ式中T t —混凝土不同龄期的绝热温升T(t)—混凝土最高绝热温升ξ—不同龄期水化热温升与混凝土厚度有关值经计算列于下表7-11不同龄期的绝热温升（℃）表7-11②不同龄期混凝土中心最高温度Ｔmax＝T j＋T t式中T max—不同龄期混凝土中心最高温度T j—混凝土浇筑温度T t—不同龄混凝土绝热温升计算结果列于表7-12不同龄期混凝土中心最高温度表7-123）混凝土温度应力本底板按外约束为二维时的温度应力(包括收缩)来考虑计算①各龄期混凝土的收缩变形值及收缩当量温差a.各龄期收缩变形&y(t)＝&0y(1-e-0.01t)×M1×M2x……xMn式中&y(t)—龄期t时混凝土的收缩变形值&0y—混凝土的最终收缩值,取3.24×10-4/℃M1．M2……Mn各种非标准条件下的修正系数本工程根据用料及施工方式修正系数取值如表7-13修正系数取值表7-13经计算得出收缩变形如表7-15各龄期混凝土收缩变形值 表7-15b.各龄期收缩当量温差将混凝土的收缩变形换算成当量温差式中—各龄期混凝土收缩当量温差(℃)&y (t)—各龄期混凝土收缩变形—混凝土的线膨胀系数，取10×10-6/℃ 计算结果列于表7-16各龄期收缩当量温差 表7-16②各龄期混凝土的最大综合温度差 ΔT(t)＝T j ＋T(t)＋T y (t)-T q 式中ΔT(t)—各龄期混凝土最大综合温差T j —混凝土浇筑温度,取26℃ T(t)—龄期t 时的绝热温升 T y (t)—龄期t 时的收缩当量温差T q —混凝土浇筑后达到稳定时的温度,取年平均气温25℃计算结果列表7-17各龄期混凝土最大综合温度差 表7-17③各龄期混凝土弹性模量 E(t)＝E h (1-e -0.09t )式中E(t)—混凝土龄期t 时的弹性模量(MPa)E h —混凝土最终弹性模量(MPa) C 30混凝土取3.0×104(MPa) 计算结果列表7-18混凝土龄期t 时的强性模量 表7-18④混凝土徐变松驰系数、外约束系数、泊桑比及线膨胀系数 a.松驰系数,根据有关资料取值列表7-19混凝土龄期t 时的松驰系数 表7-19b.外约束系数(R) 按一般土地基，取R=0.5c.混凝土泊桑比(μ) 从取0.15d.混凝土线膨胀系数(α) α取10×10-6/℃⑤不同龄期混凝土的温度应力 σ(t)=-RS T E t h t t ⨯⨯-∆⨯⨯)()()(1μα式中σ(t)—龄期t 时混凝土温度(包括收缩)应力E (t)—龄期t 时混凝土弹性模量 α—混凝土线膨胀系数ΔT(t)—龄期t 时混凝土综合温差 μ—混凝土泊桑比S h(t)—龄期t 时混凝土松驰系数 R —外约束系数 计算结果列表7-20不同龄期混凝土温度(包括收缩)应力 表7-204)结论C 30混凝土 28d R L =1.43(MPa) 同龄期混凝土 R L (12d)=0.75R1=1.07(MPa) 所以:()07.196.173.043.112=>==k R d L σ由计算可知基础在露天养护期间混凝土有可能出现裂缝，在此期间混凝土表面应采取养护和保温措施，使养护温度加大，综合温度减小，则可控制裂缝出现。

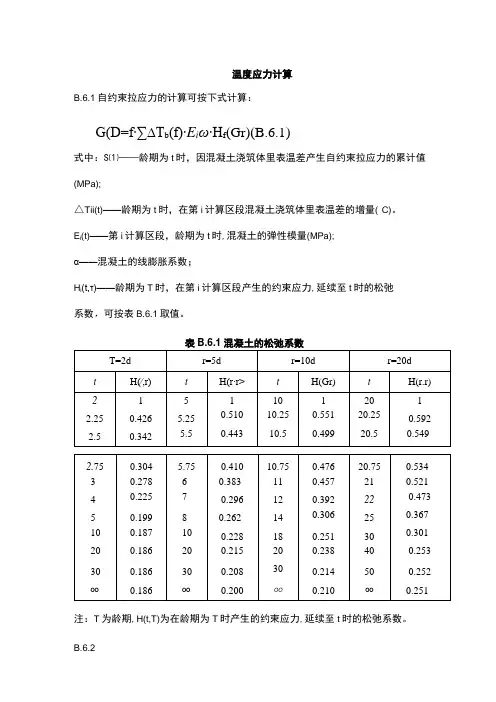
温度应力计算B.6.1自约束拉应力的计算可按下式计算：G(D=f∙∑∆T b(f)∙E iω∙H f(Gr)(B.6.1)式中：S⑴——龄期为t时，因混凝土浇筑体里表温差产生自约束拉应力的累计值(MPa);△Tii(t)——龄期为t时，在第i计算区段混凝土浇筑体里表温差的增量(°C)。

E i(t)——第i计算区段，龄期为t时,混凝土的弹性模量(MPa);α——混凝土的线膨胀系数；H i(t,τ)——龄期为T时，在第i计算区段产生的约束应力,延续至t时的松弛系数，可按表B.6.1取值。

注：T为龄期,H(t,T)为在龄期为T时产生的约束应力,延续至t时的松弛系数。

B.6.2混凝土浇筑体里表温差的增量可按下式计算：∆T b(0=∆T1(r)-∆T l(z-J) (B.6.2) 式中：j——为第i计算区段步长(d)。

B.6.3在施工准备阶段，最大自约束应力可按下式计算：Ozm B X=S∙E(力∙∆Tι∏wx∙H(t9τ)(B.6.3)式中：Ozmax --- 最大自约束应力(MPa)；△Timax一混凝土浇筑后可能出现的最大里表温差(℃)；E(t)——与最大里表温差"lmax相对应龄期t时，混凝土的弹性模量(MPa)；H(t,T)——在龄期为T时产生的约束应力,延续至t时(d)的松弛系数。

B.6.4外约束拉应力可按下式计算：HσM=∑∆T2j(0∙E iω∙H,(f")∙R iω1Z z I==I(R6.4-1) ∆T2,(r)=∆T2(r-J)-∆T2(r)(R6.4-2)R iω=1 ----------------- 71- ------ ---- (R6.4-3)c0sh(Vτ⅛7),⅜)式中：σ×(t)——龄期为t时,因综合降温差,在外约束条件下产生的拉应力(M Pa);△T2i(t)——龄期为t时，在第i计算区段内,混凝土浇筑体综合降温差的增量(o C)eμ——混凝土的泊松比，取0.15;Ri(t)——龄期为t时，在第i计算区段，外约束的约束系数。