北师大版九年级数学下册第二章二次函数 第13课 二次函数的应用(2)——抛物线型问题课件
- 格式:pptx
- 大小:825.88 KB
- 文档页数:18



2.4 二次函数的应用(2)教材分析:如果一个人经商,那么他最应该考虑的问题是什么呢?当然是怎样才能获得最大利润,这正是二次函数的应用范畴。
因为二次函数的图象是抛物线,在确定自变量的取值范围后,总能取到最大值或最小值。
若自变量的取值包括顶点的横坐标,就可以将二次函数化为顶点式,更易得到最大值或最小值。
本节课中关键问题是把实际问题转化为数学问题,把二次函数知识运用于实践,并对结果进行合理的解释。
在实际情景中用二次函数知识解决最优问题,首先要读懂问题,实际问题往往叙述部分较长,使人感到问题很难,想解决问题就要克服畏难情绪,明确要解决的问题是什么;其次,分析问题中各个量之间的相互关系;再次是把问题和相互关系表示成数学式子;在此基础上,利用学过的数学知识一步一步地解决问题。
教学目标:(一)知识与技能经历探索T恤衫销售中最在利润问题的过程,体会二次函数是一种最优化问题的数学模型。
能够分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出问题的最大/最小值。
(二)过程与方法经历销售中最大利润问题的探究过程,发展学生运用数学知识解决实际问题的能力。
(三)情感、态度与价值观体会数学与人类社会的密切联系,初步感受二次函数的应用价值,增进学生对数学的理解和学好数学的信心。
认识到数学是解决实际问题和进行交流的工具,让学生认识数学与人类生活的密切联系及对人类历史发展的作用,了解数学对促进社会进步和发展人类理性精神的作用。
教学重点:经历探究销售中最大利润问题的过程,能够分析和表示实际问题中变量之间的二次函数关系,初步获得利用数学方法解决实际问题的经验。
教学难点:分析和表示不同背景下实际变量间的二次函数关系,运用二次函数的知识解决实际问题。
教学方法:教师指导下的学生自主学习法。
教具准备:PPT课件教学过程:一.温故知新前面学习了二次函数及其图象与性质,知道抛物线的三要素是:开口方向、对称轴、顶点坐标。
同时,列方程解应用题的一般步骤是:审、设、列、解、检、答。


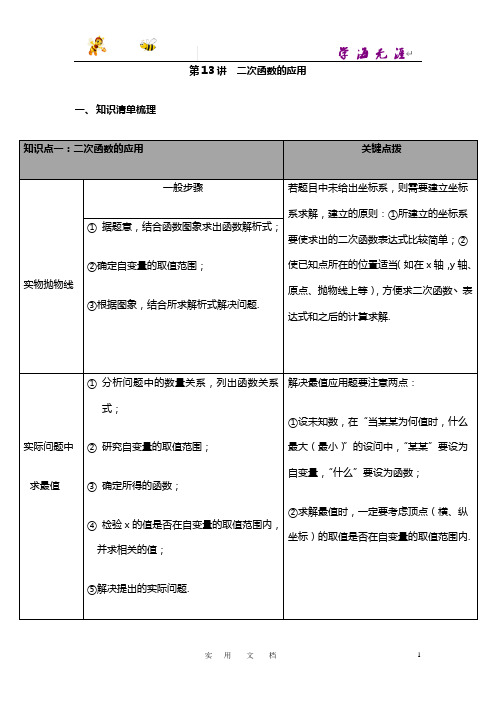
第13讲二次函数的应用
一、知识清单梳理
知识点一:二次函数的应用关键点拨
实物抛物线
一般步骤若题目中未给出坐标系,则需要建立坐标
系求解,建立的原则:①所建立的坐标系
要使求出的二次函数表达式比较简单;②
使已知点所在的位置适当(如在x轴,y轴、
原点、抛物线上等),方便求二次函数丶表
达式和之后的计算求解.
①据题意,结合函数图象求出函数解析式;
②确定自变量的取值范围;
③根据图象,结合所求解析式解决问题.
实际问题中求最值①分析问题中的数量关系,列出函数关系
式;
②研究自变量的取值范围;
③确定所得的函数;
④检验x的值是否在自变量的取值范围内,
并求相关的值;
⑤解决提出的实际问题.
解决最值应用题要注意两点:
①设未知数,在“当某某为何值时,什么
最大(最小)”的设问中,“某某”要设为
自变量,“什么”要设为函数;
②求解最值时,一定要考虑顶点(横、纵
坐标)的取值是否在自变量的取值范围内.
结合几何图形①根据几何图形的性质,探求图形中的关系
式;
②根据几何图形的关系式确定二次函数解
析式;
③利用配方法等确定二次函数的最值,解决
问题
由于面积等于两条边的乘积,所以几何问
题的面积的最值问题通常会通过二次函数
来解决.同样需注意自变量的取值范围.。