当前位置：文档之家 › 函数单调性课件(公开课)ppt

函数单调性课件(公开课)ppt

  • 格式：ppt
  • 大小：691.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

函数的单调性课件(共17张PPT)

函数的单调性课件(共17张PPT)
如果我们以x表示时间间隔（单位：h),y表示记忆保持量，则 不难看出，图3-7中，y是的函数，记这个函数为y =f(x).
这个函数反映出记忆具有什么规律？你能从中得到什么启发？
调动思维，探究新知 在在活初初动中中2，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
问题情境：我们知道，“记忆”在我们的学习过程中 扮演着非常重要的角色，因此有关记忆的规律一直都 是人们研究的课題。德国心理学家艾宾浩斯曾经对记 忆保持量进行了系统的实验研究，并给出了类似图37所示的记忆规律．
创设情境，生成问题 在在活初初动中中1，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
△x表示自变量x的增量，△y表示因变量y的增量． 这时，对于属于这个区间上的任意两个不相等的值x1,x2: 这个数是增函数的充要条件是yx ＞0； 这个数是增函数的充要条件是y ＜0.
x
调动思维，探究新知 在在活初初动中中2，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
因此，函数f(x)=3x+2在（- ,+ ）上是增函数.
巩固练习，提升素养 在活初动中3，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
数学Biblioteka 基础模块（上册）第三章 函数
3.1.3 函数的单调性

函数单调性与最值公开课一等奖课件省赛课获奖课件

函数单调性与最值公开课一等奖课件省赛课获奖课件

x b
0a
x b
从几何上看, y = f (x) 在 [a, b] 上单增(或单减)，
其图形是一条沿 x 轴正向上升(或下降)的曲线。
上升的曲线每点处的切线斜率均为正，
即 f ( x) 0 ;
下降的曲线每点处的切线斜率均为负， 即 f ( x) 0 .
定 理：
设函数 y f x在 a,b连续, 在 a,b 可导,
y
x 0
二. 极值的求法. 由上图可知，函数取到极值处，曲
线的切线都是水平的，但有水平切线的 点不一定都是函数的极值点。
定理 1：（必要条件）
设 f (x)在 x0 处可导，且在 x0 处获得极
值，则必有 f ( x0 ) 0 .
阐明：
1.使导数 f ( x)为 0 的点，称为 f (x) 的驻点。 可导函数的极值点必是驻点， 但 驻点不一定是极值点。
定义：设 f x在a,b内有定义，x0 a,b.
对 x U ( xˆ0 , ),
若 f (x0) > f (x), 则称 f (x0)为 f (x)的一种 极大值， x0 称为极大值点；
若 f (x0) < f (x), 则称 f (x0)为 f (x)的一种
极小值， x0 称为极小值点。 极大值(点)与极小值(点)统称极值(点)。
2. 证明方程根的唯一性
例3：证明方程 x5 5x 1 0 在 1，0内
有唯一的实根。 证：先证明根的存在性：
设 f x x5 5x 1 且在 1，0 连续，
f 1 5 0, f 0 1 0，
由零点定理, f (x) = 0 在 (-1,0) 内最少有一根; 再证明根的唯一性：
sec3 x sin x(2 cos3 x) 0

《函数的单调性》示范公开课教学PPT课件【高中数学人教版】

《函数的单调性》示范公开课教学PPT课件【高中数学人教版】

（2）它在定义域I上的单调性是怎样的？证明你的结论．
答案：图象略．
（1）（－∞，0）∪（0，＋∞）．
（2）当k＞0时，y＝ k 在区间（－∞，0）和（0，＋∞）上单调递减； x
当k＜0时，y＝ k 在区间（－∞，0）和（0，＋∞）上单调递增． x
目标检测
44．画出反比例函数y＝
k x
的图象．
（1）这个函数的定义域I是什么？
新知探究
追问5 函数f（x）＝|x|，f（x）＝－x2各有怎样的单调性？
f（x）＝|x|在区间（－∞，0]上单调递减， 在区间[0，＋∞）上单调递增； f（x）＝－x2在区间（－∞，0]上单调递增， 在区间[0，＋∞）上是单调递减．
新知探究
问题4 如何用符号语言准确刻画函数值随自变量的增大而增大 （减小）呢？
证明：由x1，x2∈（1，＋∞），得x1＞1，x2＞1，
所以x1x2＞1，x1x2－1＞0．
由x1＜x2，得x1－x2＜0，
于是（x1－x2）（
x1x2 1 x1 x2
）＜0，即y1＜y2．
所以，函数y＝x＋ 1 在区间（1，＋∞）上的单调递增． x
新知探究
追问 你能用单调性定义探究y＝x＋ 1 在整个定义域内的单调性吗？ x
图1
图2
图3
图1的特点是：从左至右始终保持上升；
图2与图3的特点是：从左至右有升也有降．
新知探究
★资源名称： 【数学探究】函数值的变化情况 ★使用说明：本资源通过操作展示动画，使学生观察函数值随着自变量值的变化而变化的情 况．通过交互式动画的方式，运用了本资源，可以吸引学生的学习兴趣，增加教学效果，提高教 学效率． 注：此图片为动画缩略图，如需使用资源，请于资源库调用

函数的单调性(公开课课件)

函数的单调性(公开课课件)

04 函数单调性的应用举例
利用函数单调性求最值问题
极值问题
通过判断函数在某一点的单调性 ，可以确定该点是否为极值点， 从而求得函数的最值。
最值问题
利用函数在整个定义域上的单调 性，可以确定函数在定义域上的 最大值和最小值。
利用函数单调性解不等式问题
单调性比较法
通过比较两个函数的单调性，可以确定它们的大小关系，从而解决一些不等式问题。
02
建议学生多参与数学建模和数学竞赛等活动，提高数学应用发展
03
学生可以通过阅读数学期刊、参加学术会议等方式，了解数学
学科的最新发展动态和前沿研究领域。
THANKS FOR WATCHING
感谢您的观看
单调性分析法
利用函数的单调性，可以分析不等式的解集和边界情况。
利用函数单调性解决实际问题
优化问题
在经济学、金融学等领域中，经常需要解决一些优化问题，如最优化生产、最优化投资等。利用函数 单调性可以找到最优解或近似最优解。
决策问题
在企业管理、市场营销等领域中，经常需要做出一些决策，如选择最佳的营销策略、确定最优的产品 价格等。利用函数单调性可以分析不同决策方案的效果，从而做出更好的决策。
03 函数单调性的判定方法
导数法判定函数单调性
总结词
通过求导数判断函数的单调性
详细描述
求函数的导数，然后分析导数的符号，如果导数大于0，则函数在该区间内单调递增；如 果导数小于0，则函数在该区间内单调递减。
举例
对于函数$f(x) = x^3$，其导数$f'(x) = 3x^2$，在$x > 0$时，$f'(x) > 0$，因此函数 $f(x)$在$x > 0$时单调递增。

函数单调性课件(公开课)ppt

函数单调性课件(公开课)ppt
函数单调性课件(公开课)
目录
• 函数单调性的定义与性质 • 判断函数单调性的方法 • 单调性在解决实际问题中的应用 • 函数单调性的深入理解 • 函数单调性的实际案例分析
01 函数单调性的定义与性质
函数单调性的定义
函数单调性是指函数在某个区间内的增减性。如果函数在某个区间内单调递增， 则表示函数值随着自变量的增加而增加；如果函数在某个区间内单调递减，则表 示函数值随着自变量的增加而减小。
的计算过程。
单调性与微分方程的关系
要点一
单调性决定了微分方程解的稳定 性
对于一阶线性微分方程，如果其系数函数在某区间内单调 递增（或递减），则该微分方程的解在此区间内是稳定的 。
要点二
单调性是研究微分方程的重要工 具
通过单调性可以判断微分方程解的存在性和唯一性，以及 研究解的动态行为。
05 函数单调性的实际案例分 析
总结词
利用单调性证明或解决不等式问题
详细描述
单调性在解决不等式问题中起到关键作用。通过分析函数的单调性，我们可以证明不等式或解决与不等式相关的 问题。例如，利用单调性可以证明数学归纳法中的不等式，或者在比较大小的问题中利用单调性进行判断。
单调性在函数极值问题中的应用
总结词
利用单调性求解函数的极值
详细描述
函数单调性的定义可以通过函数的导数来判断。如果函数的导数大于0，则函数在该 区间内单调递增；如果函数的导数小于0，则函数在该区间内单调递减。
函数单调性的性质
函数单调性具有传递性，即如果函数在区间I上单调递增，且 在区间J上单调递增，则函数在区间I和J的交集上也是单调递 增的。
函数单调性具有相对性，即如果函数在区间I上单调递增，且 另一个函数在区间J上单调递增，则这两个函数在区间I和J的 交集上也是单调递增的。

函数的单调性(公开课课件)

函数的单调性(公开课课件)
详细描述
单调减函数是指函数在某个区间内，对于任意两个自变量$x_1$和$x_2$（$x_1 < x_2$），如果$x_1$和$x_2$ 都在这区间内，那么函数值$f(x_1) geq f(x_2)$。也就是说，函数的图像随着$x$的增加而下降。
严格单调函数的定义
总结词
严格单调函数是指函数在某个区间内，严格满足单调增或单调减条件的函数。
利用单调性解方程
利用函数的单调性，可以求解方程。
通过分析函数的单调性，可以确定方程解的范围，从而求解方程。例如，对于一元二次方程$ax^2 + bx + c = 0$，如果$a > 0$，则函数$f(x) = ax^2 + bx + c$在区间$(-infty, -frac{b}{2a})$上单调递减，在区间$(-frac{b}{2a}, +infty)$上单调递增 ，因此方程的解必定落在$(-frac{b}{2a}, +infty)$区间内。
函数单调性的反例
04
单调增函数的反例
总结词
非严格单调增函数
详细描述
有些函数在其定义域内并非严格单调递增，即存在某些区间内函数值先减小后 增大。例如，函数$f(x) = x^3$在区间$(-2, -1)$内是单调减函数。
单调减函数的反例
总结词
非严格单调减函数
详细描述
有些函数在其定义域内并非严格单调递减，即存在某些区间 内函数值先增大后减小。例如，函数$f(x) = frac{1}{x}$在区 间$(1, +infty)$内是单调增函数。
详细描述
单调增函数是指函数在某个区间内，对于任 意两个自变量$x_1$和$x_2$（$x_1 < x_2$ ），如果$x_1$和$x_2$都在这区间内，那么 函数值$f(x_1) leq f(x_2)$。也就是说，函数 的图像随着$x$的增加而上升。

函数的单调性和极值省公开课一等奖全国示范课微课金奖PPT课件

函数的单调性和极值省公开课一等奖全国示范课微课金奖PPT课件

第4页
分析：从图形看 若函数在区间(a,b)内单调递增，我
们发觉在（a，b）上切线斜率为正，即 在（a，b）内每一点处导数值为正
若函数在区间(a,b)内单调递减，发觉 在（a，b）上切线斜率为负，即在(a,b)内 每一点处导数值为负，
第5页
结论： 设函数y=f(x)在某个区间内有导数
，假如在这个区间内y'>0，那么y=f(x)为 这个区间内增函数；假如在这个区间内 y'<0，那么y=f(x)为这个区间内减函数.
令 f (x) 0 , 得 x 1, x 2
x (, 1) 1 (1 , 2) 2 (2, )
f (x)
0
0
f (x)
2
1
y
故 f (x) 单调增区间为
2
(, 1), (2, ); 1
f (x)单调减区间为 (1, 2).
o
12 x
第8页
用导数法确定函数单调性时步骤是： （1）求出函数导函数 （2）求解不等式f `(x)>0，求得其解集，
第21页
3、已知过曲线y=x3/3上点P切线方程为12x3y=16，则点P坐标为 .
4、函数f(x)=x3-3x+1减区间为( )
(A) (-1,1)
(B) (1,2)
(C) (-∞,-1)
(D) (-∞,-1) ，(1, +∞)
5、若函数y=a(x3-x)递减区间为( 3 , )3，则
a取值范围为( )
y'>0
增函数
y'<0
减函数
证实函数单调性惯用方法： （1）定义法 （2）导数法
第6页
例1 求函数 f(x)=x3-3x 的单调区间 解 （1）该函数的定义区间为（-, ）； （2）f/(x)=3x2-3=3(x+1)(x-1),令 f/(x)=0,得 x=-1,x=1

函数的单调性(公开课课件)

函数的单调性(公开课课件)

VS
单调性与极值大小的关系
单调性可以用来比较不同区间上的极值大 小。
单调性与最值的关系
单调性与最值点的关系
单调性可以用来判断函数在某点是否为最值 点。
单调性与最值大小的关系
单调性可以用来比较不同区间上的最值大小 。
THANKS FOR WATCHING感Biblioteka 您的观看CHAPTER 03
函数单调性的应用
利用单调性求参数范围
通过函数的单调性，我们可以确定参数的取值范围，进而解决一些数学问题。
在函数中，如果函数在某区间内单调递增或递减，那么我们可以根据函数值的变化趋势，确定参数的取值范围。例如，如果 函数$f(x)$在区间$(a, b)$内单调递增，且$f(x_0) = 0$，那么对于任意$x in (a, b)$，都有$f(x) > 0$，从而可以得出参数的 取值范围。
单调性可以通过函数的导数来判断，如果函数的导数大于等于0，则函数在该区 间内单调递增；如果函数的导数小于等于0，则函数在该区间内单调递减。
单调增函数和单调减函数
01
单调增函数是指函数在某个区间 内随着自变量的增加而增加。
02
单调减函数是指函数在某个区间 内随着自变量的增加而减少。
函数单调性的几何意义
导数与函数单调性
总结词
导数可以判断函数的单调性，当导数大于0时，函数单调递增；当导数小于0时 ，函数单调递减。
详细描述
导数表示函数在某一点的切线斜率。如果导数大于0，说明切线斜率为正，函数 在该区间内单调递增；如果导数小于0，说明切线斜率为负，函数在该区间内单 调递减。
复合函数的单调性
总结词
复合函数的单调性取决于内外层 函数的单调性以及复合方式。

函数的单调性公开课课件

函数的单调性公开课课件

在函数值比较中的应用
1 2
利用单调性比较函数值大小
对于同一区间内的两个函数值，如果函数在该区 间内单调，则可以直接比较它们的大小。
确定函数值的范围
通过判断函数的单调性，可以确定函数在某个区 间内的取值范围。
3
举例
比较sin(π/4)和sin(π/6)的大小。由于正弦函数 在[0, π/2]区间内单调递增，因此sin(π/4) > sin(π/6)。
06
复合函数的单调性
复合函数的定义和性质
复合函数的定义
设函数$y=f(u)$的定义域为$D_f$， 函数$u=g(x)$的定义域为$D_g$， 且$g(D_g) subseteq D_f$，则称函 数$y=f[g(x)]$为$x$的复合函数。
复合函数的性质
复合函数保持原函数的定义域、值域 、周期性、奇偶性等基本性质。
以直观地判断函数在各个 区间内的单调性。
判断单调区间
根据图像的形状和走势， 确定函数在各个区间内的 单调性。
图像的绘制
通过描点法、图像变换法 等方法，绘制出函数的图 像。
04
常见函数的单调性
一次函数
一次函数单调性
一次函数$f(x) = ax + b$（$a neq 0$）在其定 义域内单调增加或减少，取决于系数$a$的正负。
总结与展望
课程总结
函数的单调性定义
详细解释了函数单调性的定义，包括增函数、减函数以及常数函 数的特性。
判断函数单调性的方法
介绍了如何通过导数、二阶导数以及函数的图像来判断函数的单调 性。
函数单调性的应用
举例说明了函数单调性在解决实际问题中的应用，如优化问题、经 济学中的边际分析等。

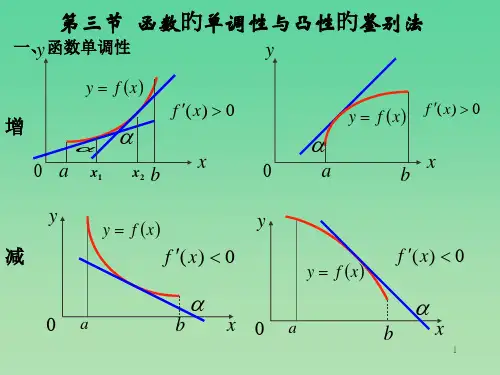
函数单调性和凹凸性省公开课获奖课件说课比赛一等奖课件

函数单调性和凹凸性省公开课获奖课件说课比赛一等奖课件
(1).若在 (a,b) 内 f ( x) 0 , 则 f (x) 在[a, b] 上 单调 增长. (2).若在 (a,b) 内 f (x) 0 , 则 f (x) 在[a, b] 上 单调 降低.
证 (1). 设 x1 , x2 (a, b), ( x1 x2 ) , 应用拉格朗日中值定理
11
x3
2 5x 1
33
9
9
9 3 x4
令 y 0 得 x1 1/ 5, 当 x2 0 时, y不存在.
列表： x (,1/ 5 ) 1/ 5 (1/ 5,0) 0
(0, )
y
0
不存在
y
有拐点 无拐 点
综上，曲线在(,1/ 5 ) 为上凸旳
点
1 5,Biblioteka 6 53 25是拐点.
在 (-1/5, )上为下凸旳.
上凸旳。
问题：拟定函数在那些区间上图形上凸旳，那些区间上图 形是下凸旳，即求函数旳凸向区间。
8
例1.判断曲线 y x3 旳凸向
解 y 3x2 y 6x
x 0 时, y 0, 曲线 在 (, 0)内是上凸旳. x 0 时, y 0, 曲线 在 (0,)内时是下凸旳.
定义 曲线上上凸弧与下凸弧旳分界点,称为拐点.
如例1中,点(0,0) 是曲线 y x3 旳拐点.
y y x3
0
•
x
注意 1.若点 (x0, f (x0)) 是拐点,则 f ( x0 ) 0.或f ( x0 )不存在
2.由f ( x0 ) 0. 或不存在 所拟定旳点(x0, f (x0 )) 未必是拐点.
如 f ( x) x4 , f (0) 0, 但点 (0,0) 不是拐点.
2
例1. 鉴定函数 y x sin x 在 [0,2 ] 上旳单调性.

函数单调性课件ppt

函数单调性课件ppt

导数与函数单调性
01
02
03
导数大于0
函数在对应区间内单调递 增
导数小于0
函数在对应区间内单调递 减
导数等于0
函数可能存在拐点或不可 导点
复合函数的单调性
同增异减
内外层函数单调性相同，则复合 函数单调递增；内外层函数单调 性不同，则复合函数单调递减。
注意拐点
复合函数在拐点处可能改变单调 性。
常见函数的单调性
函数单调性课件
目录
• 函数单调性的定义 • 判断函数单调性的方法 • 函数单调性的应用 • 函数单调性的实例分析 • 函数单调性的综合练习
01
函数单调性的定义
函数单调性的定义
函数单调性是指函数在某个区间内的 增减性。如果函数在某个区间内单调 递增，那么对于该区间内的任意两个 数$x_1$和$x_2$，当$x_1 < x_2$时 ，有$f(x_1) < f(x_2)$；反之，如果 函数在某个区间内单调递减，那么对 于该区间内的任意两个数$x_1$和 $x_2$，当$x_1 < x_2$时，有 $f(x_1) > f(x_2)$。
03
函数单调性的应用
利用单调性证明不等式
总结词
单调性是证明不等式的一种有效工具 ，通过比较函数在不同区间的增减性 ，可以推导出不等式的正确性。
详细描述
利用单调性证明不等式的基本思路是 ，首先确定函数在指定区间上的单调 性，然后根据单调性定义，比较函数 值的大小，从而证明不等式。
利用单调性求函数的极值
VS
单调性是函数的一种固有属性，与函 数的定义域和值域无关，只与函数的 增减性有关。
单调增函数和单调减函数
01
单调增函数是指函数在某个区间 内单调递增的函数。对于任意两 个数$x_1$和$x_2$，当$x_1 < x_2$时，有$f(x_1) < f(x_2)$。

函数的单调性公开课课件

函数的单调性公开课课件
函数的单调性公开课 课件
目录
• 引言 • 函数单调性的判断方法 • 函数单调性的性质 • 函数单调性的应用 • 典型例题分析 • 课堂小结与思考题
CHAPTER 01
引言
函数的单调性定义
增函数
对于函数$f(x)$，如果在其定义域内的任意两个数$x_1$和 $x_2$（$x_1 < x_2$），都有$f(x_1) leq f(x_2)$，则称$f(x)$ 在该定义域内是增函数。
导数非正 如果一个函数在其定义域内的导数存在且非正，则该函数 在该定义域内单调减少。
单调函数的周期性
周期函数与非周期函数
单调函数可以是周期函数，也可以是非周期函数。周期函数具有重复出现的特性，而非 周期函数则不具有这种特性。
周期函数的单调性
如果一个周期函数在一个周期内单调增加（或减少），则在每个周期内都具有相同的单 调性。这意味着周期函数的图像在每个周期内都会重复相同的上升或下降趋势。
利用单调函数的性质，如增减性、连续性等，对函数值进行比较和估算。
在函数图像分析中的应用
利用函数的单调性判断函数图像的趋势
通过函数的单调性可以判断函数图像在某个区间内的上升或下降趋势，从而了解函数的整体性质。
单调函数的性质在函数图像分析中的应用
利用单调函数的性质，如拐点、极值点等，对函数图像进行进一步的分析和研究，如确定函数的最大值、 最小值等。
3
导数非负 如果一个函数在其定义域内的导数存在且非负， 则该函数在该定义域内单调增加。
单调减函数的性质
函数值随自变量增大而减小 对于任意两个自变量的值x1和x2（x1 < x2），如果函数 f(x)在区间[x1, x2]内单调减少，则有f(x1) ≥ f(x2)。

23版-函数的单调性公开课优质课件

23版-函数的单调性公开课优质课件

在函数最值问题中的应用
求函数的最值
对于闭区间上的连续函数，通过确定其单调性，可以找到函数的最大值和最小值 。例如，如果函数$f(x)$在$[a, b]$上单调增加，那么其最小值出现在$a$处，最 大值出现在$b$处。
判断函数的凸凹性
函数的单调性与凸凹性密切相关。通过确定函数的二阶导数符号，可以判断函数 的凸凹性，从而进一步分析函数的最值问题。
02 单调减函数
对于任意x1,
x2∈D，当x1<x2时，都有
f(x1)≥f(x2)，则称f(x)在区间D上是单调减函数。
03 单调函数的性质
单调函数在其定义域内具有“升降一致”的特性 ，即函数值随自变量的增大而增大（或减小）。
研究函数单调性的意义
揭示函数变化规律
通过研究函数的单调性，可以了解函数值随自变量变化而 变化的趋势和规律。
判断函数极值与最值
函数的单调性与极值、最值密切相关，通过研究函数的单 调性可以判断函数在某一区间内是否存在极值或最值。
解决实际问题
在实际问题中，很多现象或过程可以用函数来描述，通过 研究函数的单调性可以了解这些现象或过程的变化趋势， 为解决实际问题提供思路和方法。
课件内容与结构概览
• 课件内容：本课件将详细介绍函数的单调性定义、性质、判断方法以及 应用举例等内容。
在经济学等实际问题中的应用
边际分析
在经济学中，边际分析是一种重要的分析方法，它涉及到函 数的单调性和导数。通过确定函数的单调性，可以判断边际 量（如边际成本、边际收益等）的变化趋势，为经济决策提 供依据。
弹性分析
弹性是经济学中另一个重要概念，它表示一个变量对另一个 变量变化的敏感程度。函数的单调性与弹性密切相关，通过 分析函数的单调性可以判断弹性的大小和方向，进而分析市 场供求关系、价格变动等问题。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（1）如果函数 y =f(x)在区间I是单调增函数或单调减函数，那么 就说函数 y =f(x)在区间I上具有单调性。
在单调区间上，增函数的图象是上升的，减函数的图象是下降的。 （2）函数单调性是针对某个区间而言的，是一个局部性质;
判断1：函数 f (x)= x2 在 , 是单调增函数；
例1.画出下列函数图像，并写出单调区间：
y
(1) y
1 y x
1 ( x 0); x
x
1 ( , 0) , (0, ) y 的单调减区间是 _____________ x
？
讨论1：根据函数单调性的定义，
能不能说y 1 ( x 0)在定义域( , 0) (0, )上 x 是单调减函数?
类比单调增函数的研究方法定义单调减函数. y y
f(x2) f(x1) f(x1) f(x2)
x1 O x2 x 设函数y=f(x)的定义域为I,区间D I. 如果对于属于定义I域内某个区间D上 如果对于属于定义域I内某个区间D上 的任意两个自变量的值x1,x2， 的任意两个自变量的值x ,x ，
例2.画出下列函数图像，并写出单调区间：
(2) y x2 2.
( , 0] y x2 +2的单调增区间是 _______;
y x +2的单调减区间是_______.
2
y
2 1 -2 -1 -1 -2
y=-x2+2
[0, )
1
2
x
例3:下图是定义在[－5，5]上的函数y＝f（x）的图象， 根据图象说出y＝f（x）的单调区间，以及在每一单调区 间上， y＝f（x）是增函数还是减函数？ 解： y＝f（x）的单调区间有 [－5，－2），[－2，1） [1，3），[3，5]. 其中y＝f（x）在[－5，－2），[1，3）上 是减函数， 在[－2，1）， y [3，5）上是增函数.
1 2
x1 O x2 x 设函数y=f(x)的定义域为I,区间D I.
当x1<x2时，都有f(x1 ) < f(x2 )，
当x1<x2时，都有 f (x1 )
>
f(x 2 )，
那么就说在f(x)这个区间上是单调增 那么就说在f(x)这个区间上是单调 函数，D称为f(x)的单调 增 区间. 减函数，D称为f(x)的单调 减 区间. 单调区间
y y
o
x
o
x
y=kx+b (k>0)
y=kx+b (k<0)
） k 0时，在（ ， ） k 0时，在（， 上为增函数 上为减函数
（2）二次函数单调性
y ax
2
b bx c(a 0) 的对称轴为 x 2a
y ax2 bx c
a>0
a<0
单调增区间
b , 2 a
单调减区间
b , 2a
b , 2a
b , 2a
（3）反比例函数的单调性
k y x ( k 0)
结论： k 0时，函数在（ ， 0）和（ 0， ） 两个区间上都是减函数 k 0时，函数在（ ， 0）和（ 0， ） 两个区间上都是增函数
1 1 ) ( x2 ) x1 x2
取值
则 f ( x1 ) f ( x2 ) ( x1
作差
1 1 ( x1 x2 ) ( ) x1 x2
( x2 x1 ) ( x1 x2 ) x1 x2 x1 x2 1 ( x1 x2 )( ) x1 x2
当x的值增大时,函数值y也增大——图像在该区间内逐渐上升；
当x的值增大时,函数值y反而减小——图像在该区间内逐渐下降。
y
10 8 6 4
2
O -2 2 4
D
6 8 10 12
14 16
18
20
22 24
x
y
图象在区间D逐渐上升 区间D内随着x的增大，y也增大
f(x2)
f(x1) O
M
N
？
对区间D内
1 例3.判断函数 y x 在定义域 x
0, 上的单调性.
并给出证明
主要步骤 1. 任取x1，x2∈D，且x1<x2； 2. 作差f(x1)－f(x2)；
3. 变形（通常是因式分解和配方）；
4. 定号（即判断差f(x1)－f(x2)的正负）； 5. 下结论
证明：在区间
1, 上任取两个值 x1 , x2 且 x1 x2
f(x1) O
M
N
对区间D内任意
x1，x2 ，
D x 1
都 有f(x1)<f(x2) 当x1<x2时，
x2
x
定 义
设函数y=f(x)的定义域为I,区间D I. 如果对于区间D的任意 两个自变量的值x1,x2， 当x1<x2时，都有f(x1 ) < f(x2 )， 那么就说 f (x)在区间D上 是单调增函数， D称为 f (x)的单调 增区间.
y
10 8 6 4 2 O -2 2 4 6 8 10 12
14 16
18
20
22 24
x
上升
y
下降
y
局部上升或下降
y
y x 1
y x 1
y x2
o x o x o x
函数的这种性质称为函数的单调性 能用图象上动点 P（x，y）的横、纵坐标 在某一区间内， 关系来说明上升或下降趋势吗？
y
y x2
o x
下表是函数 f ( x) x 中y随x的变化 情况
2
x
… -4 -3 -2 -1 0 1 2 3
2
4
…
f ( x) x
… 16 9 4
1
0 1 4 9 16 …
分析函数值的变化可得到函数的单调性。
（1）如果函数 y =f(x)在区间I是单调增函数或单调减函数，那么 就说函数 y =f(x)在区间I上具有单调性。
在单调区间上，增函数的图象是上升的，减函数的图象是下降的。 （2）函数单调性是针对某个区间而言的，是一个局部性质; （3） x 1, x 2 取值的任意性
判断2：定义在R上的函数 f (x)满足 f (1)< f(2)， y 则函数 f (x)在R上是增函数；
f(2) f(1) O 1 2x
(1)一次函数的单调性
函数的单调性
杨阳
永 远 联 系 莫 分 华 离
罗 庚
切 莫 忘 几 何 代 数 统 一 体
隔 离 分 家 万 事 休
数 形 结 合 百 般 好
形 少 数 时 难 入 微
数 无 形 时 少 直 觉
焉 能 分 作 两 边 飞
数 与 形 本 是 相 倚 依
,
,
——
如图为五常某日24小时内的气温变化图．观察这 张气温变化图，观察图形,你能得到什么信息?
1. 两个定义：增函数、减函数的定义； 2. 两种方法: ①图象法判断函数的单调性： 增函数的图象从左到右 上升 下降 ②定义法证明函数单调性，步骤: 取值 作差变形 定号 下结论 减函数的图象从左到右
3.一个数学思想：数形结合
练习册：
x1，x2 ，
有f(x1)<f(x2)
D x 1
当x1<x2时，
x2
x
y
图象在区间D逐渐上升 区间D内随着x的增大，y也增大
f(x2)
f(x1) O
M
N
？
对区间D内任意
x1，x2 ，
有f(x1)<f(x2)
D x 1
当x1<x2时，
x2
x
y
图象在区间D逐渐上升 区间D内随着x的增大，y也增大
f(x2)
，且 x1
变 形
x1, x2 1,
x2 x1 x2 0, x1 x2 1 0
f ( x1 ) f ( x2 ) 0, f ( x1 ) f ( x2 ) 1 所以函数 y x 在区间上 1, 是增函数. x
定号
结论
1 试用定义法证明函数 f ( x) x 在区间 0, 上是单调增函数。
3
2 1 -5 -4 -3 -2 -1 O 1 -1 -2 2 3 4 5x 作图是发 现函数单 调性的方 法之一.
单调区间的书写：
函数在其定义域内某一点处的函数值 是确定的，讨论函数在某点处的单调 性无意义。若函数在区间端点处有定 义，则写成闭区间，当然写成开区间 也可以；若函数在区间端点处无定义， 则必须写成开区间。