(2)转化为不等式恒成立问题,即“若函数单调递增,则f′(x)≥0;若函数单调递
减,则f′(x)≤0”来求解,当然,在转化过程中要注意所给区间的开闭及不等式
中等号有无等细节;
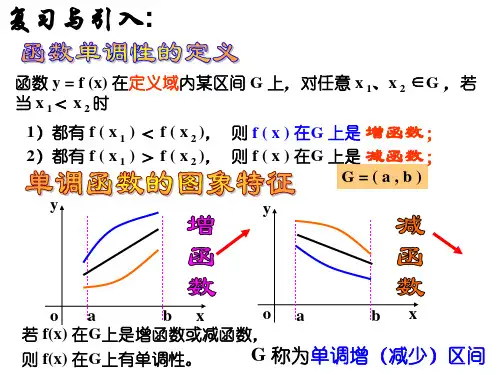
(3)要注意区分“函数在区间(a,b)上单调”与“函数的单调区间为(a,b)”.
变式 1:若函数 f(x)= 3x2 ax (a∈R)在区间(1,3)单调递增,求实数 a 的取值范围. ex
(1)[f(x)eαx]′=f′(x)eαx+αf(x)eαx;
(2)[f(x)xα]′=f′(x)xα+αf(x)xα-1.在具体题目中将α用符合题意的具体的数 值代入即可.
变式 1:定义在(0, π )的函数 f(x),函数 f′(x)是它的导函数,且恒有 2
f(x)<f′(x)tan x 成立,则( )
3
3
3
的两不等实根,
代入得
2 2
4 3 4 3
a 3
a, 3
6
,
解得
a=8.
变式 3:若函数 f(x)= 3x2 ax (a∈R)在区间(-1,1)上不单调,求实数 a 的取值范围. ex
解:因为 f′(x)= 3x2 6 a x a ,由函数 f(x)在区间(-1,1)上不单调知,
解:因为 f′(x)= 3x2 6 a x a ,由 f(x)在(1,3)上单调递增知,
ex
f′(x)≥0 在[1,3]上恒成立,即-3x2+(6-a)x+a≥0 在[1,3]上恒成立,
当
x=1
时,不等式恒成立;当
1<x≤3
时,a≤
3x2 6x 1 x
恒成立,只需
a≤
3x2 6x 1 x