第7章 多采样率数字信号处理

多采样率数字信号处理在数字语音系统中的
应用
随着数字信号处理技术的快速发展，多采样率数字信号处理在数字语音系统中发挥着重要作用。

它通过在数字语音处理过程中使用不同的采样率，提供了更高的灵活性和更好的性能。

首先，多采样率数字信号处理在数字语音编解码中提供了更高的质量和效率。

在语音编码过程中，为了减小数据量和节省传输带宽，采样率通常会降低。

然而，在一些要求高质量语音的应用中，如语音通信和语音识别，需要更高的采样率来保证声音的清晰度和真实性。

通过多采样率数字信号处理技术，可以在编码过程中灵活地提高采样率，从而提供更高质量的语音信号。

其次，多采样率数字信号处理在音频变速和音高转换中发挥重要作用。

在一些音频应用中，如音乐制作和语音合成，需要对音频进行变速和音高转换，以满足不同的需求。

通过多采样率数字信号处理技术，可以按照不同的速度和音高要求，灵活地改变采样率，从而实现音频的变速和音高转换。

此外，多采样率数字信号处理还在降噪和回声消除等音频处理算法中起到重要作用。

在一些嘈杂环境下，语音信号可能会受到环境噪声和回声的干扰。

通过多采样率数字信号处理技术，可以对输入信号进行不同采样率的处理，从而提取出噪声和回声的特征，并通过合适的算法进行降噪和回声消除，提高语音信号的清晰度和可懂性。

总之，多采样率数字信号处理在数字语音系统中具有广泛的应用。

它通过灵活调整采样率，提供了更高质量和更好性能的音频处理和编
解码功能。

因此，在设计和实现数字语音系统时，我们应充分利用多
采样率数字信号处理技术，以提升语音系统的性能。

[离散时间信号处理学习笔记]14.多采样率信号处理多采样率信号处理⼀般是指利⽤增采样、减采样、压缩器和扩展器等⽅式来提⾼信号处理系统效率的技术（These multirate techniques refer in general to utilizing upsampling, downsampling, compressors, and expanders in a variety of ways to increase the efficiency of signal-processing systems. ）本⽂章主要讨论多采样率技术中的两个研究成果：滤波与压缩器/扩展器的互换；多相分解。

尽管上⼀篇⽂章中已经讨论过这部分内容，不过由于这部分是理解本⽂所必须的关键知识点，这⾥将在时域与频域展开更详细的分析。

压缩器假设压缩器的压缩率为M，那么压缩器在时域上的表⽰为x_d[n] = x[nM]x[n]的采样频率为T，那么x_d[n]的采样频率为T_d = MT，按照，有\begin{align*} X(e^{j\omega}) &= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{T}-\frac{2\pi k}{T}\right)\right ]\\ X_d(e^{j\omega}) &= \frac{1}{MT}\sum_{r=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{MT}-\frac{2\pi r}{MT}\right)\right ] \end{align*}压缩前的序列频谱X(e^{j\omega})与压缩后的序列频谱X_d(e^{j\omega})之间有如下关系\begin{align*} X_d(e^{j\omega}) &= \frac{1}{MT}\sum_{r=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{MT}-\frac{2\pi r}{MT}\right)\right ] \\ & = \frac{1}{MT}\left\{\cdot\cdot\cdot+X_c\left[j\left(\frac{\omega}{MT}-\frac{-2\pi}{MT} \right ) \right ] +X_c\left[ j\left(\frac{\omega}{MT}-\frac{0} {MT}\right)\right ] + X_c\left[j\left(\frac{\omega}{MT}-\frac{2\pi}{MT} \right ) \right ]+\cdot\cdot\cdot \right \}\\ & = \frac{1}{MT}\left\{\cdot\cdot\cdot+X_c\left[j\left(\frac{\omega}{MT}-\frac{0}{MT} \right ) \right ]+\cdot\cdot\cdot +X_c\left[ j\left(\frac{\omega}{MT}-\frac{2(M-1)\pi} {MT}\right)\right ]\right.\\ &\quad\qquad\qquad\left.+ X_c\left[j\left(\frac{\omega}{MT}-\frac{2M\pi}{MT} \right ) \right ]+\cdot\cdot\cdot+X_c\left[j\left(\frac{\omega}{MT}-\frac{2M\pi}{MT} -\frac{2(M-1)\pi}{MT}\right ) \right ]+\cdot\cdot\cdot \right \}\\ \end{align*} \begin{align*} \qquad\quad\ &= \frac{1}{MT}\left\{\cdot\cdot\cdot+\sum_{i=0}^{M-1}X_c\left[j\left(\frac{\omega}{MT}-\frac{2i\pi}{MT} \right ) \right ]+\sum_{i=0}^{M-1}X_c\left[j\left(\frac{\omega}{MT}-\frac{2i\pi}{MT}-\frac{2\pi}{T} \right ) \right ]+\cdot\cdot\cdot\right\}\\ &= \frac{1} {MT}\sum_{k=-\infty}^{\infty} \sum_{i=0}^{M-1}X_c\left[j\left(\frac{\omega}{MT}-\frac{2\pi i}{MT}-\frac{2\pi k}{T} \right ) \right ] \\ &=\frac{1} {M}\sum_{i=0}^{M-1}\left\{\frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[j\left(\frac{\omega-2\pi i}{MT}-\frac{2\pi k}{T} \right ) \right ]\right\}\\&=\frac{1}{M}\sum_{i=0}^{M-1}X(e^{j(\omega-2\pi i)/M}) \end{align*}如下图所⽰扩展器假设扩展器的扩展率为L，那么扩展器在时域上的表⽰为x_e[n] = \left\{\begin{matrix} x[n/L], &n=0,\pm L,\pm 2L,\cdot\cdot\cdot \\ 0, &else \end{matrix}\right.扩展前的序列频谱X(e^{j\omega})与扩展后的序列频谱X_e(e^{j\omega})之间有如下关系\begin{align*} X_e(e^{j\omega}) &= \sum_{n=-\infty}^{\infty}x_e[n]e^{-j\omega n}\\ &=\sum_{n=-\infty}^{\infty}x[n/L]e^{-j\omega n}\quad n=0,\pm L,\pm 2L,\cdot\cdot\cdot\\ &=\sum_{k=-\infty}^{\infty}x[k]e^{-j\omega kL}\quad letting\ n=kL\\ &=X(e^{j\omega L}) \end{align*}如下图所⽰滤波器与压缩器互换如上⼀篇⽂章所描述的减采样就是⼀个滤波器与压缩器的级联系统。

目录1.背景 12．具体过程 22.1 整数因子抽取 22.2 整数因子内插 22.3 I/D的采样率转换 22.4多采样率数字信号处理的应用 23．实验过程 23.1整数倍抽取实验 23.2整数倍插值实验 23.3用有理因子I/D的采样率转换进行的实验 2 4．实验结果 24.1信号的整数倍抽取 24.2信号的整数倍插值 24.3用有理因子I/D的采样速率转换 25．结论 25.1整数因子抽取 25.2整数因子插值 25.3有理因子I/D的采样速率转换 26.心得体会与总结 21.背景现在实际系统中，经常要求一个数字系统能工作在多采样率状态，例如：在数字电视系统中，图像采集系统一般按4:4:4标准或4:2:2标准采集数字电视信号，再根据不同的电视质量要求将其转换成其它标准的数字电视信号（如4:2:2,4:1:1,2:1:1）进行处理。

在数字电话系统中，传输的信号既有语音信号又有传真信号，甚至有视频信号。

这些信号的频域成分相差甚远。

因此该系统应具有多种采样率，并能根据所传输的信号自动完成采样率转换。

对一个非平稳随机信号（如语音信号）做频谱分析或编码时，对不同的信号段可根据其频域成分的不同而采用不同的采样率，已到达既满足采样定理，又最大限度的减少数据量的目的。

如果以高采样率采集的数据存在冗余，这时就希望在该数字信号的基础上降低采样率。

多采样率数字信号处理是建立在单抽样率信号处理基础上的一类信号处理。

在传输信号时，由于语音﹑图像、视频信号的中心频率相差很大，所以需要以多种抽样频率来对信号采样来满足各种传输类型的需要。

2．具体过程2.1 整数因子抽取信号的抽取是实现频率降低的方法。

在第二章曾经讨论过，当采样频率大于信号最高频率的2倍时，不会产生混叠失真。

显然，当采样频率远高于信号最高频率时，采样后的信号就会有冗余数据。

此时，通过信号的抽取来降低采样频率，同样不会产生混叠失真。

Xd(n)整数因子抽取原理图：设x(n)=x(t)|t=nTs，欲使fs减少D倍，最简单的方法就是从x(n)中每D个点中抽取一个，依次组成一个新的序列xd(n),即xd(n)=x(Dn)因为是舍去部分点，故可引入冲激函数来进行抽样，得到xd(n)与x(n)之间的表达式：xd(n)=x(n) D(n)其中为周期单位脉冲序列，当且仅当n为D的整数倍时， D(n)的值为1,n为其他值时为零。

多采样率数字信号处理在数字语音系统中的应用多采样率数字信号处理在数字语音系统中的应用随着计算机技术的发展和进步，数字化语音系统得到了广泛应用和发展，为人们的生活带来了诸多便利。

其中，多采样率数字信号处理在数字语音系统中的应用尤为重要。

多采样率数字信号处理是指通过在不同的时间间隔内对信号进行采样，以获得更加准确和丰富的信息。

在数字语音系统中，多采样率数字信号处理可以用于多个方面。

首先，多采样率数字信号处理在语音编解码中起到了重要作用。

在数字通信中，语音信号是以数字信号的形式进行传输的。

在编码过程中，语音信号需要被采样，并经过一系列处理，如量化和编码压缩等，以减小数据量并保留重要信息。

多采样率数字信号处理可以提高编码的准确性和质量，从而提高语音信号的传输效果。

其次，多采样率数字信号处理在语音合成中也有广泛的应用。

语音合成是指通过计算机生成逼真的语音信号。

在语音合成过程中，需要对数字信号进行采样和处理，以模拟人声的特征和音调。

多采样率数字信号处理可以提高语音合成的自然度和逼真度，使得生成的语音信号更加接近真实的人声，提高用户体验。

此外，多采样率数字信号处理还可以在语音识别和语音增强中发挥重要作用。

在语音识别中，需要对输入的语音信号进行特征提取和模式匹配，以识别出语音中的文字内容。

多采样率数字信号处理可以提高特征的准确性和区分度，从而提高识别的准确率。

在语音增强中，可以通过多采样率数字信号处理的技术，如降噪和增益调整等，对语音信号进行优化和改善，使得信号更加清晰可辨，提高语音增强的效果。

总结起来，多采样率数字信号处理在数字语音系统中有着广泛的应用。

它可以在语音编解码、语音合成、语音识别和语音增强等方面发挥重要作用。

通过提高采样率和对信号进行处理，可以提高数字语音系统的性能和效果，为用户提供更好的语音体验。

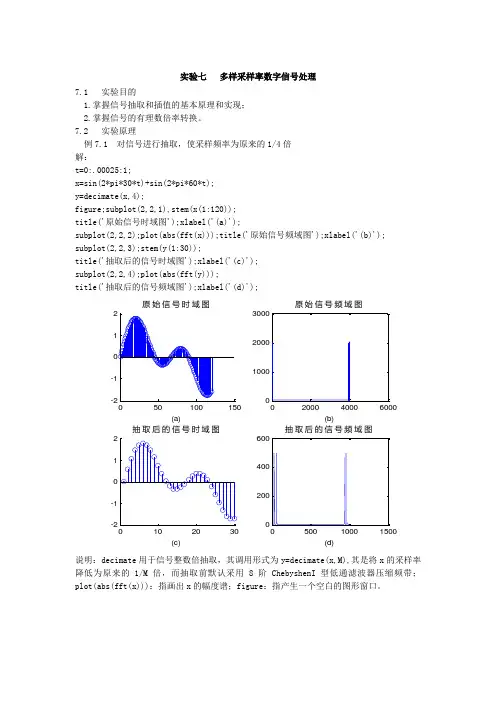
实验七 多样采样率数字信号处理7.1 实验目的1.掌握信号抽取和插值的基本原理和实现；2.掌握信号的有理数倍率转换。

7.2 实验原理例7.1 对信号进行抽取，使采样频率为原来的1/4倍 解：t=0:.00025:1;x=sin(2*pi*30*t)+sin(2*pi*60*t); y=decimate(x,4);figure;subplot(2,2,1),stem(x(1:120)); title('原始信号时域图');xlabel('(a)');subplot(2,2,2);plot(abs(fft(x)));title('原始信号频域图');xlabel('(b)'); subplot(2,2,3);stem(y(1:30));title('抽取后的信号时域图');xlabel('(c)'); subplot(2,2,4);plot(abs(fft(y)));title('抽取后的信号频域图');xlabel('(d)');050100150-2-1012原始信号时域图(a)0200040006000100020003000原始信号频域图(b)0102030-2-1012抽取后的信号时域图(c)050010001500200400600抽取后的信号频域图(d)说明：decimate 用于信号整数倍抽取，其调用形式为y=decimate(x,M),其是将x 的采样率降低为原来的1/M 倍，而抽取前默认采用8阶ChebyshenI 型低通滤波器压缩频带；plot(abs(fft(x)))：指画出x 的幅度谱；figure ：指产生一个空白的图形窗口。

例7.2 信号，采样频率f/fs=1/16,现将采样频率提高为原来的四倍。

解： n=0:30;x=cos(3*pi*n/16); y=interp(x,4);figure;subplot(2,2,1),stem(x);title('原始信号时域图');xlabel('(a)');subplot(2,2,2);plot(abs(fft(x)));title('原始信号频域图');xlabel('(b)'); subplot(2,2,3);stem(y);title('插值后的信号时域图');xlabel('(c)'); subplot(2,2,4);plot(abs(fft(y)));title('插值后的信号频域图');xlabel('(d)');10203040-1-0.500.51原始信号时域图(a)102030405101520原始信号频域图(b)50100150-2-11插值后的信号时域图(c)50100150020406080插值后的信号频域图(d)说明：interp 用于信号整数倍插值，其调用格式为y=interp(x ，L)，是将信号采样率提高L 倍。

多采样率信号处理1．绪论随着数字信号处理的发展，信号的处理、编码、传输和存储等工作量越来越大。

为了节省计算工作量及存储空间，在一个信号处理系统中常常需要不同的采样率及其相互转换，在这种需求下，多速率数字信号处理产生并发展起来。

它的应用带来许多好处，例如：可降低计算复杂度、降低传输速率、减少存储量等。

在信号处理领域，多速率信号处理最早于20世纪70年代提出，由其引出的多速率滤波在数学领域里基于多格算法解决了大量的微分等式。

在多速率数字信号处理发展中，一个突破点是70年代两通道正交镜像滤波器组应用于语音信号的压缩。

在该方法中，信号通过分析滤波器组被分成低通和高通两个子带，每个子带经过2倍抽取和量化后再进行压缩，之后可以通过综合滤波器组近似地重建出原始信号，重建的近似误差一部分源于子带信号的压缩编码，一部分是由分析和综合滤波器组产生的误差，其中最主要的误差是混叠误差，它是由分析滤波器组不是理想带限而引起的。

在很多应用系统中，混叠误差存在一定程度的影响，因此就需要对其进行改进。

多速率系统应用于通信、语音信号处理、谱分析、雷达系统和天线系统，以及在数字音频系统、子带编码技术( 用于声音和图像的压缩) 和模拟语音个人系统(如标准电话通信) 等方面的应用。

另外还应用于多相理论和多速率系统在一些非传统领域，包括：高效率信号压缩的多速率理论；高效窄带滤波器的脉冲响应序列的编码新技术的推导；可调整的多级响应FIR滤波器的设计等。

基于上述研究的发展，从20世纪80年代初开始，多速率数字信号处理技术在工程实践中得到广泛的应用，主要用于通信系统、语音、图像压缩、数字音频系统、统计和自适应信号处理、差分方程的数值解等。

多速率信号处理在基础理论和应用领域的蓬勃发展，也促进了整个数字信号处理界的发展。

2．采样率转换基础理论实现采样率转换的方法有三个：一是若原模拟信号x (t)可以再生，或是己记录下来了的话，那么可重新抽样；二是将x(n)通过D/A变成模拟信号x(t)后，对x (t)经A/D再抽样；三是发展一套算法，对抽样后的数字信号x(n)在“数字域”作采样率转换，以得到新的抽样。

实验设计：多采样率数字信号处理分析实验名称：多采样率数字信号处理一．实验目的：1. 掌握信号抽取和插值的基本原理和实现；2．掌握信号的有理数倍率转换。

二．实验原理：多采样率数字信号处理共分为3方面的问题：信号的整数倍抽取、信号的整数倍插值和信号的有理数倍速率转换。

Matlab 信号处理工具箱提供了抽取函数decimate 用于信号整数倍抽取，其调用格式为：y=decimate(x,M)y=decimate(x,M,n)y=decimate(x,M,’fir’)y=decimate(x,M,n,’fir’)其中y=decimate(x,M)将信号x 的采样率降低为原来的M1，抽取前缺省地采用8阶Chebyshev Ⅰ型低通滤波器压缩频带。

y=decimate(x,M,n)指定所采用Chebyshev Ⅰ型低通滤波器的阶数，通常13 n 。

y=decimate(x,M,’fir’)指定用FIR 滤波器来压缩频带。

y=decimate(x,M,n,’fir’) 指定所用FIR 滤波器的阶数。

Matlab 信号处理工具箱提供了插值函数interp 用于信号整数倍插值，其调用格式为：y=interp(x,L)y=interp(x,L,n,alpha)[y,b]=interp(x,L,n,alpha)其中y=interp(x,L)将信号的采样率提高到原来的L 倍。

y=interp(x,L,n,alpha)指定反混叠滤波器的长度n 和截止频率alpha ，缺省值为4和0.5。

[y,b]=interp(x,L,n,alpha)在插值的同时，返回反混叠滤波器的系数向量。

信号的有理数倍速率转换是使信号的采样率经由一个有理因子M L 来改变，可以通过插值和抽取的级联来实现。

Matlab 信号处理工具箱提供了重采样函数resample 用于有理倍数速率转换，其调用格式为：y=resample(x,L,M);y=resample(x,L,M,n);y=resample(x,L,M,n,beta);y=resample(x,L,M,b);[y,b]= y=resample(x,L,M);其中，y=resample(x,L,M);将信号x 的采样率转换为原来的M L 倍，所用的低通滤波器为kaiser 窗的FIR 滤波器。

目录一、课程设计的性质与目的 (1)二、课程设计题目 (1)1. 设计目的 (1)2. 设计要求 (1)3. 设计步骤 (2)三、课程设计要求 (2)四、设计进度安排 (2)五、设计原理 (3)1. 巴特沃斯滤波器 (3)2. 采样定理............................................. 错误！未定义书签。

3. 椭圆滤波器........................................... 错误！未定义书签。

4. 抽取与内插 (5)六、实验步骤及效果图 (6)1. 信源的时域和频域分析 (6)2. 对原始信号进行滤波 (7)3. 对滤波后的信号采样 (8)4. 椭圆滤波器滤波 (9)5. 对语音信号进行抽取和内插处理 (10)6. 语音信号的恢复 (11)7. 信号波形图对比 (12)七、问题及解决办法 (14)1. 信源的时域和频域分析原代码 (14)2. 对原始信号进行滤波原代码 (15)3. 椭圆滤波器滤波原代码 (16)八、心得体会 (17)一、课程设计的性质与目的《数字信号处理》课程是通信专业的一门重要专业基础课，是信息的数字化处理、存储和应用的基础。

通过该课程的课程设计实践，使学生对信号与信息的采集、处理、传输、显示、存储、分析和应用等有一个系统的掌握和理解；巩固和运用在《数字信号处理》课程中所学的理论知识和实验技能，掌握数字信号处理的基础理论和处理方法，提高分析和解决信号与信息处理相关问题的能力，为以后的工作和学习打下基础。

数字滤波器是一种用来过滤时间离散信号的数字系统，通过对抽样数据进行数学处理来达到频域滤波的目的。

根据其单位冲激响应函数的时域特性可分为两类：无限冲激响应（IIR）滤波器和有限冲激响应（FIR）滤波器。

二、课程设计题目多采样率数字信号处理在数字语音系统中的应用1、设计目的学习多采样率数字信号处理原理，采用整数因子抽取与整数因子内插来解决数字语音系统中的信号采样过程中存在的问题，并用MATLAB编程实现，加深对多采样率数字信号处理的理解。