《433余角和补角》导学

4.3.3余角和补角【出示目标】1．了解两个角互余或互补的意义．2．掌握同角或等角的余角相等；同角或等角的补角相等．3．理解方位角的概念，会用角描述方向，解决实际问题．【预习导学】自学指导看书学习第137、138页的内容，知道什么是补角和余角，以及它们的性质．知识探究1．一般地，如果两个角的和等于90°(直角)，就说这两个角互为余角．即其中每一个角都是另一个角的余角．几何语言表示为：如果∠1＋∠2＝90°，那么∠1与∠2互为余角．2．一般地，如果两个角的和等于180°(平角)，就说这两个角互为补角．即其中一个是另一个角的补角．几何语言表示为：如果∠1＋∠2＝180°，那么∠1与∠2互为补角．3．性质：等角的余角相等，等角的补角相等．【自学反馈】1．判断题：(1)90度的角叫余角，180度的角叫补角．(×)(2)若∠1＋∠2＋∠3＝90°则∠1，∠2，∠3互为余角．(×)(3)如果一个角有补角，那么这个角一定是钝角．(×)(4)互补的两个角不可能相等．(×)(5)钝角没有余角，但一定有补角．(√)(6)互余的两个角一定都是锐角，两个锐角一定互余．(×)(7)如果∠A＝25°，∠B＝75°，那么∠A与∠B互为余角．(×)(8)如果∠A＝x°，∠B＝(90－x)°，那么∠A与∠B互余．(√)2．已知一个角的补角是这个角的余角的3倍，求这个角的度数．解：45°.【出示目标】活动1：小组讨论1．如图，点A、O、B在同一直线上，OD平分∠AOB，∠COE ＝90°.回答下列问题：(1)写出图中所有的直角∠AOD，∠BOD，∠EOC；(2)写出图中与∠AOE相等的角∠3；(3)写出图中∠AOE所有的余角∠2，∠4；(4)写出图中∠COD的补角∠EOB；(5)写出图中∠DOE的补角∠AOC.2．如图，点O在直线AB上，OD平分∠COA，OE平分∠COB.①∠COB＋∠AOC＝180°，∠EOD＝90°.②图中互余的角有 4 对，互补的角有 5 对．活动2：活学活用1．请认真观察下图，回答下列问题：(1)图中有几对互余的角？(2)图中哪几对角是相等的角(直角除外)？为什么？解：(1)6；(2)∠C＝∠B，∠COD＝∠BOE＝∠A.2．用方位角描述下列方向．【课堂小结】1．余角、补角的概念：(1)和为90°的两个角互为余角；(2)和为180°的两个角互为补角．2．余角、补角的性质：(1)等角的余角相等；(2)等角的补角相等．【随堂训练】教学至此，敬请使用学案随堂训练部分．。

《余角和补角》导学案一、学习目标1、理解余角和补角的概念。

2、掌握余角和补角的性质，并能运用其解决简单的几何问题。

3、培养观察、分析和推理能力，体会数学在实际生活中的应用。

二、学习重点1、余角和补角的概念。

2、余角和补角的性质。

三、学习难点余角和补角性质的应用。

四、知识回顾1、角的度量单位：度、分、秒。

2、直角的度数为 90°。

五、新课导入在生活中，我们常常会遇到一些与角的数量关系有关的问题。

比如，在一幅三角板中，有两个角的度数之和等于 90°，而在一些图形中，两个角的度数之和等于180°。

那么，这些角之间有着怎样的特殊关系呢？今天我们就来学习余角和补角。

六、余角的概念如果两个角的和等于 90°（直角），就说这两个角互为余角，简称互余。

其中一个角是另一个角的余角。

例如，若∠1 ＋∠2 ＝ 90°，则∠1 与∠2 互为余角，∠1 是∠2 的余角，∠2 也是∠1 的余角。

练习 1：已知∠A ＝ 20°，则∠A 的余角为多少度？解：因为互为余角的两个角的和为 90°，所以∠A 的余角＝ 90° 20°＝ 70°七、补角的概念如果两个角的和等于 180°（平角），就说这两个角互为补角，简称互补。

其中一个角是另一个角的补角。

例如，若∠3 ＋∠4 ＝ 180°，则∠3 与∠4 互为补角，∠3 是∠4 的补角，∠4 也是∠3 的补角。

练习 2：已知∠B ＝ 110°，则∠B 的补角为多少度？解：因为互为补角的两个角的和为 180°，所以∠B 的补角＝ 180°110°＝ 70°八、余角和补角的性质1、同角（或等角）的余角相等。

2、同角（或等角）的补角相等。

证明性质 1：已知∠1 ＋∠2 ＝ 90°，∠1 ＋∠3 ＝ 90°则∠2 ＝ 90°∠1，∠3 ＝ 90°∠1所以∠2 ＝∠3证明性质 2：已知∠4 ＋∠5 ＝ 180°，∠4 ＋∠6 ＝ 180°则∠5 ＝ 180°∠4，∠6 ＝ 180°∠4所以∠5 ＝∠6练习 3：已知∠7 与∠8 互余，∠8 与∠9 互余，求证∠7 ＝∠9证明：因为∠7 与∠8 互余，所以∠7 ＋∠8 ＝ 90°因为∠8 与∠9 互余，所以∠8 ＋∠9 ＝ 90°所以∠7 ＝ 90°∠8，∠9 ＝ 90°∠8所以∠7 ＝∠9练习 4：已知∠10 与∠11 互补，∠11 与∠12 互补，求证∠10 ＝∠12证明：因为∠10 与∠11 互补，所以∠10 ＋∠11 ＝ 180°因为∠11 与∠12 互补，所以∠11 ＋∠12 ＝ 180°所以∠10 ＝ 180°∠11，∠12 ＝ 180°∠11所以∠10 ＝∠12九、余角和补角的应用1、在几何图形中，通过寻找余角和补角来求解角的度数。

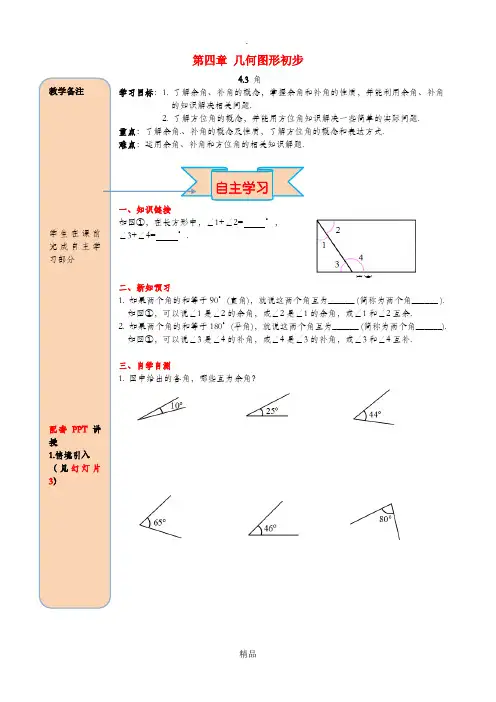
80︒65︒46︒44︒25︒10︒170︒120︒100︒150︒80︒10︒30︒60︒21434.3.3余角和补角七年级一班二班 学习目标1、在具体的现实情境中，认识一个角的余角和补角，掌握余角和补角的性质。

认识理解方位角，能确定具体物体的方位。

2、进一步提高抽象概括能力，发展空间观念和知识运用能力，学会简单的逻辑推理，并能对问题的结论进行合理的猜想。

学习重点：认识角的互余、互补关系及其性质。

认识方位角，找准方位。

学习难点：归纳出余角、补角的性质，并能用规范的语言描述性质是难点。

探 究 案探究一：余角和补角1、结合教材理解互为余角的定义：如果两个角的和是 ( )，那么这两个角叫做互为余角，其中一个角是另一个角的余角。

几何语言表示为：如果∠1+∠2= ，那么∠1与∠2互为余角，即:∠1是∠2的余角或∠2是∠1的余角。

2、理解应用⑴：图中给出的各角，哪些互为余角？3、结合教材理解互为补角的定义：如果两个角的和是 ( )，那么这两个角叫做互为补角，其中一个角是另一个角的补角。

几何语言表示为：如果∠3+∠4= °，那么∠3与∠4互为补角，即:∠3是∠4的补角或∠4是∠3的补角 4、理解应用⑵：（1）图中给出的各角，哪些互为补角？（2）填下列表：2143西北西南东南东北北西南东东结论：同一个锐角的补角比它的余角大 （3）填空：①70°的余角是 ，补角是 。

②∠α（∠α <90°）的余角是 ，它的补角是 。

如何判断两个角是互余还是互补呢？5、探究补角(余角)的性质：如图∠1 与∠2互补，∠３ 与∠４互补 ，如果∠1＝∠３,那么∠2与∠４相等吗？为什么？归纳结论：答：∠2 与∠4相等。

∵∠1与∠2互余，∠3与∠4互余 ( )∴ ∠2 = 90°─∠1，∠4 = 90°─∠3 ( )∵ ∠1=∠3 ( )∴ ∠2 =∠4 ( ) 补角性质： 根据补角的性质你能否归纳出余角的性质？例1:若一个角的补角等于它的余角4倍，求这个角的度数。

精品“正版”资料系列，由本公司独创。

旨在将“人教版”、”苏教版“、”北师大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友。

本资源创作于2020年8月，是当前最新版本的教材资源。

包含本课对应内容，是您备课、上课、课后练习以及寒暑假预习的最佳选择。

第 2学时内容：正数和负数（2）学习目标:1、会用正、负数表示具有相反意义的量.2、通过正、负数学习，培养学生应用数学知识的意识.3、通过探究，渗透对立统一的辨证思想学习重点：用正、负数表示具有相反意义的量学习难点：实际问题中的数量关系教学方法：讲练相结合教学过程一、.学前准备通过上节课的学习，我们知道在实际生产和生活中存在着两种不同意义的量,为了区分它们,我们用正数和负数来分别表示它们.问题1：“零”为什么即不是正数也不是负数呢?引导学生思考讨论,借助举例说明.参考例子:温度表示中的零上,零下和零度.二.探究理解解决问题先引导学生分析，再让学生独立完成例(1)一个月内,小明体重增加2kg,小华体重减少1kg,小强体重无变化,写出他们这个月的体重增长值;(2)2009年下列国家的商品进出口总额比上一年的变化情况是:美国减少6.4%, 德国增长1.3%,法国减少2.4%, 英国减少3.5%,意大利增长0.2%, 中国增长7.5%.写出这些国家2009年商品进出口总额的增长率.解:(1)这个月小明体重增长2kg,小华体重增长-1kg,小强体重增长0kg.(2)六个国家2009年商品进出口总额的增长率:美国-6.4%, 德国1.3%,法国-2.4%, 英国-3.5%,意大利0.2%, 中国7.5%.三、巩固练习从0表示一个也没有,是正数和负数的分界的角度引导学生理解.在学生的讨论中简单介绍分类的数学思想先不要给出有理数的概念.在例题中,让学生通过阅读题中的含义,找出具有相反意义的量,决定哪个用正数表示,哪个用负数表示.通过问题(2)提醒学生审题时要注意要求,题中求的是增长率,不是增长值.四、阅读思考问题:1.直径为30.032mm和直径为29.97的零件是否合格?2.你知道还有那些事件可以用正负数表示允许误差吗?请举例.五、小结1、本节课你有那些收获？2、还有没解决的问题吗？六、应用与拓展选做题1、甲冷库的温度是-12°C,乙冷库的温度比甲冷酷低5°C,则乙冷库的温度是.2、一种零件的内径尺寸在图纸上是9±0.05(单位:mm),表示这种零件的标准尺寸是9mm,加工要求最大不超过标准尺寸多少?最小不小于标准尺寸多少?3、吐鲁番的海拔是－155m，珠穆朗玛峰的海拔是8848m ，它们之间相差多少米？4、如果规定向东为正，那么从起点先走+40米，再走－60米到达终点，问终点在起点什么方向多少米？应怎样表示？一共走过的路程是多少米？5、10筐橘子，以每筐15㎏为标准，超过的千克数记作正数，不足的千克数记作负数。

《4．3.3 余角和补角》教案【教学目标】1．在具体情境中认识余角和补角，掌握余角和补角的性质；(重点)2．能利用余角和补角的性质进行计算和简单的推理．(重点)【教学过程】一、情境导入让学生观察意大利著名建筑比萨斜塔．比萨斜塔建于1173年，工程曾间断了两次很长的时间，历经约二百年才完工．设计为垂直建造，但是在工程开始后不久便由于地基不均匀和土层松软而倾斜．二、合作探究探究点一：余角和补角及其性质【类型一】余角和补角的概念如果α与β互为余角，则( )A．α＋β＝180° B．α－β＝180°C．α－β＝90° D．α＋β＝90°解析：如果α与β互为余角，则α＋β＝90°.故选D.方法总结：正确记忆互为余角的定义是解决问题的关键．【类型二】利用余角和补角计算求值已知∠A与∠B互余，且∠A的度数比∠B度数的3倍还多30°，求∠B 的度数．解析：根据∠A与∠B互余，得出∠A＋∠B＝90°，再由∠A的度数比∠B度数的3倍还多30°，从而得到∠A＝3∠B＋30°，再把两个算式联立即可求出∠2的值．解：∵∠A与∠B互余，∴∠A＋∠B＝90°，又∵∠A的度数比∠B度数的3倍还多30°，∴∠A＝3∠B＋30°，∴3∠B＋30°＋∠B＝90°，解得∠B＝15°.故∠B的度数为15°.方法总结：此题把角的关系结合方程问题一起解决，即把相等关系的问题转化为方程问题，利用方程组来解决．【类型三】余角、补角和角平分线的综合计算如图，已知∠AOB在∠AOC内部，∠BOC＝90°，OM、ON分别是∠AOB，∠AOC的平分线，∠AOB与∠COM互补，求∠BON的度数．解析：根据补角的性质，可得∠AOB＋∠COM＝180°，根据角的和差，可得∠AOB＋∠BOM＝90°，根据角平分线的性质，可得∠BOM＝12∠AOB，根据解方程，可得∠AOB的度数，根据角的和差，可得答案．解：由∠AOB与∠COM互补，得∠AOB＋∠COM＝180°.由角的和差，得∠AOB＋∠BOM＋∠COB＝180°，∠AOB＋∠BOM＝90°.由OM是∠AOB的平分线，得∠BOM＝12∠AOB，即∠AOB＋12∠AOB＝90°.解得∠AOB＝60°.由角的和差，得∠AOC＝∠BOC＋∠AOB＝90°＋60°＝150°.由ON平分∠AOC得∠AON＝12∠AOC＝12×150°＝75°.由角的和差，得∠BON＝∠AON－∠AOB＝75°－60°＝15°.方法总结：本题考查了余角与补角及角平分线的相关知识，利用了补角的性质，角的和差，角平分线的性质进行计算，解决问题一定要结合图形认真分析，做到数形结合．探究点二：方位角【类型一】利用方位角确定方向M地是海上观测站，从M地发现两艘船A、B的方位如图所示，下列说法中正确的是( )A．船A在M的南偏东30°方向B．船A在M的南偏西30°方向C．船B在M的北偏东40°方向D．船B在M的北偏东50°方向解析：船A在M的南偏西90°－30°＝60°方向，故A、B选项错误；船B 在M的北偏东90°－50°＝40°方向，故C正确，D错误．故选C.方法总结：用方位角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边，故描述方位角时，一般先叙述北或南，再叙述偏东或偏西．【类型二】方位角的有关计算如图所示，甲、乙、丙三艘轮船从港口O出发，当分别行驶到A、B、C 处时，经测量得甲船位于港口的北偏东44°方向，乙船位于港口的北偏东76°方向，丙船位于港口的北偏西45°方向．(1)求∠BOC的度数；(2)求∠AOB的度数．解析：(1)根据方向角的表示方法，可得∠EOB，∠EOC的度数，根据角的和差，可得答案；(2)根据方向角的表示方法，可得∠EOB，∠EOA的度数，根据角的和差，可得答案．解：如图，(1)由乙船位于港口的北偏东76°方向，丙船位于港口的北偏西45°方向，得∠EOB＝76°，∠EOC＝45°.由角的和差，得∠BOC＝∠EOB＋∠EOC ＝76°＋45°＝121°；(2)由甲船位于港口的北偏东44°方向，乙船位于港口的北偏东76°方向，得∠EOB＝76°，∠EOA＝44°.由角的和差，得∠AOB＝∠EOB－∠EOA＝76°－44°＝32°.方法总结：解决本题主要是理解方向角的表示方法，结合图形找到相应的角，然后进行计算．三、板书设计1．互余、互补(1)和为90°的两个角互余；(2)和为180°的两个角互补．2．方位角【教学反思】通过比萨斜塔这一学生熟知的著名建筑激发学生的学习兴趣，再运用现代化的教学手段，把图形的“静”变成“动”，在动态课件演示中引出概念，增强了趣味性，并且可以充分调动学生的学习兴趣，一下子把学生吸引到课堂上来．这样也把书本上原本呆板的概念激活了，使数学知识充满新鲜感，实现了书本知识和学生发现的一种沟通，增强学生对几何图形的敏感性．《4.3.3 余角和补角》同步练习能力提升1.如图,A,O,B三点在一条直线上,已知∠AOD=25°,∠COD=90°,则∠BOC的度数为()A.25°B.85°C.115°D.155°2.如果∠AOB+∠BOC=90°,∠BOC+∠COD=90°,那么∠AOB与∠COD的关系是()A.互余B.互补C.相等D.不能确定3.如图,点O在直线AB上,∠COB=∠DOE=90°,则图中相等的角的对数是()A.3B.4C.5D.74.如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是 ()A.右转80°B.左转80°C.右转100°D.左转100°5.在直线AB上任取一点O,过点O作射线OC,OD,使∠COD=90°,当∠AOC=30°时,∠BOD的大小是()A.60°B.120°C.60°或90°D.60°或120°6.如图,将两块三角板的直角顶点重合后叠放在一起,若∠1=40°,则∠2= .7.如图,射线OP表示的方向是.8.如图,桌面上平放着一块三角板和一把直尺,小明将三角板的直角顶点紧靠直尺的边缘,他发现无论是将三角板绕直角顶点旋转,还是将三角板沿直尺平移,∠1与∠2的和总是保持不变,则∠1与∠2的和是度.9.学校、电影院、公园在平面图上的标点分别为A,B,C,如果电影院在学校的正东方向上,公园在学校的南偏西25°的方向上,那么平面图上的∠CAB= 度.10.互余的两个角的度数之比为3∶7,则这两个角的度数分别是多少?11.如图,一只蚂蚁从点O出发,沿北偏东45°的方向爬行2.5 cm,碰到障碍物(记作B)后折向北偏西60°的方向爬行3 cm(此时位置记作点C).(1)画出蚂蚁的爬行路线;(2)求出∠OBC的度数.注:如图,,∠1=∠2★12.如图所示,已知O是直线AB上一点,∠AOE=∠FOD=90°,OB平分∠COD,图中与∠DOE互余的角有哪些?与∠DOE互补的角有哪些?并说明理由.创新应用★13.按如图所示的方法折纸,然后回答问题:(1)∠2是多少度的角?为什么?(2)∠1与∠3有何关系?(3)∠1与∠AEC,∠3和∠BEF分别有何关系?★14.根据互余和互补的定义知,20°角的补角为160°,余角为70°,160°-70°=90°;25°角的补角为155°,余角为65°,155°-65°=90°;50°角的补角为130°,余角为40°,130°-40°=90°;75°角的补角为105°,余角为15°,105°-15°=90°……观察以上几组数据,你能得到什么结论?写出你的结论.参考答案能力提升1.C因为∠AOC=∠COD-∠AOD=90°-25°=65°,所以∠BOC=180°-∠AOC=180°-65°=115°.2.C3.C因为∠COB=90°,所以∠AOC=180°-∠BOC=180°-90°=90°,所以∠AOC=∠BOC=∠DOE;因为∠BOD+∠COD=∠EOC+∠COD=90°,所以∠EOC=∠BOD;因为∠AOE+∠EOC=∠COD+∠EOC=90°,所以∠AOE=∠COD,共5对.4.A如图,∠ECF=20°,∠FCD=60°,要从BC方向转向CD方向,需转过的角为∠ECD=∠ECF+∠FCD=20°+60°=80°,即右转80°.5.D根据题意画图为如图①和图②,在图①中∠BOD的度数是60°,在图②中∠BOD的度数是120°,所以∠BOD的度数是60°或120°.6.40°7.南偏西62°8.90由图形知∠1,∠2与直角三角板的直角形成一个平角,所以无论是将三角板绕直角顶点旋转,还是将三角板沿直尺平移,形成的始终是一个平角.所以∠1与∠2的和是90度.9.11510.解:设这两个角的度数分别为3x°,7x°,由题意,得3x°+7x°=90°,解得x°=9°,3x°=27°,7x°=63°.答:这两个角的度数分别是27°,63°.11.解:(1)如图.(2)∠OBC=90°-60°+90°-45°=75°.12.解:与∠DOE互余的角有∠EOF,∠BOD,∠BOC;与∠DOE互补的角有∠BOF,∠COE.理由:∠DOE+∠EOF=90°,∠DOE+∠BOD=∠BOE=180°-∠AOE=90°,∠DOE+∠BOC=∠DOE+∠BOD=90°,∠DOE+∠BOF=∠AOF+∠BOF=180°,∠DOE+∠COE=∠DOE+∠BOF=180°.创新应用13.解:(1)∠2=90°.因为折叠,则∠1与∠3的和与∠2相等,而这三个角加起来,正好是平角∠BEC,所以∠2=×180°=90°.(2)因为∠1与∠3组成的大角和∠2相等,且三个角加起来恰好是一个平角,所以∠1+∠3=90°.所以∠1与∠3互余.(3)因为∠1与∠AEC的和为180°,∠3与∠BEF的和为180°,所以∠1与∠AEC互补,∠3与∠BEF互补.14.解:设一个角的度数为x°,则补角为(180-x)°,它的余角为(90-x)°.因为180-x-(90-x)=90,所以一个角的补角比它的余角大90°.第四章几何图形初步4.2 直线、射线、线段《第1课时直线、射线、线段》导学案【学习目标】：1. 了解余角、补角的概念，掌握余角和补角的性质，并能利用余角、补角的知识解决相关问题.2. 了解方位角的概念，并能用方位角知识解决一些简单的实际问题.【重点】：了解余角、补角的概念及性质，了解方位角的概念和表达方式.【难点】：运用余角、补角和方位角的相关知识解题.【自主学习】一、知识链接如图①，在长方形中，∠1+∠2= °，∠3+∠4= °.二、新知预习1. 如果两个角的和等于90°(直角)，就说这两个角互为______ (简称为两个角______ ).如图①，可以说∠1是∠2的余角，或∠2是∠1的余角，或∠1和∠2互余.2. 如果两个角的和等于180°(平角)，就说这两个角互为______ (简称为两个角______).如图①，可以说∠3是∠4的补角，或∠4是∠3的补角，或∠3和∠4互补.三、自学自测1. 图中给出的各角，哪些互为余角？2. 图中给出的各角，哪些互为补角？四、我的疑惑_________________________________________________________________ _____________________________________________________________________ 【课堂探究】一、要点探究探究点1：有关余角和补角的计算例1 若一个角的补角等于它的余角的 4 倍，求这个角的度数.方法总结：余补角问题中，若角之间有比较明显的倍分关系，可尝试将较小的角设为未知数，列方程解答.例2 如图，已知O为AD上一点，∠AOC与∠AOB互补，OM，ON分别为∠AOC，∠AOB的平分线，若∠MON=40°，试求∠AOC与∠AOB的度数．观察与思考：∠α∠α的余角∠α的补角5°32°45°77°62°23′x°(0＜x＜90)观察可得结论：锐角的补角比它的余角大_____.针对训练1.如果∠a=36°，那么∠a的余角等于（）A．54° B．64° C．144° D．134°2.如图，将一副直角三角板如图放置，若∠AOD=18°，则∠BOC的度数为_____.第2题图变式题图【变式题】一副三角板按如图方式摆放，且∠1的度数比∠2的度数大44°，则∠1=______.3.已知∠A与∠B互余，且∠A的度数比∠B度数的3倍还多30°，求∠B的度数.探究点2：余角和补角的性质思考：∠1 与∠2，∠3都互为补角，∠2 与∠3 的大小有什么关系？例3 如图，O为直线AB上一点，OD平分∠AOC，∠DOE=90°．（1）∠AOD的余角是_______________，∠COD的余角是_________________;（2 ）OE是∠BOC的平分线吗？请说明理由．针对训练如图，已知∠AOB=90°，∠AOC=∠BOD，则与∠AOC互余的角有__________.探究点3：方位角八大方位正东：正南：正西：正北：西北方向：西南方向：东北方向：东南方向：例4 如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上. 同时，在它北偏东40°，南偏西10°，西北 (即北偏西45°)方向上又分别发现了客轮B，货轮C和海岛D. 仿照表示灯塔方位的方法画出表示客轮B，货轮C 和海岛D方向的射线.针对训练1. 如图，说出下列方位(1) 射线 OA 表示的方向为 .(2) 射线 OB 表示的方向为 .(3) 射线 OC 表示的方向为 . .(4) 射线 OD 表示的方向为 .2.费俊龙、聂海胜乘坐“神舟”六号遨游太空时，我国当时派出远望一号~四号船队，跟踪检测. 其中远望一、二号停在太平洋洋面上，某一时刻，分别测得神舟六号在北偏东60°和北偏东30°的方向，你能在下图中画出当时神舟六号所处的位置吗？二、课堂小结【当堂检测】1.一个角的余角是它的2倍，这个角的度数是（）A．30°B．45°C．60°D．75°2.下列说法正确的是（）A．一个角的补角一定大于它本身B．一个角的余角一定小于它本身C．一个钝角减去一个锐角的差一定是一个锐角D．一个角的余角一定小于其补角3.已知∠A与∠B互余，∠B与∠C互补，若∠A=60°，则∠C的度数是_______.4.∠1与∠2 互余，∠1 = (6x + 8)°，∠2 = (4x－8)°，则∠1= ，∠2= .5. 请认真观察下图，回答下列问题：(1)图中有哪几对互余的角？(2) 图中哪几对角是相等的角(直角除外)？为什么？6 垃圾打捞船A和B都停驻在湖边观测湖面，从A船发现它的北偏东60°方向有白色漂浮物，同时，从B船也发现该白色漂浮物在它的北偏西30°方向.(1) 试在图中确定白色漂浮物C的位置；(2) 点C在点A的北偏东60°的方向上，那么点A在点C的________方向上.A. 南偏东30°B. 南偏西30°C. 南偏东60°D. 南偏西60°。

合作交流
（1）找一副三角板中互余的两个角.
（2）说出一个锐角，同伴尝试回答这个角的余角和补角.
思考：(1)是不是所有的角都有余角和补角？
(2)如何求∠α的余角和补角？
结论：(1)钝角没有_____，只有______.
(2)∠α的余角为___________；∠α的补角为________________.
[活动五]归纳小结，深化新知
本节课你学习了哪些知识？
在探索知识的过程中，你用了哪些方法？对你今后的学习有什么帮助？
[活动六]分层作业，课堂检测
1.教科书第139页练习第3、4题，教科书第140页习题4.3第13题.
2.思维拓广：一个角的补角比它的余角的2倍还大25°，求这个角.
思考：通过练习，你能发现同一个角的余角之间有什么关系？补角之间呢？两个相等的角的余角或补角之间又有什么关系呢？
性质:同角（等角）的_____相等.
同角（等角）的_____相等.
[活动三]应用新知，形成技能
例点A、O、B在同一条直线上，射线OD和射线OE分别平分∠AOC和∠COB，图中哪些角互为余角？
[活动二]探索归纳，学习新知
定义：一般地，如果两个角的和等于90°（直角），就说这两个角互为余角，即其中一个角是另一个角的余角.
类似地，如果两个角的和等于180°（平角），就说这两个角互为补角，即其中一个角是另一个角的补角.
想一想：
如图，若∠1+∠2=90°，则∠1与∠2互为_____；∠1的余角是______；∠2是______的余角；
课题：4.3.3余角和补角（1）
姓名：班级：授课时间:
课型
新授课
备课教师
刘会英
审核
学
习

课题：4.3.3余角和补角编号：第44号主备人：复备人：审核人：科研处审核：1.知道余角和补角的定义,能求一个角的余角和补角.2.明白“同角(等角)的余角相等,同角(等角)的补角相等”,并能应用余角、补角的性质进行简单的计算和说理.3.知道方位角的定义,会画方位角,能用方位角描述物体相对于某点的方向.4.重点:余角和补角的定义及性质,方位角的画法.【问题探究】阅读教材P137~138,回答下列问题.探究一:1.如果两个角的和等于就说这两个角互为余角,即其中一个角是另一个角的余角.2.如果两个角的和等于 ,就说这两个角互为补角,即其中一个角是另一个角的补角.【讨论】1.画出一个锐角的余角和补角,互补、互余的两角是否一定有公共顶点或公共边呢?2.如果∠1+∠2=90°,能否说∠1是余角,∠2是余角呢?为什么?∠1+∠2=180呢?【预习自测】已知∠α=35°,则∠α的余角是()A.35°B.55°C.65°D.145°探究二:1.(1)如果∠1与∠α互余,∠2与∠α互余,那么∠1与∠2相等吗?为什么?(2)如果∠1与∠α互余,∠2与∠β互余,∠α=∠β,那么∠1与∠2相等吗?为什么?2.(1)如果∠1与∠β互补,∠2与∠β互补,那么∠1与∠2相等吗?为什么?(2)如果∠1与∠α互补,∠2与∠β互补,∠α=∠β,那么∠1与∠2相等吗?为什么?【预习自测】如图,直线CD过点O,且OC平分∠AOB,说出∠AOD与∠BOD的大小关系和理由?【归纳】( )的余角相等, ( )的补角相等.探究三:请画出表示下列方向的射线.①南偏东25°;②北偏西60°;③西南方向(即南偏西45°).【归纳】1.方位角通常是以南、北方向为角的,另一边为角的.2.东北方向,即45°;东南方向,即45°;西北方向,即45°;西南方向,即45°.【预习自测】如图,点A位于点O的(B)A.南偏东35°B.北偏西65°C.南偏东65°D.南偏西65°互动探究1:25°的余角和补角分别是多少度?一个角的补角比它的余角大多少度?[变式训练]一个角的余角比它的补角的还多1°,求这个角.(方法指导:在解决几何问题时,常设未知数列方程求解,即将几何问题转化为代数问题.)互动探究2:如图,A、O、D三点在同一条直线上,∠AOB=∠COD,问其中哪几对角互为补角?[变式训练]OE平分∠AOC,OD平分∠COB,则∠EOD= ,∠2的余角为,∠2的补角为.互动探究3:如图,点O是直线AB上一点,OC平分∠AOB,∠DOE=90°,∠AOD和∠COE相等吗?为什么?[变式训练]除直角外,上题中还有哪些相等的角?请说明理由.【方法归纳交流】要说明两个角相等,只要说明这两个角是的余角(或补角)即可.互动探究4:在一幅学校的地图上,有教学楼、食堂、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,只知道图书馆在教学楼的东北方向,在食堂的南偏西60°方向,你能确定图书馆的位置吗?。

§4.3.3余角和补角第一课时学案一、课标对本课时的具体要求：理解余角、补角的概念，探索并掌握同角（等角）的余角相等，同角（等角）的补角相等的性质。

二、本课时的知识网络三、本课时的重点、难点【重点】认识角的互余、互补关系及其性质，【难点】通过简单的推理，归纳出余角、补角的性质，并能用规范的语言描述性质是难点。

四、学习目标1、在具体的现实情境中，认识一个角的余角和补角，2、掌握余角和补角的性质。

五、学习过程（一）多媒体出示活动指导，在明确的活动要求和问题引领下引导学生积极参与探讨和自主学习。

（5分钟）（学生根据要求，自读课本，完成学案所给的问题，在明确的引领下引导学生积极参与探讨和学习）（二）展示交流 探究新知(10分钟) 探究活动1：如图，是一个放在直线上的直角三角板，它的两个锐角∠CAB 与∠CBA 之间有什么关系？ ∠ABC 与∠CBD 有什么关系？答：两个锐角∠CAB 与∠CBA 的和等于 ，∠ABC 与∠CBD 的和等于 . 2.互为余角的定义：就说这两个角互为余角。

如图，若∠1=230，∠2=670，∠1与∠2互为 ；若∠AOB=900，∠3与∠4互为 。

3.互为补角的定义：如果两个角的和是180°(平角)，那么这两个角叫做 ，其中一个角是另一个角的。

如图，若∠5=230，∠6=1570，∠5与∠6互为 ；若∠AOB=1800，∠7与∠8互为 。

练习：填下列表：【设计意图】根据学生的情况，我主要采取自主探究、小组交流的方式学习余角和补角的概念，引导学生通过直观计算，总结规律，从而化抽象的概念12 34A O B2143为简明的关系，帮助学生正确理解并掌握。

（三）探讨释疑，突破难点(10分钟)探究活动3：如图:已知∠AOC，利用三角板分别画它的余角和补角．（只要满足条件的角都可以） 问：从中发现了什么？结论： 。

结论： 。

再问：如果两个角相等，那么它们的余角和补角有什么关系？如图∠1 与∠2互余，∠３ 与∠４互余 ，如果∠1＝∠３，那么∠2与∠４相等吗？为什么？结论： 。

《余角与补角》导学案莱州市文峰中学徐冬梅〖学习目标〗1．在具体情境中了解补角、余角、等概念，掌握“同角或等角的余角相等”，“同角或等角的补角相等”的结论，并能解决一些实际问题。

2．经历观察、操作、推理、交流的过程，增强学好数学的信心。

3．建立空间观念，发展推理能力和有条理表达的能力。

4．通过解决生活中的实际问题，明确知识来源于生活又服务于生活，养成热爱科学的态度。

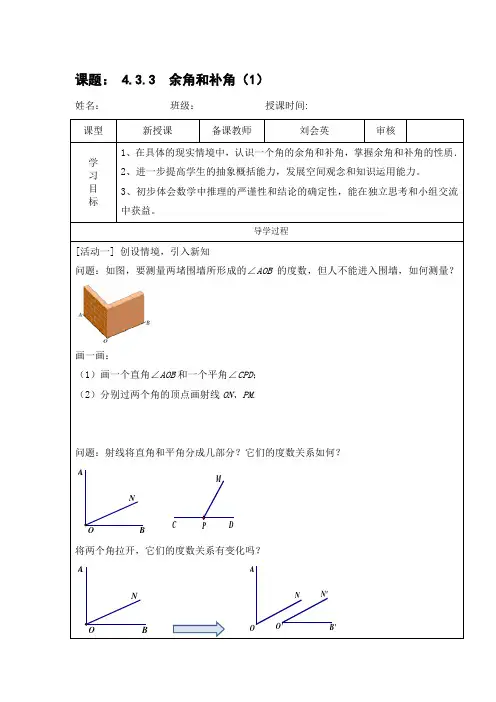
〖教学过程〗(一)创设情境，引出课题生活中处处可见道路、房屋、山川、桥梁。

在大自然的杰作和人类的创造物中，蕴含着无数的相交线和平行线。

在这一章里，我们将发现相交线和平行线的一些特征，并探索两条直线平行的条件。

我们还将利用圆规和没有刻度的直尺，尝试着作一些美丽的图案（二）探究新知动手试试：将纸按虚线折叠，然后展开由此产生了一些小角，如∠1、∠2、∠3、∠4,请同学们用所学的知识及量角器进行讨论:∠1﹢∠2＝°∠2﹢∠3＝°∠3﹢∠4＝°∠1﹢∠4＝°互余定义互补定义找一找，看谁找的准：1.图中给出的各角中,哪些互为余角?哪些互为补角?2.如图，点O为直线AB上一点，∠AOC=90°,OD是∠BOC内的一条射线。

图中哪些角互为余角?哪些角互为补角?比一比看谁算得快∠α∠α的余角∠α的补角想一想:1、钝角有余角吗？2、直角有余角吗？3、同一个角的补角比它的余角大多少度？我们一起来已知，一个角的补角加上20°后等于这个角余角的3倍，求这个角学以致用1.意大利首都罗马著名的比萨斜塔建于12世纪,由于地面下沉,它已经倾斜.而它以“斜而不倒”闻名于世。

已知斜塔与地面所成的角中,较小的角85°,较大的角是多少度?比萨斜塔已经倾斜了多少度?2.要测量两堵墙所成的∠AOB的度数，但人不能进入围墙，如何测量？思考探究（一）∠1和∠2互余，∠3和∠4互余，如果∠2=∠4，那么，∠1和∠3相等吗？为什么？思考探究（二）∠1和∠2互补，∠3和∠4互补，如果∠2=∠4，那么，∠1和∠3相等吗？为什么？思考探究（三）一、已知:∠AOC＝90°, ∠DOE＝90°1、图中有互余的角吗,请找出来2、∠1与∠3什么关系？二、如图，你知道∠1、∠2、∠3这三个角之间的关系吗？余角的性质补角的性质(三)性质应用•∠AOE是平角，∠AOC是直角，∠COD与∠COB互余，∠COD=28°35′•求∠AOB的度数学以致用：1.模拟实验2.你知道吗？打台球的游戏中，台球击到桌沿又反弹回来的路线，就象光的反射定律中入射光线与反射光线的路线是一样的。

第四章几何图形初步4.3 角学习目标：1. 了解余角、补角的概念，掌握余角和补角的性质，并能利用余角、补角的知识解决相关问题.2. 了解方位角的概念，并能用方位角知识解决一些简单的实际问题.重点：了解余角、补角的概念及性质，了解方位角的概念和表达方式.难点：运用余角、补角和方位角的相关知识解题.一、知识链接如图①，在长方形中，∠1+∠2= °，∠3+∠4= °.图①二、新知预习1. 如果两个角的和等于90°(直角)，就说这两个角互为______ (简称为两个角______ ).如图①，可以说∠1是∠2的余角，或∠2是∠1的余角，或∠1和∠2互余.2. 如果两个角的和等于180°(平角)，就说这两个角互为______ (简称为两个角______).如图①，可以说∠3是∠4的补角，或∠4是∠3的补角，或∠3和∠4互补.三、自学自测1. 图中给出的各角，哪些互为余角？自主学习教学备注学生在课前完成自主学习部分配套PPT讲授1.情境引入（见幻灯片3）2. 图中给出的各角，哪些互为补角？四、我的疑惑__________________________________________________________________________________________________________________________________________________________________一、要点探究探究点1：有关余角和补角的计算例1 若一个角的补角等于它的余角的4 倍，求这个角的度数.方法总结：余补角问题中，若角之间有比较明显的倍分关系，可尝试将较小的角设为未知数，列方程解答.例2如图，已知O为AD上一点，∠AOC与∠AOB互补，OM，ON分别为∠AOC，∠AOB的平分线，若∠MON=40°，试求∠AOC与∠AOB的度数．课堂探究教学备注配套PPT讲授2.探究点1新知讲授（见幻灯片4-12）观察与思考：∠α∠α的余角∠α的补角5°32°45°77°62°23′x°(0＜x＜90)观察可得结论：锐角的补角比它的余角大_____.针对训练1.如果∠a=36°，那么∠a的余角等于（）A．54°B．64°C．144°D．134°2.如图，将一副直角三角板如图放置，若∠AOD=18°，则∠BOC的度数为_____.第2题图变式题图【变式题】一副三角板按如图方式摆放，且∠1的度数比∠2的度数大44°，则∠1=______.3.已知∠A与∠B互余，且∠A的度数比∠B度数的3倍还多30°，求∠B的度数.探究点2：余角和补角的性质思考：∠1 与∠2，∠3都互为补角，∠2 与∠3 的大小有什么关系？教学备注配套PPT讲授3.探究点2新知讲授（见幻灯片13-17）例3 如图，O为直线AB上一点，OD平分∠AOC，∠DOE=90°．（1）∠AOD的余角是_______________，∠COD的余角是_________________;（2 ）OE是∠BOC的平分线吗？请说明理由．针对训练如图，已知∠AOB=90°，∠AOC=∠BOD，则与∠AOC互余的角有__________________.探究点3：方位角八大方位正东：正南：正西：正北：西北方向：西南方向：东北方向：东南方向：例4如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上. 同时，在它北偏东40°，南偏西10°，西北(即北偏西45°)方向上又分别发现了客轮B，货轮C和海岛D. 仿照表示灯塔方位的方法画出表示客轮B，货轮C和海岛D方向的射线.针对训练教学备注配套PPT讲授4.探究点3新知讲授（见幻灯片18-23）1. 如图，说出下列方位(1) 射线OA 表示的方向为.(2) 射线OB 表示的方向为.(3) 射线OC 表示的方向为. .(4) 射线OD 表示的方向为.2.费俊龙、聂海胜乘坐“神舟”六号遨游太空时，我国当时派出远望一号~四号船队，跟踪检测. 其中远望一、二号停在太平洋洋面上，某一时刻，分别测得神舟六号在北偏东60°和北偏东30°的方向，你能在下图中画出当时神舟六号所处的位置吗？二、课堂小结1.一个角的余角是它的2倍，这个角的度数是（）A．30°B．45°C．60°D．75°当堂检测教学备注配套PPT讲授5.课堂小结2.下列说法正确的是（）A．一个角的补角一定大于它本身B．一个角的余角一定小于它本身C．一个钝角减去一个锐角的差一定是一个锐角D．一个角的余角一定小于其补角3.已知∠A与∠B互余，∠B与∠C互补，若∠A=60°，则∠C的度数是_______.4.∠1与∠2 互余，∠1 = (6x + 8)°，∠2 = (4x－8)°，则∠1= ，∠2= .5. 请认真观察下图，回答下列问题：(1)图中有哪几对互余的角？(2) 图中哪几对角是相等的角(直角除外)？为什么？6 垃圾打捞船A和B都停驻在湖边观测湖面，从A船发现它的北偏东60°方向有白色漂浮物，同时，从B船也发现该白色漂浮物在它的北偏西30°方向.(1) 试在图中确定白色漂浮物C的位置；(2) 点C在点A的北偏东60°的方向上，那么点A在点C的________方向上.A. 南偏东30°B. 南偏西30°C. 南偏东60°D. 南偏西60°如有侵权请联系告知删除，感谢你们的配合！教学备注6.当堂检测（见幻灯片24-28）。

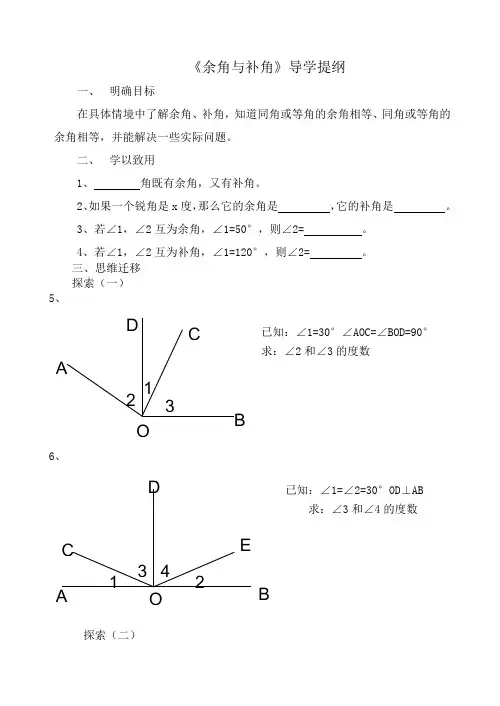
《余角与补角》导学提纲一、 明确目标在具体情境中了解余角、补角，知道同角或等角的余角相等、同角或等角的余角相等，并能解决一些实际问题。

二、 学以致用1、 角既有余角，又有补角。

2、如果一个锐角是x 度，那么它的余角是 ，它的补角是 。

3、若∠1，∠2互为余角，∠1=50°，则∠2= 。

4、若∠1，∠2互为补角，∠1=120°，则∠2= 。

三、思维迁移 探索（一）5、已知：∠1=30°∠AOC=∠BOD=90° 求：∠2和∠3的度数6、已知：∠1=∠2=30°OD ⊥AB求：∠3和∠4的度数探索（二）3ADC 21O ABOC DE123 47、已知：AB 、CD 相较于O ，∠1=110° 求：∠2和∠3的度数8、已知：O 在直线AB 上， ∠1=∠2=30°求：∠AOD 和∠BOC 的度数四、走进生活9、由于开学初的那场大风雪，使路边绿化带中的有些小树发生了倾斜。

老师发现了这样的一棵小树（如图），假如你是位园林工作者，你应该怎样做才能把小树扶正？（小树与地面形成的夹角是∠AOF=70 °，先利用已有的工具如三角板、量角器等把图画出来，再求出应该向什么方向转动多少度？）EOF A1 2 3ABCD OABC D12O10、已知：O 是直线EF 上的一点，∠BOF=∠BOE=∠AOC=90° 问题：（1）哪个角与∠AOF 互为余角？ 哪个角与∠BOC 互为补角？（2）如果∠AOF=60 °，那么∠BOC 是多少度？六、自我检测11、已知：∠1=42°，∠1，∠2互为余角，则∠2= 。

12、已知：∠1+∠2=180°，∠1+∠3=180°，∠2=40°，则∠3= 。

13、打台球时，可以选择适当的方向用白球击打红球，反弹后红球直接入袋，此时∠1=∠2，如图CD ⊥EF ，你能找出∠1的余角和补角吗？EFAC OB七、课后拓展1、如果∠1=60°，则∠1的余角的补角是2、如果一个锐角是x 度，那么它的余角是 ，它的补角是 。

4．3.3 余角和补角一、导学学习目标1．在具体的现实情境中，认识一个角的余角和补角； 2．掌握余角和补角的性质；3．了解方位角，能确定具体物体的方位． 学习重点：掌握余角和补角的性质；学习难点：正确求出一个角的余角和补角． 自主学习，研读教材将一张长方形纸片，沿一个角折叠后，折痕与长方形的边形成了4个角. 如图.回答问题1．互为余角的定义：如果两个角的和等于90°，那么这两个角互为余角． 思考：2．互为补角的定义：如果两个角的和等于180°，那么这两个角互为补角． 问题1：以上定义中的“互为”是什么意思？3.练习题 巩固新知同角的余角相等；∵∠1与∠2互余，∠1与∠3互余，O60°30°BOCAD213∴∠2＝90 °－∠1，∠3＝90 °－∠1∴∠2＝∠330°二.探究1243等角的余角相等。

理由:∵∠1与∠2互余∴∠2=90o -∠1∵∠3与∠4互余∴∠4=90o -∠3又∵∠1=∠3∴∠2=∠4解：∠2与∠4相等如图，∠1和∠2互余，∠3和∠4互余，若∠1=∠3，那么∠2与∠4相等吗？为什么？同理：同角或等角的补角相等 2. 你知道表示方向的一个成语吗?“四面”—东、南、西、北“八方”--东、南、西、北和东北、东南、西北、西南东西北南O正东：正南：正西：正北：西北方向：西南方向：东北方向：东南方向：射线OA ABCD45°EGFH45°八大方位45°45°射线OB 射线OC 射线OD射线OE 射线OF 射线OH 射线OG三.检测1.一个角是70°39′，求它的余角和补角。

2、∠A 的补角是它的3倍，∠A 是多少度？BAOC3、如图两堵墙围一个角∠AOB ，但人不能进入围墙，我们如何去测这个角的大小呢？四.拓展1、课堂小结2、强化训练（见课件题型）。

在小组 课堂探究 内交流 1． 如果∠1 与∠2 互余， 与∠3 互余， ∠1 那么∠2 与∠3 相等吗？ 展示． 为什么？
2． 如果∠1 与∠2 互补， 与∠3 互补， ∠1 那么∠2 与∠3 相等吗？ 为什么？
3．如果∠1 与∠2 互余，∠3 与∠ Nhomakorabea 互余，并且∠1＝∠3，那么∠ 2 与∠4 相等吗？
SH-7-073
这节课采用的是多媒体教学，但又不是完全的依靠多媒体手段。力图让学生 对图形有直观的感受，节约了教学时间又提高了教学效率。通过有效的活动 来引导学生，获得实际的结论。 在引入方面比较新颖的涉及了福州的本土文化教育，白塔和巫塔，以及与世 界奇观比萨斜塔的对比，以实际生活中的图片引入，直观的理解概念，从视 觉和听觉两方面给予学生构建概念的方法。 说明生活中处处存在数学的图形。 在对概念理解透彻的基础上，对余角性质的教学采用了学生直接动手作图的 方法教学。从实践中理解性质的本质，并能简单的应用。 从余角概念和性质构建的基础上，类比思想构建补角的概念和性质，这种数 学学习方法需要及时地渗透。例题部分较为典型。 （二）对教师在课堂教学实施中的表现反思 这节课中，能够和学生良好的配合完成教学。整节课虽然完整的上完了，可 是在类比补角的时候，整个流程显得比较急躁，可以将内容讲的更详实、缓 慢些，不用对练习的完成量多做要求。典型例题大部分学生可以完成，但是 个别学生的回答没有给予及时的肯定，对学生的鼓励措施不够。因此对于一 堂真正好的课，应该时刻注意着学生显现出的丝毫变化，抓住机会，完善学 生的知识系统。 （三）对教学活动的反思 对于课堂上的教学活动主要采用了教师引导、学生观察并动手活动，思考的 过程。通过多媒体的演示可以得到很好的效果，配合学生动手作图对概念和 性质的理解效果有所提高。

2022年七年级人教版数学433余角和补角导学案课题学习目标4.3.3余角和补角课时主备人1．认识一个角的余角和补角，掌握余角和补角的性质2．学会简单的逻辑推理，并能对问题的结论进行合理的猜想。

3.初步体会数学中推理的严谨性和结论的确定性学习过程一、探索新知：1、定义：自学指导一：自学课本141页，并填空（1）如果两个角的和是，那么这两个角叫做（2）如果两个角的和是，那么这两个角叫做反馈练习：填下列表：∠a5°32°45°77°62°23′某°∠a的余角∠a的补角注意：ⅰ）锐角∠的余角是（90°—∠）∠的补角是（180°—∠）ⅱ）互余和互补是两个角的数量关系，与它们的位置无关。

2、探究补角(余角)的性质：（1）∠1与∠2互余，∠3与∠4互余，如果∠1＝∠3,那么∠2与∠4相等吗？结论：（2）如图∠1与∠2互补，∠３与∠４互补，如果∠1＝∠3,那么∠2与∠4相等吗？结论：2413几何语言：∠1与∠2互余，∠3与∠4互余又∠1＝∠3∠2=∠4北反馈练习：141页练习3、方位角OA的方向是OB的方向是OC的方向是OD的方向是反馈练习：144页12题二、尝试应用例1:一个角的补角是它的3倍,这个角是多少度西东南例2:若一个角的补角等于它的余角4倍，求这个角的度数。

三、归纳小结四、自我检测1、如果∠1与∠2互余，则∠1+∠2=2、如果∠1+∠2=90°，∠2+∠3=90°，则∠1∠3理由是3、若∠=40°，则它的余角是，补角是4、如果一个角的补角是120°，则这个角的余角是（）A、150°B、90°C、60°D、30°5、如图∠AOB=∠COD=90°，∠AOD=,∠BOC=，则等于（）A、180°B、120°C、90°D、不能确定6、如图，已知∠AOC=∠BOD=98°,∠BOC=62°,则∠AOD的度数为（）A、137°B、134°C、133°D、132°7、如图，OC是∠BOD的平分线，OB是∠AOD的平分线，且∠COD=30°，则∠AOC的度数为（）A、60°B、80°C、90°D、120°BCDABACDBADCO(5题图)(6题图)(7题图)8、甲看乙的方位是北偏东30°，则乙看甲的方向是（）A、南偏西30°B、南偏东60°C、南偏东30°D、南偏西60°10、一个角的补角加上10°的和等于这个角余角的3倍，求这个角的余角和补角选作：1、如图所示，AOB80,OM是AOB内任意一条射线，若OC平分AOM,OD平分BOM,求COD的度数2、已知线段AB=10,点C为线段上任意一点，点M平分AC,点N平分BC，求线段MN的长度MCABD3、如图，将书页斜折过去，使A得顶点落到A处,BC为折痕，BD为ABE的平分线求CBD的度数ABCADE。

数学：4.3.3《余角和补角（1）》学案（人教版七年级上）【学习目标】在具体的现实情境中，认识一个角的余角和补角； 【重点难点】正确求出一个角的余角和补角。

【导学指导】 一、知识链接 思考：（1） 在一副三角板中同一块三角板的两个锐角和等于多少度？ （2） 如图1，已知∠1=61°，∠2=29°，那么∠1+∠2= 。

（3） 如 图 2，已知点A 、O 、B 在一直线上 ，∠COD=90°，那么∠1+∠2= 。

二、自主探究1.互为余角的定义： 思考：（1） 如图3，已知∠1=62°,∠2=118°,那么 ∠1+∠2＝（2） 如图4，A 、O 、B 在同一直线上，∠1+∠2=2.互为补角的定义：2图 190°12图 212Ａ Ｏ Ｂ图 412图 3 CODOEDCBA问题1：以上定义中的“互为”是什么意思？问题2：若 ∠1+∠2 +∠3 =180° ，那么∠1、∠2、∠3互为补角吗？ 3.新知应用：例1:若一个角的补角等于它的余角4倍，求这个角的度数。

例2：如图，∠AOC ＝∠COB ＝90°，∠DOE ＝90°，A 、O 、B 三点在一直线上 （1）写出∠COE 的余角，∠AOE 的补角； （2）找出图中一对相等的角，并说明理由；【课堂练习】：课本141页练习1、2、3；【要点归纳】：【拓展训练】：1、一个角的余角比它的补角的31还少︒20，求这个角的度数。

2、若α∠和β∠互余，且α∠：β∠=7：2，求α∠、β∠的度数。

【总结反思】：2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．如图，若延长线段AB 到点C ，使BC=AB ，D 为AC 的中点，DC=5cm ，则线段AB 的长度是（ ）A.10cmB.8cmC.6cmD.4cm2．若∠β=25°31'，则∠β的余角等于（ ） A.64°29'B.64°69'C.154°29'D.154°69'3．如图，两块直角三角板的直顶角O 重合在一起，若∠BOC=15∠AOD ，则∠BOC 的度数为（ ）A ．30° B. 45° C．54° D．60° 4．下列解方程去分母正确的是( ) A.由，得2x ﹣1＝3﹣3x B.由，得2x ﹣2﹣x ＝﹣4 C.由，得2y-15=3yD.由，得3(y+1)＝2y+65．甲、乙两工程队开挖一条水渠各需10天、15天，两队合作2天后，甲有其他任务，剩下的工作由乙队单独做，还需多少天能完成任务？设还需x 天，可得方程（ ）A.11()21101515x+⨯+= B.11015x x+= C.2211015x ++= D.2211015x ++= 6．中国古代问题：有甲、乙两个牧童，甲对乙说：“把你的羊给我一只，我的羊数就是你的羊数的2倍”．乙回答说：“最好还是把你的羊给我一只，我们羊数就一样了”．若设甲有x 只羊，则下列方程正确的是（ ） A.x+1=2（x ﹣2） B.x+3=2（x ﹣1） C.x+1=2（x ﹣3）D.1112x x +-=+ 7．已知一个多项式与3x 2+9x 的和等于3x 2+4x ﹣1,则这个多项式是（ ） A ．﹣5x ﹣1B ．5x+1C ．﹣13x ﹣1D ．13x+18．定义一种正整数n “F ”的运算：①当n 是奇数时，()31F n n =+；②当n 是偶数时，()2kn F n =(其中k 是使得2k n为奇数的正整数......，)两种运算交替重复运行.例如，取24n =，则： 243105F F F −−−→−−−→−−−→⋅⋅⋅⋅⋅⋅第一次第二次第三次②①②，若13n =，则第2019次“F ”运算的结果是( ) A.1B.4C.2019D.201949．下列判断正确的是（ ） A ．-a 不一定是负数 B ．|a|是一个正数C ．若|a|=a ，则a ＞0；若|a|=-a ，则a ＜0D ．只有负数的绝对值是它的相反数10．现有五种说法：①-a 表示负数；②绝对值最小的有理数是0；③3×102x 2y 是5次单项式；④5x y-是多项式．其中正确的是（ ） A.①③B.②④C.②③D.①④11．如果水位升高1米记为+1米，那么水位下降2米应记为（ ） A.﹣1米B.+1米C.﹣2米D.+2米12．已知a ，b ，c 是有理数，且a+b+c=0，abc （乘积）是负数，则||||||b c a c a b a b c +++++的值是（ ）A.3B.﹣3C.1D.﹣1二、填空题13．如果∠A 的余角是26°，那么∠A 的补角为_______°．14．如图，在灯塔O 处观测到轮船A 位于北偏西54°的方向，同时轮船B 在南偏东15°的方向，那么∠AOB=_______°．15．关于x 的方程ax ﹣2x ﹣5＝0(a≠2)的解是_____． 16．已知关于x 的一元一次方程2019x +5＝2019x+m 的解为x ＝2018，那么关于y 的一元一次方程52019y-﹣5＝2019（5﹣y ）﹣m 的解为_____．17．如图所示，若三角形纸片内有100个点，连同三角形的顶点共103个点，其中任意三点都不共线.现以这些点为顶点作三角形，并把纸片剪成小三角形，这样的小三角形的个数是______.18．观察下列图形，它是把一个三角形分别连接这个三角形三边的中点，构成4个小三角形，挖去中间的一个小三角形(如图1)；对剩下的三个小三角形再分别重复以上做法，…将这种做法继续下去(如图2，图3…)，则图5中挖去三角形的个数为______19．若a,b 是整数，且ab ＝12，|a|＜|b|，则a+b=________ . 20．与原点的距离为 2 个单位的点所表示的有理数是________． 三、解答题21．如图，长方形ABCD 中，AB ＝4cm ，BC ＝8cm ．点P 从点A 出发，沿AB 匀速运动；点Q 从点C 出发，沿C→B→A→D→C 的路径匀速运动．两点同时出发，在B 点处首次相遇后，点P 的运动速度每秒提高了3cm ，并沿B→C→D→A 的路径匀速运动；点Q 保持速度不变，继续沿原路径匀速运动，3s 后两点在长方形ABCD 某一边上的E 点处第二次相遇后停止运动．设点P 原来的速度为xcm/s ． （1）点Q 的速度为 cm/s （用含x 的代数式表示）； （2）求点P 原来的速度．（3）判断E 点的位置并求线段DE 的长．22．已知，O 是直线AB 上的一点，COD ∠是直角，OE 平分BOC ∠．()1如图1，若AOC 30∠=，求DOE ∠的度数；()2在图1中，若AOC a ∠=，直接写出DOE ∠的度数(用含a 的代数式表示)； ()3将图1中的DOC ∠绕顶点O 顺时针旋转至图2的位置．①探究AOC ∠和DOE ∠的度数之间的关系，写出你的结论，并说明理由；②在AOC ∠的内部有一条射线OF ，满足：AOC 4AOF 2BOE AOF ∠∠∠∠-=+，试确定AOF ∠与DOE ∠的度数之间的关系，说明理由．23．如图所示，一幅地图上有A ，B ，C 三地，地图被墨迹污染，C 地具体位置看不清楚了，但知道C 地在A 地的北偏东30°方向，在B 地的南偏东45°方向，你能确定C 地位置吗？24．先化简，再求值：22113122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭，其中x=-1，y=23. 25．先化简，再求值：-2x 2•4x 4+（x 4）2÷x 2-（-3x 3）2，其中x 3=12． 26．现从小欣作业中摘抄了下面一道题的解题过程：计算：24÷（13-18-16）； 解：24÷（13-18-16）=24÷13-24÷18-24÷16=72-192-144 =-264；观察以上解答过程，请问是否正确？若不正确，请写出正确的解答． 27．观察下列等式： 第一个等式：122211a 132222121==-+⨯+⨯++ 第二个等式：2222223211a 1322(2)2121==-+⨯+⨯++第三个等式：3333234211a 1322(2)2121==-+⨯+⨯++ 第四个等式：4444245211a 1322(2)2121==-+⨯+⨯++按上述规律，回答下列问题：()1请写出第六个等式：6a =______=______；()2用含n 的代数式表示第n 个等式：n a =______=______； ()1234563a a a a a a +++++=______(得出最简结果)； ()4计算：12n a a a ++⋯+．28．学校准备添置一批课桌椅，原计划订购60套，每套100元，店方表示：如果多购，可以优惠．结果校方实际订购了72套，每套减价3元，但商店获得了同样多的利润．（1）求每套课桌椅的成本；（2）求商店获得的利润．【参考答案】***一、选择题1．B2．A3．A4．D5．A6．C7．A8．B9．A10．B11．C12．D二、填空题13．116°14．14115． SKIPIF 1 < 0解析：52 a-16．2023 17．201 18．121 19．7，8，13 20．±2三、解答题21．（1）2x；（2）点P原来的速度为53cm/s．（3）此时点E在AD边上，且DE=2.22．（1）15°；（2）12α；（3）①∠AOC＝2∠DOE；②4∠DOE－5∠AOF＝180°.23．画图见解析.24．-3x+y2，31 925．-4.26．错误，正确的解法见解析. 27．（1）()6266213222+⨯+⨯，6121+-7121+；（2）()2213222nn n +⨯+⨯，121n +-1121n ++；（3）1443；（4）()1122321n n ++-+.28．（1）每套课桌椅的成本为82元．（2）商店获得的利润为1080元．2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．如图，点A 、B 在线段EF 上，点M 、N 分别是线段EA 、BF 的中点，EA ：AB ：BF ＝1：2：3，若MN ＝8cm ，则线段EF 的长是（ ）A.10 cmB.11 cmC.12 cmD.13 cm2．如果一个角α的度数为13°14'，那么关于x 的方程21803x x α-=︒-的解为（ ） A.76°46'B.76°86'C.86°56'D.166°46'3．如图，直线l 是一条河，P ，Q 是两个村庄。