汽车驾驶员模型建立

驾驶员行为的多维度分析与建模随着社会的发展和交通工具的不断普及，道路交通安全越来越受到人们的关注。

而驾驶员行为是造成交通事故的主要原因之一，在交通安全领域扮演着重要的角色。

因此，对驾驶员行为进行多维度的分析和建模，对于制定交通安全策略和提高道路交通安全水平具有重要意义。

一、驾驶员行为的多维度分析驾驶员行为是指驾驶员在行驶过程中的行为表现，主要包括速度、加减速、转向、变道、超车、酒后驾驶、疲劳驾驶等，是造成交通事故的主要原因之一。

为了更好地理解驾驶员行为，可以从以下几个维度进行分析。

1. 心理维度驾驶员的个体心理特征对于其行为的影响十分重要。

例如，焦虑、紧张、疲劳等情绪都可能影响驾驶员对道路交通的感知和处理能力。

另外，驾驶员的性格特征和驾驶经验也会对其行为产生影响。

2. 生理维度驾驶员的生理特征也对其行为有一定的影响。

例如，身体状况、视力、听力、反应速度等都会影响驾驶员对道路交通的认知和处理能力。

3. 车辆维度驾驶员所驾驶的车辆也会影响其行为。

例如，车辆的品牌、型号、年份、质量等因素都会影响驾驶员对车辆的控制能力。

另外，车辆的座椅舒适度、空调温度等细节问题也可能影响驾驶员的舒适感，从而影响其驾驶行为。

4. 道路环境维度道路环境因素是指路面、天气、交通流量、路段类型等因素。

这些因素会对驾驶员的行为产生直接或间接的影响。

例如，恶劣的天气会影响驾驶员的行驶速度和车辆控制能力，高峰期通行的交通流量会影响驾驶员的红绿灯处理能力等。

二、驾驶员行为的建模通过对驾驶员行为的多维度分析，可以建立驾驶员行为的模型。

驾驶员行为模型是一种科学的描述和预测驾驶员行为的方法，可以帮助交通管理部门了解驾驶员行为的主要特征和影响因素，制定相应的交通安全政策和管理措施。

1. 传统行为模型传统的驾驶员行为模型主要包括微观和宏观模型。

微观模型建立在个体交通参与者的行为基础上，常用的微观模型有加速度-速度模型和轨迹模型等。

宏观模型主要研究车流量的变化，描述了车速、密度和流量之间的关系。

智能驾驶员模型是指采用先进的计算机技术和人工智能算法，使汽车能够像人类驾驶员一样感知和决策，从而实现自动驾驶。

在智能驾驶员模型中，IDM（Intelligent Driver Model）是一种基于交通流动力学理论的模型，用于描述车辆在道路上的运行行为，并在自动驾驶系统中发挥重要作用。

1. IDM模型的基本原理IDM模型是由D. Helbing和M. Treiber于1999年提出的，它基于微观交通流动力学理论，用于描述车辆与车辆之间的相互作用和影响。

IDM模型的基本原理包括以下几点：- 车辆之间存在相互影响和作用力，主要表现为跟驰效应和交通行为的调整。

- 车辆的加速度受到车辆之间的距离和速度差的影响，根据交通流动力学理论，车辆之间的相互作用可以用力学公式来描述。

- IDM模型将车辆间的相互作用建模为一种加速度函数，通过该函数可以计算车辆的加速度，并据此进行自动驾驶控制。

2. IDM模型的数学表达IDM模型的数学表达主要包括以下几个方面：- 车辆的加速度受到期望速度、车辆当前速度、前车距离以及速度差的影响。

根据IDM模型的描述，加速度函数可以用数学公式来表示。

- IDM模型中的参数包括期望速度、舒适加速度、期望车头距离等，这些参数的选择对于模型的精确度和鲁棒性有重要影响。

- 通过数学推导和理论分析，可以得到IDM模型的具体数学表达式。

这些数学表达式通常以微分方程或差分方程的形式呈现，并包括车辆的位置、速度、加速度等变量。

3. IDM模型的推导过程IDM模型的推导过程包括以下几个步骤：- 基于交通流动力学理论和力学原理，建立车辆之间的相互作用和加速度函数的数学模型。

- 根据车辆之间的相互作用和影响，推导出加速度函数的数学表达式。

- 通过理论分析和模型假设，确定IDM模型中的参数和变量，包括期望速度、舒适加速度、期望车头距离等。

- 将参数和变量代入加速度函数的数学表达式中，得到IDM模型的具体数学表达式。

基于路程预瞄的驾驶员模型杨浩;黄江;李攀;韩中海【摘要】为真实反映驾驶员在人-车-路闭环系统中对汽车的操纵特性,提出了一种基于路程预瞄的智能控制驾驶员模型.通过对一段路程进行预瞄,提出了用于判断目标路径相对于预瞄方向的位置关系的路程预瞄曲率阈值理论,建立了预瞄距离可变的自适应跟踪模型,同时,建立了智能控制转向盘的决策模型,提出了最优速度控制策略.CarSim和Simulink联合仿真结果显示,建立的驾驶员模型具有较高的路径跟踪精度和合理的速度控制策略.【期刊名称】《汽车技术》【年(卷),期】2019(000)002【总页数】7页(P7-13)【关键词】路程预瞄;路程预瞄曲率阈值;预瞄距离可变;模糊控制理论;最优速度控制策略【作者】杨浩;黄江;李攀;韩中海【作者单位】重庆工商职业学院,重庆 401520;重庆理工大学,汽车零部件先进制造技术教育部重点实验室,重庆400054;重庆理工大学,汽车零部件先进制造技术教育部重点实验室,重庆400054;重庆理工大学,汽车零部件先进制造技术教育部重点实验室,重庆400054;重庆理工大学,汽车零部件先进制造技术教育部重点实验室,重庆400054【正文语种】中文【中图分类】U469.71 前言驾驶员行为规律及其建模在人-车-路闭环系统的仿真、评价与优化中具有至关重要的作用。

研究人员根据预瞄理论提出了各种驾驶员模型：MacAdam提出了最优预瞄控制模型[1]，郭孔辉院士提出了单点预瞄最优曲率模型[2]，张慧豫提出了两点预瞄的新型驾驶员模型[3]，同时，汽车动力学仿真软件CarSim中采用了5点预瞄驾驶员模型。

近年来，随着控制理论的不断发展和完善，基于预瞄的各种驾驶员模型不断提出，主要有模糊控制驾驶员模型[4]、预瞄优化神经网络驾驶员模型[5]和自适应最优预瞄控制驾驶员模型[6]。

上述方法在路径跟踪方面取得了一定进展，但并没有充分反映驾驶员的预瞄行为。

郭孔辉院士的研究表明[2]，驾驶员预瞄更一般的形式是其目光不只集中于前方一点，而是着眼于前方的一段路，并争取使汽车在这一段路程内的运动误差最小，同时根据路程预瞄的有效信息和当前车速来调整预瞄距离，即预瞄距离应可变。

驾驶员行为模型和驾驶员状态监测技术实现随着汽车技术的不断改进和智能化的发展，车辆的自主驾驶技术已经逐渐走进了我们的生活，成为了当代最为热门的汽车技术之一。

而自动驾驶技术的实现离不开驾驶员行为模型和驾驶员状态监测技术。

本文将详细介绍驾驶员行为模型和驾驶员状态监测技术的实现。

一、驾驶员行为模型驾驶员行为模型是自动驾驶车辆设计的重要组成部分。

它通过对驾驶员操作动作的分析和描述，建立一个能够反映驾驶员驾驶行为的数学模型，从而进一步推断出驾驶员的意图和福利状况，为车辆控制提供有效的信息。

驾驶员行为模型包括三个方面的内容：（1）驾驶员意图推断驾驶员行为模型可以通过分析驾驶员的行为，推断驾驶员的意图，从而更好地适应不同的场景，提供更加精准的控制策略。

例如，在自动驾驶汽车中，当驾驶员希望更改目的地或者更改路线时，车辆可以根据驾驶员的意图，调整自己的方向和速度，从而达到更好的驾驶效果。

（2）驾驶员心理和生理状态识别驾驶员心理和生理状态是影响驾驶员驾驶行为的重要因素，在自动驾驶汽车中，可以通过识别驾驶员的心理和生理状态，优化车辆的控制策略，提高驾驶效率和安全性。

例如，在自动驾驶汽车中，如果车辆能够识别到驾驶员的注意力分散或疲劳等状态，可以采取相应措施，例如减速或提示驾驶员休息等，从而避免交通事故的发生。

（3）驾驶员行为预测驾驶员行为预测是指通过对驾驶员驾驶行为的分析和模拟，预测驾驶员未来的行为，为车辆控制提供更加可靠的信息。

例如，在自动驾驶汽车中，如果车辆能够准确预测驾驶员未来的驾驶行为，可以提前做好相应的准备，避免交通事故的发生。

二、驾驶员状态监测技术实现驾驶员状态监测技术是指通过对驾驶员心理和生理状态的检测和分析，为车辆控制提供。

有效的信息，使得车辆能够在车辆无人驾驶的情况下，快速反应驾驶员异常状态，采取相应的措施，提高驾驶员的安全性和控制效率。

驾驶员状态监测技术包括以下方面的内容：（1）眼动追踪技术眼动追踪技术可以监测驾驶员的注视点移动情况，识别驾驶员的视线偏移或者注意力分散等异常状态，车辆可以根据驾驶员的状态变化，调整自己的控制策略，从而保证驾驶的安全性和效率。

驾驶员状态评估模型的训练方法我折腾了好久驾驶员状态评估模型的训练方法，总算找到点门道。

我一开始真的是瞎摸索，就知道要收集数据，可收集啥样的数据都是问题呢。

我就先想到从驾驶员的基本身体数据开始，像心率啊，当时我想着这个简单，就找了些传感器来收集，还让一些朋友当志愿者。

结果发现心率能反映的情况很有限，一个人紧张或者放松时心率变化虽然有，但是光靠这个去评估驾驶员状态太片面了。

后来我又加上了面部表情的分析。

这可就难多了，就像在一团乱麻里找线头一样。

我尝试用各种开源的图像识别库，像OpenCV。

试着去识别眼睛的状态，比如说眼睛是不是半闭着，这可能就表示驾驶员疲劳了。

但是它这个识别，有时候准有时候不准的。

我后来才明白是光线影响太大了。

在强光下，眼睛的轮廓都不清晰了，识别就容易出错。

我就只能重新调整算法来适应不同的光照环境，这个过程真是漫长又痛苦，改了一次又一次，就像一个小孩学走路不断摔倒又爬起来。

再之后我又把驾驶行为数据纳入进来，像方向盘的转动角度、转动频率。

我还自己开着车记录了好多数据，差点因为太专注记录数据而自己分神驾驶了呢这可是很危险的事，还好及时缓过神。

我发现如果一个驾驶员正常行驶时，方向盘的转动是比较有规律的。

要是状态不好，比如说打瞌睡了或者走神了，转动角度就会突然变得奇怪，要么就是很长时间都不变，要么就是猛地一拐。

不过这个也有问题，路面状况也会影响这个数据，在坑洼路面，方向盘的转动也会很不规律。

在模型的选择上也是一波三折。

我开始就想用简单的线性回归模型，觉得这个好理解也好操作。

可是后来发现，驾驶员状态评估这个事儿太复杂了不是简单的线性关系就能表达的。

于是我又试了神经网络，像卷积神经网络，虽然它能处理复杂关系可是难训练啊，一不小心就过拟合了，模型就记住了每个训练数据而不是找到规律。

我觉得可能是数据不够多或者算法设置不好。

我又重新调整网络结构，减少了层数，增加了数据量这才慢慢好点。

到现在我也不能说我这个训练方法就完美了。

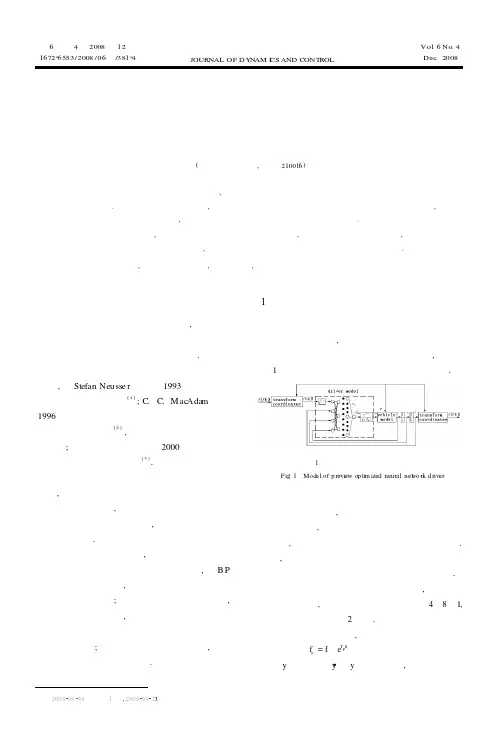
第6卷第4期2008年12月167226553/2008/06⑷/38124动力学与控制学报JOURNAL OF DY N AM I CS AND CONT ROLVol .6No .4Dec .200822收到第稿,223收到修改稿基于汽车操纵动力学的神经网络驾驶员模型徐瑾　赵又群　阮米庆(南京航空航天大学,南京　210016)摘要　作为人一车—路闭环系统的重要环节,驾驶员模型对汽车闭环系统仿真和汽车主动安全性评价都具有重要的意义.本文基于汽车操纵动力学,预瞄—跟随理论以及神经网络建立了一种驾驶员方向控制模型,即两层前馈神经网络驾驶员模型,并在此基础上建立了驾驶员—汽车闭环系统模型.对该闭环模型进行了单移线与双移线仿真试验,仿真结果与理想数据具有很好的一致性,表明该驾驶员模型是合理的,可以有效地模拟驾驶员控制汽车方向的行为特性,为进一步研究人一车一路闭环系统提供了一条可行途径.关键词　驾驶员模型,　汽车操纵动力学,　神经网络,　仿真分析引言随着车辆操纵稳定性研究的发展,将神经网络强大的自学习和非线性能力应用于驾驶员模型的建立成为目前广泛采用的技术手段之一.国内外已有多位学者基于神经网络理论建立了各种驾驶员模型,如Stefan Neusse r 等人于1993年设计了三层前馈神经网络控制器[1];C . C.Mac Ada m 等人于1996年提出了基于神经网络和预瞄传感器的汽车转向智能控制系统[2],用神经网络模仿人的行为驾驶车辆;郭孔辉院士课题组于2000年提出了预瞄优化神经网络驾驶员模型[3].虽然这些模型能获得与真实熟练驾驶员驾驶汽车非常接近的轨迹跟随效果,但都需要依据大量的实车或驾驶模拟器试验数据作为训练样本,且对于神经网络的拓扑结构需要通过试凑法多次比较确定,无形中增加了研究的难度和工作量.因此为解决上述问题,本文根据“预瞄—跟随系统理论”和人工神经网络的基本原理,将B P 算法和遗传算法相结合,建立了两层前馈预瞄优化神经网络驾驶员模型;同时基于汽车操纵动力学,获得了可靠的训练样本,从而在缺少实车试验数据的条件下为人—车—路闭环系统模型的研究提供有利的理论依据;并以单移线及双移线为例,对建立的闭环系统进行了仿真分析.1　预瞄优化神经网络驾驶员模型的建立驾驶员是依据前视轨迹信息和车辆的状态反馈信息来驾驶汽车,因此参照人工神经网络的拓扑结构和驾驶员—汽车闭环系统的功能框图,建立如图1所示的预瞄优化人工神经网络驾驶员模型.图1　预瞄优化神经网络驾驶员模型Fig .1　Model of p revi ew op ti m ized neural net w o rk d river该驾驶员模型是根据“单点预瞄假设”建立的神经网络驾驶员模型,依据预瞄时间只采集前方道路上一点的信息,模拟真实驾驶员的目光集中于前方一点处,这时道路信息的输入变量简化为一维向量.通常,基于这个假设得到的仿真结果与实际驾驶员在模拟器试验中的仿真结果能够吻合的比较理想.此驾驶员模型为两层前馈神经网络,经过多次训练结果比较,确定各层神经元数分别为4—8—1,网络的拓扑结构如图2所示.神经网络驾驶员模型的输入是一个四维向量,分别是驾驶员预瞄前方道路点的轨迹f e =fe T p S和车辆的状态反馈———侧向位移y 、侧向速度�y 和¨y 侧向加速度,这些输入经过人工神经网络各个神经元间的权值和转移函数的2008090912008092.动　力　学　与　控　制　学　报2008年第6卷叠加综合,得到神经网络的输出—理想方向盘转角δ3S W ,再经过驾驶员模型的神经滞后和操纵反应滞后环节,得到驾驶员模型的输出—方向盘转角δS W.图2　神经网络驾驶员的拓扑结构Fig .2　Topol ogi cal struct u re of neu ral net work driver2　简化驾驶员模型如图1所示绝对坐标系与车辆的相对坐标系之间需要进行坐标变换,当道路的方向角变化不大时,车辆的航向角变化也不大(ψ→0),绝对坐标系的X 、Y 轴与车辆坐标系的x 、y 轴几乎重合,则有如下近似的关系:X ≈x ;Y ≈y .在相对坐标系下得到的各个量值与在绝对坐标系下得到的也近似相等,就可以略去坐标变换这一环节,使神经网络驾驶员模型得到简化.由于人工神经网络具有极强的自学习能力,从理论上讲,只要训练样本数足够多且具有代表性,神经网络就能揭示出蕴藏在其间的任意复杂规律.描述驾驶员熟练程度的参数为神经反应滞后时间t d 、操纵反应滞后时间T h 和预瞄时间T,通过组合三个参数在各自变化范围内的不同取值,来模拟多位驾驶员驾驶同一辆汽车.在此基础上可得到有效的训练数据,从而只需利用以上建立的两层前馈神经网络,就能直接获得方向盘实际转角δSW ,这样就进一步简化了驾驶员模型.综上所述,图1所示的驾驶员模型就简化成图3所示:图3　两层前馈神经网络驾驶员模型F 3　T y f f 3　神经网络学习算法基于对现有的人工神经网络模型的分析,综合考虑实用性、高效性及针对性等各种因素,最终采用B P 改进算法———带有动量项的BP 算法,对驾驶员模型进行建模和仿真.同时针对B P 网络存在的收敛速度慢、易于陷入局部极小点、网络的泛化能力及适应能力较差等缺陷,本文参考文献[4][5],利用遗传算法G A 对改进的BP 网络的权值进行训练.G A 和BP 算法结合的步骤如下:①随机产生一组实数制位串种群,每一个位串表示网络连接权和阈值的一个集合.②对实数制位串进行解码成网络的各个连接权和阈值,运行网络,评价网络性能.③根据遗传操作,产生下一代种群,形成下一代网络.④重复②、③,直到J ≤J m a x 或达到进化代数,此时,将最终种群中的个体进行解码,从而得到通过G A 优化后的网络的连接权和阈值.J m a x 为遗传算法所要达到的性能指标.⑤将G A 优化后的网络权值和阈值作为B P 算法的网络初始权值和阈值.⑥依据动量法BP 网络权值调整公式进行网络权值和阈值的调节,评价网络性能.⑦重复⑥,直到J ≤J m in 或e (i )≤m ax ep (i =1,…,l ),其中l 为训练网络的样本数,J m in 为B P 算法所要达到的网络性能指标,即最终要求的性能指标,m ax ep 是单个样本的最大误差.此时,保存网络权值和阈值.4　获取训练样本为获得神经网络的训练样本,需要建立汽车闭环系统模型,如图4所示.由于本文主要研究侧向图4　驾驶员—汽车闭环系统模型F M f y 加速度不是很大的汽车的平面转向问题,故只需采用二自由度线性汽车模型283i g.wo -la e r -e ed or w a rd ne ura l ne t wo rk d rive r mode li g.4ode l o dri ve r -ve hic l e c l o se d -l oop s ste m.第4期徐瑾等:基于汽车操纵动力学的神经网络驾驶员模型由上图可得到人—车—路闭环系统状态方程及输出方程,具体内容参见文献[6].本文采用均匀设计的方法[7]来安排仿真试验.仿真计算涉及3个因素———驾驶员预瞄时间、神经反应滞后时间和操纵反应滞后时间,可以选择均匀设计表进行仿真试验设计,试验次数为15次.通过试验可获得由有效道路输入、汽车侧向位移、侧向速度、侧向加速度以及对应的方向盘角输入的离散值组成的15组训练样本.5　仿真试验及结果以某轿车为例,使用上述的两层神经网络驾驶员模型对驾驶员—汽车闭环系统进行单移线和双移线道路下的模拟与仿真.闭环系统仿真由驾驶员响应模块和汽车响应模块组成.其中驾驶员模块的输出作为汽车模块的输入,汽车模块的输出又反馈给驾驶员模块,仿真框图如图5所示.图5　驾驶员—汽车闭环系统仿真框图Fi g .5　Si mu l ati on bl ock diagra m of driver -vehicl e cl osed -loop s yst em图6为单移线路径下,本文建立的两层前馈神经网络驾驶员模型仿真结果和得到广泛认可的预瞄最优曲率驾驶员模型[3]仿真结果的比较,实线两层前馈神经网络驾驶员模型,虚线为预瞄最优曲率驾驶员模型图为双移线下两者的仿真结果比较对曲线进行对比分析和误差计算,得出汽车的侧向位移曲线,侧向速度、加速度曲线和方向盘转角曲线的相对误差均在5%以下,在误差允许范围内,从而说明本文建立的两层前馈神经网络驾驶员模型是合理的,而且具有以下几个优点:1)通过合理简化,与以往的“预瞄跟随”驾驶员模型相比更加简单、有效;2)采用人工神经网络从而能够允许人—车—路闭环系统高度非线性化,不再拘泥于几个简单参数的表达,可通过学习不断实现自我完善;3)可通过调整网络的拓扑结构,实现驾驶员、汽车特性因素的改变.图6　单移线仿真结果比较Fig .6　C omp aris on of s ingle lane si m ulati on res ults图7　双移线仿真结果比较Fi g .7　Comparis on of double l ane si mu l ati on results6　结束语本文基于汽车操纵动力学,结合B P 学习方法和遗传算法建立了两层前馈神经网络驾驶员模型,并与已得到广泛认可的“预瞄最优曲率”驾驶员模型进行仿真试验比较,证明该模型及其各种简化假设是合理的,模拟的结果准确有效,因此可作为进一步研究人—车—路闭环系统特性的依据.参　考　文　献　S f N ,N f I M ,3,(3)5～66383.7.1te an eu sser e t al .eu r o n con trol o r late ral veh ic l egu idance .EEE icro 19911:7动　力　学　与　控　制　学　报2008年第6卷2　C C M acadam and Gerg ory E Johns on .App licati on of ele 2mentary neura l ne t works and p revie w sens o rs for repre sen 2ting driver stee ri ng control behavior .Vehicl e Syst em D y 2nam ics ,1996,25:3～303　郭孔辉,潘峰,马凤军.预瞄优化神经网络驾驶员模型.机械工程学报,2003,39(1):26～28(Guo K ong 2hui,Pan Feng,M a Fengju .Preview op ti m ized a rtificialneura l ne t w ork driv e r model .Chines e Journa l ofM echanica l Engineering,2003,39(1):26～28(in Chi nese ))4　穆阿华,周绍磊,刘青志等.利用遗传算法改进B P 学习算法.计算机仿真,2005,22(2):150～151(M uAhua ,Zhou Shao l e i,Liu Zhiqing .U sing gene tic alg orith m to i mprove B P tra ining a lg orith m.Co m puter Si mula ti on,2005,22(2):150～151(in Chine s e ))5　朱海峰,李伟,张林.基于BP 神经网络整定的P I D 控制.动力学与控制学报,2005,3(4):93～96(Zhu Haifeng,Li We i,Zhang Lin .P I D control based on BP neura l net 2work adjusting .J ourna l of D ynam ics a nd Control,2005,3(4):93～96(in Chi nese))6　吴杰,赵又群,吴珂.基于逆问题求解的汽车操纵性能分析.中国机械工程,2006,17(4):435～439(Wu J ie,Zhao Y ouqun,Wu Ke .Analysis of lane -change vehic l e maneuverabilit y based on s oluti on of inverse p r oble m s .Chi 2na Mechanica l Engineering,2006,17(4):435～439(in Chinese ))7　方开泰,马长兴.正交与均匀试验设计.北京:科学出版社,2001(Fang Kaita i,Ma Changxing .O rt hog onal and uni 2for m ex pe ri mental desi gn .B eijing:Science Publishing House,2001(in Chi nese ))8　赵又群,王立公,何小明等.四轮转向汽车运动稳定性分析.中国机械工程,2003,14(14):1246～1248(ZhaoY ouqun,W ang L i gong,He Xiao m ing .Moti on stability anal 2ysis of 4WS vehicle .China Mecha nica l E ngineering,2003,14(14):1246～1248(i n Chine se))R S ,3S THE ART IF IC IAL NEURAL NET W O RK D R IVER M OD EL BASEDO N VE H ICL E HAN DL ING DYNA M IC S3Xu Jin Zhao Y ouqun Ruan Miqing(N a nj ing U niv ersity of Aerona utics a nd Astronautics ,N a nj ing 210016,China )Abstrac t A s a crucia l link of the drive r 2vehicle 2r oad closed 2l oop syste m ,the driver model p lays an i m portant r ole in the si mula tion of vehicle close 2l oop syste m and the evalua tion of vehicle active safety .B ased on the Vehi 2c le Handling Dyna m ic s,the P r eview 2Foll ow theor y and the A rtificial N eural Net work,this paper e stablished a di 2rec tiona l contr ol driver model —Two 2Laye r 2Feedf or ward A rtificia l Neur al Net work D riverModel and the driver 2ve 2hic le closed -l oop system model .U sing the cl ose 2l oop syste m mode l,single and double lane change si m ulati ons were pe r f or med .The results show good agr ee m ent with the ideal da ta .It indicates that this driver model is rea 2sonable enough to si m ulate the driver ’s behavi or pr ope rty and p r ovide a feasible way t o the f urther inve stigation ofthe driver 2vehicle 2r oad cl osed 2l oop syste m.Key wor ds driver model,　vehic le handling dyna m ics,　neural net work,　si m ulati on analysis483ec e i ve d 9ep t embe r 2008revised 2pe te mbe r 2008.。