材料力学(单辉组)第四章扭转

材料力学 804一、参考教材：《材料力学I、II》，第四版，高等教育出版社，单辉祖编著。

二、课程内容的基本要求：第一章：绪论第二章：轴向拉压应力第三章：轴向拉压变形第四章：扭转第五章：弯曲内力第六章：弯曲应力第七章：弯曲变形第八章：应力分析和强度理论第九章：组合变形第十章：压杆稳定第十一章：能量方法第十二章：动载荷第十三章：应力分析的实验方法三、应该掌握的内容和重点内容第一章绪论材料力学的任务、基本概念，变形体的基本假设，杆件变形的基本形式。

第二章轴向拉压应力1、轴向拉（压）的概念、内力、截面法、轴力的计算和轴力图的画法。

2、轴向拉（压）杆件横截面及斜截面上的应力计算；许用应力；强度条件及应用。

3、材料在拉伸、压缩时的机械性能。

4、剪切面、挤压面的概念及其判定；剪应力和挤压的公式及其计算。

重点：1、轴力及轴力图的画法。

2、拉（压）应力及强度计算。

3、材料的主要性能。

第三章轴向拉压变形1、轴向拉（压）杆件的变形，纵向变形、弹性模量、抗拉刚度、横向变形、泊松比等概念；虎克定律及其应用。

2、桁架节点位移计算。

3、简单静不定问题的计算。

重点：1、轴向拉（压）变形计算。

2、静不定问题的分析和计算。

第四章扭转1、外力扭矩的计算，扭矩、扭矩图。

2、圆轴扭转时横截面上的应力分布和计算；强度条件及其应用。

3、圆轴扭转时变形和刚度计算；材料的扭转破坏实验。

4、扭转静不定问题的计算。

重点：1、圆轴扭转应力和强度计算。

2、圆轴扭转变形和刚度计算。

3、简单扭转静不定的计算。

第五章弯曲内力1、平面弯曲、剪力、弯矩的概念。

2、剪力方程、弯矩方程的列法；剪力图与弯矩图的画法。

3、利用微分关系画剪力图和弯矩图。

重点：剪力图与弯矩图的画法。

第六章弯曲应力1、纯弯曲的概念和平面假设；平面图形的几何性质。

2、弯曲正应力公式及应用；弯曲剪应力计算。

3、弯曲强度计算；提高梁的强度的主要措施。

重点：弯曲正应力分析与强度计算。

第七章弯曲变形1、挠度、转角及其关系；挠曲线微分方程式；积分法、叠加法求梁的变形。

第二章轴向拉压应力与材料的力学性能2-1试画图示各杆的轴力图。

题2-1图解：各杆的轴力图如图2-1所示。

图2-12-2试画图示各杆的轴力图，并指出轴力的最大值。

图a与b所示分布载荷均沿杆轴均匀分布，集度为q。

题2-2图(a)解：由图2-2a(1)可知，qxqaxF-=2)(N轴力图如图2-2a(2)所示，qaF2m ax,N=图2-2a(b)解：由图2-2b(2)可知，qaF=RqaFxF==R1N)(22R2N2)()(qxqaaxqFxF-=--=轴力图如图2-2b(2)所示，qa F =m ax N,图2-2b2-3 图示轴向受拉等截面杆，横截面面积A =500mm 2，载荷F =50kN 。

试求图示斜截面m -m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。

题2-3图解：该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N10508263=⨯=⨯⨯==－A F σ 斜截面m -m 的方位角，50-=α故有MPa 3.41)50(cos MPa 100cos 22=-⋅==ασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅== αστα杆内的最大正应力与最大切应力分别为MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示，图中还同时画出了低应变区的详图。

试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ，并判断该材料属于何种类型（塑性或脆性材料）。

题2-5解：由题图可以近似确定所求各量。

220GPa Pa 102200.001Pa10220ΔΔ96=⨯=⨯≈=εσEMPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。

2-7 一圆截面杆，材料的应力-应变曲线如题2-6图所示。

若杆径d =10mm ，杆长 l =200mm ，杆端承受轴向拉力F = 20kN 作用，试计算拉力作用时与卸去后杆的轴向变形。

第4章 扭转§4-1 概述工程上的轴是承受扭转变形的典型构件，如图4-1所示的攻丝丝锥，图4-2所示的桥式起重机的传动轴以及齿轮轴等。

扭转有如下特点：1．受力特点：在杆件两端垂直于杆轴线的平面内作用一对大小相等，方向相反的外力偶——扭转力偶。

其相应内力分量称为扭矩。

2．变形特点：横截面绕轴线发生相对转动，出现扭转变形。

若杆件横截面上只存在扭矩一个内力分量，则这种受力形式称为纯扭转。

§4-2 外力偶矩与扭矩的计算 扭矩图1．外力偶矩 m如图4-3所示的传动机构，通常外力偶矩不是直接给出的，而是通过轴所传递的功率mN和转速n 由下列关系计算得到的。

nN m 9550= (4-1a) 如轴在m 作用下匀速转动φ角，则力偶做功为φm A =，由功率定义ωφm dtd m dt dA N =⋅==。

角速度ω与转速n （单位为转/分，即r/min ）。

关系为60/2n πω=（单位为弧度/秒，rad/s ）。

由于1kW=1000N ·m/s ，N 千瓦的功率相当于每秒钟作功N W ×=1000，单位为N ·m ；而外力偶在1秒钟内所作的功为m n 2m W ⋅=⋅=πω/60 （N ·m ）由于二者作的功应该相等，则有m n N ⋅=×π21000/60由此便得（4-1）式。

式中：N —传递功率（千瓦，kW ） —转速（r/min ）n 如果传递功率单位是马力(PS)，由于1PS=735.5 N ·m/s ，则有nN m 7024=（N ·m ） (4-1b) 式中：N —传递功率（马力，PS ）n —转速（r/min ）2．扭矩T求出外力偶矩后，可进而用截面法求扭转内力——扭矩。

如图4-4所示圆轴，由m 0=∑x m ，从而可得A —A截面上扭矩T−m T ， m T =0=T 称为截面A —A 上的扭矩；扭矩的正负号规定为：按右手螺旋法则，T 矢量离开截面为正，指向截面为负。

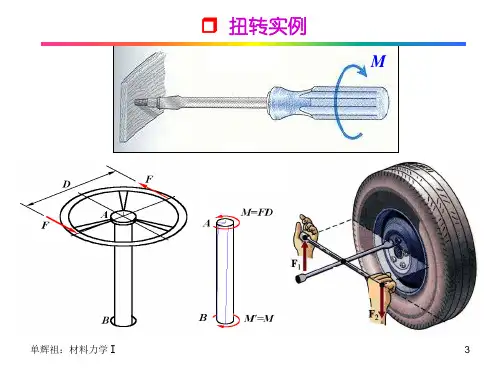
精选全文完整版第四章 扭转§4—1 工程实例、概念一、工程实例1、螺丝刀杆工作时受扭。

2、汽车方向盘的转动轴工作时受扭。

3、机器中的传动轴工作时受扭。

4、钻井中的钻杆工作时受扭。

二、扭转的概念受力特点：杆两端作用着大小相等方向相反的力偶，且作用面垂直杆的轴线。

变形特点：杆任意两截面绕轴线发生相对转动。

轴：主要发生扭转变形的杆。

§4—2 外力偶矩、扭矩一、外力：m （外力偶矩）1、已知：功率 P 千瓦(KW ），转速 n 转／分(r ／min ； rpm)。

外力偶矩：m)(N 9549⋅=nPm 2、已知：功率 P 马力(Ps)，转速 n 转／分(r ／min ；rpm)。

外力偶矩：m)(N 7024⋅=nPm 二、内力：T （扭矩） 1、内力的大小：（截面法）mT m T mx==-=∑002、内力的符号规定：以变形为依据，按右手螺旋法则判断。

（右手的四指代表扭矩的旋转方向，大拇指代表其矢量方向，若其矢量方向背离所在截面则扭矩规定为正值，反之为负值。

）3、注意的问题：（1）、截开面上设正值的扭矩方向；（2）、在采用截面法之前不能将外力简化或平移。

4、内力图（扭矩图）：表示构件各横截面扭矩沿轴线变化的图形。

作法：同轴力图：§4—3 薄壁圆筒的扭转 一、薄壁圆筒横截面上的应力(壁厚0101r t ≤,0r ：为平均半径） 实验→变形规律→应力的分布规律→应力的计算公式。

1、实验：2、变形规律：圆周线——形状、大小、间距不变，各圆周线只是绕轴线转动了一个不同的角度。

纵向线——倾斜了同一个角度，小方格变成了平行四边形。

3、切应变（角应变、剪应变）：直角角度的改变量。

4、定性分析横截面上的应力(1) 00=∴=σε ；（2）00≠∴≠τγ因为同一圆周上切应变相同，所以同一圆周上切应力大小相等。

⑶ 因为壁厚远小于直径，所以可以认为切应力沿壁厚均匀分布,而且方向垂直于其半径方向。