当前位置：文档之家 › 材料力学第4章扭转

材料力学第4章扭转

  • 格式：ppt
  • 大小：2.25 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

第四章 扭转(张新占主编 材料力学)

第四章 扭转(张新占主编 材料力学)

2M A M e M B 0 （2）
联立式（1）与式（2），得
Me MB 3
MA MB Me 3
26
4.6 等直圆轴扭转时的应变能
圆轴在外力偶作用下发生扭转变形，轴内将积蓄应变能。这种 应变能在数值上等于外力所做的功。
T1 在位移 d1上所做的功为 dW T1d1
PB M eB M eC 9549 n 796(N m) PA M eA 9549 1910(N m) n PD M eD 9549 318(N m) n
5
（2）求扭矩（扭矩按正方向假设） 1-1 截面
M M M
x
0
T1 M eB 0
T1 M eB 796N m
d1 85.3 mm
取 d1 85.3 mm。 BC段：同理，由扭转强度条件得 d2 67.4 mm ，由扭转刚度条件得
d 2 74.4 mm
取 d 2 74.4 mm。
23
（2）将轴改为空心圆轴后，根据强度条件和刚度条件确定轴的 外径D。 由强度条件得 D 96.3 mm 由刚度条件得 D 97.3 mm 取 D 97.3 mm ，则内径为
T Me
M e RdA RRd 2R 2
A 0
2
Me 2 2R
8
二、切应力互等定理
M
z
0
（dy）dx （ dx）dy
得到

切应力互等定理：在单元体在相互垂直的一对平面上，切应力 同时存在，数值相等，且都垂直于两个平面的交线，方向共同 指向或共同背离这一交线。 纯剪应力状态：单元体上四个侧面上只有切应力，而无正应力 作用

材料力学课件第3-4章

材料力学课件第3-4章

L M x( x) d x
0 GIP (x)
28
3.5 圆轴扭转时的变形与刚度条件
二. 刚度条件
对等直轴:
d
dx
Mx GIP
单位长度的扭转角
等直圆轴扭转
max
M x max GIP
180
[ ](o /m)
对阶梯轴: 需分段校核。
max
M x max GIP
180
[ ](ο /m)
2. 给出功率, 转速
(kw)
Me = 9549
P n
(N. m)
(r/min)
5
3.2 外力偶矩的计算 扭矩和扭矩图 二.横截面上的内力
截面法求内力： 截，取，代，平
Mx 称为截面上的扭矩
Mx 0 Mx Me 0 即 Mx Me
按右手螺旋法：
指离截面为正，
M x 指向截面为负。
6
3.2 外力偶矩的计算 扭矩和扭矩图
10
3.3 薄壁圆筒的扭转 纯剪切
一. 薄壁筒扭转实验
nm
t
实验观察 分析变形
x
r
nm l
mn没变 x = 0
x = 0
Me
nm
γ
Me
φ
x
r没变 = 0
= 0
nm
Me
nm
Mx
x
n m Mx
11
3.3 薄壁圆筒的扭转 纯剪切
Me Mx
nm
Mx
n m Mx
由于轴为薄壁,所以认
为 沿t 均布.即 =C
max
M x max Wp
31.5 103 m
M x max d 3
16

材料力学第四章 扭转

材料力学第四章 扭转
则上式改写为
max
T GI p
180
(/m)
×
例５ 图示圆轴，已知mA =1kN.m， mB =3kN.m， mC
=2kN.m；l1 =0.7m，l2 =0.3m；[]=60MPa，[ ]=0.3°/m，
G=80GPa；试选择该轴的直径。
mA
mB mC 解： ⑴按强度条件
A
l1
B l2 C
max
9.55
200 300
6.37
(kN m)
×
n D
m2 1 m3 2 m1 3 m4
n A 1 B 2 C 3D
②求扭矩（扭矩按正方向假设）
m 0 , T1 m2 0, T1 m2 4.78kN m m 0; T2 m1 m2 0
T2 m2 m3 (4.78 4.78) 9.56kN m
T
2 r02
t
T 2 A0
t
T
A0为平均半径所作圆的面积。
×
三、切应力互等定理：
´
a
b
dy
´
c
z
dx
d t
mz 0; t dxdy t dxdy
'
这就是切应力互等定理：在单元体相互垂直的两个截面
上，切应力必然成对出现，且数值相等，两者都垂直于两平
面的交线，其方向或共同指向交线，或共同背离交线。
垂直，则杆件发生的变形为扭转变形。
A
B O
A
BO
m
m
——扭转角（两端面相对转过的角度）
——剪切角，剪切角也称切应变。
×
§4–2 扭转的内力—扭矩与扭矩图
一、扭矩 圆杆扭转横截面的内力合成
结果为一合力偶，合力偶的力偶 矩称为截面的扭矩，用T 表示之。 m

材料力学 第4章_扭转

材料力学 第4章_扭转
z


d x d z d y d y d z d x 0

返回
4. 切应力互等定理

切应力互等定理： 也称切应力双生定理， 指在单元体相互垂直的两 个面上，切应力必成对存 在，且数值相等；两者都 垂直于两个平面的交线， 方向共同指向或背离这一 交线。


纯剪切
BC B
TCD mB mC 700N m
(b)
TDA mA 1146N m
可见:主动轮与从动轮位置不 同,轴内最大扭矩也不同,显 然(a)方案比(b)方案合理。
返回
§4.3 圆轴扭转时的应力与强度条件
返回总目录
一、薄壁圆筒扭转时的切应力 1. 变形现象 圆周线大小、形状、间距 不变，纵向线相同倾斜。 2. 横截面上应力分析 因纵向纤维无正应变， 有角应变，因此横截面上 无，有， 与圆周相切。 又因壁很薄，可近似认 为沿壁厚应力相等。
第4章 扭转
第4章 扭转
§4.1 扭转的概念 §4.2 外力偶矩、扭矩和扭矩图
§4.3 圆轴扭转时的应力与强度条件
§4.4 圆杆扭转时的变形及刚度条件
§4.5 非圆截面杆的扭转概念
§4.1 扭转的概念
返回总目录
工程中的受扭转杆件
拧紧螺母的工具杆产生扭转变形
返回
工程中的受扭转杆件
返回
工程中的受扭转杆件
r
d dx
横截面上任一点的 ⊥半 径，并与该点到轴线的距离 成正比。
返回
4. 应力公式 静力关系
T

dA
横截面上分布内力系对 圆心的矩等于扭矩T。

T d A A d d 2 G d A G d A A dx dx A

材料力学第4章扭转变形

材料力学第4章扭转变形

1 1
T
1 1
T
1
Me
+
B
x
T Me
Me
B
T图 x
例 一传动轴如图，转速n = 300r/min； 主动轮输 入的功率P1= 500kW，三个从动轮输出的功率分 别为： P2= 150kW， P3= 150kW， P4= 200kW。 试作轴的扭矩图。
解： 首先必须计算作用在各轮上的外力偶矩
M2 1
2 T
1
1 T
1
材料不同），可见在两
杆交界处的切应力是不
同的。
d
D
§4. 7 非圆截面杆扭转的概念
对非圆截面杆的扭转问题，主要介绍矩形截面 杆的扭转。
试验现象
横向线变 成曲线
横截面发生 翘曲不再保 持为平面
平面假设不再 成立，可能产 生附加正应力
自由扭转 翘曲不受限制。 纵向纤维无伸长 横截面上无正应力
T
max
O
max
D
d
T
Ip
max
T Wp
圆截面的极惯性矩Ip和扭转截面系数Wp —几何性质 实心圆截面：
d
O
d
O
d D d
Ip
2 d A πd 4
A
32
Wp
Ip d /2
πd 3 16
Ip
2 d A πD4
A
32
1 4
Wp
Ip D /2
πD 3 16
1 4
4-4 圆轴扭转强度条件与合理设计
B 0
按叠加原理：
B BB BM 0
BB、BM分别为MB、Me 引起的在杆端B的扭转角。
线弹性时，物理关系(胡克定理)为

材料力学第四章

材料力学第四章

一、 传动轴如图19-5（a ）所示。

主动轮A 输入功率kW N A 75.36=，从动轮D C B 、、输出功率分别为kW N kW N N D C B 7.14,11===，轴的转速为n =300r/min 。

试画出轴的扭矩图。

解 （1）计算外力偶矩：由于给出功率以kW 为单位，根据（19-1）式：117030075.3695509550=⨯==n N M A A (N ·m )3513001195509550=⨯===n N M M B C B (N ·m )4683007.1495509550=⨯==n N M D D (N ·m )（2）计算扭矩：由图知，外力偶矩的作用位置将轴分为三段：AD CA BC 、、。

现分别在各段中任取一横截面，也就是用截面法，根据平衡条件计算其扭矩。

BC 段：以1n M 表示截面Ⅰ－Ⅰ上的扭矩，并任意地把1n M 的方向假设为图19-5（b ）所示。

根据平衡条件0=∑x m 得：01=+B n M M3511-=-=B n M M (N ·m )结果的负号说明实际扭矩的方向与所设的相反，应为负扭矩。

BC 段内各截面上的扭矩不变，均为351N ·m 。

所以这一段内扭矩图为一水平线。

同理，在CA 段内：M n Ⅱ＋0=+B C M MⅡn M = －B C M M -= －702(N ·m ) AD 段：0=D n M M －Ⅲ468==D n M M Ⅲ(N ·m )根据所得数据，即可画出扭矩图[图19－5（e ）]。

由扭矩图可知，最大扭矩发生在CA 段内，且702max =n M N ·m二、 如图19-15所示汽车传动轴AB ，由45号钢无缝钢管制成，该轴的外径D =90mm ，壁厚t =2.5mm ，工作时的最大扭矩M n ＝1.5kN·m ，材料的许用剪应力][τ＝60MPa 。

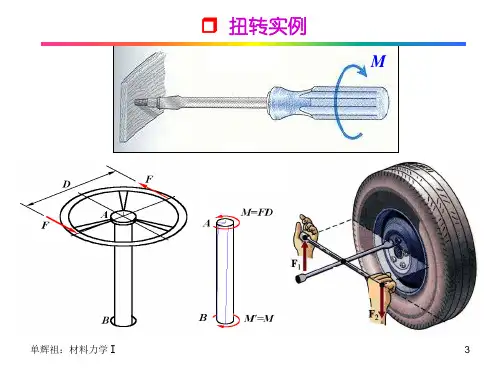
《材料力学》第四章 扭转

《材料力学》第四章 扭转

第四章 扭转§4—1 工程实例、概念一、工程实例1、螺丝刀杆工作时受扭。

2、汽车方向盘的转动轴工作时受扭。

3、机器中的传动轴工作时受扭。

4、钻井中的钻杆工作时受扭。

二、扭转的概念受力特点：杆两端作用着大小相等方向相反的力偶，且作用面垂直杆的轴线。

变形特点：杆任意两截面绕轴线发生相对转动。

轴：主要发生扭转变形的杆。

§4—2 外力偶矩、扭矩一、外力：m （外力偶矩）1、已知：功率 P 千瓦(KW ），转速 n 转／分(r ／min ； rpm)。

外力偶矩：m)(N 9549⋅=nPm 2、已知：功率 P 马力(Ps)，转速 n 转／分(r ／min ；rpm)。

外力偶矩：m)(N 7024⋅=nPm 二、内力：T （扭矩） 1、内力的大小：（截面法）mT m T mx==-=∑002、内力的符号规定：以变形为依据，按右手螺旋法则判断。

（右手的四指代表扭矩的旋转方向，大拇指代表其矢量方向，若其矢量方向背离所在截面则扭矩规定为正值，反之为负值。

）3、注意的问题：（1）、截开面上设正值的扭矩方向；（2）、在采用截面法之前不能将外力简化或平移。

4、内力图（扭矩图）：表示构件各横截面扭矩沿轴线变化的图形。

作法：同轴力图：§4—3 薄壁圆筒的扭转 一、薄壁圆筒横截面上的应力(壁厚0101r t ≤,0r ：为平均半径） 实验→变形规律→应力的分布规律→应力的计算公式。

1、实验：2、变形规律：圆周线——形状、大小、间距不变，各圆周线只是绕轴线转动了一个不同的角度。

纵向线——倾斜了同一个角度，小方格变成了平行四边形。

3、切应变（角应变、剪应变）：直角角度的改变量。

4、定性分析横截面上的应力(1) 00=∴=σε ；（2）00≠∴≠τγ因为同一圆周上切应变相同，所以同一圆周上切应力大小相等。

⑶ 因为壁厚远小于直径，所以可以认为切应力沿壁厚均匀分布,而且方向垂直于其半径方向。

材料力学：第四章 扭转

材料力学：第四章 扭转

回顾: 极惯性矩、抗扭截面系数的计算
抗扭截面系数 极惯性矩
薄壁圆管 扭转切应力
回顾: 圆轴扭转强度条件 & 应力计算公式
薄壁圆管扭 转切应力
圆轴扭转 强度条件
max
[ ] u
n
扭转极限应力τu =
扭转屈服应力ts (塑性材料) 扭转强度极限tb (脆性材料)
§5 圆轴扭转变形与刚度计算
单辉祖：材料力学Ⅰ
14
例题
例 2-1 MA=76 Nm, MB=191 Nm, MC=115 Nm, 画扭矩图 解：用截断法,列力偶
矩平衡方程,和x轴正向 相同者取正 (1) 1-1截面
单辉祖：材料力学Ⅰ
(2) 2-2截面 T2 MC 115 N m
(3) 画扭矩图
15
§3 圆轴扭转横截面上的应力
单辉祖：材料力学Ⅰ
64
薄壁杆扭转
开口与闭口薄壁杆
截面中心线
－截面壁厚平分线
薄壁杆
－壁厚<<截面中心线 长度的杆件
闭口薄壁杆
－截面中心线为封闭曲线的薄壁杆
开口薄壁杆
－截面中心线为非封闭曲线的薄壁杆
单辉祖：材料力学Ⅰ
65
闭口薄壁杆扭转应力与变形
假设 切应力沿壁厚均匀分布, 并平行于中心线切线 应力公式
单辉祖：材料力学Ⅰ
62
例题
例 7-1 试比较闭口与开口薄壁圆管的抗扭性能,设 R0＝20d
解：1. 闭口薄壁圆管
2. 开口薄壁圆管
3. 抗扭性能比较
单辉祖：材料力闭学Ⅰ口薄壁杆的抗扭性能远比开口薄壁杆好
63
§8 薄壁杆扭转
开口与闭口薄壁杆 闭口薄壁杆扭转应力与变形 开口薄壁杆扭转简介 薄壁杆合理截面形状 例题

周建方版材料力学习题解答[第四章]

周建方版材料力学习题解答[第四章]

δ3 3 1 2( 2 1 )
3
2 2
1
4
2Fl EA
Fl EA
(4
2 1) Fl EA
4-6 求图 4-18 所示节点 B 的水平位移和竖向位移。 AB 杆和 BC 杆的抗拉刚度 EA相同。
解：
C
根据静力学容易求得：
FBC
A
FAB B
BD
E GH F
题 4-6 图
FAB F FBC 2 F
2
EA
2
EA
4-5（c）
D
A
C
FO1A
FO1C
FO2C
δ1 δ2
(一）受力分析，反力计算
M C 0 FO1A F
F
M D 0 F 2l FO1C 2l 0
B (二）求变形
因此：FO1C 2F
1
FO1Al EA
Fl EA
2
FO1C 2l EA
2 2
2F 2l EA
2 2 2 Fl EA
1 8
ql 4 EI
5ql 4 24EI
4-15(b)解
（一） C C C1 C2 Fl2 Fl2l 3Fl2 2EI EI 2EI
（二）求 wB
wB
wB1
wB2
Fl3 3EI
Ml2 2EI
Fl3 Fl3 Fl3 3EI 2EI 6EI
ql (2)
(B') 1 ql 2 2
A dx B x
题 4-4 图
4-5 试计算以下各题刚性梁 AB 的 B 处位移（图 4-17）。其它杆件为弹性杆，刚度 EA。
（a）
q
A FDC
D
D' C C'

同济大学材料力学第四章 扭转 3学时

同济大学材料力学第四章 扭转 3学时

N马力 m 7.02 n
(kN m)
N KW m 9.55 n
(kN m)
第四章 扭转/二 外力偶矩、扭矩和扭矩图
2 求扭转内力的方法—截面法
Ⅰ
Ⅰ
3 受扭圆轴横截面上的内力—扭矩
I
Mn
I
第四章 扭转/二 外力偶矩、扭矩和扭矩图
4 扭矩的符号规定—右手螺旋法则
mI I
m
Mn
扭 矩 符 号 规 定 ：
m1
d1
m2
d2
m3
I P1 I P2
d1
A
0.8kN· m
0.8m
B
1.0m
C
32 d 2 4 236cm 4 32
25.1cm
4
AB
BC
M n1L1 0.0318rad GI P1
M n 2 L2 0.0079rad GI P 2
1.5kN· m
AC AB BC 0.0318rad 0.0079rad 0.0239rad
0
τ
τ
σmin
τ
45 0
0
σmax
第四章 扭转/三 圆轴扭转时的强度计算
3 圆轴扭转时的强度条件 为保证圆轴安全工作，要求轴内的最大工作切 应力不超过材料的许用切应力，即：
max
式中的许用扭转切应力 ,是根据扭转试验, 并考虑适当的工作安全系数确定的.
M n max WP
159.2
第四章 扭转/二 外力偶矩、扭矩和扭矩图
课堂练习 图示圆轴中，各轮上的转矩分别为mA＝4kN·m， mB＝10kN·m, mC＝6kN · m，试求1－1截面和2－2截面上的 轮 扭矩，并画扭矩图。

材料力学课件 第四章扭转

材料力学课件 第四章扭转
4. 公式讨论： ① 仅适用于各向同性、线弹性材料，在小变形时的等圆截面
直杆。
② 式中：T—横截面上的扭矩，由截面法通过外力偶矩求得。
—该点到圆心的距离。
Ip—截面极惯性矩，纯几何量，无物理意义。
17
Ip A 2dA 单位：mm4，m4。
③ 尽管由实心圆截面杆推出，但同样适用于空心圆截面杆，
只是Ip值不同。
一、传动轴的外力偶矩 传递轴的传递功率、转数与外力偶矩的关系：
m
9.55
P n
(kN
m)
其中：P — 功率，千瓦（kW） n — 转速，转/分（rpm）
m
7.024
P n
(kN
m)
其中：P — 功率，马力（PS） n — 转速，转/分（rpm）
m
7.121
P n
(kN
m)
其中：P — 功率，马力（HP） n — 转速，转/分（rpm）
22
[例2]有一阶梯形圆轴，如图(a)所示轴的直径分别d为1 50mm,d2 80mm 。扭转力偶矩分别为 Me1 0.8kN m ，Me2 1.2kN m ，M e3 2kN m。若 材料的许用切应力 [ ] 40MPa ，试校核该轴的强度。
解： 方法一（理论计算法） 用截面法求出圆轴各段的扭矩，如图(b)所示。 由扭矩图可见，CD段和DB段的直径相同，但DB段的扭矩大 于CD段，故这两段只要校核DB段的强度即可。AC段的扭矩 虽然也小于DB段，但其直径也比DB段小，故AC段的强度也 需要校核。
2GI p
W
U ;
64PR3n Gd 4
P K
;
K
Gd 4 64R3n
为弹簧常数。
36
[例3] 圆柱形密圈螺旋弹簧的平均直径为：D=125mm，簧丝直 径为：d =18mm，受拉力 P=500N 的作用，试求最大剪应力 的近似值和精确值；若 G =82GPa，欲使弹簧变形等于 6mm， 问：弹簧至少应有几圈？

材料力学扭转

材料力学扭转

材料力学扭转材料力学是研究材料在外力作用下的变形和破坏规律的一门学科，而扭转则是材料力学中非常重要的一种变形形式。

在工程实践中，我们经常会遇到各种扭转现象，比如轴承、螺纹、螺栓等零部件的扭转变形。

因此，了解材料力学中的扭转现象对于工程设计和实际应用具有重要意义。

首先，我们来看一下什么是扭转。

扭转是指材料在外力作用下沿着一定轴线发生的旋转变形。

在扭转过程中，材料内部会受到剪切应力的作用，从而导致材料发生扭转变形。

扭转变形不仅会影响材料的外观和尺寸，还会对材料的力学性能产生影响。

在材料力学中，我们通常用剪切模量来描述材料的扭转性能。

剪切模量是指材料在扭转过程中所表现出的抗扭转能力。

剪切模量越大，材料的抗扭转能力就越强，反之则越弱。

因此，在工程设计中，我们需要根据材料的剪切模量来选择合适的材料，以满足工程的扭转性能要求。

除了剪切模量，材料的断裂韧性也是影响材料扭转性能的重要因素。

断裂韧性是指材料在扭转过程中抵抗断裂的能力。

材料的断裂韧性越大，其扭转性能就越好，能够更好地抵抗扭转变形和破坏。

因此，在工程设计中，我们还需要考虑材料的断裂韧性，以确保材料在扭转过程中不会发生过早的断裂。

此外，材料的微观结构也会对其扭转性能产生影响。

晶粒的大小、形状以及晶界的性质都会影响材料的扭转性能。

一般来说，晶粒越细小，晶界越强化，材料的扭转性能就会越好。

因此，在材料的制备过程中，我们需要通过控制材料的微观结构来提高其扭转性能。

总的来说，材料力学中的扭转现象是工程设计中不可忽视的重要问题。

了解材料的扭转性能，选择合适的材料，并通过控制材料的微观结构来提高其扭转性能，对于保证工程零部件的稳定性和可靠性具有重要意义。

希望本文能够对大家对材料力学中的扭转问题有所帮助。

材料力学-圆杆扭转时的变形及刚度条件

材料力学-圆杆扭转时的变形及刚度条件

扭转剪应力公式是圆轴在弹性范围内导出的，其适用条件是：
1. 必须是圆轴，否则横截面将不再保持平面，变形协调公式
将不再成立。
d
dx
2. 材料必须满足胡克定律，而且必须在弹性范围内加载，只有
这样，剪应力和剪应变的正比关系才成立：
G
d
dx
二者结合才会得到剪应力沿半径方向线性分布的结
何斌
Page 28
材料力学
第4章 圆轴扭转
连接件强度计算的工程意义
两个或多个构件相连 —— 1. 用 钉子、铆钉等联结 2. 焊接 3. 其它
联接件体系（联接件、被联接构件）的受力特点： 力在一条轴线上传递中有所偏离（与拉压情况不同）
问题：1. 力传递的偏离引起什么新的力学现象？ 2. 如何计算联接件、被联接构件的强度？
何斌
Page 12
材料力学
例 题1
第4章 圆轴扭转
θ M x θ ＝1.5 ＝1.5 π rad / m
GIp
2m 2 180
I
＝π D4 p 32
1－α 4
，α＝ d D
轴所能承受的最大扭矩为
M x
θ
GI
＝1.5 p2
π 180
rad/m G
π D4 32
1－α 4
1.5π
受扭圆轴的相对扭转角
圆杆受扭矩作用时，dx微段的两截面绕轴线相对转动 的角度称为相对扭转角
d M x dx
GIP沿轴线方向积分，得到源自d M x dxl
l GIp
何斌
Page 6
材料力学
第4章 圆轴扭转
圆杆扭转时的变形及刚度条件
受扭圆轴的相对扭转角
对于两端承受集中扭矩的等截面圆轴，两端面的相

材料力学-第4章 扭转

材料力学-第4章 扭转
18
材料力学－第4章 扭转
圆轴扭转横截面上的应力

变 形
O
dx
ρ
R A

d
O’
( ) G G
d
dx
应变特征

B B´
A


B B´
应力分布

C
C
D D´

D D´
应力公式
BB Rd G G G AB dx
19
材料力学－第4章 扭转
圆轴扭转横截面上的应力
材料力学
第四章 扭 转
1
材料力学－第4章 扭转
内容提纲：
• • • • • • • • 概述及示例 外力偶矩、扭矩和扭矩图 圆轴扭转横截面上的应力 圆轴扭转破坏与强度条件 圆轴扭转变形与刚度条件 扭转静不定问题 非圆截面轴扭转 薄壁杆扭转
2
材料力学－第4章 扭转
概述及示例
3
材料力学－第4章 扭转
9
材料力学－第4章 扭转
扭力偶矩计算与扭矩
• 在工程中，功率常用千瓦 Pkw (kW) 或马力 P 给出，角 速度用转速 n(r/min (转/分钟)) 给出，则外力偶矩的计算 公式为
PkW M e 9549 nr /min M e 7024 P 马力 nr /min
1 Pkw (千瓦) 1000 N m /s 1 P (马力) 735.5 N m /s

45o
32
材料力学－第4章 扭转
圆轴扭转破坏与强度条件
从破坏类型可见，对于脆性材料（如铸 铁），其破坏机理是斜截面上的最大拉应力 因此，本质上讲，应对斜截面上的正应力 进行强度计算。然而，由于斜截面上的正应力和 横截面上的剪应力间有固定的关系，所以，习惯 上仍按最大剪应力进行强度计算

材料力学课件(路桥)第4章扭转

材料力学课件(路桥)第4章扭转
计算过程中需要考虑材料的弹性模量、泊松比、剪切模量等参数，以及 结构的几何尺寸和边界条件。
强度条件的工程意义
满足强度条件是保证路桥工程安全性和 稳定性的基础。
通过满足强度条件，可以防止桥梁结构 在承受外力矩和扭矩时发生破坏或过度
变形。
在路桥工程的设计、施工和运营过程中 ，需要定期进行检测和维护，以确保结
扭矩的量纲
扭矩的量纲是力和长度（L）的乘积，表示为ML^2。
量纲是描述物理量本质属性的方式，通过量纲可以判断物理量的性质和相互关系 。
03
扭转的应力分析
切应力与剪切应变的关系
切应力与剪切应变的关系是线 性的，即剪切应变与切应力成 正比。
在剪切弹性范围内，切应力与 剪切应变之间的关系可以用剪 切弹性模量来描述。
扭转过程中，杆件上各点的角位移和 剪切变形程度不同，导致杆件横截面 绕其自身轴线发生转动。
扭转的物理现象
01
杆件在扭转时，横截面上的正应 力分布不均匀，呈现出剪切变形 的特点。
02
杆件上各点的剪切变形程度与该 点到轴线的距离成正比，导致横 截面上的切向力分布不均匀。
扭转的分类
根据杆件上所受外力矩的方向， 扭转可分为左旋和右旋两种类型
构的强度和稳定性。
05
扭转的刚度条件
刚度条件的定义
刚度条件是指在材料力学中，杆件在受到扭矩作用时，其横 截面上的剪切应力和剪切变形之间的关系。
刚度条件是材料力学中一个重要的基本概念，它描述了杆件 在扭矩作用下抵抗变形的能力。
刚度条件的计算方法
根据材料力学的基本理论，刚度条件可以通过杆件的剪切 弹性模量和剪切应变来计算。
材料力学课件(路桥)第4章 扭转
目录 CONTENTS

第四章：扭转

第四章：扭转

2 2
64.22
45.02
0.611
A1
d12
58.62
小 结 在最大切应力相同的情况下，空心轴所用的材料是实心轴的
61.1%，自重也减轻了 38.9%。其原因是：圆轴扭转时，横截面上应力
呈线性分布，越接近截面中心，应力越小，此处的材料就没有充分发挥 作用。做成空心轴，使得截面中心处的材料安置到轴的外缘，材料得到 了充分利用，而且也减轻了构件的自重。但空心轴的制造要困难些，故 应综合考虑。
解：1）用截面法求各段扭矩 AB 段：
1
2
T1 MA 900 N m
BC 段：
T
T2 M c 600 N m
600Nm
画出扭矩图如图所示
900Nm
第五节：圆轴扭转时的变形
AB 截面 极惯性矩
I P1
πd14 32
BC 截面 极惯性矩
2）C 截面相对于 A 截面的转角
IP2
πd
4 2
32
第一节：扭转的概念
扭转：是杆的又一种基本变形形式。其受力特点是：构件两 端受到两个作用面与杆的轴线垂直的、大小相等的、转向相 反的力偶矩作用，使杆件的横截面绕轴线发生相对转动。
扭转角：任意两横截面间的相对角位移。如图所示的 φ 角。
轴：工程中以扭转为主要变形的构件。如钻探机的钻杆，电 动机的主轴及机器的传动轴等。
叠加原理
CA CB BA
AB 段：
BA =
T1l1 GI P1
×
1800
=-0.8110
BC 段：
CB =
T2l2 GI P2
×
1800
=0.9810
CA CB BA 0.9810 (0.8110 ) 0.17 0

材料力学课件-第四章 扭转-薄壁杆件的扭转

材料力学课件-第四章 扭转-薄壁杆件的扭转
部分加厚由于最小壁厚不变，最大应力不变。部分加厚后甚至由于应力集中更危险。
例2：某等壁厚d闭口薄壁杆受扭矩T，中心线周长S，轴的最大扭转切应力与扭转变形:(1)在 S/2中心线长度上壁厚增加一倍到2d；(2)在很小的局部受损伤壁厚减薄到d/2。
解：(2)第2种情形
局部减薄对积分值影响甚微，可以忽略不计。
最大应力增加一倍。
定性研究结论：强度是局部量，刚度是整体量。
例3：比较扭转切应力与扭转变形
解：
R0
R0
比较
（1）闭口薄壁圆管
（2）开口薄壁圆管
(狭长矩形)
作业 4-22 4-27 4-35 4-36
谢谢
薄壁圆管
思考：公式的精度？
在线弹性情况下，精确解为
思考：公式（1）和（2）的适用范围？
(1)
(2)
误差
T
dx
a
b
c
d
二、闭口薄壁杆的扭转变形
dx
ds
分析方法讨论:
由静力学、几何和物理三方面求解所遇到的困难：几何形状复杂。
新方法探索：
尝试能量法。
一未知量
无未知量
问题可解
二、闭口薄壁杆的扭转变形
假设：切应力沿壁厚均匀分布，其方向平行于中心线 假设依据：
T
dx
a
b
c
d
a
b
c
d
2
1
dx
1
1
2
2
薄，切应力互等定理
利用切应力互等定理，转化为研究纵向截面切应力，利用平衡方程求解.
截面中心线所围面积 的2倍
思考：O点位置可否任选，如截面外？
ds
o
ds
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(2)计算扭矩
从受力情况看，在轴的AB，BC，CD三段内，各横截面上的扭矩是不相等的。
现在用截面法，根据平衡方程计算各段内的扭矩。 在AB段，用截面1—1截取，取左段为研究对象，并假设该截面上的扭矩T1为 正，如图4.5(c)所示。由平衡方程 MA+T1=0 于是有 T1=-MA=-1 910 N²m ，得
相反的切应力′，于是组成力偶矩为(′dxdz)dy的力偶。根据平衡方 程 ，得 ′dxdz)dy
( dydz)dx=( 于是
如图4.7(a)所示的单元体在其两对相互垂直的平面上只有切应力而无正应力 。这种应力状态称为纯剪切应力状态。显然，薄壁圆筒发生扭转时处于纯剪
切应力状态。由于这种单元体的前、后两平面上无任何应力，所以可将其改
图4.3 根据平衡方程 ，即
T-Me=0
得 T=Me
显然，若截取后取右段为研究对象，则在同一横截面上可求得扭矩的数值大
小相等而方向相反。为使同一横截面上的扭矩正、负号一致，对扭矩的符号 规定如下：按右手螺旋法则确定扭矩矢量T，当T的指向与横截面的外法线方
向一致时，扭矩为正(见图4.4(a))，反之，为负(见图4.4(b))。
依据上述分析，可知薄壁圆筒的扭转时，横截面上各处的切应力值均相等， 其方向与圆周相切。由于横截面上的扭矩都是该截面上的应力与横面积dA之 乘积的合成，如图4.6(d)所示，可得
所以
(2)切应力互等定理 在承受扭转的薄壁圆筒上，用两个横截面、两个径向截面和两个圆柱面截取 出边长分别为dx，dy，dz的单元体，并放大为图4.7(a)所示。单元体的左、 右两侧面是圆筒横截面的一部分，所以有切应力。切应力值根据公式(4.2) 计算，数值相等但图4.7方向相反，于是组成一个力偶矩为( dydz)dx的力偶 。为保持平衡，单元体的上、下两个面必须有切应力，并组成力偶以与力偶 ( dydz)dx相平衡。由 可知，上、下两个面上存在大小相等、方向
在研究扭转的应力和变形之前，先介绍作用于轴上的
外力偶矩及横截面上的内力。
4.2.1外力偶矩的计算 以工程中常见的传动轴为例，作用在轴上的外力偶矩与轴传递的功率和转速 有关。若已知轴传递的功率为Pk，单位kW，转速为n，单位r/min，则圆轴在 每分钟内传递的功为 W=Pk²t=Pk³103³60 外力偶矩Me在每分钟内完成的功为 W′=Me²φ =Me³2π ³n 由于W′=W，所以作用在轴上的外力偶矩
图4.1
上述杆件的受力可简化为如图4.2所示，其受力特点是在杆件 两端作用两个大小相等、方向相反、且作用面垂直于杆件轴线 的力偶。变形特点是杆件的任意两个横截面绕其轴线作相对的 转动。扭转时杆件两个横截面相对转动的角度称为相对扭转角 ，一般用φ 表示(见图4.2)。
图4.2
4.2外力偶矩的计算扭矩与扭矩图
4.3圆轴扭转时的应力
本节讨论等直圆轴扭转时的应力。先通过研究薄壁圆筒的扭转寻求扭转时横 截面上的应力和应变的分布规律及其二者之间的关系，再进一步从等直圆轴
受扭时的变形几何关系、物理关系和静力关系３个方面综合分析，推导圆轴
扭转时的应力计算公式。
4.3.1纯剪切 (1)薄壁圆筒的扭转 设一等厚薄壁圆筒，其壁厚δ 远小于其平均半径为r，两端承受外力偶矩Me ，如图4.6(a)所示。圆筒任一横截面上的扭矩都是由截面上的应力与微面积 dA之乘积合成的，因此横截面上的应力只能是切应力。
图4.6
为得到沿横截面圆周各点处切应力的变化规律，可在薄壁圆筒受扭前，在筒 表面画出一组等间距的纵向线和圆周线，形成一系列的矩形小方格。然后在 两端施加外力偶矩Me，圆筒发生扭转变形。由此可以观察到： ①圆筒表面各纵向线在小变形下仍保持直线，但都倾斜了同一微小角度γ 。 ②各圆周线的形状、大小和间距都保持不变，但绕轴线旋转了不同的角度。 因筒壁很薄，所以可将圆周线的转动视为整个横截面绕轴线的转动，圆筒两 端截面的相对扭转角为φ ，如图4.6(b)所示。此外，圆筒任意两横截面之间 也有相对转动，从而使筒表面的各矩形小方格的直角都改变了相同的角度γ ，如图4.6(c)所示，这是横截面上切应力作用的效果，又因薄壁圆筒δ r ，所以可近似认为切应力沿壁厚不变。
第4章 扭转
4.1扭转的概念和实例 工程中，受扭构件是很常见的。例如，汽车转向轴，当汽车转向时，驾驶员 通过方向盘把力偶作用在转向轴的上端，在转向轴的下端则受到来自转向器
的阻力偶作用，如图4.1(a)所示。又如轴承传动系统的传动轴工作时，电动
机通过皮带轮把力偶作用在一端，在另一端则受到齿轮的阻力偶作用，如图 4.1(b)所示。
负号表明截面1—1上的实际扭矩方向与假设方向相反，按照扭矩的符号规定 ，该截面上扭矩是负的。
同理，可求得截面2—2和截面3—3上的扭矩分别为
T2=-3 820 N²m9T3=5 730 N²m (3)绘制扭矩图
根据上述计算，绘制扭矩图如图4.5(f)所示。可以看出，该轴的最大扭矩发
生在CD段，且Tmax=5 730 N²m。
用平面图加以表示，如图4.7(b)所示。
图4.7
(3)剪切胡克定律 通过薄壁圆筒的扭转实验可以得到材料在纯剪切应力状态下应力与应变之间 的关系。 试验结果表明，当切应力低于材料的剪切比例极限时，相对扭转角φ 与扭矩
应用时需要注意功率和转速的单位。
4.2.2扭矩与扭矩图 杆件上的外力偶矩确定后，就可用截面法计算任意横截面上的内力。以如图 4.3(a)所示的圆轴为例，假想用m—m截面将圆轴一分为二，并取其左段为研 究对象(见图4.3(b))。由于整个轴是平衡的，则左段也处于平衡状态，这就 要求m—m横截面上的内力必须归结为一个力偶矩，称为扭矩，用T表示。
图4.4
下面举例说明扭矩的计算和扭矩图的绘制。
例4.1如图4.5(a)所示的传动轴，已知轴的转速n=300 r/min，主动轮C输入
功率PC=360 kW，3个从动轮A，B，D输出功率分别为PA=60 kW，PB=120 kW， PD=15
解(1)计算外力偶矩 根据公式(4.1)计算作用于各轮上的外力偶矩