云南省曲靖市师宗县五龙民族中学2014秋九年级数学上册 22.2 用函数的观点看一元二次方程(第2课时)教案

教学时间课题《二次函数》小结与复习（2）课型新授课教学目标知识和能力会用待定系数法求二次函数的解析式，能结合二次函数的图象掌握二次函数的性质，能较熟练地利用函数的性质解决函数与圆、三角形、四边形以及方程等知识相结合的综合题。

过程和方法情感态度价值观教学重点用待定系数法求函数的解析式、运用配方法确定二次函数的特征。

教学难点会运用二次函数知识解决有关综合问题。

教学准备教师多媒体课件学生“五个一”课堂教学程序设计设计意图一、例题精析，强化练习，剖析知识点用待定系数法确定二次函数解析式．例：根据下列条件，求出二次函数的解析式。

(1)抛物线y＝ax2＋bx＋c经过点(0，1)，(1，3)，(－1，1)三点。

(2)抛物线顶点P(－1，－8)，且过点A(0，－6)。

(3)已知二次函数y＝ax2＋bx＋c的图象过(3，0)，(2，－3)两点，并且以x＝1为对称轴。

(4)已知二次函数y＝ax2＋bx＋c的图象经过一次函数y＝－3/2x＋3的图象与x轴、y轴的交点；且过(1，1)，求这个二次函数解析式，并把它化为y＝a(x－h)2＋k的形式。

学生活动：学生小组讨论，并让学生阐述解题方法。

教师归纳：二次函数解析式常用的有三种形式：(1)一般式：y＝ax2＋bx＋c (a≠0)(2)顶点式：y＝a(x－h)2＋k (a≠0) (3)两根式：y＝a(x－x1)(x－x2) (a≠0)当已知抛物线上任意三点时，通常设为一般式y＝ax2＋bx＋c形式。

当已知抛物线的顶点与抛物线上另一点时，通常设为顶点式y＝a(x－h)2＋k形式。

当已知抛物线与x轴的交点或交点横坐标时，通常设为两根式y＝a(x－x1)(x－x2)强化练习：已知二次函数的图象过点A(1，0)和B(2，1)，且与y轴交点纵坐标为m。

(1)若m为定值，求此二次函数的解析式；(2)若二次函数的图象与x轴还有异于点A的另一个交点，求m的取值范围。

二、知识点串联，综合应用例：如图，抛物线y＝ax2＋bx＋c过点A(－1，0)，且经过直线y＝x－3与坐标轴的两个交点B、C。

22.2 用函数观点看一元二次方程 教 学 目 标 知 识和能 力复习巩固用函数y ＝ax 2＋bx ＋c 的图象求方程ax 2＋bx ＋c ＝0的解 过 程和方 法让学生体验函数y ＝x 2和y ＝bx ＋c 的交点的横坐标是方程x 2＝bx ＋c 的解的探索过程，掌握用函数y ＝x 2和y ＝bx ＋c 图象交点的方法求方程ax 2＝bx ＋c 的解。

情 感态 度价值观 提高学生综合解题能力，渗透数形结合思想。

教学重点用函数图象法求方程的解以及提高学生综合解题能力 教学难点提高学生综合解题能力，渗透数形结合的思想 教学准备 教师 多媒体课件 学生 “五个一”课 堂 教 学 程 序 设 计 设计意图一、复习巩固1．如何运用函数y ＝ax 2＋bx ＋c 的图象求方程ax 2＋bx ＋c 的解?2．完成以下两道题：(1)画出函数y ＝x 2＋x －1的图象，求方程x 2＋x －1＝0的解。

(精确到0.1)(2)画出函数y ＝2x 2－3x －2的图象，求方程2x 2－3x －2＝0的解。

教学要点1．学生练习的同时，教师巡视指导， 2．教师根据学生情况进行讲评。

解：略函数y ＝2x 2－3x －2的图象与x 轴交点的横坐标分别是x 1＝－12和x 2＝2，所以一元二次方程的解是x 1＝－12和x 2＝2。

二、探索问题问题1：(P23问题4)育才中学初三(3)班学生在上节课的作业中出现了争论：求方程x 2＝12x 十3的解时，几乎所有学生都是将方程化为x 2－12x －3＝0，画出函数y ＝x 2－12x －3的图象，观察它与x 轴的交点，得出方程的解。

唯独小刘没有将方程移项，而是分别画出了函数y ＝x 2和y ＝12x ＋2的图象，如图(3)所示，认为它们的交点A 、B 的横坐标－32和2就是原方程的解． 提问： 1. 这两种解法的结果一样吗? 2．小刘解法的理由是什么? 让学生讨论，交流，发表不同意见，并进行归纳。

课堂小结
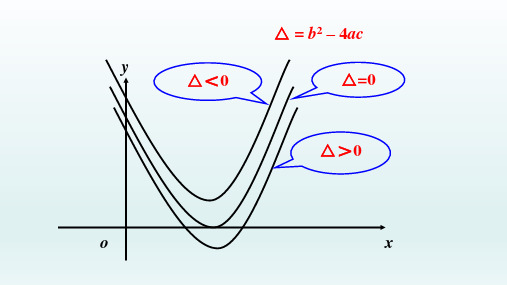
二次函数y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系：
二次函数y=ax2+bx+c 的图象和x轴交点
一元二次方程
ax2+bx+c= 0的根
一元二次方程ax2+bx+c= 0
根的判别式Δ=b2-4ac
有两个交点有两个不相等的实数根
只有一个交点
有两个相等的实数根没有交点没有实数根b2–4ac> 0 b2–4ac = 0 b2–4ac < 0
随堂练习
1.不与x 轴相交的抛物线是（）
A. y = 2x 2–3
B. y =－2 x 2+ 3
C. y = －x 2–3x
D. y =－2(x +1)2－3
2.若抛物线y = ax 2+bx +c ，当a >0，c <0时，图象与x 轴交点情况是
（）
A. 无交点
B. 只有一个交点
C. 有两个交点
D. 不能确定
D C
3. 如果关于x 的一元二次方程x 2－2x +m =0有两个相等的实数根，
则m =＿＿＿，此时抛物线y=x 2－2x +m 与x 轴有＿＿个交点.
4.已知抛物线y =x 2–8x + c 的顶点在x 轴上，则c =＿＿.
11165.若抛物线y =x 2+ bx + c 的顶点在第一象限,则方程x 2+ bx + c =0 的根的情况是＿＿＿＿＿.b 2－4ac < 0。

教学时间课题《二次函数》小结与复习（1）课型新授课教学目标知识和能力理解二次函数的概念，掌握二次函数y＝ax2的图象与性质；会用描点法画抛物线，能确定抛物线的顶点、对称轴、开口方向，能较熟练地由抛物线y＝ax2经过适当平移得到y＝a(x－h)2＋k的图象。

过程方法情感态度价值观教学重点用配方法求二次函数的顶点、对称轴，根据图象概括二次函数y＝ax2图象的性质。

教学难点二次函数图象的平移。

教学准备教师多媒体课件学生“五个一”课堂教学程序设计设计意图一、结合例题精析，强化练习，剖析知识点1．二次函数的概念，二次函数y＝ax2(a≠0)的图象性质。

例：已知函数是关于x的二次函数，求：(1)满足条件的m值；(2)m为何值时，抛物线有最低点?求出这个最低点．这时当x为何值时，y随x的增大而增大?(3)m为何值时，函数有最大值?最大值是什么?这时当x为何值时，y随x的增大而减小?学生活动：学生四人一组进行讨论，并回顾例题所涉及的知识点，让学生代表发言分析解题方法，以及涉及的知识点。

教师精析点评，二次函数的一般式为y＝ax2＋bx＋c(a≠0)。

强调a≠0．而常数b、c可以为0，当b，c同时为0时，抛物线为y＝ax2(a≠0)。

此时，抛物线顶点为(0，0)，对称轴是y轴，即直线x＝0。

(1)使是关于x的二次函数，则m2＋m－4＝2，且m＋2≠0，即：m2＋m－4＝2，m＋2≠0，解得；m＝2或m＝－3，m≠－2(2)抛物线有最低点的条件是它开口向上，即m＋2＞0，(3)函数有最大值的条件是抛物线开口向下，即m＋2＜0。

抛物线的增减性要结合图象进行分析，要求学生画出草图，渗透数形结合思想，进行观察分析。

强化练习；已知函数是二次函数，其图象开口方向向下，则m＝_____，顶点为_____，当x_____0时，y随x的增大而增大，当x_____0时，y随x的增大而减小。

2。

用配方法求抛物线的顶点，对称轴；抛物线的画法，平移规律，例：用配方法求出抛物线y＝－3x2－6x＋8的顶点坐标、对称轴，并画出函数图象，说明通过怎样的平移，可得到抛物线y＝－3x2。