2015年秋新人教A版高中数学选修4-1：2.4《弦切角的性质》练习及答案

一、选择题1．如图2－4－12所示，AB 是⊙O 的直径，MN 与⊙O 切于点C ，AC ＝12BC ，则sin ∠MCA ＝( )图2－4－12A.12 B.22 C.32D.55【解析】 由弦切角定理，得 ∠MCA ＝∠ABC .∵sin ∠ABC ＝AC AB＝AC AC 2＋BC 2＝AC 5AC ＝55，故选D. 【答案】 D图2－4－132．如图2－4－13所示，AB 是⊙O 的直径，EF 切⊙O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 的长为( )A ．2B ．3C ．2 3D ．4【解析】 连接BC .∵AB 是⊙O 的直径， ∴AC ⊥BC ，由弦切角定理可知， ∠ACD ＝∠ABC ，∴△ABC ∽△ACD ，∴AC AD ＝AB AC， ∴AC 2＝AB ·AD ＝6×2＝12， ∴AC ＝23，故选C. 【答案】 C3．如图2－4－14，PC 与⊙O 相切于C 点，割线PAB 过圆心O ，∠P ＝40°，则∠ACP 等于( )图2－4－14A ．20°B ．25°C ．30°D ．40°【解析】 如图，连接OC ， ∵PC 切⊙O 于C 点， ∴OC ⊥PC ，∵∠P ＝40°， ∴∠POC ＝50°， 连接BC ，∵OC ＝OB ， ∴∠B ＝12∠POC ＝25°，∴∠ACP ＝∠B ＝25°.【答案】 B4．如图2－4－15所示，已知AB 、AC 与⊙O 相切于B 、C ，∠A ＝50°，点P 是⊙O 上异于B 、C 的一动点，则∠BPC 的度数是( )A ．65°B．115°C．65°或115°D．130°或50°图2－4－15【解析】当点P在优弧BC上时，由∠A＝50°，得∠ABC＝∠ACB＝65°.∵AB是⊙O的切线，∴∠ABC＝∠BPC＝65°.当P点在劣弧BC上时，∠BPC＝115°.故选C.【答案】 C二、填空题5．(2012·广东高考)如图2－4－16所示，直线PB与圆O相切于点B，D是弦AC上的点，∠PBA＝∠DBA.若AD＝m，AC＝n，则AB＝________.图2－4－16【解析】利用弦切角定理及相似三角形求解．∵PB切⊙O于点B，∴∠PBA＝∠ACB.又∠PBA＝∠DBA，∴∠DBA＝∠ACB，∴△ABD ∽△ACB . ∴AB AC ＝AD AB， ∴AB 2＝AD ·AC ＝mn ， ∴AB ＝mn . 【答案】mn6. 如图2－4－17，点P 在圆O 直径AB 的延长线上，且PB ＝OB ＝2，PC 切圆O 于C 点，CD ⊥AB 于D 点，则CD ＝__________.图2－4－17【解析】 连接OC ，∵PC 切⊙O 于点C ， ∴OC ⊥PC ，∵PB ＝OB ＝2，OC ＝2， ∴PC ＝23，∵OC ·PC ＝OP ·CD ， ∴CD ＝2×234＝ 3.【答案】3三、解答题7．如图2－4－18所示，△ABT 内接于⊙O ，过点T 的切线交AB 的延长线于点P ，∠APT 的平分线交BT 、AT 于C 、D .求证：△CTD 为等腰三角形．图2－4－18【证明】 ∵PD 是∠APT 的平分线， ∴∠APD ＝∠DPT .又∵PT 是圆的切线，∴∠BTP ＝∠A . 又∵∠TDC ＝∠A ＋∠APD ， ∠TCD ＝∠BTP ＋∠DPT ， ∴∠TDC ＝∠TCD ， ∴△CTD 为等腰三角形．8．(2012·辽宁高考)如图2－4－19，⊙O 和⊙O ′相交于A ，B 两点，过A 作两圆的切线分别交两圆于C ，D 两点，连接DB 并延长交⊙O 于点E .证明：图2－4－19(1)AC ·BD ＝AD ·AB ； (2)AC ＝AE .【证明】 (1)由AC 与⊙O ′相切于A ，得∠CAB ＝∠ADB ，同理∠ACB ＝∠DAB ，所以△ACB ∽△DAB .从而AC AD ＝ABBD，即AC ·BD ＝AD ·AB .(2)由AD 与⊙O 相切于A ，得∠AED ＝∠BAD . 又∠ADE ＝∠BDA ，得△EAD ∽△ABD . 从而AE AB ＝ADBD ，即AE ·BD ＝AD ·AB .综合(1)的结论知，AC ＝AE .9．(2013·辽宁高考)如图2－4－20，AB 为⊙O 的直径，直线CD 与⊙O 相切于E ，AD 垂直CD 于D ，BC 垂直CD 于C ，EF 垂直AB 于F ，连接AE ，BE .图2－4－20证明：(1)∠FEB ＝∠CEB ； (2)EF 2＝AD ·BC .【证明】 (1)由直线CD 与⊙O 相切，得∠CEB ＝∠EAB . 由AB 为⊙O 的直径，得AE ⊥EB ，从而∠EAB ＋∠EBF ＝π2；又EF ⊥AB ，得∠FEB ＋∠EBF ＝π2.从而∠FEB ＝∠EAB .故∠FEB ＝∠CEB .(2)由BC ⊥CE ，EF ⊥AB ，∠FEB ＝∠CEB ，BE 是公共边，得Rt △BCE ≌Rt △BFE ，所以BC ＝BF .类似可证Rt △ADE ≌Rt △AFE ，得AD ＝AF . 又在Rt △AEB 中，EF ⊥AB ，故EF 2＝AF ·BF ， 所以EF 2＝AD ·BC .10．如图，△ABC 内接于圆O ，AB ＝AC ，直线MN 切圆O 于点C ，弦BD ∥MN ，AC 与BD 相交于点E .(1)求证：△ABE ≌△ACD ； (2)若AB ＝6，BC ＝4，求AE .【解】 (1)证明：由已知得∠ABE ＝∠ACD ，∠BAE ＝∠EDC ， 又∵BD ∥MN ，∴∠DCN ＝∠EDC ， ∴∠BAE ＝∠DCN .又直线MN 切圆O 于点C ， ∴∠CAD ＝∠DCN . ∴∠CAD ＝∠BAE .又AB ＝AC ，∴△ABE ≌△ACD . (2)由于△ABE ≌△ACD ，则BE ＝CD ， 由(1)得∠CAD ＝∠BAE ，∴BC ＝CD .∴BE ＝CD ＝4. 在△ABE 和△CDE 中，∠BAE ＝∠EDC ，∠EBA ＝∠ECD ， ∴△ABE ∽△DCE .∴BE CE ＝ABCD .∴BE AC －AE ＝AB CD . ∴46－AE ＝64， 解得AE ＝103.。

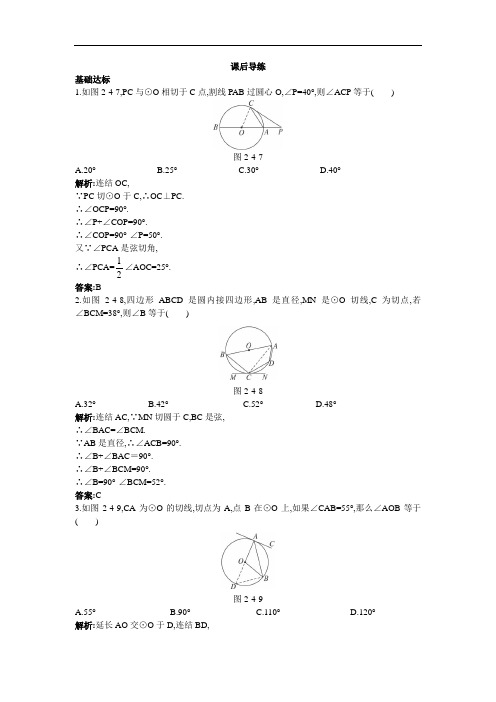
课后导练基础达标1.如图2-4-7,PC 与⊙O 相切于C 点,割线PAB 过圆心O,∠P=40°,则∠ACP 等于( )图2-4-7 A.20° B.25° C.30° D.40° 解析:连结OC,∵PC 切⊙O 于C,∴OC ⊥PC. ∴∠OCP=90°.∴∠P+∠COP=90°. ∴∠COP=90°-∠P=50°. 又∵∠PCA 是弦切角, ∴∠PCA=21∠AOC=25°. 答案:B2.如图2-4-8,四边形ABCD 是圆内接四边形,AB 是直径,MN 是⊙O 切线,C 为切点,若∠BCM=38°,则∠B 等于( )图2-4-8 A.32° B.42° C.52° D.48° 解析:连结AC,∵MN 切圆于C,BC 是弦, ∴∠BAC=∠BCM.∵AB 是直径,∴∠ACB=90°. ∴∠B+∠BAC ＝90°. ∴∠B+∠BCM=90°. ∴∠B=90°-∠BCM=52°. 答案:C3.如图2-4-9,CA 为⊙O 的切线,切点为A,点B 在⊙O 上,如果∠CAB=55°,那么∠AOB 等于( )图2-4-9A.55°B.90°C.110°D.120° 解析:延长AO 交⊙O 于D,连结BD,∵AC 切⊙O 于A,AB 是弦, ∴∠D=∠CAB. 又∵∠D=21∠AOB, ∴∠AOB=2∠CAB=110°. 答案:C4.如图2-4-10,∠ABC=90°,O 是AB 上一点,⊙O 切AC 于D,交AB 于E,连结DB 、DE 、OC,则图中与∠CBD 相等的角共有( )图2-4-10A.1个B.2个C.3个D.4个 解析:∵AB ⊥BC,∴BC 与⊙O 相切,BD 为弦. ∴∠CBD=∠BED. 同理,∠CDB=∠BED. ∴∠CBD=∠CDB. 又OC ⊥BD,DE ⊥BD, ∴DE ∥OC.∴∠BED=∠BOC. ∴∠CBD=∠BOC. ∴共3个. 答案:C5.如图2-4-11,AB 、AC 与⊙O 相切于B 、C,∠A=50°,点P 是圆上异于B 、C 的一动点,则∠BPC 的度数是( )图2-4-11A.65°B.115°C.65°或115°D.130°或50° 解析:点P 可能位置有两种情况,点P 在优弧上或在劣弧上.图2-4-12(1)如图2-4-12,在优弧上, ∵AB 、AC 是切线,∴∠ABC=∠P 1,∠ACB=∠P 1,∠ABC=21(180°-∠A)=65°. (2)如图2-4-13,在劣弧上,可在优弧上任取一点Q,图2-4-13由(1)知∠Q=65°,∵四边形BP 2CQ 内接于圆O, ∴∠BP 2C+∠Q=180°. ∴∠BP 2C=180°-∠Q=115°. 综上,∠BPC=65°或115°. 答案:C 温馨提示本题运用了运动变化思想、分类思想和化归思想. 综合运用6.如图2-4-14,AD 是圆内接△ABC 的∠A 的平分线,交圆于D,E 为BC 中点,BF 为圆的切线,DF ⊥BF. 求证:DE=DF.图2-4-14证明:连结BD,∵BF 是切线,BD 是弦, ∴∠DBF=∠BAD. ∵=,∴∠DBC=∠DAC.又∵AD 是∠BAC 的平分线,∴∠BAD=∠DAC.∴∠DBF=∠DBE, 即BD 是∠EBF 的平分线. ∵∠BAD=∠DAC,∴=,即D 是中点.∵E 是BC 中点,∴DE ⊥BC. ∴DE=DF.7.如图2-4-15,梯形ABCD 中,AB ∥DC,AD=BC,以AD 为直径的⊙O 交AB 于点E,⊙O 的切线EF 交BC 于F,求证:EF ⊥BC.图2-4-15证明:∵AD是直径,∴∠AED=90°.∴∠DEF+∠BEF=90°.∵EF切⊙O于点E,DE是弦,∴∠DEF=∠A.∴∠A+∠BEF=90°.∵AD=BC,AB∥DC,∴∠B=∠A.∴∠B+∠BEF=90°.∴∠BFE=90°.∴EF⊥BC.8.两圆内切于点P,大圆的弦AD交小圆于点B、C.求证:∠APB=∠CPD.图2-4-16证明:过P作两圆的公切线MN.∵PB是小圆弦,MN是切线,∴∠BPM=∠BCP.∵PA是大圆弦,MN是切线,∴∠APM=∠D.∴∠BPM-∠APM=∠BCP-∠D.又∠BCP=∠D+∠CPD,∴∠BCP-∠D=∠CPD.∴∠APB=∠CPD.9.如图2-4-17,AB是⊙O的弦,CD是经过⊙O上一点M的切线.图2-4-17求证:(1)AB∥CD时,AM=MB.(2)AM=MB时,AB∥CD.证明:(1)∵AB∥CD,∴∠A=∠AMC.∵CD切⊙O于M,AM是弦,∴∠AMC=∠B.∴∠A=∠B.∴AM=BM.(2)∵AM=MB,∴∠A=∠B.又∵CD切⊙O于M,AM是弦,∴∠AMC=∠B.∴∠AMC=∠A.∴AB∥CD.拓展探究10.如图2-4-18,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动且总保持PQ=PO,过Q作⊙O的切线交BA的延长线于点C.图2-4-18(1)当∠QPA=60°时,请你对△QCP的形状作出猜想,并证明;(2)当QP⊥AO时,△QCP的形状是___________三角形.(3)由(1)、(2)得出的结论,请你进一步猜想,当点P在线段AM上运动到任何位置时△QCP一定是___________三角形.解析:(1)△QCP是等边三角形,证明:连结OQ,则CQ⊥OQ.∵PQ=PO,∠QPC=60°,∴∠POQ=∠PQO=30°.∴∠C=∠CQO-∠POQ=60°.∴∠CQP=∠C=∠QPC=60°.∴△QPC是等边三角形.(2)等腰直角(解析:略)(3)等腰(解析:略)备选习题11.如图2-4-19,BC为⊙O直径,DE切⊙O于A点,BD⊥DE于D,若∠ABD=50°,则的度数为_________________.图2-4-19解析:∵BD⊥DE,∴∠BDA=90°.∴∠ABD+∠BAD=90°.∴∠BAD=90°-50°=40°.∵AB是弦,AD是切线,∴∠C=∠BAD=40°.∴BC是直径.∴∠BAC=90°.∴∠C+∠ABC=90°.∴∠ABC=90°-∠C=50°.∴的度数为100°.答案:100°12.如图2-4-20,AB为⊙O的直径,DA、DE为⊙O两切线,A、C为切点,A、B、E共线,若的度数为60°,则∠CAD的度数为____________,∠E的度数为_____________.图2-4-20解析:∵度数为60°,∴∠BAC=30°,∠BCE=30°.∵AD为切线,∴BA⊥AD.∴∠BAC+∠CAD=90°.∴∠CAD=90°-∠BAC=60°.∵AB为直径,∴∠ACB=90°.∴∠ABC=90°-∠BAC=30°.∴∠E=∠ABC-∠BCE=30°.答案:60°30°13.两圆内切于点P,大圆的弦AB切小圆于C，求证：∠APC＝∠CPB.图2-4-21证明:过P作两圆公切线MN,设PB交小圆于D,连结CD.∵PC是小圆弦,MN切小圆于P,∴∠MPC=∠PDC.∵PA是大圆弦,MN切大圆于P,∴∠MPA=∠B.∴∠MPC-∠MPA=∠PDC-∠B.∵∠PDC=∠B+∠BCD,∴∠PDC-∠B=∠BCD.∴∠APC=∠BCD.又AB切小圆于C，CD是小圆弦,∴∠BCD=∠CPB.∴∠APC=∠CPB.14.如图2-4-22,△ABC中,过A与BC相切于D的圆分别交AB、AC于E、F,且EF∥BC. 求证:AD平分∠A.图2-4-22证明:连结DF,∵BC 切圆于D,DF 是弦, ∴∠3=∠2.∵EF ∥BC,∴∠3=∠4. 又∠1=∠4,∴∠1=∠2,即AD 平分∠BAC.15.如图2-4-12(1),OA 和OB 是⊙O 的半径,且OA ⊥OB,P 是OA 上任一点,BP 的延长线交⊙O 于Q,过Q 的⊙O 的切线交OA 的延长线于R,易证RP=RQ(不要求证明). (1)现将PA 向上平移至图2-4-23(2)位置,结论还成立吗?若成立,请证明.(2)若将PA 向上平移至⊙O 外,结论还成立吗?如图2-4-23(3),若成立,请证明.(1) (2) (3)图2-4-23解析:(1)成立.证明:连结OQ,则QR ⊥OQ. ∴∠PQR+∠BQO=90°.∵∠RPQ=∠1,∠1+∠B=90°, ∴∠RPQ+∠B=90°.又OB=OQ,∴∠B=∠BQO. ∴∠PQR=∠RPQ.∴RP=RQ. (2)结论仍然成立.证明:连结OQ,则OQ ⊥RQ. ∴∠RQO=90°.∴∠RQP+∠BQO=90°.∵OA ⊥PA,∴∠P+∠ABP=90°. 又∠PBA=∠OBQ,∵OB=OQ, ∴∠OBQ=∠OQB.∴∠P=∠PQR.∴RP=RQ.。

课后训练1．如图，O 的半径为2 cm,O 切AC 于D ，切BE 于E ，∠ACB ＝60°,则CE 的长为（ ）．A ．3cmB ．23cm 3C ．3cm 3D ．23cm2．如图,AB 是O 的直径,直线EF 切O 于B ，C 、D 为O 上的点，∠CBE ＝40°，AD CD =,则∠BCD 的度数是( )．A ．110°B ．115°C ．120°D ．135°3．如图，在圆的内接四边形ABCD 中，AC 平分∠BAD ，EF 切O 于C 点，那么图中与∠DCF 相等的角的个数是( )．A ．4B ．5C ．6D ．74．如图，BD 为O 的直径，AB 、AE 切O 于B 、C ，∠BDC ＝65°,则∠BAC ＝________。

5．如图，已知AB 与O 相切于点M ，MC MD =，且MC 、MD 为14圆周长,则∠AMC ＝__________。

6．已知,如图，△ABC内接于O,DC切O于C点，BC平分∠ACD，则△ABC为________．7．如图，AB是O的直径，CD是O的切线，C为切点，AC 平分∠BAD．求证：AD⊥CD．8．如图，P是O的半径OA上的一点，D在O上，且PD＝PO.过点D作O的切线交OA的延长线于点C，延长DP交O于K，连接KO，OD．(1）证明：PC＝PD；(2)若该圆的半径为5，CD∥KO，求出OC的长．如图,BC为O的直径,AB AD=，过点A的切线与CD的延长线交于点E.(1）试猜想∠AED是否等于90°？为什么？（2）若25AD=，ED∶EA＝1∶2，求O的半径．(3）在（2）的条件下求∠CAD的正弦值．参考答案1.答案：B解析：∵CD、CE是O的切线，∴OC平分∠ECD．∴∠OCE＝12∠ECD＝12(180°－∠ACB)＝12(180°－60°）＝60°.∴CE＝OE cot60°＝323233⨯=(cm）．2。

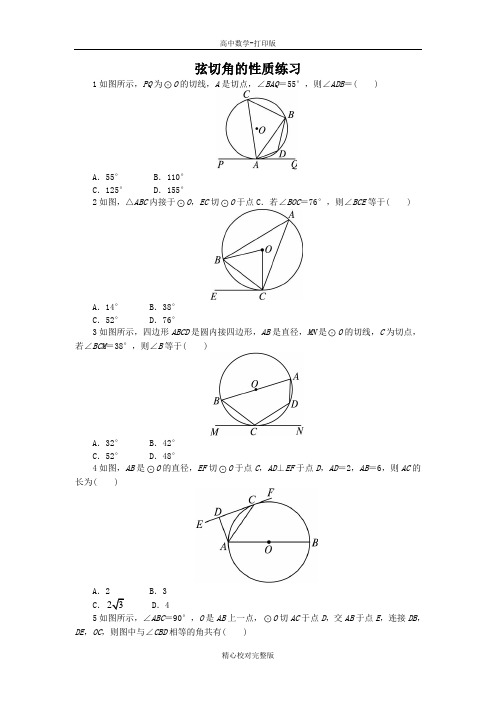
弦切角的性质练习1如图所示，PQ为O的切线，A是切点，∠BAQ＝55°，则∠ADB＝( )A．55° B．110°C．125° D．155°2如图，△ABC内接于O，EC切O于点C．若∠BOC＝76°，则∠BCE等于( )A．14° B．38°C．52° D．76°3如图所示，四边形ABCD是圆内接四边形，AB是直径，MN是O的切线，C为切点，若∠BCM＝38°，则∠B等于( )A．32° B．42°C．52° D．48°4如图，AB是O的直径，EF切O于点C，AD⊥EF于点D，AD＝2，AB＝6，则AC的长为( )A．2 B．3C．．45如图所示，∠ABC＝90°，O是AB上一点，O切AC于点D，交AB于点E，连接DB，DE，OC，则图中与∠CBD相等的角共有( )A．1个 B．2个C．3个 D．4个6如图，AD切O于点F，FB，FC为O的两弦，请列出图中所有的弦切角________．7如图，AB是O的直径，直线CE与O相切于点C，AD⊥CE于D，若AD＝1，∠ABC ＝30°，则O的面积是__________．8如图，AB是O的直径，PB，PE分别切O于B，C，若∠ACE＝40°，则∠P＝__________.9如图所示，BA是O的直径，AD是O的切线，切点为A，BF，BD分别交AD于点F，D，交O于E，C，连接CE.求证：BE·BF＝BC·B D．10如图，△ABC内接于O，AB＝AC，直线MN切O于点C，弦BD∥MN，AC与BD相交于点E.(2)求证：BE＝B C．参考答案1答案：C ∵PQ是切线，∴∠C＝∠BAQ＝55°.又∵四边形ADBC内接于圆，∴∠ADB＝180°－∠C＝180°－55°＝125°. 2答案：B ∵EC为O的切线，∴∠BCE＝∠BAC＝12∠BOC＝38°.3答案：C 连接AC，如图所示.∵MN切圆于C，BC是弦，∴∠BAC＝∠BCM.∵AB是直径，∴∠ACB＝90°.∴∠B＋∠BAC＝90°.∴∠B＋∠BCM＝90°，∴∠B＝90°－∠BCM＝52°. 4答案：C 连接BC，如图所示.∵EF是O的切线，∴∠ACD＝∠ABC.又AB是O的直径，∴∠ACB＝90°.又AD⊥EF，∴∠ACB＝∠ADC.∴△ADC∽△ACB.∴AB AC AC AD.∴AC2＝AD·AB＝2×6＝12，∴AC＝5 答案：C ∵AB⊥BC，∴BC与O相切，BD为弦. ∴∠CBD＝∠BED.同理可得∠CDB＝∠BED，∴∠CBD＝∠CDB.连接OD.∵OD＝OB，OC＝OC，∴Rt△COD≌Rt△COB.∴CB＝CD，∠DCO＝∠BCO.∴OC⊥BD.又DE⊥BD，∴DE∥OC.∴∠BED＝∠BOC，∴∠CBD＝∠BOC.∴与∠CBD相等的角共有3个.6 答案：∠AFB，∠AFC，∠DFC，∠DFB7 答案：4π∵DE是切线，∴∠ACD＝∠ABC＝30°.又AD⊥CD，∴AC＝2AD＝2.又∵AB是直径，∴∠ACB＝90°.又∠ABC＝30°，∴AB＝2AC＝4，∴OA＝12AB＝2.∴O的面积为S＝π·OA2＝4π.8答案：80°如图所示，连接BC，则∠ACE＝∠ABC，∠ACB＝90°.又∠ACE＝40°，则∠ABC＝40°.所以∠BAC＝90°－∠BCA＝90°－40°＝50°，∠ACP＝180°－∠ACE＝140°.又AB是O的直径，则∠ABP＝90°.又四边形ABPC的内角和等于360°，所以∠P＋∠BAC＋∠ACP＋∠ABP＝360°.所以∠P＝80°.9 答案：分析：要证BE·BF＝BC·BD，只需证BE BCBD BF，即证明△BEC∽△BDF.由∠DBF为公共角，只需再找一组角相等，为此，过点B作O的切线，构造弦切角.证明：如图，过点B作O的切线BG，则AB⊥BG.又AD是O的切线，∴AD⊥AB，∴BG∥AD，∴∠GBC＝∠BDF.又∵∠GBC＝∠BEC，∴∠BEC＝∠BDF.又∠CBE＝∠DBF，∴△BEC∽△BDF.∴BE BCBD BF.∴BE·BF＝BC·BD.10 答案：分析：(1)很明显∠ABE＝∠ACD，只需证明∠BAE＝∠CAD，转化为证明∠BAE ＝∠CDB，∠CDB＝∠DCN，∠DCN＝∠CAD.(2)转化为证明∠BEC＝∠ECB.证明：(1)∵BD∥MN，∴∠CDB＝∠DCN.又∠BAE＝∠CDB，∴∠BAE＝∠DCN.又直线MN是O的切线，∴∠DCN＝∠CAD.∴∠BAE＝∠CAD.又∠ABE＝∠ACD，AB＝AC，∴△ABE≌△ACD.(2)∵∠EBC＝∠BCM，∠BCM＝∠BDC.∴∠EBC＝∠BDC.∴CB＝CD＝4.∵∠BEC＝∠EDC＋∠ECD，∠ECD＝∠ABE，∴∠BEC＝∠EBC＋∠ABE＝∠ABC.又AB＝AC，∴∠ABC＝∠ECB.∴∠BEC＝∠ECB.∴BE＝BC.。

四弦切角的性质课后篇巩固探究一、A组1.如图,MN与☉O相切于点M,Q和P是☉O上两点,∠PQM=70°,则∠NMP等于()A.20°B.70°C.110°D.160°解析:∵∠NMP是弦切角,∴∠NMP=∠PQM=70°.答案:B2.如图,已知AB和AC分别是☉O的弦和切线,点A为切点,AD为∠BAC的平分线,且交☉O于点D,BD的延长线与AC交于点C,AC=6,AD=5,则CD的长度等于()A.3B.4C.5D.6解析:由题意,得∠CAD=∠ABC.因为AD为∠BAC的平分线,所以∠CAD=∠DAB,从而∠CBA=∠DAB,所以DB=AD=5,且△ACD∽△BCA,于是,即,解得CD=4(负值舍去).答案:B3.如图,四边形ABCD是圆的内接四边形,AB是直径,MN是☉O的切线,切点为C.若∠BCM=38°,则∠B=()A.32°B.42°D.48°解析:如图,连接AC.∵∠BCM=38°,MN是☉O的切线,∴∠BAC=38°.∵AB为☉O的直径,∴∠BCA=90°.∴∠B=90°-38°=52°.答案:C4.如图,AB是☉O的直径,EF切☉O于点C,AD⊥EF于点D,AD=2,AB=6,则AC的长为()A.2B.3C.2D.4解析:如图,连接BC.∵EF是☉O的切线,∴∠ACD=∠ABC.又AB是☉O的直径,∴∠ACB=90°.又AD⊥EF,∴∠ACB=∠ADC.∴△ADC∽△ACB.∴.∴AC2=AD·AB=2×6=12,∴AC=2.答案:C5.如图,若AB切☉O于A,AC,AD为☉O的弦,且,则∠C与∠CAB的关系是.解析:因为,所以∠ADC=∠ACD.又由弦切角定理可得∠BAC=∠ADC,故∠C=∠CAB.答案:∠C=∠CAB6.已知AB是☉O的弦,PA是☉O的切线,A是切点.如果∠PAB=30°,那么∠AOB=. 解析:∵弦切角∠PAB=30°,∴它所夹的弧所对的圆周角等于30°,所对的圆心角等于60°.答案:60°7.已知PA是圆O的切线,切点为A,PO交圆O于B,C两点,AC=,∠PAB=30°,则线段PB的长为.解析:连接OA,∵PA为☉O的切线,∴∠OAP=90°,∠C=∠PAB=30°,∴∠OBA=∠OAB=60°,∴∠P=∠PAB=30°,∴PB=AB.又AC=,BC为☉O的直径,∴∠CAB=90°,∴AB=1,∴PB=1.答案:18.如图,☉O1与☉O2交于A,B两点,过☉O1上一点P作直线PA,PB分别交☉O2于点C和点D,EF切☉O1于点P.求证:EF∥CD.证明:连接AB,∵EF是☉O1的切线,由弦切角定理知,∠FPA=∠PBA.又在☉O2中,四边形ABDC为圆内接四边形,∴∠C=∠ABP,∴∠FPA=∠C,∴EF∥CD.9.如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于,直线ED交BC的延长线于F.若AD∶AE=2∶1,求tan∠F的值.解:如图,连接BD.∵AC为☉O的切线,∴∠ADE=∠ABD.∵∠A=∠A,∴△ADE∽△ABD,∴,即,∴.∵BE为☉O的直径,∴∠BDE=90°,∴tan∠ABD=.∵∠F+∠BEF=90°,∠ABD+∠BEF=90°,∴∠ABD=∠F,∴tan∠F=tan∠ABD=.二、B组1.如图,在圆的内接四边形ABCD中,AC平分∠BAD,EF切☉O于C点,则图中与∠DCF相等的角的个数是()A.4B.5C.6D.7解析:∠DCF=∠DAC,∠DCF=∠BAC,∠DCF=∠BCE,∠DCF=∠BDC,∠DCF=∠DBC.答案:B2.如图,☉O和☉O'相交于A,B两点,过点A作两圆的切线,分别交两圆于C,D两点.若BC=2,BD=4,则AB的长为()A.2B.2C.4D.6解析:∵AC,AD分别是两圆的切线,∴∠C=∠BAD,∠D=∠BAC.∴△ACB∽△DAB.∴.∴AB2=BC·DB=2×4=8,解得AB=2(负值舍去).答案:A.AB切☉O于点A,圆周被AC所分成的优弧与劣弧之比为3∶1,则夹劣弧的弦切角∠BAC=.解析:∵优弧与劣弧之比为3∶1,∴劣弧所对的圆心角为90°,所对的圆周角为45°,故由弦切角定理可知,弦切角∠BAC=45°.答案:45°4.导学号52574036如图,AB是圆O的直径,点C在圆O上.延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=.解析:连接OC.∵AB为圆O的直径,∴AC⊥BC.又BC=CD,∴AB=AD=6,∠BAC=∠CAD.又CE为圆O的切线,则OC⊥CE.∵∠ACE为弦切角,∴∠ACE=∠B.∴∠ACE+∠CAD=90°.∴CE⊥AD.又AC⊥CD,∴CD2=ED·AD=2×6=12,即CD=2.∴BC=2.答案:25.如图,△ABC内接于☉O,AB=AC,直线XY切☉O于点C,BD∥XY,AC,BD相交于E.(1)求证:△ABE≌△ACD;6 cm,BC=4 cm,求AE的长.(1)证明:因为XY是☉O的切线,所以∠1=∠2.因为BD∥XY,所以∠1=∠3,故∠2=∠3.因为∠3=∠4,所以∠2=∠4.因为∠ABD=∠ACD,又因为AB=AC,ABE≌△ACD.(2)解:易知∠3=∠2,∠ABC=∠ACB,所以△BCE∽△ABC,,即AC·CE=BC2.因为AB=AC=6 cm,BC=4 cm,所以6·(6-AE)=16,故AE= cm.6.导学号52574037如图,AB为☉O的直径,直线CD与☉O相切于E,AD⊥CD于D,BC ⊥CD于C,EF⊥AB于F,连接AE,BE.∠FEB=∠CEB;(2)EF2=AD·BC.证明:(1)由直线CD与☉O相切,得∠CEB=∠EAB.由AB为☉O的直径,得AE⊥EB,从而∠EAB+∠EBF=.又EF⊥AB,得∠FEB+∠EBF=.从而∠FEB=∠EAB,故∠FEB=∠CEB.(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,得Rt△BCE≌Rt△BFE,所以BC=BF.同理可证Rt△ADE≌Rt△AFE,得AD=AF.在Rt△AEB中,EF⊥AB,故EF2=AF·BF,所以EF2=AD·BC.。

人教新课标A版选修4-1数学2.4弦切角的性质同步检测A卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）如图，经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，则∠BAC所对的弧的度数为（）A . 40°B . 100°C . 120°D . 30°2. （2分）如图，在⊙O中，AB是弦，AC是⊙O的切线，A是切点，过 B作BD⊥AC于D，BD交⊙O于E点，若AE平分∠BAD，则∠BAD=（）A . 30°B . 45°C . 50°D . 60°3. （2分）(2016·天津模拟) 如图，圆O的直径AB长度为10，CD是点C处的切线，AD⊥CD，若BC=8，则CD=（）A .B .C .D .4. （2分） PT切⊙O于T，割线PAB经过O点交⊙O于A、B，若PT=4，PA=2，则cos∠BPT=（）A .B .C .D .5. （2分）若图中，PA切⊙O于点A，PCB交⊙O于C、B两点，且PCB过点O，AE⊥BP交⊙O于E，则图中与∠CAP相等的角的个数是（）A . 1B . 2C . 3D . 46. （2分） (2017高一下·河北期末) 如图所示，在圆的内接四边形中，平分，切于点，那么图中与相等的角的个数是（）A . 4B . 5C . 6D . 77. （2分）如图，直线BC切⊙O于B，AB=AC，AD=BD，则∠A=（）A . 35°B . 36°C . 40°D . 50°8. （2分） (2017高二上·信阳期末) 如图，已知四边形ABCD是圆内接四边形，且∠BCD=120°，AD=2，AB=BC=1，现有以下结论：①B，D两点间的距离为；②AD是该圆的一条直径；③CD= ；④四边形ABCD的面积S= ．其中正确结论的个数为（）A . 1B . 2C . 3D . 49. （2分）如图⊙O中，弦AB与弦CD相交于点P，∠B=38°，∠APD=80°，则∠A等于（）A . 38°B . 42°C . 80°D . 118°10. （2分） (2016高二下·五指山期末) 如图，四边形ABCD是⊙O的内接四边形，延长BC到E，已知∠BCD：∠ECD=3：2，那么∠BOD等于（）A . 120°B . 136°C . 144°D . 150°二、填空题 (共5题；共5分)11. （1分）如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=， AB=BC=3．AC 的长为________ ．12. （1分）如图，已知点D在圆O直径AB的延长线上，过D作圆O的切线，切点为C．若CD=， BD=1，则圆O的面积为________ ．13. （1分）如图，从圆O外一点P作圆O的割线PAB、PCD，AB是圆O的直径，若PA=4，PC=5，CD=3，则∠CBD=________ ．14. （1分）如图，AB的延长线上任取一点C，过C作圆的切线CD，切点为D，∠ACD的平分线交AD于E，则∠CED=________15. （1分）如图，AB、AC是⊙O的两条切线，切点分别为B、C．若∠BAC=60°，BC=6，则⊙O的半径为________ ．三、解答题 (共10题；共70分)16. （10分） (2015高三上·苏州期末) 如图，四边形么BDC内接于圆，BD=CD，过C点的圆的切线与AB的延长线交于E点．（1）求证：∠EAC=2∠DCE；（2）若BD⊥AB，BC=BE，AE=2，求AB的长．17. （5分）(2016·城中模拟) 如图，在△ABC和△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD，⊙O是以AB 为直径的圆，DC的延长线与AB的延长线交于点E．（Ⅰ）求证：DC是⊙O的切线；（Ⅱ）若EB=6，EC=6 ，求BC的长．18. （5分）如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE，与CD的延长线交于E，AE⊥CD，垂足为点E．（Ⅰ）证明：DA平分∠BDE；（Ⅱ）如果AB=4，AE=2，求对角线CA的长．19. （5分）如图，∠PAQ是直角，圆O与射线AP相切于点T，与射线AQ相交于两点B，C．求证：BT平分∠OBA．20. （10分）(2016·大连模拟) 如图所示，已知圆O1与圆O2相交于A，B两点，过点A作圆O1的切线交圆O2于点C，过点B作两圆的割线，分别交圆O1 ，圆O2于点D，E，DE与AC相交于点P．（1）求证：AD∥EC；（2）若AD是圆O2的切线，且PA=3，PC=1，AD=6，求DB的长．21. （10分）(2017·白山模拟) 如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA 的延长线上．（1）若 = ， =1，求的值；（2）若EF2=FA•FB，证明：EF∥CD．22. （5分）(2017·镇江模拟) 如图，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A 作l的垂线AD，AD分别与直线l、圆交于点D、E．求∠DAC的度数与线段AE的长．23. （5分）(2017·唐山模拟) 如图，A、B、C为⊙O上三点，B为的中点，P为AC延长线上一点，PQ 与⊙O相切于点Q，BQ与AC相交于点D．（Ⅰ）证明：△DPQ为等腰三角形；（Ⅱ）若PC=1，AD=PD，求BD•QD的值．24. （10分）如图，AB切O于点D，直线AD交O于D，E两点，BC⊥DE，垂足为C．（1）证明：CBD=DBA；（2）若AD=3DC，BC=，求O的直径．25. （5分）(2017·榆林模拟) 如图，已知PA与圆O相切于点A，经过点O的割线PBC交圆O于点B，C，∠APC 的平分线分别交AB，AC于点D，E．（Ⅰ）证明：∠ADE=∠AED；（Ⅱ）若AC=AP，求的值．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题；共5分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共10题；共70分) 16-1、16-2、17-1、18-1、19-1、20-1、20-2、21-1、21-2、22-1、23-1、24-1、24-2、25-1、。

高中数学学习材料马鸣风萧萧*整理制作2.4弦切角的性质一、选择题1．如图，⊙O内切于△ABC，切点分别为D、E、F.已知∠B＝50°，∠C＝60°，连接OE、OF、DE、DF，那么∠EDF等于()．A．40°B．55°C．65°D．70°2．如图所示，AB是⊙O的直径，EF切⊙O于C，AD⊥EF于D，AD＝2，AB＝6，则AC的长为()．A．2 B．3C．2 3 D．43．如图所示，经过⊙O上的点A的切线和弦BC的延长线相交于点P，若∠CAP＝40°，∠ACP＝100°，则∠BAC所对的弧的度数为()．A．40°B．100°C．120°D．30°4．如图所示，AB是⊙O直径，直线EF切⊙O于B，C、D为⊙O上的点，∠CBE ＝40°，AD＝CD，则∠BCD的度数是()．A．110°B．115°C．120°D．135°5．如图所示，AC切⊙O于点A，∠BAC＝25°，则∠B的度数为()．A．25°B．45°C．60°D．65°6．已知P A 、PB 是⊙O 的两条切线，点A 、B 为切点，AC 是⊙O 的直径，∠BAC ＝20°，则∠P 的大小为( )．A ．40°B ．50°C ．60°D ．65°二、填空题7．如图所示，已知AB 与⊙O 相切于点M ，且MC MD ，且MC 、MD 为14圆周长，则∠AMC ＝________，∠BMC ＝________，∠MDC ＝________，∠MOC ＝______.8．如图所示，AB 、AC 是⊙O 的两条切线，切点分别为B 、C ，D是优弧BC 上的点，已知∠BAC ＝80°，那么∠BDC ＝________.三、解答题9．如图所示，已知BC 是⊙O 的弦，P 是BC 延长线上一点，P A 与⊙O 相切于点A ，∠ABC ＝25°，∠ACB ＝80°，求∠P 的度数．10． 如图所示，△ABC 内接于⊙O ，AB ＝AC ，直线XY 切⊙O 于点C ，弦BD ∥XY ，AC 、BD 相交于E .(1)求证：△ABE ≌△ACD ；(2)若AB ＝6 cm ，BC ＝4 cm ，求AE 的长．2.4弦切角的性质一、选择题1.B2.C3.C4.B5.D6.A二、填空题7．45° 135° 45° 90° 8. 50°三、解答题9. 解 因为P A 与⊙O 相切于点A ，所以∠P AC ＝∠ABP ＝25°.又因为∠ACB ＝80°，所以∠ACP ＝100°. 又因为∠P AC ＋∠PCA ＋∠P ＝180°，所以∠P ＝180°－100°－25°＝55°.10. (1)证明 因为XY 是⊙O 的切线，所以∠1＝∠2.因为BD ∥XY ，所以∠1＝∠3，∴∠2＝∠3. 因为∠3＝∠4，所以∠2＝∠4.因为∠ABD ＝∠ACD ，又因为AB ＝AC ， 所以△ABE ≌△ACD .(2)解 因为∠3＝∠2，∠ABC ＝∠ACB ，所以△BCE ∽△ACB ，BC AC ＝CE CB ，AC ·CE ＝BC 2.因为AB ＝AC ＝6 cm ，BC ＝4 cm ，所以6·(6－AE )＝16.所以AE ＝103 cm.。

《弦切角的性质》同步练习一、选择题1．P在⊙O 外，PM 切⊙O 于C ，PAB 交⊙O 于A ，B ，则( )A ．∠MCB ＝∠B B ．∠PAC ＝∠PC ．∠PCA ＝∠BD ．∠PAC ＝∠BCA2．如图，PC 与⊙O 相切于C 点，割线PAB 过圆心O ，∠P ＝40°，则∠ACP 等于( )A ．20°B ．25°C ．30°D ．40°3．如图，AB 是⊙O 的直径，EF 切⊙O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 的长为( )A ．2B ．3C ．2 3D ．44．如图，AB 是⊙O 的直径，P 在AB 的延长线上，PD 切⊙O 于C 点，连接AC ，若AC ＝PC ，PB ＝1，则⊙O 的半径为( )A ．1B ．2C ．3D ．4PE 分别切⊙O 于B ，C ，若∠ACE ＝40°，则∠P ＝________.6．如图，点P 在圆O 直径AB 的延长线上，且PB ＝OB ＝2，PC 切圆O 于C 点，CD ⊥AB 于D点，则CD ＝________.7．如图，过圆O 外一点P 分别作圆的切线和割线交圆于A ，B ，且PB ＝7，C 是圆上一点使得BC ＝5，∠BAC ＝∠APB ，则AB ＝________.8.如图，AB 是半圆O 的直径，C 是圆周上一点(异于A ，B)，过C 作圆O 的切线l ，过A 作直线l 的垂线AD ，垂足为D ，AD 交半圆于点E.求证：CB ＝CE.9.如图所示，△ABC 内接于⊙O ，AB ＝AC ，直线XY 切⊙O 于点C ，弦BD ∥XY ，AC ，BD 相交于点E.(1)求证：△ABE ≌△ACD ；(2)若AB ＝6 cm ，BC ＝4 cm ，求AE 的长．答案和解析一、选择题1．P 在⊙O 外，PM 切⊙O 于C ，PAB 交⊙O 于A ，B ，则( )A ．∠MCB ＝∠B B ．∠PAC ＝∠PC ．∠PCA ＝∠BD ．∠PAC ＝∠BCA解析：选C 由弦切角定理知∠PCA ＝∠B.2．如图，PC 与⊙O 相切于C 点，割线PAB 过圆心O ，∠P ＝40°，则∠ACP 等于( )A ．20°B ．25°C ．30°D ．40°解析：选B 连接OC.∵PC 切⊙O 于C 点，∴OC ⊥PC.∵∠P ＝40°，∴∠POC ＝50°.连接BC ，则∠B ＝12∠POC ＝25°， ∴∠ACP ＝∠B ＝25°.3．如图，AB 是⊙O 的直径，EF 切⊙O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 的长为( )A ．2B ．3C ．2 3D ．4解析：选C 连接BC ，则∠ACB ＝90°，又AD ⊥EF ，∴∠ADC ＝90°，即∠ADC ＝∠ACB ，又∵∠ACD ＝∠ABC ，∴△ABC ∽△ACD ，∴AC AD ＝AB AC， ∴AC2＝AD ·AB ＝12，即AC ＝2 3.4．如图，AB 是⊙O 的直径，P 在AB 的延长线上，PD 切⊙O 于C 点，连接AC ，若AC ＝PC ，PB ＝1，则⊙O 的半径为( )A ．1B ．2C ．3D ．4解析：选A连接BC.∵AC ＝PC ，∴∠A ＝∠P.∵∠BCP ＝∠A ，∴∠BCP ＝∠P.∴BC ＝BP ＝1.由△BCP ∽△CAP 得PC PA ＝PB PC. ∴PC2＝PB ·PA ，即AC2＝PB ·PA.而AC2＝AB2－BC2，设⊙O 半径为r ，则4r2－12＝1·(1＋2r)，解得r ＝1.PE 分别切⊙O 于B ，C ，若∠ACE ＝40°，则∠P ＝________.解析：连接BC ，∵AB 是⊙O 的直径，∴∠ACB ＝90°.又∠ACE ＝40°，∴∠PCB ＝∠PBC ＝50°.∴∠P ＝80°.答案：80°6．如图，点P 在圆O 直径AB 的延长线上，且PB ＝OB ＝2，PC 切圆O 于C 点，CD ⊥AB 于D 点，则CD ＝________.解析：连接OC.∵PC 切⊙O 于C 点，∴OC ⊥PC.∵PB ＝OB ＝2，OC ＝2.∴PC ＝2 3.∵OC ·PC ＝OP ·CD ，∴CD ＝2×234＝ 3. 答案： 37．如图，过圆O 外一点P 分别作圆的切线和割线交圆于A ，B ，且PB ＝7，C 是圆上一点使得BC ＝5，∠BAC ＝∠APB ，则AB ＝________.解析：由PA 为⊙O 的切线，BA 为弦，得∠PAB ＝∠BCA ，又∠BAC ＝∠APB ，于是△APB ∽△CAB ，所以PB AB ＝AB BC. 而PB ＝7，BC ＝5，故AB2＝PB ·BC ＝7×5＝35，即AB ＝35.答案：358.如图，AB 是半圆O 的直径，C 是圆周上一点(异于A ，B)，过C 作圆O 的切线l ，过A 作直线l 的垂线AD ，垂足为D ，AD 交半圆于点E.求证：CB ＝CE.证明：连接AC ，BE ，在DC 延长线上取一点F ，因为AB 是半圆O 的直径，C 为圆周上一点， 所以∠ACB ＝90°，即∠BCF ＋∠ACD ＝90°.又因为AD ⊥l ，所以∠DAC ＋∠ACD ＝90°.所以∠BCF ＝∠DAC.又因为直线l 是圆O 的切线，所以∠CEB ＝∠BCF ，又∠DAC ＝∠CBE ，所以∠CBE ＝∠CEB ，所以CB ＝CE.9.如图所示，△ABC 内接于⊙O ，AB ＝AC ，直线XY 切⊙O 于点C ，弦BD∥XY ，AC ，BD 相交于点E.(1)求证：△ABE ≌△ACD ；(2)若AB ＝6 cm ，BC ＝4 cm ，求AE 的长．解：(1)证明：因为XY 是⊙O 的切线，所以∠1＝∠2.因为BD ∥XY ，所以∠1＝∠3，所以∠2＝∠3.因为∠3＝∠4，所以∠2＝∠4.因为∠ABD ＝∠ACD ，又因为AB ＝AC ，所以△ABE ≌△ACD.(2)因为∠3＝∠2，∠ABC ＝∠ACB ，所以△BCE ∽△ACB ，所以BC AC ＝CE CB， 即AC ·CE ＝BC2.因为AB ＝AC ＝6 cm ，BC ＝4 cm ，所以6·(6－AE)＝16.所以AE ＝103(cm)．。