单自由度系统的振动阻尼

单自由度系统自由衰减振动 及固有频率、阻尼比的测定一、 实验目的1、了解单自由度系统模型的自由衰减的振动的有关概念；2、学习用频谱分析信号的频率。

3、学习测试单自由度系统模型阻尼比的方法。

二、 实验仪器实验仪器：INV1601B 型振动教学实验仪、INV1601T 型振动教学实验台、加速度传感器、调速电机或配重块、MSC-1力锤（橡胶头）。

软件：INV1601型DASP 软件。

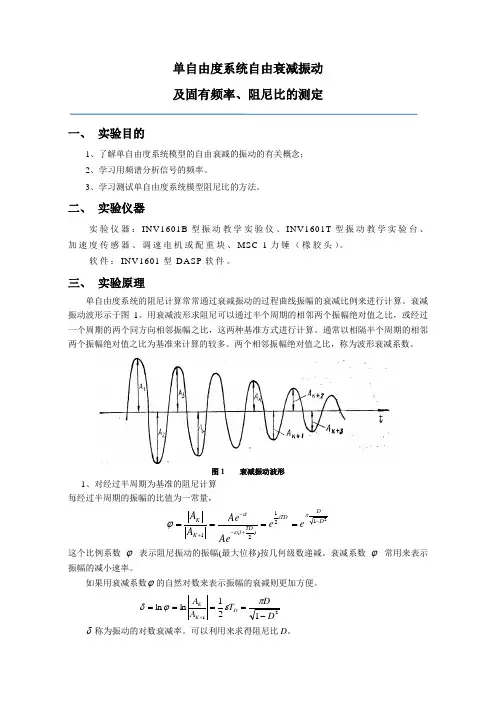
三、 实验原理单自由度系统的阻尼计算常常通过衰减振动的过程曲线振幅的衰减比例来进行计算。

衰减振动波形示于图1。

用衰减波形求阻尼可以通过半个周期的相邻两个振幅绝对值之比，或经过一个周期的两个同方向相邻振幅之比，这两种基准方式进行计算。

通常以相隔半个周期的相邻两个振幅绝对值之比为基准来计算的较多。

两个相邻振幅绝对值之比，称为波形衰减系数。

图1 衰减振动波形1、对经过半周期为基准的阻尼计算 每经过半周期的振幅的比值为一常量，2121)2(1D D TD TDt t K K eeAeAe A A -+--+====πεεεϕ这个比例系数ϕ 表示阻尼振动的振幅(最大位移)按几何级数递减。

衰减系数 ϕ 常用来表示振幅的减小速率。

如果用衰减系数ϕ的自然对数来表示振幅的衰减则更加方便。

21121lnln D D T A A D K K -====+πεϕδδ称为振动的对数衰减率。

可以利用来求得阻尼比D 。

22δπδ+=D引入常用对数101010303.2lg ,4343.0lg lg ln lg lg δδδϕδϕδ======ee ee 便得22)(lg 862.1lg )lg 733.0(1lg 733.0ϕϕϕϕ+=+=D在实际阻尼波形振幅读数时，由于基线甚难处理，阻尼较大时，基线差一点， ϕ 就相差很大，所以往往读取相邻两个波形的峰峰值之比，211+++++K K K K A A A A在211+++=K K K K A A A A 时，2111++++++==K K K K K K A A A A A A ϕ这样，实际阻尼波形读取数值就大为方便，求得阻尼比也更加正确。

振动系统的自由度和阻尼对振动的影响如何一、振动系统的自由度振动系统的自由度是指系统在空间中独立运动的数量。

在物理学中，一个自由度通常指的是一个物体在某个参考系下可以独立运动的程度。

对于振动系统来说，自由度决定了系统的复杂程度和可能的状态。

1.单自由度系统：指系统在空间中只能沿一个方向或一个轴进行振动。

例如，一根弹簧振子就是一个单自由度系统。

2.多自由度系统：指系统在空间中有多个方向或多个轴可以进行振动。

例如，一个弹簧-质量系统，如果它可以在三维空间中的任意方向振动，则它是一个三自由度系统。

二、阻尼对振动的影响阻尼是振动系统中能量耗散的机制，它会使振动的振幅逐渐减小，直至振动停止。

阻尼对振动的影响主要表现在以下几个方面：1.阻尼比：阻尼比是描述阻尼特性的一个参数，定义为阻尼力与恢复力的比值。

阻尼比越大，系统的振动衰减越快，振幅减小得越迅速。

2.阻尼对振动幅值的影响：在初始阶段，阻尼对振动幅值的影响较小，但随着振动时间的增加，阻尼作用逐渐明显，振幅逐渐减小。

3.阻尼对振动周期的影响：阻尼对振动周期没有直接影响，振动周期仅与系统的弹性特性和质量有关。

4.阻尼对振动稳定性的影响：适当的阻尼可以提高振动的稳定性，防止系统发生过度振动或共振。

然而，过大的阻尼可能会导致系统过早地停止振动，影响某些应用中的振动性能。

三、自由度和阻尼的相互作用自由度和阻尼的相互作用表现在以下几个方面：1.自由度越多，系统可能出现的振动状态越多，同时阻尼对振动的影响也越复杂。

2.在多自由度系统中，各个自由度之间的振动可能会相互耦合，使得系统的振动特性更加复杂。

3.阻尼的存在可能会影响自由度之间的耦合关系，从而改变系统的振动特性。

综上所述，振动系统的自由度和阻尼对振动的影响是多方面的，它们相互作用决定了系统的振动特性。

了解这些知识点有助于我们更好地分析和解决实际问题。

习题及方法：1.习题：一个单自由度弹簧振子在无阻尼状态下做简谐振动，其质量为m，弹簧常数为k，振动的初始位移为A。

单自由度系统的受迫振动理论曾凡林哈尔滨工业大学理论力学教研组本讲主要内容1、单自由度系统的无阻尼受迫振动2、单自由度系统的有阻尼受迫振动1、单自由度系统的无阻尼受迫振动受迫振动在外加激振力作用下的振动称为受迫振动。

km简谐激振力是一种典型的周期变化的激振力。

简谐激振力随时间的变化关系可写成：)sin(j w +=t H F 其中：H 称为激振力的力幅，即激振力的最大值；ω是激振力的角频率；j 是激振力的初相角。

（1）振动微分方程m 取物块的平衡位置为坐标原点，x 轴向下为正。

物块的受力为恢复力F e 和激振力F 。

F e F方程两边同除以m ，并令, 得到：m k =20w H h m=)sin(d d 2022j w w +=+t h x tx ——无阻尼受迫振动微分方程的标准形式解可以写成：12xx x =+x 1 对应齐次方程的通解; x 2 对应的是特解。

齐次方程的通解可写为：)sin(01q w +=t A x 特解可写为：2sin()x b t w j =+将x 2 代入微分方程，得到:)sin()sin()sin(22j w j w w j w w +=+++-t h t b t b 解得：220ww -=hb 微分方程的全解为：)sin()sin(2200j w ww q w +-++=t ht A x 结果表明：无阻尼受迫振动是由两个谐振动合成的。

第一部分是频率为固有频率的自由振动；第二部分是频率为激振力频率的振动，称为受迫振动。

第一部分会逐渐衰减，而第二部分则是稳定的。

0sin()A t w q +220sin()ht w f w w+-1、单自由度系统的无阻尼受迫振动（2）受迫振动的振幅2220sin()hx t w j w w=+-系统的受迫振动为简谐振动，振动频率也等于激振力的频率，振幅大小与运动的初始条件无关，而与振动系统的固有频率ω0、激振力的频率ω、激振力的力幅H 相关。

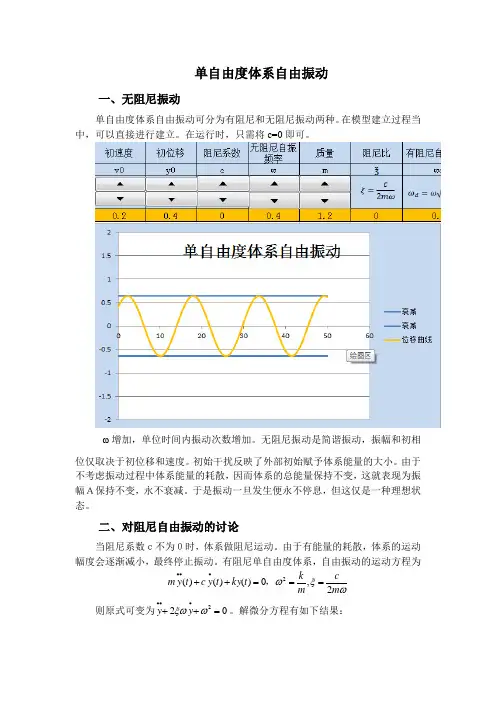
单自由度体系自由振动一、无阻尼振动单自由度体系自由振动可分为有阻尼和无阻尼振动两种。

在模型建立过程当中，可以直接进行建立。

在运行时，只需将c=0即可。

ω增加，单位时间内振动次数增加。

无阻尼振动是简谐振动，振幅和初相位仅取决于初位移和速度。

初始干扰反映了外部初始赋予体系能量的大小。

由于不考虑振动过程中体系能量的耗散，因而体系的总能量保持不变，这就表现为振幅Ａ保持不变，永不衰减。

于是振动一旦发生便永不停息，但这仅是一种理想状态。

二、对阻尼自由振动的讨论当阻尼系数ｃ不为０时，体系做阻尼运动。

由于有能量的耗散，体系的运动幅度会逐渐减小，最终停止振动。

有阻尼单自由度体系，自由振动的运动方程为ωξωm c m k t ky t y c t y m 2,0)()()(2===++∙∙∙， 则原式可变为022=++∙∙∙ωξωy y 。

解微分方程有如下结果：2.1 当1<ξ时，即小阻尼运动，方程的解为：)sin(A )sin cos ()(000ϕωωωξωωξωξω+=++=--t e t y v t y e t y d t d d d t 其中2200201)(ξωωωξω-=++=d d y v y A可画出小阻尼体系自由振动时的ｙ－ｔ曲线如图所示：是一条逐渐衰减的波动曲线2.2 当1>ξ时，即大阻尼的情况，方程的解为：⎥⎥⎦⎤⎢⎢⎣⎡-+--+=-t ch y t sh v y e t y o t ωξωξξξωωξ11)1()(20220 上式不含有简谐振动的因子，是因为体系受干扰后偏离平衡位置所积蓄起来的初始能量在恢复平衡位置的过程中全部消耗克服阻尼，由于阻尼很大，不足以引起振动。

当初始速度，初始位移都大于０时，可画出大阻尼体系自由振动时的ｙ－ｔ曲线如图所示：2.3 当1=ξ时，即临界阻尼的情况，方程的解为：[]t v t y e t y t 00)1)(++=-ωω（当初始速度，初始位移都大于０时，可画出临界阻尼体系自由振动时的ｙ－ｔ曲线如下图所示；当体系在临界阻尼时，其运动衰减的最快，即他能在最短时间内无振动的回到平衡位置。

单自由度系统固有频率和阻尼比的测定实验一、实验内容1、 学习分析系统自山衰减振动的波形；2、 验证固有频率的存在；3、 山衰减振动波形确定系统固有频率和阻尼比;二、实验设备(1)式中，a )= yi K/M 为系统固有频率，H = C/2M 为阻尼系数，g = (co 勿阻尼比。

3 W “ A M 一 +C 一 + Kx = O dr dt右〕〃 3 c d 兀 2 c 111 ——+ 2n 一 + a)x = 0 dr dt振动与控制实验设备、位移传感器、测振仪、计算机与分析软件(10)则:对于小俎尼情形M < 1,其方程有解如下:设t=0时，系统的位置和速度分别为xo 和切，则A = hV °少一卩I~T ⑷x( ^y/2 -ir tan (p = (5)其衰减振动有如下特点：1、 振动周期大于无阻尼时的自由振动周期，即TigT _ 2龙一 2礼2龙_T1①J/—询]一§2 J]_§2系统固有频率为：⑹fo = L =........ > • T 片口 (7)2、 振幅按指数函数衰减'设相邻两次振动的振幅分别为Ai 和Ai+i.则减幅系数为:“二字二严 4+1对数减幅系数 J = ln;； = n7； 另外，相隔•个周期的两次振动，城幅之比设为卩，则(8)⑼x = Ae ,,f,i sin (6?/ + A o ) (2)式中人■系统初始振il 喘，%・初相位，①■衰减振动圆频率°并且有：© = -jar -n 1 = (3)q = In 7 = j/z7]四、实验步骤1.试验1:采用1个质量块，施加较小的力使得悬臂梁产生自由衰减振动。

2.试验2：釆用1个质量块，施加较大的力使得悬臂梁产生自由衰减振动。

3.设定周期数j,此试验取30,读出j个波形所经历的时间t,记录其波形的幅值。

4.计算系统阻尼比纟和固定频率厶五、数据处理与实验结果分析表5-1原始数据记录试验2试验2XI10.36XI29.60Y1116.75Y1123.11X214.14X233.40Y2110.48Y211&04dX 3.78dX 3.80dYI-6.27dYI-5.09试验1（单个质量块，力F较小）：山试验所测数据计算得到的周期为：7 = 3.78/30 = 0.126$,九二 * = 7.936H?振幅之比设为仍，则30} - In 〃 j = In(1.60) = 0.47q = In 行二In(1.28) = 0.25為则有㈠务X , =49.86 *1.60 」4+j10.48 0 47歸莎”124,则有7；.= ——=0.126$ 30x0.124沖+（洁）+2.487x,o_3试验2（单个质量块，力F 较大）：山试验所测数据讣算得到的周期为：7 = 3.80/30 = 0.126$,九二丄=7.936 血 振幅之比设为〃门则A. 23.11_ ”厂石 18.04= 1,28III以上数据处理结果可以得到/试验2和试验2在不同大小的作用力下，悬3臂梁的固有频率一致，均为7.69HZO试验3 （两个质量块）：【」」试验所测数据讣算得到的周期为：r = 3.94/ 30 = 0.1315,/o= 1 =7.6\4H 乙姑宀已严992+ （需）-7.96V 7；A -=£222 = 2.06x10- 〜e 47.96 六、试验思考1＞试验过程较为简单，只是通过给悬臂杆一个外力后让其振动，测量到它的振 动波形图就行了。

2、单自由度系统的有阻尼受迫振动单自由度系统的受迫振动理论单自由度系统的受迫振动理论（1）振动微分方程kOx②恢复力F e , 方向指向平衡位置O ，大小与偏离平衡位置的距离成正比。

kxF -=e ③黏性阻尼力F d , 方向与速度方向相反，大小与速度大小成正比。

d dd x xF cv ct=-=-物块的运动微分方程为：22d d sin()d d x x m kx c H t t tw =--+方程两边同除以m ，并令：(ω0, 固有角频率) , (δ, 阻尼系数),得到：mk =20w 2c md =2202d d 2sin()d d x x x h t t td w w ++=——有阻尼受迫振动微分方程的标准形式①激振力F , 简谐激振力。

sin()F H t w =H h m =解可以写成：12xx x =+x 1 对应齐次方程的通解; x 2 对应的是特解。

欠阻尼的情况下( δ<ω0)，齐次方程的通解可写为：1e )t x A d q -=+特解可写为：)sin(2e w -=t b x ε表示受迫振动的相位角落后于激振力的相位角2、单自由度系统的有阻尼受迫振动单自由度系统的受迫振动理论将x 2 代入微分方程，得到:220sin()2cos()sin()sin()b t b t b t h t w w e d w w e w w e w --+-+-=将等式右边的h sin(ωt )做一个变换，得到:sin()sin[()]h t h t w w e e =-+cos sin()sin cos()h t h t e w e e w e =-+-代入微分方程，整理得到:)cos(]sin 2[)sin(]cos )([220=--+---e w e w d e w e w w t h b t h b 对任意瞬时t ，上式都必须是恒等式，所以有：cos )(220=--e w w h b 0sin 2=-e w d h b 2222204)(wd w w +-=hb 2202tan w w dwe -=于是，微分方程的通解为：e)sin()tx A b t d q w e -=++-式中，A 和θ为积分常数，由运动的初始条件确定。

阻尼器阻尼比计算公式
阻尼器阻尼比的计算公式可以根据所涉及的物理系统的特定情
况而有所不同。

一般来说，在振动系统中，阻尼比通常表示为ζ
（希腊字母zeta）。

对于简单的单自由度振动系统，阻尼比可以通
过以下公式计算：
阻尼比ζ = c / (2 √(k m))。

其中，c表示系统的阻尼系数，k表示系统的弹簧刚度，m表示
系统的质量。

这个公式适用于线性阻尼器的情况。

对于其他类型的阻尼器，比如非线性阻尼器或者涉及复杂动力
学特性的系统，阻尼比的计算公式可能会更加复杂。

在这种情况下，需要根据具体的系统特性和动力学方程来确定阻尼比的计算方法。

总的来说，阻尼比的计算公式是根据特定系统的物理特性和动
力学方程来确定的。

针对不同的系统，可能需要采用不同的计算方
法来确定阻尼比。

希望这个回答能够帮助到你。

单自由度阻尼比计算公式在振动系统中，自由度是指系统中独立运动的个数。

而阻尼比则是描述振动系统中阻尼效应的一个重要参数。

在单自由度振动系统中，阻尼比可以通过以下公式进行计算：阻尼比= (2 × 阻尼系数) / 临界阻尼其中，阻尼系数是指振动系统中阻尼力与速度的比值，临界阻尼是指在没有外力作用下，振动系统从任何位置开始振动后，恢复到平衡位置所需的时间最短，且不再发生振动的阻尼状态。

在实际工程中，阻尼比的计算对于设计和分析振动系统的性能至关重要。

阻尼比的大小直接影响振动系统的响应特性，包括振幅、频率和相位等。

阻尼比的计算公式基于振动系统的动力学方程，通过对振动系统进行建模和求解，可以得到该公式。

在实际应用中，可以通过实验测量阻尼比，或者通过数值模拟和计算来获得阻尼比的数值。

阻尼比的大小对于振动系统的稳定性和响应特性有重要影响。

当阻尼比小于临界阻尼时，振动系统会出现过阻尼的现象，振动衰减缓慢，且振动系统的响应时间较长。

当阻尼比等于临界阻尼时，振动系统达到最快的响应速度，但不会产生振动。

当阻尼比大于临界阻尼时，振动系统会出现欠阻尼的现象，振动衰减迅速，但可能会产生持续的振动。

阻尼比的大小还与振动系统的材料和结构特性有关。

不同的材料和结构对振动的阻尼效应有不同的影响。

例如，在建筑结构中，阻尼比的大小可以通过增加结构的阻尼材料来调节，以改善结构的抗震性能。

在工程实践中，根据振动系统的要求和性能指标，可以选择合适的阻尼比。

通常情况下，阻尼比的选择需要考虑振动系统的稳定性、响应速度和振动衰减等方面的要求。

单自由度阻尼比计算公式是工程领域中重要的计算公式之一。

通过计算阻尼比，可以评估振动系统的响应特性和稳定性，为设计和分析振动系统提供重要的依据。

在实际应用中，需要根据具体情况选择合适的阻尼比，以满足振动系统的性能要求。