圆管明渠均匀流标准计算书

表7-3
不同充满度时无压圆管形管道的水力要素
充满度 α=h/d
0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50
过水断面 A（m2）
0.0147d2 0.0408d2 0.0739d2 0.0118d2 0.1535d2 0.1981d2 0.2449d2 0.2933d2 0.3427d2 0.3926d2
无压圆管均匀流是明渠均匀流的一种。所谓 无压圆管是指不满流的圆管，城市排水中的 污水与雨水管道均属于无压圆管均匀流。
第三节 无压圆管均匀流的水力计算
一、无压圆管均匀流的水力特性
1、无压圆管均匀流的水力要素
充满度α： h d
过水断面A：
A
8
d2
sin
水力半径R： Rd1sin
4 4
图7-4 无压圆管过水断面
水面宽度 B
过水断面积 A
湿周 x
水力半径 R
B
h
b
b
bh
b2h
bh b 2h
B
m
b
b2mh
bmh
bmhh
b2h 1m2b2h 1m2
B d
h
2
hdh
d2 8
sin*
1 d 2
d 4
1
sin
*式中 以弧度计
2.明渠的底坡 明渠渠底纵向倾斜的程度称为底坡。
以符号i表示，等于渠底线与水平线夹
管径或暗渠 高
H（mm）
500～900
≥1000
最大设计充满 度 （α=h/d或h/H）
0.7
0.75
3、无压圆管均匀流的水力计算方法
1）解析法。即由明渠均匀流基本公式 QAC Ri 直接求解。

② 污水管道内沉积的污泥可能分解析出一些有害气体。 故需要留出适当的空间，以利通风，防止爆炸。 ③ 管道部分充满时，管道内水流速度和流量比满流时大 一些。
0.24n 0.24 0.03
Q k i 76.55 0.0005 1.71m3 / s
§ 7-3 明渠水力最优断面和允许流速 §7-3 明渠水力最优断面和允许流速
1、水力最优断面
Q Ac Ri Q f i, n,断面形状，尺寸
水力最优断面：当 i、n 及 A 大小一定时，使渠道能通过的
A 为相应于正常水深 h 时的过水断面面积
正常水深（h0）：明渠均匀流的水深，沿程不变的水深。
在明渠均匀流中，断面尺寸和n一定， k f h
h0 f 断面尺寸, n,Q,i
对某一给定的渠道，则有 Q f h0
⑴曼宁公式（爱尔兰）
V
1
21
R3J 2
n
C
1
1
R6
n
§ 7-2 明渠均匀流的计算公式
§ 7-4 明渠均匀流水力计算的基本问题
解： Q Ac Ri k i
k Q 40 2305 m3 / s
i 0.0003
5
又 k Ac
R
A
1 n
1
R6
1 R 2
A
R
2 3
n
A3
2
n 3
A b mhh b 1.5 2.65 2.65 b 3.97 2.65
b 2h 1 m2 b 2 2.65 11.52 b 9.54
i z 0.5 0.0005 L 1000
A b mhh 3 1.5 0.8 0.8 3.36m2
b 2 1 m2 h 3 20.8 11.52 5.88m

明渠恒定均匀流
§6-1 明渠恒定均匀流的特性及其计算公式
明渠水流： 渠槽或河槽中液流具有与大气相 通的自由表面 恒定流：运动要素不随时间变化。
均匀流： 流线为平行直线，运动要素沿程不变。
棱柱形渠道：横断面形状、尺寸均沿程不变 的长直渠道，A=f(h)。
梯形断面：
过水断面面积 A (b mh)h
一断面，然后分别对这些断面进行水力
计算，最后进行叠加。
2 n 1 3 Ri i Ai Ri i i 1 ni
Q Ai C i
i 1
n
Q，求i。
确定渠道的断面尺寸：已知Q、i、n、m，
求断面尺寸b和h。
确定渠道的断面尺寸： (1)b一定，求h 假定若干不同的h值，绘出Q=f(h)曲线， 找出对应的h。 (2)h一定，求b 假定若干不同的b值，绘出Q=f(b)曲线， 找出对应的b。
(3)按梯形水力最佳断面条件，确定b和h。 确定边坡系数m，计算宽深比β m，根据 h=f(β m)得出h。 (4)已知 Q、v、i、n、m，求断面尺寸b和h。
V 2
明渠均匀流的计算公式： 谢才公式：v C RJ C Ri
1 y 巴甫洛夫斯基公式：C R , y f (n, R) n Q AV AC Ri K i （K：流量模数）
1 曼宁公式： C R n
1 6
粗糙系数n反映河、渠壁面对水流阻力的
大小，与渠道壁面材料、水位高低、施工质
量及渠道修成后的运行管理等有关。
设计n值偏大，设计阻力偏大，断面尺寸
偏大,实际流速＞设计流速；
设计n值偏小，设计阻力偏小，断面尺寸
偏小,实际流速＜设计流速；
水力最佳断面：流量一定时过水断面最小

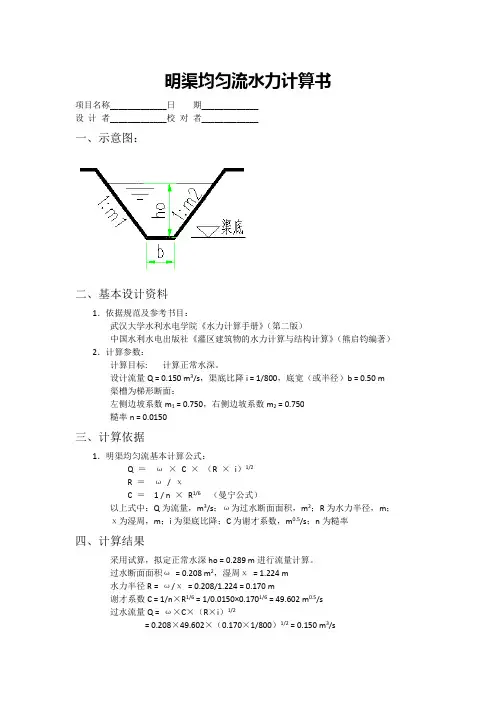
明渠均匀流水力计算书项目名称_____________日期_____________设计者_____________校对者_____________一、示意图：二、基本设计资料1．依据规范及参考书目：武汉大学水利水电学院《水力计算手册》（第二版）中国水利水电出版社《灌区建筑物的水力计算与结构计算》（熊启钧编著）2．计算参数：计算目标: 计算正常水深。

设计流量Q = 0.150 m3/s，渠底比降i = 1/800，底宽（或半径）b = 0.50 m渠槽为梯形断面：左侧边坡系数m1 = 0.750，右侧边坡系数m2 = 0.750糙率n = 0.0150三、计算依据1．明渠均匀流基本计算公式：Q ＝ω×C ×（R ×i）1/2R ＝ω/ χC ＝ 1 / n ×R1/6（曼宁公式）以上式中：Q为流量，m3/s；ω为过水断面面积，m2；R为水力半径，m；χ为湿周，m；i为渠底比降；C为谢才系数，m0.5/s；n为糙率四、计算结果采用试算，拟定正常水深ho = 0.289 m进行流量计算。

过水断面面积ω= 0.208 m2，湿周χ= 1.224 m水力半径R = ω/χ= 0.208/1.224 = 0.170 m谢才系数C = 1/n×R1/6 = 1/0.0150×0.1701/6 = 49.602 m0.5/s过水流量Q = ω×C×（R×i）1/2= 0.208×49.602×（0.170×1/800）1/2 = 0.150 m3/s当正常水深ho = 0.289 m时，计算流量与设计流量大约相等，ho = 0.289 m即为所求。

0.0200 0.0225 0.0250
0.0225 0.0250 0.0275
0.0250 0.0300 0.0250 0.0300 0.0330 0.035~0.045 0.0120 0.0140 0.0150 0.0150 0.0150 0.0170 0.0250 0.0275~0.03 0.0225
形断面)
湿周χ
水力系数 C
校核流量
26.50538 1.935 100.745 1.964 44.65222 100.00
原始数据 常数 过程数据 计算结果
Q＜1 m3/s 毛渠 支渠以下的固定渠道，渠床弯曲，养护一般 岩石 经过良好修整 经过中等修整无凸出部分 经过中等修整有凸出部分 未经修整有凸出部分 各种材料护面 抹光的水泥抹面 不抹光的水泥抹面 光滑的混凝土护面 料石砌护 砌砖护面 粗糙的混凝土护面 浆砌块石护面 干砌块石护面 卵石铺砌
糙率n值
渠道名称 电站尾水段
底宽b 20
水深h 2.3
明渠均匀流流量计算公式(梯形断面)
边坡系数 断面面积
m
A
糙率n
比降i
m2
1.00 51.29 0.025 0.001
1
m=△B/h
渠道糙率n参考值 渠道特征
Q＞25m3/s 平整顺直, 养护良好 平整顺直, 养护一般 渠床多石, 杂草丛生, 养护较差
1＜Q＜25m3/s 平整顺直, 养护良好 平整顺直, 养护一般 渠床多石, 杂草丛生, 养护较差

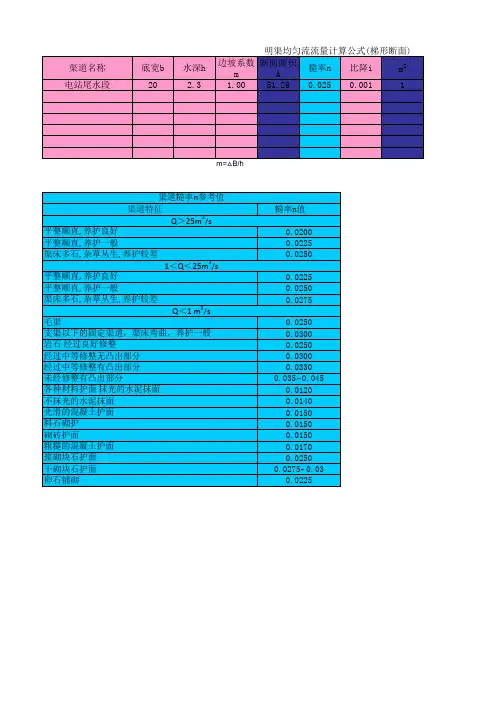
明渠均匀流计算公式含义
明渠均匀流是指水流在充满整个河道断面的情况下，流动速度均匀且河底坡度
恒定的流动状态。

为了计算明渠均匀流的流量，我们可以使用一种被广泛接受和使用的公式，称为曼宁公式。

曼宁公式描述了明渠均匀流的速度和流量之间的关系。

该公式的含义是：流量（Q）等于河道断面的横截面积（A）乘以流速（V）和河底粗糙程度的函数，即：Q = A * V * S
其中，Q表示流量，单位为立方米每秒（m³/s）；A表示河道断面的横截面积，单位为平方米（m²）；V表示流速，单位为米每秒（m/s）；S表示河底粗糙程度（即曼宁系数），是一个无单位的常数。

曼宁公式的标准形式是：
Q = (1/n) * A * R^(2/3) * S^(1/2)
其中，n是河道的曼宁系数，它描述了河道内各类摩阻力之和对水流阻力的影响，是根据河道底床的粗糙程度、植被情况以及河水的特性而确定的一个常数。

R
表示水力半径，可以通过河道的横截面积除以湿周来计算。

通过使用曼宁公式，我们可以计算得到明渠均匀流的流量，从而对水资源的管理、河流工程设计以及洪水预报等方面提供有价值的信息。

这个公式已经被广泛应用在水利工程领域，为工程师们提供了一个有力的工具，以便更好地理解和管理水的流动。

再论圆管明渠均匀流正常水深的直接计算公式文辉;李风玲【摘要】Based on the summarization of the existing formulae for normal depth of uniform flows in circular tube open channels, the dimensionless parameter a and the dimensionless normal depth p are introduced to perform mathematical transformation of the basic equation for uniform flows in circular tube open channels. A new explicit formula for the normal water depth of the uniform flows in circular tube open channels is proposed by means of the curve fitting and optimization principles. According to the requirements of Structural design code for special structures of water supply and waste water engineering and Design specification for hydraulic engineering, the scope of project application for the proposed formula is determined considering the specific situations of projects. The error analysis and case studies indicate that the proposed explicit formula has advantages of concise form and high precision. The maximum relative error is less than 0.72% , and it is convenient for designers to directly use it.%在总结前人圆管明渠均匀流正常水深计算公式的基础上,引入无量纲参数α和无量纲正常水深β,对圆管明渠均匀流基本方程进行数学变换,应用曲线拟合和优化原理,提出新的圆管明渠均匀流正常水深的直接计算公式；根据给水排水工程和水利工程设计规范的要求,并考虑工程实际情况,确定计算公式的工程适用范围.误差分析和计算实例表明:该公式形式简捷,精度较高,在工程适用范围内最大相对误差小于0.72％,可以方便工程设计人员在设计中直接使用.【期刊名称】《水利水电科技进展》【年(卷),期】2012(032)006【总页数】3页(P15-17)【关键词】圆管;明渠;均匀流;正常水深;圆形断面;超越函数方程【作者】文辉;李风玲【作者单位】惠州学院建筑与土木工程系,广东惠州516007;惠州学院建筑与土木工程系,广东惠州516007【正文语种】中文【中图分类】TV131.4圆管具有结构形式简单和力学条件好等特点，是给水排水工程和水利工程中应用最广泛的输水形式。

思考题2：非棱柱体渠道中，流线也会是平行直线，故水流也可能 形成均匀流。 A、正确； B 、错误；
思考题3：各种渠道中：①平底坡渠道；②正底坡、长直渠道；③正 底坡、棱柱形，长直渠道；④正底坡、非棱柱形渠道；⑤逆坡底渠 道；能否产生均匀流？为什么？
16
（三）明渠均匀流的计算公式
17
明渠均匀流的计算公式
5 1
当i、n、A = 给定 ： Q → Qmax
R →Rmax 或 →min
1）水力最优断面的明渠均匀流，当i，n，A给定时，水力 半径R 最大，即湿周χ最小的断面能通过最大的流量。 2）水力最优断面的明渠均匀流，通过已知流量时面积最 小。工程量最小，过水能力最强。
22
思考题
1、哪个断面的过水能力 大？
30
明渠最大设计流速
明渠类别 粗砂或贫亚粘土 亚粘土
vmax m s vmax m s
1.6 2.0
vmax m s
0.8 1.0
明渠类别 草皮护面 干砌块石
粘土
石灰岩或中砂岩
1.2
4.0
浆砌块石或浆砌 砖
混凝土
3.0
4.0
•
最小流速要求：v>0.3-0.4m/s（避免水草滋生）
学习重点
1、明渠均匀流水力计算；
2
主要内容
明渠均匀流概述
明渠均匀流的特性和形成条件 明渠均匀流的计算公式 水力最佳断面及允许流速 明渠均匀流的水力计算
无压圆管均匀流的水力计算
复式断面渠道的水力计算
3
（一）明渠均匀流概述
4
1. 明渠水流概述
明渠：天然的河道、人工渠道。 明渠水流：明渠中流动的液体，是一种具有自由液面的流动，水 流表面压强为大气压，即相对压强为零。 明渠水流特点： 液体通过明渠流动时，形成与大气相接触的自由水面，表面各点压 强均为大气压强，所以明渠水流为无压流。（管流则是压力流）

第六章
明渠均匀流
明渠均匀流属于明渠水流的一种。
运动要素不 随时间变化
恒定流
非均匀流 均匀流
明渠水流
流线为相互 平行的直线
表面相对压强为 非恒定流 零，为无压流
本章纲要:
第一节 概述 第二节 明渠均匀流的计算公式 第三节 明渠水力最优断面和允许流速 第四节 明渠均匀流水力计算的基本问题 第五节 无压圆管均匀流的水力计算 第六节 复式断面渠道的水力计算
第二节 明渠均匀流的基本计算公式 谢才公式
谢才公式 J=i
vC Ri
vC RJ
断面平均 流速(m/s)
水力半径(m)
R
适用范围: R<0.5m且
n<0.02
谢才系数 (m1/2/s)
曼宁公式
c
1
1
R6
n
巴氏公式 c 1 R y
n
n：粗糙系数
适用范围: 0.1m≤R≤3m 且0.01l<n<0.04
沿程断面形状 尺寸是否变化
棱柱形 渠道
f (h)
断面形 状多样
明渠
底坡i=sinθ
非棱柱 f(h,s)
形渠道 过水断面面
i<0 顺坡
积与水深、 位置有关
i=0 平坡
i>0 逆坡
第一节 概述 二、明渠均匀流的特征
水力特征
几何角度
运动学角度
能量角度 力学角度
质点做等速 直线运动 （均匀流）
概述 二、明渠均匀流的特征 几何特征
1、梯形水力最优断面计算 问题本质？
确定适当的水深h和渠底宽b， 使断面流量Q最大。
Q
i 5/最大，即在 面积ω一定时，湿周最小。

第六章 明渠均匀流一、一、概念：明渠是具有自由表面液体的渠道 分类（据形成）： 天然渠道→天然河流人工渠道→人工河流、不满流的排水管渠明渠流——明渠中流动的液体又称重力流（依靠重力作用而产生） 也称无压流（自由表面相对大气压为0） 分类： 恒定流 均匀流 非恒定流 非均匀流注意特殊性：A 随θ的变化而变化，故不可能发生非恒定均匀流动。

2、水流运动的影响因素： 过水断面形状过水断面尺寸底坡的大小 2、 据影响把明渠分为： 1、棱柱形渠道 非棱柱性渠道 2、顺坡、平坡和逆坡渠道 二、1、 1、 棱柱形渠道：凡是断面形状、尺寸沿程不变，过水断面仅随水深变化而变化的常直渠道。

过水断面面积随形状沿程变化的渠道，称非棱柱形渠道。

棱柱断面 断面规则的长直人工渠道，同管径的排水管道、涵洞 非棱柱断面 连接两条在断面形状、尺寸，不同渠道的过渡段。

渠道断面类型：矩形、梯形、圆形、半圆形、此外有组合型、三角型（复式）、抛物线型、卵型2、 2、 顺坡、平坡、逆坡渠道：底坡——渠道底面的坡度，用i 表示，通常是指单位渠长。

l 上的渠道高差，即θsin =∆=lz iz∆——渠底高差l ——对应z ∆的相应渠长θ——渠底与水平线的夹角一般渠道底坡都很小，即θ很小，实际中，为方便测量渠长和水深，故常用θtg 代替θsin ，水平渠长代替水流方向渠长，铅垂水深代替垂直于底坡的水深。

底坡分类：顺坡：0>i ，渠底沿程降低的底坡。

平坡：0=i ，渠底水平，平坡 逆坡：0<i ，渠底沿程升高。

意义：底坡i 反映了重力在流动方向上的分力，表征水流推动力的大小，i 愈大，重力沿水流方向分力愈大，流速愈快。

§6-1 明渠均匀流的形成条件和水力特征一、一、明渠均匀流的形成条件：1、 1、 明渠均匀流——水深、断面平均流速沿程都不变的流动。

⑴ 渠底必须沿程降低，即0>i 并且要在较长一段距离内保持不变。

（是重力流，依靠重力分力驱使水流运动，保证流动流向必须有恒定不变的作用力。

0.089709
1.114719
1300
0.014
0.1
0.81
4.028
0.376312
0.085016
1.176249
1200
0.014
0.1
0.81
4.0280.365550源自0802231.246528
1100
0.014
0.1
0.81
4.028
0.3542
0.075318
1.327696
1000
0.054273
1.84252
600
0.014
0.1
0.81
4.028
0.28433
0.048535
2.060386
500
0.014
0.1
0.81
4.028
0.266146
0.042525
2.351554
要求坡度小，所以选取坡度为1:1500管径D=0.39时流速V=1.06,V不淤＜V＜V不冲，所以满足要求。
0.014
0.1
0.81
4.028
0.342171
0.07029
1.422684
900
0.014
0.1
0.81
4.028
0.329349
0.06512
1.535615
800
0.014
0.1
0.81
4.028
0.315583
0.05979
1.672507
700
0.014
0.1
0.81
4.028
0.300671
取糙率为0.014，设计流量为0.1时，i=1:500至1:1500进行试算，结果如下：

（4) 排水管的最小设计流速：对污水管道，当管径小于等于500mm，为0.7m/s；当 管径大于500mm，为0.8m/s。
管径或暗渠高 150~300 350~450 500~900 》1000
最大设计充满度 0.6 0.7 0.75 0.8
恒定明渠流非均匀流的产生条件及特征
明渠非均匀流：
非均匀流(壅水曲线） aI
得
Q 2
q 2
hk 3 gb2 3 g
Q2
g
Ak3 Bk
b3hk3 b
b2hk3
式中: q 称为单宽流量，单位为m2/s 。
qQ b
由于 q vcr hcr
得
hk
vk2
g
2 vk2
2g
上式说明，当矩形断面渠道中出现临界流时，临界水深为流速水头的两倍。
3 临界坡度
当已知流量Q，在一定断面形状、渠壁粗糙系数的棱柱体渠道中作均匀流动时，正常 水深将随渠底坡度i的不同而变化。当正常水深恰好等于临界水深时的渠底坡度称为临 界底坡，并以icr 表示。
管内水深达到80%管径时，流量接近满管 流时的流量;
管内水深达到直径一半时，流速接近满管 流时的流速。
A,B计算公式
5/3

A 4arcsin
sin(4arcsin
)
2/3
43.14 sin(4arcsin )
2/3
B 4arcsin
sin(4arcsin )
2/3
sin(4arcsin )
dE d
Q2
Q2 dA
dh
(h dh
2gA2 )
1
gA3
dh
0
E
h
Q 2
2gA2

明渠均匀流水力计算书
项目名称_____________日期_____________
设计者_____________校对者_____________
一、示意图：
二、基本设计资料
1．依据规范及参考书目：
武汉大学水利水电学院《水力计算手册》（第二版）
中国水利水电出版社《灌区建筑物的水力计算与结构计算》（熊启钧编著）2．计算参数：
计算目标: 计算流量。

正常水深ho = 3.20 m，渠底比降i = 1/7000，底宽（或半径）b = 1.50 m
渠槽为梯形断面：
左侧边坡系数m1 = 2.500，右侧边坡系数m2 = 2.500
糙率n = 0.0250
三、计算依据
1．明渠均匀流基本计算公式：
Q ＝ω×C ×（R ×i）1/2
R ＝ω/ χ
C ＝ 1 / n ×R1/6（曼宁公式）
以上式中：Q为流量，m3/s；ω为过水断面面积，m2；R为水力半径，m；
χ为湿周，m；i为渠底比降；C为谢才系数，m0.5/s；n为糙率
四、计算结果
过水断面面积ω= 30.400 m2，湿周χ= 18.733 m
水力半径R = ω/χ= 30.400/18.733 = 1.623 m
谢才系数C = 1/n×R1/6 = 1/0.0250×1.6231/6 = 43.362 m0.5/s
过水流量Q = ω×C×（R×i）1/2
= 30.400×43.362×（1.623×1/7000）1/2 = 20.071 m3/s。

顺坡、正坡 i > 0
平坡 i = 0
逆坡、负坡 i < 0
在平底渠道中i=0，流段重力在顺流方向分力
G sinθ=0；
在逆坡渠道中，流段重力的分力Gsinθ与摩阻力 Ff的方向一致，因而都不可能满足Gsinθ＝Ff 的平衡
条件，故在平底及逆坡渠段中，不可能产生均匀流动， 只有在顺坡渠道中，才有可能产生均匀流。
从力学观点看，明渠均匀流是一种等速直线运动。则作用于流段上所有外 力在流动方向的分量必相互平衡，即
Fp1 Gsin Fp2 Ff 0 式中为渠底与水平线的夹角 。
因为均匀流中过水断面上的压强按静水压强分布，而且各过水断面的水深 及过水断面积相同，故P1=P2。则由上式可得
Gsin Ff
上式标明：明渠均匀流中摩阻力Ff与水流重力在流动方向的分力相平衡。
本章的重点
明渠均匀流的特性和形成条件； 明渠流水力计算应考虑的几个问题； 明渠均匀流水力计算的类型和方法。
9
9.1 概述
明 渠
9.2 件
明渠均匀流的特征及其形成条
均 9.3 明渠均匀流的水力计算
匀
流 9.4 无压圆管均匀流
9
9.1 概述
明 渠
9.1.1 明渠流动的特点
均
9.1.2 明渠的分类
匀
流
水深时，渠道过不了设计流量（比设计流量小）。 通过一定流量时，实际水深比设计计算的水深大， 可能造成水漫渠顶事故。
•
各种土质、衬砌材料渠道的糙率表
表 人工渠道的糙率
渠道衬砌材料 土渠： 夯实光滑的土面 砾石（直径20~60mm）渠面 散布粗石块的土渠面 野草丛生的砂壤土或砾石渠面
n
0.017~0.020 0.025~0.030 0.033~0.04 0.04~0.05

明渠均匀流水力计算方法及Basic 程序使用说明明渠均匀流水力计算的主要内容包括如下两个方面：一是校核已成渠道的过水能力；或者由实测流量资料确定已成渠道的糙率；二是设计新的渠道即确定底宽(b)或水深(h)或底坡(i)。

为了应用方便，这两类问题可以汇编成一个电算程序来解决。

一、明渠均匀流水力计算的数学公式：明渠均匀流水力计算的基本公式是连续方程及谢才公式。

3/23/56/1/1X A n i Q X A R R n C Ri C V V A Q ∙=⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==∙=∙=令 1nQ Y ∙=，3/23/5x A K =只要根据不同的横断面类型找出A 与x 的表达式，就可以解决各种情况下的明渠均匀流水力计算问题。

工程中较为常用的是梯形和u 形断面型式，其相应的过水断面面积和湿周的表达式，分别如下：梯形断面：()h mh b A ∙+=212m h b x ++=对于不同的问题，编写程序时可分别应用下述不同的公式。

(1)计算流量：n i K Q ∙=(2)计算底坡：2⎪⎭⎫ ⎝⎛∙=K Q n i(3)计算糙率：Q i K n ∙=(4)计算正常水深，应用迭代公式，()h K y h ∙=6.0/ (5)计算底宽或半径R ，用迭代公式：b xy b ∙=二、Basic 原程序5 REM 梯形断面明渠均匀流水力计算10 INPUT “J=”;J20 ON J GOTO 30,150,270,390,58030 INPUT “H=”;H: INPUT “N=”;N : INPUT “I=”;I50 INPUT “B=”;B: INPUT “M=”;M60 GOSUB 860130 Q=K*SQR(I)/N140 PRINT “Q=”;INT(1000*Q+0.5)/1000145 END150 INPUT “Q=”;Q: INPUT “N=”;N: INPUT “H=”;H170 INPUT “B=”;B: INPUT “M=”;M180 GOSUB 860190 I=(Q*N/K)^2200 PRINT “I=”;INT(1000*I+0.5)/1000205 END270 INPUT “H=”;H: INPUT “Q=”;Q : INPUT “I=”;I280 INPUT “B=”;B: INPUT “M=”;M290 GOSUB 860300 N=K*SQR(I)/Q310 PRINT “N=”;INT(1000*N+0.5)/1000320 END390 INPUT “Q=”;Q: INPUT “N=”;N: INPUT “I=”;I392 Y=Q*N/SQR(I)395 INPUT “B=”;B: INPUT “M=”;M:H=5400 GOSUB 860430 H1=H*(Y/K)^0.6450 IF ABS(H-H1)<0.001 THEN 470460 H=H1 : GOTO 400470 PRINT “H=”;INT(1000*H+0.5)/1000480 END580 INPUT “Q=”;Q: INPUT “N=”;N: INPUT “I=”;I590 Y=Q*N/SQR(I)600 INPUT “H=”;H: INPUT “M=”;M:B=5610 GOSUB 860620 B1=B*Y/K630 IF ABS(B-B1)<0.001 THEN 650640 B=B1 : GOTO 610650 PRINT “H=”;INT(1000*H+0.5)/1000660 END860 A=(B+M*H)*H:P=B+2*H*SQ R(1+M*M)870 K=A^(5/3)/(P^(2/3))880 RETURN三、有关程序的说明：1、程序只适用于计算梯形(矩形)断面，对于其它的的断面类型，可根据具体情况修改子程序中的断面面积A及湿周x的表达式即可。

l y 4.5h
1 l y (4.5h 5 ) 2
l0 (2.5 ~ 3.0)l y
恒定明渠非均匀渐变流动的基本微分方程
假设: (1)沿程流速变化缓慢，符合渐变流条件，可应用总流伯努利方程； (2)只有沿程损失，不考虑局部损失； (3)不均匀流微小流程上的沿程损失可按均匀流计算。 写总流的伯努利方程
h0 hk
i ik ,
h0 hk
用波速来判别明渠流的型态
当c=v时， 为c’零，渠中水流为缓、急流的分界 状态，称为临界流。 这时的流速称为临界流速，以vcr表示，
缓流 急流 临界流
v v v
vcr
gh
gh gh gh
2、佛汝德数 ——缓流和急流的判别标准 佛汝德数为 缓流 急流
明渠均匀流 临界流动
Q Ak Ck Rk ik
Q 2
g
3 Ak Bk
联立解似上两式，可得
g k ik 2 Ck Bk
在流量、渠道断面形状、尺寸和粗糙系数一定时 缓流，缓坡渠道 临界流，临界坡渠道 急流，急流渠道
正常水深与临界水深之间的关系
i ik ,
h0 hk
i ik ,
hw (h
引入6-26和6-35
1v12
2g
) (h
2 1v2
2g
) e e
(h h) 3 hw 4hh
由上式可知，在给定流量下，能量损失的大小与跃高h”-h’成正比，跃高愈 高则能量损失愈大。
水跃长度经验公式：
l l y l0
3.共轭水深的计算
Q 2
gA 1
yc1 A1
Q 2
gA2
yc 2 A2

1无压圆管均匀流的水力计算
无压圆管指不满流的圆管。

在排水工程中被广泛使用。

对于长直的圆管，i>0，粗糙系数保持沿程不变时，管中水流可以认为是明渠均匀流。

见图6—6—3。

直径为d，水深为h的圆形管道，其过水断面面积A、湿周χ和水力半径R计算公
式如下：
无压圆管均匀流水力计算的基本公式仍是
或
为了避免繁琐的计算，可以利用图6-6-4来计算。

图中纵坐标为充满度α＝
h/d，横坐标为无量纲流量Q/Q
0和无量纲流速v/v。

Q
和v
为圆管满流时的流量
和流速。

Q与v则表示充满度h／d时的流量和流速。

从图中可以看出，最大流
量发生在h／d=0.95时，这时Q/Q
=1．087，因为这时的AR2／3最大；最大流速发
生在h／d=0．81时，这时v/v
=1．16。

因为这时的水力半径R最大，水深再加大时，过水断面面积虽有增加，但湿周增加得更快，使R反而减小。

[例6-6-3]无压长涵管，直径d=1．5m，底坡i=0．002，粗糙系数n=0．014，流
量Q=2．5m3／s，渠中水流为均匀流。

求水深h。

[解] 先求满管流时的Q
查图6—6—4得
所以。