雷达信号分析(第2章)信号分析基础
- 格式:pdf
- 大小:350.57 KB
- 文档页数:23




第二章 信号分析基础1、信号分析中常用函数包括:δ函数、sinc(t)函数、复指数函数e st① δ函数具有“抽样(乘积)、筛选(积分)、卷积”特性,其拉氏变换和傅氏变换的值均为1。
② 卷积特性的表达式为)()()()()(t f d t f t t f =-=*⎰+∞∞-ττδτδ,τ为两信号之间的时差。
③ sinc(t)函数又称为闸门函数、滤波函数或内插函数,分别对应其用处:闸门(或抽样)、低通滤波、采样信号复原时sinc(t)函数叠加构成非采样点波形。
④ 复指数函数e st 中出现的“负频率”是与负指数相关联的,是数学运算的结果,并无确切的物理含义。
2、一个信号不能够在时域或频域都是有限的。
3、信号的时域统计分析:均值x μ、均方值ψ2x 、方差σ2x 。
三者具有如下关系:2x2x 2x μσψ+= 式中,ψ2x (又称平均功率,平均能量的一种表达)表达了信号的强度; σ2x 描述了信号的波动量; μ2x 描述了信号的静态量。
4、各态历经过程:此过程中的任一个样本函数x(t)都经历了过程的各种状态,从它的一个样本函数x(t)中可以提取到整个过程统计特征的信息。
5、相关函数的性质:① 自相关函数R x (τ)是τ的偶函数,满足:)()(ττ-=x x R R 。
② 互相关函数R xy (τ)是τ的非奇非偶函数,满足:)()(ττ-=yx xy R R 。
③ 当τ=0时,自相关函数具有最大值。
对于功率信号,若均值μx =0,则在τ=0点处,有ψ2x =σ2x =R x (τ)。
④ 周期信号的R x (τ)仍然是与原信号同频率的周期信号,但不具有原信号的相位信息。
⑤ 两周期信号(同频)的R xy (τ)仍然是与原信号同频率的周期信号,但保留了原信号的相位信息。
⑥ 两个不同频的周期信号互不相关,其互相关函数R xy (τ)=0。
⑦ 随机信号的R x (τ)将随|τ|值增大而很快趋于0。
有限带宽白噪声信号的R x (τ)是一个sinc(τ)型函数,即可说明。


雷达信号基本知识声明 | 本号聚焦相关知识分享,内容观点不代表本号立场,可追溯内容均注明来源,若存在版权等问题,请联系(158****1905,微信同号)删除,谢谢。
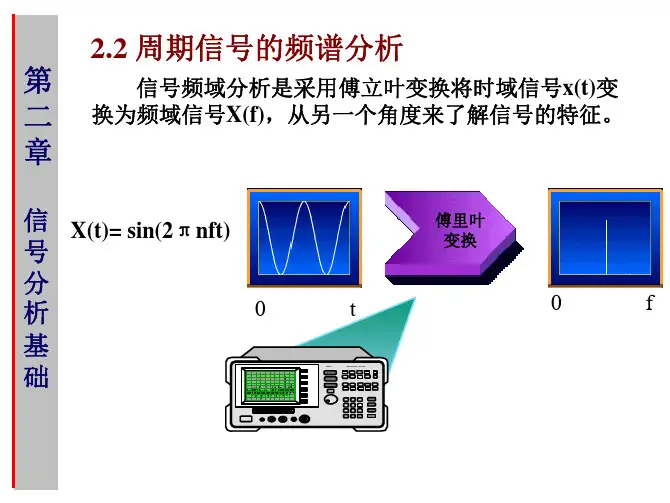
1. 非线性调频信号(NLFM)由前面介绍,我们知道为了解决单载频脉冲信号的局限性,在现代雷达系统中,人们普遍使用具有大时宽带宽积的脉冲压缩信号。
脉冲压缩技术:在发射端,通过对相对较宽的脉冲进行调制使其同时具有大的带宽,从而得到大时宽带宽积的发射信号;在接收端,对接收的回波信号进行压缩处理,得到较窄的脉冲。
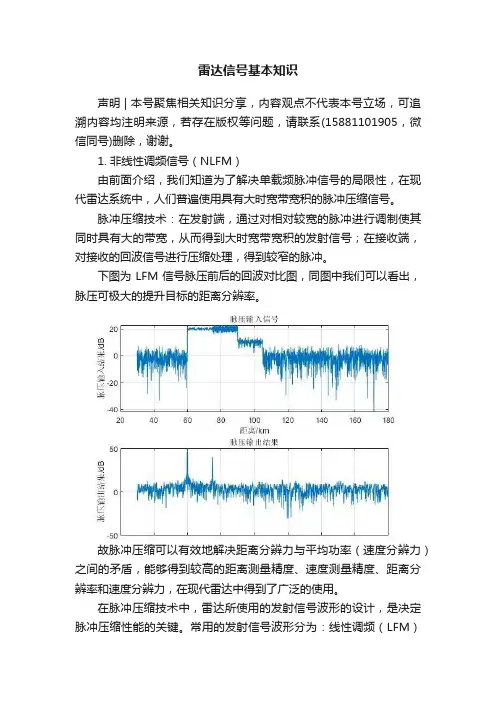
下图为 LFM 信号脉压前后的回波对比图,同图中我们可以看出,脉压可极大的提升目标的距离分辨率。
故脉冲压缩可以有效地解决距离分辨力与平均功率(速度分辨力)之间的矛盾,能够得到较高的距离测量精度、速度测量精度、距离分辨率和速度分辨力,在现代雷达中得到了广泛的使用。
在脉冲压缩技术中,雷达所使用的发射信号波形的设计,是决定脉冲压缩性能的关键。
常用的发射信号波形分为:线性调频(LFM)信号,非线性调频(NLFM)信号和相位编码(PSK)信号等,本文主要讨论的是NLFM信号。
LFM 信号的产生和实现都比较容易,是研究最早、应用较为广泛的一种脉冲压缩信号。
LFM 信号的频率在脉冲宽度内与时间变化成线性关系。
LFM 信号最大的优点是匹配滤波器对回波信号的脉冲多普勒频移不敏感,即使回波信号具有较大的多普勒频移,采用原有的匹配滤器仍然能得到较好的脉冲压缩结果,因而可简化信号处理系统。
LFM信号波形如下图所示。
但 LFM 信号匹配滤波器输出响应的旁瓣较高,为了抑制旁瓣常需要进行加权处理,但这会造成主瓣展宽,并导致信噪比损失。
此外,LFM 信号的缺点是会产生多普勒耦合时移现象,不能同时独立提供距离和速度的测量值。
LFM 信号经过匹配滤波器后的输出响应及主副瓣图形如下图所示。
为了解决以上问题,现代雷达也经常采用非线性调频(NLFM)信号。
NLFM 信号的频率随着时间做非线性变化,其突出的优点是直接进行匹配滤波即可得到较低的旁瓣而无需加权处理,因而避免了引入加权所带来的信噪比损失问题。

