机械制图之曲面体的投影

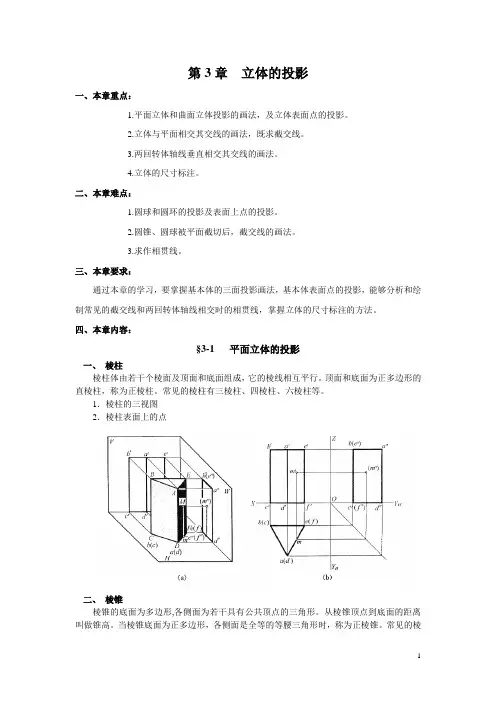
第3章立体的投影一、本章重点：1.平面立体和曲面立体投影的画法，及立体表面点的投影。

2.立体与平面相交其交线的画法，既求截交线。

3.两回转体轴线垂直相交其交线的画法。

4.立体的尺寸标注。

二、本章难点：1.圆球和圆环的投影及表面上点的投影。

2.圆锥、圆球被平面截切后，截交线的画法。

3.求作相贯线。

三、本章要求：通过本章的学习，要掌握基本体的三面投影画法，基本体表面点的投影，能够分析和绘制常见的截交线和两回转体轴线相交时的相贯线，掌握立体的尺寸标注的方法。

四、本章内容：§3-1 平面立体的投影一、棱柱棱柱体由若干个棱面及顶面和底面组成，它的棱线相互平行。

顶面和底面为正多边形的直棱柱，称为正棱柱。

常见的棱柱有三棱柱、四棱柱、六棱柱等。

1．棱柱的三视图2．棱柱表面上的点二、棱锥棱锥的底面为多边形,各侧面为若干具有公共顶点的三角形。

从棱锥顶点到底面的距离叫做锥高。

当棱锥底面为正多边形，各侧面是全等的等腰三角形时，称为正棱锥。

常见的棱锥有三棱锥、四棱锥、六棱锥。

1. 棱锥的三视图2．棱锥表面上的点§3-2曲面立体的投影曲面立体的表面是由一母线绕定轴旋转而成的，故称曲面立体，也称为回转体。

常见的回转体有圆柱、圆锥、圆球和圆环等。

一、圆柱1．圆柱面的形成圆柱面可看作一条直线AB围绕与它平行的轴线OO回转而成。

OO称为回转轴，直线AB称为母线，母线转至任一位置时称为素线。

这种由一条母线绕轴回转而形成的表面称为回转面，由回转面构成的立体称为回转体。

2．圆柱的三视图3．圆柱表面上的点二、圆锥1．圆锥面的形成圆锥面可看作由一条直母线围绕和它相交的轴线回转而成。

2．圆锥的三视图3．圆锥表面上的点三、圆球1．圆球面的形成圆球面可看作一圆（母线），围绕它的直径回转而成。

2．圆球的三视图3．圆球表面上的点四、圆环1．圆环的形成圆环面可看作由一圆母线，绕一与圆平面共面但不通过圆心的轴线回转而成。

图中的回转轴是铅垂线。

曲面立体表面点的投影(总9页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除《机械制图》课程教案《第三章立体表面交线的投影作图§3－1 立体表面上点的投影》教案授课教师：杨秋颖班级：机加14-1 时间：课题：曲面立体的投影及表面取点教学方法：讲授法教学目的：1、讲解曲面立体的种类及其三视图画法2、讲解在圆柱和圆锥体表面取点、取线的作图方法目的要求：1、能够熟练掌握圆柱和圆锥体的三视图画法2、能够熟练运用利用点所在的面的积聚性法和辅助线法在曲面立体表面取点、取线教学重点：1、曲面立体的种类及其三视图画法。

2、在曲面立体表面取点、取线的作图方法教学难点：在圆柱和圆锥体表面取点、取线的作图方法【教学媒体和资源利用】多媒体课件【教学过程设计】组织教学—引入—新授—小结—学生练习—作业（a ）立体图 （b ）投影图 图3－4 圆柱的投影及表面上的点 边画图边讲解作图方法与步骤。

总结圆柱的投影特征：当圆柱的轴线垂直某一个投影面时，必有一个投影为圆形，另外两个投影为全等的矩形。

（2）圆柱面上点的投影 方法：利用点所在的面的积聚性法。

（因为圆柱的圆柱面和两底面均至少有一个投影具有积聚性。

）举例：如图3－4（b ）所示，已知圆柱面上点M 的正面投影m ′，求作点M 的其余两个投影。

因为圆柱面的投影具有积聚性，圆柱面上点的侧面投影一定重影在圆周上。

又因为m ′ 可见，所以点M 必在前半圆柱面的上边，由m ′ 求得m ″，再由m ′ 和m ″ 求得m 。

第二课时（二）曲面立体的投影及表面取点1、圆锥圆锥表面由圆锥面和底面所围成。

如图3－5（a ）所示，圆锥面可看作是一条直母线SA 围绕与它平行的轴线SO 回转而成。

在圆锥面上通过锥顶的任一直线称为圆锥面的素线。

（1）圆锥的投影画圆锥面的投影时，也常使它的轴线垂直于某一投影面。

举例：如图3－5（b ）所示圆锥的轴线是铅垂线，底面是水课件展示平面，图3－5（c）是它的投影图。

机械制图教案-点、直线和曲面的投影1. 引言本教案介绍了机械制图中点、直线和曲面的投影方法。

通过研究这些技巧，学生将能够准确地表示三维物体在二维平面上的投影。

2. 知识点2.1 点的投影- 点的投影是将三维空间中的点投射到二维平面上的方法。

- 介绍点的正投影和侧投影的概念。

- 研究如何根据点在三维空间中的坐标计算它的投影坐标。

2.2 直线的投影- 直线的投影是将三维空间中的直线投射到二维平面上的方法。

- 介绍直线在正投影和侧投影中的表现形式。

- 研究如何根据直线在三维空间中的两点坐标计算它的投影坐标。

2.3 曲面的投影- 曲面的投影是将三维空间中的曲面投射到二维平面上的方法。

- 介绍曲面在正投影和侧投影中的表现形式。

- 研究如何根据曲面在三维空间中的参数方程计算它的投影形状。

3. 教学方法- 理论讲解：介绍点、直线和曲面在投影中的基本概念和原理。

- 实例演示：通过具体的例子演示点、直线和曲面的投影计算方法。

- 练指导：提供一些练题和题答案，让学生巩固所学知识。

4. 教学评估- 口头提问：对学生进行口头提问，检验他们对点、直线和曲面投影知识的掌握程度。

- 练测验：提供一些练题，让学生进行实际计算，评估他们的运用能力。

5. 资源需求- 投影仪：用于展示理论部分的演示和示例图形。

- 教材：提供相关理论知识和练题。

- 计算工具：学生可以使用计算器进行投影计算。

6. 教学计划本教案按照以下教学计划进行：7. 教学目标- 理解点、直线和曲面的投影概念。

- 学会计算点、直线和曲面的投影坐标。

- 能够应用投影技巧解决实际问题。

8. 总结本教案涵盖了机械制图中点、直线和曲面的投影方法。

通过系统研究这些知识点，学生将能够准确地表示三维物体在二维平面上的投影，为日后的机械制图实践打下坚实的基础。

注意：以上文档为教案提纲，实际编写时需适量扩展内容，以确保教案的完整性和详细性。

第2章立体的投影2.1 立体及其表面上的点与线立体由其表面所围成，可分为两类：表面都是平面的平面立体和表面是曲面或曲面与平面的曲面立体。

一、平面立体平面立体由若干多边形所围成，因此，绘制平面立体的投影，可归结为绘制它的所有多边形表面的投影，也就是绘制这些多边形的边和顶点的投影。

多边形的边是平面立体的轮廓线，分别是平面立体的每两个多边形表面的交线。

当轮廓线的投影为可见时，画粗实线；不可见时，画虚线；当粗实线与虚线相重合时，应画粗实线。

常见的平面立体有棱柱和棱锥。

1、棱柱2、棱锥平面立体的投影的外围轮廓总是可见的，应画粗实线；而在投影的外围轮廓内部的图线，则应根据线、面的投影分析，按前遮后、上遮下、左遮右直接判断投影的可见性，决定画粗实线或虚线，必要时还可利用交叉两直线的重影点的可见性进行判断。

二、曲面立体曲面立体由曲面或曲面与平面所围成。

有的曲面立体有轮廓线，即表面之间的交线，如圆柱；有的曲面立体有尖点，如圆锥；有的曲面立体全部由光滑的曲面所围成，如圆球。

在画曲面立体的投影时，除了画出轮廓线和尖点外，还要画出曲面投影的转向轮廓线。

曲面立体的转向轮廓线是切于曲面的诸投射线与投影面的交点的集合，也就是这些投射线所组成的平面或柱面与曲面的切线的投影，常常是曲面的可见投影和不可见投影的分界线。

曲面立体的投影就是它的所有曲面表面或曲面表面与平面表面的投影，也就是曲面立体的轮廓线、尖点的投影和曲面投影的转向轮廓线。

常见的曲面立体有圆柱、圆锥、圆球，圆环。

1、圆柱圆柱由圆柱面、顶面和底面所围成。

圆柱面由直线绕与它平行的轴线旋转而成。

因此，画圆柱的投影就是画顶面和底面及轮廓线、圆柱面投影的转向轮廓线、轴线。

当圆柱的轴线与投影面垂直时，圆柱面在轴线垂直的投影面上的投影具有积聚性。

因此，作圆柱表面2、 圆锥圆锥由圆锥面和底面所围成。

圆锥面由直线绕与它相交的轴线旋转而成。

因此，画圆锥的投影就是画尖点（即锥顶）、底面及轮廓线、圆锥面投影的转向轮廓线、轴线。