机械制图之立体的投影

机械制图之立体的投影引言在机械制图中，立体的投影是一个非常重要的概念。

立体的投影是将三维物体在二维平面上反映出来的一种方法，能够在制图过程中更加清晰地表达物体的形状、结构和尺寸。

本文将介绍机械制图中立体的投影的基本原理和常见的投影方法。

立体的投影原理立体的投影是基于投影原理来实现的。

在机械制图中，通常使用平行投影和透视投影两种方法。

平行投影平行投影是指通过平行投影线来投影物体的方法。

在平行投影中，投影线与物体平面平行，物体上各点在投影面上的投影位置与物体上的位置相对应，从而构成了物体的平行投影。

平行投影主要分为正射投影和斜投影两种。

正射投影是投影线与投影面垂直的一种投影方法，适用于表达物体的外形和尺寸。

斜投影是指投影线与投影面不垂直的投影方法，适用于表达物体在空间中的位置和形状。

透视投影透视投影是指通过透视原理来投影物体的方法。

在透视投影中，投影线与投影面相交，物体上的各点在投影面上的位置与物体上的位置不完全对应，从而构成了物体的透视投影。

透视投影能够更加真实地反映物体在空间中的位置和形状，适用于表达物体的逼真程度和透视效果。

常见的投影方法在机械制图中，常见的立体投影方法包括主视图、剖视图和投影视图。

主视图主视图是指将物体在三个主要投影面上的投影呈现出来的一种视图。

主视图包括前视图、俯视图和左视图。

前视图是指物体在前方投影面上的投影，能够表达物体的前方形状和尺寸。

俯视图是指物体在上方投影面上的投影，能够表达物体的上方形状和尺寸。

左视图是指物体在左侧投影面上的投影，能够表达物体的左侧形状和尺寸。

主视图通常以正交投影的方式呈现，即投影线与投影面相互垂直。

剖视图是指将物体通过截面呈现出来的一种视图。

在剖视图中，物体被切割，并将切面投影到投影面上。

剖视图能够表达物体的内部结构和细节。

剖视图常用于显示物体的内部零部件和装配方式，便于理解和分析。

投影视图投影视图是指将物体在其他投影面上的投影呈现出来的一种视图。

第二章立体的投影§2—1 liti表面上的点与线立体由其表面所围成，可分为两类：表面都是平面的平面立体和表面是曲面或曲面与平面的曲面立体。

一、平面立体平面立体由若干多边形所围成，因此，绘制平面立体的投影，可归结为绘制它的所有多边形表面的投影，也就是绘制这些多边形的边和顶点的投影。

多边形的边是平面立体的轮廓线，分别是平面立体的每两个多边形表面的交线。

当轮廓线的投影为可见时，画粗实线；不可见时，画虚线；当粗实线与虚线重合时，应画粗实线。

工程上常用的平面立体是棱柱和棱锥(包括棱台)。

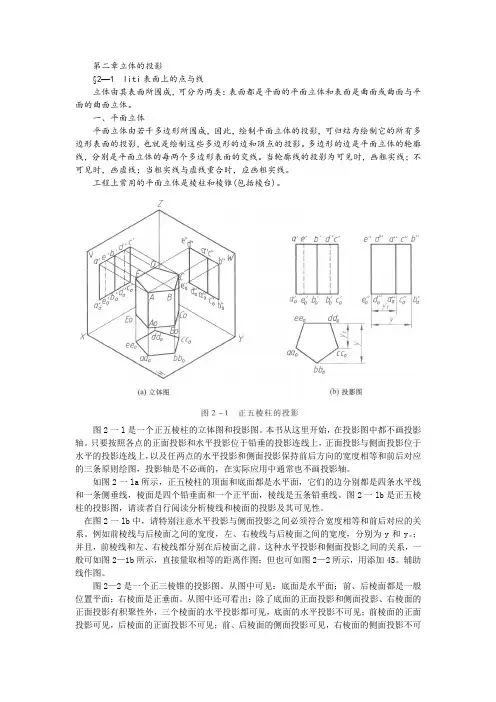
图2一l是一个正五棱柱的立体图和投影图。

本书从这里开始，在投影图中都不画投影轴。

只要按照各点的正面投影和水平投影位于铅垂的投影连线上，正面投影与侧面投影位于水平的投影连线上，以及任两点的水平投影和侧面投影保持前后方向的宽度相等和前后对应的三条原则绘图，投影轴是不必画的，在实际应用中通常也不画投影轴。

如图2一la所示，正五棱柱的顶面和底面都是水平面，它们的边分别都是四条水平线和一条侧垂线，棱面是四个铅垂面和一个正平面，棱线是五条铅垂线。

图2一lb是正五棱柱的投影图，请读者自行阅读分析棱线和棱面的投影及其可见性。

在图2一lb中，请特别注意水平投影与侧面投影之间必须符合宽度相等和前后对应的关系。

例如前棱线与后棱面之间的宽度，左、右棱线与后棱面之间的宽度，分别为y和y。

；并且，前棱线和左、右棱线都分别在后棱面之前。

这种水平投影和侧面投影之间的关系，一般可如图2—1b所示，直接量取相等的距离作图；但也可如图2—2所示，用添加45。

辅助线作图。

图2—2是一个正三棱锥的投影图。

从图中可见：底面是水平面；前、后棱面都是一般位置平面；右棱面是正垂面。

从图中还可看出：除了底面的正面投影和侧面投影、右棱面的正面投影有积聚性外，三个棱面的水平投影都可见，底面的水平投影不可见；前棱面的正面投影可见，后棱面的正面投影不可见；前、后棱面的侧面投影可见，右棱面的侧面投影不可见。

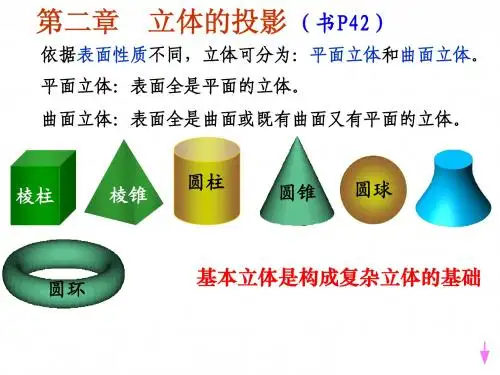
第四章立体的投影根据围成立体的表面不同，我们可将立体作如下分类：1．平面立体：棱柱、棱锥、棱台2．曲面立体：一般曲面体，回转体（圆柱、圆锥、圆台、球、圆环等）§4-1 平面立体的投影及其表面取点由于平面立体的表面均为平面，各表面相交形成棱线．．，故可将绘制平面立体的投影归结为绘制其各表面的投影；或者归结为绘制各棱线及各顶点的投影。

平面立体投影的作图原则：1. 分别作出各顶点的三面投影，然后依次连接同面相邻的点。

2. 可见棱线用粗实线绘制，不可见棱线用细实线绘制。

一．棱柱（一）棱柱的三面投影1．投影分析分析各条棱线的位置。

2．作图步骤（1）先画对称线；（2）再画积聚投影；（二）棱柱表面上取点基本思路：1. 点与表面有从属关系。

2. 从积聚投影出发。

3. 注意点的可见性分析。

二．棱锥（一）棱锥的投影1．投影分析底面为水平面；三个侧棱面为一般位置平面和侧垂面；分析各条棱线的位置。

2．作图步骤（1）先画底面的水平投影和另两个投影；（2）再画出锥顶的三面投影；（3）连接锥顶和底面三个顶点的同面投影。

（二）棱锥表面上取点基本思路：1. 点与表面有从属关系。

2. 先作辅助线的投影，再作点的投影。

3. 判断可见性：可见面上的点即可见。

辅助线作法：1.过顶点和欲求点作辅助线，并延长至底边（点从属辅助线）。

2.过欲求点作底边的平行线（利用平行性）。

三．棱台棱台为截去顶部的棱锥，作图方法与棱锥类似。

（一）作图步骤：1．画顶面和底面的三面投影；2．连接顶面和底面的顶点的同面投影。

（二）表面取点作辅助线：方法与棱锥相同，但由于棱台没有顶点，多作底边的平行线。

§4-2 回转体的投影及其表面取点、线工程上最常见的曲面立体是回转体。

回转体的形成：由母线（直线或曲线）绕其轴线旋转而成。

回转体的特性：母线的任一具体位置称为素线；母线上各点的运动轨迹皆为垂直于轴线的圆——纬圆一．圆柱(直母线∥轴线)（一）圆柱的投影1．投影分析（1）圆（2）圆圆柱面为铅垂面；（3）水平投影积聚；正面和侧面投影画出圆柱面的最大轮廓线（最左、最右、最前、最后素线）2．作图步骤（1）先画轴线；（2）再画积聚性的投影（圆）；（3）根据投影关系画出其它两个投影（同样大小的矩形）。

第2章立体的投影2.1 立体及其表面上的点与线立体由其表面所围成，可分为两类：表面都是平面的平面立体和表面是曲面或曲面与平面的曲面立体。

一、平面立体平面立体由若干多边形所围成，因此，绘制平面立体的投影，可归结为绘制它的所有多边形表面的投影，也就是绘制这些多边形的边和顶点的投影。

多边形的边是平面立体的轮廓线，分别是平面立体的每两个多边形表面的交线。

当轮廓线的投影为可见时，画粗实线；不可见时，画虚线；当粗实线与虚线相重合时，应画粗实线。

常见的平面立体有棱柱和棱锥。

1、棱柱2、棱锥平面立体的投影的外围轮廓总是可见的，应画粗实线；而在投影的外围轮廓内部的图线，则应根据线、面的投影分析，按前遮后、上遮下、左遮右直接判断投影的可见性，决定画粗实线或虚线，必要时还可利用交叉两直线的重影点的可见性进行判断。

二、曲面立体曲面立体由曲面或曲面与平面所围成。

有的曲面立体有轮廓线，即表面之间的交线，如圆柱；有的曲面立体有尖点，如圆锥；有的曲面立体全部由光滑的曲面所围成，如圆球。

在画曲面立体的投影时，除了画出轮廓线和尖点外，还要画出曲面投影的转向轮廓线。

曲面立体的转向轮廓线是切于曲面的诸投射线与投影面的交点的集合，也就是这些投射线所组成的平面或柱面与曲面的切线的投影，常常是曲面的可见投影和不可见投影的分界线。

曲面立体的投影就是它的所有曲面表面或曲面表面与平面表面的投影，也就是曲面立体的轮廓线、尖点的投影和曲面投影的转向轮廓线。

常见的曲面立体有圆柱、圆锥、圆球，圆环。

1、圆柱圆柱由圆柱面、顶面和底面所围成。

圆柱面由直线绕与它平行的轴线旋转而成。

因此，画圆柱的投影就是画顶面和底面及轮廓线、圆柱面投影的转向轮廓线、轴线。

当圆柱的轴线与投影面垂直时，圆柱面在轴线垂直的投影面上的投影具有积聚性。

因此，作圆柱表面2、 圆锥圆锥由圆锥面和底面所围成。

圆锥面由直线绕与它相交的轴线旋转而成。

因此，画圆锥的投影就是画尖点（即锥顶）、底面及轮廓线、圆锥面投影的转向轮廓线、轴线。