2013年北京二模数学几何综合题汇编(无需编辑)

2013朝阳中考数学二模试题及答案北京市朝阳区九年级综合练习（二）数学试卷2013.6学校班级姓名考生须知1．本试卷共6页，共五道大题，25道小题，满分120分. 考试时间120分钟.2．在试卷和答题卡上准确填写学校名称、班级、姓名和准考证号.3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效.4．在答题卡上，选择题、作图题用2B铅笔作答，其它试题用黑色字迹签字笔作答. 5．考试结束，将本试卷、答题卡和草稿纸一并交回.一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的．1．-2的绝对值是A．-2 B．12-C．12D．22．我国质检总局规定，针织内衣等直接接触皮肤的制品，每千克的衣物上甲醛含量应在0.000075千克以下．将0.000075用科学记数法表示为 A ．57.510 B.57.510C ．40.7510D.675103．如图，在△ABC 中，DE ∥BC ,如果AD =3，BD =5，那么DE BC的值是 A. 35 B.925C. 38D. 584．从分别标有1到9数字的9张卡片中任意抽取一张，抽到所标数字是3的倍数的概率为A ．19B ．18C ．29 D ．135．如图，圆锥的底面半径OA 为2，母线AB 为3，则这个圆锥的侧面积为A.3πB. 6πC. 12πD. 18π6．如图，下列水平放置的几何体中，主视图不．E DAB O二、填空题（本题共16分，每小题4分） 9．在函数23yx 中，自变量x 的取值范围是 ．10．分解因式：32242xx x= ．11．如图，在⊙O 中，直径CD AB 于点E ，点F 在弧AC 上，若∠BCD ＝32°，则∠AFD 的度数为 ． 12．如图，在平面直角坐标系xOy 中，直线AB与x 、y 轴分别交于点A 、B ，且A (-2，0)，B (0，1)，在直线 AB 上截取BB 1=AB ，过点B 1分别作x 、y 轴的垂线，垂足分别为点A 1 、C 1，得到矩形OA 1B 1C 1；在直线 AB 上截取B 1B 2= BB 1，过点B 2分别作x 、y 轴的垂线，垂足分别为点A 2 、C 2，得到矩形OA 2B 2C 2；在直线 AB 上截取B 2B 3= B 1B 2，过点B 3分别作x 、y 轴的垂线，垂足分别为点A 3 、yxA 2A 3C 3C 2A 1C 1O B3B 2B 1BAC 3，得到矩形OA 3B 3C 3；……则第3个矩形OA 3B 3C 3的面积是 ；第n 个矩形OA n B n C n 的面积是 （用含n 的式子表示，n 是正整数）．三、解答题（本题共30分，每小题5分） 13．计算：()219342452-⎛⎫︒ ⎪⎝⎭．14．计算：2312()111x x x -÷-+-　．15．如图，为了测量楼AB 的高度，小明在点C 处测得楼AB 的顶端A 的仰角为30º，又向前走了20米后到达点D ，点B 、D 、C 在同一条直线上，并在点D 测得楼AB 的顶端A 的仰角为60º，求楼AB 的高．16．已知：如图，E 、F 为BC 上的点，BF=CE ，点A 、D 分别在BC的两侧，且AE ∥DF ，AE =DF ． 求证：AB ∥CD ．17．如图，在平面直角坐标系xOy 中，一次函数y kx=－2的图象与x 、y 轴分别交于点A 、B ，与反比例函数32y x =-（x ＜0）的图象交于点y MFDBE3()2M n -，．（1）求A 、B 两点的坐标；（2）设点P 是一次函数y kx =－2图象上的一点，且满足△APO 的面积是△ABO 的面积的2倍，直接写出点P 的坐标．18．某新建小区要铺设一条全长为2200米的污水排放管道，为了尽量减少施工对周边居民所造成的影响，实际施工时，每天铺设的管道比原计划增加10%，结果提前5天完成这一任务，原计划每天铺设多少米管道？四、解答题（本题共20分，每小题5分） 19．如图，在平行四边形ABCD 中，AD = 4，∠DFAB =105º，E 是BC 边的中点，∠BAE =30º，将△ABE 沿AE 翻折，点B 落在点F 处，连接FC ，求四边形ABCF 的周长．20．如图，在△ABC 中，AC=BC ，D 是BC 上的一点，且满足∠BAD ＝12∠C ，以AD 为直径的⊙O 与AB 、AC 分别相交于点E 、F .（1）求证：直线BC 是⊙O 的切线；（2）连接EF ，若tan ∠AEF ＝43，AD ＝4，求BD 的长.21．今年“五一”假期，小翔参加了学校团委组织的一项社会调查活动，了解他所在小区家庭的教育支出情况．调查中，小翔从他所在小区的500户家庭中，随机调查了40个家庭，并将调查结果制成了部分统计图表．F EOB（注：每组数据含最小值，不含最大值）根据以上提供的信息，解答下列问题：（1）频数分布表中的a = ，b = ；（2）补全频数分布直方图；（3）请你估计该小区家庭中，教育支出不足1500元的家庭大约有多少户？分组频数 频率1100~13002 0.050 1300~15006 0.150 1500~170018 0.450 1700~19009 0.225 1900~2100a b 2100~23002 0.050合计401.0004 8 12 16 20 (户(元)教育支出频教育支出频数22．阅读下列材料：小华遇到这样一个问题，如图1, △ABC 中，∠ACB =30º，BC =6，AC =5，在△ABC 内部有一点P ，连接PA 、PB 、PC ，求PA +PB +PC的最小值．小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分离，然后再将它们连接成一条折线，并让折线的两个端点为定点，这样依据“两点之间，线段最短”，DABP图2AB图3ACB P图1就可以求出这三条线段和的最小值了．他先后尝试了翻折、旋转、平移的方法，发现通过旋转可以解决这个问题．他的做法是，如图2，将△APC 绕点C顺时针旋转60º，得到△EDC，连接PD、BE，则BE的长即为所求．（1）请你写出图2中，PA+PB+PC的最小值为；（2）参考小华的思考问题的方法，解决下列问题：①如图3，菱形ABCD中，∠ABC=60º，在菱形ABCD内部有一点P，请在图3中画出并指明长度等于PA+PB+PC最小值的线段（保留画图痕迹，画出一条即可）；②若①中菱形ABCD的边长为4，请直接写出当PA+PB+PC值最小时PB的长．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．已知关于x的一元二次方程x2 (4 m)x 1 m = 0．（1）求证：无论m取何值，此方程总有两个不相等的实数根；（2）此方程有一个根是 3，在平面直角坐标系xOy中，将抛物线y x2 (4 m)x 1 m向右平移3个单位，得到一个新的抛物线，当直线y x b与这个新抛物线有且只有一个公共点时，求b的值．24．如图，在平面直角坐标系xOy中，抛物线y ax 2 bx 4与x 轴交于点A ( 2，0)、B (6，0)，与y 轴交于点C ，直线CD ∥x轴，且与抛物线交于点D ，P 是抛物线上一动点．（1）求抛物线的解析式；（2）过点P 作PQ ⊥CD 于点Q ，将△CPQ绕点C 顺时针旋转，旋转角为α（0º﹤α﹤90º），当cos α=35，且旋转后点P 的对应点'P 恰好落在x 轴上时，求点P 的坐标．y xBAD C O备用图yxBA D CO25. 在□ABCD 中，E 是AD 上一点，AE =AB ，过点E 作直线EF ，在EF 上取一点G ，使得∠EGB =∠EAB ，连接AG .（1）如图1，当EF 与AB 相交时，若∠EAB =60°，求证：EG =AG +BG ；（2）如图2，当EF 与AB 相交时，若∠EAB =α（0º﹤α﹤90º），请你直接写出线段EG 、AG 、BG 之间的数量关系（用含α的式子表示）；（3）如图3，当EF 与CD 相交时，且∠EAB =90°，请你写出线段EG 、AG 、BG 之间的数量关系，并证明你的结论.图DG图DG F图DA GF北京市朝阳区九年级综合练习（二）数学试卷参考答案2013.6一、选择题（本题共32分，每小题4分） 题号 1 2 3 4 5 6 7 8 答案 DBCDBBCA二、填空题（本题共16分，每小题4分） 9. x ≥23 10. 22(1)x x 11. 32° 12.24，2n 2+2n三、解答题（本题共30分，每小题5分） 13. 解：)219342452-⎛⎫︒⎪⎝⎭24312……………………………………………………4分1. ………………………………………………………………………5分14. 解：2312111x x x()()3(1)11(1)1(1)x x x x x x ⎡⎤++=-⎢⎥+-+-⎣⎦221x ………………………………2分()()2242111x x x x +=÷+--…………………………………………………………………3分()()()()1124112x x x x x +-+=⋅+-…………………………………………………………4分2x =+.……………………………………………………………………………………5分15. 解： 由题意可知∠ACB =30°，∠ADB =60°，CD =20，在Rt △ABC 中，()3tan 30=20AB BC BD =⋅︒+.………………………………1分在Rt △ABD 中，tan 60=3AB BD BD =⋅︒………………………………………2分∴()3BD BD +，……………………………………203……………………3分∴BD=.………………………………………………10…………………………4分∴AB=.……………………………………………103………………………5分16. 证明：∵AE∥DF，∴∠AEB＝∠DFC. ………………………………………………………………1分∵BF=CE，∴BF+EF＝CE+EF.即BE＝CF. ………………………………………………………………………2分在△ABE和△DCF中，AE DFAEB DFCBE CF∴△ABE≌△DCF. ………………………………………………………………3分 ∴∠B =∠C . ………………………………………………………………………4分∴AB ∥CD . … ……………………………………………………………………5分17. 解：（1）∵点3()2M n -，在反比例函数32y x =-（x ＜0）的图象上，∴1n .…………………………………………………………………………1分∴3()2M -，1. ∵一次函数y kx =－2的图象经过点3()2M -，1，∴3122k . ∴2k .∴一次函数的解析式为22y x =--. ∴A (-1，0)，B (0，-2) . ………………………………………………………3分（2）P 1(-3，4)，P 2(1，-4) . ………………………………………………………5分18. 解：设原计划每天铺设x 米管道．…………………………………………………1分由题意，得220022005(110%)x x=++ ……………………………………………3分解得40x =． ……………………………………………………………4分经检验40x =是原方程的根． …………………………………………………5分答：原计划每天铺设40米管道．四、解答题（本题共20分，每小题5分） 19．解：作BG ⊥AE ，垂足为点G ， ∴∠BGA ＝∠BGE ＝90º.在平行四边形ABCD 中，AD = 4，∵E 是BC 边的中点， ∴11 2.22BE EC BC AD ====……………………………………………………1分∵∠BAE =30º，∠ABC =105º， ∴∠BEG =45º.由已知得△ABE ≌△AFE .∴AB =AF ，BE ＝FE ，∠BEF =90º. 在Rt △BGE 中， BG ＝GE 2.……… ………………………………………………………………2分在Rt △ABG 中， ∴AB =AF =2 2.………………………………………………………………………3分在Rt △ECF 中，222 2.FC EF EC =+= ………………………………………………… ……4分∴四边形ABCF 的周长4 2.+……………………………………………………5分20. （1）证明：在△ABC 中，∵AC=BC ，∴∠ CAB = ∠B .∵∠ CAB +∠B +∠C ＝180º，GFC B∴2∠B+∠C＝180º.∴1B C＝290º. ……………………………………………………1分∵∠BAD＝1∠C，2∴B BAD＝90º.∴∠ADB＝90º.∴AD⊥BC.∵AD为⊙O直径的，∴直线BC是⊙O的切线.…………………………………………………2分（2）解：如图，连接DF，∵AD是⊙O的直径，∴∠AFD = 90º. ……………………………………………………………………3分∵∠ADC＝90º，∴∠ADF+∠FDC＝∠CD+∠FDC＝90º.∴∠ADF＝∠C. …………………………………………………………………4分∵∠ADF ＝∠AEF ，tan ∠AEF ＝43， ∴tan ∠C ＝tan ∠ADF ＝43在Rt △ACD 中，设AD ＝4x ，则CD ＝3x .∴225.AC AD DC x +=∴BC ＝5x ，BD ＝2x . ∵AD ＝4， ∴x ＝1. ∴BD ＝2. …………………………………………………………………………5分 21．解：（1）a =3，FE OBb=0.075；……………………………………………………………2分（2）………………………3分（3）500(0.050.15)100⨯+=.所以该小区家庭中，教育支出不足1500元的家庭大约有100户.…………5分21．解：（1）61………………………………………………………………………………1分A（2）①如图，…………………………………………2分BD；……………………………………………………………………………3分(343. …………………………………………………………………………5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23. （1）证明：∵△=()()2---.………………………………………441m m………1分=2412-+m m=()228m-+…………………………………………………………2分∴△＞0.…………………………………………………………………3分∴无论m 取何值，方程总有两个不相等的实数根.（2）把x =-3代入原方程，解得m =1. …………………………………………………4分∴23y x x=+.即23924y x ⎛⎫=+-⎪⎝⎭.依题意，可知新的抛物线的解析式为239'24y x ⎛⎫=--⎪⎝⎭. ………………………5分即2'3y xx=+∵抛物线'y 与直线y x b =+只有一个公共点，∴23x x x b-=+..…………………………………………………………………6分即240xx b --=. ∵△=0. ∴()()2440b --⨯-=.解得b =-4. ……………………………………………………………………7分 24. 解：（1）根据题意得424036640a b a b -+=⎧⎨++=⎩，．…………………………………………………………1分 解得1343a b ⎧=-⎪⎪⎨⎪=⎪⎩，．所以抛物线的解析式为214433y x x =-++.………………………………2分（2）如图1，过点Q 的对应点'Q 作EF ⊥CD 于点E ，交x 轴于点F .设P (x ，y )，则CQ = x ，PQ =4- y . 由题意可知'CQ = CQ = x ，''P Q =PQ =4-y ，∠CQP =∠C ''Q P =90°.∴'''''QCQ CQ E P Q F CQ E ∠+∠=∠+∠=90°. ∴'''P Q F QCQ α∠=∠=.……………………………………………………3分又∵cos α=35，∴4'5EQ x =　，3'(4)5FQ y =-.y EQCP∴43(4)455x y +-=. ∵214433y xx =-++， 整理可得2145x=.∴125x =225x=-.∴85-8(25P ，.………………………………………………………………5分 如图2，过点Q 的对应点'Q 作EF ⊥CD 于点E ，交x 轴于点F .设P (x ，y )，则CQ =- x ，PQ =4- y . 可得'''P Q F QCQ α∠=∠=.……………………………………………………6分又∵cos α=35，∴4'5EQ x =-　，3'5FQ =. ∴434(4)55x y -+=-. ∵214433y xx =-++， 整理可得2145x=.∴125x =，225x =-∴yxEF P'Q'BAQ DC OP85+8(25P -，.……………………………………………………………7分∴85-8(25)P ，或85+8(25P -，.25. 解：（1）证明：如图，作∠GAH =∠EAB 交GE 于点H .∴∠GAB =∠HAE . ………………………………………………………………1分∵∠EAB =∠EGB ，∠APE =∠BPG ， ∴∠ABG =∠AEH. ∵又AB =AE ，∴△ABG ≌△AEH . ………………2分∴BG =EH ，AG =AH . ∵∠GAH =∠EAB =60°， ∴△AGH 是等边三角形. ∴AG =HG . ∴EG=AG +BG . …………………………………………………………………3分PH D G F(2) 2sin .2EG AG BG α=+…………………………………………………………5分（3）2.EG AG BG -……………………………………………………………6分如图，作∠GAH =∠EAB 交GE于点H .∴∠GAB =∠HAE .∵∠EGB =∠EAB =90°， ∴∠ABG +∠AEG =∠AEG +∠AEH =180°.∴∠ABG =∠AEH .∵又AB =AE ，∴△ABG ≌△AEH . ………………7分∴BG =EH ，AG =AH .∵∠GAH =∠EAB =90°， ∴△AGH 是等腰直角三角形. 2=HG . ∴HEDG-…………………………………………EG AG BG2.………………8分说明：各解答题其它正确解法请参照给分.九年级数学试卷第31页（共6页）。

北京市通州区2013年初三二模试卷数 学 2013. 5.27一、选择题（本题共24分，每小题3分）在每道小题给出的四个备选答案中，只有一个是符合题目要求的，请将所选答案前的 字母按规定要求填在答题纸第1-8题的相应位置上． 1．5-的绝对值是A ．-5B ．5C ．15- D ．152．节约是一种美德，节约是一种智慧．据不完全统计，全国每年浪费食物总量折合粮食可养活约3亿5千万人．将数350000000用科学记数法表示为A ．35 ⨯ 107B ．3.5⨯ 108C ．0.35⨯ 109D ． 3.5 ⨯ 1093．如图，在△ABC 中，DE ∥BC ，若AD ∶DB=2∶1，则AE ∶EC 的值是A ．1∶2B ．1∶3C ．2∶3D ． 2∶14. 下列运算中，正确的是A ．43a a -=B ．236a a a = C ．22a a a ÷= D ．()326aa =5． ⊙O 1和⊙O 2的半径分别为3cm 和5cm ，若O 1O 2=8cm ，则⊙O 1和⊙O 2的位置关系是A ．外切B ．相交C ．内切D ．内含 6．已知一个多边形的内角和是它的外角和的3倍，则这个多边形的边数是A ．6B ．8C ．3D ．10 7. 一个盒子中装有四张完全相同的卡片，分别写着2cm ，3cm ，4cm 和5cm ，现随机从盒中任取出三张卡片，以卡片上的数量分别作为三条线段的长度，则这三条线段能构成直角三角形的概率是A ．21B ．31C ．41D ．518．如图，菱形ABCD 和菱形ECGF 的边长分别为3和4，∠A =120°，则图中阴影部分的面积是AB ．349C ．32D ．E DCAG F DA二、填空题（本题共12分，每小题3分）9．分解因式：2312m - = ______．10．已知a b >，则12a c +_________12b c +．(填“>”、“<”或“=”) 11()210y += ，则yx = .12. 如图，Rt △ABC 中，∠BAC =90°，AB =3，AC =4，点P 为BC 上一动点，连接P A ，以P A ，PC 为邻边作平行四边形P AQC ，连接PQ ，则PQ 的最小值为 .三、解答题（本题共30分，每小题5分） 13()01 3.142cos 45π---︒．14．已知：如图点C E B F ，，，在同一直线上，AC DF ∥,AC DF =，CB FE =．求证：△ABC ≌△DEF .15.已知221a a +=-，求()()()2122a a a a +--+的值．16．用配方法解方程：2410x x -+=.17.如图，在□ABCD 中，E 是对角线AC 的中点，EF ⊥AD 于F ，∠B=60°，AB=4，∠ACB=45°，求DF 的长．FEDCBAFEDBAQP C18. 如图，在直角坐标系xoy 中，点A 是反比例函数y 1=xk的图象上一点，AB ⊥x 轴的正 半轴于点B ，C 是OB 的中点，一次函数y 2=ax +b 的图象经过A 、C 两点，并交y 轴于 点D (0,－2)，若S △AO D =4. （1）求反比例函数和一次函数的表达式；（2）观察图象，请指出在y 轴的右侧，当y 1＞y 2时x 的取值范围.四、解答题（本题共19分，第19题7分,第20题6分,第21题6分）19. 小明参加班长竞选，需进行演讲答辩与民主测评，民主测评时一人一票，按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图.(1)求评委给小明演讲答辩分数的众数，以及民主测评为“良好”票数的扇形圆心角度数； (2)求小明的综合得分是多少？(3)在竞选中，小亮的民主测评得分为82分，如果他的综合得分不小于小明的综合得分，他的演讲答辩得分至少要多少分？20．如图，AB 是⊙O的直径，弦DE 垂直平分半径OA ，C 为垂足，DE ＝3，连接BD ，过点E 作EM ∥BD ，交BA 的延长线于点M ． (1) 求证：EM 是⊙O 的切线；(2) 若弦DF 与直径AB 相交于点P ，当∠APD ＝45º时，求图中阴影部分的面积．y xO DC B A民主测评票数统计图良好优秀70％一般10％演讲答辩评委评分统计图21. 已知关于x 的一元二次方程2(3)3=0mx m x +++. （1）求证：方程有两个实数根；（2）当此方程有一个根是3时，求关于x 的二次函数2(3)3y mx m x =+++的表达式； （3）在（2）的条件下，若点A 1()x n ，与点B 2()x n ，(12x x ≠)在关于x 的二次函数2(3)3y mx m x =+++的图象上，将此二次函数的图象在AB 上方的部分沿AB 翻折，图象的其它部分保持不变，得到一个新图象，当这个新图象与x 轴恰好只有两个公共点时，n 的取值范围是_________________________________________.五、解答题（本题共15分，第22题7分,第23题8分）22. 如图，点O 是等边ABC △内一点，β=∠AOB , α=∠BOC ．将B O C △绕点C 按顺时针方向旋转60得ADC △，连接OD ．（1）当=110β,150α=时，试判断AOD △（2）请写出AOD △是等边三角形时α 、β的度数.α= 度； β= 度.（3）探究：若=110β，则α为多少度时，AOD △是等腰三角形？（只要写出探究结果）α= ；23.已知抛物线y =a （x ﹣m ）2+n 与y 轴交于点A ，它的顶点为点B ，点A 、B 关于原点O的对称点分别为C 、D ．若A 、B 、C 、D 中任何三点都不在一直线上，则称四边形ABCD 为抛物线的伴随四边形，直线AB 为抛物线的伴随直线．（1）如图1，求抛物线y =（x ﹣2）2+1的伴随直线的表达式．（2）如图2，若抛物线y =a （x ﹣m ）2+n （m ＞0）的伴随直线是y =x ﹣3，伴随四边形的面积为12，求此抛物线的表达式．（3）如图3，若抛物线y =a （x ﹣m ）2+n 的伴随直线是y =﹣2x +b （b ＞0），且伴随四边形ABCD 是矩形．用含b 的代数式表示m 、n 的值.图3Ox y y x O 图2图1ABC D O x y通州区初三数学毕业考试参考答案及评分标准2013．5 一、选择题：1．B 2．B 3．D 4．D 5．A 6．A 7．C 8．C 二、填空题：9.()()322m m +-； 10.>； 11. 12； 12. 125；三、解答题：()01 3.142cos 45π---︒13. 解：原式=1122--⨯， ……………… 4分； =11-，=2- . ……………… 5分. 14. 证明： ∵AC DF ∥，∴C F ∠=∠， ……………… 1分；在△ABC 和△DEF 中∵ .AC DF C F CB FE =⎧⎪∠=∠⎨⎪=⎩，， ……………… 4分；∴△ABC ≌△DEF . ……………… 5分. 15． 解：原式=()()()2122a a a a +--+，=()22224a a a +--， ……………… 2分； =22224a a a +-+，=224a a ++. ……………… 3分；FECBA由221a a +=-，∴原式=143-+=. ……………… 5分.16. 解：241x x -=-， .................. 1分； 24414x x -+=-+， (2)分；()223x -=， (3)分；2x -= ……………… 4分；2x =， (5)分.∴12x =22x =17. 解:过点C 作CG AD ⊥于点G . ……………… 1分；∵四边形ABCD 是平行四边形，∴60D B ∠=∠=，4CD AB ==，AD ∥BC ，∴45CAD ACB ∠=∠=，在Rt △CGD 中，90CGD ∠=o，4CD =， ∴ sin GCCDG CD∠=， ∴sin 604GC ==o， ∴GC = ……………… 2分； ∴ 2GD =，在Rt △CGA 中，90CGA ∠=o，45CAD ∠=o，∴AG CG == ……………… 3分； ∵ E 是AC 的中点，EF ⊥AD ，CG AD ⊥GFE DBA∴AF FG == ……………… 4分；∴2DF FG GD =+=+ ……………… 5分.18.解：（1）过点A 作AE y ⊥轴于点E .∵S △AO D =4，D (0,－2)∴142OD AE ⨯⨯=， ∴1242AE ⨯⨯=， ∴4AE =， ……………… 1分；∵AB ⊥x 轴，y 轴⊥x 轴， ∴四边形AEOB 是矩形，∴4OB AE ==，∵C 是OB 的中点， ∴2OC =，∴C (2，0)， ……………… 2分； ∵一次函数y 2=ax +b 的图象经过C 、D 两点， ∴202a b b +=⎧⎨=-⎩，，解得：12a b ⎧⎨=-⎩=，，∴一次函数的表达式为22y x =-. ……………… 3分； 当4x =时，2422y =-=， ∴A (4，2)，∵点A 是反比例函数y 1=xk的图象上一点， ∴8k =，EyxO DC B A∴反比例函数的表达式为18y x=. ……………… 4分； (2)当y 1＞y 2时，x 的取值范围为04x <<. ……………… 5分. 四、解答题19. （1）94，72o……………… 2分； （2）()19594929094935++++=，. ……………… 3分；70％×50×2+20％×50×1=80， ……………… 4分； 小明的综合得分是93×0.4+80×0.6=85.2 . ……………… 5分； (3) 设小亮的演讲答辩得分为x 分，根据题意得：0.4820.685.2x +⨯≥， ……………… 6分； 解得：90x ≥，演讲答辩得分至少要90分. ……………… 7分.20．(1)证明：连接OD 、OE .∵AB 是⊙O 的直径，弦DE 垂直平分半径OA ，∴»»AD AE =，1122OC OD OE ==， ∴ 60DOC EOC ∠=∠=，………………1分；∴1302B DOC ∠=∠=， ∵EM ∥BD ，∴30M B ∠=∠=， ……………… 2分； ∴306090M EOC ∠+∠=+=，∴90MEO ∠=，∴EM 是⊙O 的切线. ……………… 3分； (2) 连接OF .∵AB 是⊙O 的直径，弦DE 垂直平分半径OA ，∴1322DC CE DE ===， 在Rt △COE 中，sin CEEOC OE ∠=，sin 3260OE ==∴OE = ……………… 4分；∵∠APD ＝45º，∠DCP ＝90º， ∴∠CDP ＝45º，∵»»EFEF =， ∴∠EOF ＝90º， ……………… 5分；∴图中阴影部分的面积是211334242EOFEOF S Sππ-=-=-扇形. ……………… 6分.21. 已知关于x 的一元二次方程2(3)3=0mx m x +++. （1）求证：方程有两个实数根；证明：△=()2343m m +-⨯， ……………… 1分； =26912m m m ++-，=()230m -≥. ……………… 2分； ∴方程有两个实数根.（2）当此方程有一个根是3时，求关于x 的二次函数2(3)3y mx m x =+++的表达式； 解：当3x =时，()93330m m +++=，∴1m =-. ……………… 3分； ∴223y x x =-++. ……………… 4分； （3）n 的取值范围是24n <<，0n =. ……………… 6分.22. （1）结论：AOD △是直角三角形，证明：由题意可得：△ACD ≌△BCO , 60OCD ∠=， ∴CO =CD ，150ADC α∠=∠=，∴△OCD 是等边三角形， ……………… 1分；∴60CDO ∠=，∴1506090ADO ADC CDO ∠=∠-∠=-=， ……………… 2分； ∴AOD △是直角三角形.（2）α= 120 度； β= 120 度. ……………… 4分； （3） （只要写出探究结果）α= 125 或110或 140； ……………… 7分. 23.解：（1）由题意可知：A (0，5)，B (2，1)， ……………… 1分； 设伴随直线AB 的表达式为y kx b =+，∴215k b b +=⎧⎨=⎩，，解得25k b =-⎧⎨=⎩，，∴抛物线y =（x ﹣2）2+1的伴随直线的表达式为25y x =-+. …… 2分； （2）令0x =，得3y =-，∴A (0，-3)，由题意可知：顶点B (m ，n )在伴随直线y =x ﹣3上， ∴n =m -3，∴B (m ，m-3)， ……………… 3分； ∵点A 、B 关于原点O 的对称点分别为C 、D ， ∴C (0，3) ，D (-m ，-m+3)， 过点B 作BE y ⊥轴于点E . ∵ m ＞0， ∴ BE m =，∵伴随四边形ABCD 的面积为12， ∴12122AC BE ⨯⨯⨯=，y=x-3E yxODCBA图2∴612m =，∴2m =， ……………… 4分； ∴B (2，-1)，∴ ()221y a x =--，把A (0，-3)代入()221y a x =--中， 得：12a =-， ∴抛物线的表达式为()21212y x =---. ……………… 5分；（3）∴伴随直线AB ；y =﹣2x +b （b ＞0）与x 轴、y 轴分别交于点F (2b，0) ，A (0，b )， ∴C (0，-b )∵伴随四边形ABCD 是矩形，∴顶点B (m ，n )在y 轴右侧的直线y =﹣2x +b 上， ∠ABC ＝90º，∴B (m ，-2m+b )，过点B 作BE y ⊥轴于点E . ∴E (0，-2m+b )， ∴tan OF BAE OA ∠==tan CECBE BE∠=，或证△ABE ∽△BCE … 6分； ∴222bm b b m-+=， ∴45m b =， ……………… 7分；∴43255n b b b =-⨯+=-. ……………… 8分.注：出现其他解法酌情给分.FE 图3O xyDCBA。

2013年北京市海淀区高考数学二模试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项.1. 集合A ={x|(x −1)(x +2)≤0}，B ={x|x <0}，则A ∪B =( ) A (−∞, 0] B (−∞, 1] C [1, 2] D [1, +∞)2. 已知数列{a n }是公比为q 的等比数列，且a 1⋅a 3=4，a 4=8，则a 1+q 的值为（ ） A 3 B 2 C 3或−2 D 3或−33. 如图，在边长为a 的正方形内有不规则图形Ω．向正方形内随机撒豆子，若撒在图形Ω内和正方形内的豆子数分别为m ，n ，则图形Ω面积的估计值为（ ）Ama nB nam Cma 2nDna 2m4. 某空间几何体的三视图如图所示，则该几何体的表面积为（ ）A 180B 120C 276D 3005. 在四边形ABCD 中，“∃λ∈R ，使得AB →=λDC →，AD →=λBC →”是“四边形ABCD 为平行四边形”的（ ）A 充分而不必要条件B 必要而不充分条件C 充分必要条件D 既不充分也不必要条件6. 用数字1，2，3，4，5组成没有重复数字的五位数，且5不排在百位，2，4都不排在个位和万位，则这样的五位数个数为（ ） A 32 B 36 C 42 D 487. 双曲线C 的左右焦点分别为F 1，F 2，且F 2恰为抛物线y 2＝4x 的焦点，设双曲线C 与该抛物线的一个交点为A ，若△AF 1F 2是以AF 1为底边的等腰三角形，则双曲线C 的离心率为（ ） A √2 B 1+√2 C 1+√3 D 2+√38. 若数列{a n }满足：存在正整数T ，对于任意正整数n 都有a n+T =a n 成立，则称数列{a n }为周期数列，周期为T ．已知数列{a n }满足a 1=m(m >0)，a n+1={a n −1，a n >1，1an，0<a n ≤1，则下列结论中错误的是( )A 若a 3=4，则m 可以取3个不同的值B 若m =√2，则数列{a n }是周期为3的数列 C ∀T ∈N ∗且T ≥2，存在m >1，使得{a n }是周期为T 的数列 D ∃m ∈Q 且m ≥2，使得数列{a n }是周期数列二、填空题：本大题共6小题，每小题5分，共30分. 9. 在极坐标系中，极点到直线ρcosθ=2的距离为________．10. 已知a =ln 12，b =sin 12，c =2−12，则a ，b ，c 按照从大到小排列为________．11. 直线l 1过点(−2, 0)且倾斜角为30∘，直线l 2过点(2, 0)且与直线l 1垂直，则直线l 1与直线l 2的交点坐标为________．12. 在△ABC 中，∠A =30∘，∠B =45∘，a =√2，则b =________；S △ABC =________． 13. 正方体ABCD −A 1B 1C 1D 1的棱长为1，若动点P 在线段BD 1上运动，则DC →⋅AP →的取值范围是________．14. 在平面直角坐标系中，动点P(x, y)到两条坐标轴的距离之和等于它到点(1, 1)的距离，记点P 的轨迹为曲线为W ． (I)给出下列三个结论： ①曲线W 关于原点对称；②曲线W 关于直线y =x 对称；③曲线W 与x 轴非负半轴，y 轴非负半轴围成的封闭图形的面积小于12；其中，所有正确结论的序号是________；(II)曲线W 上的点到原点距离的最小值为________．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15. 已知函数f(x)=1−√2sin(x−π4)．（1）求函数f(x)的定义域； （2）求函数f(x)的单调增区间．16. 福彩中心发行彩票的目的是为了获取资金资助福利事业，现在福彩中心准备发行一种面值为5元的福利彩票刮刮卡，设计方案如下：（1）该福利彩票中奖率为50%；（2）每张中奖彩票的中奖奖金有5元，50元和150元三种；（3）顾客购买一张彩票获得150元奖金的概率为p ，获得50元奖金的概率为2%．（1）假设某顾客一次性花10元购买两张彩票，求其至少有一张彩票中奖的概率； （2）为了能够筹得资金资助福利事业，求p 的取值范围．17. 如图1，在直角梯形ABCD 中，∠ABC =∠DAB =90∘，∠CAB =30∘，BC =2，AD =4．把△DAC 沿对角线AC 折起到△PAC 的位置，如图2所示，使得点P 在平面ABC 上的正投影H 恰好落在线段AC 上，连接PB ，点E ，F 分别为线段PA ，PB 的中点．（1）求证：平面EFH // 平面PBC ；（2）求直线HE与平面PHB所成角的正弦值；（3）在棱PA上是否存在一点M，使得M到P，H，A，F四点的距离相等？请说明理由．18. 已知函数f(x)=e x，A(a, 0)为一定点，直线x=t(t≠0)分别与函数f(x)的图象和x轴交于点M，N，记△AMN的面积为S(t)．（1）当a=0时，求函数S(t)的单调区间；（2）当a>2时，若∃t0∈[0, 2]，使得S(t0)≥e，求a的取值范围．19. 已知椭圆M:x2a2+y2b2=1(a>b>0)的四个顶点恰好是一边长为2，一内角为60∘的菱形的四个顶点．（1）求椭圆M的方程；（2）直线l与椭圆M交于A，B两点，且线段AB的垂直平分线经过点(0,−12)，求△AOB（O为原点）面积的最大值．20. 设A是由m×n个实数组成的m行n列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”．（1）数表A如表1所示，若经过两次“操作”，使得到的数表每行的各数之和与每列的各数（2）数表A如表2所示，若必须经过两次“操作”，才可使得到的数表每行的各数之和与每列的各数之和均为非负整数，求整数a的所有可能值；表2（3）对由m×n个实数组成的m行n列的任意一个数表A，能否经过有限次“操作”以后，使得到的数表每行的各数之和与每列的各数之和均为非负整数？请说明理由．2013年北京市海淀区高考数学二模试卷（理科）答案1. B2. D3. C4. B5. C6. A7. B8. D9. 210. c>b>a11. (1,√3)12. 2,√3+1213. [0, 1]14. ②③,2−√215. 解：（1）∵ sin(x−π4)≠0，∴ x−π4≠kπ，k∈Z，则函数的定义域为{x|x≠kπ+π4, k∈Z}；（2）∵ f(x)=1−cos 2x−sin2xsinx−cosx =1+(cosx+sinx)=1+sinx+cosx=1+√2sin(x+π4)，又∵ y=sinx的单调递增区间为(2kπ−π2, 2kπ+π2)，k∈Z，令2kπ−π2<x+π4<2kπ+π2，解得：2kπ−3π4<x<2kπ+π4，又注意到x≠kπ+π4，则f(x)的单调递增区间为(2kπ−3π4, 2kπ+π4)，k∈Z．16. 解：（1）设至少一张中奖为事件A，则P(A)=1−0.52=0.75…（2）设福彩中心卖出一张彩票可能获得的资金为ξ，则ξ可以取5，0，−45，−145…故ξ的分布列为所以ξ的期望为Eξ=5×50%+0×(50%−2%−p)+(−45)×2%+(−145)×p=2.5−90%−145p…所以当1.6−145p>0时，即p<8725…所以当0<p<8725时，福彩中心可以获取资金资助福利事业…17. 解：（1）∵ 点P在平面ABC上的正投影H恰好落在线段AC上，所以PH⊥平面ABC，所以PH⊥AC，∵ 在直角梯形ABCD中，∠ABC=∠DAB=90∘，∠CAB=30∘，BC=2，AD=4，∴ AC=4，∠CAB=60∘，∴ △ADC是等边三角形，故H是AC的中点，∴ HE // PC同理可证EF // PB，又HE∩EF=E，CP∩PB=P，∴ 平面EFH // 平面PBC；（2）在平面ABC内过H作AC的垂线，如图建立空间直角坐标系，则A(0, −2, 0)，P(0, 0, 2√3)，B(√3, 1, 0)因为E(0, −1, √3)，HE →=(0, −1, √3)，设平面PHB 的法向量n →=(x, y, z)， ∵ HB →=(√3, 1, 0)，HP →=(0, 0, 2√3)，∴ {HP →⋅n →=0˙，即{√3x +y =0z =0，令x =√3，则y =−3， ∴ n →=(√3, −3, 0)…8分 cos <n →，HE →>=|n →|⋅|HE →|˙=32×2√3=√34∴ 直线HE 与平面PHB 所成角的正弦值为√34 （3）存在，事实上记点E 为M 即可因为在直角三角形PHA 中，EH =PE =EA =12PA =2在直角△PHB 中，PB =4，EF =12PB =2，所以点E 到P ，H ，A ，F 四点的距离相等 18. 解：（1） 因为S(t)=12|t −a|e t ，其中t ≠a…当a =0，S(t)=12|t|e t ，其中t ≠0当t >0时，S(t)=12te t ，S′(t)=12(t +1)e t ，所以S ′(t)>0，所以S(t)在(0, +∞)上递增，… 当t <0时，S(t)=−12te t ，S′(t)=−12(t +1)e t ，令S′(t)=−12(t +1)e t >0，解得t <−1，所以S(t)在(−∞, −1)上递增令S′(t)=−12(t +1)e t <0，解得t >−1，所以S(t)在(−1, 0)上递减 …综上，S(t)的单调递增区间为(0, +∞)，(−∞, −1)，S(t)的单调递增区间为(−1, 0) （2）因为S(t)=12|t −a|e t ，其中t ≠a 当a >2，t ∈[0, 2]时，S(t)=12(a −t)e t因为∃t 0∈[0, 2]，使得S(t 0)≥e ，所以S(t)在[0, 2]上的最大值一定大于等于e ， S′(t)=−12[t −(a −1)]e t ，令S ′(t)=0，得t =a −1…当a −1≥2时，即a ≥3时S′(t)=−12[t −(a −1)]e t >0对t ∈(0, 2)成立，S(t)单调递增，所以当t =2时，S(t)取得最大值S(2)=12(a −2)e 2令12(a −2)e 2≥e ，解得 a ≥2e +2， 所以a ≥3…当a −1<2时，即a <3时S′(t)=−12[t −(a −1)]e t >0对t ∈(0, a −1)成立，S(t)单调递增，S′(t)=−12[t −(a −1)]e t <0对t ∈(a −1, 2)成立，S(t)单调递减， 所以当t =a −1时，S(t)取得最大值S(a −1)=12e a−1，令S(a −1)=12e a−1≥e ，解得a ≥ln2+2，所以ln2+2≤a <3… 综上所述，ln2+2≤a… 19. 解：（1）因为椭圆x 2a2+y 2b 2=1(a >b >0)的四个顶点恰好是一边长为2，一内角为60∘的菱形的四个顶点，∴ a =√3，b =1，椭圆M 的方程为：x 23+y 2=1...4分（2）设A(x 1, y 1)，B(x 2, y 2)，因为AB 的垂直平分线经过点(0, −12)，显然直线AB 有斜率， 当直线AB 的斜率为0时，AB 的垂直平分线为y 轴，则x 1=−x 2，y 1=y 2， 所以S △AOB=12|2x 1||y 1|=|x 1||y 1|=|x 1|⋅√1−x 123=√x 12(1−x 123)=√13x 12(3−x 12)，∵ √x 12(3−x 12)≤x 12+(3−x 12)2=32，∴ S △AOB ≤√32，当且仅不当|x 1|=√62时，S △AOB 取得最大值为√32...7分 当直线AB 的斜率不为0时，则设AB 的方程为y =kx +t ， 所以{y =kx +tx 23+y 2=1，代入得到(3k 2+1)x 2+6ktx +3t 2−3=0， 当△=4(9k 2+3−3t 2)>0，即3k 2+1>t 2①，方程有两个不同的实数解； 又x 1+x 2=−6kt3k 2+1，x 1+x 22=−3kt3k 2+1...8分所以y 1+y 22=t 3k 2+1，又y 1+y 22+12x 1+x 22−0=−1k ，化简得到3k 2+1=4t②代入①，得到0<t <4，…10分 又原点到直线的距离为d =√k 2+1，|AB|=√1+k 2|x 1−x 2|=√1+k 2⋅√4(9k 2+3−3t 2)3k 2+1，所以S △AOB =12|AB||d|=2√k 2+1√1+k 2⋅√4(9k 2+3−3t 2)3k 2+1，化简得：S △AOB =14√3(4t −t 2)...12分∵ 0<t <4，所以当t =2时，即k =±√73时，S △AOB 取得最大值为√32． 综上，S △AOB 取得最大值为√32...14分法3：改变第1列得：改变第4列得：（写出一种即可） …（2） 每一列所有数之和分别为2，0，−2，0，每一行所有数之和分别为−1，1；则第一行之和为2a −1，第二行之和为5−2a ，{2a −1≥05−2a ≥0，解得a =1，a =2．… ②如果操作第一行则每一列之和分别为2−2a ，2−2a ，2a −2，2a 解得a =1 … 综上a =1 …（3） 证明：按要求对某行（或某列）操作一次时，则该行的行和（或该列的列和） 由负整数变为正整数，都会引起该行的行和（或该列的列和）增大，从而也就使得数阵中mn 个数之和增加，且增加的幅度大于等于1−(−1)=2， 但是每次操作都只是改变数表中某行（或某列）各数的符号，而不改变其绝对值，显然，数表中mn 个数之和必然小于等于∑∑|nj=1m i=1a ij |， 可见其增加的趋势必在有限次之后终止，终止之时必然所有的行和与所有的列和均为非负整数，故结论成立 …。

顺义区2013届初三第二次统一练习数学试卷学校 姓名 准考证号 考生须知1．本试卷共6页，共五道大题，25道小题，满分120分．考试时间120分钟． 2．在试卷和答题卡上准确填写学校名称、姓名和准考证号． 3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答． 5．考试结束，将本试卷、答题卡和草稿纸一并交回．一、选择题（本题共32分，每小题4分） 下面各题均有四个选项，其中只有一个．．是符合题意的． 1．9的算术平方根是A ．9B ．3-C ．3D ． 3± 2．如下书写的四个汉字，其中为轴对称图形的是A ．B ． C. D.3．一副扑克牌，去掉大小王，从中任抽一张，恰好抽到的牌是8的概率是 A ．154B ．113C ．152D ．144．把代数式269ab ab a -+分解因式，下列结果中正确的是A ．2(3)a b +B ．(3)(3)a b b +-C ．2(4)a b -D ．2(3)a b - 5．函数y kx k =-与ky x=（0k ≠）在同一直角坐标系中的图象可能是6．如图，AEBD ∥，1120240∠=∠=°，°，则C ∠的度数是Ａ．10° Ｂ．20° Ｃ．30° Ｄ．40°7．若22a a -=-，则a 的取值范围是A ．2a >B ．0a >C ．2a ≤D ．0a ≤ 8．右图中是左面正方体的展开图的是二、填空题（本题共16分，每小题4分） 9．函数23xy x -=-中，自变量x 的取值范围是 .10．甲、乙两个旅游景点今年5月上旬每天接待游客的人数如图所示，甲、乙两景点日接待游客人数的方差大小关系为：2S 甲 2S 乙．11．若把代数式257x x ++化为2()x m k -+的形式，其中m 、k 为常数，则k m -= .12．正方形111A B C O ， 2221A B C C ,，3332A B C C ， …按如图所示的方式放置．点1A ，2A ，3A ，…和点1C ，2C ，3C …分别在直线(0)y kx b k =+>和x 轴上，已知点1(1,1)B ，2(3,2)B ，则点6B 的坐标是 ， 点n B 的坐标是 ． 三、解答题（本题共30分，每小题5分） 13．计算：201273tan 30()4(32)2-+︒+--．14．解方程：21133x x x-+=--.15．已知220x x +-=，求代数式2(2)(3)(3)(1)x x x x x -++--+的值．A ．B ．C ．D ．A 3A 2A 1B 3B 2B 1C 3C 2C 1Oyx16．已知：如图，在ABC ∆中，AC BC =，90ACB ∠=︒，MN 是过点C 的一条直线，AM MN ⊥于M ，BN MN ⊥于N . 求证: AM CN =17．列方程或方程组解应用题:某企业向四川雅安地震灾区捐助价值17.6万元的甲、乙两种帐篷共200顶，已知甲种帐篷每顶800元，乙种帐篷每顶1000元，问甲、乙两种帐篷各多少顶？18. 如图，在平面直角坐标系xOy 中，一次函数22y x =-+的图象与x 轴相交于点B ，与y 轴相交于点C ，与反比例函数图象相交于点A ，且2AB BC =. (1) 求反比例函数的解析式；（2）若点P 在x 轴上，且APC ∆的面积等于12，直 接写出点P 的坐标．四、解答题（本题共20分，每小题5分）19．已知：如图，四边形ABCD 中，对角线AC 、BD 相交于点E ，90ABC ACD ∠=∠=︒,62AB BC ==,2tan 3CDE ∠=. 求对角线BD 的长和ABD ∆的面积.20．已知：如图，O ⊙是Rt △ABC 的外接圆，∠ABC =90°，点P 是O ⊙外一点，PA 切O ⊙于点A ，且PA=PB ． （1）求证：PB 是O ⊙的切线；（2）已知PA =23，BC =2，求O ⊙的半径．A NMCB EDCBAOABCP21．甲、乙两学校都选派相同人数的学生参加综合素质测试，测试结束后，发现每名参赛学生的成绩都是70分、80分、90分、100分这四种成绩中的一种，并且甲、乙两学校的学生获得100分的人数也相等．根据甲学校学生成绩的条形统计图和乙学校学生成绩的扇形统计图，解答下列问题：（1）求甲学校学生获得100分的人数，并补全统计图；（2）分别求出甲、乙两学校学生这次综合素质测试所得分数的中位数和平均数，以此比较哪个学校的学生这次测试的成绩更好些．22． 问题：如果存在一组平行线a b c ，请你猜想是否可以作等边三角形ABC 使其三个顶点分别在,,a b c 上.小明同学的解答如下：如图1所示，过点A 作AM b ⊥于M ，作60MAN ∠=︒，且AN AM =，过点N 作CN AN ⊥交直线c 于点C ,在直线b 上取点B 使BM CN =，则ABC ∆为所求．(1) 请你参考小明的作法,在图2中作一个等腰直角三角形DEF 使其三个顶点分别在,,a b c 上，点D 为直角顶点；(2) 若直线,a b 之间的距离为1， ,b c 之间的距离为2， 则在图2中，DEF S ∆= ，在图1中，AC = ．甲学校学生成绩的条形统计图乙学校学生成绩的扇形统计图207080134人数分数59010060°90°120°90°100分90分80分70分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．已知抛物线232y x mx =+-．（1）求证：无论m 为任何实数，抛物线与x 轴 总有两个交点；（2）若m 为整数，当关于x 的方程2320x mx +-=的两个有理数根都在1-与43之间 （不包括-1、43）时，求m 的值． （3）在(2）的条件下，将抛物线232y x mx =+-在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新图象G ，再将图象G 向上平移n 个单位，若图象G 与过点（0，3）且与x 轴平行的直线有4个交点，直接写出n 的取值范围是 ．24．如图，直线MN 与线段AB 相交于点O , 点C 和点D 在直线MN 上，且45ACN BDN ∠=∠=︒.(1) 如图1所示，当点C 与点O 重合时 ，且AO OB =，请写出AC 与BD 的数量关系和位置关系；（2）将图1中的MN 绕点O 顺时针旋转到如图2所示的位置，AO OB =，（1）中的AC与BD 的数量关系和位置关系是否仍然成立？若成立，请证明；若不成立，请说明理由； （3）将图2中的OB 拉长为AO 的k 倍得到如图3，求ACBD的值．1xyOABCDEFxyO25． 已知抛物线214y x bx c =-++与x 轴交于,A B 两点，与y 轴交于点C ，连结AC BC ，，D 是线段OB 上一动点，以CD 为一边向右侧作正方形CDEF ，连结BF ．若8O B C S ∆=，AC BC =．（1）求抛物线的解析式； （2）求证：BF AB ⊥； （3）求FBE ∠的度数；（4）当D 点沿x 轴正方向移动到点B 时，点E 也随着运动，则点E 所走过的路线长 是 ．顺义区2013届初三第二次统一练习数学试题参考答案及评分参考一、选择题 号 案二、填空题9. 3x ≠ ； 10．22S S >乙甲 ； 11．134； 12．6(63B ，32) ， 1(21,2)n n n B -- ． 三、解答题13．解：原式=3333443+⨯+- …………………………………………4分 =43 ……………………………………………… 5分 14． 解：方程两边同乘以(3)x -，得， ………………………………………… 1分213x x --=-． ………………………………………… 2分解方程得 2x =． ………………………………………… 3分 当2x =时，30x -≠ ……………………………… 4分所以，原方程的根为2x = …………………………………………5分15．解：原式= 222443(23)x x x x x x -+++---…………………………………… 3分 =22244323x x x x x x -+++-++=27x x ++ ………………………………………… 4分 ∵220x x +-= ， ∴22x x +=∴原式=2+7=9 ………………………………………………5分 16．证明：∵,,AM MN BN MN ⊥⊥∴ 90AMC CNB ∠=∠=︒ ……………………………………………1分90MAC ACM ∠+∠=︒ ∵ 90ACB ∠=︒∴ 90BCN ACM ∠+∠=︒ ∴ MAC BCN ∠=∠在AMC ∆和CNB ∆中∵AMC CNB MAC BCN AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩……………………………………………3分 ∴AMC ∆≌CNB ∆ …………………………………………… 4分 ∴AM CN = ……………………………………………5分17．解：设甲种帐篷x 顶，乙种帐篷y 顶 ……………………………………1分 依题意，得2008001000176000x y x y +=⎧⎨+=⎩ …………………………………3分解以上方程组，得x =120，y =80答：甲、乙两种帐篷分别是120顶和80顶. ………………………………5分18．（1）由已知可得点(1,0)B ，点(0,2)C …………1分 ∴1,2OB CO ==过点A 作AD x ⊥轴于点D∴ BOC ∆∽BDA ∆ …………………2分 ∴12CO OB BC AD DB AB === ∴ 24,22AD CO DB OB ====∴ 点(3,4)A - …………………………3分 设反比例函数解析式为(0)ky k x=≠，点(3,4)A -在图象上， ∴ 12k =-∴ 反比例函数的解析式为12y x=-…………………………………4分 （2） 点(5,0)P 或(3,0)P - ………………………………………………5分 19．解：过点B 作BF AC ⊥于F∵90ABC ACD ∠=∠=︒, 62AB BC ==， ∴ 6BF AF CF === …………………1分 90BFC ACD ∠=∠=︒∴BF ∥CD∴ FBE CDE ∠=∠ …………………… 2分∴ 2tan tan 3FBE CDE ∠=∠= 即23EF BF = ∴ 4EF =∴2,3EC CD == ……………………………3分 ∴222264213BE BF EF =+=+=22222313D E E C C D =+=+=∴313BD BE DE =+= ……………………………………4分(2) 114522ABD ABE ADE S S S AE BF AE CD ∆∆∆=+=⋅+⋅= ……………5分20．解：（1）证明：连接OBOA OB =，PA PB = ∴ OAB OBA ∠=∠，PAB PBA ∠=∠．∴OAB PAB OBA PBA ∠+∠=∠+∠．即PAO PBO ∠=∠． ………………1分 又∵PA 是O ⊙的切线，∴90PAO ∠=°∴90PBO ∠=°∴OB PB ⊥．又∵OB 是O ⊙的半径，∴PB 是O ⊙的切线． …………………2分（2）解：连接OP ，交AB 于点D ．∵PA PB =，OA OB =，∴点P 和点O 都在线段AB 的垂直平分线上． ∴OP 垂直平分线段AB ． ∴ AD BD = ∵OA OC =∴112OD BC ==……………………………………3分∵90PAO PDA ∠=∠=°，APO DPA ∠=∠ ∴APO DPA △∽△ ∴AP PO DP PA= ∴2AP PO DP =·．……………………………………4分∴()2PO PO OD AP -=即()2223PO PO -=，解得4PO =．在Rt APO △中，222OA PO PA =-=，即O ⊙的半径为2． …………………………………………5分21．解：（1）设甲学校学生获得100分的人数为x ．由题意和甲、乙学校学生成绩的统计图得O AB C PD12356x x =+++ 得2x =所以甲学校学生获得100分的人数有2人．图(略) …………………………………2分(2）由（1）可知： 甲学校的学生得分与 相应人数为：乙学校的学生得分与 相应人数为：所以，甲学校学生分数的中位数为90（分）．甲学校学生分数的平均数为 270380590210051585.823526x ⨯+⨯+⨯+⨯==≈+++甲（分）…………3分乙学校学生分数的中位数为80（分） 乙学校学生分数的平均数为 370480390210050025083.3343263x ⨯+⨯+⨯+⨯===≈+++乙（分） …4分由于甲学校学生分数的中位数和平均数都大于乙学校学生分数的中位数和平均 数，所以甲学校学生的数学竞赛成绩较好． ……………………5分22. 解:(1)作图 …………………………………………………………2分 (2 ) 5DEF S ∆= …………………………………………………………3分AC =2213…………………………………………………………5分 23．解：（1）∵△=2243(2)24m m -⨯⨯-=+，分数 70 80 90 100 人数 2 3 5 2分数 70 80 90 100 人数 3 4 32∴无论m 为任何实数，都有2240m ∆=+>………………………… 1分 ∴抛物线与x 轴总有两个交点． …………………………………… 2分（2）由题意可知：抛物线232y x mx =+-的开口向上，与y 轴交于（0，-2）点，∵方程2320x mx +-=的两根在-1与43之间， ∴当x =-1和43x =时，0y >． 即320,16420.33m m -->⎧⎪⎨+->⎪⎩ ………………………………………… 4分 解得 512m -<<． ………………………………………… 5分 因为 m 为整数，所以 m =-2，-1，0 ．当 m=-2时， 方程的判别式△=28，根为无理数，不合题意.当 m=-1时， 方程的判别式△=25，根为1221,3x x ==-，符合题意. 当 m=0时， 方程的判别式△=24，根为无理数，不合题意.综上所述 m =-1 . ………………………………………… 6分（3）n 的取值范围是11312n <<．………………………………… 7分 24.(1) ,AC BD AC BD =⊥ ； ………………………………………… 2分（2） 仍然成立.证明: 过点A 作AE MN ⊥于E ,过点B 作BF MN ⊥于F∴90AEO BFO ∠=∠=︒∵AOE BOF ∠=∠,AO OB =∴AOE ∆≌BOF ∆∴AE BF = ………………………………………… 3分∵45ACN BDN ∠=∠=︒ ∴2,2AC AE BD BF ==∴ AC BD = ………………………………………… 4分延长AC 与DB 的延长线相交点H∴45DCH ACN ∠=∠=︒又∵45BDN ∠=︒∴90CHD ∠=︒∴AC BD ⊥ ………………………………………… 5分(3) 过点A 作AE MN ⊥于E ,过点B 作BF MN ⊥于F易证 AOE ∆∽BOF ∆∴ AE AO BF OB=． ………………………………………… 6分 ∵ OB kAO =，∴ 1AO OB k=． 由（2）知 2,2AC AE BD BF ==．212AC AE AE BD BF k BF=== ．………………………………………7分 25. 解：（1）由AC BC =，可知此抛物线的对称轴是y 轴，即0b =所以(0,),(4,0)C c B c由182OBC S OB OC ∆=⨯⨯=，得4c = 抛物线解析式为 2144y x =-+ …………………………………………2分 （2）由（1）得(0,4),(4,0)C B所以224590ACB OCB ∠=∠=⨯︒=︒ ………………………………3分 在ADC ∆和BFC ∆中90ACD DCB BCF ∠=︒-∠=∠，,AC BC DC FC ==所以ADC ∆≌BFC ∆ ………………………………………… 4分 所以45FBC CAD ∠=∠=︒所以90ABF ABC CBF ∠=∠+∠=︒所以BF AB ⊥ …………………………………………5分（3）作EM x ⊥轴，交x 于点M易证ODC ∆≌DME ∆所以4DM OC ==，OD EM =又因为4OD OB BD BD DM BD BM =-=-=-=所以BM EM =因为90EMB ∠=︒所以45MBE MEB ∠=∠=︒ …………………………………………7分（4）由（3）知，点E 在定直线上当D 点沿x 轴正方向移动到点B 时，点E 所走过的路线长等于42BC = ………………………………8分。

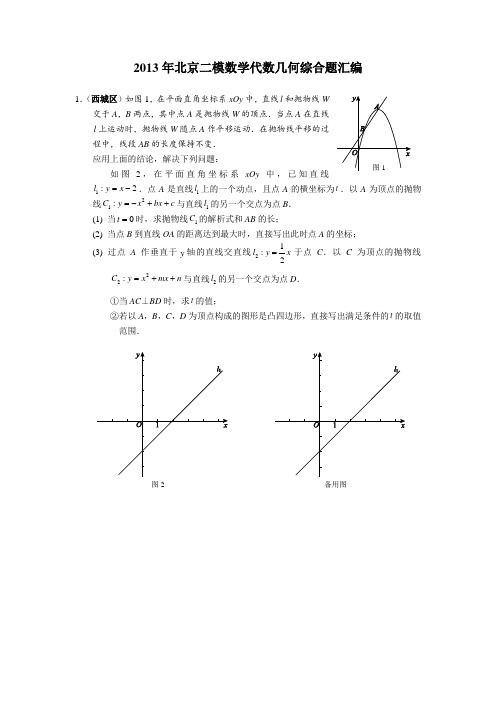
2013年北京二模数学代数几何综合题汇编1．（西城区）如图1，在平面直角坐标系xOy 中，直线l 和抛物线W交于A ，B 两点，其中点A 是抛物线W 的顶点．当点A 在直线l 上运动时，抛物线W 随点A 作平移运动．在抛物线平移的过程中，线段AB 的长度保持不变． 应用上面的结论，解决下列问题：如图2，在平面直角坐标系xOy 中，已知直线1:2l y x =-．点A 是直线1l 上的一个动点，且点A 的横坐标为t ．以A 为顶点的抛物线21:C y x bx c =-++与直线1l 的另一个交点为点B ． (1) 当0t =时，求抛物线1C 的解析式和AB 的长；(2) 当点B 到直线OA 的距离达到最大时，直接写出此时点A 的坐标；(3) 过点A 作垂直于y 轴的直线交直线21:2l y x =于点C ．以C 为顶点的抛物线22:C y x mx n =++与直线2l 的另一个交点为点D ．①当AC ⊥BD 时，求t 的值；②若以A ，B ，C ，D 为顶点构成的图形是凸四边形，直接写出满足条件的t 的取值范围．图2 备用图2．（海淀区）在平面直角坐标系xOy 中，点的坐标是，过点作直线垂直轴，点是直线上异于点的一点，且.过点作直线的垂线m ，点在直线m 上，且在直线的下方，.设点的坐标为.（1） 判断△OBC 的形状，并加以证明； （2） 直接写出与的函数关系式（不要求写自变量的取值范围）；（3） 延长交（2）中所求函数的图象于点.求证：CD =CO ×DO .A 0,2()A l yB l A ÐOBA =a B lC l ÐOCB =2a C x ,y ()y x COD3. （东城区）定义：P，Q分别是两条线段a和b上任意一点，线段PQ长度的最小值叫做线段a与线段b的距离. 已知O(0，0)，A(4，0)，B(m，n)，C(m+4，n)是平面直角坐标系中的四点.（1）根据上述定义，当m=2，n=2时，如图1，线段BC与线段OA的距离是_____；当m=5，n=2时，如图2，线段BC与线段OA的距离是______ .（2）如图3，若点B落在圆心为A，半径为2的圆上，求线段BC与线段OA的距离d.（3）当m的值变化时，动线段BC与线段OA的距离始终为2，若线段BC的中点为M，直接写出点M随线段BC运动所形成的图形的周长.4．（石景山区）（1）如图1，把抛物线2y x =-平移后得到抛物线1C ，抛物线1C 经过点(4,0)A -和原点(0,0)O ，它的顶点为P ，它的对称轴与抛物线2y x =-交于点Q ，则抛物线1C 的解析式为____________；图中阴影部分的面积为_____．（2）若点C 为抛物线1C 上的动点，我们把90ACO ∠=时的△ACO 称为抛物线1C 的内接直角三角形.过点(1,0)B 做x 轴的垂线l ，抛物线1C 的内接直角三角形的两条直角边所在直线AC 、CO 与直线l 分别交于M 、N 两点，以MN 为直径的⊙D 与x 轴交于E 、F 两点,如图2.请问：当点C 在抛物线1C 上运动时，线段EF 的长度是否会发生变化？请写出并证明你的判断．图1图25.（丰台区）如图，把△OAB 放置于平面直角坐标系xOy 中，90OAB ∠=︒，32,2OA AB ==，把△OAB 沿轴的负方向平移2OA 的长度后得到△DCE .（1）若过原点的抛物线2+yax bx c =+经过点B 、E ，求此抛物线的解析式； （2）若点在该抛物线上移动，当点P 在第一象限内时，过点作轴于点，连结.若以、、为顶点的三角形与以B 、C 、E 为顶点的三角形相似，直接写出点的坐标；（3）若点M (-4，n ) 在该抛物线上，平移抛物线，记平移后点M 的对应点为M ′，点B 的对应点为B ′．当抛物线向左或向右平移时，是否存在某个位置，使四边形M ′B ′CD 的周长最短？若存在，求出此时抛物线的解析式；若不存在，请说明理由．6. （大兴区）已知：如图，在平面直角坐标系xOy中，四边形ABCD是菱形，顶点A．C．D均在坐标轴上，且AB=5，sinB=45．（1）求过A．C．D三点的抛物线的解析式；（2）记直线AB的解析式为y1=mx+n，（1）中抛物线的解析式为y2=ax2+bx+c，求当y1＜y2时，自变量x的取值范围；（3）设直线AB与（1）中抛物线的另一个交点为E，P点为抛物线上A、E两点之间的一个动点，当P点在何处时，△PAE的面积最大？并求出面积的最大值．7. （昌平区）如图，已知半径为1的1O e 与x 轴交于A B ，两点，OM 为1O e 的切线，切点为M ，圆心1O 的坐标为(20)，，二次函数2y x bx c =-++的图象经过A B ，两点． （1）求二次函数的解析式；（2）求切线OM 的函数解析式；（3）线段OM 上是否存在一点P ，使得以P O A ，，为顶点的三角形与1OO M △相似．若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．8. （顺义区）已知抛物线c bx x y ++-=241与x 轴交于A 、B ，与y 轴交于点C ，连 AC 、BC ，D 是线段OB 上一动点，以CD 为一边向右侧作正方形CDEF ，连结BF 。

房山区2013年初三统一练习(二模)数学考生须 知1.本试卷共6页，共五道大题，25道小题，满分120分，考试时间120分钟。

2.在试卷和答题纸上准确填写学校名称、姓名和准考证号。

3.试题答案一律填涂或书写在答题纸上，在试卷上作答无效。

4.在答题纸上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5.考试结束，将本试卷、答题纸和草稿纸一并交回。

一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的．用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑．1．-2的倒数为A ．2 B.-2 C.21 D.21- 2．国家统计局22日公布的2012年统计公报显示，我国2012年全年研究与试验发展(R ＆D)经费支出10240亿元，比上年增长17.9％，占国内生产总值的1.97％.将10240用科学记数法表示应为A ．4100240.1⨯B ．5100240.1⨯C ．410240.10⨯D.41010240.0⨯3．在直角坐标系中，点M （1，2）关于y 轴对称的点的坐标为A.（1，-2）B.（2，-1）C. （-1，2）D. （-1，-2）4、如图：⊙A 、⊙B 、⊙C 两两不相交，且半径均为1，则图中三个阴影扇形的面积之和为（ ）A .πB .π21C .π2D .π415.某场射击比赛中，第一小组10人第一轮射击成绩分别为8、9、9、10、7、8、8、9、8、8（单位：环），则这组数据的众数和中位数分别为 A ．8、8B ．8、9C ．7、8D ．9、86.若两圆的半径分别是2和3，圆心距为5，则这两圆的位置关系是 A ．内切 B ．相交 C ．外切 D ．外离7.若一个多边形的内角和等于720，则这个多边形的边数是 A ．5B ．6C ．7D ．8ABC第4题图8.在正方体的表面上画有如图所示的粗线，则其展开后正确的是二、填空题（本大题共16分，每小题4分）：9．图象过点A （-1，2）的反比例函数的解析式为_____________． 10．分解因式：22363a ab b -+= __________． 11．如图，△ABC 中，D 为AB 上一点，且∠ACD=∠B ，若AD=2，BD=52，则AC= ．12．观察下列等式：①23a a +=；②65a a +=；③127a a +=；④209a a+=…；则根据此规律第6个等式为 ，第n 个等式为 ．三、解答题（本大题共30分，每小题5分）：13． 计算：8-2sin ４５°+02π-（）212---（）．14．解不等式组:31422x x x -≥⎧⎨=⎩，并把它的解集在数轴上表示出来.15.已知 210a a --=，求代数式aa aa a a +⋅-+-2111的值．16已知：如图，点C 、D 在线段AB 上，E 、F在AB 同侧，DE 与CF 相交于点O ，且AC =BD ， AE =BF ，A B ∠=∠.求证：DE =CF .17.如图，直线AB 过点A ，且与y 轴交于点B .DCB A第11题图D.C.B.A. B.A.第8题图A C D BE FO 第16题图 xy-33Bo（1）求直线AB 的解析式；（2）若P 是直线AB 上一点，且⊙P 的半径为1，请直接写出⊙P 与坐标轴相切时点P 的坐标；18．据媒体报道，2010年北京市民到郊区旅游总人数约5000万人，2012年市民到郊区旅游总人数增长到约7200万人.求这两年北京市民到郊区旅游总人数的年平均增长率.四、解答题（本大题共20分，每小题5分）： 19.如图，四边形ABCD 中，AB ∥CD ，AB =13，CD =4，点E 在边AB 上，DE ∥BC ．若CB CE =，且3tan =∠B ，求四边形ABCD 的面积.20. 如图，在△ABC 中，∠ABC=∠ACB ，以AC 为直径的⊙O 分别交AB 、BC 于点M 、N ，点P 在AB 的延长线上，且∠CAB=2∠BCP.（1）求证：直线CP 是⊙O 的切线；（2）若BC=25，sin ∠BCP=55，求⊙O 的半径及△ACP的周长. 21. 某学校为了进一步丰富学生的体育活动，欲增购一些体育器材，为此对该校一部分学生进行了一次“你最喜欢的体育活动”的问卷调查（每人只选一项）．根据收集到的数据，绘制成如下统计图（不完整）请根据图中提供的信息，完成下列问题： M NACOP B第20题图 第19题图 ABC D E图1 球类 40% 跳绳 其它 踢毽15% 第21题图1 100 90 80 7060 50 403020 100 球类 跳绳 踢毽 其它 类别30 4080 人数图2 第21题图2（1）在这次问卷调查中，一共抽查了 名学生； （2）请将上面两幅统计图补充完整；（3）在图1中，“踢毽”部分所对应的圆心角为 度；（4）如果全校有1860名学生，请问全校学生中，最喜欢“球类”活动的学生约有多少人？22.如图1，在矩形MNPQ 中，点E ，F ，G ，H 分别在边NP ，PQ ，QM ，MN 上， 当4321∠=∠=∠=∠时，我们称四边形EFGH 为矩形MNPQ 的反射四边形. 已知：矩形ABCD 的四个顶点均为边长为1的正方形网格的格点，请解决下列问题：（1）在图2中，点E ，F 分别在BC ，CD 边上，请作出矩形ABCD 的反射四边形EFGH ，并求出反射四边形EFGH 的周长.（2）在图3中作出矩形ABCD 的所有反射四边形，并判断它们的周长之间的关系.五、解答题（本大题共22分，第23题7分，第24题7分，第25题8分）23.已知二次函数217=22y x kx k ++-．（1）求证：不论k 为任何实数，该函数的图象与x 轴必有两个交点；（2）若该二次函数的图象与x 轴的两个交点在点A （1，0）的两侧，且关于x 的一元二次方程k 2x 2＋(2k ＋3)x ＋1=0有两个不相等的实数根，求k 的整数值； （3）在（2）的条件下，关于x 的另一方程 x 2＋2(a ＋k )x ＋2a －k 2＋6 k －4=0 有大于0且小于3的实数根，求a 的整数值．第22题图2 F D C E A B 第22题图 3D CA B4321E H G FD C A B 第22题图1 M N Q P D CA B备用图24.（1）如图1，正方形ABCD 中，E 、F 分别是BC 、CD 边上的点，且满足BE=CF ，联结AE 、BF 交于点H..请直接写出线段AE 与BF 的数量关系和位置关系； （2）如图2，正方形ABCD 中，E 、F 分别是BC 、CD 边上的点，联结BF ，过点E 作EG ⊥BF 于点H ，交AD 于点G ，试判断线段BF 与GE 的数量关系，并证明你的结论； （3）如图3，在（2）的条件下，联结GF 、HD. 求证：①FG+BE ≥2BF;②∠HGF=∠HDF.25.已知抛物线()()22-43-2-3m m x m x m y ++=的最低点A 的纵坐标是3，直线b mx y +=经过点A ，与y 轴交于点B ，与x 轴交于点C.（1）求抛物线与直线AB 的解析式.（2）将直线AB 绕点O 顺时针旋转90°，与x 轴交于点D ，与y 轴交于点E ，求sin ∠BDE 的值.（3）过B 点作x 轴的平行线BG,点M 在直线BG 上，且到抛物线的对称轴的距离为6，设点N 在直线BG 上，请你直接写出使得∠AMB+∠ANB=450的点N 的坐标.y x3O14-112345-125-2第25题图第24题图 1F B CA DEH 第24题图 2FBC D AGEH第21题图3FBCADGEH初三数学综合练习（二）参考答案及评分标准一、选择题：1.D ；2.A ；3. C ；4. B ；5.A ；6.C ；7.B ；8.D. 二、填空题：9..2y x =- ； 10..23()a b - 11.3 ； 12.1342=+aa ； 122+=++n a n n a . 三、解答题：13.解： 原式=4122222-+⨯- -------------------------------4分 32-= ------------------------------5分14. 解：由不等式413-≥-x ，得≥x -1． -----------------------1分 由不等式22+<x x ，得2<x ． -----------------------2分 ∴ 原不等式组的解集是21<<-x ． -----------------------3分 ∴ 原不等式组的解集在数轴上表示为：-5-4-3-2-143210-------------------------5分15． 解： ∵2111a a a a a a +-∙-+ =1a -11a a +∙-1aa a +（） ------------------1分 =1a -11a - ----------------------------------2分=11a aa a ---（）=21a a-- ------------------------------------------3分∵210a a --=，∴21a a -=． --------------------------------------4分 当21a a -=时,原式=-1 ---------------------------------------5分16．证明：∵ AC =BD ,∴ AD =BC . -----------------------------------------1分 ∵ A B ∠=∠ ，AE =BF ------------------------------------3分 ∴ △ADE ≌△BCF . - -----------------------------------4分 ∴ DE =CF . ------------------------------5分17.解：（1）由图可知：A （-3，-3），B （0,3） ------------1分设直线AB 的解析式为y=kx+b （k ≠0）则333k b b -+=-⎧⎨=⎩，解得23k b =⎧⎨=⎩.∴直线AB 的解析式为y=2x+3. ------------2分 （2）P 1（-2，-1），P 2（-1，1），P 3（1，5）. ------------5分18．解：设这两年北京市民到郊区旅游总人数的年平均增长率为x -------1分 根据题意，得5000（1+x ）=7200 ------------------------2分 解得2.01=x ，2.22-=x -----------------------3分 ∵增长率不能为负，∴只取x =0.2=20% ------------------------4分 答：这两年北京市民到郊区旅游总人数的年平均增长率为20％. ------5分19.解：过点C 作AB CF ⊥于点F . -------1分∵AB ∥CD ，DE ∥BC∴四边形BCDE 为平行四边形 ------------2分 ∴BE=CD∵CD=4 ，∴BE=4. ∵CB CE =，BE CF ⊥∴BF=2 --------------------------------3分 在Rt△BCF 中， 3tan =∠B ，2=BF∴6=CF . ---------------------------------4分∴四边形ABCD 的面积=6)94(21⨯+=39 ----------------------5分20.证明：（1）连接AN ，∵∠ABC=∠ACB ，∴AB=AC ，∵AC 是⊙O 的直径，∴AN ⊥BC ， ∴∠CAN=∠BAN ，BN=CN ， ∵∠CAB=2∠BCP ，∴∠CAN=∠BCP ， ------------------------1分MNACO P B D∵∠CAN ＋∠ACN=90°， ∴∠BCP ＋∠ACN=90°， ∴CP ⊥AC∵OC 是⊙O 的半径∴CP 是⊙O 的切线. ------------------------2分 解：（2）∵∠ANC=90°，sin ∠BCP=55， ∴CN AC =55， ∴AC=5，∴⊙O 的半径为52----------------3分 过点B 作BD ⊥AC 于点D ，由（1）得BN=CN=12BC=5， 在Rt △CAN 中，AN=22AC CN -=25在△CAN 和△CBD 中， ∠ANC=∠BDC=90°，∠ACN=∠BCD ，∴△CAN ∽△CBD ， ∴BC BDAC AN=，∴BD=4. （3）在Rt △BCD 中，CD=22BC BD -=2， ∴AD=AC —CD=5—2=3， ∵BD ∥CP ，∴BD AD CP AC =, BPABDC AD =∴CP=203, 310=BP ---------------------- -----------------4分∴△APC 的周长是AC ＋PC ＋AP=20； -------------------------5分21. 解：(1)200 ………1分(2)图略 ………3分 (3)54 ………4分 (4)744人 ………5分22. 解：（1）如图，∴四边形EFGH 即为所求，且周长为58 ------------------2分（2）如图：GFDCEHA BD CABDCAB指明结果（略） -------------------4分 矩形ABCD 的反射四边形的周长为定值． -------------------5分23.（1）证明：△1=222174421422b ac k k k k ==+----（）222113=113k k k =++-+-（）＞0∴不论k 为任何实数，该函数的图象与x 轴必有两个交点 -------------1分（2）∵二次函数217=22y x kx k ++-的图象与x 轴的两个交点在点（1，0）的两侧， 且二次函数开口向上∴当x=1时，函数值y ＜0, 即17122k k ++-＜0，解得k ＜53-----------------------------2分 ∵关于x 的一元二次方程k 2x 2＋(2k ＋3)x ＋1=0有两个不相等的实数根∴k ≠0且△2=222224234=41294=129b ac k k k k k k =+++--+-（）＞0∴k ＞34-且k ≠0 ------------------------------------4分 ∴34-＜k ＜53且k ≠0 ∴k=1 --------------------------------5分 （3）由（2）可知，k=1∴x 2＋2(a ＋1)x ＋2a ＋1=0解得x 1=-1，x 2=-2a -1 ---------------------------------6分根据题意，0＜-2a -1＜3∴122a --＜＜ ∴a 的整数值为-1. -------------------------------7分24（1）AE=BF 且AE ⊥BF. -----------------------------------------------1分（2）判断：BF=GE. -------------------------------------------------2分 证明：过点A 作AM ∥GE 交BC 于M∵EG ⊥BF∴AM ⊥BF∴∠BAM+∠ABF=90° ∵正方形ABCD∴AB=BC ，AD ∥BC ，∠ABC=∠BCD=90° ∴∠CBF+∠ABF=90° ∴∠BAM=∠CBF∴△ABM ≌△BCF∴AM=BF -------------------------------------------------3分 ∵AM ∥GE 且AD ∥BC ∴AM=GE∴BF=GE -------------------------------------------------4分 （3）①：过点B 作BN ∥FG ，且使BN=FG 联结NG 、NE∴四边形NBFG 是平行四边形∴BF=NG ，BF ∥NG由（2）可知，BF ⊥GE ，且BF=GE∴NG ⊥EG 且NG=EG∴△NGE 为等腰直角三角形 由勾股定理得NE=2NG ∴NE=2BF.当点F 与点D 不重合，点E 与点C 不重合时，N 、B 、E 三点不共线此时，在△BEN 中，NB+BE ＞NE ，即FG+BE ＞2BF. -------------------------------5分 当点F 与点D 重合，点E 与点C 重合时，N 、B 、E 三点共线 此时，NB+BE=NE，即FG+BE=2BF.----------------------------------------------6分②：∵正方形ABCD ∴∠ADC=90°以GF 为直径作⊙P ，则点D 在⊙P 上 ∵∠GHF=90° ∴点H 也在⊙P 上∴∠HGF=∠HDF. ---------------------------------------------7分M F B C DA G E H NF BCA DG EH P FBCADGEH25. 解：（1）∵抛物线的对称轴x=)3(2)3(22m m a b ---=-=1 且抛物线()()22-43-2-3m m x m x m y ++=的最低点A 的纵坐标是3∴抛物线的顶点为A （1，3）∴0652=+-m m∴m=3或m=2,∵3-m ﹥0， ∴ m=2, -----------------------------1分∴直线为b y +=x 2∴抛物线的解析式为：224y x x =-+ --------------------------------2分 直线AB 为:y=2x+1； ----------------------------3分（2）令x=0,则y=1, ）令y=0,则x=21-, ∴B （0,1），C （-21，0） 将直线AB 绕O 点顺时针旋转900，设DE 与BC 交于点F∴D(1,0),E(0, 21) 090=∠CFD -------------------------4分 ∴OB=OD=1 OC=21, ∴ CD=23 25=CB 2=BD∵DF CB OB CD ⨯=⨯∴553=DF ------------------------5分 ∴55=BF ∴ Si n ∠BDE=BD BF =1010 -----------6分 (3) 12(5,1),(3,1)N N - --------8分G F B C E D。

P FEDCB A PFE D C B A 2013北京模拟：立体几何综合【高三二模题组】 1、（2013昌平二模，理16）如图，在四棱锥P A B C D -中，底面A B C D 是边长为2的正方形，侧面P A D ⊥底面A B C D，且2P A P D A D ==，E ，F 分别是P C 、B D 的中点（I ）求证：E F ∥平面P A D ；（II ）求证：平面P A B ⊥平面P D C ；（III ）在线段A B 上是否存在点G ，使得二面角C P D G --的余弦值为13？2、（2013昌平二模，文17）如图，在四棱锥P A B C D -中，底面A B C D 是边长为2的正方形，侧面P A D ⊥底面A B C D，且22P A P D A D ===，E ，F 分别是P C 、B D 的中点（I ）求证：E F ∥平面P A D ； （II ）求三棱锥P B C D -的体积；（III ）在线段A B 上是否存在点G ，使得C D ⊥平面E F G ？3、（2013丰台二模，文17）如图，多面体E D A B C 中，A C ，B C ，C E 两两垂直，A D C E ∥，E D D C ⊥，12A D C E =，M 为B E 中点（I ）求证：D M ∥平面A B C ；（II ）求证：平面B D E ⊥平面B C D 。

4、（2013丰台二模，理17）如图1，等腰直角三角形A B C 底边4A B =，点D 在线段A C 上，D E A B ⊥于E ，现将△A D E 沿D E 折起到△P D E 的位置，如图2 （I ）求证：P B D E ⊥；（II ）若P E B E ⊥，直线P D 与平面P B C 所成的角为30°，求P E 的长。

图1 图2 5、（2013海淀二模，文17）如图，在直角梯形A B C D 中，A D B C ∥，90A D C ∠=°，B A B C =，把△B A C 沿A C 折起到△P A C 的位置，使得P 点在平面A D C 上的正投影O 恰好落在线段A C 上，如图2所示，点E ，F 分别为棱P C 、C D 的中点 （I ）求证：平面O E F ∥平面APD ；（II ）求证：C D ⊥平面P O F ；（III ）在棱P C 上是否存在一点M ，使得M 到点P ，O ，C ，F 四点距离相等？请说明理由。

【解析分类汇编系列三：北京2013（二模）数学理】9：圆锥曲线一、选择题1 ．（2013北京东城高三二模数学理科）过抛物线24yx =焦点的直线交抛物线于A ,B 两点,若10AB =,则AB 的中点到y 轴的距离等于 （ ）A ．1B ．2C ．3D ．4【答案】D抛物线24y x =的焦点（1，0），准线为l ：1x =-，设AB 的中点为 E ，过 A 、E 、B 分别作准线的垂线，垂足分别为 C 、F 、D ，EF 交纵轴于点H ，如图所示：则由EF 为直角梯形的中位线知522AC BD ABEF +===，所以1514EH EF =-=-=,即则B 的中点到y轴的距离等于4．选D.2．（2013北京朝阳二模数学理科试题）若双曲线22221(0,0)x y a b a b-=>>的渐近线与抛物线22y x =+有公共点,则此双曲线的离心率的取值范围是（ ）A ．[3,)+∞B ．(3,)+∞C ．(1,3]D ．(1,3)【答案】A双曲线的渐近线为b y x a =±，不妨取b y x a =，代入抛物线得22bx x a=+，即220b x x a -+=，要使渐近线与抛物线22y x =+有公共点，则2()80ba∆=-≥，即228b a ≥，又22228b c a a =-≥，所以229c a ≥，所以29,3e e ≥≥。

所以此双曲线的离心率的取值范围是[3,)+∞，选A.3 ．（2013北京海淀二模数学理科）双曲线C 的左右焦点分别为12,F F ,且2F 恰为抛物线24y x =的焦点,设双曲线C 与该抛物线的一个交点为A ,若12AF F ∆是以1AF 为底边的等腰三角形,则双曲线C 的离心率为 （ ）AB ．1C ．1D ．2+【答案】B抛物线的焦点为(1,0)，即2(1,0)F ,所以双曲线中1c =。

双曲线C 与该抛物线的一个交点为A ，（不妨设在第一象限）若12AF F ∆是以1AF 为底边的等腰三角形，则抛物线的准线过双曲线的左焦点。