第三节__三重积分的计算(2)

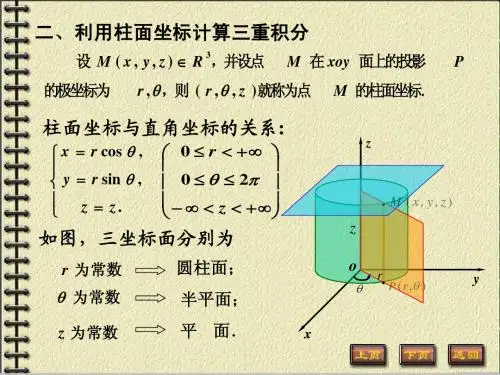
三重积分的常用计算方法1直角坐标系法：适用于被积区域不含圆形的区域 2柱面坐标法：适用被积区域的投影为圆时3球面坐标系法：适用于被积区域包含球的一部分第三节 三重积分一、三重积分的概念设f x y z (,,)是空间闭区域Ω上的有界函数,将Ω任意地分划成n 个小区域 ∆∆∆v v v n12,,,其中∆v i表示第i 个小区域,也表示它的体积.在每个小区域∆v i 上任取一点(,,)ξηζi i i,作乘积 f v i i i i(,,)ξηζ∆作和式 f v i i i i i n(,,)ξηζ∆=∑1以λ记这n 个小区域直径的最大者, 若极限lim (,,)λξηζ→=∑01f v i i i i i n∆ 存在,则称此极限值为函数f x y z (,,)在区域Ω上的三重积分,记作f x y z dv (,,)Ω⎰⎰⎰,即 f x y z dv f v i i i i i n(,,)lim (,,)Ω∆⎰⎰⎰∑=→=λξηζ01其中dv 叫体积元素.自然地,体积元素在直角坐标系下也可记作成dxdydz .二、三重积分的计算1、利用直角坐标计算三重积分假设积分区域Ω的形状如下图所示Ω在xoy 面上的投影区域为D xy , 过D xy 上任意一点, 作平行于z 轴的直线穿过Ω内部, 与Ω边界曲面相交不多于两点. 亦即, Ω的边界曲面可分为上、下两片部分曲面.S z z x y 11:(,)= , S z z x y 22:(,)=其中z x y 1(,), z x y 2(,)在D xy 上连续, 并且 z x y z x y 12(,)(,)≤.如何计算三重积分f x y z dv (,,)Ω⎰⎰⎰呢?不妨先考虑特殊情况f x y z (,,)≡1,则[]dv dxdydz z x y z x y d D xyΩΩ⎰⎰⎰⎰⎰⎰⎰⎰==-21(,)(,)σ即 dvdxdydz z x y z x y D xyΩ⎰⎰⎰⎰⎰⎰=12(,)(,)一般情况下,类似地有dv dxdy f x y z dz z x y z x y D xyΩ⎰⎰⎰⎰⎰⎰=(,,)(,)(,)12显然积分f x y z dzz x y z x y (,,)(,)(,)12⎰只是把f x y z (,,)看作z 的函数在区间[(,),(,)]z x y z x y 12上对z 求定积分, 因此,其结果应是x y ,的函数, 记F x y f x y z dz z x y z x y (,)(,,)(,)(,)=⎰12那么 f x y z dv F x y dxdy D xy(,,)(,)Ω⎰⎰⎰⎰⎰=如上图所示, 区域D xy 可表示为a xb y x y y x ≤≤≤≤,()()12从而F x y dxdy dx F x y dy D aby x y x xy(,)(,)()()⎰⎰⎰⎰=12综上讨论, 若积分区域Ω可表示成a xb y x y y x z x y z z x y ≤≤≤≤≤≤,()(),(,)(,)1212则 f x y z dv dx dyf x y z dz aby x y x z x y z x y (,,)(,,)()()(,)(,)Ω⎰⎰⎰⎰⎰⎰=1212这就是三重积分的计算公式, 它将三重积分化成先对积分变量z , 次对y ,最后对x 的三次积分.如果平行于 z 轴且穿过Ω内部的直线与边界曲面的交点多于两个,可仿照二重积分计算中所采用的方法, 将Ω剖分成若干个部分,(如ΩΩ12,),使在Ω上的三重积分化为各部分区域( ΩΩ12,)上的三重积分,当然各部分区域 (ΩΩ12,) 应适合对区域的要求.例如,求f x y z dv (,,)Ω⎰⎰⎰,其中Ω为 14222≤++≤x y z .将面将区域剖分成上下两个部分区域Ω1222014=≥≤++≤{(,,)|,}x y z z x y zΩ2222014=≤≤++≤{(,,)|,}x y z z x y z则 fdv fdv fdv ΩΩΩ⎰⎰⎰⎰⎰⎰⎰⎰⎰=+12例1计算xyzdxdydz Ω⎰⎰⎰, 其中Ω为球面x y z 2221++=及三坐标面所围成的位于第一卦限的立体. 解:(1)、画出立体的简图(2)、找出立体Ω在某坐标面上的投影区域并画出简图Ω在xoy 面上的投影区域为 D x y x y xy :,,22100+≤≥≥(3)、确定另一积分变量的变化范围在已知积分变量x y ,的变化范围为D xy 的情况下, 再确定另一积分变量z 的变化范围. 在D xy 内任取一点, 作一过此点且平行于z 轴的直线穿过区域Ω, 则此直线与Ω边界曲面的两交点之竖坐标即为z 的变化范围.0122≤≤--z x y(4)、选择一种次序,化三重积分为三次积分⎰⎰⎰⎰⎰⎰⎰⎰----Ω--==222210221101010)1(21x y x x dy y x xy dxxyzdzdy dxxdydzxyzddxx x x x x x dx xy y x xy dy xy y x xy dxx x ⎰⎰⎰⎰⎥⎦⎤⎢⎣⎡-----=⎥⎦⎤⎢⎣⎡--=--=--102223210104232103310)1(81)1(41)1(41814141)212121(224812462481246224124241cos sin 81cos sin 41cos sin 41cos cos sin 81cos sin 41cos sin 412052033320204232=⋅⋅⋅⋅-⋅⋅⋅⋅-⋅⋅=--=⎥⎦⎤⎢⎣⎡--=⎰⎰⎰⎰ππππtdt t tdt t dt t tdtt t t t t t2、利用柱面坐标计算三重积分 （1）、柱面坐标设M x y z (,,)为空间的一点,该点在xoy 面上的投影为P ,P 点的极坐标为r ,θ,则r z ,,θ三个数称作点M 的柱面坐标.规定r z ,,θ的取值范围是0≤<+∞r ，02≤≤θπ，-∞<<+∞z柱面坐标系的三组坐标面分别为r =常数,即以z 轴为轴的圆柱面； θ=常数,即过z 轴的半平面； z =常数,即与xoy 面平行的平面.点M 的直角坐标与柱面坐标之间有关系式x r y r z z ===⎧⎨⎪⎪⎩⎪⎪cos sin θθ（2）、三重积分f x y z dv(,,)Ω⎰⎰⎰在柱面坐标系中的计算公式用三组坐标面r =常数,θ=常数,z =常数,将Ω分割成许多小区域,除了含Ω的边界点的一些不规则小区域外,这种小闭区域都是柱体.考察由r z ,,θ各取得微小增量dr d dz ,,θ所成的柱体,该柱体是底面积为rdrd θ,高为dz 的柱体,其体积为dv rdrd dz =θ这便是柱面坐标系下的体积元素, 并注意到(1)式有f x y z dv f r r z rdrd dz (,,)(cos ,sin ,)ΩΩ⎰⎰⎰⎰⎰⎰=θθθ (2)(2)式就是三重积分由直角坐标变量变换成柱面坐标变量的计算公式.(2)式右端的三重积分计算,也可化为关于积分变量z r ,,θ的三次积分,其积分限要由z r ,,θ在Ω中的变化情况来确定. 3、用柱面坐标r z ,,θ表示积分区域Ω的方法(1)、找出Ω在xoy 面上的投影区域D xy , 并用极坐标变量r ,θ表示之； (2)、在D xy 内任取一点(,)r θ, 过此点作平行于z 轴的直线穿过区域, 此直线与Ω边界曲面的两交点之竖坐标( 将此竖坐标表示成r ,θ的函数 )即为z 的变化范围.例1求下述立体在柱面坐标下的表示形式Ω1: 球面x y z 2221++=与三坐标面所围成的立体且位于第一卦限内的部分.Ω2: 由锥面z x y =+22与平面z =1所围成的立体.Ω1在xoy 面上的投影区域为 D x y x y xy ():,,122100+≤≥≥, 其极坐标下的表示形式为 0201≤≤≤≤θπ,rz 在Ω1的变化范围是 0122≤≤--z x y ,即012≤≤-z rΩ12020101:,,≤≤≤≤≤≤-θπr z rΩ2在xoy 面上的投影区域为 D x y xy ():2221+≤, 其极坐标下的表示形式为 0201≤≤≤≤θπ,r z 在Ω2的变化范围是 x y z 221+≤≤即 r z ≤≤1故 Ω202011:,,≤≤≤≤≤≤θπr r z三、利用球坐标计算三重积分 1. 球面坐标如图所示,空间任意一点),,(z y x M 也可用三个数θφ,,r 唯一表示。

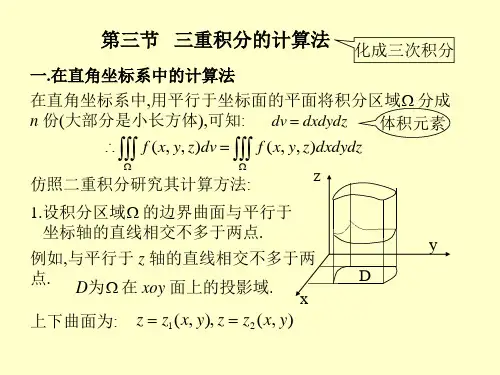
第三节 三重积分的计算一、 利用直角坐标系计算三重积分 三重积分的定义：∑⎰⎰⎰=→=ni i i i i V f dV z y x f 1),,(lim),,(∆ςηξλΩ． 三重积分中体积元素可表示为dxdydz dV =，于是⎰⎰⎰⎰⎰⎰=ΩΩdxdydz z y x f dV z y x f ),,(),,(．三重积分的计算是将其化为计算一个定积分和一个二重积分，最终都要转化为计算三次定积分．１、 坐标面投影法（先一后二计算法） 由上次课的引例知，三重积分⎰⎰⎰ΩdV z y x f ),,(可看成为体密度为),,(z y x f 且占有空间区域Ω的立体的质量．设区域Ω在xOy 面上的投影区域为D ，以D 的边界为准线作平行于z 轴的柱面，将V 分为上下两个曲面，其方程分别为),(:22y x z z =∑ ),(:11y x z z =∑设它们为D 上的单值连续函数，且),(),(21y x z z y x z ≤≤，用垂直于x轴和y 轴的平面将区域D 分为若干个细长条，对应于小区域σd 高度为dz 的小薄片的质量近似等于dz d z y x f σ),,(，所以细长条的质量用微元法求得为σσd dz z y x f dz d z y x f y x z y x z y x z y x z ]),,([),,(),(),(),(),(2121⎰⎰=再将其在区域D 上求二重积分，得到立体的质量为⎰⎰⎰⎰⎰⎰=Dy x z y x z d dz z y x f dV z y x f σΩ]),,([),,(),(),(21上面公式对于一般情形仍然成立，于是我们有下面结果． 当积分区域Ω可以表示为:Ω⎩⎨⎧∈≤≤xyD y x y x z z y x z ),(),(),(21 其中xy D 为Ω在xOy 面上的投影，此时称Ω为xy －型区域． 则有计算公式⎰⎰⎰⎰⎰⎰=xyD y x z y x z dxdy dz z y x f dV z y x f ]),,([),,(),(),(21Ω．进一步，如果D 是x －型区域，即Ω可表示为如下不等式组Ω：⎪⎩⎪⎨⎧≤≤≤≤≤≤),(),( )()( 2121y x z z y x z x y y x y b x a 则⎰⎰⎰⎰⎰⎰=Dy x z y x z dxdy dz z y x f dxdydz z y x f ]),,([),,(),(),(21Ω⎰⎰⎰=),(),()()(2121),,(y x z y x z x y x y ba dz z y x f dy dx由于上面计算公式实际上是先求一个单积分，再求一个二重积分，因此称为先一后二计算法．类似地，积分区域还有yz －型区域，zx －型区域，都有类似公式．例如对于yz －型区域，Ω可表示为⎩⎨⎧∈≤≤),(),(),(21yz D z y z y x x z y x 则有公式⎰⎰⎰⎰⎰⎰=yzD z y x z y x d dx z y x f dV z y x f σΩ]),,([),,(),(),(21例１ 计算三重积分⎰⎰⎰Vxdxdydz ，其中V 为三个坐标面和平面12=++z y x 所围成的闭区域．解 从图上看出，积分区域可以用如下不等式组表示为⎪⎩⎪⎨⎧--≤≤-≤≤≤≤yx z x y x 210 21010 由上面公式有481)2(41)21(10322101021021010=+-=--==⎰⎰⎰⎰⎰⎰⎰⎰⎰----dx x x x dyy x x dx xdz dy dx xdxdydz xy x x V例２ 求由抛物面z y x -=+622，平面0=x ，0=y ，1=x ，2=y 及z y 4=所围成的立体的体积．解 从立体图形看出，区域V 可以用不等式组表示为⎪⎩⎪⎨⎧--≤≤≤≤≤≤2264/ 2010y x z y y x 6492264201===⎰⎰⎰⎰⎰⎰--y x y Vdz dy dx dV V ． ２、 坐标投影法（截面法或先二后一法）如果将空间区域Ω向z 轴作投影得一投影区间],[q p ，且Ω能够表示为Ω：⎩⎨⎧≤≤∈qz p D y x z),(．其中z D 是过点),0,0(z 且平行于xOy 面的平面截Ω所得的平面区域，就称Ω为z 型空间区域。