(精选)三重积分的计算方法与例题

三重积分的各种计算方法计算： ()f x y z dxdydz Ω⎰⎰⎰，，. 当积分区域Ω的表面用柱(/球)坐标表示时方程简单，且被积函数 () f x y z ，， 用柱(/球)坐标表示时，可变量分离时，可将其转化为用柱(/球)坐标( )F z d d dz ρρθρθΩ⎰⎰⎰，，()2s ()in r F r drd d θϕϕθϕΩ⎰⎰⎰，或，计算三重积分比较简单。

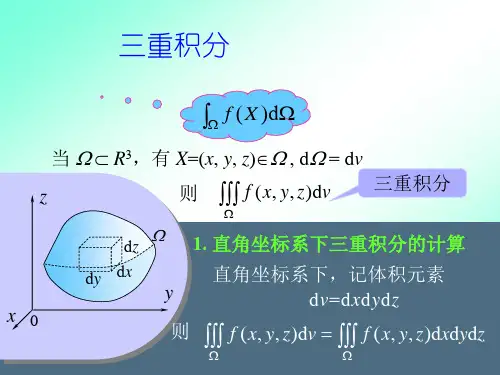
—— 重积分的换元积分法_____________________________________________________________________三重积分的计算是化为三次积分进行的。

其实质是计算一个定积分（一重积分）和一个二重积分。

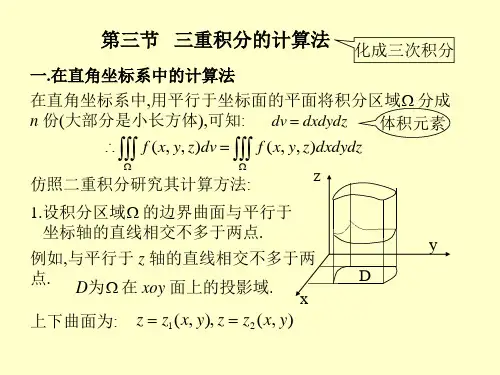
从顺序看：_____________________________________________________________________1. 如果先做定积分21() z z f x y z dz ⎰，，，再做二重积分(,)xyD F x y d σ⎰⎰，就是投影法，也即 “先一后二”。

步骤为：找Ω及在xoy 面投影区域D 。

过D 上一点() x y ，“穿线”确定z 的积分限，完成了“先一”这一步（定积分）；进而按二重积分的计算步骤计算投影区域D 上的二重积分，完成“后二”这一步，即()()21,,(,,)[(,,)]xy z x y D z x y f x y z dv f x y z dz d σΩ=⎰⎰⎰⎰⎰⎰_____________________________________________________________________2. 如果先做二重积分⎰⎰zD d z y x f σ),,(再做定积分⎰21)(c c dz z F ，就是截面法，也即“先二后一”。

步骤为：确定Ω位于平面1 z c =与2 z c =之间，即12[,]z c c ∈，过z 作平行于xoy 面的平面截Ω，截面z D 。

高等数学三重积分例题一、计算三重积分∭_varOmega z dV，其中varOmega是由锥面z = √(x^2)+y^{2}与平面z = 1所围成的闭区域。

1. 利用柱坐标计算在柱坐标下x = rcosθ，y = rsinθ，z = z，dV = rdzdrdθ。

锥面z=√(x^2)+y^{2}在柱坐标下就是z = r。

由锥面z = r与平面z = 1所围成的闭区域varOmega，其在柱坐标下的范围为：0≤slantθ≤slant2π，0≤slant r≤slant1，r≤slant z≤slant1。

2. 计算积分则∭_varOmegaz dV=∫_0^2πdθ∫_0^1rdr∫_r^1zdz。

先计算关于z的积分：∫_r^1zdz=(1)/(2)(1 r^2)。

再计算关于r的积分：∫_0^1r×(1)/(2)(1 r^2)dr=(1)/(2)∫_0^1(rr^3)dr=(1)/(2)((1)/(2)-(1)/(4))=(1)/(8)。

最后计算关于θ的积分：∫_0^2πdθ = 2π。

所以∭_varOmegaz dV=(1)/(8)×2π=(π)/(4)。

二、计算三重积分∭_varOmega(x + y+z)dV，其中varOmega是由平面x = 0，y = 0，z = 0及x + y+z = 1所围成的四面体。

1. 利用直角坐标计算对于由平面x = 0，y = 0，z = 0及x + y + z=1所围成的四面体varOmega，其范围为0≤slant x≤slant1，0≤slant y≤slant1 x，0≤slant z≤slant1 x y。

则∭_varOmega(x + y + z)dV=∫_0^1dx∫_0^1 xdy∫_0^1 x y(x + y + z)dz。

2. 计算积分先计算关于z的积分：∫_0^1 x y(x + y+z)dz=(x + y)z+(1)/(2)z^2big|_0^1 x y=(x + y)(1 x y)+(1)/(2)(1 x y)^2展开得x + y-(x^2+2xy + y^2)+(1)/(2)(1 2x 2y+x^2+2xy + y^2)进一步化简为x + y x^2-2xy y^2+(1)/(2)-x y+(1)/(2)x^2+xy+(1)/(2)y^2即(1)/(2)-x^2-xy (1)/(2)y^2。

三重积分先一后二例题（最新版）目录1.引言：介绍三重积分的概念和计算方法2.三重积分的计算顺序：先一后二3.例题分析：详细解答一个三重积分例题，展示先一后二的计算过程4.总结：回顾三重积分的计算方法和注意事项正文一、引言三重积分是数学中的一个重要概念，它在物理、工程等领域有着广泛的应用。

三重积分的计算方法相对复杂，需要掌握一定的技巧。

在解决三重积分问题时，有一种常见的计算顺序，即先一后二。

接下来，我们将通过一个具体的例题，来详细讲解这种计算方法。

二、三重积分的计算顺序：先一后二在解决三重积分问题时，我们通常按照以下顺序进行计算：1.首先解决第一个积分，即对变量 x 的积分2.然后解决第二个积分，即对变量 y 的积分3.最后解决第三个积分，即对变量 z 的积分这种计算顺序可以帮助我们简化问题，更容易地求解三重积分。

三、例题分析下面，我们通过一个具体的例题，来展示三重积分先一后二的计算过程。

例题：计算三重积分∫∫∫f(x, y, z)dxdydz解：1.首先，解决第一个积分，即对变量 x 的积分。

我们可以将 f(x, y, z) 看作是一个关于 x 的函数，对它进行积分，得到一个关于 y 和 z 的函数。

∫f(x, y, z)dx = F(y, z)2.然后，解决第二个积分，即对变量 y 的积分。

此时，我们将 F(y, z) 看作是一个关于 y 的函数，对它进行积分，得到一个关于 z 的函数。

∫F(y, z)dy = G(z)3.最后，解决第三个积分，即对变量 z 的积分。

对 G(z) 进行积分，得到最终的结果。

∫G(z)dz = H(z) + C其中，C 为积分常数。

通过以上计算过程，我们可以看到，按照先一后二的顺序计算三重积分，可以简化问题，更容易地求解。

四、总结在解决三重积分问题时，先一后二的计算顺序是一种有效的方法。

通过先解决第一个积分，再解决第二个积分，最后解决第三个积分，可以简化问题，更容易地求解。

三重积分的计算方法例题摘要：一、三重积分的概念及应用场景二、三重积分的计算方法1.重积分的计算2.重积分的换元法3.重积分的性质4.重积分的几何意义三、实例解析四、总结与拓展正文：一、三重积分的概念及应用场景三重积分是一种多元函数的积分形式，通常表示为对空间中一个几何体内部的属性进行积分。

它在物理学、工程学、经济学等领域具有广泛的应用。

三重积分的计算方法有多种，包括重积分、换元法等。

二、三重积分的计算方法1.重积分的计算重积分是指对一个空间函数在某个区域内的值进行积分。

求解重积分的过程通常包括以下步骤：确定被积函数、确定积分区域、选择积分顺序、进行积分计算。

2.重积分的换元法重积分的换元法是一种求解重积分的高效方法。

通过引入一个新的变量，将复杂的重积分问题转化为简单的一重积分问题。

换元法的关键在于选择合适的换元函数，使得积分过程变得简洁。

3.重积分的性质重积分具有线性、可交换、满足乘法公式等性质。

这些性质使得重积分在实际计算中具有很好的灵活性，可以简化计算过程。

4.重积分的几何意义重积分在几何上的意义是对一个立体图形的质量进行求解。

具体来说，重积分可以表示为空间曲线长度、曲面面积或体积的函数。

这为求解空间几何问题提供了理论依据。

三、实例解析以一个球体的体积为例，介绍三重积分的计算过程。

设球体的半径为R，球体的密度为ρ。

我们需要求解球体内部某一区域内质量的分布。

1.确定被积函数：球体内部的密度函数，即ρ(x, y, z)。

2.确定积分区域：球体内部，用球坐标系表示为x^2 + y^2 + z^2 <R^2。

3.选择积分顺序：先对z积分，再对y积分，最后对x积分。

4.进行积分计算：利用重积分公式，计算出球体内部的质量分布。

四、总结与拓展本文详细介绍了三重积分的计算方法，包括重积分、换元法等。

通过实际应用场景和实例解析，加深了对三重积分的理解。

在实际问题中，三重积分有着广泛的应用，掌握其计算方法有助于解决诸多实际问题。

三重积分计算详解例题当我们进行三重积分计算时，通常会遇到一个三维空间中的函数，我们希望求解该函数在某个特定区域上的体积、质量、质心等物理量。

下面我将以一个具体的例题来详细解释三重积分的计算过程。

假设我们要计算函数f(x, y, z) = x^2 + y^2 + z^2在球体x^2 + y^2 + z^2 <= 1上的体积。

首先，我们需要确定积分的顺序，由于球体的形状对称性较好，我们选择球坐标系进行积分。

球坐标系下，积分区域为0 ≤ r ≤ 1, 0 ≤ θ ≤ π, 0 ≤ φ ≤ 2π。

接下来，我们可以按照r、θ、φ的顺序进行积分。

首先对r进行积分，然后是θ，最后是φ。

具体的计算过程如下：∫∫∫(球体内部) x^2 + y^2 + z^2 dV = ∫[0, 2π] ∫[0, π] ∫[0, 1] (r^2) r^2 sin(θ) dr dθ dφ。

其中，dV = r^2 sin(θ) dr dθ dφ是球坐标系下的体积元素。

对r进行积分后得到，∫[0, 2π] ∫[0, π] ∫[0, 1] r^4sin(θ) dr dθ dφ = 2π ∫[0, π] sin(θ) dθ ∫[0, 1]r^4 dr.继续计算可得，2π (-cos(π) + cos(0)) (1/5) = 2π (2) (1/5) = 4π/5。

因此，函数f(x, y, z) = x^2 + y^2 + z^2在球体x^2 + y^2+ z^2 <= 1上的体积为4π/5。

这就是对三重积分计算的详细解释。

在实际应用中，我们可以根据具体情况选择合适的坐标系和积分顺序，通过逐步积分来求解体积、质心等物理量。

希望这个例题能够帮助你更好地理解三重积分的计算过程。

三重积分的计算方法：三重积分的计算是化为三次积分进行的。

其实质是计算一个定积分（一重积分）和一个二重积分。

从顺序看：如果先做定积分⎰21),,(z z dz z y x f ，再做二重积分⎰⎰Dd y x F σ),(，就是“投影法”，也即“先一后二”。

步骤为：找Ω及在xoy 面投影域D 。

多D 上一点（x,y ）“穿线”确定z 的积分限，完成了“先一”这一步（定积分）；进而按二重积分的计算步骤计算投影域D 上的二重积分，完成“后二”这一步。

σd dz z y x f dv z y x f Dz z ⎰⎰⎰⎰⎰⎰Ω=21]),,([),,(如果先做二重积分⎰⎰zD d z y x f σ),,(再做定积分⎰21)(c c dz z F ，就是“截面法”，也即“先二后一”。

步骤为：确定Ω位于平面21c z c z ==与之间，即],[21c c z ∈，过z 作平行于xoy 面的平面截Ω，截面z D 。

区域z D 的边界曲面都是z 的函数。

计算区域z D 上的二重积分⎰⎰zD d z y x f σ),,(，完成了“先二”这一步（二重积分）；进而计算定积分⎰21)(c c dz z F ，完成“后一”这一步。

dz d z y x f dv z y x f c c D z]),,([),,(21σ⎰⎰⎰⎰⎰⎰Ω=当被积函数f （z ）仅为z 的函数（与x,y 无关），且z D 的面积)(z σ容易求出时，“截面法”尤为方便。

为了简化积分的计算，还有如何选择适当的坐标系计算的问题。

可以按以下几点考虑：将积分区域Ω投影到xoy 面，得投影区域D(平面)（1） D 是X 型或Y 型，可选择直角坐标系计算（当Ω的边界曲面中有较多的平面时，常用直角坐标系计算）（2） D 是圆域（或其部分），且被积函数形如)(),(22xyf y x f +时，可选择柱面坐标系计算（当Ω为圆柱体或圆锥体时，常用柱面坐标计算）（3）Ω是球体或球顶锥体，且被积函数形如)(222z y x f ++时，可选择球面坐标系计算以上是一般常见的三重积分的计算方法。

每日一题327：三重积分计算的五种常用思路、方法及典型题分析练习题【注】如果公式显示不全，请在公式上左右滑动显示！练习327 ：计算三重积分其中积分区域为：先自己思考，动手尝试探索一下解题思路与解题过程，写写解题步骤，然后再对照下面的答案！【注1】每日一题参考解答思路一般不仅仅是为了解题，而重在分享、拓展思路，更多重在基本知识点的理解、掌握与应用！参考解答一般仅提供一种思路上的参考，过程不一定是最简单的，或者最好的，并且有时候可能还有些许小错误！希望在对照完以后，不管是题目有问题，还是参考解答过程有问题，希望学友们能不吝指出！如果有更好的解题思路与过程，也欢迎通过公众号会话框或邮件以图片、或Word文档形式发送给管理员，管理员将尽可能在第一时间推送和大家分享，谢谢！【注2】每日一题题目并非咱号完全原创，一般来自各类参考书或网络资源，由学友改编、整理并由咱号免费推送分享。

练习参考解答【注】如果公式显示不全，请在公式上左右滑动显示！练习327 ：计算三重积分其中积分区域为：【参考解答】：【思路一】由积分区域为上半球域，被积函数有两项的平方和，考虑球坐标方法计算三重积分. 建立球坐标变换如下则依据建立的球坐标系，可知积分域的球坐标变量范围为所以由三重积分的球坐标计算公式，得【思路二】由积分区域为上半球域，用平行于面的平面截取所得区域为圆域，即且. 又被积函数包含有项，故可以考虑先二后一的截面法计算三重积分. 并且二重积分由于积分区域为圆域，并且包含项，故可考虑极坐标方法，故得【思路三】由积分区域为上半球面和面围成，所以为简单的型区域，故可以考虑三重积分先一后二的投影法来计算三重积分，并且在面上的投影区域为根据投影区域的图形特征和被积函数包含有项，故对于后面的二重积分考虑极坐标方法计算，故得【注】：对于先一后二方法，如果先不计算定积分，直接将三重积分写成二重积分用极坐标描述的累次积分表达式，并且将的积分上下限和被积函数中的变量用极坐标变量描述，即则积分方法即为三重积分的柱坐标计算方法. 对于柱坐标、球坐标变换计算方法其实就是三重积分的换元法. 比如由球坐标变换关系式可得雅克比行列式的绝对值为故由三重积分换元法公式可以得到三重积分的球坐标计算公式，类似有柱坐标变换的换元结果.关于三重积分计算的一般思路与方法的详细分析与讨论可以参见视频课堂“《高等数学》解题思路与典型考题解析”课程中的“三重积分计算的一般思路与方法及三种坐标系下积分的计算步骤”章节中的五个教学视频：·第1节：三重积分计算的一般思路与步骤·第2节：计算三重积分的“先一后二”投影法的思路与步骤实例分析·第3节：柱坐标系中计算三重积分的思路与步骤实例分析·第4节：计算三重积分的“先二后一”截面法的思路与步骤实例分析·第5节：球坐标系中计算三重积分的思路与步骤实例分析另外在“第四届、第八届、第九届全国大学生数学竞赛预赛非数学类试题解析”等在线课堂对三重积分的柱坐标、球坐标和换元法分别进行了深入的分析与探讨！。