实验七分支限界法

分⽀限界法实验（单源最短路径）算法分析与设计实验报告第七次实验基本思想：附录：完整代码（分⽀限界法）Shorest_path.cpp//单源最短路径问题分⽀限界法求解#include#include#include#include"MinHeap2.h"using namespace std;templateclass Graph //定义图类{friend int main();public:void shortest_path(int); private:int n, //图的顶点数*prev; //前驱顶点数组Type **c, //图的邻接矩阵*dist; //最短距离数组};templateclass MinHeapNode //最⼩堆中的元素类型为MinHeapNode{friend Graph;public:operator int() const{return length;}private:int i; //顶点编号Type length; //当前路长};//单源最短路径问题的优先队列式分⽀限界法templatevoid Graph::shortest_path(int v){MinHeap> H(1000);//定义最⼩堆的容量为1000//定义源为初始扩展结点MinHeapNode E;//初始化源结点E.i=v;E.length=0;dist[v]=0;while(true)//搜索问题的解空间{for(int j=1;j<=n;j++)if((c[E.i][j]!=0)&&(E.length+c[E.i][j]{//顶点i到顶点j可达，且满⾜控制约束//顶点i和j之间有边，且此路径⼩于原先从源点i到j的路径长度dist[j]=E.length+c[E.i][j];//更新dist数组prev[j]=E.i;//加⼊活结点优先队列MinHeapNode N;N.i=j;N.length=dist[j];H.Insert(N);//插⼊到最⼩堆中}try{H.DeleteMin(E); // 取下⼀扩展结点}catch (int){break;}if(H.currentsize==0)//优先队列空{break;}}}int main(){int n=11;int prev[12]={0,0,0,0,0,0,0,0,0,0,0,0};//初始化前驱顶点数组intdist[12]={1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000};//初始化最短距离数组cout<<"单源图的邻接矩阵如下："<int **c=new int*[n+1];for(int i=1;i<=n;i++) //输⼊图的邻接矩阵{c[i]=new int[n+1];for(int j=1;j<=n;j++){cin>>c[i][j];}}int v=1; //源结点为1Graph G;G.n=n;G.c=c;G.dist=dist;G.prev=prev;clock_t start,end,over; //计算程序运⾏时间的算法start=clock();end=clock();over=end-start;start=clock();G.shortest_path(v);//调⽤图的最短路径查找算法//输出从源结点到⽬的结点的最短路径cout<<"从S到T的最短路长是："<for(int i=2;i<=n;i++)//输出每个结点的前驱结点{cout<<"prev("<}for(int i=2;i<=n;i++) //输出从源结点到其他结点的最短路径长度{cout<<"从1到"<}for(int i=1;i<=n;i++) //删除动态分配时的内存{delete[] c[i];}delete[] c;c=0;end=clock();printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显⽰运⾏时间cout< system("pause");return 0;}MinHeap.h#includetemplateclass Graph;templateclass MinHeap //最⼩堆类{templatefriend class Graph;public:MinHeap(int maxheapsize=10); //构造函数，堆的⼤⼩是10~MinHeap(){delete[] heap;} //最⼩堆的析构函数int Size() const{return currentsize;} //Size()返回最⼩堆的个数T Max(){if(currentsize) return heap[1];} //第⼀个元素出堆MinHeap& Insert(const T& x); //最⼩堆的插⼊函数MinHeap& DeleteMin(T& x); //最⼩堆的删除函数void Initialize(T x[],int size,int ArraySize); //堆的初始化void Deactivate();void output(T a[],int n);private:int currentsize,maxsize;T *heap;};templatevoid MinHeap::output(T a[],int n) //输出函数，输出a[]数组的元素{for(int i=1;i<=n;i++)cout<cout<}templateMinHeap::MinHeap(int maxheapsize){maxsize=maxheapsize;heap=new T[maxsize+1]; //创建堆currentsize=0;}templateMinHeap& MinHeap::Insert(const T& x){if(currentsize==maxsize) //如果堆中的元素已经等于堆的最⼤⼤⼩return *this; //那么不能在加⼊元素进⼊堆中int i= ++currentsize;while(i!=1 && x{heap[i]=heap[i/2];i/=2;}heap[i]=x;return *this;}templateMinHeap& MinHeap::DeleteMin(T& x) //删除堆顶元素{if(currentsize==0){cout<<"Empty heap!"<return *this;}x=heap[1];T y=heap[currentsize--];int i=1,ci=2;while(ci<=currentsize){if(ciheap[ci+1])ci++;if(y<=heap[ci])break;heap[i]=heap[ci];i=ci;ci*=2;}heap[i]=y;return *this;}templatevoid MinHeap::Initialize(T x[],int size,int ArraySize) //堆的初始化{ delete[] heap;heap=x;currentsize=size;maxsize=ArraySize;for(int i=currentsize/2;i>=1;i--){T y=heap[i];int c=2*i;while(c<=currentsize){if(cheap[c+1])c++;if(y<=heap[c])break;heap[c/2]=heap[c];c*=2;}heap[c/2]=y;}}templatevoid MinHeap::Deactivate() {heap=0;}。

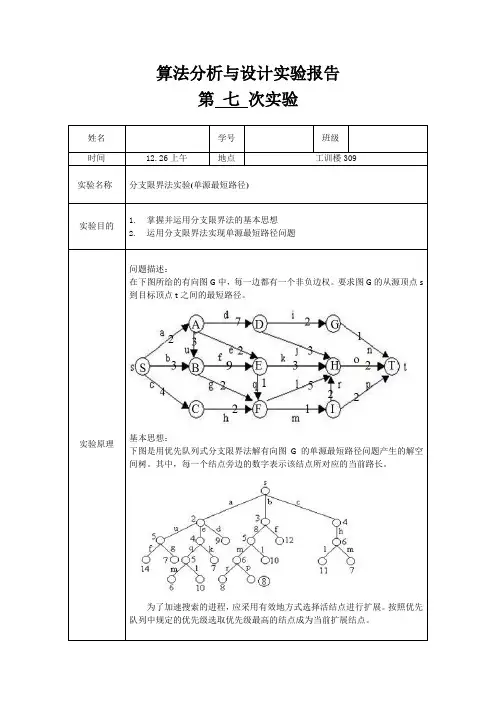
算法分析与设计实验报告第七次实验姓名学号班级时间12.26上午地点工训楼309实验名称分支限界法实验(单源最短路径)实验目的1.掌握并运用分支限界法的基本思想2.运用分支限界法实现单源最短路径问题实验原理问题描述：在下图所给的有向图G中，每一边都有一个非负边权。

要求图G的从源顶点s 到目标顶点t之间的最短路径。

基本思想：下图是用优先队列式分支限界法解有向图G的单源最短路径问题产生的解空间树。

其中，每一个结点旁边的数字表示该结点所对应的当前路长。

为了加速搜索的进程，应采用有效地方式选择活结点进行扩展。

按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。

catch (int){break;}if(H.currentsize==0) //优先队列空{break;}}}上述有向图的结果：测试结果附录：完整代码（分支限界法）Shorest_path.cpp//单源最短路径问题分支限界法求解#include<iostream>#include<time.h>#include<iomanip>#include"MinHeap2.h"using namespace std;template<class Type>class Graph //定义图类{friend int main();public:void shortest_path(int); private:int n, //图的顶点数*prev; //前驱顶点数组Type **c, //图的邻接矩阵*dist; //最短距离数组};template<class Type>class MinHeapNode //最小堆中的元素类型为MinHeapNode{friend Graph<Type>;public:operator int() const{return length;}private:int i; //顶点编号Type length; //当前路长};//单源最短路径问题的优先队列式分支限界法template<class Type>void Graph<Type>::shortest_path(int v){MinHeap<MinHeapNode<Type>> H(1000);//定义最小堆的容量为1000//定义源为初始扩展结点MinHeapNode<Type> E;//初始化源结点E.i=v;E.length=0;dist[v]=0;while(true)//搜索问题的解空间{for(int j=1;j<=n;j++)if((c[E.i][j]!=0)&&(E.length+c[E.i][j]<dist[j])){//顶点i到顶点j可达，且满足控制约束//顶点i和j之间有边，且此路径小于原先从源点i到j的路径长度dist[j]=E.length+c[E.i][j];//更新dist数组prev[j]=E.i;//加入活结点优先队列MinHeapNode<Type> N;N.i=j;N.length=dist[j];H.Insert(N);//插入到最小堆中}try{H.DeleteMin(E); // 取下一扩展结点}catch (int){break;}if(H.currentsize==0)//优先队列空{break;}}}int main(){int n=11;int prev[12]={0,0,0,0,0,0,0,0,0,0,0,0};//初始化前驱顶点数组intdist[12]={1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000 };//初始化最短距离数组cout<<"单源图的邻接矩阵如下："<<endl;int **c=new int*[n+1];for(int i=1;i<=n;i++) //输入图的邻接矩阵{c[i]=new int[n+1];for(int j=1;j<=n;j++){cin>>c[i][j];}}int v=1; //源结点为1Graph<int> G;G.n=n;G.c=c;G.dist=dist;G.prev=prev;clock_t start,end,over; //计算程序运行时间的算法start=clock();end=clock();over=end-start;start=clock();G.shortest_path(v);//调用图的最短路径查找算法//输出从源结点到目的结点的最短路径cout<<"从S到T的最短路长是："<<dist[11]<<endl;for(int i=2;i<=n;i++)//输出每个结点的前驱结点{cout<<"prev("<<i<<")="<<prev[i]<<" "<<endl;}for(int i=2;i<=n;i++) //输出从源结点到其他结点的最短路径长度{cout<<"从1到"<<i<<"的最短路长是："<<dist[i]<<endl;}for(int i=1;i<=n;i++) //删除动态分配时的内存{delete[] c[i];}delete[] c;c=0;end=clock();printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间cout<<endl;system("pause");return 0;}MinHeap.h#include<iostream>template<class Type>class Graph;template<class T>class MinHeap //最小堆类{template<class Type>friend class Graph;public:MinHeap(int maxheapsize=10); //构造函数，堆的大小是10~MinHeap(){delete[] heap;} //最小堆的析构函数int Size() const{return currentsize;} //Size()返回最小堆的个数T Max(){if(currentsize) return heap[1];} //第一个元素出堆MinHeap<T>& Insert(const T& x); //最小堆的插入函数MinHeap<T>& DeleteMin(T& x); //最小堆的删除函数void Initialize(T x[],int size,int ArraySize); //堆的初始化void Deactivate();void output(T a[],int n);private:int currentsize,maxsize;T *heap;};template<class T>void MinHeap<T>::output(T a[],int n) //输出函数，输出a[]数组的元素{for(int i=1;i<=n;i++)cout<<a[i]<<" ";cout<<endl;}template<class T>MinHeap<T>::MinHeap(int maxheapsize){maxsize=maxheapsize;heap=new T[maxsize+1]; //创建堆currentsize=0;}template<class T>MinHeap<T>& MinHeap<T>::Insert(const T& x){if(currentsize==maxsize) //如果堆中的元素已经等于堆的最大大小return *this; //那么不能在加入元素进入堆中int i= ++currentsize;while(i!=1 && x<heap[i/2]){heap[i]=heap[i/2];i/=2;}heap[i]=x;return *this;}template<class T>MinHeap<T>& MinHeap<T>::DeleteMin(T& x) //删除堆顶元素{if(currentsize==0){cout<<"Empty heap!"<<endl;return *this;}x=heap[1];T y=heap[currentsize--];int i=1,ci=2;while(ci<=currentsize){if(ci<currentsize && heap[ci]>heap[ci+1])ci++;if(y<=heap[ci])break;heap[i]=heap[ci];i=ci;ci*=2;}heap[i]=y;return *this;}template<class T>void MinHeap<T>::Initialize(T x[],int size,int ArraySize) //堆的初始化{delete[] heap;heap=x;currentsize=size;maxsize=ArraySize;for(int i=currentsize/2;i>=1;i--){T y=heap[i];int c=2*i;while(c<=currentsize){if(c<currentsize && heap[c]>heap[c+1])c++;if(y<=heap[c])break;heap[c/2]=heap[c];c*=2;}heap[c/2]=y;}}template<class T>void MinHeap<T>::Deactivate(){heap=0; }。

一、课题名称用分枝限界法求解单源最短路径问题二、课题内容和要求设计要求：学习算法设计中分枝限界法的思想，设计算法解决数据结构中求解单源最短路径问题，编程实现：（1）给出指定源点的单源最短路径；（2）说明算法的时间复杂度。

三、需求分析1.实现极小堆的创建，用来存储活结点表。

2.实现循环队列的创建、初始化、入队、出队等操作。

3.实现分支限界法来实现求解单元最短路径的算法。

4.实现最短路径的正确输出。

四、概要设计建立工程MinPath.dsw,加入源文件main.cpp，头文件CirQueue.h,init.h，Minpath.h和output.h. CirQueue.h中实现极小堆的创建，循环队列的创建、初始化、入队、出队等操作，Minpath.h中实现分支限界法来实现求解单元最短路径的算法。

output.h中实现最短路径的正确输出。

如下图所示：实验用例如下，通过邻接矩阵的方式写在init.h 中：五、详细设计12581134 69 7103 43292212223733352main函数：#include<iostream.h>#include"init.h"#include"CirQueue.h"#include"MinPath.h"#include"output.h"void main(){int k;int q;cout<<"------------欢迎使用本系统---------------"<<endl;cout<<"------------请选择单元路径的起点：---------------"<<endl;cout<<"------------提示：输入"<<1<<"到"<<n-1<<"之间的整数---------------"<<endl;cin>>k;cout<<"------------请选择单元路径的终点：---------------"<<endl;cin>>q;while(k<1||k>11){cout<<"------------提示：输入"<<1<<"到"<<n-1<<"之间的数，请重新输入---------------"<<endl;cin>>k;}MinPath(k);output(k,q);}init.hconst int size = 200;const int inf = 1000; //两点距离上界置为1000const int n = 12; //图顶点个数加1int prev[n]; //图的前驱顶点int dist[] = {0,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf}; //最短距离数组int c[n][n] = {{0,0,0,0,0,0,0,0,0,0,0,0},{0,0,2,3,4,inf,inf,inf,inf,inf,inf,inf},{0,inf,0,3,inf,7,2,inf,inf,inf,inf,inf},{0,inf,inf,0,inf,inf,9,2,inf,inf,inf,inf},{0,inf,inf,inf,0,inf,inf,2,inf,inf,inf,inf},{0,inf,inf,inf,inf,0,inf,inf,3,3,inf,inf},{0,inf,inf,inf,inf,inf,0,1,inf,3,inf,inf},{0,inf,inf,inf,inf,inf,inf,0,inf,5,1,inf},{0,inf,inf,inf,inf,inf,inf,inf,0,inf,inf,3},{0,inf,inf,inf,inf,inf,inf,inf,inf,0,inf,2},{0,inf,inf,inf,inf,inf,inf,inf,inf,2,inf,2},{0,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,0},}; //图的邻接矩阵CirQueue.hclass MinHeapNode//创建极小堆用来存储活结点表{public :int i; //顶点编号int length; //当前路长};class CirQueue//循环队列{private:int front,rear;//头指针和尾指针MinHeapNode data[size];public:CirQueue()//初始化建空队列{front = rear = 0;}void queryIn(MinHeapNode e)//元素入队操作{if((rear +1)%size != front)//队列未满{rear = (rear+1)%size; //插入新的队尾元素data[rear] = e; //在队尾插入元素 }}void queryOut()//元素出队操作{if(rear != front){front = (front+1)%size; //删除队头元素}}MinHeapNode getQuery()//读取队头元素，但不出队 {if(rear != front){return data[(front+1)%size];}return data[1];}bool empty()//判断队列是否为空{return front == rear;}bool full()//判断队列是否为满{return (rear +1)%size == front;}};//CirQueue结束MainPath.hvoid MinPath(int v){CirQueue s;//定义源为初始扩展结点MinHeapNode e;e.i = v;e.length = 0;dist[v] = 0;s.queryIn(e); //将源节点加入队列while(true){for(int j = 1;j<n;j++){if(j>=n){break;}MinHeapNode m = s.getQuery();if((c[m.i][j]<inf)&&(m.length + c[m.i][j] < dist[j]))//顶点i到顶点j可达，且从源出发途经i到j的路径长度小于当前最优路径长度{dist[j] = m.length + c[m.i][j];prev[j] = m.i;MinHeapNode mi;//加入活结点优先队列mi.i = j;mi.length = dist[j];if(s.full()){break;}s.queryIn(mi); //元素入队}}//for循环结束if(s.empty()){break;}s.queryOut(); //当该结点的孩子结点全部入队后，删除该结点 }//while循环结束}//方法结束output.hvoid output(int k,int q){int q1=q;if(dist[q1]==1000){cout<<"------------找不到此路径---------------"<<endl;return;}cout<<"最短路径长为: "<<dist[q1]<<endl;cout<<"单源最短路径为: ";int a[12]={0};int t =q1;int s=0;for(int i=0;t!=k;i++){a[i] = prev[t];t = prev[t];s=s+1;}for(i=s-1;i>-1;i--) {cout<<a[i]<<" ";}cout<<q1;cout<<endl<<"------------欢迎使用本系统---------------"<<endl; }六、测试数据及其结果分析1.选择起点：1，终点：111到11最短路径长为8，为1->3->7->10->11所获得。

分支限界法实验报告引言分支限界法是一种解决组合优化问题的常用方法，该方法通过对问题空间进行分割，并使用上、下界进行限制，从而快速得到较优解。

在本次实验中，我们主要使用分支限界法解决旅行商问题（TSP），即给定一组城市和各城市之间的距离，求解经过所有城市且距离之和最小的路径。

实验目的本次实验的目的是通过编写程序，利用分支限界法求解旅行商问题，并分析算法的效率和求解结果的优劣。

实验过程问题模型我们使用邻接矩阵来表示城市之间的距离，并通过回溯法和分支限界法来求解最优解。

其中，回溯法用于生成所有可能的路径，而分支限界法则用于剪枝和获取最优解。

在分支限界法中，我们将问题抽象为一个树形结构，树的每个节点代表选择了某一条路径。

同时，我们定义一个上界来限制搜索的范围，并实时更新下界以筛选一些无效的路径。

通过不断剪枝和对路径进行排序，我们最终可以得到最优解。

算法实现我们使用Python语言实现了分支限界法求解旅行商问题的算法。

具体实施步骤如下：步骤1：生成邻接矩阵根据给定的城市和距离，我们首先生成一个邻接矩阵，用于表示各个城市之间的距离。

步骤2：初始化数据结构我们使用一个优先队列来保存当前搜索的路径，并将起始城市加入队列。

同时，我们定义一个全局变量来保存最优路径和当前最优路径的长度。

步骤3：搜索路径通过递归的方式，不断进行路径的搜索。

在搜索过程中，我们使用上、下界和分支限界来进行剪枝操作，并实时更新最优路径信息。

步骤4：输出结果最终，我们得到的最优路径就是旅行商问题的解。

我们将其输出，并统计算法的运行时间。

实验结果实验数据我们使用了一个包含20个城市的实例进行测试，城市之间距离的数据如下：城市距离-1 -2 101 - 3 15... ...19-20 12结果分析经过多次实验，我们得到了最优路径如下：1 -> 3 -> 10 -> 5 -> 17 ->2 -> 12 -> 11 -> 4 -> 9 -> 16 -> 6 -> 19 -> 18-> 13 -> 20 -> 15 -> 8 -> 7 -> 14 -> 1该路径的总距离为123，是经过所有城市且距离之和最小的路径。

第1篇一、实验目的1. 理解并掌握分枝限界法的基本原理和实现方法。

2. 通过实际编程，运用分枝限界法解决实际问题。

3. 比较分析分枝限界法与其他搜索算法（如回溯法）的优缺点。

4. 增强算法设计能力和编程实践能力。

二、实验内容本次实验主要涉及以下内容：1. 分支限界法的基本概念和原理。

2. 分支限界法在单源最短路径问题中的应用。

3. 分支限界法的实现步骤和代码编写。

4. 分支限界法与其他搜索算法的对比分析。

三、实验环境1. 操作系统：Windows 102. 编程语言：Python3.83. 开发环境：PyCharm四、实验步骤1. 算法描述：分支限界法是一种用于解决组合优化问题的算法，其基本思想是在问题的解空间树中，按照一定的搜索策略，优先选择有潜力的节点进行扩展，从而减少搜索空间，提高搜索效率。

2. 程序代码：下面是使用Python实现的分支限界法解决单源最短路径问题的代码示例：```pythonimport heapqclass Node:def __init__(self, vertex, distance, parent): self.vertex = vertexself.distance = distanceself.parent = parentdef __lt__(self, other):return self.distance < other.distancedef branch_and_bound(graph, source):初始化优先队列和已访问节点集合open_set = []closed_set = set()添加源节点到优先队列heapq.heappush(open_set, Node(source, 0, None))主循环，直到找到最短路径while open_set:弹出优先队列中最小距离的节点current_node = heapq.heappop(open_set)检查是否已访问过该节点if current_node.vertex in closed_set:continue标记节点为已访问closed_set.add(current_node.vertex)如果当前节点为目标节点，则找到最短路径if current_node.vertex == target:path = []while current_node:path.append(current_node.vertex)current_node = current_node.parentreturn path[::-1]遍历当前节点的邻居节点for neighbor, weight in graph[current_node.vertex].items():if neighbor not in closed_set:计算新节点的距离distance = current_node.distance + weight添加新节点到优先队列heapq.heappush(open_set, Node(neighbor, distance, current_node))没有找到最短路径return None图的表示graph = {0: {1: 2, 2: 3},1: {2: 1, 3: 2},2: {3: 2},3: {1: 3}}源节点和目标节点source = 0target = 3执行分支限界法path = branch_and_bound(graph, source)print("最短路径为：", path)```3. 调试与测试：在编写代码过程中，注意检查数据结构的使用和算法逻辑的正确性。

实验七分支限界法（2学时）一、实验目的与要求1、掌握旅行商售货员问题的分支限界算法；2、区分分支限界算法与回溯算法的区别，加深对分支限界法的理解。

二、实验题：某售货员要到若干城市去推销商品，已知各城市之间的路程(或旅费)。

他要选定一条从驻地出发，经过每个城市一次，最后回到驻地的路线，使总的路程(或总旅费)最小。

三、实验提示旅行商问题的解空间是一个排列树。

有两种实现的方法。

第一种是只使用一个优先队列，队列中的每个元素中都包含到达根的路径。

另一种是保留一个部分解空间树和一个优先队列，优先队列中的元素并不包含到达根的路径。

以下为第一种方法。

由于我们要寻找的是最小耗费的旅行路径，因此可以使用最小耗费分枝定界法。

在实现过程中，使用一个最小优先队列来记录活节点，队列中每个节点的类型为MinHeapNode。

每个节点包括如下区域： x（从1到n的整数排列，其中x[0] = 1 ），s（一个整数，使得从排列树的根节点到当前节点的路径定义了旅行路径的前缀x[0:s], 而剩余待访问的节点是x [s + 1 : n - 1 ]），cc（旅行路径前缀，即解空间树中从根节点到当前节点的耗费），lcost（该节点子树中任意叶节点中的最小耗费）， rcost（从顶点x[s : n - 1]出发的所有边的最小耗费之和）。

当类型为MinHeapNode( T )的数据被转换成为类型T时，其结果即为lcost的值。

分枝定界算法的代码见程序程序首先生成一个容量为100的最小堆，用来表示活节点的最小优先队列。

活节点按lcost 值从最小堆中取出。

接下来，计算有向图中从每个顶点出发的边中耗费最小的边所具有的耗费MinOut。

如果某些顶点没有出边，则有向图中没有旅行路径，搜索终止。

如果所有的顶点都有出边，则可以启动最小耗费分枝定界搜索。

根的孩子B作为第一个E-节点，在此节点上，所生成的旅行路径前缀只有一个顶点1，因此s=0, x[0]=1, x[1:n-1]是剩余的顶点（即顶点2 ， 3 ，.， n ）。