当前位置：文档之家 › 一阶电路瞬态响应

一阶电路瞬态响应

  • 格式：ppt
  • 大小：1.71 MB
  • 文档页数：58

下载文档原格式

  / 58

合集下载

一阶电路的瞬态分析

一阶电路的瞬态分析

（1）计算 t = 0+ 电路时，电容电压不变，因此
电容等效于一直流电压源，数值为 UC (0- ) 。
UC (0- )
UC (0- )
电路分析
（2）计算 t = 0+ 电路时，电感电流不变，因此
电感等效于一直流电流源，数值为 iL (0- ) 。
iL (0- )
iL (0- )
由原电路画出t=0­时的等效电 路，得：
iL (0- ) =
US R1 + R3
= 1A,
uC (0- ) = iL (0- ) × R3 = 4V
当t=0 瞬间，闭合，由换路定则可知：
iL (0+ ) = iL (0- ) = 1 A， uC (0+ ) = uC (0- ) = 4V
t=0+时刻的等效电路如图b）所示，它是一个典型的直流电 阻电路，其中 uL (0+ ) = uC (0+ ) - R3iL (0+ ) = 0V
iC
(0+
)
=
-iL
(0-
)
=
-
US R1 + R2
,
UR2 (0+ )
= il (0- )R2
=US
R2 R1 + R2
U L (0+ ) = -U R2 + UC (0- ) = 0
电路分析
R1
R2
K
Us
C uc
iL L
等效电路如图
R1
uR2 R2
iC
uc(0 )
Us
uL iL(0 )
电路分析
+ uC
=
U

RC电路瞬态响应过程和RLC谐振电路

RC电路瞬态响应过程和RLC谐振电路
3．学习用示波器观察分析RC电路旳响应。 4．从响应曲线中求RC电路旳时间常数。
二、 RLC谐振电路试验研究
1、掌握谐振频率以及品质因数旳测量措施。 2、了解谐振电路特征频率特征，加深对谐振 电路旳认识。 3、了解谐振电路旳选频特征、通频带及其应用。
理论基础（一）
1．一阶RC电路旳零输入响应（放电过程） 电路在无鼓励情况下，由储能元件旳初始状态引起旳响应
试验内容（二）
5、Δf和Q值 根据谐振曲线计算Δf值，必要时需要补测若干点。
用Δf和f0计算Q值旳大小。 6、将电阻R增大至1k Ω ， 反复内容2~5，自制表格统计分析。
试验内容（二）
二、RLC并联谐振电路试验
1、按图构成试验电路 L=40mH, C=0.1μF, R=56kΩ.电感分别选用内阻不同旳两
试验内容（二）
一、RLC串联谐振电路试验
1、按图构成试验电路 L=40mH, C=0.1μF, R=100Ω.电感分别
选用内阻不同旳两种； 用示波器测量ui和uo 信号源输出ui为正弦波，
电压1V
试验内容（二）
2、找出电路旳谐振频率f0 将示波器旳一种输入端接在电阻R旳两端，使信号源旳
0
(t 0)
能够得出电容器上旳电压和电流随时间变化旳规律：
t
t
uC (t) uC (0 )e RC U0e
(t 0)
t
iC
(t
)
uC
(0 )e R
RC
U0
t
e
R
(t 0)
τ = RC为时间常数
理论基础（一）
2．一阶RC电路旳零状态响应（充电过程） 所谓零状态响应是指初始状态为零，而输入不为零所产生

第五章 一阶电路的瞬态分析-117页PPT资料

第五章 一阶电路的瞬态分析-117页PPT资料

电感电压电流 iL(0),UL(0) ， 电阻电压U R 2 (0 ) 。
解：开关闭合时的电容电压 U C ( 0 _ )
K
Us
R1
R2
C uc
iL L
与电感电流 i L ( 0 ) 为
U C(0)U SR 1R 2R 2, iL(0)R 1 U SR 2
由换路定则， U C ( 0 ) U C ( 0 ) ,iL ( 0 ) iL ( 0 )
i1
uC1 R1
5et
A
t 0
R=R2//R3=1.2Ω 2=RC2=2.4s uC 2(0+)=uC 2(0－)=3V
i2uR C21.5e2t.4 A t0
i2 R2 R3
+
C2
uC2

R1 i1
C1 +
u C1

Is
i2 R2 i
K R3
+
C2 uC2

i IS i1 i2 1 5 e t 1 .5 e 2 t.4At 0
第五章 一阶电路的瞬态分析
第一节 概述
电路结构，参数或电源的改变，称为换路。 电路从一种稳定状态转为另一种稳定状态，称为 过渡过程。
（1）对于纯电阻电路，电路中电压和电流的变
化是“立即”完成的。
K
R2
K闭合
I1

Us R1
，K打开 I 1 0
Us R1
R3
I1
（2）对于存在电容和电感的电路，电容元件的 电压（电荷）和电感元件的电流（磁链）变化一 般需要时间。（过渡过程时间）。
由初始条件UC(0)U0 得 k U 0 电容电压响应（变化规律）： UC(t)U0et

浙江大学实验报告：一阶RC电路的瞬态响应过程实验研究

浙江大学实验报告：一阶RC电路的瞬态响应过程实验研究

三墩职业技术学院实验报告课程名称：电子电路设计实验指导老师：成绩：__________________实验名称：一阶RC电路的瞬态响应过程实验研究实验类型：探究类同组学生姓名：__一、实验目的二、实验任务与要求三、实验方案设计与实验参数计算（3.1 总体设计、3.2 各功能电路设计与计算、3.3完整的Array实验电路……）四、主要仪器设备五、实验步骤与过程六、实验调试、实验数据记录七、实验结果和分析处理八、讨论、心得一、实验目的1、熟悉一阶RC电路的零状态响应、零输入响应过程。

2、研究一阶RC电路在零输入、阶跃激励情况下，响应的基本规律和特点。

3、学习用示波器观察分析RC电路的响应。

4、从响应曲线中求RC电路的时间常数。

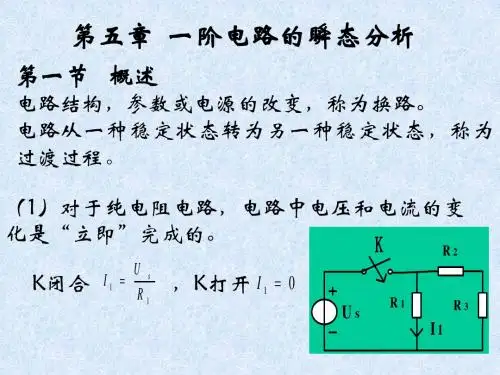
二、实验理论基础1、一阶RC电路的零输入响应（放电过程）零输入响应：电路在无激励情况下，由储能元件的初始状态引起的响应，即电路初始状态不为零，输入为零所引起的电路响应。

（实际上是电容器C 的初始电压经电阻R 放电过程。

）在图1中，先让开关K 合于位置a ，使电容C 的初始电压值0)0(U u c =-，再将开关K 转到位置b 。

电容器开始放电，放电方程是可以得出电容器上的电压和电流随时间变化的规律：式中τ=RC 为时间常数，其物理意义是衰减到1/e （36.8%）)0(u c 所需要的时间，反映了电路过渡过程的快慢程度。

τ越大，暂态响应所持续的时间越长，即过渡过程的时间越长；图1)0(0≥=+t dtdu RCu CC )0()0()(0≥-=-=---t e RU Reu t i tRCt C C τ)(u t C )0()0()(0≥==---t eU eu t u tRCt C C τ)(u t C反之，τ越小，过渡过程的时间越短。

时间常数可以通过相应的衰减曲线来反应，如图2。

由于经过5τ时间后，已经衰减到初态的1%以下，可以认为经过5τ时间，电容已经放电完毕。

图22、一阶RC 电路的零状态响应（充电过程）所谓零状态响应是指初始状态为零，而输入不为零所产生的电路响应。

电工学I(电路与电子技术)[第三章一阶电路的瞬态分析]山东大学期末考试知识点复习

电工学I(电路与电子技术)[第三章一阶电路的瞬态分析]山东大学期末考试知识点复习

第三章一阶电路的瞬态分析3．1．1 换路定则在换路瞬间(t=0)，根据能量不能跃变的原理，则有电感电流不能跃变和电容电压不能跃变。

即t=0－表示换路前终了瞬间；t=0＋表示换路后初始瞬间。

换路定则主要用来确定换路瞬间，即t=0时刻电感电流和电容电压的初始值，然后再根据基本定律确＋时刻其他各个电量的初值。

定t=0＋3．1．2 储能公式电感储存的磁场能量与电流有关；电容储存的电场能量与电压有关。

且注意：电感电压可以跃变；电容电流可以跃变；电阻只耗能不储能，故不产生瞬态过程，其中的电压和电流均可发生跃变。

3．1．3“三要素法”公式即f(t)=稳态分量+瞬态分量，其中f(t)表示一阶线性电路瞬态过程中的任意变量(电流或电压)；f(∞)表示换路后电路已达到稳定状态时电流或电压的稳态值；f(0+)表示瞬态变量的初始值；时间常数τ是表征瞬态过程进行快慢的参数，它的大小反映了电路中能量储存或释放的速度，τ愈大，则瞬态过程时间愈长。

对于RC电路：τ=RC。

对于RL电路：τ=L／R。

注意：这里的R、L和C都是等效值，其中的R是取换路后的电路，从储能元件两端看进去的一个等值电阻。

“三要素法”只适用于求解直流电源激励的一阶线性电路的瞬态响应。

3．1．4 RC串联电路的矩形波脉冲响应特点对于RC串联电路，当输入信号为连续的矩形波脉冲周期信号时，在不同的电路时间常(τ=RC)下，从电阻或电容两端会获得不同的输出电压波形，从而使输出信号与输入信号之间可形成近似的一种微分关系或积分关系。

3．2．1 本章重点(1)换路瞬间(t=0+)各电量初始值的确定。

换路定则仅适用于换路瞬间，可根据它来确定t=0+时电路电压和电流之值。

即瞬态过程的初始值，其方法如下。

①由t=0-时的等效电路求出u C(0-)和i L(0-)。

如果换路前电路处于稳态，则电感视为短路，电容视为开路。

②在t=0+的电路中，用换路定则确定的u C(0+)和i L(0+)出t=0+的等效电路。

2第二节一阶系统的瞬态响应

2第二节一阶系统的瞬态响应
表3-1 列出了一阶系统在各种典型输入下的响应。 为了减小调节时间（提高快速性），必须减小时间常数T。 下面是减小时间常数的一个方法：
R(s) E(s) 1 Ts + 1 C(s)
1 单位斜坡响应函数：R(s) = 2 s
通过反馈，使得时间常数减小了 一半。反馈后的传递函数如下：
Φ(s) = 0.5 0.5Ts + 1
t − s T
− 1 1 1 −1 −1 1 c (t ) = L [ × ]= L [ − ] =1− e T Ts + 1 s s s+ 1 T
Hale Waihona Puke C(t)1 0.8 0.6 0.4 0.2
斜率=1/T
C(∞)
0.95 0.98 0.632
可见，调整时间只与时间常数T有关。
Wednesday, December 29, 2010
第二节 一阶系统的瞬态响应
Wednesday, December 29, 2010
1
一阶系统的数学表现形式：其微分方程是一阶的，或其传 递函数的特征方程是 s的一次方程。 典型的一阶系统的结构图如下：
R(s) E(s)
-
k s
C(s)
C(s) 1 其闭环传递函数为： (s) = Φ = R(s) Ts +1 1 式中， T = ,称为时间常数。 k
Wednesday, December 29, 2010
4
小结
一阶系统的传递函数和典型结构图 一阶系统的单位阶跃响应（单调上升曲线，调 整时间） 一阶系统的单位斜坡响应 系统对输入信号导数的响应等于对输入信号响 应的导数 减小一阶系统时间常数的方法（为什么要减小 时间常数？）
Wednesday, December 29, 2010

第3章_时域瞬态响应分析_3.2一阶系统的瞬态响应

第3章_时域瞬态响应分析_3.2一阶系统的瞬态响应

(t ≥ 0)
1 斜率 − 2 T
1 0.368 T
1 − t /T xo (t ) = e T
T
一阶系统三种典型输入信号及响应关系： 一阶系统三种典型输入信号及响应关系：
xi (t ) = t
输 入
xt (t ) = t − T + Te x1 (t ) = 1 − e 1 1 −T t xδ (t ) = e T
x0(t) 1
1/T
xo(t)=1-e-t/T
86.5%
0
63.2%
95.0%
98.2%
T
2T
3T
4T
t
特点 一阶惯性系统总是稳定的，无振荡。 （1）一阶惯性系统总是稳定的，无振荡。 曲线上升到0.632的高度 。 反过来 ， 的高度。 （ 2 ） 经过时间 T ， 曲线上升到 的高度 反过来， 如果用实验的方法测出响应曲线达到0.632的时间 ， 的时间， 如果用实验的方法测出响应曲线达到 的时间 即是惯性环节的时间常数。 即是惯性环节的时间常数。 经过时间3 响应曲线达稳定值的95 95％ （3）经过时间 3T～ 4T，响应曲线达稳定值的95％～ 98％ 可以认为其调整过程已经完成， 98 ％ ， 可以认为其调整过程已经完成 ， 故一般取调 整时间( 整时间(3～4)T。 响应曲线的切线斜率为1/T。 （4）在t＝0处，响应曲线的切线斜率为 。
注意： 该性质只适用于线性定常系统， 注意 ： 该性质只适用于线性定常系统 ， 不适用于 线性时变系统和非线性系统。 线性时变系统和非线性系统。
1 T T = 2− + s s s+ 1 T
单位斜坡响应为 x0 (t ) = t − T + Te

2第二节一阶系统的瞬态响应

2第二节一阶系统的瞬态响应

y (t )
y ( )
y ( ) %
( 2或5)
t
0 td
ts
峰值时间tp 和超调量d%： 一阶系统的单位阶跃响应曲线为单调上升的指数曲线， 没有振荡，所以峰值时间和超调量不存在。
3.2.7 减小一阶系统时间常数的措施
一阶系统的时间常数T对系统性能起着非常重要的作用，时 间常数不仅影响一阶系统的响应速度，还影响系统跟踪输入信 号的精度。 对于不同的输入信号，时间常数越大，系统的响应速度越慢， 跟踪精度越低。 对于大多数的实际工程系统，通常希望有较小的时间常数。 [方法一] 通过负反馈减小时间常数 : 1 原系统为 : G ( s ) ，加入负反馈如下图： Ts 1 反馈后系统的闭环传递函数为： R s Y s 1

t2 T
t 2 2.30259 T
所以上升时间tr为： tr t2 t1 2.197 T
3.2.6 一阶系统的瞬态性能指标
调整时间ts :假设系统的误差 带宽度为,则根据调整时间的 定义有: t s 1 % 1 e T 得： 4T， 2 t s T ln % 3T， 5
-
100 s
C (s)
k
时ts≤0.1秒
由此可知：对一阶系统而言反馈加深可使调节时间减小。
反馈加深对系统的响应还有什么影响？
100 1 100 1 10 1 1 s Y ( s) ( ) 100 1 0.3 s s 30 s 3 s s 30 s
y (t ) 10 (1 e 30 t ) 3
上式的拉氏反变换称为一阶系统的单位斜坡响应 ：
y(t ) t T (1 e ), t 0

一阶电路瞬态响应

一阶电路瞬态响应
电工电子学(Ⅰ)
25
一阶电路的瞬态响应
一阶线性电路的概念
一阶电路的瞬态响应分析 一阶电路的三要素分析法
电工电子学(Ⅰ)
26
一阶线性电路的概念(1)
iL t=0t=0+ 4A 4A iC 0 -6A iR 2A 2A uC 12V 12V uL 0 0
21
电工电子学(Ⅰ)
例4电路如图4所示。求在开关s闭合瞬 间(t＝0+)各元件中的电流及其两端电压？ 当电路到达稳态时又各等于多少?设在t＝0时，电路中的储能元件均未储能。
R1
S (t 0)
例2：如图所示电路，计算开关K闭合后各元 件的电压和各支路电流的初始值。开关闭合前 电容电压为零值。
i R1 i1
解 : 因为 uC(0–)=0, 根 据
t=0 E
iC
R2
uR2
换路定律， uC(0+)=0, 作 出t=0+电路如图所示:
应用克希荷夫定律 列出电路方程如下：
电工电子学(Ⅰ) E
uR1
8
iL 2 (0) 0
L2
iR1
t= 0t= 0+ 0
iR2
0
iL1
iL2
iC1
0
iC2
0
uR2
0
uL1
0
uL2
0
uC1
uC2
0 0
0 0
0 0
0 0
24
1A -1A
1A 1A
2V -8V 8V
8V
电工电子学(Ⅰ)
电路中除元件uC、iL以外的 电容电流、电感电压以及电阻支路 电流、电压，t=0+时刻初始值是可 以突变也可以不突变的，这些电 流、电压的初始值，不能用换路定 则直接求解。

电工电子技术课程课件一阶电路瞬态响应

电工电子技术课程课件一阶电路瞬态响应
学习一阶电路瞬态响应 的基本分析方法。
阶电路瞬态响应的数学模型
一阶电路的微分方程
通过微分方程描述一阶电路 的瞬态响应。
一阶电路的传递函数
了解一阶电路传递函数的定 义和应用。
瞬态响应的数学表达式
掌握瞬态响应的数学表达式 及其意义。
一阶电路瞬态响应的实际分析
1
电路初始状态的确定
确定电路的初始电流和电压状态。
未来发展方向和趋势
展望一阶电路瞬态响应领域的未来发展方向和趋势。
电工电子技术课程课件一 阶电路瞬态响应
欢迎学习电工电子技术课程中的一阶电路瞬态响应。本课件内容涵盖了基础 知识回顾、数学模型、实际分析和总结与展望等内容。让我们一起深入了解 吧！
基础知识回顾
电路一阶线性元件 的定义
了解一阶线性元件的概 念和特性。
RC电路的基本概念
掌握RC电路的组成和工 作原理。
一阶电路的瞬态分 析基本方法
瞬态响应的电流、电压关系
2
及其图像
分析瞬态响应过程中电流和电压的
关系以及图像。
3
实际应用中的瞬态响应分析
探索一阶电路瞬态响应在实际应用 中的分析方法和应用场景。
总结与展望
一阶电路瞬态响应的重要性
总结一阶电路瞬态响应对电路性能的重要影响。
瞬态响应分析的应用范围
探讨瞬态响应分析在工程领域中的广泛应用。

第3章一阶电路的瞬态响应

第3章一阶电路的瞬态响应

－
t

其中：
uc ( )
uc ( 0 )
电容电压的终值 电容电压的初值
τ=RC
RC电路的时间常数
三个值就可以唯一确定 ！
（2）RL电路的暂态分析
i L ( t ) i L ( ) [ i L (0 ) i L ( )] e
－ t

电路的时间常数：
τ=L/R
注意：时间常数中的R值为电 路拿掉C或L后的二端网络的等 效电阻值。
iS uR
10mA S S
iR
2k 2k +
iC
1k
iL
2k
uC 10V
C -
uL
5mA
L
开关闭合： 用电压源V0= uC （0+）代替电 容； 用电流源I0=iL （0+）代替电感。
iS uR
10mA S
iR
2k +
iC
1k
iL
2k
5mA uL
10V
-
t = 0＋时刻：
注意：
t=0+时刻，除电容uC、电感iL 以外，各个电流、电压的初始值 是可以突变也可以不突变，这些 电流、电压的初始值，不能用换 路定则直接来求解。 电容、电感已储能和未储能两 种状态的处理不同。
能量不能跃变也是电路中产生 瞬态的原因。
2、换路：
电路的接通、切断、短路、电源电 压的改变或电路中元件参数的改变。 即：条件改变。 当电路中含有L、C时，由于换路 引起电路中的电压和电流发生变化， 就会引起电路中的能量关系发生变化， 而这种变化是不能跃变的。
3、电路中瞬态产生的条件 电路必须进行换路； 电路必须有储能元件L或C ； 电路换路前后储能元件储存的 能量发生改变。

一阶系统的瞬态响应

一阶系统的瞬态响应
欠阻尼瞬态响应是介于无阻尼振荡和过阻尼瞬态响应之间的一种状态，系统在激励作用下做衰减振动 。
详细描述
在欠阻尼瞬态响应中，一阶系统的输出呈现衰减振荡的特点，其幅度随着时间的推移逐渐减小，直到 达到稳定状态。这种响应通常出现在系统具有一定的阻尼效应，但不足以阻止振动的发生。
过阻尼瞬态响应
总结词
过阻尼瞬态响应是一种一阶系统的瞬态响应形式，其特点是系统在激励作用下立即达到 稳态值，不发生振动。
THANKS FOR WATCHING
感谢您的观看
在控制系统中的重要性
基础性
一阶系统作为最简单的动态系统，是 理解和分析更复杂系统的基础。
实际应用
在实际的工程系统中，许多实际系统 的动态行为可以用一阶系统近似描述 。
瞬态响应与稳态响应的区别
瞬态响应
描述系统在输入信号作用下的动态行为，包括过渡过程和达 到稳态所需的时间。
稳态响应
描述系统在输入信号的长期影响下达到的稳态输出，与时间 无关。
传递函数表示
01
02
03
传递函数定义
一阶系统可以用传递函数 表示，如 $G(s) = frac{b}{as + b}$，其中 $s$ 是复变量。
极点和零点
传递函数的极点和零点决 定了系统的动态响应特性。
稳定性分析
通过极点和零点分析系统 的稳定性。
动态响应分析
时间响应
根据系统的微分方程或传递函数，分析系统的动态响应过程。
02
一阶系统的数学模型
微分方程描述
微分方程描述
一阶系统通常由一个一阶微分方程描述，如 $frac{dx}{dt} = ax(t) + b$，其中 $x(t)$ 是系统状态，$a$ 和 $b$ 是系统参数。

电路的一阶瞬态响应

电路的一阶瞬态响应
(1)、对称方波通过微分电路(高通滤波器)
微分电路如图3-1所示，该电路的时常数为T=RC ，若 输入的方波的脉宽τ 远大于电路的时常数T，则输出的波形 为尖脉冲；若方波的脉宽τ 远小3 T τ
R
图3-1
微分电路
τ＞3~6T
从频域角度分析，微分电路实质上是一个高通滤波器，其 系统函数为： H(s)=S／(S+1/RC)
C R
图3-4
串联谐振电路
当方波加至串联谐振电路时，将引起电路的谐振，振荡
0 1 LC 的频率为： 此时只要满足方波的频率 1 认为是阶跃响应。
0 ，就可以把响应的前半周
三、实验电路(见下页) ： 四、实验前预习内容：
1、计算微分电路的截止频率（R=10KHZ,C=1000PF),并画 出幅拼特性曲线； 2、计算积分电路的截止频率（R=20KHZ,C=1000PF),并画 出幅拼特性曲线； 3、计算LC低通滤波器的截止频率（L=10mH,C=0.1μ F)； 4、计算图3-4所示串联谐振电路的阶跃响应，并画图。
吉伯斯现象。 2、阶跃响应的观测 阶跃响应则是指单位阶跃信号作用下系统的零状态响 应。我们用冲激响应和阶跃响应来描述系统的时域特性。由 于普通示波器无法捕捉到t=0时刻的瞬间跳变，所以我们用 方波作为激励信号；只要方波的重复周期T1足够大 (T1>>阶 跃响应建立的时间tr) ，则方波前半周的信号就可以看成是 阶跃信号，若将此方波通过系统其响应的前半周就可以认为 是阶跃响应。本实验的线性系统为一串联谐振系统，如图 3-4所示。 L
六、实验报告要求：
1、叙述实验内容及实验步骤； 2、按照实验内容中的要求详细记录所测得的波形，并对 所得波形进行相应的理论解释。
其截止频率为：ω c＝1/RC 当方波通过高通率波器时，基波及低次谐波分量将受到 衰减，从而产生平顶失真；而且RC越小(截止频率越大)失真 越大，即波形越尖；反之波形失真较小，波形较平坦。 (2)、对称方波通过积分电路(低通滤波器) 积分电路如图3-2所示，该电路的时常数为T=RC ，若 输入的方波的脉宽τ 远大于电路的时常数T，则输出的波形 近似方波；若方波的脉宽τ 远小于电路的时常数T，则输出 的精度大大降低，波形接近三角波如图3-2所示。

一阶系统瞬态响应

一阶系统瞬态响应

3.2 一阶系统的瞬态响应可用一阶微分方程描述的系统，称为一阶系统。

典型的一阶系统微分方程式为(3.7)系统的传递函数为(3.8)式中T为系统的时间常数，K为系统的放大系数，y(t)为系统的输出变量，x(t)为系统的输入变量。

3.2.1 一阶系统的单位阶跃响应一阶系统的单位阶跃响应为(3.9)将式（3.9）展开为部分分式(3.10)对式（3.10）两边进行拉普拉斯变换，得到(3.11)式（3.10）即一阶系统的单位阶跃响应。

图3.4给出了响应y(t)的变化曲线：这是一条指数曲线。

在t=0时，曲线的斜率最大。

(3.12)曲线斜率随时间增加不断下降。

当t时，斜率为零，动态过程结束。

这时的响应记为=K，即单位阶跃信号经过了一阶系统后被放大了K倍。

过t=0点做响应曲线的切线，与表示的直线交于P点。

P点所对应的时间t=T，而此时响应值y(T)=0.632K。

工程上常用这个特征来判断实验曲线是不是一阶系统的响应曲线。

图3.4 一阶系统的单位阶跃响应y(t)的瞬态响应曲线从t=0到逐渐变缓。

y(t)变化的几个典型值见表3.1。

从表3.1可以看出，一阶系统瞬态响应的主要部分是在动态过程初始阶段内完成的。

理论上来看，只有在时，一阶系统的单位阶跃响应动态过程才能结束。

在实际工程中，当输出响应进入到一定的误差范围后，就可以认为动态过程已经结束。

我们用调节时间来描述动态过程的长短。

就是一个系统的动态性能指标。

工业上常取的误差范围为2%或5%，若取2%的误差范围，则若取5%的误差范围，则一阶系统的时间常数是决定系统动态特性的参数。

T的大小表明了一阶系统惯性的大小。

T越大，也越大，说明系统响应变化得慢。

T越小，即系统惯性小，也越小，输出响应变化得就快。

3.2.2 一阶系统的单位斜坡响应一阶系统单位斜坡响应的拉普拉斯变换为展开成部分分式后得到(3.14)求（3.14）式的拉普拉斯变换，得到(3.15)图3.5给出了一阶系统的单位斜坡响应曲线。

浙江大学_一阶RC电路的瞬态响应过程实验研究 _RLC谐振实验研究-推荐下载

浙江大学_一阶RC电路的瞬态响应过程实验研究 _RLC谐振实验研究-推荐下载



U0
R
t
t
e
(t 0)
(t 0)
先让开关 K 合于位置 b，当 t = 0 时，将开关 K 转到位置 a。电容器开始充电，充电方程为： 初始值：uC(0-)=0，可以得出电压和电流随时间变化的规律：
uC
RC duC dt
t
uC (t) US 1 e RC US 1 e
定义传递函数(或网络函数)为输出电压与输入电压之比，即
H
(
)

VR VS

R
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关，1系电过，力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层，机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2，高总而中体且资配可料置保试时障卷，各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高；中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整，处核或理对者高定对中值某资，些料审异试核常卷与高弯校中扁对资度图料固纸试定，卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置，跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等，料，编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气，线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术，技含以来术线及避槽系免、统不管启必架动要等方高多案中项；资方对料式整试，套卷为启突解动然决过停高程机中中。语高因文中此电资，气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技，进术合行，理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对：于于在调差分试动线过保盒程护处中装，高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时，术，作是应为指采调发用试电金人机属员一隔，变板需压进要器行在组隔事在开前发处掌生理握内；图部同纸故一资障线料时槽、，内设需，备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切，验除线报从缆告而敷与采设相用完关高毕技中，术资要资料进料试行，卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

一阶电路瞬态分析

一阶电路瞬态分析

1 K
4 L iL
+
uL
t = 0时闭合开关k , 求 uL(0+)
-
uL ( 0 ) 0 uL ( 0 ) 0

10 2A 先求 i L (0 ) 1 4

由换路定律: 0+电路 1
iL(0+)= iL(0-) =2A
4
+
10V 2A uL
uL ( 0 ) 2 4 8V
1.
二. 换路定律（开闭定则） 1 t 1 0 1 uC ( t ) i ( )d i ( )d C C C t 1 + i uC (0 ) i ( )d uc C 0 - C t = 0+时刻


t 0
i ( )d
q =C uC
y( t ) y( 0 )e

t

2. 衰减快慢取决于时间常数。RC电路 = RC, RL电路 = L/R
R等
C
= R等C
3. 同一电路中所有响应具有相同的时间常数。 4.一阶电路的零输入响应和初始值成正比，称为零输入线性。
§5-3 零输入响应
K(t=0)
uC (0-)=U0
§5-4 一阶电路的零状态响应
一、RC电路的零输入响应
K(t=0)
uC (0-)=U0
i
R
pt
解: uR uC 0
d uC i C dt
C
uC
–
+
uR
–
+
d uC RC uC 0 dt uC ( 0 ) U 0
设 uC Ae
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初值（0+）
短路
uC 0
C
终值（∞）
开路
iC 0
开路
L
短路
iL 0 uL 0
L

C
u U0
电压源 + 短路

开路
U0

C
iC 0
iL I 0
电流源 + I0 开路
短路
L
uL 0
L
14
电路中初始值的确定(3)

例1: 如图1所示电路，换路前开关S闭合电路处 于稳态,求换路后电容电压的初始值 uC(0+),iR(0+)。 R K 解:由于换路前电 4k i t=0 u 路处于稳态，电容相 8k 12V 2 mF R 当于开路，作出t=0– 等 图1 效电路如图所示。 R
W L (T ) W L (T ) WC (T ) WC (T )
12
电路中初始值的确定(1)

换路定则仅适用于换路瞬间，可根据它来确定t=0+时 电路电压和电流之值。即瞬态过程的初始值，其方法 如下：
1．由t=0–时的等效电路求出uC(0–)和iL(0–)。如果换路前 电路处于稳态，则电感视为短路，电容视为开路。 2．在t=0+的电路中，用换路定则确定uc(0+)和iL(0+)求出 t=0+的等效电路。
电工电子学(Ⅰ)
11
换路定则内容(3)
如果换路发生在任意时刻t=T，则换路定则 表达式为：
i L (T ) i L (T ) uC (T ) uC (T )
L (T ) L (T ) q C (T ) q C (T )
电工电子学(Ⅰ)
8
iL 2 (0) 0
L2
iR1
t= 0t= 0+ 0
iR2
0
iL1
iL2
iC1
0
iC2
0
uR2
0
uL1
0
uL2
0
uC1
uC2
0 0
0 0
0 0
0 0
24
1A -1A
1A 1A
2V -8V 8V
8V
电工电子学(Ⅰ)
电路中除元件uC、iL以外的 电容电流、电感电压以及电阻支路 电流、电压，t=0+时刻初始值是可 以突变也可以不突变的，这些电 流、电压的初始值，不能用换路定 则直接求解。
1.电路必须进行换路——即电路的接通，断开、短 路、开路，电源电压改变或电路参数改变。 2.电路中必须有储能元件L或C；
电工电子学(Ⅰ) 3.换路前后储能元件储存的能量发生改变。
9
换路定则内容(1)
由于电路的换路，使电路中的能量发生变化，而这 种变化是不能跃变的——必须是连续的。
设t=0为换路瞬间，t=0–表示换路前的终了瞬间， t=0+表示换路后的初始瞬间，0–和0+在数值上都等于0， 但0–是t从负值趋近于0，0+是t从正值趋近于0，从t=0– 到t=0+瞬间，电感元件中储存的磁场能量，WL 和电容 元件中储存的电场能量WC是不能跃变的，即
一阶电路的矩形波响应
本章小结
电工电子学(Ⅰ)
3
换路定则
瞬态的概念 电路中瞬态产生的原因 换路定则内容
电路中初始值的确定
电工电子学(Ⅰ)
4
瞬态的概念（1）
前面几章我们所讨论的是电路的稳定 状态。所谓稳定状态，就是电路中的电流 和电压在给定的条件下已到达某一稳态值, 对交流讲是指它的幅值到达稳定。稳定状 态简称稳态。电路的过渡过程往往为时短 暂，所以电路在过渡过程中的工作状态常 称为瞬态，因是个过渡过程又称为瞬态过 程。瞬态过程虽然为时短暂，但在不少实 际工作中却是极为重要的。
第 3 章
一阶电路瞬态响应
1
本章教学基本要求
• 理解电路的瞬态、换路定则和时间常数的基本概念；
• 掌握一阶电路瞬态分析的三要素法。
• 理解零输入响应、零状态响应、瞬态响应、稳态响应
和全响应的概念。
• 本章讲授学时: 3学时 自学学时: 8学时
电工电子学(Ⅰ)
2
主要内容
换路定则 一阶电路的瞬态响应
R1
S (t 0)

2
L1 1H

U S 10V
C2
图4
R2
2mF
C1
1mF
解：因为换路前电容元 件和电感元件均未储能，所 以：
8
L2
2H
i L1 (0) i L 2 (0) 0 uC 1 (0) uC 2 (0) 0
iL1 (0) iL1 (0) iL 2 (0) iL 2 (0) 0 电工电子学(Ⅰ) uC1 (0) uC 2 (0) uC1 (0) uC 2 (0) 0
u C (0 ) u C (0 ) 8V
用 8V 电 压 源 代 替 uC(0+) 画 出 t=0+的等效电路见图所示。
iR (0+) R2
8k
+ uC (0+) –
t=0＋的电路
电工电子学(Ⅰ)
uC (0 ) 8 i R (0 ) 1mA R2 8
16
电路中初始值的确定(5)
例2：如图所示电路，计算开关K闭合后各元 件的电压和各支路电流的初始值。开关闭合前 电容电压为零值。
i R1
解: 因为 uC(0–)=0,根 据
t=0 E
i1
iC
R2
uR2
换路定律，uC(0+)=0,作 出t=0+电路如图所示:
应用克希荷夫定律 列出电路方程如下：
电工电子学(Ⅰ) E
uR1
C
uC
iC(0+) i(0+) R1 i1(0+) R 2 uR1(0+) + – uR2(0+) uC(0+) =0
电工电子学(Ⅰ)
25
一阶电路的瞬态响应
一阶线性电路的概念
一阶电路的瞬态响应分析 一阶电路的三要素分析法
电工电子学(Ⅰ)
26
一阶线性电路的概念(1)


什么是一阶电路? 只含有一个储能元件或可等效为一个储能元件 的线性电路，不论是简单的或复杂的，它的微分方 程都是一阶常系数线性微分方程。这种电路称为一 阶线性电路。 一阶电路的等效模型 对于一阶线性电路,由于只含有一个独立的储能 元件(L或C）,电路可分割成两个部分： 线性 电阻网络 N

2
L1
iL1 (0) 0
iC1
uC1 (0) 0
i R1 i R 2 iC 1 iC 2 1A

U S 10V
iR 2
iC 2
R2
C1
uR 2 uL1 uL 2 8V uR1 i R1 R1 2V
uR1
0
C 2 uC 2 (0) 0
22
由此画出t=0+时的等效电路如下图4a：
R1
S (t 0)

iR1
R1
2
L1 1H

U S 10V
C2
图4
R2
2mF
C1
1mF
S (t 0)

2
L1
iL1 (0) 0
iC1
uC1 (0) 0
8
L2

U S 10V
iR 2
iC 2
R2
C1
2H
C 2 uC 2 (0) 0
E iC (0 ) R2
t=0+电路
E i1 (0 ) R1
R1 R2 R R1 R2
18
E E E i (0 ) i1 (0 ) ic (0 ) R1 R2 R
电工电子学(Ⅰ)
电路中初始值的确定(7)
例3:在图3所示电路中，已知:R1=4Ω,R2=6Ω, R3=3Ω,C=0.1µF,L=1mH,US=36V,开关S闭合已经很 长时间,在t=0时将开关S断开,试求电路中各变量的 初始值。
解：画出t=0-的电路如图3图（b）所示： 电容C以开路代 替，电感L以短路代替。
电工电子学(Ⅰ)
19
求出uC(0-)和iL(0-)
R2 // R3 uC (0 ) US R1 R2 // R3 12V
uC (0 ) i L ( 0 ) R3 4A
画出 t=0+的电路如图（c）所示：电容C以电压源代替，电 感L以电流源代替。
6
电路中瞬态产生的原因(1)
瞬态过程的产生是由于物质所具有的能量 不能跃变而造成的。电路中产生瞬态的主要原 因是由于电路的接通、切断、短路、电源电压 的改变或电路中元件参数的改变等（称为换路） 引起电路中的电压和电流发生变化，当电路中 含有电感元件和电容元件的时候，就会引起电 路中的能量关系发生变化，即：使电感储存的 磁场能量发生变化，或使电容中储存的电场能 量发生改变等，而这种变化也是不能跃变的。
iR US , R1 R2
t
iC 0, uC 0 WC 0
iL 0, uL 0 WL 0
uR
R2 US R1 R2
t 0 t
iC 0,
WC
t 0 t
US iL , R
WL
uC U S
1 2 CU S 2
uL 0
1 2 Li L 2
电工电子学(Ⅰ)
5
瞬态的概念(2)

日常生活中的瞬态现象
自然界事物的运动，在一定条件下有 一定的稳定状态，当条件改变时，就要过 渡到新的稳定状态。 在电路中也同样存在瞬态过程，例如， 在RC串联的直流电路中，其中电流为零， 而电容元件上的电压等于电源电压，这是电 路已经达到稳定状态时的情况。