初三数学第4讲：三角形一边的平行线判定定理

第三讲：三角形一边的平行线判定定理一、知识要点：1、三角形一边的平行线判定定理：如果一条直线截三角形的两边所得的对应线段成比例，那么这条直线平行于三角形的第三边。

数学表达：如图，直线DE 截△ABC 得两边AB 、AC ， 若①AD AE DB EC =,②AD AE AB AC =,③BD ECAB AC=中之一为已知条件，则DE ∥BC 2、三角形一边的平行线判定定理推论：如果一条直线截三角形两边的延长线（这两边的延长线在第三边的同侧）所得的对应线段成比例，那么这条直线平行于三角形的第三边。

数学表达：若点D 、E 分别在射线AB 、AC 上，如图（1）或分别在他们的方向延长线上如图（2），且具备上述条件①、②、③之一，则D E ∥BC. 牛刀小试：1、如图，△ABC 中，点D 、E 分别在边AB 、AC 上。

判断在下列条件下能否推出D E ∥BC,为什么？（1）23AD DB =,AE=2，AC=3 （2）25AD AB =,25DE BC =（3）23AD DB =,53AC CE =2、△ABC 中，直线DE 交AB 于点D ，交AC 于点E ，那么能推出D E ∥BC 的条件是（）A 、AB 3=AD 2,EC 1=AE 2B 、AD 2=AB 3,DE 2=BC 3 C 、AD 2=DB 3,CE 2=AE 3D 、AD 3=AB 4,AE 3=EC 4二、典型例题例1、如图EF ∥BC ，31=AC AF ，BF=4，FD=2，求证：EF ∥ADADEDCBAEFBC例2、如图所示，M 为AB 的中点，EF ∥AB,连接EM 、FM ，分别交AF 、BE 于点C 、D ，连接CD 。

求证：CD ∥AB.分析：判定两直线平行的方法一般有四种：（1）通过“三线八角”的相等或互补判定两直线平行；（2）通过三角形、梯形中位线定理判定两直线平行；（3）通过平行四边形的判定间接证平行；（4）通过比例线段证平行。

基础知识点三角形一边的平行线性质定理：平行于三角形一边的直线截其他两边所在直线，截得的对应线段成比例。

如图(1)，若DE//BC ，则AD AE DB EC =或AD AE AB AC =或DB CEAB AC =如图(2)，若DE//BC ，则AB AC AE AD =或AB AC EB DC =或EA DAEB DC=EDE（2）（1）CBADC BA三角形一边的平行线性质定理推论：平行于三角形一边的直线截其他两边所在的直线，截得的三角形的三边与原三角形的三边对应成比例。

如图(1)已知：△ABC 中，点D 、E 分别在AB 、AC 上，且DE//BC ，则AD DE AEAB BC AC==; 如图(2)已知：△ABC 中，点D 、E 分别在CA 、BA 的延长线上，且DE//BC ，则AB BC ACAE DE AD==. EDE（2）（1）CBADC BA同高(或等高)的两个三角形的面积之比等于对应底边的比（2）（1）DCBADCBA如图(1)：ABD ADCS BDSDC =如图(2)：若AD//BC,则ADC ABCS ADSBC=三角形重心(三中线交点)：三角形的重心到一个顶点的距离，等于它到这个顶点对边中点的距离的两倍。

1、三角形三条中线交于一点，三角形三条中线的交点叫做三角形的重心。

2、三角形的重心到一个顶点的距离，等于它到这个顶点对边中点距离的两倍。

例题解析如图，在ABC ∆中，DE //BC ，下列各式中错误的是( ). A.AD AB AE AC = B.BD EC AD AE = C.AD DE DB BC = D.AE DEAC BC =答案：C变式：如图，已知在ABC ∆中，DE //BC ，EF //CD ，那么下列线段的比中与AEAC相等的有( )个。

①AF AB②AF AD ③FD FB④ADABA.0B.1C.2D.3答案：C,①和④例题讲解:在△ABC 中，DE//BC ，DE 与AB 相交于D ，与AC 相交于E 。

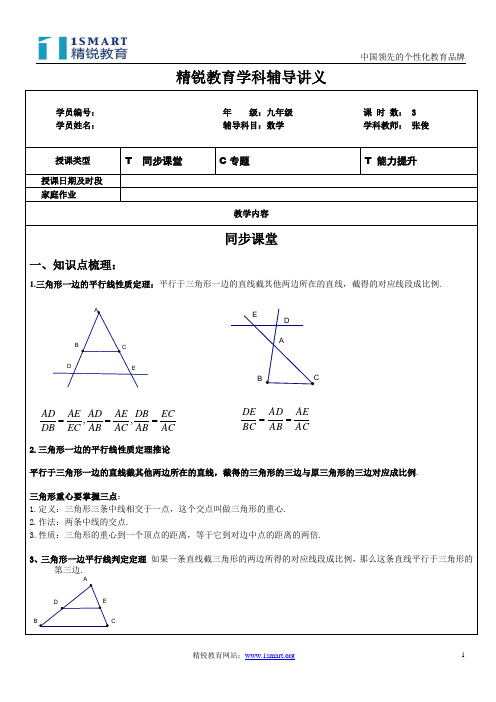
精锐教育学科辅导讲义学员编号： 年 级：九年级 课 时 数： 3 学员姓名： 辅导科目：数学 学科教师： 张俊授课类型 T 同步课堂C 专题 T 能力提升授课日期及时段 家庭作业教学内容同步课堂一、知识点梳理：1.三角形一边的平行线性质定理：平行于三角形一边的直线截其他两边所在的直线，截得的对应线段成比例.EDABCAEDCBAC AE AB AD BC DE == 2.三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线，截得的三角形的三边与原三角形的三边对应成比例. 三角形重心要掌握三点：1.定义：三角形三条中线相交于一点，这个交点叫做三角形的重心.2.作法：两条中线的交点.3.性质：三角形的重心到一个顶点的距离，等于它到对边中点的距离的两倍.3、三角形一边平行线判定定理 如果一条直线截三角形的两边所得的对应线段成比例，那么这条直线平行于三角形的第三边.,,AD AE AD AE DB EC DB EC AB AC AB AC===ABCDE三角形一边的平行线判定定理推论 如果一条直线截三角形两边的延长线（这两边的延长线在第三边的同侧）所得的对应线段成比例，那么这条直线平行于三角形的第三边.AEDCB4、平行线分线段成比例定理：两条直线被三条平行的直线所截，截得的对应线段成比例.FED CB A用符号语言表示： ΘAD ∥BE ∥CF,,,AB DE BC EF AB DEBC EF AC DF AC DF∴===. 平行线等分线段定理：两条直线被三条平行的直线所截，如果在一直线上所截得的线段相等，那么在另一直线上所截得的线段也相等.（一）、比例式 比例式：1、设2y －3x ＝0（y ≠0），则yyx +＝ ． 比例中项：1、已知线段a=2，b=8，若线段c 是线段a 与b 的比例中项，则c ＝ ． （二）、A 字型1、在△ABC 中，已知点D 、E 分别在边AB 、AC 上，DE ∥BC ．如果AD ＝1cm ，AB ＝3cm ，DE ＝4cm ，那么BC ＝ cm ．2、已知：在△ABC 中，点D 、E 分别在边AB 、AC 上，DE ∥BC ．如果AD ＝4cm ，AB ＝6cm ，DE ＝3cm ，那么BC ＝ cm ．3、如图，在△ABC 中，DE ∥B C ，DB AD ＝21， 则BCDE＝ ．AD CEB4、已知：如图，在△ABC 中，BD 是∠ABC 的平分线，过点D 作DE ∥CB ，交AB 于点E ，DC AD ＝31， DE ＝6，则AB ＝ ．（三）、X 型 1、如图，AB//CD ，AD 与BC 交于点O ，若35 OD OC ，则BOAO= ．2、如图，E 是平行四边形ABCD 边AD 上一点，且AE ∶ED=1∶2，CE 与BD 交于点O ，则BO ：OD= ．（四）、中间比1、如图，在△ABC 中，DE ∥BC ，DF ∥AB ，那么下列比例式中正确的是（ ）（A ）EB AE ＝FC BF ； （B ）EB AE ＝FB CF ；（C ）BC DE ＝DC AD； （D ）BC DE ＝AB DF ． （五）、重心1、如果直角三角形的斜边长为18，那么这个直角三角形的重心到直角顶点的距离为 ．2、在△ABC 中，∠ACB ＝90°，AC ＝3.6，BC ＝4.8，点G 为△ABC 的重心，则点G 到AB 中点的距离为 ．3、如图，BE 、CD 是△ABC 的边AC 、AB 上的中线，且相交于点F ．则FCDF＝ ．4、如图，已知点O 是△ABC 的重心，过点O 作EF ∥BC ，分别交AB 、AC 于点E 、F ，若BC ＝6，则EF ＝ ．DACBOE DABC ODBCEFBCDE B CE AF OBAECFD专题一、填空题：1．若():1:2x y y -=，则:x y =___ _． 2．已知线段a ，b ，c 满足关系式a bb c=，且3b =，则ac =_ _． 3．已知345x y z==，且18x y z -+=，则2x y z ++= ． 4．如图1－1所示，在△ABC 中，D ，E 分别在AB ，AC 上，且DE ∥BC ，=3AD ，=5AB ，=1CE ，那么=AC ．ABCD E1－1A BCDE F1－2ABCDE1－31－4E D CBAF5．如图1－2所示，在△ABC 中，DE ∥BC ，如果12AD DB =，那么EFBF= ． 6．如图1-3所示，在△ABC 中，BD 平分ABC ∠，交AC 于D ，DE ∥BC ，交AB 于点E ，若=6AB ，=4DE ，则=BC ．7．如图1－4所示，EF 平行BC ，FD 平行AB ，=18AE ，=12BE ，=14CD ，则=BD ．A BCDE1－5G1－6FEDCBA1－7F EDCBAABCDEF1－88．如图1－5所示，△ABC 中，DE ∥BC ，4AB =，8AC =，DB AE =，则AE = ．9．如图1－6所示，△ABC 中，DE ∥FG ∥BC ，若::=2:5:9DE FG BC ，则::AD DF =FB ． 10．如图1－7所示，AB ⊥BC 于B ，EF ⊥BC 于F ， DC ⊥BC 于C ，=4AB ，=14DC ，且:=2:3BF FC ．则EF 的值为 ．11．如图1-8所示，ABCD Y 中，DE 平分ADC ∠，=2AB ，=3AD ，则=DF FE ： ． 12．如图1－9所示，直角梯形ABCD 中，AD ∥BC ，BC DC ⊥，3=AD ，6=BC ，4=CD ，则=AO ． 1－9DCBAO13．如图1－10所示，△ABC 中，DE ∥AC ，FD ∥AB ，则ABDFAC DE +的值为 ． 1－10FE DCBAABC DEF1－11A BCDEF1－12O 1-13E DC BA14．在△ABC 中，如果5==AC AB 厘米，8=BC 厘米，那么这个三角形的重心G 到BC 的距离是 ． 15．如图1－11所示，E 为ABCD Y 的边AD 延长线上一点，且D 为AE 的黄金分割点，即AE AD 215-=，BE 交DC 于点F ，已知15+=AB ，则CF 的长是 ．16．如图1－12所示，梯形ABCD 中，AD ∥BC ，AC ，BD 相交于点O ，过O 点做AD 的平行线交AB 于点E ，交CD 于F ，若3=AD ，5=BC ，则=EF ． 17．如果线段a ，b 满足222350a ab b --=，则ab的值是 ．18．平行四边形ABCD 中，对角线BD 的四等分点为1O ，2O ，3O ，1AO 的延长线交BC 于E ，3EO 的延长线交AD 于F ，则:AF FD = ．19．如图1－13所示，在△ABC 中，C ∠90=o ，3AC =，D 为BC 上一点，过点D 作DE BC ⊥交AB 于点E ，若1ED =，2BD =．则DC 的长为 ．20．如图1－14所示，边长为8的正△ABC ，DE ∥BC ，面积比:1:4BCD ABC S S =△△，则EC = ．1-14E D CBAQF1-15EDCB AHF 1-16EDCBA21．若a b c k b c a c a b===+++，则k = ． 22．如图1－15所示，四边形ABCD ，EQ ∥CD ，EF ∥AB ，则EF EQAB CD+= ． 23．如图1－16所示，E 是△ABC 中BC 边的中点，F 是BC 边上任一点，过F 作FH ∥AE ，交BA 的延长线于点D ，交CA 于点H ，则FD FHAE AE+= ．24．已知::2:3:5a b c =，5a b c ++=，求a ，b ，c 的值 ． 25．已知31212358a a a b b b ===，则1212a ab b ++= ，1313a a b b ++= ． 26．已知23a c b d ==，则44a cb d--= ． 27．已知::2:3:4a b c =，则有23a b ca++= ．28．2，3，6的第四比例项是 ．二、解答题：1．如图1－31所示，B ，C 是△APM 边AP 上的两点，过B 作BN ∥AM 交PM 于N ，过N 作ND ∥MC 交AP 于D ． 求证：PA PCPB PD=． N1-31D C B MAP2．如图1－32所示，梯形ABCD 中，AD ∥BC ，对角线AC ，BD 相交于O ，过O 作AD 的平行线与两腰分别相交于E ，F ，比较OE 与OF 的大小关系，并说明理由．O1-32D CBEA F3．已知线段a ，b ，c 如图1－33所示，求作线段x ，使2bc x a=． c b a 1-334．如图1－34所示，在△ABC 中，12==AC AB ，4=BC ，BD 平分ABC ∠，DE ∥BC ． 求△ADE 的周长．1－34E DCBA5．如图1－35所示，已知在△ABC 中，EFCD 是菱形，且3AD =，5=BF ．求菱形EFCD 的边长．1－35F E DCBA6．如图1－36所示，平行四边形ABCD 的对角线AC 与BD 相较于点O ，E 是CD 的中点，AE 交BD 与点F ． 求FODF的值．DCBEAF1-36O7．如图1－37所示，在△ABC 中，EF ∥BC ,DF ∥EC ．求证：AE 是AB AD 与的比例中项．1-37F AE BCD ADEBCF1-388．如图1－38所示，在△ABC 中，AB AD 31=，延长BC 到点F ，使得BC CF 31=．连接DF ，交AC 于点E ， 求证：（1）EF DE =；（2）EC AE 2=．9．如图1－39所示，AD ∥EF ∥BC ，5AD =，7BC =，E 是AB 的黄金分割点，BE AE >． 求EF 的长．ADE BCF1-3910．如图1－40所示，已知E 是平行四边形ABCD 的边CD 上的一点，连接AE 并延长交BC 的延长线于点F ． 求证：DC DE FB AD ::=．1-40CBED AF11．已知a ，b ，c ，d 四条线段能够成比例，2=a 厘米，3=b 厘米，5=c 厘米．求线段d 的长度．12．如图1－41所示，在ABCD Y 中，E 是AB 的中点，=AF 12DF ，EF 交AC 于点G ．求AC AG的值． ADE BCF1-41G13．如图1－42所示，D 为△ABC 中BC 上一点，EF ∥BC 交AD 于点H ．求证：EH BD HF CD=． HADEBCF1-4214．如图1－43所示，在△ABC 中，AD BC ⊥于点D ，BE AC ⊥于点E ，H 为AC 上一点，且AH AD =，过点H 作HF ∥BC 交AB 于点F ． 求证：FH BE =．HAD EBCF 1-43课后总结：能力提升一、填空题：1．如图1—61所示，梯形ABCD 中，DC ∥AB ，DC =3，AB =5, E 是DA 的黄金分割点，且EF ∥AB 交BC 于点F ，则EF = ．1-61D CBE AF B 2A 2C 2A 1B 1C 11-62CBA 1-63DC BEA FE nE 3E 2E 1D nD 3D 21-64D 1CBA2．如图1—62所示，点1A ，2A ，1B ，2B ，1C ，2C 分别是△ABC 的边BC ，CA ，AB 的三等分点，若△ABC 的周长是m ，则六边形1A 2A 1B 2B 1C 2C 的周长是 ．3．如图1—63所示，AD ∥EF ∥BC ,AD =12，BC =17，AE :EB =2:3，则EF = ．4．△ABC 中，BC =a ，若1D ，1E 分别是BC ，AC 的中点，则1D 1E =12a ；若2D ，2E 分别是1D B ，1E C 的中点，则2D 2E =113()224a a a +=；若3D ，3E 分别是2D B ，2E C 的中点，则3D 3E =137()248a a a +=；…；若n D ，n E 分别是1n D B -，1n E C -的中点，则n n D E = ．5．如图1—64所示，△ABC 中，BC =a ． （1）若1AD =13AB ，1AE =13AC ，则11D E = ；（2）若12D D =113D B ，12E E =113E C ，则22D E = ；（3）若1n n D D -=113n D B -，1n n E E -=113n E C -，则n n D E = ．6．如图1—65所示，已知DE ∥BC ，且BF ：EF =3：2，则AC ：AE = ，AD ：DB = ．1-65DC BEAFM1-66DCBEAF 1-67DCBEAFO1-68DCBEAF7．如图1—66所示，四边形ABCD 中，==90A C ∠∠o，M 为BD 上一点，ME AB ⊥于点E ,MF CD ⊥于点F ，则MF MEBC AD+= ． 8．如图1—67所示，AF ∥BE ∥CD ，AF =12，BE = 19，CD =28．则FE ：ED 的值等于 ．9．如图1—68所示，ABCD Y的对角线AC 与BD 相交于点O ，E 是CD 的中点，AE 交BD 于点F ．则DF ：FO = ．10．如图1－69所示，DC ∥MN ∥PQ ∥AB ，2=DC ，5.3=AB ，PA MP DM ==，则=MN ，=PQ ．1-69ABD C Q M P N FABCDE1-701-71MkN A CEFDBL 3L 2L 111．如图1－70所示，在梯形ABCD 中，AB ∥CD ，CD AB 3=，E 为对角线AC 的中点，直线BE 交AD 于点F ，则FD AF :的值等于 ．12．如图1－71所示，1L ∥2L ∥3L ， 4.2CN =，3AM =，5BM =，12EF =，则=DN ，=EK ． 13．如图1－72所示，已知EFDFBC AB =,则1l ∥2l ∥3l ，此命题是 （真、假）命题． 1-72A BCD EF321课后作业：1．如图1－83所示，已知D 是△ABC 中AC 边的中点，过点D 的任意直线交AB 于点E ，交BC 的延长线于点F ． 求证：BE CF BF EA ⋅=⋅．1-83EFC BDA2．如图1－84所示，在△ABC 中，D 是AB 的中点，E 是AC 上一点，延长DE 交BC 的延长线于点F ．求证：FCBF EC AE =． 1-84F DAB EC3．如图1－85所示，D ，E 是△ABC 的AB ，BC 边上的点，连接DE 并延长交AC 的延长线于点F ，AC AB DE BD ::=．求证：△EFC 是等腰三角形．F D AB EC1-854．如图1－86所示，已知四边形ABCD 是正方形，FG ∥CD ．求证：GF BF =．G 1-86CE B A D F5．如图1－87所示，在平行四边形ABCD 中，E 为AB 中点，G 是对角线AC 上一点，且:1:5AG GC =，EG 的延长线交AD 与点F ．求:DF FA 的值．G 1-87CEB A D F6．如图1－88所示，D 为△ABC 中AC 边上的一点，E 为CB 延长线上的一点，EB AD =，DE 交AB 于点F ．求证：AC DF BC EF ⋅=⋅．1－88AB CDE F7．如图1－89（1）所示，AB ⊥BD ，CD ⊥BD ，垂足分别为点B ，D ，AD 和BC 相交于点E ，EF ⊥BD ，垂足为点F ，我们可以证明111+=AB CD EF成立（不要求证明）． 若将图1－89（1）中的垂线改为斜交，如图1－89（2），AB ∥CD ，AD 与BC 相交于点E ．过点E 作EF ∥AB ，交BD 于点F ．则：（1）111+=AB CD EF 还成立吗？如果成立，请给出证明；如果不成立，请说明理由； （2）请找出面积ABD S △，BED S △和BDC S △间的关系式，并给出证明．（2）（1）AD BC F E 1-89EF C BD A8．如图1－91所示，如果M 是△ABC 中BC 边的中点，P 是CM 上任一点，过点P 作PR ∥AM ，交BA 延长线于点Q ，交CA 于点R ．求证：BM BC AM PR AM PQ =+． 1－91MRQP C B A9．如图1－90（1）所示，D 是△ABC 的BC 边上的中点，过点D 的一条直线交AC 于点F ，交BA 的延长线于点E ，AG ∥BC 交EF 于点G ，我们可以证明EG DC ⋅=ED ⋅AG 成立（不要求证明）． （1）如图l －90（2）所示，若将图1－90（1）中的过点D 的一条直线交AC 于点F ，改为交CA 的延长线于点F ，交BA 的延长线于点E ，改为交BA 于点E ，其他条件不变，则AG ED DC EG ⋅=⋅还成立吗？如果成立，请给出证明；如果不成立，请说明理由；（2）根据图1－90（2）所示，请你找出EG ，FD ，ED ，FG 四条线段之间的关系，并给出证明；（3）如图l －90（3）所示，若将图1－90（1）中的过点D 的一条直线交AC 于点F ，改为交CA 的反向延长线于点F ，其他条件不变，则（2）得到的结论是否成立？1－90（3）（2）（1）A FG E B D C A G B D C FE EFC DB G A10．如图1－92所示，已知△ABC 中=90ACB ∠o ，以BC 为边向外作正方形BCDE ，连接AE 交BC 于点F ，作FG ∥AC 交AB 于点G ．求证：FG FC =．1－92A B CDGFE11．如图1－93所示，△ABC 中，DE ∥BC ，CD ，BE 交于点O ，过点O 作MN ∥BC ，分别交AB ，AC 于点M ，N ．求证：MNBC DE 211=+． 1－93N ME O DC B A12．如图1－94所示，以AC ，BC 为底向AB 同侧作两个顶角相等的等腰△ADC ，△CEB ，若AE ，DC 交于点P ，BD ，CE 交于点Q ．求证：CQ CP =．AP C DQB E1－9413．如图1－95所示，BD ∥FG ，BE ∥FC ．求证：DC ∥EG ．1－95G FEDCB A14．如图1－96所示，在平行四边形ABCD 中，E 是边AB 的中点，点F 在边BC 上，且BF CF3=，EF 与BD相交于点G ．求证：BG DG 5=．1－96AB C D EF G15．如图1－97所示，在等腰△ABC 中，AC AB =，底边BC 外接正方形BCDE ，AD ，AE 分别交BC 于点F ，G ，过F 点作FH ∥CD 交AC 于H ．求证：HF GF =．1－97A B C DE F HG16．如图l －98所示，已知：梯形ABCD ，AB ∥CD ，且7=AB ，4=CD ，延长AD ，BC 交于点E ，过E 作平行于AB 的直线，分别交AC ，BD 的延长线于M ，N ．求：MN 的长．1－98A B C DE N M17．如图1－99所示，在平行四边形ABCD 中，EH 交BA ，BC 延长线于E ，H 点，且交AD ，DC 于F ，G ，交BD 于P 点．求证：EP PF PH PG ⋅=⋅．P 1-99EFC BDAG H18．如图1－100所示，在四边形ABCD 中，AB ∥CD ，对角线AC ，BD 相交于F ，EG 过F 点且与AB 平行． 求证：2EG EG AB CD+=． 1-100G FEDC BA19．如图1－101所示，△ABC 中，AP 平分BAC ∠，BE AP ⊥，垂足为Q ，BE 交AC 的延长线于E ，M 为BC 的中点，延长AM 交BE 于N ，连结NP ．求证：NP ∥AB ．QAB CE MN P 1-101。

沪教版初三数学上册知识点梳理重点题型（常考知识点）巩固练习相似形及比例线段（基础）知识讲解【学习目标】1、能通过生活中的实例认识图形的相似，能通过观察直观地判断两个图形是否相似；2、了解比例线段的概念及有关性质；3、探索相似图形的性质，知道两相似多边形的主要特征，并根据相似多边形的特征识别两个多边形是否相似，并会运用性质进行相关的计算，提高推理能力.【要点梳理】要点一、相似图形在数学上，我们把形状相同的图形称为相似图形或相似形.要点诠释：(1) 相似图形就是指形状相同，但大小不一定相同的图形；(2) “全等”是“相似”的一种特殊情况，即当“形状相同”且“大小相同”时，两个图形全等；要点二、相似多边形【：图形的相似二、图形的相似 2】相似多边形的概念：如果两个多边形的对应角相等，对应边的长度成比例，我们就说它们是相似多边形．要点诠释：（1）相似多边形的定义既是判定方法，又是它的性质．（2）相似多边形对应边的比称为相似比．要点三、比例线段【：图形的相似预备知识】1．成比例线段：对于四条线段a、b、c、d，如果其中两条线段的比与另两条线段的比相等，如a:b=c:d，我们就说这四条线段是成比例线段，简称比例线段．2．比例的性质：（1）基本性质：若a:b=c:d，则ad=bc；（2）合比性质：如果如果（3）等比性质：如果（4）比例中项：若a:b=b:c，则=ac，b称为a、c的比例中项．要点诠释：通常四条线段a,b,c,d的单位应该一致，但有时为了计算方便，a,b的单位一致，c,d的单位一致也可以。

要点四、黄金分割如果点P把线段AB分割成AP和PB,(AP>PB)两段，其中AP是AB和PB的比例中项，那么就称这种分割为黄金分割，点P是线段AB的黄金分割点.≈0.618AB(叫做黄金分割值).要点诠释：线段的黄金分割点有两个.【典型例题】类型一、相似图形1. 下面给出了一些关于相似的命题，其中真命题有（）（1）菱形都相似；（2）等腰直角三角形都相似；（3）正方形都相似；（4）矩形都相似；（5）正六边形都相似．A.1个B.2个C.3个D.4个【答案】C.【解析】解：（1）所有菱形的对应角不一定相等，故菱形不一定都相似；（2）等腰直角三角形都相似，正确；（3）正方形都相似，正确；（4）矩形对应边比值不一定相等，不矩形不一定都相似；（5）正六边形都相似，正确，故符合题意的有3个．故选：C．【总结升华】此题主要考查了相似图形，应注意：①相似图形的形状必须完全相同；②相似图形的大小不一定相同；③两个物体形状相同、大小相同时它们是全等的，全等是相似的一种特殊情况．举一反三：【变式】如图，左边是一个横放的长方形，右边的图形是把左边的长方形各边放大两倍，并竖立起来以后得到的，这两个图形是相似的吗？【答案】这两个图形是相似的，这两个图形形状是一样，对应线段的比都是1:2，虽然它们的摆放方法、位置不一样，但这并不会影响到它们的相似性.类型二、相似多边形2. 如图，已知四边形相似于四边形，求四边形的周长.【答案与解析】∵四边形相似于四边形∴，即∴∴四边形的周长.【总结升华】先根据相似多边形的对应边的比相等，求出四边形的未知边的长，然后即可求出该四边形的周长举一反三：【变式】如图所示的相似四边形中，求未知边x、y的长度和角的大小.【答案】根据题意，两个四边形是相似形，得，解得.3. 如图，在矩形ABCD中，AB=2AD，线段EF=10，在EF上取一点M，分别以EM、MF为一边作矩形EMNH、MFGN，使矩形MFGN与矩形ABCD相似.令MN=x，当x为何值时，矩形EMNH的面积S有最大值？最大值是多少？【答案与解析】解：∵矩形MFGN与矩形ABCD相似，当时，S有最大值，为.【总结升华】借助相似，把最值问题转移到函数问题上，是解决这类题型最好方法之一.类型三、比例线段4.（2016•兰州模拟）若a：b=2：3，则下列各式中正确的式子是（）A．2a=3b B．3a=2b C．D．【思路点拨】根据比例的性质，对选项一一分析，选择正确答案．【答案】B．【解析】A、2a=3b⇒a：b=3：2，故选项错误；B、3a=2b⇒a：b=2：3，故选项正确；C、=⇒b：a=2：3，故选项错误；D、=⇒a：b=3：2，故选项错误．故选B．【总结升华】考查了比例的性质．在比例里，两个外项的乘积等于两个内项的乘积．举一反三：【变式】判断下列线段a、b、c、d是否是成比例线段：(1)a=4，b=6，c=5，d=10；(2)a=2，b=，c=，d=．【答案】(1) ∵，，∴，∴线段a、b、c、d不是成比例线段．(2) ∵，，∴，∴线段a、b、c、d是成比例线段．5. 主持人站在舞台的黄金分割点处最自然得体，如果舞台AB长为20米，一个主持人现站在舞台AB的黄金分割点点C处，则下列结论一定正确的是（）①AB：AC=AC：BC；②AC≈6.18米；③；④．A. ①②③④B. ①②③C. ①③D. ④【答案】D.【解析】解：AB的黄金分割点为点C处，若AC＞BC，则AB：AC=AC：BC，所以①不一定正确；AC≈0.618AB≈12.36或AC≈20﹣12.36=7.64，所以②错误；若AC为较长线段时，AC=AB=10（﹣1），BC=10（3﹣）；若BC为较长线段时，BC=AB=10（﹣1），AC=10（3﹣），所以③不一定正确，④正确．故选D．【总结升华】黄金分割知识的理解和运用要结合生活实践.沪教版初三数学上册知识点梳理重点题型（常考知识点）巩固练习相似形及比例线段（基础）巩固练习【巩固练习】一．选择题1. 在比例尺为1︰1 000 000的地图上，相距3 cm的两地，它们的实际距离为（）A.3 kmB.30 kmC.300 kmD.3 000 km2. （2016•滨江区模拟）由5a=6b（a≠0），可得比例式（）A．B．C．D．3.如图，用放大镜将图形放大，这种图形的改变是（）A．相似B．平移 C．轴对称D．旋转4. 某学习小组在讨论“变化的鱼”时，知道大鱼与小鱼是相似图形，如图所示，则小鱼上的点(a，b)对应大鱼上的点( )A．(-2a，-2b) B．(-a，-2b) C．(-2b，-2a) D．(-2a，-b)5. 一个三角形三边的长分别为3，5，7，另一个与它相似的三角形的最长边是21，则此三角形其它两边的和是（）A．19 B．17 C．24 D．216. .△ABC与△A1B1C1相似且相似比为，△A1B1C1与△A2B2C2相似且相似比为，则△ABC与△A2B2C2的相似比为 ( )A．B．C．或D．二. 填空题7. 两地实际距离为1 500 m，图上距离为5 cm，这张图的比例尺为_______.8. （2016•浦东新区一模）已知，那么= ．9．判定两个多边形相似的方法是：当两个多边形的对应边_______,对应角_______时，两个多边形相似.10.已知则11.两个三角形相似，其中一个三角形两个内角分别是40°，60°，则另一个三角形的最大角为______,最小角为____________.12. （2015春·庆阳校级月考）要制作两个形状相同的三角形框架，其中一个三角形框架的三边长分别为4、5、6，另一个三角形框架的一条最短边长为2，则另外一个三角形的周长为 .三综合题13. 已知，求的值.14. （1）已知a、b、c、d是成比例线段，其中a=3dcm,b=2cm,c=6cm,求线段d的长；（2）已知线段a、b、c，a=4cm，b=9cm，线段c是线段a和b的比例中项，求线段c的长．15. 市场上供应的某种纸有如下特征：每次对折后，所得的长方形均和原长方形相似，则纸张(矩形)的长与宽应满足什么条件？【答案与解析】一、选择题1．【答案】B．【解析】图上距离︰实际距离＝比例尺．2.【答案】D.【解析】A、⇒ab=30，故选项错误；B、⇒ab=30，故选项错误；C、⇒6a=5b，故选项错误；D、⇒5（a﹣b）=b，即5a=6b，故选项正确．故选D．3．【答案】A【解析】根据相似图形的定义知，用放大镜将图形放大，属于图形的形状相同，大小不相同，所以属于相似变换．故选A．4．【答案】 A【解析】由图可知，小鱼和大鱼的相似比为1：2，若将小鱼放大1倍，则小鱼和大鱼关于原点对称.5．【答案】C【解析】相似三角形对应边的比相等6．【答案】A【解析】相似比AB︰A1B1=，A1B1︰A2B2=，计算出AB︰A2B2.二、填空题7.【答案】.1：30 000【解析】比例尺=图上距离︰实际距离.8.【答案】．【解析】∵的两个内项是y、1，两个外项是x、3，∴，根据合比定理，知==4；又∵上式的两个内项是x和4，两个外项是x+y和1，∴．9.【答案】成比例；相等.10.【答案】【解析】提示：设11.【答案】80°，40°.12.【答案】7.5.【解析】设另一个三角形周长是x.∵一个三角形的三边长是4,5,6，∴这个三角形的周长为：4+5+6=15.∵与它相似的另一个三角形最短的一边长是2，∴，解得：x=7.5.∴另一个三角形的周长是7.5.三、解答题13.【解析】设=k则∴==14.【解析】解：（1）∵a、b、c、d是成比例线段，∴a：b=c：d，∵a=3cm，b=2cm，c=6cm，∴d=4cm；(2)∵线段c是线段a和b的比例中项，a=4cm，b=9cm.∴c2=ab=36，解得：c=±6，又∵线段是正数，∴c=6cm.15.【解析】如图，为了方便分析可先画出草图，根据题意知两个矩形的长边之比应等于短边之比.设矩形的长为，宽为，由相似多边形的特征得，即纸张的长与宽之比为.沪教版初三数学上册知识点梳理重点题型（常考知识点）巩固练习三角形一边的平行线知识讲解【学习目标】1、掌握三角形一边的平行线性质定理及推论；判定定理及推论；以及平行线分线段成比例定理的推导与应用；2、了解三角形的重心的意义和性质并能应用它解题；3、经历运用分类思想针对图形运动的不同位置分别探究的过程,初步领略运用运动观点、化归和分类讨论等思想进行数学思考的策略.【要点梳理】要点一、三角形一边的平行线性质定理及推论1.性质定理：平行于三角形一边的直线截其他两边所在的直线，截得的对应线段成比例.2.推论：平行于三角形一边的直线截其他两边所在的直线，截得的三角形的三边与原三角形的三边对应成比例.要点诠释：(1)主要的基本图形：分A型和X型；A型 X型（2）常用的比例式：3.三角形的重心：三角形三条中线的交点叫做三角形的重心.要点诠释：(1)重心的性质：三角形的重心到一个顶点的距离，等于它到这个顶点对边中点的距离的二倍.（2）重心的画法：两条中线的交点.要点二、三角形一边的平行线判定定理及推论1.判定定理：如果一条直线截三角形的两边所得的对应线段成比例，那么这条直线平行于三角形的第三边.2.推论：如果一条直线截三角形两边的延长线（这两边的延长线在第三边的同侧）所得的对应线段成比例，那么这条直线平行于三角形的第三边.要点诠释：判断平行线的条件中，只能是被截的两条直线的对应线段成比例(被判断的平行线本身不能参与作比例).要点三、平行线分线段成比例定理1.性质定理：两条直线被三条平行的直线所截，截得的对应线段成比例.2.平行线等分线段定理：两条直线被三条平行的直线所截，如果在一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等.要点诠释：（1）平行线等分线段定理是平行线分线段成比例定理的特例；（2）平行线分线段成比例没有逆定理；(3) 由于平行线分线段成比例定理中，平行线本身没有参与作比例，因此，有关平行线段的计算问题通常转化到“A”、“X”型中.【典型例题】类型一、三角形一边的平行线性质定理1. 如图已知直线截△ABC三边所在的直线分别于E、F、D三点且AD=BE.求证：EF：FD=CA：CB.【答案与解析】过D作DK∥AB交EC于K点.则，，即又∵AD=BE，∴.【总结升华】运用三角形一边的平行线性质定理，即只要有平行线就可推出对应线段成比例.举一反三【变式】如图,在⊿ABC, DG∥EC, EG∥BC,求证:【答案】∵DG∥EC,∴,∵EG∥BC,∴,∴,即.2.已知，△ABC中，G是三角形的重心， AG⊥GC，AG=3，GC=4，求BG的长.【答案与解析】延长BG交AC于点D,∵G是三角形的重心，∴点D是线段AC的中点，又∵AG⊥GC，AG=3，GC=4，∴AC=5，即DG=2.5，∵BG:GD=2:1.∴BG=5.【总结升华】三角形的重心到一个顶点的距离，等于它到这个顶点对边中点的距离的二倍.类型二、三角形一边的平行线判定定理3. 如图，AM是△ABC的中线，P是AM上任意一点，BP、CP的延长线分别交AC、AB于E、D两点.求证：DE∥BC.【答案与解析】延长AM到H，使HM=MP，连接BH、CH∵BM=MC∴四边形BPCH是平行四边形∵BH∥CD，CH∥BE在△ABH和△ACH中，有，∴DE∥BC【总结升华】平行线所截得的对应线段成比例，而两条平行线中的线段与所截得的线段不成比例.举一反三【变式】如图，在△ABC（AB＞AC）的边AB上取一点D，在边AC 上取一点E,使AD=AE,直线DE和BC的延长线交于点P,求证：.【答案】过点C作CF∥AB交DP于点F,∵CF∥AB，∴∠ADE=∠EFC∵AD=AE,∴∠ADE=∠AED=∠FEC∴∠EFC=∠FEC∴CF=CE∵CF∥AB∴,即.类型三、平行线分线段成比例定理4. （2016•兰州）如图，在△ABC中，DE∥BC，若=，则=（）A．B．C．D．【思路点拨】直接利用平行线分线段成比例定理写出答案即可．【答案】C．【解析】解：∵DE∥BC，∴==，故选C．【总结升华】本题考查了平行线分线段成比例定理，了解定理的内容是解答本题的关键，属于基础定义或定理，难度不大．举一反三【变式】（2015•舟山）如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C，直线DF分别交l1，l2，l3于点D，E，F，AC 与DF相交于点G，且AG=2，GB=1，BC=5，则的值为（）A. B. 2 C. D.【答案】D提示：∵AG=2，GB=1，∴AB=AG+BG=3，∵直线l1∥l2∥l3，∴=，沪教版初三数学上册知识点梳理重点题型（常考知识点）巩固练习三角形一边的平行线【巩固练习】一．选择题1.（2016•杭州）如图，已知直线a∥b∥c，直线m交直线a，b，c 于点A，B，C，直线n交直线a，b，c于点D，E，F，若=，则=（）A．B．C．D．12. 如图，在△ABC中，DE∥BC，则下列比例式成立的是( )A．B． C．D．3. 在△ABC中，点D在AB上，点E在AC上，且DE∥BC，，则等于( )A．B．C． D．4. 如图，△ABC中，DE∥AC交AB、BC于D、E，如果AB=7cm，AC=5cm，AD=3cm，则DE=( )A．B． C．D．5. 如图，在△ABC中，如果DE∥BC，DF∥AC，则下列比例式中不正确的是( )A．B．C． D．6. 如图，△ABC中，G是BC中点，E是AG中点，CE的延长线交AB于D，则EC：DE的值为( )A．2 B．3 C．D．二. 填空题7. （2016•无锡一模）如图，直线AD∥BE∥CF，BC=AC，DE=4，那么EF的值是．8. 如图，DE∥BC,BF:EF=4:3，则AC:AE=____________.9．已知点G是△ABC的重心，AD是BC边上的中线，如果GD=2cm，那么AD=______.10. 如图，△PMN,点A,B分别在MP,NP的延长线上，,则________.11. 如图，四边形ABCD中，AC、BD相交于点P,若AP=8，CP=12，BC=15.则AD=_________.12.（2015•香坊区三模）如图，△ABC中，D、F在AB边上，E、G 在AC边上，DE∥FG∥BC，且AD：DF：FB=3：2：1，若AG=15，则EC 的长为 .三.综合题13. 如图，已知，AB∥CD∥EF，OA=14，AC=16，CE=8，BD=12，求OB、DF的长.14.已知：如图，在△ABC中，AB=AC，且，EG∥CD．证明：AE=AF．15. 如图，△ABC中，AD是中线，点F在AD上，且AF：FD=1：2，BF的延长线交AC于E，求AE：EC=？【答案与解析】一、选择题1.【答案】B．【解析】∵a∥b∥c，∴==．故选B．2．【答案】 D.3．【答案】 C.【解析】∵DE∥BC，∴,又∵，∴,即=.4．【答案】D.【解析】∵DE∥AC，∴，又∵AB=7cm，AC=5cm，AD=3cm，∴BD=4，即DE=.5．【答案】C.【解析】提示：∵ DE∥BC，DF∥AC，∴DE=CF, DF=CE.6.【答案】B.【解析】作GM∥CD交AB于点M,∵E是AG中点，∴MG=2DE,又∵G是BC中点，∴CD=2MG=4DE∴EC=3DG,即EC:DE=3:1.二、填空题7.【答案】2．【解析】∵BC=AC，∴=，∵AD∥BE∥CF，∴=，∵DE=4，∴=2，∴EF=2．8.【答案】4:3.【解析】∵DE∥BC, BF:EF=4:3，∴9.【答案】6cm.【解析】∵点G是重心，∴AG:GD=2:1，又∵GD=2，∴AG=4，即AD=6cm.10.【答案】3:2.【解析】∵，∴.11.【答案】10.12.【答案】9.【解析】∵DE∥FG∥BC，∴=，而AD：DF：FB=3：2：1，∴=，∴=，∴EC=9．三、解答题13. 【解析】∵AB∥CD∥EF，∴,又∵OA=14，AC=16，BD=12，∴OB=.同理,CE=8，∴DF=6.14.【解析】证明：∵EG∥CD，∴=，且，∴=，∴=，即=，∵AB=AC，∴AE=AF．15.【解析】作DG∥BE,∵AD是中线，∴EG=GC,又∵AF：FD=1：2，∴EG=2AE,即EC=4AE,∴AE:EC=1:4.沪教版初三数学上册知识点梳理重点题型（常考知识点）巩固练习相似三角形的判定--知识讲解（基础）【学习目标】1、了解相似三角形的概念，掌握相似三角形的表示方法及判定方法；2、进一步探索相似三角形的判定及其应用，提高运用“类比”思想的自觉性，提高推理能力.【要点梳理】要点一、相似三角形在和中，如果我们就说与相似，记作∽.k就是它们的相似比，“∽”读作“相似于”.要点诠释：(1)书写两个三角形相似时，要注意对应点的位置要一致，即∽，则说明点A的对应点是A′，点B的对应点是B′，点C的对应点是C′；(2)对于相似比，要注意顺序和对应的问题，如果两个三角形相似，那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时，两个三角形全等.要点二、相似三角形的判定定理【高清课程名称：相似三角形的判定（1）高清：394497：相似三角形的判定】1．判定方法（一）：平行于三角形一边的直线和其他两边相交，所构成的三角形和原三角形相似.2．判定方法（二）：如果两个三角形的三组对应边的比相等，那么这两个三角形相似.3．判定方法（三）：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似.要点诠释：此方法要求用三角形的两边及其夹角来判定两个三角形相似，应用时必须注意这个角必需是两边的夹角，否则，判断的结果可能是错误的.4．判定方法（四）：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.要点诠释：要判定两个三角形是否相似，只需找到这两个三角形的两个对应角相等即可，对于直角三角形而言，若有一个锐角对应相等，那么这两个三角形相似.要点三、相似三角形的常见图形及其变换：【典型例题】类型一、相似三角形1. 下列能够相似的一组三角形为( ).A.所有的直角三角形B.所有的等腰三角形C.所有的等腰直角三角形D.所有的一边和这边上的高相等的三角形【答案】C【解析】A中只有一组直角相等，其他的角是否对应相等不可知；B中什么条件都不满足；D中只有一条对应边的比相等；C中所有三角形都是由90°、45°、45°角组成的三角形，且对应边的比也相等.答案选C.【总结升华】根据相似三角形的概念，判定三角形是否相似，一定要满足三个角对应相等，三条对应边的比相等.举一反三：【变式】给出下列几何图形：①两个圆；②两个正方形；③两个矩形；④两个正六边形；⑤两个等边三角形；⑥两个直角三角形；⑦两个菱形．其中，一定相似的有（填序号）．【答案】①②④⑤.类型二、相似三角形的判定2. 如图所示，已知中，E为AB延长线上的一点，AB=3BE，DE与BC相交于F，请找出图中各对相似三角形，并求出相应的相似比.【思路点拨】充分利用平行寻找等角，以确定相似三角形的个数. 【答案与解析】∵四边形ABCD是平行四边形，∴ AB∥CD，AD∥BC，∴△BEF∽△CDF，△BEF∽△AED.∴△BEF∽△CDF∽△AED.∴当△BEF∽△CDF时，相似比；当△BEF∽△AED时，相似比；当△CDF∽△AED时，相似比.【总结升华】此题考查了相似三角形的判定（有两角对应相等的两三角形相似）与性质（相似三角形的对应边成比例）.解题的关键是要仔细识图，灵活应用数形结合思想.举一反三：【高清课程名称：相似三角形的判定（2）高清：394499：例4及变式应用】【变式】如图，AD、CE是△ABC的高，AD和CE相交于点F，求证：AF·FD=CF·FE．【答案】∵ AD、CE是△ABC的高,∴∠AEF=∠CDF=90°,又∵∠AFE=∠CFE,∴△AEF∽△CDF.∴, 即AF·FD=CF·FE．3. （2016•福州）如图，在△ABC中，AB=AC=1，BC=，在AC边上截取AD=BC，连接BD．（1）通过计算，判断AD2与AC•CD的大小关系；（2）求∠ABD的度数．【思路点拨】（1）先求得AD、CD的长，然后再计算出AD2与AC•CD的值，从而可得到AD2与AC•CD的关系；（2）由（1）可得到BD2=AC•CD，然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC，依据相似三角形的性质可知∠DBC=∠A，DB=CB，然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数．【答案与解析】解：（1）∵AD=BC=1，BC=，∴AD=，DC=1﹣=．∴AD2==，AC•CD=1×=．∴AD2=AC•CD．（2）∵AD=BC，AD2=AC•CD，∴BC2=AC•CD，即．又∵∠C=∠C，∴△BCD∽△ACB．∴，∠DBC=∠A．∴DB=CB=AD．∴∠A=∠ABD，∠C=∠BDC．设∠A=x，则∠ABD=x，∠DBC=x，∠C=2x．∵∠A+∠ABC+∠C=180°，∴x+2x+2x=180°．解得：x=36°．∴∠ABD=36°．【总结升华】本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角形内角和定理的应用，证得△BCD∽△ABC是解题的关键．4. 已知：如图，△ABC中，AB＝AC，AD是中线，P是AD上一点，过C作CF∥AB，延长BP交AC于E，交CF于F．求证：BP2＝PE·PF．【思路点拨】从求证可以判断是运用相似，再根据BP2＝PE·PF，可以判定所给的线段不能组成相似三角形，这就需要考虑线段的等量转移了.【答案与解析】连接，，，是的中垂线，，，，．，．又，∽，，．【总结升华】根据求证确定相似三角形，是解决此类题型的捷径.举一反三：【变式】如图，F是△ABC的AC边上一点，D为CB延长线一点，且AF=BD,连接DF, 交AB于E. 求证：.【答案】过点F作FG∥BC,交AB于G.则△DBE∽△FGE△AGF∽△ABC∵,又∵AF=BD,∴∵△AGF∽△ABC∴,即.沪教版初三数学上册知识点梳理重点题型（常考知识点）巩固练习相似三角形的判定--巩固练习（基础）【巩固练习】一、选择题1. 下列判断中正确的是( ).A.全等三角形不一定是相似三角形B.不全等的三角形一定不是相似三角形C.不相似的三角形一定不全等D.相似三角形一定不是全等三角形2．已知△ABC的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′ 相似, 那么△A′B′C′ 的第三边长应该是 ( ).A. B. C. D.3．（2015•大庆校级模拟）如图，小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△ABC相似的是（）A．B．C．D．4. （2016•盐城）如图，点F在平行四边形ABCD的边AB上，射线CF交DA的延长线于点E，在不添加辅助线的情况下，与△AEF相似的三角形有（）A．0个B．1个C．2个D．3个5．在矩形ABCD中，E、F分别是CD、BC上的点，若∠AEF＝90°，则一定有（）.A．ΔADE∽ΔAEF B．ΔECF∽ΔAEF C．ΔADE ∽ΔECF D．ΔAEF∽ΔABF6. 如图所示在平行四边形ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为( ).A. B.8 C.10 D.16二、填空题7. （2016•娄底）如图，已知∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是．（只需写一个条件，不添加辅助线和字母）8如图所示，∠C=∠E=90°，AD=10，DE=8，AB=5，则AC=________.9.如图所示，在直角坐标系中有两点A(4，0)，B(0，2)，如果点C 在x轴上(C与A不重合)，当点C的坐标为________或________时，使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).10.如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED=1，BD=4，那么AB=__________.11.如图，CD∥AB，AC、BD相交于点O,点E、F分别在AC、BD上，且EF∥AB,则图中与△OEF相似的三角形为_________.12．如图，点E是平行四边形ABCD的边BC延长线上一点，连接AE 交CD于点F,则图中相似三角形共有_________对.三．解答题13. 如图，在△ABC中，DE∥BC，AD＝3，AE＝2，BD＝4，求的值及AC、EC的长度．14. 如图在梯形ABCD中，AD∥BC，∠A＝90°，且，求证：BD⊥CD．15.如图，在△ABC中，已知∠BAC=90°，AD⊥BC于D，E是AB上一点，AF⊥CE于F，AD交CE于G点，（1）求证：AC2=CE•CF；（2）若∠B=38°，求∠CFD的度数．【答案与解析】一．选择题1.【答案】C.2.【答案】A.【解析】根据三边对应成比例，可以确定，所以第三边是3.【答案】B.【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、只有选项B的各边为1、、与它的各边对应成比例．故选B．4.【答案】C．【解析】∵四边形ABCD是平行四边形，∴AD∥BC，AB∥DC，∴△AEF∽△CBF，△AEF∽△DEC，∴与△AEF相似的三角形有2个．5.【答案】C.【解析】∵∠AEF＝90°, ∴∠1+∠2=90°，又∵∠D=∠C=90°，∴∠3+∠2=90°，即∠1=∠3，∴△ADE∽△ECF.6.【答案】C.【解析】∵ EF∥AB，∴，∵，∴，，∴ CD=10，故选C.二. 填空题7.【答案】AB∥DE．【解析】∵∠A=∠D，∴当∠B=∠DEF时，△ABC∽△DEF，∵AB∥DE时，∠B=∠DEF，∴添加AB∥DE时，使△ABC∽△DEF．8.【答案】 3 .【解析】∵∠C=∠E，∠CAB=∠EAD，∴△ACB∽△AED，∴，BC=4，在Rt△ABC中，.9．【答案】；.10.【答案】4.【解析】∵AB⊥BD，ED⊥BD，∴∠B=∠D=90°，又∵AC⊥CE，∴∠BCA+∠DCE=90°，∴∠BCA=∠E,∴△ABC∽△CDE.∵C是线段BD的中点，ED=1，BD=4∴BC=CD=2∴,即AB=4.11.【答案】△OAB,△OCD.12.【答案】3.【解析】∵平行四边形ABCD，∴AD∥BE.AB∥CD∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.三综合题13.【解析】∵DE∥BC，∴△ADE∽△ABC，∵，，∴，∴AC＝，∴EC＝AC－AE＝．14.【解析】∵AD∥BC，∴∠ADB＝∠DBC，又∵，∴△ABD∽△DCB，∴∠A＝∠BDC，∵∠A＝90°，∴∠BDC＝90°，∴BD⊥CD ．15.【解析】解：（1）∵AD⊥BC，∴∠CFA=90°，∵∠BAC=90°，∴∠C FA=∠BAC，∵∠ACF=∠FCA，∴△CAF∽△CEA，∴=，∴CA2=CE•CF；（2）∵∠CAB=∠CDA，∠ACD=∠BCA，∴△CAD∽△CB A，∴=，∴C A2=CB×CD，同理可得：CA2=CF×CE，∴CD•BC=CF•CE，∴=，∵∠DCF=∠ECB，∴△CDF∽△CEB，∴∠CFD=∠B，∵∠B=38°，∴∠CFD=38°．沪教版初三数学上册知识点梳理重点题型（常考知识点）巩固练习相似三角形的性质及应用--知识讲解（基础）【学习目标】1、探索相似三角形的性质，能运用性质进行有关计算；2、通过典型实例认识现实生活中物体的相似，能运用图形相似的知识解决一些简单的实际问题（如何把实际问题抽象为数学问题）. 【要点梳理】要点一、相似三角形的性质【高清课程名称：相似三角形的性质及应用高清：394500：相似形的性质】1．相似三角形的对应角相等，对应边的比相等.2. 相似三角形中的重要线段的比等于相似比.相似三角形对应高，对应中线，对应角平分线的比都等于相似比.要点诠释：要特别注意“对应”两个字，在应用时，要注意找准对应线段.3. 相似三角形周长的比等于相似比∽，则由比例性质可得：4. 相似三角形面积的比等于相似比的平方∽，则分别作出与的高和，则要点诠释：相似三角形的性质是通过比例线段的性质推证出来的.要点二、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度，通常使用“在同一时刻物高与影长的比例相等”的原理解决.【高清课程名称：相似三角形的性质及应用高清：394500：应用举例及总结】要点诠释：测量旗杆的高度的几种方法：平面镜测量法影子测量法手臂测量法标杆测量法2.测量距离测量不能直接到达的两点间的距离，常构造如下两种相似三角形求解。

三角形一边的平行线是九年级数学上学期第一章第二节的内容，本讲主要讲解三角形一边平行线判定定理及推论，以及平行线分线段成比例定理；重点是理清该判定定理及其推论之间的区别和联系，难点是灵活运用本节的三个定理及两个推论，并理解和掌握“作平行线”这一主要的作辅助线的方法，为学习相似三角形的性质和判定做好准备．1、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例，那么这条直线平行于三角形的第三边．2、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线（这两边的延长线在第三边的同侧）所得的对应线段成比例，那么这条直线平行于三角形的第三边．如图，在ABC ∆中，直线l 与AB 、AC 所在直线交于点D 和点E ，如果AD AEDB EC=那么l //BC ．三角形一边的平行线（二）内容分析知识结构模块一：三角形一边的平行线判定定理及推论知识精讲lABCD EABCD EABCDE ll【例1】在ABC ∆中，点D 、E 分别在边AB 、AC 上，根据下列条件，试判断DE 与BC 是 否平行．（1）3AD cm =，4DB cm =， 1.8AE cm =， 2.4CE cm =； （2）6AD cm =，9BD cm =，4AE cm =，10AC cm =； （3）8AD cm =，16AC cm =，6AE cm =，12AB cm =；（4）2AB BD =，2AC CE =．【难度】★【答案】（1）平行；（2）平行；（3）不平行；（4）平行．【解析】（1）34AD AE DB CE ==，可推知平行；（2）6CE AC AE =-=，23AD AE BD CE ==，可推知平行； （3）23AD AB =，38AE AC =，不相等，可推知不平行； （4）根据线段大小和位置关系，得AD BD =，AE CE =，1AD AEBD CE==，可推知平行． 【总结】考查三角形一边平行线判定定理的内容，根据比例性质进行相关变形应用．【例2】如图，::1:3AM MB AN NC ==，则:MN BC =． 【难度】★ 【答案】1:4．【解析】由::1:3AM MB AN NC ==，根据三角形一边平行 线的判定定理，可知//MN BC ，根据三角形一边平行线 的性质定理和比例的合比性，可得::1:4MN BC AN AC ==．【总结】考查三角形一边平行线性质定理及其判定定理，先判定再应用．例题解析A BCNMA B CEF【例3】如图，PMN ∆中，点A 、B 分别在MP 和NP 的延长线上，且38AP BP AM BN ==，则MNBA= ．【难度】★【答案】53．【解析】由38AP BP AM BN ==，由比例合比性，可得35AP BP PM PN ==，根据三角形一边平行线的判定定理的推论，可知//MN AB ，根据三角形一边平行线的性质定理，可得53MN PM BA AP ==．【总结】考查三角形一边平行线性质定理及其判定定理，先判定再应用．【例4】如图，ABC ∆中，E 点在边AB 上，F 点在边AC 上，下列命题中不正确的是（ ）（A ）若EF //BC ，则AE AF EB FC = （B ）若AE AFEB FC=，则EF //BC （C ）若EF //BC ，则AE EFAB BC=（D ）若AE EFAB BC=，则EF //BC 【难度】★ 【答案】D【解析】A 、B 、C 选项都可由三角形一边平行线性质定理及其判定定理可判定正确，D 选项不符合定理判定内容．【总结】考查三角形一边平行线性质定理及其判定定理的内容．AB PNMABCDE F ABCD O【例5】如图，点D 、F 在ABC ∆的边AB 上，点E 在边AC 上，且DE //BC ，AF ADAD AB=．求证：EF //DC ．【难度】★ 【答案】略．【解析】证明：//DE BC ， AD AE DB EC ∴=， 则AD AEAB AC=． 又AF AD AD AB =， AF AEAD AC∴=， ∴EF //DC ． 【总结】考查三角形一边平行线性质定理及其判定定理，先利用性质证明比例线段相等再进行判定应用．【例6】如图，四边形ABCD 中，AC 、BD 相交于点O ，若A O D OC O B O=，8AO =，20CO =，15BC =，求AD 的长．【难度】★【答案】6．【解析】AO DO CO BO =， //AD BC ∴， 820AD AO BC CO ∴==．代入可计算，得：6AD =．【总结】考查三角形一边平行线性质定理及其判定定理，先判定再应用．【例7】点D 、E 分别在ABC ∆的边AB 、AC 上，如果DE ADBC AB=，能否得到DE //BC ，为什么？【难度】★★ 【答案】不能得到平行【解析】在AC 上必能找到一点E 使得DE //BC ，同时在AC 上能找到一点'E 使得'DE DE =，即等腰三角形存在，此时仍满足'DE ADBC AB=，但显然'DE 不与BC 平行． 【总结】考查三角形一边平行线判定定理内容的内容把握．ABC DEFM B C D NMABCD EF【例8】如图，M 为AB 的中点，EF //AB ，联结EM 、FM 分别交AF 、BE 于点C 和点D ．求证：CD //AB ．【难度】★★ 【答案】略． 【解析】证明：EF //AB ，EF EC EF DFAM CM BM DM∴==，．M 为AB 的中点， A M B M∴=． E C D FC MD M∴=， ∴CD //AB ． 【总结】考查三角形一边平行线性质定理及其判定定理，先判定再应用．【例9】如图，MC //ND ，且::PB AB PD CD =．求证：BN //AM ．【难度】★★ 【答案】略． 【解析】证明：MC //ND ， PD PNCD MN ∴=．::PB AB PD CD =，PN PBMN AB∴=， ∴BN //AM ．【总结】考查三角形一边平行线性质定理及其判定，先应用性质证明比例线段相等再判定．【例10】如图，D 、F 是ABC ∆的AB 边上的两点，满足2AD AF AB =．联结CD ，过点F 作FE //DC ，交边AC 于点E ，联结DE ．求证：DE //BC ．【难度】★★ 【答案】略．【解析】证明：FE //DC ， A F A EA D A C ∴=． 又2AD AF AB =， 即AF ADAD AB=， A E A DA C A B∴=， ∴DE //BC ． 【总结】考查三角形一边平行线性质定理及其判定，先应用性质证明比例线段相等再判定．ABCA’B’C’OA BCDEFGH【例11】如图，AC //''A C ，BC //''B C ．求证：AB //''A B ．【难度】★★ 【答案】略．【解析】证明：AC //''A C ，BC //''B C ，''''OA OC OB OC OA OC OB OC ∴==，， ''OA OBOA OB ∴=，∴AB //''A B ．【总结】考查三角形一边平行线性质定理及其判定，先应用性质证明比例线段相等再判定．【例12】将上题中的四边形OABC 绕点O 旋转180︒得下图，而其他已知条件不变，结论还成立吗？【难度】★★ 【答案】成立．【解析】证明：AC //''A C ，BC //''B C ，''''OA OC OB OC OA OC OB OC ∴==，，''OA OBOA OB ∴=．∴AB //''A B ．【总结】考查三角形一边平行线性质定理及其判定定理的推论，先应用性质证明比例线段相等再判定．【例13】点D 、E 分别在ABC ∆的边AB 、AC 上，且DE //BC ，以DE 为一边作平行四边形DEFG ，延长BG 、CF 交于点H ，连接AH ，求证：AH //EF ．【难度】★★ 【答案】略． 【解析】证明：DE //BC ， D E A EB C A C∴=． 又四边形DEFG 为平行四边形， //DE FG DE FG ∴=，．F G H F B C H C ∴=， A E H F A C H C ∴=， A E H FE CF C ∴=， ∴AH //EF ．【总结】考查三角形一边平行线性质定理及其判定定理的推论，先应用性质证明比例线段相等再判定．AB CA’B’C’OA B CDEF G【例14】如图，在菱形ABCD 中，点E 、F 分别在边BC 、CD 上，BAF DAE ∠=∠，AE 与BD 交于点G ，又DF ADFC DF =．求证：四边形BEFG 是平行四边形．【难度】★★ 【答案】略． 【解析】证明：BAF DAE ∠=∠，BAE DAF ∴∠=∠．又四边形ABCD 是菱形，//AB AD BC CD ABE ADF AD BC ∴===∠=∠，，．A B E A D F ∴≅．BE DF ∴=且有AD GDBE GB=． B E D F A D G DB C C D D F G B ∴==，， //EF BD ∴．又DF AD FC DF =， DF GDFC GB ∴=， //FG BC ∴． 即证四边形BEFG 是平行四边形．【总结】平行四边形的证明，先从判定定理出发，考虑哪个判定定理的应用，然后根据题目条件进行分析证平行．【例15】如图，E 、F 、G 、H 分别是四边形ABCD 各边的点，且AE FD EB AF =， BG HC GC DH =，连接EH 、GF 相交于点O ．求证：OE GO FO OH =．【难度】★★★ 【答案】略．【解析】证明：连结EF 、BD 、GH ．A E F D EB A F=，即AE AFEB FD =， //EF BD ∴． 又BG HC GC DH =，即GC HCBG DH=，//GH BD ∴． //EF GH ∴， OE OFOH OG∴=， 即OE GO FO OH =． 【总结】观察题目条件的形式，可知题目考查三角形一边平行线性质及其判定定理，先判定再利用性质进行变形应用．ADB CEF P Q【例16】如图，在梯形ABCD 中，AD //BC ，AD a =，BC b =，E 、F 分别是AD 、BC的中点，且AF 交BE 于P ，CE 交DF 于Q ，求PQ 的长．【难度】★★★【答案】abPQ a b =+．【解析】AD //BC ， AE PE ED EQBF BP FC QC∴==，． 又E 、F 分别是AD 、BC 的中点，A E D EB F FC ∴==，， PE EQBP QC ∴=， ////P Q B C A D ∴．P Q E P P QP F P B B C E B A DA F EB ∴===，，1PQ PQAD BC ∴+=． 代入，求得：abPQ a b=+．【总结】考查三角形一边平行线性质定理及其判定定理的，先应用性质证明比例线段相等再判定．由三线平行模型可得出结论．【例17】如图，点G 是ABC ∆的重心，过点G 作直线k ，交AB 于点E ，交AC 于点F ．求证：1BE CFAE AF +=．【难度】★★★ 【答案】略．【解析】证明：分别过点B 和点C 作BM 和CN 平行于直线 AD ，分别交AB 、AC 于点M 、点N ．则有////BM AG CN ，BE BM CF CNAE AG AF AG∴==，， BE CF BM CNAE AF AG+∴+=． 又G 是ABC ∆的重心，根据重心的性质，BD CD ∴=且有2AG DG =， 即此时DG 为梯形MBCN 的中位线．2BM CN DG AG ∴+==，即可证1BE CFAE AF+=． 【总结】根据重心的特殊性质构造平行线段，用比例线段的转化建立一个三直线平行的模型解决问题．1、平行线分线段成比例定理两条直线被三条平行的直线所截，截得的对应线段成比例． 如图，直线1l //2l //3l ，直线m 与直线n 被直线1l 、2l 、3l 所截，那么DF EGFB GC=．2、平行线等分线段定理两条直线被三条平行的直线所截，如果一条直线上截得的线段相等，那么另一条直线上截得的线段也相等．【例18】如图，1l //2l //3l ，3AB =，8AC =，10DF =，求DE 、EF 的长．【难度】★ 【答案】152544DE EF ==，． 【解析】根据平行线分线段成比例定理和比例的合比 性，可得AB DE AC DF =，代入求得154DE =，则254EF DF DE =-=． 【总结】考查平行线分线段成比例定理结合比例的合比性质的应用．模块二：平行线分线段成比例定理知识精讲例题解析BCD E FG1l 2l3l BC1l 2l3l A DEFABCDEF【例19】如图，直线1l 、2l 、3l 分别交直线4l 于点A 、B 、C ，交直线5l 于点D 、E 、F ，且1l //2l //3l ．已知3AB =，5AC =，9DF =，求DE 、EF 的长．【难度】★ 【答案】271855DE EF ==，． 【解析】根据平行线分线段成比例定理和比例的合比性， 可得AB DE AC DF =，代入求得275DE =，则185EF DF DE =-=． 【总结】考查平行线分线段成比例定理结合比例的合比性质的应用，两条直线交叉时仍成立．【例20】命题“梯形ABCD 中，AD //BC ，点E 、F 在AB 、CD 上，且::AE EB DF FC =，则EF //BC ”是（选填“真”或“假”）命题．【难度】★ 【答案】真．【解析】过点A 作CD 的平行线，根据三角形一边平行线的判定定理易证得命题成立． 【总结】平行线分线段成比例定理，实际是三角形一边平行线性质定理的变形应用，即将一条直线进行平移即可．【例21】如图，ABC ∆中，90C ∠=︒，四边形EDFC 为内接正方形，5AC =，3BC =，则:AE DF =．【难度】★ 【答案】5:3．【解析】:::5:3AE DF AE DE AC BC ===． 【总结】考查图形中相等比例线段的转化．CB A 5l 1l 2l 3l4l DE F【例22】已知线段a 、b 、c ，求作线段x ，使::a b c x =． 【难度】★ 【答案】略．【解析】作法：在平面内任作一条直线1l ，在1l 上顺次截取 AB a BC b ==，，过点A 任作一条射线2l ，在2l 上截取线段AD c =，连结BD ，过点C 作//CE BD 交射线2l 于点E ，线段DE 即为所求．【总结】考查三角形一边平行线性质定理的应用，平行情况下截得的对应线段长度比例相等．【例23】如图，已知线段AB ，在线段AB 上求作一点C ，使得:1:2AC BC =． 【难度】★★ 【答案】略【解析】作法：过点A 任作一条射线l （不与AB 重合），在l 上顺次截取一个合适的线段， 使得AD DE EF ==， 连结BF ，过点D 作//DC BF 交线段AB 于点C ，点C 即为所求．【总结】考查三角形一边平行线性质定理的应用，平行情况下截得的对应线段长度比例相等．【例24】如图，ABC ∆中，90C ∠=︒，点G 是三角形的重心，8AB =． （1）求GC 的长；（2）过点G 的直线MN //AB ，交AC 于点M ，交BC 于点N ，求MN 的长．【难度】★★【答案】（1）83GC =；（2）163MN =．【解析】（1）延长CG 交AB 于点D ，则CD 为ABC 斜边AB 上的中线，则有142CD AB ==，根据重心的性质，即可得2833GC CD ==，．（2）由MN //AB 易得G 为Rt AMN 斜边MN 的中线，故1623MN GC ==【总结】考查三角形重心的性质与直角三角形斜边中线相结合，根据平行可得出线段相等的判定．b c ABA BCNMG D【例25】如图，D 是线段BC 上一点，且23BD DC =，CE 交AB 于点F ，:1:3AE ED =，求:AF BF 的值．【难度】★★ 【答案】2:15．【解析】过点A 作//AM BC 交CF 的延长线于点M ， 根据三角形一边平行线的性质定理，则有13AM AE DC ED ==．又23BD DC =，即()23BC DC DC -=． 可得25DC BC =， 则215AM BC =．由//AM BC 可得：::2:15AF BF AM BC ==．【总结】考查三角形一边平行线的性质，由已知和所求比例构造平行．【例26】如图，AB 、CD 、EF 都垂直于直线l ，12AB =，7EF =，:2:3BD DF =，求CD 的长．【难度】★★ 【答案】10．【解析】过点F 作//FN EA 交CD 于点M ，交AB 于点N．AB 、CD 、EF 都垂直于直线l ，////A B C D E F ∴，则四边形EFMC 、CMNA 、EFNA 都为平行四边形．7E F C M N A ∴===， 5B N A B A N ∴=-=．:2:3B D D F =， 35DF BF ∴=． 由平行可得：35DM DF BN BF ==，代入得：3DM =，10CD CM DM =+=． 【总结】考查平行线分线段成比例定理，往往通过平行线的平移转化到一个三角形中三角形一边平行线性质定理的应用．ABCDEFlM NA BCDEFO【例27】如图，ABC ∆中，M 为BC 中点，O 为AM 上一点，BO 的延长线交AC 于点D ， CO 的延长线交AB 于点E ，PQ //BC ，且PQ 过点O 与AB 、AC 分别交于点P 和点Q ．求证：（1）PO OQ =；（2）DE //BC ．【难度】★★ 【答案】略． 【解析】证明：（1）PQ //BC ，∴////PO BM OQ CM ，．PO AO OQ AO BM AM CM AM ∴==，， PO OQBM CM∴=．由M 为BC 中点，即可证得PO OQ =．（2）连结DE ． PQ //BC ，EO PO DO OQEC BC DB BC∴==，．由（1）可得PO OQ =，EO DO EC DB ∴=，EO DOOC OB∴=，∴DE //BC ． 【总结】考查三角形一边平行线的判定定理，注意根据相等的比例作为中间量进行等比例转换．【例28】如图，在等腰梯形ABCD 中，AB //CD ，两对角线AC 和BD 相交于点O ，过点O作EF //AB ，且10EF =，若:1:3AE ED =，求梯形ABCD 中位线的长．【难度】★★【答案】403．【解析】AB //CD ，AB AO BOCD OC OD∴==． A O B OA CB D∴=． 又EF //AB ，//EF CD ∴．又:1:3AE ED =，1144EO AO AE FO BO AO CD AC AD CD BD AC ∴======，．152E O F O E F ∴===，12042033DC EO AB CD ∴====，． 即梯形中位线长为()14023AB CD +=．【总结】充分利用三角形一边平行的性质和比例合比性进行计算，关键点在于判断中点，对于非等腰梯形也可得到相同的结论．ABCD E O PQM【例29】如图，已知点A 、C 、E 和点B 、F 、D 分别是O ∠两边上的点，且AB //ED ， BC //EF ．求证：AF //CD ．【难度】★★ 【答案】略． 【解析】证明：AB //ED ，OA OBOE OD∴=， 即OB OE OA OD ⋅=⋅．又BC //EF ， O B O CO F O E∴=， 即OB OE OC OF ⋅=⋅． O A O D O C O F∴⋅=⋅， 即OA OFOC OD=， ∴AF //CD ． 【总结】考查三角形一边平行线的性质及其判定定理，多用相等比例线段进行转化．【例30】如图，M 、N 分别是ABC ∆两边AB 、AC 的中点，P 是MN 上任一点，延长BP 、CP 交AC 、AB 于K 、H ，求AH AKHB KC +的值． 【难度】★★★ 【答案】1．【解析】过点A 作//DE BC ，分别交CH 、BK 的延长线于点D 、点E ．由//DE BC ，则有//AD BC ，//AE BC ，故AH AD AK AEHB BC KC BC==，． ∴=AH AK AD AE DEHB KC BC BC++=． 又M 、N 分别为AB 、AC 的中点，∴MN 为ABC 的中位线，∴//MN BC 且1=2MN BC ，//MN DE ．又M 、N 分别为AB 、AC 的中点，∴PM 、PN 分别为ABE 、ACD 的中位线，∴1122PM AE PN AD ==，，∴()12PM PN AE AD +=+，即12MN DE =．由此DE BC =，故1AH AKHB KC +=．【总结】根据题目所求的比例线段，构造平行线，在图形中形成“A ”字型和“X ”字型的构造，先判定再应用，进行比例线段的综合应用．AC EF O【例31】如图，矩形ABCD 中，AC 、BD 相交于点O ，OE BC ⊥于点E ． （1）连接DE 交OC 于点F ，作FG BC ⊥于点G ，求证：点G 是线段BC 的一个三等 分点；（2）请你仿照（1）的作法，在原图上作出BC 的一个四等分点（要求保留作图痕迹，可不写作法及证明过程）．【难度】★★★【答案】（1）略；（2）如图点M 即为所求． 【解析】（1）证明：四边形ABCD 是矩形， 90BCD OB OD ∴∠=︒=，． 又OE BC ⊥，//OE CD ∴，12OE OB OFCD OD FC ∴===． FG BC ⊥，//FG OE ∴， 2CG FC GE OF∴==． 由OB OD =可知E 为BC 中点， 2163CG BC ∴==．即点G 是线段BC 的一个三等分点（2）延长EO 交AD 于点H ，连结CH 交DE 于点P ，过点P 作PM BC ⊥交BC 于点M ，易证点M 为EC 中点，即图中点M 即为所求．【总结】考查对三角形一边平行线性质定理的构造和应用，注意对图形中“A ”字型和“X ”字型的构造，先判定再应用，进行比例线段的综合应用．ABDE F G OHP M【例32】如图，ABC ∆中，12BC =，AC =45C ∠=︒，P 是BC 边上的一个动点， 过点P 作PD //AB 与AC 相交于点D ，连接AP ，设线段BP 的长为x ，APD ∆的面积为y ．（1）求y 与x 之间的函数关系式，并指出函数的定义域；（2）是否存在一个位置的点P ，使APD ∆的面积等于APB ∆的面积的13？如果存在，求出BP的长；如果不存在，请说明理由．【难度】★★★【答案】（1）()2140123y x x x =-+<<；（2）存在，8BP =．【解析】（1）过点P 作PE AC ⊥于点E ． 由BP x =，可得12PC x =-，又45C ∠=︒，故)12PE CE x ==-． 又//PD AB ，故BP AD BC AC=，代入可得：AD x ．故)()2111124012223y PE AD x x x x x =⋅=-=-+<<． （2）过点A 作AF BC ⊥于点F ．由45C AC ∠=︒=，，可得：8AF CF ==， 故142ABPSAF BP x =⋅=． 又APD ∆的面积是APB ∆面积的13，∴2114433y x x x =-+=⨯，解得：8x =，即8BP =．【总结】考查三角形中一边平行线性质的综合应用，同时在题目中，注意对于特殊角的利用．ABCD PEF【习题1】如图，ABC ∆中，点D 、E 分别在边AB 、AC 上，已知=3AD ，5AB =，2AE =，43EC =，由此判断DE 和BC 的位置关系是，理由是 ． 【难度】★【答案】平行，三角形一边平行线的判定定理【解析】2BD AB AD =-=，则有AD AEBD EC =，根据三角形一边平 行线的判定定理可知平行．【总结】考查三角形一边平行线判定定理的内容掌握．【习题2】ABC ∆中，直线DE 交AB 于点D ，交AC 于点E ，以下能推出DE //BC 的条件 是（ ）．（A ）23AB AD =，12EC AE =（B ）23AD AB =，23DE BC = （C ）23AD DB =，23CE AE =（D ）43AD AB =，43AE EC =【难度】★ 【答案】A【解析】根据比例的合比性，可知只有A 选项中满足2AB AEBD EC==，根据三角形一边平行 线的判定定理可知A 选项正确，其它都不满足．【总结】考查三角形一边平行线的判定定理，需要结合比例的合比性等性质进行判断．【习题3】在ABC ∆中，点D 、E 分别在边AB 和BC 上，2AD =，3DB =，10BC =，要使DE //AC ，则BE =．【难度】★ 【答案】6．【解析】根据三角形一边平行线的判定定理，要得到DE //AC ，则必有DB BEAB BC=， 即3=2+310BE，即可求得6BE =． 【总结】考查三角形一边平行线的判定定理，注意性质和判定的相互转化．随堂检测ABCD E【习题4】如图，ABC ∆中，DE //BC ，AF ADDF DB=，求证：EF //CD ． 【难度】★ 【答案】略． 【解析】证明：DE //BC ，AD AEDB EC∴=． 又AF AD DF DB =，AF AEDF EC∴=． ∴EF //CD ．【总结】考查三角形一边平行线性质及其判定定理，先利用性质构造等比例线段再判定．【习题5】如图，已知AD //BE //CF ，它们依次交直线1l 、2l 于点A 、B 、C 和点D 、E 、F ．（1）如果6AB =，10BC =，8EF =，求DE 的长； （2）如果:3:5DE EF =，24AC =，求AB 、BC 的长． 【难度】★★【答案】（1）245；（2）915AB BC ==，．【解析】（1）根据平行线等分线段成比例定理，则有 DE AB EF BC =，代入可求得245DE = （2）根据平行线等分线段成比例定理，则有35AB DE BC EF ==，根据比例的合比性，则有38AB AC =，代入可得9AB =，15BC AC AB =-=【总结】考查平行线等分线段成比例定理和比例的合比性的综合应用．1l 2lABC D E FACD EFABCDEF O【习题6】如图，平行四边形ABCD 中，AC 、BD 相交于点O ，2AB =，3BC =，1AF =，BA 的延长线交OF 的延长线于点E ，求AE ．【难度】★★ 【答案】2．【解析】延长FO 交线段BC 于点G ．四边形ABCD 是平行四边形，////3A D B C A B C DA DBC ∴==，，．又由AO CO =，可得1GC AF ==，2B G B C G C ∴=-=． 由//AF BG ，可得12AE AF BE BG ==，即122AE AE =+，解得：2AE =．【总结】平行四边形中容易出现“A ”字型和“X ”字型，利用平行可进行相应的等比例转化解决问题．【习题7】如图，在ABC ∆中，点E 、F 分别在AB 、AC 上，且EF //BC ，D 为BC 的中 点，ED 、FD 的延长线分别交AC 、AB 的延长线于点H 、点G ，连接HG ，求证：EF //GH ．【难度】★★ 【答案】略． 【解析】证明：EF //BC ，GD BD DH CDGF EF EH EF∴==，． 又BD CD =，GD DHGF EH∴=． 根据比例的合比性，即GD DHDF DE=， //EF GH ∴．【总结】考查三角形一边平行线性质及其判定定理，根据平行进行等比例转化．ABCDE F G GA BCDFGH【习题8】如图1，在菱形ABCD中，点G是CD边上的一点，联结BG交AC于F，过F作FH//CD交BC于H，可以证明结论FH FGAB BG=成立（不必证明）．（1）如图2，上述条件中，若点G在CD的延长线上，其他条件不变时，结论FH FGAB BG=是否仍成立？若成立，请给出证明；若不成立，请说明理由；（2）在（1）的条件下，若已知4AB=，60ADC∠=︒，9CG=，求线段BG与FG的长．图1 图2【难度】★★★【答案】（1）成立；（2）BG FG=【解析】（1）证明：四边形ABCD是菱形，//AB CD AB CD∴=，．FH//CD，//FH AB∴，FH CFAB CA∴=．由//AB CG，FG FCFB FA∴=，根据比例的合比性FG FCBG CA=，F H F GA B B G∴=．（2）过点B作BM DC⊥交DC延长线于点M．四边形ABCD是菱形，4//BC AB AD BC∴==，．60ADC∠=︒，60BCM∴∠=︒，122CM BC BM∴===，由9CG=，可得11GM=，BG∴===由//AB CG得94GF CGFB AB==，913GFGB∴=．代入即得：FG=【总结】平行四边形中容易出现“A”字型和“X”字型，利用平行可进行相应的等比例转化解决问题，同时注意对图形中一些特殊角的运用，实际上在上图中产生了三个等边三角形，利用等边三角形也可以解决问题．A BCDFGHMABC DEFOP【习题9】如图，矩形ABCD 中，对角线AC 、BD 相交于点O ，4AB =，3BC =，在线段 AB 上取一点P ，过点P 作AC 的平行线交BC 于点E ，连接EO ，并延长交AD 于点F ，连接PF ．（1）求证：PF //BD ；（2）设的AP 长为x ，PEF ∆的面积为y ，求y 与x 的函数关系式，并写出它的定义域． 【难度】★★★【答案】（1）略；（2）()233044y x x x =-+<<．【解析】（1）证明：//PE AC ，AP CEAB BC ∴=． 又四边形ABCD 为矩形， //AO CO AD BC AD BC ∴==，，．由此可得CE AF =．AP AFAB AD∴=，∴PF //BD ． （2）解：由（1）可得PF //BD ，//PE AC ，故34AF AD AP AB ==，34BE BC BP AB ==，AP x =，则4BP x =-，34AF x =，33344BE BP x ==-，同时由于CE AF =，DF BE =，1134622ABCD ABEF S S ∴==⨯⨯=矩形梯形APF BPE ABEF y S S S ∆∆∴=--梯形11622AP AF BP BE =-⋅-⋅()221313642424x x =-⋅-⋅-()233044x x x =-+<<．【总结】考查三角形一边平行线性质运用时，经常可以将对应边的比例关系转化到一个三角形中相应边的比例关系，并且在平行四边形中，过对称中心的点平分平行四边形的周长和面积，且截得的线段都相等．【作业1】在A ∠的一边上顺次有B 、C 两点，在另一边上顺次有D 、E 两点，又下列条件能判断//BD CE 的个数是（）．（1）3AB cm =，4BC cm =， 1.8AD cm =， 2.2DE cm =； （2）:2:3AB AD =， 1.8AE cm =， 1.2AC cm =； （3）5AB cm =，6BC cm =， 4.4AE cm =， 2.4DE cm =； （4）10AB cm =，15AC cm =，10BD cm =，15EC cm =． （A ）1个（B ）2个（C ）3个（D ）4个【难度】★ 【答案】C【解析】根据三角形一边平行线的判定定理，可知（2）（3）都满足AB ADAC AE=，可得到//BD CE ， （1）不满足；同时，在（4）的条件下，ABD ∆和ACE ∆都是等腰三角形，且有公共底角A ∠， 由此可知两三角形每个角都对应相等，也可得到平行．【总结】考查三角形一边平行线的判定定理的条件，一般只考虑有公共夹角的情况，但有时候在等腰三角形中需要进行更详细分析再得出结论．【作业2】ADE ∆中，点B 和点C 分别在AD 、AE 上，且2AB BD =，2AC CE =，则:BC DE =．【难度】★ 【答案】2:1．【解析】由2AB BD =，2AC CE =，即有12AD AE AB AC ==． 故//DE BC ，可得：::2:1BC DE AB AD ==．【总结】考查三角形一边平行线的性质和判定定理，先判定再利用性质得出结论．课后作业ABCDE F ON M【作业3】已知点D 、E 分别是ABC ∆的边AB 、AC 的反向延长线上的点，如果25AD AB =，当AEAC为何值时，//DE BC ？ 【难度】★【答案】25．【解析】25AE AD AC AB ==．【总结】考查三角形一边平行线性质判定定理的推论，在反向延长线上也成立．【作业4】如图，在ABC ∆中，点D 、E 、F 分别在AC 、AB 、BC 上，且3DE =， 4.5BF =，25AD AE AC AB ==．求证：EF //AC ．【难度】★★ 【答案】略．【解析】证明：25AD AE AC AB ==，//DE BC ∴， 25D E A E B C A B ∴==．由3DE =，可得7.5BC =，则有35BF BE BC AB ==， ∴EF //AC ．【总结】考查三角形一边平行线性质定理的应用，也可通过证明四边形CDEF 是平行四边形间接证得．【作业5】如图，在梯形ABCD 中，EF //AB //CD ，两对角线AC 和BD 相交于点O ，且分别与EF 相交于点M 、N ，下列比例式中正确的是（ ） （A ）AO BO AB CO DO CD == （B ）AM BN MN CM DN AB ==（C ）AE AB BF DE CD CF == （D ）BD AC AB DN CM MN ==【难度】★★ 【答案】A【解析】根据三角形一边平行线的性质定理及其推论可知A 正确．【总结】考查三角形一边平行线的性质定理及其推论，找准相应比例线段，确立好对应关系．AB CDEFA BCD EFG1l 2l 3l ABCD E FG1l 2l【作业6】如图，1l //2l ，:2:5AF FB =，:4:1BC CD =，则不成立的是（ ） （A ）:2:1AE EC = （B ）:2:5FG GD = （C ）:2:5GF FD = （D ）:1:2AG BC = 【难度】★★ 【答案】B【解析】由1l //2l ，可得:::2:5AG BD GF FD AF FB ===，B 错误，C 正确； 又根据:4:1BC CD =，可得:2:41:2AG BC ==，:2:1AG CD =，由平行可得：::2:1AE EC AG CD ==，A 、D 正确．【总结】考查三角形一边平行线的性质定理，注意根据题目已知条件进行等比例转化．【作业7】如图，直线1l //2l //3l ，若5AB cm =，8BC cm =，2EG cm =，3GF cm =，求线段DE 与GC 的长．【难度】★★ 【答案】258DE cm =，245GC cm =． 【解析】根据平行线分线段成比例定理，可以得到DE ABEF BC =， 即5238DE =+，可得258DE cm =．由12//l l ，可得：EG BG DE AB =，代入可解得：165BG =， 245GC BC BG cm ∴=-=．【总结】考查平行线分线段成比例定理，往往可以在过程中应用三角形一边的平行线性质定理进行比例转化和计算．AB【作业8】如图，已知线段AB ，在线段AB 上求作一点C，使得:AC BC = 【难度】★★★ 【答案】略．【解析】作法：在平面内任作一等腰直角三角形DEF ，其中点E 为其直角顶点，以点F 为 圆心，FD 长为半径画弧交EF 的延长线于点G，则:EF FG =，过点A 任作一条 射线l ，在l 上顺次截取AM EF =，MN FG =，连结NB ，过点M 作//MC NB 交线段AB于点C ，点C 即为所求．【总结】考查三角形一边平行线性质定理的应用，平行情况下截得的对应线段长度比例相等，关键在于构造比为【作业9】梯形ABCD 中，点E 在AB 上，点F 在CD 上，且AD a =，BC b =． （1）如图（a ），如果点E 、F 分别为AB 、CD 的中点，求证：EF //BC 且2a bEF +=； （2）如图（b ），如果AE DF mEB FC n==，判断EF 和BC 是否平行，并证明你的结论，并用a 、 b 、m 、n 的代数式表示EF ．【难度】★★★【答案】（1）略；（2）平行，an bmEF m n+=+． 【解析】（1）证明：过点F 作//MN AB 交AD 延长线于点M ，交BC 于点N ， 则四边形ABNM 为平行四边形，AB MN AM BN ∴==，．F 为CD 中点，由平行可得F 为MN 中点，即12FN MN =，DM CN =．E 为AB 中点，1122BE AB MN NF ∴===．由//MN AB ，∴四边形EBNF 为平行四边形，//EF AB ∴且EF AM BN ==．即()()()111222EF AM BN a DM b CN a b =+=++-=+．（2）证明：过点F 作//MN AB 交AD 延长线于点M ，交BC 于点N ， 则四边形ABNM 为平行四边形，AB MN AM BN ∴==，．由//DM CN ，DM MF DFCN FN CF∴==． AE DF EB FC =，AE MF EB FN ∴=，AB MNEB FN ∴=，EB FN ∴=． 由//MN AB ，∴四边形EBNF 为平行四边形．//EF AB ∴且EF AM BN ==． 由DM DF m CN FC n ==，可得AM a m b BN n -=-，即EF a mb EF n-=-，解得：an bmEF m n+=+．【总结】考查梯形中位线性质的证明，实际上也是平行线分线段成比例定理的一种逆运用，通过平移构造并证明平行线段．F EA (D)B CNMNMM【作业10】已知MN //EF //BC ，点A 、D 为直线MN 上的两动点，AD a =，BC b =，AE mBE n=． （1）当点A 、D 重合，即0a =时（如图1），试求EF ； （用含a 、b 、m 、n 的代数式表示）（2）请直接应用（1）的结论解决下面问题：当A 、D 不重合，即0a ≠， ①如图2这种情况时，试求EF ；（用含a 、b 、m 、n 的代数式表示）②如图3这种情况时，试猜想EF 与a 、b 之间有何种数量关系？并证明你的猜想．【难度】★★★ 【答案】（1）mb EF m n =+；（2）①mb na EF m n +=+；②mb naEF m n-=+． 【解析】（1）0a =时，EF AE m BC AB m n ==+，可得mbEF m n=+； （2）①过点D 作//DH AB 交EF 于点G ，交BC 于点H ， 易得EG AD BH a CH b a ====-，． 同时由平行可得：FG AE mCH AB m n==+， 则()m b a FG m n-=+，∴()m b a mb naEF EG FG a m n m n-+=+=+=++． ②过点A 作//AH DC 交EF 延长线于点G ，交BC 延长线于点H ， 易得FG AD CH a BH b a ====+，，同时由平行可得：EG AE mBH AB m n==+，则()m b a FG m n +=+， ()m b a m b n aE F E G F G a m n m n+-=-=-=++． 【总结】考查平行线分线段成比例定理，通过平移转化到一个三角形中对应边成比例即可．H。

基础知识点三角形一边平行线的判定定理:如果一条直线截三角形两边所得的对应线段成比例，那么这条直线平行于三角形的第三边。

(由成比例得平行)A如图，若EC AE DB AD =(或AC AE AB AD =或ACEC AB BD =)，则DE//BCD EB C三角形一边平行线的判定定理的推论：如果一条直线截三角形两边的延长线(这两条延长线在第三边的同侧)所得的对应线段成比例，那么这条直线平行于第三边。

若CE AC BD AB =(或AE AC AD AB =或AC EC AD BD =) 若AC AE AB AD =(或EC AE BD AD =或CEAC BD AB =) 则DE//BC 则DE//BC例题解析例题解析:在△ABC 中，点D 、E 在边AB 、AC 上，根据下列给定的条件，试判断DE 与BC 是否平行？ 并说明理由.(1)AD=3cm ，DB=4cm ，AE=1.8cm ，CE=2.4cm ；(2)AD=6cm ，BD=9cm ，AE=4cm ，AC=10cm;答案：(1)是；(2)不是.变式:在△ABC 中，点D 、E 在边AB 、AC 上，根据下列给定的条件，试判断DE 与BC 是否平行？ 并说明理由.(1)AD=8cm ，AC=16cm ，AE=6cm ，AB=12cm;(2)AB=3BD ，AE=32AC;(3)AB=2BD ，AC=2CE.答案：(1)不是；(2)是；(3)是.例题解析:如图，点D 、E 分别在AB 、AC 上，以下能推得DE//BC 的条件是( )。

A.AD:AB=DE:BCB.AD:DB=DE:BCC.AD:DB=AE:ECD.AE:AC=AD:DB 答案:解析：∵AD:DB=AE:EC ，∴DE//BC ，故选:C ．变式:在△ABC 中，点D 、E 分别在边AB 、AC 上，下列条件中不能判定DE//BC 的是( )。

A.= B.= C.= D.=解析：∵=，∴DE//BC ，选项A 不符合题意；∵=，∴DE//BC ，选项B 不符合题意； ∵=，∴DE//BC ，选项C 不符合题意；=，DE//BC 不一定成立，选项D 符合题意.故选：D ．例题解析:已知:如图，点D ，F 在△ABC 的边AB 上，点E 在边AC 上，且DE//BC ，ABAD AD AF =，求证:EF//DC. 解答:证明:∵DE//BC ，∴AC AE AB AD =， ∵AB AD =，∴AC AD =，∴ADAC =，∴EF//DC.变式:如图，在△ABC 中，EF//CD ，DE//BC 。

基础知识点三角形一边平行线的判定定理:如果一条直线截三角形两边所得的对应线段成比例，那么这条直线平行于三角形的第三边。

(由成比例得平行)A如图，若EC AE DB AD =(或AC AE AB AD =或ACEC AB BD =)，则DE//BCD EB C三角形一边平行线的判定定理的推论：如果一条直线截三角形两边的延长线(这两条延长线在第三边的同侧)所得的对应线段成比例，那么这条直线平行于第三边。

若CE AC BD AB =(或AE AC AD AB =或AC EC AD BD =) 若AC AE AB AD =(或EC AE BD AD =或CEAC BD AB =) 则DE//BC 则DE//BC例题解析例题解析:在△ABC 中，点D 、E 在边AB 、AC 上，根据下列给定的条件，试判断DE 与BC 是否平行？ 并说明理由.(1)AD=3cm ，DB=4cm ，AE=1.8cm ，CE=2.4cm ；(2)AD=6cm ，BD=9cm ，AE=4cm ，AC=10cm;答案：(1)是；(2)不是.变式:在△ABC 中，点D 、E 在边AB 、AC 上，根据下列给定的条件，试判断DE 与BC 是否平行？ 并说明理由.(1)AD=8cm ，AC=16cm ，AE=6cm ，AB=12cm;(2)AB=3BD ，AE=32AC;(3)AB=2BD ，AC=2CE.答案：(1)不是；(2)是；(3)是.例题解析:如图，点D 、E 分别在AB 、AC 上，以下能推得DE//BC 的条件是( )。

A.AD:AB=DE:BCB.AD:DB=DE:BCC.AD:DB=AE:ECD.AE:AC=AD:DB 答案:解析：∵AD:DB=AE:EC ，∴DE//BC ，故选:C ．变式:在△ABC 中，点D 、E 分别在边AB 、AC 上，下列条件中不能判定DE//BC 的是( )。

A.= B.= C.= D.=解析：∵=，∴DE//BC ，选项A 不符合题意；∵=，∴DE//BC ，选项B 不符合题意； ∵=，∴DE//BC ，选项C 不符合题意；=，DE//BC 不一定成立，选项D 符合题意.故选：D ．例题解析:已知:如图，点D ，F 在△ABC 的边AB 上，点E 在边AC 上，且DE//BC ，ABAD AD AF =，求证:EF//DC. 解答:证明:∵DE//BC ，∴AC AE AB AD =， ∵AB AD =，∴AC AD =，∴ADAC =，∴EF//DC.变式:如图，在△ABC 中，EF//CD ，DE//BC 。