当前位置：文档之家 › 中心对称第一课时优质优秀课件

中心对称第一课时优质优秀课件

  • 格式：ppt
  • 大小：1.56 MB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

《中心对称》(第1课时)ppt课件

《中心对称》(第1课时)ppt课件

九年级 上册
23.2 中心对称（第1课时）
课件说明
• 本节课从旋转变换引入中心对称的概念，先让学生从 旋转的角度观察两个图形之间的关系，类比旋转得出 中心对称的定义，渗透了从一般到特殊的思想方法． 在此基础上，通过探究成中心对称的两个图形的对称 中心与对应点所连线段之间的关系得到中心对称的性 质，并能运用中心对称的性质画出一个图形关于某一 点中心对称的对称图形．
D A
O C
B
2．中心对称的性质
问题5 中心对称是特殊的旋转，它有哪些性质？
C
A
B
O B′
A′
C＇
思考： （1）点 O 在线段 AA＇上吗？如果在，在什么位置？ （2）△ABC 和△A ＇B＇C＇ 有什么关系？ （3）你能从这个探究中得到什么结论？
中心对称的性质
（1）中心对称的两个图形， 对称点所连线段都经 过对称中心，而且被对称中心所平分；
6．布置作业
教科书第 66 页，练习 1，2 题．
这两个图形在旋转后能重合的对应点叫做关于对称 中心的对称点．
问题3 中心对称与一般的旋转的联系和区别？
联系：中心对称和一般的旋转都是绕着某一点进行 旋转；
区别：中心对称的旋转角度都是180°，一般的 旋转的旋转角度不固定，中心对称是特殊的旋转．
问题4 对称中心和对称点是如何确定的？ 你能指 出下图中的对称点吗？
例1 （1）如左图，选择点 O 为对称中心，画出点
A 关于点 O 的对称点 A＇；
（2）如右图，选择点 O 为对称中心，画出与 △ABC关于点 O 对称的△A＇B＇C＇．
A
A
C′
·
·B′
O
A′
·
O
B
中心对称图形(优质课比赛课件)

中心对称图形(优质课比赛课件)

中心对称图形(优质课比赛课件)
目录 Contents
• 中心对称图形的定义与性质 • 中心对称图形的分类与特点 • 中心对称图形的性质证明 • 中心对称图形在日常生活中的应用 • 中心对称图形的美学价值 • 中心对称图形的拓展与思考
01
中心对称图形的定义与性质
定义
总结词
中心对称图形是指关于某一点对称的图形，即图形绕着某点 旋转180度后与自身重合。
建筑学中的应用
1 2
建筑设计中的中心对称
中心对称的建筑形式给人以稳重、庄严和平衡的 感觉，常用于大型公共建筑和宗教建筑。
建筑立面和内部布局
建筑立面和内部布局中，中心对称的元素可以增 强建筑的视觉效果，给人以和谐、统一的感觉。
3
建筑结构和功能
中心对称的建筑结构有助于提高建筑的稳定性和 抗震性能，同时也有利于建筑的功能布局和使用。
艺术创作中的应用
绘画和雕塑
中心对称的构图和造型在绘画和 雕塑中广泛应用，可以创造出平
衡、和谐的艺术作品。
摄影
在摄影中，通过中心对称的构图 可以突出主题，增强画面的视觉
冲击力。
图案设计
中心对称的图案设计在纺织品、 平面设计等领域应用广泛，可以 创造出富有艺术感的视觉效果。
其他领域的应用
自然科学
在物理学、化学和生物学中，中心对称的现象广 泛存在，如晶体结构、分子形状等。
检查其是否能与原图重合来进行判断。
02
中心对称图形的分类与特点
中心对称图形的分类
中心对称图形可以分为两类：旋 转对称图形和镜面对称图形。
旋转对称图形是指围绕一个固定 点旋转一定角度后能与自身重合 的图形，如圆形、正多边形等。
镜面对称图形是指关于某一直线 对称的图形，如长方形、正方形
2021年人教版数学九年级上册23 中心对称(第一课时)课件

2021年人教版数学九年级上册23 中心对称(第一课时)课件


A．点 E C．点 G
B．点 F D．点 H
8
3．如图，△ABC 与△A′B′C′关于点 O 成中心对称，则下列结论不成立的是 ( D)
A．点 A 与点 A′是对称点 C．AB∥A′B′
B．BO＝B′O D．∠ACB＝∠C′A′B′
9
4．如图，在△ABC 中，AB＝AC，△ABC 与△FEC 关于点 C 成中心对称，连 接 AE、BF.若四边形 ABFE 为矩形，则∠ACB 为( C )
另外两个矩形，得到连接各自中心
的第二条线段，两条线段交于点G，
点G即为重心．
22
图2
►在有欢声笑语的校园里，满地都是雪，像一块大地毯。房檐上挂满了冰凌 ，一根儿一根儿像水晶一样，真美啊！我们一个一个小脚印踩在大地毯上 ，像画上了美丽的图画，踩一步，吱吱声就出来了，原来是雪在告我们： 和你们一起玩儿我感到真开心，是你们把我们这一片寂静变得热闹起来。 对了，还有树。树上挂满了树挂，有的树枝被压弯了腰，真是忽如一夜春 风来，千树万树梨花开。真好看呀！ ►冬天，一层薄薄的白雪，像巨大的轻软的羊毛毯子，覆盖摘在这广漠的荒 原上，闪着寒冷的银光。
B．(－ 3，2)，( 3，－2)
C．(－ 3，2)，(2，－ 3)
D．－ 27，
221， 27，－
21 2
14
8．如图，四边形 ABCD 是中心对称图形，对称中心为点 O，过点 O 的直线与 AD、BC 分别交于点 E、F，则图中相等的线段有( C )
A．3 对 C．5 对
B．4 对 D．6 对
►走进颐和园，眼前是繁华的苏州街，现在依稀可以想象到当年的热闹场面， 苏州街围着一片湖，沿着河岸有许多小绿盘子里装着美丽的荷花。这里是 仿照江南水乡--苏州而建的买卖街。当年有古玩店、绸缎店、点心铺等， 店铺中的店员都是太监、宫女妆扮的，皇帝游览的时候才营业。我正享受 着皇帝的待遇，店里的小贩都在卖力的吆喝着。 ►走近一看，我立刻被这美丽的荷花吸引住了，一片片绿油油的荷叶层层叠 叠地挤在水面上，是我不由得想起杨万里接天莲叶无穷碧这一句诗。荷叶 上滚动着几颗水珠，真像一粒粒珍珠，亮晶希望对您有帮助，谢谢 晶的。 它们有时聚成一颗大水珠，骨碌一下滑进水里，真像一个顽皮的孩子！
优质课中心对称市公开课一等奖省优质课获奖课件

优质课中心对称市公开课一等奖省优质课获奖课件

第9页
【针对训练】 D
第10页
探究点三 中心对称性质应用
Ø 活动三：阅读教材64页例1，相互交流思索 下面问题 ：
第11页
（1）怎样找到点A对应点？ （2）怎样找到A，B，C三点对应点？
第12页
【针对训练】
第13页
第14页
●总结梳理 内化目标
1. 中心对称． 2.中心对称性质． 3.中心对称作图方法．
（2）什么叫中心对称？什么叫对称中心？什 么叫关于中心对称点？
第4页
第5页
【针对训练】 B
第6页
（3）
（4）
第7页
探究点二 中心对称性质推导
Ø 活动二：阅读教材第65页内容, 相互交流 思索下面问题 ： (1)教材是怎样证实A，O，A′三点在一条 直线上？ (2)中心对称性质有哪些？
第8页
中心对称判别方法
第15页
●达标检测 反思目标A第16页第17页第18页
第19页
第20页
第21页
课后作业
• 上交作业：教科书第69页第1题 ． • 课后作业：“学生用书”“课后作业”部分
．
第22页
第2页
学习目标
• 1． 认识两个图形关于某一点中心对 称本质.
• 2. 了解中心对称性质，并能够判断 两个图形是否成中心对称.
• 3. 会画某图形关于某点对称图形， 会确定对称中心.
第3页
● 合作探究 达成目标
探究点一 中心对称概念
活动一：阅读教材第64页内容,相互交流思 索下面问题 ：
(1)在图23.2-1及图23.2-2两图中，图形旋 转了多少度？旋转后有什么改变？
中心对称图形课件第一课时

中心对称图形课件第一课时


圆既是轴对称图形，又是中心对称图形。对称轴 是每一条直径所在直线；对称中心是圆心 。
轴对称图形与中心对称图形的比较
中心对称图形与轴对称图形有 什么区别与联系？
轴对称图形
中心对称图形
1 有一条对称轴——直线 有一个对称中心——点 2 图形沿轴对折（翻转180° ） 图形绕中心旋转180°
3 翻转前后的图形完全重合 旋转前后的图形完全重合
（1）轴对称图形也是中心对称图形。（× ） （2）旋转对称图形也是中心对称图形。（× ）
（3）平行四边形、长方形和正方形都是中心对
称图形，对角线的交点是它们的对称中心。（√ ）
（4）角是轴对称图形也是中心对称图形。（ × ）
（5）在成中心对称的两个图形中，对应线段
平行（或在同一直线上）且相等。
（√ ）
26个英文大写正体字母中，哪些是轴对称图 形，哪些是中心对称图形？
ABCDEF GHI JKL M NO P Q R S T U V WX YZ
下面扑克牌中，哪些牌的牌面是中心对称图形？
观察下列标志，它们分别是何种对称图形？
填一填
下面图形中,哪些是中心对称图形?哪些是轴 对称图形?指出它们的对称中心或对称轴?
中心对称图形
随堂练习
1. 选择题： （1）下列图形中即是轴对称图形又是中心对称
图形的是（ C ） A. 角 B. 等边三角形 C. 线段 D. 平行四边形
（2）下列多边形中，是中心对称图形而不是 轴对称图形的是（ A ）
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
2. 判断下列说法是否正确。
2.中心对称图形只有一个对称中心， 而轴对称可有几条不同的对称轴，
3.如果一个图形既是轴对称图形 ， 又是中心对称图形，那么对称中心 一定在对称轴上。
《中心对称》PPT课件

《中心对称》PPT课件


2．如图，在平行四边形 ABCD 中，对角线 AC，BD 相交于点 O， 则与△AOB 成中心对称的三角形是( B ) A．△BOC B．△COD C．△AOD D．△ACD
3．下列各组图形中，△A′B′C′与△ABC 成中心对称的是( A )
4．中心对称的两个图形，对称点所连线段都经过_对__称__中__心___， 而且被对称中心所_平__分_____，且这两个图形全等．
温馨提示： 此PPT
可修改编辑
【答案】D
8．作点 A 关于点 O 的对称点时，连接 AO 并延长__一__倍____，即 可得到点 A 的对称点；作某个图形关于点 O 的对称图形时， 先作出图形的_每__个__关__键__点_____关于点 O 的对称点，然后顺次 连接各对称点即可．
9．(2019·舟山)如图，在直角坐标系中，已知菱形 OABC 的顶点 A(1，2)，B(3，3)．作菱形 OABC 关于 y 轴的对称图形 OA′B′C′， 再作图形 OA′B′C′关于点 O 的中心对称图形 OA″B″C″，则点 C 的对应点 C″的坐标是( A ) A．(2，－1) B．(1，－2) C．(－2，1) D．(－2，－1)
(3)在图③中，画出△ABC 绕着点 C 按顺时针方向旋转 90°后的 三角形． 解：如图③，△DEC为所求作的三角形．
13．如图，在△ABC 中，∠A＝90°，点 D 为 BC 的中点，DE⊥ DF，DE 交 AB 于点 E，DF 交 AC 于点 F，试写出线段 BE， EF，FC 之间的数量关系，并说明理由．
1. 说得太好了，老师佩服你，为你感到骄傲！ 2. 你的设计(方案、观点)富有想象力，极具创造性。 3. 我非常欣赏你的想法，请说具体点，好吗? 4. 某某同学的解题方法非常新颖，连老师都没想到，真厉害！ 5. 让我们一起为某某喝彩！同学们在学习过程中，也要敢于猜想，善于猜想，这样才能有所发现，有所创造! 三、表扬类
2中心对称第一课时课件9张

2中心对称第一课时课件9张


180°)后重合
180°后重合
折叠后与另一图形重合 旋转后与另一图形重合
对称点的连线被对称轴 对称点连线经过对称中
垂直平分
心,且被对称中心平分
小结 谈谈你的收获？
A C
• 证明：
1点A是点A绕点O旋转180 后得到的，即线段
OA绕点O旋转180 得到线段OA，所以点O在线 段AA上，且OA=OA，即点O是线段AA的中点。 点O是线段AA的中点。 同样地，点O也是线段BB和CC的中点。
C A′
O B′
B
A
C′
练习
解法二：根据视察，B、B′及C、C ′应分别是两 组对应点，连结BB′ 、CC′ ，它们相交于点O， 则点O即为所求（如图）．
C A′
O B′
B A
C′
想一想
中心对称与轴对称有什么区分?又有什么联系?
轴对称
中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折(翻折 图形绕对称中心旋转
关于这个点对称或中心对称，这个点就叫做 对称中心，这两个图形中的对应点叫做关于中 心的对称点.
△OCD和△OAB关于
点O 对称，对称点
B
C
是 A和C,B和D,O和O..
探究
旋转三角板，画关于点O对称的两个三角形：
第一步，画出△ABC；
第二步，以三角板的一个顶点 O为中心，把三角板旋转 180°，画出△A′B′C′ ； 第三步，移开三角板.
练习
2.画一个与已知四边形ABCD成中心对称的图形． （1）以顶点A为对称中心； （2）以Bห้องสมุดไป่ตู้边的中点为对称中心．
N
F
B
A
B．
《中心对称》PPT课件 人教版九年级数学

《中心对称》PPT课件 人教版九年级数学


如图，已知等边三角形ABC和点O，画△A′B′C′,使
△A′B′C′和△ABC关于点O成中心对称.
作法： 1.连接AO并且延长AO至A′，使AO=A′O；
A
C′
B′
O
2.连接BO并且延长BO至B′，使BO=B′O；
3.连接CO并且延长CO至C′，使CO=C′O；
B
C
则△A′B′C′即为所求.
A′
课堂小结
中心对称，由此图中阴影部分的三个三
角形就可以转化到直角△ADC中，易得
阴影部分的面积为3．
巩固练习
如图，点O是平行四边形的对称中心，
点A、C关于点O对称，有AO=CO， D F
C
那么OE=OF吗？
O
A
EB
解：∵平行四边形是中心对称图形，O是对称中心.
EF经过点O，分别交AB、CD于E、F. ∴点E、F是关于点O的对称点.
探究新知
【思考】两个图形成中心对称需要具备什么条件？
两个图形成中心对称须具备三个条件： ①能找到一个对称中心； ②旋转角为180°； ③这两个图形旋转后能重合.
探究新知
填一填： 如图，△OCD与△OAB关于点O中心对称 ，则 __O__是对称中心，点A与___C__是对称点， 点B 与__D__是对称点. C
就是成轴对称的图形. （×）
课堂检测
2. 如下所示的4组图形中，左边数字与右边数字成中心 对称的有（ D ）
A.1组
B.2组
C.3组
D.4组
3.如图，已知△AOB与△DOC成中心对称，△AOB的面积
是6，AB＝3，则△DOC中CD边上的高是（ B ）
A.2
B.4
C.6
D.8
教学课件：中心对称ppt1

教学课件：中心对称ppt1

A′B′
A
B′
O
B
A′
线段A′B'即为所求的线段
3 如图，选择点O为对称中心,画出与△ABC关
于点O对称的△A′B′C′. 解:
B′
A′
C′
△A′B′C′即为所求的三角形。
B’ A’ C’
O D’
已知四边形ABCD 和点O。画四边形 A′B′C′D′，使它与 已知四边形关于这 一点对称
D
C
A B
探究二：△ABC与△A′B′C′有什么关系？。
1、中心对称的两个图形，对称点所 连线段经过对称中心，而且被对称中 心所平分。
2、中心对称的两个图形是全等形。
1 、点的中心对称点的作法
AOΒιβλιοθήκη 作法： A′ 1、作射线OA；
2、截取OA＝OA′。
点A′就是所要求的对称点。
2、线段的中心对称线段的作法
作法： 以点O为对称中心,作出线段AB的对称线段
四边形A′B′C′D′就是所要求四边形。
如图，已知△ABC与 △A’B’C’中心对称， 求出它们的对称中心O。
C
A’ O B’
B A
C’
点O就是所要求的对称中心。
1.（金华·中考）如图，在平面直角坐标系中， 若△ABC与 △A1B1C1关于点E成中心对称， 则对称中心E点的坐标是 .
【解析】由中心对称图形对应点的连线交于一点，可知E点 的坐标是（3，-1）. 答案：（3，-1）
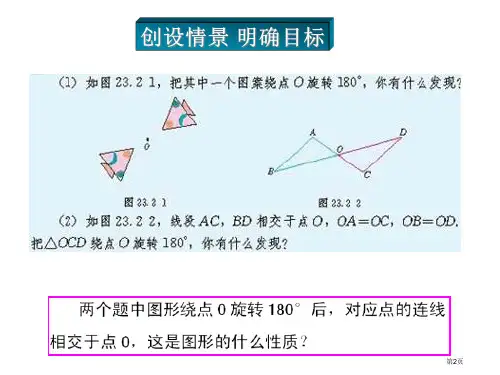
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC，BD相交于点O，OA=OC，OB=OD．把 △OCD绕 点O旋转180°,你有什么发现?
O
重合
B
（2） C
重合
九年级数学中心对称4省公开课获奖课件市赛课比赛一等奖课件

九年级数学中心对称4省公开课获奖课件市赛课比赛一等奖课件

B’ B
A C’
解法一：根据观察，B、B’应是相应点，连结BB’，用刻度尺 找出BB’旳中点O，则点O即为所求（如图）
C A’
O B’
B
A
C’
解法二：根据观察，B、B’及C、C’应是两组相应点，连结 BB’、CC’，BB’、CC’相交于点O，则点O即为所求（如图）。
C A’
O B’
B A
C’
2. 如图，已知等边三角形ABC和点O，画△A’B’C’,使 △A’B’C’和△ABC有关点O成中心对称。
名称 定义 性质
中心对称
把一种图形绕着某一种点旋转180 ,假如他 能够与另一种图形重叠，那么就说这两个图 形有关这点对称，这个点叫做对称中心,两个 图形有关点对称也称中心对称，这两个图形 中旳相应点叫做有关中心旳对称点
①两个图形完全重叠； ②相应点连线都经过对称中心，而且被对称 中心平分
中心对称图形 假如一种图形绕着一种点旋 转180 后旳图形能够与原来 旳图形重叠，那么这个图形 叫做中心对称图形，这个点 就是它旳对称中心
正方形是中心对称图形吗？正方形绕 两条对角线旳交点旋转多少度能与原 来旳图形重叠？能由此验证正方形旳 某些特殊性质吗？
旋转 2700
正方形是中心对称图形吗？正方形 绕两条对角线旳交点旋转多少度能 与原来旳图形重叠？能由此验证正 方形旳某些特殊性质吗？
旋转 3600
正方形是中心对称图形吗？正方形绕两条对角线旳交 点旋转多少度能与原来旳图形重叠？能由此验证正方 形旳某些特殊性质吗？
； 悉尼驾照翻译
3. 判断下列说法是否正确 （1）轴对称图形也是中心对称图形。（×） （2）旋转对称图形也是中心对称图形。（× ）
（3）平行四边形、长方形和正方形都是中心对称图 形，对角线旳交点是它们旳对称中心。（√ ）
人教版九年级上册数学中心对称图形优秀ppt课件

人教版九年级上册数学中心对称图形优秀ppt课件

中心对称图形形状匀称美观，很多建筑物和工艺品上 常采用这种图形作装饰图案.另外，具有中心对称图形形 状的物体，能够在平面内绕对称中心平稳地旋转，在生 产中旋转的零部件的形状常设计成中心对称图形，如水 泵叶轮等.
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
返回
旋转
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT) 人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
o O
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT) 人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT) 人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
中心对称图形
1什么是中心对称？
2中心对称有什么性质？
A
定义: 把一个图形绕着 某一点旋转180 °，如 果它能够与另一个图 形重合，那么就说这 两个图形关于这个点 对称或中心对称，这 个点叫做对称中心， 能够互相重合的一对 点叫做对称点。
C`
B`
O
B
C
A`
性质: ①两个图形全等；
②对应点所连线段都经过对称中 心，并且被对称中心平分
中心对称与中心对称图形有什么区别与联系？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中心对称第一课时优质课 件
你知道旋转的性质吗？
旋转的性质
对应点到旋转中心的距离相等 对应点与旋转中心所连线段的夹角等于旋转角
旋转前、后的图形全等
游戏
两人玩摆放棋子游戏，每 人轮流把一枚棋子摆放在圆 形盘上，依次下去，最后棋 子摆不下者为输方。问：要 赢此盘棋，应采取 什么绝招？
观察与探究
(1)把其中一个图案绕点O旋转180°,你有什么发现?
1.两个图形是全等形 性
2.对称轴是对应点连 线的垂直平分线
1.两个图形是全等形
2.对称中心是对应点连 线的中点
质 3.对应线段或延长线相 交,交点在对称轴上
3.对应点连线都经过 对称中心
快速抢答 判断
1.线段的两个端点关于它的中点对称.
2.矩形一组对边关于对角线交点对称.
3.正方形一组对角的顶点关于对角线 交点对称.
B´
A
C´
D
O.
D´ A´
C B
如图，已知△ABC与△A’B’C’中心对称，求
出它们的对称中心O。 C
A’ B’
B A
C’
3/10/2021
游戏
两人玩摆放棋子游戏，每人轮流把 一枚棋子摆放在圆形盘上，依次下 去，最后棋子摆不下者为输方。问： 要赢此盘棋，应采取什么绝招？
方法：首先把棋子
摆在对称中心，然后 每次都根据对方棋子 的位置找出中心对称 的位置来摆放，一定 能获胜.
则A’是所求的点
例2、已知线段AB和O点，画出线段AB关于点O的
对称线段A’B’
B'
连结AO并延长到A’，使OA’＝OA，A
则得A的对称点A’
O
连结BO并延长到B’，使OB’＝OB，
A'
则得B的对称点B’
连结A’B’，则线段A’B’是所画线段
B
例3，已知四边形ABCD和O点，画出四边形ABCD
关于O点的对称图形。
有一个对称中心——点
图形绕对称中心旋转180° 后重合 旋转后与另一图形重合
对称点连线经过对称中心,
且被对称中心平分
轴对称
中心对称
定 1.有一条对称轴—直线 1.有一个对称中心—点 义 三 2.图形绕对称轴翻转180度 2.图形绕中心旋转180度
要 点 3.翻转后与另一图形重合 3.旋转后与另一图形重合
C'
快速抢答
如图，将△AOB绕点O旋转180°得△DOE， 则下列正确的是（ ）
3/10/2021
探究交流
A
点O是AA′的中点。
C
△ABC≌△A′BC′
问题1 分别连接对称点AA′，BB′，CC′。点O在线段AA′上 吗？如果在，在什么位置？请说明理由。
问题2 △ABC与△A′B′C′有什么关系？为什么？
4.全等的两个图形一定是关于中心对称的.
画一个图形与已知图形关于某一点成中心对称
1、已知A点和O点，画出点A关于点O的对称点A'。
A
O
2、已知线段AB和O点，画出线段AB关于点O的对称 线段A’B’。
A O
B
三、中心对称的作图
例1、已知A点和O点，画出点A关于点O的对称点A'
A
O
A'
连结OA， 并延长到A’，使OA’=OA，
想一想 中心对称与轴对称有什么区别?又有什么联系?
A
C1
B1
O
B
C
A1
定义
轴对称
中心对称
1 有一条对称轴——直线
有一个对称中心——点
2 图形沿轴对折（翻转180°） 图形绕中心旋转180°
3 翻转后和另一个图形重合 旋转后和另一个图形重合
3/10/2021
轴对称 与中心对称定义、性质对比图：
轴对称
3/10/2021
一、中心对称的概念
把一个图形绕着某一个点
旋转180°后，如果它能够与另
一个图形完全重合，那么称这两
个图形关于这个点对称，也叫中
心对称。这个点叫做对称中心。
这两个图形中的对应点叫做关于
中心的对称点。
C
A
△ABC与△A`B`C`
B'
关于点O对称,点O
O
B
是对称中心对应点A
A'
和A`关于点O对称
C
A
B
● B′ O
A′
C′
1、中心对称的两个图形，对称点所连线段经过对 称中心，而且被对称中心所平分。
2、中心对称的两个图形是全等形。
3/10/2021
二、中心对称的性质：
1、关于中心对称的两个图形是全等形。
2、关于中心对称的两个图形，对称点的连
线都经过对称中心，并且被对称中心平分。
△ABC≌ △A`B`C`
C
A、O、A`三点共线
A
B、O、B`三点共线
B'
O
C、O、C`三点共线
B
A'
OA=OA` OB=OB` OC=OC`
C'
讨论：中心对称与轴对称的区
别：
L
A
A/
A O
A/
轴对称
有一条对称轴——直线 图形沿对称轴对折(翻折 180°)后重合 折叠后与另一图形重合 对称点的连线被对称轴垂直 平分
中心对称
中心对称
定 1 有一条对称轴—直线 有一个对称中心—点。
2 图形沿轴对折，(翻 图形绕中心旋转180度。 转达180度。)
义 3 翻转后与另一个图形 旋转后与另一个图形重合。 重合。
性 1 两个图形是全等形。 两个图形是全等形。
质 2 对称轴是对称点连线 对称点连线都过对称中心，
的垂直平分线。
且被对称中心平分。
(2)线段AC，BD相交于点O，OA=OC，OB=OD．把 △OCD绕点O旋转180°,你有什么发现?
O
重合
3/10/2021
B
（2 C
重合）
情景
观察下面的两组图形，看一看各组中两个图 形的形状、大小是否相同？ 怎样将一个图形旋转得到另一个图形？
3/10/2021
情景1
观察下面的两组图形，看一看各组中两个图 形的形状、大小是否相同？ 怎样将一个图形旋转得到另一个图形？
中心对称的实际应用
具有数学美。中心对称在许多建筑、 工艺品、商标等方面常用于图案装饰。