下载文档原格式
双向渐进式概念格生成算法双向渐进式概念格生成算法是一种用于数据挖掘和知识表示的算法，其目的是从给定的数据集中生成一个概念格，以便帮助我们理解数据集中事物之间的关系。
本文旨在介绍双向渐进式概念格生成算法的概念和应用。
双向渐进式概念格生成算法，简称BicP, 使用渐进式的方法生成概念格。
渐进式概念格生成是一种快速而有效的算法，它能够处理非常大的数据集，以及快速处理交互式查询。
算法最初由 Zhang 和 Chen 提出，它是单向的渐进生成算法的变体，在算法完成过程中，会在生成的结果中得到初始状态和终止状态的完全的概念格。
文章主要从以下几个方面进行介绍：1. 概念格的概念2. BicP生成算法3. 算法的优势和应用概念格的概念在谈论BicP的概念之前，我们需要了解概念格的概念。
在计算机科学和形式概念分析中，概念格是一个用于表示对象和关系的形式概念结构。
它通过将关系描述为对两个事物之间的“包含”关系来描述事物之间的关系，从而表示了一个有限集中事物之间的组织结构。
概念格在知识表示，信息检索和数据挖掘等领域具有广泛的应用。
在业务分析方面，它被广泛应用于文本分类、信息提取、基于语义标注的数据管理、Web搜索和推荐系统等方面。
BicP生成算法BicP生成算法可以被解释为一种增量概念格生成算法，它使用了两个方向的搜索。
该算法通过两个搜索过程来确定未知区域和缺失数据，从而对数据进行完整的覆盖。
其中一个搜索过程是开始于极小概念，即遍历完整个数据集的值集，另一个搜索过程是由极大概念开始，即逆序遍历完整个数据集的值集。
这两次搜索的结果组合起来，构成了完整的概念格。
BicP生成算法的具体步骤如下：1. 算法开始于极小概念，即以单元格为初始状态开展正向搜索2. 然后在这个单元格的基础上，从元素集合中选择一个属性，将单元格分裂成若干个子单元格3. 对于每个子单元格，从属性域中选择一个值，然后将其递归地纳入到生成的子概念格中4. 递归进行，直到搜索到所有单元格被分裂为极大的概念格为止。
从封建主义向资本主义过渡期间的欧洲政事形式1、相关定义1.1、”虚伪的形式”的概念余华在1986年提出”虚伪的形式”的文学理论,打破了传统的现实主义写作手法。
用他自己的话说”我开始使用一种‘虚伪的形式’,所谓虚伪,是针对人们被日常生活围困的经验而言,这种经验使人们沦陷在缺乏想象的环境里,我们的文学只能在缺乏想象的茅屋里度日如年,也因此无法期待文学会出现奇迹。
” 简单地说,余华开始创造一个与现实生活完全不同的的世界,在这世界里人们所认同的理性法则失效,联系人与人之间纽带是利益,亲情、友情、爱情早已丧失,人们缺乏对自我价值的认知,每一个人只不过是被命运安排到人世间,为达到某种目的的工具,最后任凭命运牵引走向早已安排好的结局中去。
与俄国形式主义思想家和克莱夫贝尔的”有意味的形式”相似的是,余华强调文学作品对现实生活的反叛,形式主义理论也认为艺术作品应保持独立性与超功利性,艺术品的创造应该是脱离现实生活与社会历史的制约的”纯形式”,反对将艺术作为某种政治的或道德目的的手段。
而克莱夫贝尔也提出只有脱离现实层面而上升到审美体验才能真正体会出作品中的审美情感。
余华曾经说过”生活是不真实的,生活事实上是真假杂乱和鱼目混珠”,他反对传统作家为了迎合当代社会需要而进行文学创作,认为这样的描写只是在翻译”生活给我提供的东西”,做出了一种看似荒诞的文学表达方式的创新,作为这种尝试的结果,余华也说”使我自由地接近真实”。
但是笔者认为余华所提出的”虚伪的形式”并不是完全意义上的单纯追求形式而忽略生活内涵的观点。
余华提到的”日常生活围困的经验”不过是浮于表面的人们肤浅的认识,余华要利用荒诞的笔法,为了毫不掩饰地撕开生活中看似稳固的逻辑秩序的虚假面具,将充满原始欲望的丑陋的非理性的真实暴露出来。
他关注的是人性深层次的追求,目的是为了”写出更广阔的意义”。
在余华”虚伪的形式”的观念主导下,暴力、血腥、死亡、苦难等在传统文学作品中极少出现的词语却成了余华作品的主题,也正是由于这种对于”形式”的重视使得余华早期作品体现出叙述方式的精心雕琢,把人物与事件当成符号,忽视人物的性格而更多地展现欲望,从根本上触及了在人们心里根深蒂固的致命要害,让我们对于理性世界里看似和谐稳定的生活产生怀疑,这便达到了余华利用这种特殊的叙述方式所期待的效果,”作为先锋小说家的余华就不仅是符号的单纯玩弄,更在于通过这种貌似混乱,不合逻辑手段来表现他关注世界的独特方式,这也是”虚伪的作品”与”另一种真实”达成的合一。
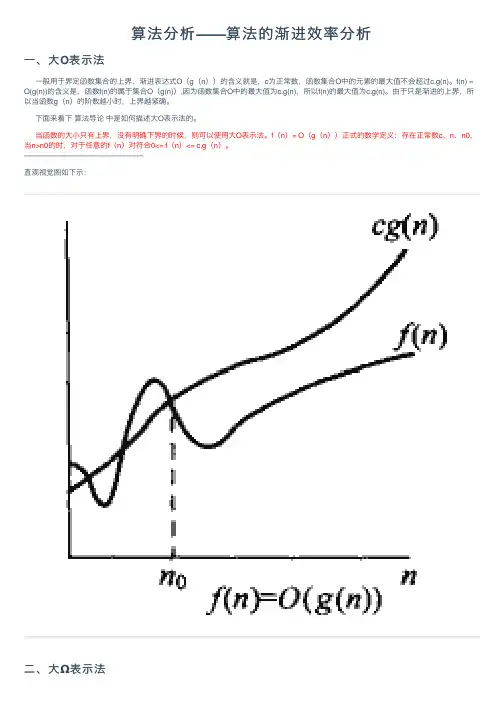
算法分析——算法的渐进效率分析⼀、⼤O表⽰法⼀般⽤于界定函数集合的上界，渐进表达式O（g（n））的含义就是，c为正常数，函数集合O中的元素的最⼤值不会超过c.g(n)。
f(n) = O(g(n))的含义是，函数f(n)的属于集合O（g(n)）,因为函数集合O中的最⼤值为c.g(n)，所以f(n)的最⼤值为c.g(n)。
由于只是渐进的上界，所以当函数g（n）的阶数越⼩时，上界越紧确。
下⾯来看下算法导论中是如何描述⼤O表⽰法的。
当函数的⼤⼩只有上界，没有明确下界的时候，则可以使⽤⼤O表⽰法。
f（n）= O（g（n））正式的数学定义：存在正常数c、n、n0，当n>n0的时，对于任意的f（n）对符合0<= f（n）<= c.g（n）。
————————————————直观视觉图如下⽰：⼆、⼤Ω表⽰法⼀般⽤于界定函数集合的下界，渐进表达式Ω（g（n））的含义就是，函数集合Ω中的元素的最⼩值不会低于c.g(n)。
f(n) = Ω（g（n））的含义是，函数f(n)的属于集合Ω（g（n））,因为函数集合Ω中的最⼩值为c.g(n)，所以f(n)的最⼩值为c.g(n)。
算法导论中是如何描述⼤Ω表⽰法的。
当函数的⼤⼩只有下界，没有明确的上界的时候，可以使⽤⼤Ω表⽰法。
f（n）= Ω（g（n））正式的数学定义：存在正常数c、n、n0，当n>n0的时，对于任意的f（n）对符合0<= c.g（n）<= f（n）。
直观视觉图如下所⽰：三、⼤θ表⽰法⽤于界定函数的渐进上界和渐进下界。
当f（n）= θ（g（n））的时候，代表着g（n）为f（n）的渐进紧确界。
⽽θ渐进描述符在所有的渐进描述符中是最严格的⼀个，因为它既描述了函数的上界，有描述了函数的下界。
算法导论中是如何描述⼤θ表⽰法的。
f（n）= θ（c.g（n））正式的数学定义：存在正常数c1、c2、n、n0，当n>n0的时，对于任意的f（n）对符合c1.g（n）<= f（n）<= c2.g（n），c1.g（n）、c2.g（n）都是渐进正函数（当n趋于⽆穷⼤的时候，f（n）为正）。
模糊形式概念并行构造算法张卓;柴玉梅;王黎明;范明【期刊名称】《模式识别与人工智能》【年(卷),期】2013(26)3【摘要】Formal concept analysis ( FCA) is extensively applied in various fields of computer. Currently, constructing fuzzy concepts directly is still one of most important issues of the FCA field. However, the construction process is always with exponential time complexity. In order to improve the efficiency of building fuzzy concepts, a parallel algorithm called Parallel Fuzzy Next Closure (ParaFuNeC) is presented. It is parallel developed from the serial construction algorithm of fuzzy concepts. The proposed method maps the combination search space of fuzzy set into the natural number interval, so that search space is simply expressed, divided and traversed through natural number. Moreover, the algorithm produces balanced and independent sub-search spaces according to the number of CPU in present computing environment. It also avoids the time costs of synchronization and communication among parallel tasks. By the time complexity analysis and experimental evaluation of the proposed algorithm, it is proved that the speedup ratio of the proposed algorithm increases proportionally to the number of CPU in the case of large-scale computing tasks. Besides, the criterion of serial fraction is used to analyze the scalability of the proposed algorithm in experiments. The results showthat the algorithm ParaFuNeC also has better scalability in the case of large-scale computing tasks.% 形式概念分析理论已经广泛地应用于计算机诸多领域。
实值形式背景下概念格的渐进式并行构造算法郭泽蔚;姜麟;李金海【摘要】经典的形式概念分析主要应用于属性值为布尔值的形式背景中,然而在很多实际应用领域,由于问题的复杂性,更多的形式背景中属性值为普通实值.这种实值虽然更为适合用来刻画实际问题的不确定性,但由于算法的复杂性大,当数据背景比较大时,传统意义上的算法并不能有效地解决概念的抽取问题.随着高性能并行技术的发展与成熟,并行计算机的成本与费用越来越低,通过适当的并行化手段,将其应用于形式概念分析领域可以显著提高算法的效率.文中基于实值形式背景,提出了一种构造实值概念格的渐进式算法,且通过对渐进式构造过程的分析,将算法并行化.通过数值实验对比了串行与并行算法的运算时间,给出了该算法并行化的加速效率.%Classical formal concept analysis is mainly used in the formal context whose attributes are Booleanvalued.However,in many fields of practical applications,due to the complexity of the problem,attributes are ordinary real-valued in more backgrounds.Although this kind of attributes are more appropriate for describing the uncertainty of practical problem,the high complexity makes traditional algorithms less effective in extracting concepts when the data under consideration is relatively large.With the development and maturity of high-performance parallel technology,the expense and cost of parallel computers become less and less,so it deserves to apply parallel technology in formal concept analysis for improving the efficiency of mining concepts.Based on the real formal context,this paper puts forward an incremental algorithm which is used to extract real-valued concept lattice.And then through analyzing the process of incrementallyupdating,the algorithm is parallelized.Finally,numerical experiments are conducted to compare serial and parallel algorithms,which verifies the acceleration efficiency of the proposed parallel algorithm.【期刊名称】《西北大学学报（自然科学版）》【年(卷),期】2018(048)003【总页数】8页(P335-342)【关键词】实值形式背景;概念格构造;渐进式算法;并行化【作者】郭泽蔚;姜麟;李金海【作者单位】昆明理工大学理学院,云南昆明650500;昆明理工大学理学院,云南昆明650500;昆明理工大学数据科学研究中心,云南昆明650500【正文语种】中文【中图分类】TP18形式概念分析(Formal concept analysis)是20世纪80年代初期由德国教授R.Wille提出的一种用于发现知识的理论。
形式概念分析通过构造概念格来进行数据的处理,也称概念格理论[1]。
以往关于概念格的研究主要集中于经典的形式背景,即属性值为Boolean值,然而,由于现实中数据的复杂性,更多的形式背景中的属性值是区间形式的普通实值。
经典的概念格主要应用于发现二值(或多值)形式背景的概念构造,因此,传统形式背景中概念格的构造方法并不适用于实值形式背景[3-4]。
而实值形式背景概念格的构造存在算法复杂性大等缺陷,现阶段围绕这一类问题的研究也缺少较好的普适性,故进一步讨论实值概念格的构造具有一定的意义。
Matlab已成为数值计算领域的主流工具,其拥有的并行计算工具箱(Parallel computing toolbox,PCT)和并行计算服务(Distributed computing server,DCS)可以实现基于多处理器平台和集群平台的多种并行计算任务,利用PCT和DCS,用户无需关心多核、多处理器之间以及集群之间的底层数据通信,可以将更多的精力放在并行算法的设计,充分利用Matlab提供的数值计算模块和数据显示功能,高效便捷的完成并行计算任务[5]。
经典形式背景下的建格算法并不适用于处理实值形式背景下的概念格,而串行算法在数据规模较大的情况下计算效率较低。
针对实值形式背景的特点,结合经典概念格的渐进式构造思想,本文首先给出了计算实值概念格的方法；然后提出了一种实值概念格计算的渐进式构造算法,并对其进行改进,得到并行算法,应用Matlab对串、并算法进行程序的实现；最后通过数值实验对该算法的串行与并行运行效率作了对比,对该算法在特定实值条件下的并行化可行性进行了评估。
1 实值形式背景与实概念格1.1 实集定义1[6] 设R为实数集。
对于μ,v∈R,称I=[μ,v]为R上的一个实区间,其中μ和v 分别称为实区间I的上界和下界。
如果μ>v,则称实区间I是空的,记为[,]。
显然,当I=[μ,v]非空时,I就是由μ到v之间的全部实数构成的集合。
对于两个实区间I1=[μ1,v1]和I2=[μ2,v2],它们的交Inter(I1,I2)满足:Inter(I1,I2)=[max(μ1,μ2),min(ν1,ν2)]定义{I1,I2}的闭包为Closure({I1,I2})=n个实区间的闭包算子可表示如下:Closure({I1,I2,…,In})=Closure({Closure({I1,I2}),…,In})在此基础上,定义两个实区间集D={I1,I2,…,Ir}和的并运算和交运算分别为定义2[6] 设U={x1,x2,…,xn}是一个维度为n的对象集,A是R上所有实区间组成的集合,P(A)是A的幂集。
U上的一个实集通过其特征函数来定义,即均为实区间集,每个表明了元素xi在实集中的所有可能的取值。
则可表示为并记U上所有实值构成的集合为R(U)。
一般地,假设每个中的实区间均两两不相交。
为了简洁起见,与记为等价,并把U上的实空集表示为:集合中的交运算和并运算也同样适用于实集,实集中有两种交(并)运算,分别为L-交(并)和S-交(并)。
下面给出定义[7]。
设为U={x1,x2,…,xn}上的两个实集,称主要小于记为如果对任意的存在使得μ′≤μ且ν′≥ν;称主要包含于记作如果对任意的xi∈U,有成立和的L-交,L-并分别定义为其次,介绍S-交和S-并。
称严格小于记为如果对任意的存在使得μ≤μ′且ν≥ν′;称严格包含于记作如果对任意的xi∈U,有成立和的S-交,S-并分别定义为1.2 实值形式背景与实概念格设U={x1,x2,…,xn}为一个非空有限对象集,A={a1,a2,…,am}为一个非空有限属性集。
定义在笛卡尔积U×A上的一个实二元关系是指它的每个关系值均为实区间集,即对任意的是一个实区间集。
定义3[8] 称三元组为一个实值形式背景,如果是U×A上的一个实二元关系。
例1 表1给出了一个实值形式背景。
表1 实值形式背景abcd x1{[5,7],[8,9]}{[10,11]}{[7,9],[11,14]}{[5,8]}x2{[6,8]}{[7,9],[11,12]}{[9,12],[14,17]}{[4,4],[7,8]}x3{[9,11]}{[8,10]}{[10,12]}{[1,5]} x4{[10,11]}{[9,10]}{[9,10]}{[1,5]}设为实值形式背景,X⊆U。
对任意的a∈A,记:可以看出,f(a)是由取并得到的一个实区间集,即f(a)包含且仅包含a属性下所有对象对应的实区间;g(a)是由取交得到的一个实区间集,即g(a)包含且仅包含a属性下所有对象对应实区间的交集。
定义4[6] 设为实值形式背景,P(U)是U的幂集。
算子∧,↑:P(U)→R(A)和∨,↓:R(A)→P(U)定义为:(∀X∈P(U))∀(∀(∀X∈P(U))∀(∀从上式中可以看出,X∧是A上的一个实集,它的每个特征函数值为是使得每个均主要小于的对象x全体构成的集合。
X↑和B↓可类似地进行解释。
利用上述4个算子,可以定义两种实概念[3]:L-实概念和S-实概念。
具体地,对于如果有且则称序对为的一个L-实概念;如果有且则称序对为的一个S-实概念。
与传统的概念格相似,这里不论是L-实概念还是S-实概念,都称X为的外延,为的内涵[6]。
继而,根据上述判断条件,可以得到表1中实值形式背景的所有满足条件的L-实概念:根据前面的讨论,对于实值形式背景,可构造两类实概念格:L-实概念格和S-实概念格。
然而,这两种概念格框架的构建及相关讨论是类似的,故在此只给出基于L-实概念格构建的背景属性框架。
需要指出的是,只要将该约简框架的中所有与L-实概念格相关的符号都替换为S-实概念格中相应的符号,就可以得到基于S-实概念格构建的实值形式属性背景框架。
1.3 概念格的构造算法概念格的构造过程实际上就是概念聚类的过程,概念格一个重要的属性就是其完备性使得对于同样的一个数据集,每次生成的格都是唯一的,即对象、属性的排列顺序和格构造算法均不会影响其构造的结果。
因此,现有的关于概念格的构造算法都是为了提高建格的效率,减少建格的复杂度而设计的[9]。
经典形式背景概念格的串行构造算法大致可分为两类:批处理算法、渐进式算法。
批处理算法主要思想:首先要生成所有的格节点,即原形式背景中所有的概念的集合,然后根据它们之间的前驱-后继关系生成边,完成格的构造。
比较经典的有Bordat算法[10-11]。
