全国卷理科数学高三一轮复习资料、强化训练、复习补习资料-33总复习：平面向量的数量积及应用(基础)

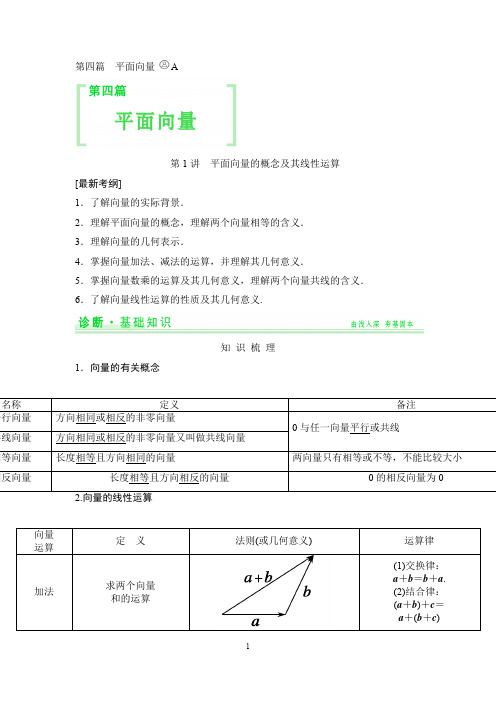
第四篇平面向量A第1讲平面向量的概念及其线性运算[最新考纲]1．了解向量的实际背景．2．理解平面向量的概念，理解两个向量相等的含义．3．理解向量的几何表示．4．掌握向量加法、减法的运算，并理解其几何意义．5．掌握向量数乘的运算及其几何意义，理解两个向量共线的含义．6．了解向量线性运算的性质及其几何意义.知识梳理1．向量的有关概念三角形法则平行四边形法则三角形法则a(1)|λa|＝|λ||a|；向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ，使得b＝λa.辨析感悟1．对共线向量的理解(1)若向量a，b共线，则向量a，b的方向相同．(×)(2)若a∥b，b∥c，则a∥c.(×)(3)(2018·郑州调研改编)设a与b是两个不共线向量，且向量a＋λb与2a－b共线，则λ＝－12.(√)(4)(2018·陕西卷改编)设a，b为向量，则“|a·b|＝|a|·|b|”是“a∥b”的充分必要条件．(√)2．对向量线性运算的应用 (5)AB →＋BC →＋CD →＝AD →.(√)(6)(教材习题改编)在△ABC 中，D 是BC 的中点，则AD →＝12(AC →＋AB →)．(√)第69页[感悟·提升]1．一个区别 两个向量共线与两条线段共线不同，前者的起点可以不同，而后者必须在同一直线上．同样，两个平行向量与两条平行直线也是不同的，因为两个平行向量可以移到同一直线上． 2．两个防范 一是两个向量共线，则它们的方向相同或相反；如(1)；二是注重零向量的特殊性，如(2).考点一 平面向量的有关概念【例1】 给出下列命题：①若|a |＝|b |，则a ＝b ；②若A ，B ，C ，D 是不共线的四点，则AB →＝DC →是四边形ABCD 为平行四边形的充要条件；③若a ＝b ，b ＝c ，则a ＝c ；④a ＝b 的充要条件是|a |＝|b |且a ∥b .其中真命题的序号是________．解析 ①不正确．两个向量的长度相等，但它们的方向不一定相同． ②正确．∵AB →＝DC →， ∴|AB →|＝|DC →|且AB →∥DC →，又∵A ，B ，C ，D 是不共线的四点， ∴四边形ABCD 为平行四边形；反之，若四边形ABCD 为平行四边形，则AB →∥DC →且|AB →|＝|DC →|，因此，AB →＝DC →. ③正确．∵a ＝b ，∴a ，b 的长度相等且方向相同； 又b ＝c ，∴b ，c 的长度相等且方向相同， ∴a ，c 的长度相等且方向相同，故a ＝c .④不正确．当a ∥b 且方向相反时，即使|a |＝|b |，也不能得到a ＝b ，故|a |＝|b |且a ∥b 不是a ＝b 的充要条件，而是必要不充分条件．综上所述，正确命题的序号是②③. 答案 ②③规律方法 对于向量的概念应注意以下几条：(1)向量的两个特征：有大小和方向，向量既可以用有向线段和字母表示，也可以用坐标表示；(2)相等向量不仅模相等，而且方向要相同，所以相等向量一定是平行向量，而平行向量则未必是相等向量；(3)向量与数量不同，数量可以比较大小，向量则不能，但向量的模是非负实数，故可以比较大小．【训练1】 设a 0为单位向量，①若a 为平面内的某个向量，则a ＝|a |a 0；②若a 与a 0平行，则a ＝|a |a 0；③若a 与a 0平行且|a |＝1，则a ＝a 0.上述命题中，假命题的个数是( )．A ．0B ．1C ．2D ．3解析 向量是既有大小又有方向的量，a 与|a |a 0的模相等，但方向不一定相同，故①是假命题；若a 与a 0平行，则a 与a 0的方向有两种情况：一是同向，二是反向，反向时a ＝－|a |a 0，故②③也是假命题．综上所述，假命题的个数是3. 答案 D考点二 平面向量的线性运算例2】 如图，在平行四边形OADB 中，设OA →＝a ， OB →＝b ，BM →＝13 BC →， CN →＝13 CD →.试用a ，b 表示OM →， O N →及MN →.解 由题意知，在平行四边形OADB 中， BM →＝13B C →＝16 BA →＝16( OA →－OB →)＝16(a －b )＝16a －16b ， 则OM →＝OB →＋BM →＝b ＋16a －16b ＝16a ＋56b . ON →＝23 OD →＝23(OA →＋OB →)＝23(a ＋b )＝23a ＋23b ， MN →＝ON →－OM →＝23(a ＋b )－16a －56b ＝12a －16b .规律方法 (1)进行向量运算时，要尽可能地将它们转化到三角形或平行四边形中，充分利用相等向量、相反向量，三角形的中位线及相似三角形对应边成比例等性质，把未知向量用已知向量表示出来．(2)向量的线性运算类似于代数多项式的运算，实数运算中的去括号、移项、合并同类项、提取公因式等变形手段在线性运算中同样适用．【训练2】 (1) (2018·四川卷)如图，在平行四边形ABCD 中，对角线AC 与BD 交于点O ，AB →＋AD →＝λ AO →，则λ＝________.(2)(2018·泉州模拟)已知P ，A ，B ，C 是平面内四点，且P A →＋PB →＋PC →＝AC →，那么一定有 ( )． A.PB →＝2CP →B.CP →＝2PB →C.AP →＝2PB →D.PB →＝2AP →解析 (1)∵AB →＋AD →＝AC →＝2AO →，∴λ＝2. (2)∵P A →＋PB →＋PC →＝AC →＝PC →－P A →， ∴PB →＝－2P A →＝2AP →. 答案 (1)2 (2)D考点三 向量共线定理及其应用【例3】 (2018·郑州一中月考)设两个非零向量a 与b 不共线．(1)若AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )．求证：A ，B ，D 三点共线； (2)试确定实数k ，使k a ＋b 和a ＋k b 共线．审题路线 (1)由向量的加法，得BD →＝BC →＋CD →⇒用a ，b 表示BD →⇒得到BD →与AB →的关系式⇒由向量共线定理，得BD →与AB →共线⇒再看是否有公共点⇒得到证明的结论．(2)假设存在实数k ⇒利用向量共线定理⇒列出方程⇒根据a ，b 是两个不共线的向量⇒得出方程组⇒解得k 值．(1)证明 ∵AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )． ∴BD →＝BC →＋CD →＝2a ＋8b ＋3(a －b )＝5(a ＋b )＝5AB →. ∴AB →，BD →共线，又它们有公共点B ， ∴A ，B ，D 三点共线．(2)解 假设k a ＋b 与a ＋k b 共线， 则存在实数λ，使k a ＋b ＝λ(a ＋k b )， 即(k －λ)a ＝(λk －1)b .又a ，b 是两不共线的非零向量， ∴k －λ＝λk －1＝0.∴k 2－1＝0.∴k ＝±1.规律方法 (1)证明三点共线问题，可用向量共线解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得出三点共线． (2)向量a ，b 共线是指存在不全为零的实数λ1，λ2，使λ1a ＋λ2b ＝0成立，若λ1a＋λ2b ＝0，当且仅当λ1＝λ2＝0时成立，则向量a ，b 不共线.第70页【训练3a ＋(2λ－1)b ，若c 与d 同向，则实数λ的值为_____． 解析 由于c 与d 同向，所以c ＝k d (k ＞0)， 于是λa ＋b ＝k [a ＋(2λ－1)b ]， 整理得λa ＋b ＝k a ＋(2λk －k )b .由于a ，b 不共线，所以有⎩⎨⎧λ＝k ，2λk －k ＝1，整理得2λ2－λ－1＝0，所以λ＝1或λ＝－12. 又因为k ＞0，所以λ＞0，故λ＝1. 答案 11．向量的加、减法运算，要在所表达的图形上多思考，多联系相关的几何图形，比如平行四边形、菱形、三角形等，可多记忆一些有关的结论．2．对于向量共线定理及其等价定理，关键要理解为位置(共线或不共线)与向量等式之间所建立的对应关系．要证明三点共线或直线平行都是先探索有关的向量满足向量等式b ＝λa ，再结合条件或图形有无公共点证明几何位置．方法优化3——准确把握平面向量的概念和运算【典例】 (2018·浙江卷)设a ，b 是两个非零向量．( )． A ．若|a ＋b |＝|a |－|b |，则a ⊥b B ．若a ⊥b ，则|a ＋b |＝|a |－|b |C ．若|a ＋b |＝|a |－|b |，则存在实数λ，使得b ＝λaD ．若存在实数λ，使得b ＝λa ，则|a ＋b |＝|a |－|b |[一般解法] (排除法)选项A ，若b ＝－a ，则等式|a ＋b |＝|a |－|b |成立，显然a ⊥b 不成立；选项B ，若a ⊥b 且|a |＝|b |，则|a |－|b |＝0，显然，|a ＋b |＝2|a |≠0，故|a ＋b |＝|a |－|b |不成立；选项D ，若b ＝a ，则|a |－|b |＝0，显然，|a ＋b |＝2|a |≠0，故|a ＋b |＝|a |－|b |不成立． 综上，A ，B ，D 都不正确，故选C.[优美解法] (数量积法)把等式|a ＋b |＝|a |－|b |两边平方，得(a ＋b )2＝(|a |－|b |)2， 即2a ·b ＝－2|a |·|b |，而a ·b ＝|a ||b |cos<a ，b >， 所以cos<a ，b >＝－1.又因为<a ，b >∈[0，π]，所以<a ，b >＝π，即a ，b 为方向相反的共线向量．故C 正确．[反思感悟] 部分学生做错的主要原因是：题中的条件“|a ＋b |＝|a |－|b |”在处理过程中误认为“|a ＋b |＝|a －b |”，从而得到“a ⊥b ”这个错误的结论． 【自主体验】在△OAB 中，OA →＝a ，OB →＝b ，OD 是AB 边上的高，若AD →＝λAB →，则实数λ＝ ( )． A.a ·(a －b )|a －b |B.a ·(b －a )|a －b |C.a ·(a －b )|a －b |2D.a ·(b －a )|a －b |2解析 由AD →＝λAB →，∴|AD →|＝λ|AB →|.又∵|AD →|＝|a |cos A ＝|a |·a ·(a －b )|a ||b －a |＝a ·(a －b )|b －a |，|AB →|＝|b －a |，∴λ＝a ·(a －b )|b －a |2＝a ·(a －b )|a －b |2.故选C.答案 C基础巩固题组(建议用时：40分钟)一、选择题1．若O ，E ，F 是不共线的任意三点，则以下各式中成立的是( )． A.EF →＝OF →＋OE → B.EF →＝OF →－OE → C.EF →＝－OF →＋OE → D.EF →＝－OF →－OE → 解析 由图可知EF →＝OF →－OE →.答案 B 2.(2019·汕头二模)如图，在正六边形ABCDEF 中，BA →＋CD →＋EF →等于( )． A ．0 B.BE → C.AD → D.CF →解析 因为ABCDEF 是正六边形，故BA →＋CD →＋EF →＝DE →＋CD →＋EF →＝CE →＋EF →＝CF →. 答案 D3．对于非零向量a ，b ，“a ＋b ＝0”是“a ∥b ”的( )． A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件解析 若a ＋b ＝0，则a ＝－b ，所以a ∥b .若a ∥b ，则a ＝λb ，a ＋b ＝0不一定成立，故前者是后者的充分不必要条件． 答案 A4．(2019·开封模拟)下列命题中，正确的是( )． A ．若|a |＝|b |，则a ＝b 或a ＝－b B ．若a ·b ＝0，则a ＝0或b ＝0 C ．若k a ＝0，则k ＝0或a ＝0D ．若a ，b 都是非零向量，则|a ＋b |＞|a －b |解析 对于A ，显然不能得知a ＝b 或a ＝－b ，因此选项A 不正确；对于B ，易知不正确；对于C ，易知正确；对于D ，注意到(a ＋b )2－(a －b )2＝4a ·b ，显然a ·b 与零的大小关系不确定，因此选项D 不正确．综上所述，选C. 答案 C5．(2019·兰州质检)若点M 是△ABC 所在平面内的一点，且满足5AM →＝AB →＋3AC →，则△ABM 与△ABC 的面积比为( )． A.15 B.25 C.35 D.45 解析设AB 的中点为D ，由5AM →＝AB →＋3AC →，得3AM →－3AC →＝2AD →－2AM →，即3CM →＝2MD →.如图所示，故C ，M ，D 三点共线，且MD →＝35CD →，也就是△ABM 与△ABC 对于边AB 的两高之比为3∶5，则△ABM 与△ABC 的面积比为35，选C. 答案 C 二、填空题6．(2019·湖州月考)给出下列命题： ①向量AB →的长度与向量BA →的长度相等；②向量a 与b 平行，则a 与b 的方向相同或相反； ③两个有共同起点而且相等的向量，其终点必相同； ④两个有公共终点的向量，一定是共线向量；⑤向量AB →与向量CD →是共线向量，则点A ，B ，C ，D 必在同一条直线上． 其中不正确命题的序号是________． 解析 ①中，∵向量AB →与BA →为相反向量， ∴它们的长度相等，此命题正确．②中若a 或b 为零向量，则满足a 与b 平行，但a 与b 的方向不一定相同或相反，∴此命题错误．③由相等向量的定义知，若两向量为相等向量，且起点相同，则其终点也必定相同，∴该命题正确．④由共线向量知，若两个向量仅有相同的终点，则不一定共线，∴该命题错误． ⑤∵共线向量是方向相同或相反的向量，∴若AB →与CD →是共线向量，则A ，B ，C ，D 四点不一定在一条直线上，∴该命题错误． 答案 ②④⑤7．在▱ABCD 中，AB →＝a ，AD →＝b ，AN →＝3NC →，M 为BC 的中点，则MN →＝________(用a ，b 表示)．解析 由AN →＝3NC →，得4AN →＝3 AC →＝3(a ＋b )，AM →＝a ＋12b ，所以MN →＝AN →－AM →＝34(a ＋b )－⎝ ⎛⎭⎪⎫a ＋12b ＝－14a ＋14b .答案 －14a ＋14b8．(2019·泰安模拟)设a ，b 是两个不共线向量，AB →＝2a ＋p b ，BC →＝a ＋b ，CD →＝a －2b ，若A ，B ，D 三点共线，则实数p 的值为________．解析 ∵BD →＝BC →＋CD →＝2a －b ，又A ，B ，D 三点共线， ∴存在实数λ，使AB →＝λBD →.即⎩⎨⎧2＝2λ，p ＝－λ，∴p ＝－1.答案 －1 三、解答题9．在△ABC 中，D ，E 分别为BC ，AC 边上的中点，G 为BE 上一点，且GB ＝2GE ，设AB →＝a ，AC →＝b ，试用a ，b 表示AD →，AG →. 解 AD →＝12(AB →＋AC →)＝12a ＋12b ；AG →＝AB →＋BG →＝AB →＋23BE →＝AB →＋13(BA →＋BC →) ＝23AB →＋13(AC →－AB →)＝13AB →＋13AC →＝13a ＋13b .10．若a ，b 是两个不共线的非零向量，a 与b 起点相同，则当t 为何值时，a ，t b ，13(a ＋b )三向量的终点在同一条直线上？ 解 设OA →＝a ，OB →＝t b ，OC →＝13(a ＋b )，∴AC →＝OC →－OA →＝－23a ＋13b ，AB →＝OB →－OA →＝t b －a . 要使A ，B ，C 三点共线，只需AC →＝λAB →. 即－23a ＋13b ＝λ(t b －a )＝λt b －λa . 又∵a 与b 为不共线的非零向量， ∴有⎩⎪⎨⎪⎧ －23＝－λ，13＝λt⇒⎩⎪⎨⎪⎧λ＝23，t ＝12.∴当t ＝12时，三向量终点在同一直线上．能力提升题组 (建议用时：25分钟)一、选择题1．(2018·济南一模)已知A ，B ，C 是平面上不共线的三点，O 是△ABC 的重心，动点P 满足OP →＝13⎝ ⎛ 12OA →＋12OB →＋⎭⎫2OC →，则点P 一定为三角形ABC 的( )． A ．AB 边中线的中点B ．AB 边中线的三等分点(非重心)C ．重心D ．AB 边的中点解析 设AB 的中点为M ，则12OA →＋12OB →＝OM →，∴OP →＝13(OM →＋2OC →)＝13OM →＋23OC →，即3OP →＝OM →＋2OC →，也就是MP →＝2PC →，∴P ，M ，C 三点共线，且P 是CM 上靠近C 点的一个三等分点． 答案 B2．在△ABC 中，点O 在线段BC 的延长线上，且与点C 不重合，若AO →＝x AB →＋(1－x )AC →，则实数x 的取值范围是( )． A ．(－∞，0) B ．(0，＋∞) C ．(－1,0) D ．(0,1)解析 设BO →＝λ BC →(λ＞1)，则AO →＝AB →＋BO →＝AB →＋λ BC →＝(1－λ)AB →＋λ AC →，又AO →＝x AB →＋(1－x )AC →，所以x AB →＋(1－x )AC →＝(1－λ)AB →＋λ AC →.所以λ＝1－x ＞ 1，得x ＜0. 答案 A 二、填空题3．若点O 是△ABC 所在平面内的一点，且满足|OB →－OC →|＝|OB →＋OC →－2OA →|，则△ABC 的形状为________．解析 OB →＋OC →－2OA →＝OB →－OA →＋OC →－OA →＝AB →＋AC →， OB →－OC →＝CB →＝AB →－AC →，∴|AB →＋AC →|＝|AB →－AC →|. 故A ，B ，C 为矩形的三个顶点，△ABC 为直角三角形． 答案 直角三角形 三、解答题 4.在△ABC 中，E ，F 分别为AC ，AB 的中点，BE 与CF 相交于G 点，设AB →＝a ，AC →＝b ，试用a ，b 表示AG →. 解 AG →＝AB →＋BG →＝AB →＋λBE →＝AB →＋λ2(BA →＋BC →)＝⎝ ⎛⎭⎪⎫1－λ2AB →＋λ2(AC →－AB →)＝(1－λ)AB →＋λ2AC →＝(1－λ)a ＋λ2b .又AG →＝AC →＋CG →＝AC →＋m CF →＝AC →＋m 2(CA →＋CB →) ＝(1－m )AC →＋m 2AB →＝m2a ＋(1－m )b ， ∴⎩⎪⎨⎪⎧1－λ＝m 2，1－m ＝λ2，解得λ＝m ＝23，∴AG →＝13a ＋13b .第70页[最新考纲]1．了解平面向量的基本定理及其意义． 2．掌握平面向量的正交分解及其坐标表示． 3．会用坐标表示平面向量的加法、减法与数乘运算． 4．理解用坐标表示的平面向量共线的条件.知 识 梳 理1．平面向量基本定理如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2.其中，不共线的向量e 1，e 2叫做表示这一平面内所有向量的一组基底． 2．平面向量的坐标运算(1)向量加法、减法、数乘向量及向量的模 设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ＋b ＝(x 1＋x 2，y 1＋y 2)，a －b ＝(x 1－x 2，y 1－y 2)，λa ＝(λx 1，λy 1)，|a |＝x 21＋y 21.(2)向量坐标的求法①若向量的起点是坐标原点，则终点坐标即为向量的坐标．②设A (x 1，y 1)，B (x 2，y 2)，则AB →＝(x 2－x 1，y 2－y 1)，|AB →|＝(x 2－x 1)2＋(y 2－y 1)2. 3．平面向量共线的坐标表示设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b ⇔x 1y 2－x 2y 1＝0.辨 析 感 悟1．对平面向量基本定理的理解(1)平面内的任何两个向量都可以作为一组基底．(×)(2)若a ，b 不共线，且λ1a ＋μ1b ＝λ2a ＋μ2b ，则λ1＝λ2，μ1＝μ2. (√) (3)(2018·广东卷改编)已知a 是已知的平面向量且a ≠0.关于向量a 的分解，有下列四个命题，请判断它们的正误： ①给定向量b ，总存在向量c ，使a ＝b ＋c .(√)②给定向量b 和c ，总存在实数λ和μ，使a ＝λb ＋μc ；(√)③给定单位向量b 和正数μ，总存在单位向量c 和实数λ，使a ＝λb ＋μc ； (√) ④给定正数λ和μ，总存在单位向量b 和单位向量c ，使a ＝λb ＋μc . (×)2．平面向量的坐标运算(4)(教材习题改编)已知点A (2,1)，B (－1,3)，则AB →＝(－3,2)．(√)(5)若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件可表示成x 1x 2＝y 1y 2.(×)(6)(2018·湘潭调研改编)已知向量a ＝(4，x )，b ＝(－4,4)，若a ∥b ，则x 的值为－4.(√)[感悟·提升]1．向量坐标与点的坐标的区别 在平面直角坐标系中，以原点为起点的向量OA →＝a ，点A 的位置被向量a 唯一确定，此时点A 的坐标与a 的坐标统一为(x ，y )，但应注意其表示形式的区别，如点A (x ，y )，向量a ＝OA →＝(x ，y )．当平面向量OA →平行移动到O 1A 1→时，向量不变即O 1A 1→＝OA →＝(x ，y )，但O 1A 1→的起点O 1和终点A 1的坐标都发生了变化．2．两个防范 一是注意能作为基底的两个向量必须是不共线的，如(1)．二是注意运用两个向量a ，b 共线坐标表示的充要条件应为x 1y 2－x 2y 1＝0，如(5).考点一 平面向量基本定理的应用【例1】 如图，在平行四边形ABCD 中，M ，N 分别为DC ，BC 的中点，已知AM →＝c ，AN →＝d ，试用c ，d 表示AB →，AD →.解 法一 设AB →＝a ，AD →＝b ， 则a ＝AN →＋NB →＝d ＋⎝ ⎛⎭⎪⎫－12b ，①b ＝AM →＋MD →＝c ＋⎝ ⎛⎭⎪⎫－12a .②将②代入①，得a ＝d ＋⎝ ⎛⎭⎪⎫－12⎣⎢⎡⎦⎥⎤c ＋⎝ ⎛⎭⎪⎫－12a ，∴a ＝43d －23c ＝23(2d －c )，③将③代入②，得b ＝c ＋⎝ ⎛⎭⎪⎫－12×23(2d －c )＝23(2c －d )．∴AB →＝23(2d －c )，AD →＝23(2c －d )． 法二 设AB →＝a ，AD →＝b .因M ，N 分别为CD ，BC 的中点， 所以BN →＝12b ，DM →＝12a ， 因而⎩⎪⎨⎪⎧c ＝b ＋12a ，d ＝a ＋12b⇒⎩⎪⎨⎪⎧a ＝23(2d －c )，b ＝23(2c －d )，即AB →＝23(2d －c )，AD →＝23(2c －d )．规律方法 (1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．(2)用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．【训练1】 在梯形ABCD 中，AB ∥CD ，AB ＝2CD ，M ，N 分别为CD ，BC 的中点，若A B →＝λAM →＋μAN →，则λ＋μ＝( )．A.15B.25C.35D.45解析 因为AB →＝AN →＋NB →＝AN →＋CN →＝AN →＋(CA →＋AN →)＝2AN →＋CM →＋MA →＝2AN →－14AB →－AM →，所以AB →＝85AN →－45AM →，所以λ＋μ＝45. 答案 D考点二 平面向量的坐标运算【例2】 已知A (－2,4)，B (3，－1)，C (－3，－4)，设AB →＝a ，BC →＝b ，CA →＝c ，且CM →＝3c ，CN →＝－2b . (1)求3a ＋b －3c ；(2)求满足a ＝m b ＋n c 的实数m ，n ； (3)求M ，N 的坐标及向量MN →的坐标．解 由已知得a ＝(5，－5)，b ＝(－6，－3)，c ＝(1,8)．(1)3a ＋b －3c ＝3(5，－5)＋(－6，－3)－3(1,8)＝(15－6－3，－15－3－24)＝(6，－42)．(2)∵m b ＋n c ＝(－6m ＋n ，－3m ＋8n )＝(5，－5)， ∴⎩⎨⎧ －6m ＋n ＝5，－3m ＋8n ＝－5，解得⎩⎨⎧m ＝－1，n ＝－1. (3)设O 为坐标原点，∵CM →＝OM →－OC →＝3c ， ∴OM →＝3c ＋OC →＝(3,24)＋(－3，－4)＝(0,20)， ∴M 的坐标为(0,20)． 又CN →＝ON →－OC →＝－2b ，∴ON →＝－2b ＋OC →＝(12,6)＋(－3，－4)＝(9,2)， ∴N 的坐标为(9,2)，∴MN →＝(9－0,2－20)＝(9，－18)．规律方法 向量的坐标运算主要是利用加、减、数乘运算法则进行的．若已知有向线段两端点的坐标，则应先求出向量的坐标，解题过程中要注意方程思想的运用及运算法则的正确使用．【训练2】 (1)已知平面向量a ＝(1,1)，b ＝(1，－1)，则向量12a －32b ＝ ( )． A ．(－2，－1) B ．(－2,1) C ．(－1,0) D ．(－1,2)第72页(2)在平行四边形ABCD 中，AC 为一条对角线，若AB ＝(2,4)，AC ＝(1,3)，则BD →＝( )．A ．(－2，－4)B ．(－3，－5)C ．(3,5)D ．(2,4) 解析 (1)12a ＝⎝ ⎛⎭⎪⎫12，12，32b ＝⎝ ⎛⎭⎪⎫32，－32， 故12a －32b ＝(－1,2)．(2)由题意得BD →＝AD →－AB →＝BC →－AB →＝(AC →－AB →)－AB →＝AC →－2AB →＝(1,3)－2(2,4)＝(－3，－5)． 答案 (1)D (2)B考点三 平面向量共线的坐标表示【例3】 平面内给定三个向量a ＝(3,2)，b ＝(－1,2)，c ＝(4,1)． (1)若(a ＋k c )∥(2b －a )，求实数k ；(2)若d 满足(d －c )∥(a ＋b )，且|d －c |＝5，求d 的坐标．审题路线 (1)分别求出(a ＋k c )与(2b －a )的坐标⇒利用向量平行的充要条件列方程⇒解关于k 的方程；(2)设d 的坐标⇒根据已知条件列出方程组⇒解方程组，得到d 的坐标．解 (1)a ＋k c ＝(3＋4k,2＋k )，2b －a ＝(－5,2)， 由题意得2×(3＋4k )－(－5)×(2＋k )＝0， 解得k ＝－1613.(2)设d ＝(x ，y )，则d －c ＝(x －4，y －1)， 又a ＋b ＝(2,4)，|d －c |＝5，∴⎩⎨⎧ 4(x －4)－2(y －1)＝0，(x －4)2＋(y －1)2＝5，解得⎩⎨⎧ x ＝3，y ＝－1或⎩⎨⎧x ＝5，y ＝3. ∴d 的坐标为(3，－1)或(5,3)．规律方法 a ∥b 的充要条件有两种表达方式： (1)a ∥b (b ≠0)⇔a ＝λb (λ∈R )；(2)设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b ⇔x 1y 2－x 2y 1＝0.两种充要条件的表达形式不同．第(1)种是用线性关系的形式表示的，而且有前提条件b ≠0，而第(2)种无b ≠0限制．【训练3】 (1)(2019·衡水中学一检)已知向量a ＝(1,2)，b ＝(1,0)，c ＝(3,4)．若λ为实数，(a ＋λb )∥c ，则λ＝ ( )． A.12 B.14 C ．1 D ．2(2)已知梯形ABCD ，其中AB ∥CD ，且DC ＝2AB ，三个顶点A (1,2)，B (2,1)，C (4,2)，则点D 的坐标为________．解析 (1)由于a ＋λb ＝(1＋λ，2)，故(a ＋λb )∥c ⇒4(1＋λ)－6＝0，解得λ＝12，故选A.(2)∵在梯形ABCD 中，DC ＝2AB ，∴DC →＝2 AB →. 设点D 的坐标为(x ，y )，则 DC →＝(4,2)－(x ，y )＝(4－x,2－y )， AB →＝(2,1)－(1,2)＝(1，－1)，∴(4－x,2－y )＝2(1，－1)，即(4－x,2－y )＝(2，－2)， ∴⎩⎨⎧ 4－x ＝2，2－y ＝－2，解得⎩⎨⎧x ＝2，y ＝4，故点D 的坐标为(2,4)． 答案 (1)A (2)(2,4)1．平面向量基本定理的本质是运用向量加法的平行四边形法则，将向量进行分解．2．向量的坐标表示的本质是向量的代数表示，其中坐标运算法则是运算的关键，通过坐标运算可将一些几何问题转化为代数问题处理，从而向量可以解决平面解析几何中的许多相关问题．3．在向量的运算中要注意待定系数法、方程思想和数形结合思想的运用．思想方法3——方程思想在平面向量线性运算中的应用【典例】 (2018·北京卷)向量a ，b ，c 在正方形网格中的位置如图所示．若c ＝λa ＋μb (λ，μ∈R )，则λμ＝________.解析 以向量a 和b 的交点为坐标原点建立如图所示的坐标系，令每个小正方形的边长为1个单位，则A (1，－1)，B (6,2)，C (5，－1)，所以a ＝AO →＝(－1,1)，b ＝OB →＝(6,2)，c ＝BC →＝(－1，－3)．由c ＝λa ＋μb 可得⎩⎨⎧－1＝－λ＋6μ，－3＝λ＋2μ，解得⎩⎪⎨⎪⎧λ＝－2，μ＝－12，所以λμ＝4. 答案 4[反思感悟] (1)用已知向量来表示另外一些向量是用向量解题的基本要领，要尽可能地转化到平行四边形或三角形中去．(2)利用向量共线建立方程组，用方程的思想求解．【自主体验】1．设e 1，e 2是平面内一组基底，且a ＝e 1＋2e 2，b ＝－e 1＋e 2，则向量e 1＋e 2可以表示为另一组基底a ，b 的线性组合，即e 1＋e 2＝________a ＋________b . 解析 由题意，设e 1＋e 2＝m a ＋n b .又a ＝e 1＋2e 2，b ＝－e 1＋e 2，所以e 1＋e 2＝m (e 1＋2e 2)＋ n (－e 1＋e 2)＝(m －n )e 1＋(2m ＋n )e 2. 又e 1，e 2是平面内一组基向量， 所以⎩⎨⎧m －n ＝1，2m ＋n ＝1，则⎩⎪⎨⎪⎧m ＝23，n ＝－13.答案23 －132．已知向量a ＝⎝ ⎛⎭⎪⎫8，x 2，b ＝(x,1)，其中x >0，若(a －2b )∥(2a ＋b )，则x ＝________.解析 a －2b ＝⎝ ⎛⎭⎪⎫8－2x ，x 2－2，2a ＋b ＝(16＋x ，x ＋1)， 由题意得(8－2x )·(x ＋1)＝⎝ ⎛⎭⎪⎫x 2－2·(16＋x )，整理得x 2＝16，又x >0，所以x ＝4. 答案 4基础巩固题组(建议用时：40分钟)一、选择题1．(2019·华东师大附中模拟)如图，设O 是平行四边形ABCD 的两条对角线AC ，BD 的交点，下列向量组：①AD →与AB →；②DA →与BC →；③CA →与DC →；④OD →与OB →，其中可作为这个平行四边形所在平面的一组基底的是( )． A ．①② B ．③④ C ．①③ D ．①④解析 ①中AD →与AB →不共线，可作为基底；②中DA →与BC →为共线向量，不可作为基底；③中CA →与DC →是两个不共线的向量，可作为基底；④中OD →与OB →在同一条直线上，是共线向量，不可作为基底．综上，只有①③中的向量可以作为基底，故选C. 答案 C2．(2019·揭阳二模)已知点A (－1,5)和向量a ＝(2,3)，若AB →＝3a ，则点B 的坐标为( )．A ．(7,4)B ．(7,14)C ．(5,4)D ．(5,14)解析 设点B 的坐标为(x ，y )，则AB →＝(x ＋1，y －5)． 由AB →＝3a ，得⎩⎨⎧ x ＋1＝6，y －5＝9，解得⎩⎨⎧x ＝5，y ＝14.答案 D 3.如图，在△OAB 中，P 为线段AB 上的一点，OP →＝x OA →＋y OB →，且BP →＝2 P A →，则( )．A ．x ＝23，y ＝13B ．x ＝13，y ＝23 C ．x ＝14，y ＝34 D ．x ＝34，y ＝14解析 由题意知OP →＝OB →＋BP →，又BP →＝2 P A →，所以OP →＝OB →＋23BA →＝OB →＋23(OA →－OB →)＝23OA →＋13OB →，所以x ＝23，y ＝13. 答案 A4．(2018·惠州模拟)已知向量a ＝(－1,1)，b ＝(3，m )，a ∥(a ＋b )，则m ＝( )．A ．2B ．－2C ．－3D ．3解析 a ＋b ＝(2，m ＋1)，由a ∥(a ＋b )，得(－1)×(m ＋1)－2×1＝0，解得m ＝－3. 答案 C5．(2019·许昌模拟)在△ABC 中，点P 在BC 上，且BP →＝2P C →，点Q 是AC 的中点，若P A →＝(4,3)，PQ →＝(1,5)，则BC →等于( )． A ．(－2,7) B ．(－6,21) C ．(2，－7) D ．(6，－21)解析 BC →＝3 PC →＝3(2 PQ →－P A →)＝6 PQ →－3 P A →＝(6,30)－(12,9)＝(－6,21)． 答案 B 二、填空题6．若三点A (2,2)，B (a,0)，C (0，b )(ab ≠0)共线，则1a ＋1b 的值为________． 解析 AB →＝(a －2，－2)，AC →＝(－2，b －2)， 依题意，有(a －2)(b －2)－4＝0， 即ab －2a －2b ＝0，所以1a ＋1b ＝12. 答案 127．已知向量OA →＝(3，－4)，OB →＝(0，－3)，OC →＝(5－m ，－3－m )，若点A ，B ，C 能构成三角形，则实数m 满足的条件是________．解析 由题意得AB →＝(－3,1)，AC →＝(2－m,1－m )，若A ，B ，C 能构成三角形，则AB →，AC →不共线，则－3×(1－m )≠1×(2－m )，解得m ≠54. 答案 m ≠548．(2018·江苏卷)设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC .若DE →＝λ1 AB →＋λ2 AC →(λ1，λ2为实数)，则λ1＋λ2的值为________． 解析 DE →＝DB →＋BE →＝12AB →＋23BC →＝12AB →＋23(BA →＋AC →)＝－16AB →＋23AC →，所以λ1＝－16，λ2＝23， 即λ1＋λ2＝12. 答案 12 三、解答题9．已知a ＝(1,2)，b ＝(－3,2)，当k 为何值时，k a ＋b 与a －3b 平行？平行时它们是同向还是反向？解 k a ＋b ＝k (1,2)＋(－3,2)＝(k －3,2k ＋2)， a －3b ＝(1,2)－3(－3,2)＝(10，－4)，法一 当k a ＋b 与a －3b 平行时，存在唯一实数λ使k a ＋b ＝λ(a －3b )，由(k －3,2k ＋2)＝λ(10，－4)得，⎩⎨⎧k －3＝10λ，2k ＋2＝－4λ.解得k ＝λ＝－13， ∴当k ＝－13时，k a ＋b 与a －3b 平行， 这时k a ＋b ＝－13a ＋b ＝－13(a －3b )． ∵λ＝－13<0，∴k a ＋b 与a －3b 反向． 法二 ∵k a ＋b 与a －3b 平行，∴(k －3)×(－4)－10×(2k ＋2)＝0，解得k ＝－13， 此时k a ＋b ＝⎝ ⎛⎭⎪⎫－13－3，－23＋2＝－13(a －3b )．∴当k ＝－13时，k a ＋b 与a －3b 平行，并且反向．10．已知点O 为坐标原点，A (0,2)，B (4,6)，OM →＝t 1 OA →＋t 2 AB →. (1)求点M 在第二或第三象限的充要条件；(2)求证：当t 1＝1时，不论t 2为何实数，A ，B ，M 三点都共线．(1)解 OM →＝t 1OA →＋t 2AB →＝t 1(0,2)＋t 2(4,4)＝(4t 2,2t 1＋4t 2)．当点M 在第二或第三象限时，有⎩⎨⎧4t 2＜0，2t 1＋4t 2≠0，故所求的充要条件为t 2＜0且t 1＋2t 2≠0， (2)证明 当t 1＝1时，由(1)知OM →＝(4t 2,4t 2＋2)． ∵AB →＝OB →－OA →＝(4,4)，AM →＝OM →－OA →＝(4t 2,4t 2)＝t 2(4,4)＝t 2 AB →， ∴AM →与AB →共线，又它们有公共点A ， ∴A ，B ，M 三点共线．能力提升题组 (建议用时：25分钟)一、选择题1．(2018·保定模拟)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，设向量p ＝(a ＋c ，b )，q ＝(b －a ，c －a )，若p ∥q ，则角C 的大小为( )． A ．30° B ．60° C ．90° D ．120° 解析 由p ∥q ，得(a ＋c )(c －a )＝b (b －a )， 整理得b 2＋a 2－c 2＝ab ，由余弦定理得cos C ＝a 2＋b 2－c 22ab ＝12， 又0°<C <180°，∴C ＝60°. 答案 B 2.(2019·中山模拟)如图所示，A ，B ，C 是圆O 上的三点，CO 的延长线与线段BA 的延长线交于圆O 外一点D ，若OC →＝m OA →＋n OB →，则m ＋n 的取值范围是( )． A ．(0,1) B ．(1，＋∞) C ．(－∞，－1) D ．(－1,0)解析 由点D 是圆O 外一点，可设BD →＝λ BA →(λ＞1)，则 OD →＝OB →＋λ BA →＝λ OA →＋(1－λ)OB →.又C ，O ，D 三点共线，令OD →＝－μ OC →(μ＞1)，则OC →＝－λμOA →－1－λμOB →(λ＞1，μ＞1)，所以m ＝－λμ，n ＝－1－λμ，且m ＋n ＝－λμ－1－λμ＝－1μ∈(－1,0)． 答案 D 二、填空题3．(2019·南京质检)设OA →＝(1，－2)，OB →＝(a ，－1)，OC →＝(－b,0)，a >0，b >0，O 为坐标原点，若A ，B ，C 三点共线，则1a ＋2b 的最小值为________． 解析 AB →＝OB →－OA →＝(a －1,1)，AC →＝OC →－OA →＝(－b －1,2)．∵A ，B ，C 三点共线， ∴AB →∥AC →.∴2(a －1)－(－b －1)＝0， ∴2a ＋b ＝1.∴1a ＋2b ＝⎝ ⎛⎭⎪⎫1a ＋2b (2a ＋b )＝4＋b a ＋4ab ≥4＋2b a ·4a b ＝8.当且仅当b a ＝4a b ，即b ＝12，a ＝14时取等号． ∴1a ＋2b 的最小值是8.答案 8 三、解答题 4.如图，已知点A (1,0)，B (0,2)，C (－1，－2)，求以A ，B ，C 为顶点的平行四边形的第四个顶点D 的坐标．解 以A ，B ，C 为顶点的平行四边形可以有三种情况： ①▱ABCD ；②▱ADBC ；③▱ABDC . 设D 的坐标为(x ，y )，①若是▱ABCD ，则由AB →＝DC →，得 (0,2)－(1,0)＝(－1，－2)－(x ，y )， 即(－1,2)＝(－1－x ，－2－y )， ∴⎩⎨⎧－1－x ＝－1，－2－y ＝2，∴x ＝0，y ＝－4. ∴D 点的坐标为(0，－4)(如题图中所示的D 1)． ②若是▱ADBC ，由CB →＝AD →，得 (0,2)－(－1，－2)＝(x ，y )－(1,0)， 即(1,4)＝(x －1，y )，解得x ＝2，y ＝4. ∴D 点的坐标为(2,4)(如题图中所示的D 2)． ③若是▱ABDC ，则由AB →＝CD →，得 (0,2)－(1,0)＝(x ，y )－(－1，－2)，即(－1,2)＝(x ＋1，y ＋2)．解得x ＝－2，y ＝0. ∴D 点的坐标为(－2,0)(如题图中所示的D 3)，∴以A ，B ，C 为顶点的平行四边形的第四个顶点D 的坐标为(0，－4)或(2,4)或(－2,0).第73页第3讲平面向量的数量积[最新考纲]1．理解平面向量数量积的含义及其物理意义．2．了解平面向量的数量积与向量投影的关系．3．掌握数量积的坐标表达式，会进行平面向量数量积的运算．4．能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系.知识梳理1．平面向量的数量积(1)定义：已知两个非零向量a与b，它们的夹角为θ，则数量|a||b|cos θ叫作a 与b的数量积(或内积)，记作a·b，即a·b＝|a||b|cos θ，规定零向量与任一向量的数量积为0，即0·a＝0.(2)几何意义：数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos θ的乘积．2．平面向量数量积的性质及其坐标表示设向量a＝(x1，y1)，b＝(x2，y2)，θ为向量a，b的夹角．(1)数量积：a·b＝|a||b|cos θ＝x1x2＋y1y2.(2)模：|a|＝a·a＝x21＋y21.(3)夹角：cos θ＝a·b|a||b|＝x1x2＋y1y2x21＋y21·x22＋y22.(4)两非零向量a⊥b的充要条件：a·b＝0⇔x1x2＋y1y2＝0.(5)|a·b|≤|a||b|(当且仅当a∥b时等号成立)⇔|x1x2＋y1y2|≤x21＋y21·x22＋y22. 3．平面向量数量积的运算律(1)a·b＝b·a(交换律)．(2)λa·b＝λ(a·b)＝a·(λb)(结合律)．(3)(a＋b)·c＝a·c＋b·c(分配律)．辨析感悟1．对平面向量的数量积的认识(1)两个向量的数量积是一个向量，向量加、减、数乘运算的结果是向量．(×) (2)(2018·湖北卷改编)已知点A (－1,1)，B (1,2)，C (－2，－1)，D (3,4)，则向量AB →在CD →方向上的投影为－322.(×)(3)若a ·b ＞0，则a 和b 的夹角为锐角；若a ·b ＜0，则a 和b 的夹角为钝角．(×) 2．对平面向量的数量积的性质、运算律的理解 (4)a ·b ＝0，则a ＝0或b ＝0.(×) (5)(a ·b )·c ＝a ·(b ·c )．(×) (6)a ·b ＝a ·c (a ≠0)，则b ＝c .(×) [感悟·提升]三个防范 一是两个向量的数量积是一个数量，而不是向量，如(1)；二是在向量数量积的几何意义中，投影是一个数量，不是向量．设向量a ，b 的夹角为θ，当θ为锐角时，投影为正值；当θ为钝角时，投影为负值；当θ为直角时，投影为0；当θ＝0°时，b 在a 的方向上投影为|b |，当θ＝180°时，b 在a 方向上投影为－|b |，如(2)；当θ＝0°时，a ·b ＞0，θ＝180°，a ·b ＜0，即a ·b ＞0是两个向量a ，b 夹角为锐角的必要而不充分条件，如(3)；三是a ·b ＝0不能推出a ＝0或b ＝0，因为a ·b ＝0时，有可能a ⊥b ，如(4)．考点一 平面向量数量积的运算【例1】 (1)(2019·威海期末考试)已知a ＝(1,2)，2a －b ＝(3,1)，则a ·b ＝( )． A ．2 B ．3 C ．4 D ．5(2)(2018·江西卷)设e 1，e 2为单位向量，且e 1，e 2的夹角为π3，若a ＝e 1＋3e 2，b ＝2e 1，则向量a 在b 方向上的射影为________． 解析 (1)∵a ＝(1,2)，2a －b ＝(3,1) ∴b ＝2a －(3,1)＝2(1,2)－(3,1)＝(－1,3)． ∴a ·b ＝(1,2)·(－1,3)＝－1＋2×3＝5.(2)由于a ＝e 1＋3e 2，b ＝2e 1，所以|b |＝2，a ·b ＝(e 1＋3e 2)·2e 1＝2e 21＋6e 1·e 2 ＝2＋6×12＝5，所以a 在b 方向上的射影为|a |·cos<a ，b >＝a ·b |b |＝52. 答案 (1)D (2)52第74页规律方法 利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．【训练1】 (1)若向量a ＝(1,1)，b ＝(2,5)，c ＝(3，x )满足条件(8a －b )·c ＝30，则x ＝( )．A ．6B ．5C ．4D ．3(2)(2018·山东卷)已知向量AB →与AC →的夹角为120°，且|AB →|＝3，|AC →|＝2.若AP →＝λAB →＋AC →，且AP →⊥BC →，则实数λ的值为______． 解析 (1)8a －b ＝8(1,1)－(2,5)＝(6,3)， 所以(8a －b )·c ＝(6,3)·(3，x )＝30， 即18＋3x ＝30，解得x ＝4.故选C. (2)∵AP →⊥BC →，∴AP →·BC →＝0，∴(λAB →＋AC →)·BC →＝0，即(λAB →＋AC →)·(AC →－AB →)＝(λ－1)AB →·AC →－λAB →2＋AC →2＝0. ∵向量AB →与AC →的夹角为120°，|AB →|＝3，|AC →|＝2， ∴(λ－1)|AB →||AC →|·cos 120°－9λ＋4＝0，解得λ＝712. 答案 (1)C (2)712考点二 向量的夹角与向量的模【例2】 (1)若非零向量a ，b 满足|a |＝3|b |＝|a ＋2b |，则a 与b 夹角的余弦值为________．(2)已知向量a ，b 满足a ·b ＝0，|a |＝1，|b |＝2，则|2a －b |＝________. 解析 (1)等式平方得|a |2＝9|b |2 ＝|a |2＋4|b |2＋4a ·b ，则|a |2＝|a |2＋4|b |2＋4|a ||b |cos θ， 即0＝4|b |2＋4·3|b |2cos θ， 得cos θ＝－13.(2)因为|2a －b |2＝(2a －b )2＝4a 2＋b 2－4a ·b ＝4a 2＋b 2＝4＋4＝8，故|2a －b |＝2 2. 答案 (1)－13 (2)2 2规律方法 (1)求向量的夹角主要是应用向量的数量积公式． (2)|a |＝a ·a 常用来求向量的模．【训练2】 (1)(2019·长沙模拟)已知向量a ，b 夹角为45°，且|a |＝1，|2a －b |＝10，则|b |＝________.(2)若平面向量a ，b 满足|a |＝1，|b |≤1，且以向量a ，b 为邻边的平行四边形的面积为12，则a 和b 的夹角θ的取值范围是________． 解析 (1)由|2a －b |＝10平方得， 4a 2－4a ·b ＋b 2＝10， 即|b |2－4|b |cos 45°＋4＝10， 亦即|b |2－22|b |－6＝0， 解得|b |＝32或|b |＝－2(舍去)． (2)依题意有|a ||b |sin θ＝12， 即sin θ＝12|b |，由|b |≤1，得 12≤sin θ≤1，又0≤θ≤π， 故有π6≤θ≤5π6.答案 (1)32 (2)⎣⎢⎡⎦⎥⎤π6，5π6考点三 平面向量的垂直问题【例3】 已知a ＝(cos α，sin α)，b ＝(cos β，sin β)(0<α<β<π)． (1)求证：a ＋b 与a －b 互相垂直；(2)若k a ＋b 与a －k b 的模相等，求β－α(其中k 为非零实数)．审题路线 证明两向量互相垂直，转化为计算这两个向量的数量积问题，数量积为零即得证⇒由模相等，列等式、化简求β－α. (1)证明 ∵(a ＋b )·(a －b )＝a 2－b 2＝|a |2－|b |2 ＝(cos 2α＋sin 2α)－(cos 2β＋sin 2β)＝0， ∴a ＋b 与a －b 互相垂直．(2)解 k a ＋b ＝(k cos α＋cos β，k sin α＋sin β)， a －k b ＝(cos α－k cos β，sin α－k sin β)， |k a ＋b |＝k 2＋2k cos (β－α)＋1， |a －k b |＝1－2k cos (β－α)＋k 2.∵|k a ＋b |＝|a －k b |，∴2k cos(β－α)＝－2k cos(β－α)． 又k ≠0，∴cos(β－α)＝0.∵0<α<β<π，∴0<β－α<π，∴β－α＝π2.规律方法 (1)当向量a 与b 是坐标形式给出时，若证明a ⊥b ，则只需证明a·b ＝0⇔x 1x 2＋y 1y 2＝0.(2)当向量a ，b 是非坐标形式时，要把a ，b 用已知的不共线向量作为基底来表示且不共线的向量要知道其模与夹角，从而进行运算证明a·b ＝0.(3)数量积的运算a·b ＝0⇔a ⊥b 中，是对非零向量而言的，若a ＝0，虽然有a·b ＝0，但不能说a ⊥b .【训练3】 已知平面向量a ＝(3，－1)，b ＝⎝ ⎛⎭⎪⎫12，32.(1)证明：a ⊥b ；(2)若存在不同时为零的实数k 和t ，使c ＝a ＋(t 2－3)b ，d ＝－k a ＋t b ，且c ⊥d ，试求函数关系式k ＝f (t )．(1)证明 ∵a ·b ＝3×12－1×32＝0，∴a ⊥b . (2)解 ∵c ＝a ＋(t 2－3)b ，d ＝－k a ＋t b ，且c ⊥d ，∴c·d＝[a＋(t2－3)b]·(－k a＋t b)＝－k a2＋t(t2－3)b2＋[t－k(t2－3)]a·b＝0. 又a2＝|a|2＝4，b2＝|b|2＝1，a·b＝0，∴c·d＝－4k＋t3－3t＝0，∴k＝f(t)＝t3－3t4(t≠0)．1．计算数量积的三种方法：定义、坐标运算、数量积的几何意义，要灵活选用，和图形有关的不要忽略数量积几何意义的应用．2．求向量模的常用方法：利用公式|a|2＝a2，将模的运算转化为向量的数量积的运算．3．利用向量垂直或平行的条件构造方程或函数是求参数或最值问题常用的方法与技巧.第75页教你审题5——数量积的计算问题【典例】(2018·上海卷)在矩形ABCD中，设AB，AD的长分别为2,1.若M，N分别是边BC，CD上的点，且满足|BM→||BC→|＝|CN→||CD→|，则AM→·AN→的取值范围是________．[审题]一审：抓住题眼“矩形ABCD”；二审：合理建立平面直角坐标系，转化为代数问题解决．解析如图，以A点为坐标原点建立平面直角坐标系，则各点坐标为A(0,0)，B(2,0)，C(2,1)，D(0,1)，设|BM →||BC →|＝|CN →||CD →|＝k (0≤k ≤1)，则点M 的坐标为(2，k )，点N 的坐标为(2－2k,1)， 则AM →＝(2，k )，AN →＝(2－2k,1)，AM →·AN →＝2(2－2k )＋k ＝4－3k ，而0≤k ≤1，故1≤4－3k ≤4. 答案 [1,4][反思感悟] 在利用平面向量的数量积解决平面几何中的问题时，首先要想到是否能建立平面直角坐标系，利用坐标运算题目会容易的多． 【自主体验】(2018·江苏卷)如图，在矩形ABCD 中，AB ＝2，BC ＝2，点E 为BC 的中点，点F 在边CD 上，若AB →·AF →＝2，则AE →·BF →的值是________．解析 法一 以A 为原点，AB ，AD 所在直线分别为x 轴、y 轴建立平面直角坐标系，则A (0,0)，B (2，0)，E (2，1)，F (x,2)，∴AF →＝(x,2)，AB →＝(2，0)，AE →＝(2，1)，BF →＝(x －2，2)，∴AB →·AF →＝2x ＝2，解得x ＝1，∴F (1,2)，∴AE →·BF →＝ 2.法二 AB →·AF →＝|AB →||AF →|cos ∠BAF ＝2，∴|AF →|cos ∠BAF ＝1，即|DF →|＝1，∴|CF →|＝2－1，AE →·BF →＝(AB →＋BE →)·(BC →＋CF →)＝AB →·BC →＋AB →·CF →＋BE →·BC →＋BE →·CF →＝AB →·CF →＋BE →·BC →＝2×(2－1)×(－1)＋1×2×1＝ 2. 答案 2基础巩固题组(建议用时：40分钟)一、选择题1．(2018·湛江二模)向量a ＝(1,2)，b ＝(0,2)，则a ·b ＝( )． A ．2 B ．(0,4) C ．4 D ．(1,4) 解析 a ·b ＝(1,2)·(0,2)＝1×0＋2×2＝4. 答案 C2．(2019·绍兴质检)在边长为2的菱形ABCD 中，∠BAD ＝120°，则AC →在AB →方向上的投影为( )．A.14B.12 C ．1 D ．2解析 如图所示，AC →在AB →方向上的投影为|AC →|cos 60°＝2×12＝1. 答案 C3．(2018·山东省实验中学诊断)已知向量a ＝(3，1)，b ＝(0,1)，c ＝(k ，3)．若a ＋2b 与c 垂直，则k ＝( )． A ．－3 B ．－2 C ．－1 D ．1解析 由题意知(a ＋2b )·c ＝0，即a ·c ＋2b ·c ＝0. 所以3k ＋3＋23＝0，解得k ＝－3. 答案 A4．(2019·浙江五校联盟)若非零向量a ，b 满足|a |＝|b |，且(2a ＋b )·b ＝0，则向量a ，b 的夹角为( )． A.2π3 B.π6 C.π3 D.5π6解析 由(2a ＋b )·b ＝0，得2a ·b ＋|b |2＝0. ∴2|b |2·cos<a ，b >＋|b |2＝0，∴cos<a ，b >＝－12，。

特别提醒：①,sin()sin ,sincos 22A B C A B C A B C π++=-+==： ②锐角三角形⇒sin sin cos 2A B B π⎛⎫>-= ⎪⎝⎭⇒sin sin sin cos cos cos A B C A B C ++>++.（2）正弦定理：2sin sin sin a b c R A B C===(R 为三角形外接圆的半径). 注意：①正弦定理的一些变式： ()sin sin i a b A B :=:；()sin 2a ii A R =；()2sin iii a R A =； ②已知三角形两边及一边的对角，求解三角形时，若运用正弦定理，则务必注意可能有两解. （3）余弦定理：2222222cos ,cos 2b c a a b c bc A A bc +-=+-=等， 解三角形中含有边角混合关系的问题时，常运用正弦定理、余弦定理实现边角互化.（4）面积公式：111sin ()222a S ah ab C r a bc ===++（其中r 为三角形内切圆半径）. （5）大边对大角：当出现多个解时，常用于判断哪些是符合题意的解、哪些不是.在三角形中，sin sin A B A B >⇔>，这是“正弦定理+大边对大角”的应用.14. 致命易错点提示：（1）特殊角三角函数值、诱导公式和三角变换公式使用错误；（2）大题第一步化简错误（应在化简完后立刻检验）；（3）已知三角函数值求角、同角三角函数之间的互化、三角函数值域和最值的研究经常会忽略角的范围.第五部分 平面向量1. 向量有关概念：（1）向量的概念：既有大小又有方向的量，叫向量. 向量常用有向线段来表示.注意向量和数量的区别.（2）零向量：长度为0的向量叫零向量，记作：0，注意零向量的方向是任意的.（3）单位向量：长度为一个单位长度的向量叫做单位向量.(与AB 共线的单位向量有两个：AB±,一个同向，一个反向).（4）相等向量：长度相等且方向相同的两个向量叫相等向量，相等向量有传递性.（5）相反向量：长度相等方向相反的向量叫做相反向量, a 的相反向量是－a .（6）平行向量（也叫共线向量）：方向相同或相反的非零向量a 、b 叫做平行向量，记作：a ∥b ，规定零向量和任何向量平行.提醒：①两个向量平行与两条直线平行是不同的两个概念，两个向量平行包含基线平行与重合两种情况, 但两条直线平行不包含两条直线重合.②三点A B C 、、共线⇔AB ∥AC .2. 向量的表示方法：（1）几何表示法：用带箭头的有向线段表示，如AB ，注意前为起点，后为终点.（2）符号表示法：用一个小写的英文字母来表示，如a ，b ，c 等.（3）坐标表示法：在平面直角坐标系内，以与x 轴、y 轴正方向同向的两个单位向量i ，j 为基底，则平面内任一向量a 可表示为(),a xi y j x y =+=，称(),x y 为向量a 的坐标，a ＝(),x y 叫做向量a 的坐标表示.如果向量的起点在原点，那么向量的坐标与向量的终点坐标相同.3. 平面向量的基本定理：如果e 1和e 2是同一平面内的两个不共线向量，那么对该平面内的任一向量a ，有且只有一对实数1λ、2λ，使a =1λe 1＋2λe 2.如:（1）若(1,1),a b ==(1,1),(1,2)c -=-，则c =______（用,a b 表示）（答：1322a b -）. （2）已知ABC ∆中，点D 在BC 边上，且−→−−→−=DB CD 2，−→−−→−−→−+=AC s AB r CD ，则s r +的值是___（答：0）.4. 实数与向量的积：实数λ与向量a 的积是一个向量，记作λa ，它的长度和方向规定如下：（1）;a a λλ=（2）当λ0>时，λa 的方向与a 的方向相同;当λ0<时，λa 的方向与a 的方向相反;当λ＝0时，0a λ=，注意：λa ≠0. 5. 平面向量的数量积：（1）两个向量的夹角：对于非零向量a ，b ，作,OA a OB b ==，AOB θ∠=()0θπ≤≤称为向量a ，b 的夹角.当θ＝0时，a ，b 同向;当θ＝π时，a ，b 反向;当θ＝2π时，a ，b 垂直.（2）平面向量的数量积：如果两个非零向量a ，b ，它们的夹角为θ，我们把数量||||cos a b θ叫做a 与b 的数量积（或内积，或点积），记作：b a ⋅，即b a ⋅＝cos a b θ.规定：零向量与任一向量的数量积是0.注意数量积是一个实数，不再是一个向量.如：①2=5=，3-=⋅b a ，则a b +等于____.） ②已知非零向量,a b 满足a b a b ==-，则,a a b 〈+〉的大小为____.（答：30）（3）b 在a 上的投影为||cos b θ，它是一个实数，但不一定大于0. 如:已知3||=→a ，5||=→b ，且12=⋅→→b a ，则向量→a 在→b 上的投影为____.(答：512) （4）b a ⋅的几何意义：数量积b a ⋅等于a 的模||a 与b 在a 上的投影数量的积.（5）向量数量积的性质：设两个非零向量a ，b ，其夹角为θ，则：①0=⋅⇔⊥b a b a .②当a ，b 同向时，b a ⋅＝a b ，特别地，22||a a a a =⋅=，||a = 当a 与b 反向时，b a ⋅＝－a b .当θ为锐角时，b a ⋅＞0，且 a b 、不同向，0a b ⋅>是θ为锐角的必要非充分条件.当θ为钝角时，b a ⋅＜0，且 a b 、不反向，0a b ⋅<是θ为钝角的必要非充分条件.③非零向量a ，b 夹角θ的计算公式：||||cos b a b a =θ ④||||||b a b a ≤⋅.如 ：已知)2,(λλ=→a ，)2,3(λ=→b ，如果→a 与→b 的夹角为锐角，则λ的取值范围是______.（答：43λ<-或0λ>且13λ≠） 6．向量的运算：（1）几何运算：①向量加法：利用“平行四边形法则”进行.向量加法还可利用“三角形法则”：设,AB a BC b ==，那么向量AC叫做a 与b 的和，即a b AB BC AC +=+=.②向量的减法：用“三角形法则”：设,,AB a AC b a b AB AC CA ==-=-=那么， 由减向量的终点指向被减向量的终点.注意：此处减向量与被减向量的起点相同.（2）坐标运算：设1122(,),(,)a x y b x y ==，则：①向量的加减法运算：12(a b x x ±=±，12)y y ±.②实数与向量的积：()()1111,,a x y x y λλλλ==.③若1122(,),(,)A x y B x y ，则()2121,AB x x y y =--，即一个向量的坐标等于表示这个向量的有向线段的终点坐标减去起点坐标.④平面向量数量积：2121y y x x b a +=⋅.⑤向量的模：222222||,||a x y a a x y =+==+.⑥两点间的距离：若()()1122,,,A x y B x y ，则||AB =.7. 向量的运算律： （1）交换律：a b b a +=+，()()a a λμλμ=，a b b a ⋅=⋅.( 2 ) 结合律：()(),a b c a b c a b c a b c ++=++--=-+，)()()(b a b a b a λλλ⋅=⋅=⋅.（3）分配律：()(),a a a a b a b λμλμλλλ+=++=+， c b c a c b a ⋅+⋅=⋅+)(.如:在下列命题中：① →→→→→→→⋅-⋅=-⋅c a b a c b a )(.② →→→→→→⋅⋅=⋅⋅c b a c b a )()(. ③ 2()a b →→-2||a →=22||||||a b b →→→-⋅+. ④ 若0=⋅→→b a ，则0=→a 或0=→b . ⑤ 若,a b c b ⋅=⋅则a c =.⑥22a a =. ⑦2a bb a a ⋅=.⑧222()a b a b ⋅=⋅. ⑨222()2a b a a b b -=-⋅+.其中正确的是______.（答：①⑥⑨）提醒：（1）向量运算和实数运算有类似的地方也有区别：对于一个向量等式，可以移项，两边平方、两边同乘以一个实数，两边同时取模，两边同乘以一个向量，但不能两边同除以一个向量，即两边不能约去一个向量，切记两向量不能相除(相约). （2）向量的“乘法”不满足结合律，即c b a c b a )()(⋅≠⋅.(为什么？)8. 向量平行(共线)的充要条件：//a b a b λ⇔=22()(||||)a b a b ⇔⋅=1212x y y x ⇔-＝0.如:(1)已知(1,1),(4,)a b x ==，2u a b =+，2v a b =+，且//u v ，则x ＝___.（答：4）.(2)设(,12),(4,5),(10,)PA k PB PC k ===，则k ＝_____时，A,B,C 三点共线.（答：－2或11）9. 向量垂直的充要条件：0||||a b a b a b a b ⊥⇔⋅=⇔+=- 12120x x y y ⇔+=.如：已知(1,2),(3,)OA OB m =-=，若OA OB ⊥，则m = .（答：32）10．向量中一些常用的结论：（1）一个封闭图形首尾连接而成的向量和为零向量，要注意运用.（2）||||||||||||a b a b a b -≤±≤+，特别地，当 a b 、同向或有0⇔||||||a b a b +=+≥||||||||a b a b -=-. 当 a b 、反向或有0⇔||||||a b a b -=+≥||||||||a b a b -=+.当 a b 、不共线⇔||||||||||||a b a b a b -<±<+. (这些和实数比较类似)（3）在ABC ∆中，①若()()()112233,,,,,A x y B x y C x y ，则其重心坐标为123123,33x x x y y y G ++++⎛⎫ ⎪⎝⎭. 如 ：若ABC ∆的三边的中点坐标分别为（2，1）、（-3，4）、（-1，-1），则ABC ∆的重心坐标为_______.（答：24(,)33-） ②1()3PG PA PB PC =++⇔G 为ABC ∆的重心， 特别地，0PA PB PC P ++=⇔为ABC ∆的重心.③PA PB PB PC PC PA P ⋅=⋅=⋅⇔为ABC ∆的垂心.④向量()(0)||||AC AB AB AC λλ+≠的基线经过ABC ∆的内心. （4）P 为12P P 的中点122MP MP MP +⇔=. （5）向量 PA PB PC 、、的终点A B C 、、共线⇔存在实数αβ、，使得PA PB PC αβ=+，且1αβ+=.如：平面直角坐标系中，O 为坐标原点，已知)1,3(A ,)3,1(-B ,若点C 满足=−→−OC −→−−→−+OB OA 21λλ,其中R ∈21,λλ且121=+λλ,则点C 的轨迹是____. （答：直线AB ） 第六部分 数列1．数列的定义：数列是一个定义域为正整数集*N （或它的有限子集{}n ,,3,2,1 ）上 的特殊函数，数列的通项公式也就是相应函数的解析式.2. 一般数列的通项n a 与前n 项和n S 的关系：⎩⎨⎧≥-==-)2()1(11n S S n S a n nn 3. 等差数列的概念：（1）等差数列的判断方法：定义法1(n n a a d d +-=为常数）.（2）等差数列的通项公式：1(1)n a a n d =+-或()n m a a n m d =+-.（3）等差数列的前n 项和：1()2n n n a a S +=1(1)2n n na d -=+， 注意n S 与中间项的关系.（4）等差中项：若,,a A b 成等差数列，那么A 叫做a 与b 的等差中项,2a b A +=. 4．等差数列的性质：（1）当公差0d ≠时，等差数列的通项公式11(1)n a a n d dn a d =+-=+-是。

第四章平面向量高考导航考试要求重难点击命题展望1.平面向量的实际背景及基本概念(1)了解向量的实际背景；(2)理解平面向量的概念，理解两个向量相等的含义；(3)理解向量的几何表示.2.向量的线性运算(1)掌握向量加法、减法的运算，并理解其几何意义；(2)掌握向量数乘的运算及其几何意义，理解两个向量共线的含义；(3)了解向量线性运算的性质及其几何意义.3.平面向量的基本定理及其坐标表示(1)了解平面向量的基本定理及其意义；(2)掌握平面向量的正交分解及其坐标表示；(3)会用坐标表示平面向量的加法、减法与数乘运算；(4)理解用坐标表示的平面向量共线的条件.4.平面向量的数量积(1)理解平面向量数量积的含义及其物理意义；(2)了解平面向量的数量积与向量投影的关系；(3)掌握数量积的坐标表达式，会进行平面向量数量积的运算；(4)能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系.5.向量的应用(1)会用向量方法解决某些简单的平面几何问题；(2)会用向量方法解决某些简单的力学问题及其本章重点：1.向量的各种运算；2.向量的坐标运算及数形结合的思想；3.向量的数量积在证明有关向量相等、两向量垂直、投影、夹角等问题中的应用.本章难点：1.向量的直角坐标运算在证明向量垂直和平行问题中的应用；2.向量的夹角公式和距离公式在求解平面上两条直线的夹角和两点间距离中的应用.向量是近代数学中重要和基本的数学概念之一，它是沟通代数、几何与三角函数的一种工具，有着极其丰富的实际背景，同时又是数形结合思想运用的典范，正是由于向量既具有几何形式又具有代数形式的“双重身份”，所以它成为中学数学知识的一个交汇点.在高考中，不仅注重考查向量本身的基础知识和方法，而且常与解析几何、三角函数、数列等一起进行综合考查.在考试要求的层次上更加突出向量的实际背景、几何意义、运算功能和应用价值.他一些实际问题.知识网络4.1 平面向量的概念及线性运算典例精析题型一向量的有关概念【例1】下列命题：①向量的长度与的长度相等；②向量a与向量b平行，则a与b的方向相同或相反；③两个有共同起点的单位向量，其终点必相同；④向量AB与向量是共线向量，则A、B、C、D必在同一直线上.其中真命题的序号是.【解析】①对；零向量与任一向量是平行向量，但零向量的方向任意，故②错；③显然错；AB与CD 是共线向量，则A、B、C、D可在同一直线上，也可共面但不在同一直线上，故④错.故是真命题的只有①.【点拨】正确理解向量的有关概念是解决本题的关键，注意到特殊情况，否定某个命题只要举出一个反例即可.【变式训练1】下列各式：a•；①|a|＝a②(a •b ) •c ＝a • (b •c )； ③OA －OB ＝BA ；④在任意四边形ABCD 中，M 为AD 的中点，N 为BC 的中点，则AB ＋DC ＝2MN ； ⑤a ＝(cos α，sin α)，b ＝(cos β，sin β)，且a 与b 不共线，则(a ＋b )⊥(a －b ). 其中正确的个数为( ) A.1B.2C.3D.4【解析】选D.| a |＝a a •正确；(a •b ) •c ≠a • (b •c )； OA －OB ＝BA 正确；如下图所示，MN =MD +DC +CN 且MN =MA +AB +BN ，两式相加可得2MN ＝AB ＋DC ，即命题④正确；因为a ，b 不共线，且|a|＝|b|＝1，所以a ＋b ，a －b 为菱形的两条对角线， 即得(a ＋b )⊥(a －b ). 所以命题①③④⑤正确.题型二 与向量线性运算有关的问题【例2】如图，ABCD 是平行四边形，AC 、BD 交于点O ，点M 在线段DO 上，且DM =DO 31，点N 在线段OC 上,且ON =OC 31,设AB =a , AD =b ,试用a 、b 表示AM ，AN ，MN .【解析】在▱ABCD 中，AC ，BD 交于点O ， 所以DO ＝12DB ＝12(AB －AD )＝12(a －b )，AO ＝OC ＝12AC ＝12(AB ＋AD )＝12(a ＋b ).又DM ＝13DO ， ON ＝13OC ，所以AM ＝AD ＋DM ＝b ＋13DO＝b ＋13×12(a －b )＝16a ＋56b ，AN ＝AO ＋ON ＝OC ＋13OC＝43OC ＝43×12(a ＋b )＝23(a ＋b ). 所以MN ＝AN －AM ＝23(a ＋b )－(16a ＋56b )＝12a －16b . 【点拨】向量的线性运算的一个重要作用就是可以将平面内任一向量由平面内两个不共线的向量表示，即平面向量基本定理的应用，在运用向量解决问题时，经常需要进行这样的变形.【变式训练2】O 是平面α上一点，A 、B 、C 是平面α上不共线的三点，平面α内的动点P 满足OP ＝OA ＋λ(AB ＋AC )，若λ＝12时，则PA •(PB ＋PC )的值为 .【解析】由已知得OP －OA ＝λ(AB ＋AC )，即AP ＝λ(AB ＋AC )，当λ＝12时，得AP ＝12(AB ＋AC )，所以2AP ＝AB ＋AC ，即AP －AB ＝AC －AP ， 所以BP ＝PC ，所以PB ＋PC ＝PB ＋BP ＝0，所以PA • (PB ＋PC )＝PA •0＝0，故填0. 题型三 向量共线问题【例3】 设两个非零向量a 与b 不共线.(1)若AB ＝a ＋b ， BC ＝2a ＋8b ， CD ＝3(a －b )， 求证：A ，B ，D 三点共线；(2)试确定实数k ，使k a ＋b 和a ＋k b 共线.【解析】(1)证明：因为AB ＝a ＋b ， BC ＝2a ＋8b ， CD ＝3(a －b )， 所以BD ＝BC ＋CD ＝2a ＋8b ＋3(a －b )＝5(a ＋b )＝5AB ， 所以AB ， BD 共线.又因为它们有公共点B ， 所以A ，B ，D 三点共线. (2)因为k a ＋b 和a ＋k b 共线， 所以存在实数λ，使k a ＋b ＝λ(a ＋k b )， 所以(k －λ)a ＝(λk －1)b .因为a 与b 是不共线的两个非零向量，所以k －λ＝λk －1＝0，所以k 2－1＝0，所以k ＝±1.【点拨】(1)向量共线的充要条件中，要注意当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，要注意待定系数法的运用和方程思想.(2)证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得出三点共线.【变式训练3】已知O 是正三角形BAC 内部一点，OA +2OB +3OC =0，则△OAC 的面积与△OAB 的面积之比是（） A.32 B.23C.2D.13【解析】如图，在三角形ABC 中， OA ＋2OB ＋3OC ＝0，整理可得OA ＋OC ＋2(OB ＋OC )＝0.令三角形ABC 中AC 边的中点为E ，BC 边的中点为F ，则点O 在点F 与点E 连线的13处，即OE ＝2OF .设三角形ABC 中AB 边上的高为h ，则S △OAC ＝S △OAE ＋S △OEC ＝12•OE • (h 2＋h 2)＝12OE ·h ，S △OAB ＝12AB •12h ＝14AB ·h ，由于AB ＝2EF ，OE ＝23EF ，所以AB ＝3OE ，所以S △OACS △OAB ＝h h AB OE ••4121＝23.故选B.总结提高1.向量共线也称向量平行，它与直线平行有区别，直线平行不包括共线(即重合)的情形，而向量平行则包括共线(即重合)的情形.2.判断两非零向量是否平行，实际上就是找出一个实数，使这个实数能够和其中一个向量把另外一个向量表示出来.3.当向量a 与b 共线同向时，|a ＋b |＝|a |＋|b |； 当向量a 与b 共线反向时，|a ＋b |＝||a |－|b ||； 当向量a 与b 不共线时，|a ＋b |＜|a|＋|b |.4.2 平面向量的基本定理及其坐标表示典例精析题型一 平面向量基本定理的应用【例1】如图▱ABCD 中,M ,N 分别是DC ，BC 中点.已知AM =a ,AN =b ,试用a ，b 表示AB ，AD 与AC 【解析】易知AM ＝AD ＋DM ＝AD ＋12AB ，AN ＝AB ＋BN ＝AB ＋12AD ，即⎪⎪⎩⎪⎪⎨⎧=+=+.21,21b a AD AB AB AD 所以AB ＝23(2b －a )， AD ＝23(2a －b ).所以AC ＝AB ＋AD ＝23(a ＋b ).【点拨】运用平面向量基本定理及线性运算，平面内任何向量都可以用基底来表示.此处方程思想的运用值得仔细领悟.【变式训练1】已知D 为△ABC 的边BC 上的中点，△ABC 所在平面内有一点P ，满足PA ＋BP ＋CP ＝0，则||AD PD 等于( ) A.13B.12C.1D.2【解析】由于D 为BC 边上的中点，因此由向量加法的平行四边形法则，易知PB ＋PC ＝2PD ，因此结合PA ＋BP ＋CP ＝0即得PA ＝2PD ，因此易得P ，A ，D 三点共线且D 是P A 的中点，所以||||AD PD ＝1，即选C.题型二 向量的坐标运算【例2】 已知a ＝(1，1)，b ＝(x ，1)，u ＝a ＋2b ，v ＝2a －b . (1)若u ＝3v ，求x ；(2)若u ∥v ，求x . 【解析】因为a ＝(1，1)，b ＝(x ，1)，所以u ＝(1，1)＋2(x ，1)＝(1，1)＋(2x ，2)＝(2x ＋1，3)， v ＝2(1，1)－(x ，1)＝(2－x ，1). (1)u ＝3v ⇔(2x ＋1，3)＝3(2－x ，1) ⇔(2x ＋1，3)＝(6－3x ，3)，所以2x ＋1＝6－3x ，解得x ＝1. (2)u ∥v ⇔(2x ＋1，3)＝λ(2－x ，1)⇔⎩⎨⎧=-=+λλ3),2(12x x⇔(2x ＋1)－3(2－x )＝0⇔x ＝1.【点拨】对用坐标表示的向量来说，向量相等即坐标相等，这一点在解题中很重要，应引起重视. 【变式训练2】已知向量a n ＝(cos n π7，sin n π7)(n ∈N *)，|b|＝1.则函数y ＝|a 1＋b|2＋|a 2＋b|2＋|a 3＋b|2＋…＋|a 141＋b|2的最大值为 .【解析】设b ＝(cos θ，sin θ)，所以y ＝|a 1＋b|2＋|a 2＋b|2＋|a 3＋b|2＋…＋|a 141＋b|2＝(a 1)2＋b 2＋2(cos π7，sin π7)(cos θ，sin θ)＋…＋(a 141)2＋b 2＋2(cos 141π7，sin 141π7)(cos θ，sin θ)＝282＋2cos(π7－θ)，所以y 的最大值为284.题型三 平行(共线)向量的坐标运算【例3】已知△ABC 的角A ，B ，C 所对的边分别是a ，b ，c ，设向量m ＝(a ，b )，n ＝(sin B ，sin A )，p ＝(b －2，a －2).(1)若m ∥n ，求证：△ABC 为等腰三角形； (2)若m ⊥p ，边长c ＝2，角C ＝π3，求△ABC 的面积.【解析】(1)证明：因为m ∥n ，所以a sin A ＝b sin B . 由正弦定理，得a 2＝b 2，即a ＝b .所以△ABC 为等腰三角形. (2)因为m ⊥p ，所以m ·p ＝0，即 a (b －2)＋b (a －2)＝0，所以a ＋b ＝ab .由余弦定理，得4＝a 2＋b 2－ab ＝(a ＋b )2－3ab ， 所以(ab )2－3ab －4＝0. 所以ab ＝4或ab ＝－1(舍去). 所以S △ABC ＝12ab sin C ＝12×4×32＝ 3.【点拨】设m ＝(x 1，y 1)，n ＝(x 2，y 2)，则 ①m ∥n ⇔x 1y 2＝x 2y 1；②m ⊥n ⇔x 1x 2＋y 1y 2＝0.【变式训练3】已知a ，b ，c 分别为△ABC 的三个内角A ，B ，C 的对边，向量m ＝(2cos C －1，－2)，n ＝(cos C ，cos C ＋1).若m ⊥n ，且a ＋b ＝10，则△ABC 周长的最小值为( )A.10－5 3B.10＋5 3C.10－2 3D.10＋2 3【解析】由m ⊥n 得2cos 2C －3cos C －2＝0，解得cos C ＝－12或cos C ＝2(舍去)，所以c 2＝a 2＋b 2－2ab cosC ＝a 2＋b 2＋ab ＝(a ＋b )2－ab ＝100－ab ，由10＝a ＋b ≥2ab ⇒ab ≤25，所以c 2≥75，即c ≥53，所以a ＋b ＋c ≥10＋53，当且仅当a ＝b ＝5时，等号成立.故选B.总结提高1.向量的坐标表示，实际是向量的代数表示，在引入向量的坐标表示后，即可使向量运算完全代数化，将数与形紧密地结合起来.向量方法是几何方法与代数方法的结合体，很多几何问题可转化为熟知的向量运算.2.向量的运算中要特别注意方程思想的运用.3.向量的运算分为向量形式与坐标形式.向量形式即平行四边形法则与三角形法则，坐标形式即代入向量的直角坐标.4.3 平面向量的数量积及向量的应用典例精析题型一 利用平面向量数量积解决模、夹角问题 【例1】 已知a ，b 夹角为120°，且|a |＝4，|b |＝2，求： (1)|a ＋b |；(2)(a ＋2b ) ·(a ＋b )； (3)a 与(a ＋b )的夹角θ.【解析】(1)(a ＋b )2＝a 2＋b 2＋2a ·b ＝16＋4－2×4×2×12＝12，所以|a ＋b |＝2 3.(2)(a ＋2b ) ·(a ＋b )＝a 2＋3a ·b ＋2b 2 ＝16－3×4×2×12＋2×4＝12.(3)a ·(a ＋b )＝a 2＋a ·b ＝16－4×2×12＝12.所以cos θ＝||||)(b a a b a a ++•＝124×23＝32，所以θ＝π6.【点拨】利用向量数量积的定义、性质、运算律可以解决向量的模、夹角等问题.【变式训练1】已知向量a ，b ，c 满足：|a|＝1，|b|＝2，c ＝a ＋b ，且c ⊥a ，则a 与b 的夹角大小是 . 【解析】由c ⊥a ⇒c ·a ＝0⇒a 2＋a ·b ＝0， 所以cos θ＝－12，所以θ＝120°.题型二 利用数量积来解决垂直与平行的问题【例2】 在△ABC 中，AB ＝(2，3)， AC ＝(1，k )，且△ABC 的一个内角为直角，求k 的值. 【解析】①当∠A ＝90°时，有AB ·AC ＝0， 所以2×1＋3·k ＝0，所以k ＝－23；②当∠B ＝90°时，有AB ·BC ＝0，又BC ＝AC －AB ＝(1－2，k －3)＝(－1，k －3)， 所以2×(－1)＋3×(k －3)＝0⇒k ＝113；③当∠C ＝90°时，有AC ·BC ＝0， 所以－1＋k ·(k －3)＝0， 所以k 2－3k －1＝0⇒k ＝3±132.所以k 的取值为－23，113或3±132.【点拨】因为哪个角是直角尚未确定，故必须分类讨论.在三角形中计算两向量的数量积，应注意方向及两向量的夹角.【变式训练2】△ABC 中，AB ＝4，BC ＝5，AC ＝6， 求AB ·BC ＋BC ·CA ＋CA ·AB .【解析】因为2AB ·BC ＋2BC ·CA ＋2CA ·AB＝(AB ·BC ＋CA ·AB )＋(CA ·AB ＋BC ·CA )＋(BC ·CA ＋BC ·AB ) ＝AB ·(BC ＋CA )＋CA ·(AB ＋BC )＋BC ·(CA ＋AB ) ＝AB ·BA ＋CA ·AC ＋BC ·CB ＝－42－62－52＝－77.所以AB ·BC ＋BC ·CA ＋CA ·AB ＝－772.题型三 平面向量的数量积的综合问题【例3】数轴Ox ，Oy 交于点O ，且∠xOy ＝π3，构成一个平面斜坐标系，e 1，e 2分别是与Ox ，Oy 同向的单位向量，设P 为坐标平面内一点，且OP ＝x e 1＋y e 2，则点P 的坐标为(x ，y )，已知Q (－1，2).(1)求|OQ |的值及OQ 与Ox 的夹角；(2)过点Q 的直线l ⊥OQ ，求l 的直线方程(在斜坐标系中). 【解析】(1)依题意知，e 1·e 2＝12，且OQ ＝－e 1＋2e 2，所以OQ 2＝(－e 1＋2e 2)2＝1＋4－4e 1·e 2＝3. 所以|OQ |＝ 3.又OQ ·e 1＝(－e 1＋2e 2) ·e 1＝－e 21＋2e 1•e 2＝0. 所以OQ ⊥e 1，即OQ 与Ox 成90°角. (2)设l 上动点P (x ，y )，即OP ＝x e 1＋y e 2， 又OQ ⊥l ，故OQ ⊥QP ，即[(x ＋1)e 1＋(y －2)e 2] ·(－e 1＋2e 2)＝0.所以－(x ＋1)＋(x ＋1)－(y －2) ·12＋2(y －2)＝0，所以y ＝2，即为所求直线l 的方程.【点拨】综合利用向量线性运算与数量积的运算，并且与不等式、函数、方程、三角函数、数列、解析几何等相交汇，体现以能力立意的命题原则是近年来高考的命题趋势.【变式训练3】在平面直角坐标系xOy 中，点A (5，0).对于某个正实数k ，存在函数f (x )＝ax 2(a ＞0)，使得OP ＝λ• (||OA OA ＋||OQ OQ)(λ为常数)，其中点P ，Q 的坐标分别为(1，f (1))，(k ，f (k ))，则k 的取值范围为( )A.(2，＋∞)B.(3，＋∞)C.(4，＋∞)D.(8，＋∞)【解析】如图所示，设||OA OA ＝OM ，||OQ OQ＝ON ，OM ＋ON ＝OG ，则OP ＝λOG .因为P (1，a )，Q (k ，ak 2)，OM ＝(1，0)，ON ＝(k k 2＋a 2k 4，ak 2k 2＋a 2k 4)，OG ＝(k k 2＋a 2k 4＋1，ak 2k 2＋a 2k 4)，则直线OG 的方程为y ＝ak 2k ＋k 2＋a 2k 4x ，又OP ＝λOG ，所以P (1，a )在直线OG 上，所以a ＝ak 2k ＋k 2＋a 2k 4，所以a 2＝1－2k.因为|OP|＝1＋a2＞1，所以1－2k＞0，所以k＞2. 故选A.总结提高1.本节是平面向量这一章的重要内容，要准确理解两个向量数量积的定义及几何意义，熟练掌握向量数量积的性质及运算律；数量积不满足结合律，即(a·b)·c≠a·(b·c)；数量积不满足消去律，即a·b ＝a·c推不出b＝c.2.通过向量的数量积，可以计算向量的长度，平面内两点间的距离，两个向量的夹角，判断两直线是否垂直.3.向量的线性运算、数量积运算是平面向量的最基本知识，在解决向量与不等式、函数、方程、数列、三角函数、解析几何等综合性问题时，往往要找到其内在的联系以获得正确的解题途径.。

第五章平面向量【知识网络】向量是沟通代数与几何的重要工具，它在日常生活、生产实践以及其他相关学科中有着广泛的应用．学习和理解向量有关知识时，建议：1.注意比较与分析．向量的有关概念与我们学习过的有关知识既有联系又有区别，如：平行、相等、乘积等等．留心比较分析，可防止学习过的有关知识对现学知识的负面影响．2.能画图时尽可能多画草图．数离形时少直观，形离数时欠入微．向量具有数与形的双重特征，加减法以三角形法则、平行四边形法则为背景，平行、垂直都对应着一个方程，数形结合考察问题，常常事半功倍．3.学会联想与化归．向量知识是从日常生活、生产实践中抽象出来的，求解向量综合题，常需要适当联想，并将应用问题数学化，复杂问题熟悉化、简单化．第29课 向量的基本运算【考点指津】1. 理解向量的概念，掌握向量的几何表示，了解共线向量、相等向量等概念．2．掌握向量的加法与减法，会正确运用三角形法则、平行四边形法则．3掌握向量加法的交换律、结合律，并会用它们进行向量化简与计算．4．理解向量的减法运算可以转化为向量的加法运算．【知识在线】1．（2a ＋8b ）－（4a －2b ）=2．在△ABC 中，BC → =a ， CA → =b ，则AB → =3．设a 表示向东3km ，b 表示向北偏东30º走3km ，则a ＋b 表示的意义为4．画出不共线的任意三个向量，作图验证a －b －c =a －（b ＋c ）．5．向量a 、b 满足|a |=8，|b |=10，求|a ＋b |的最大值、最小值．【讲练平台】例1 化简以下各式：①AB → +BC → +CA → ；②AB → －AC → ＋BD → －CD → ；③OA → －OD → ＋AD → ；④NQ → ＋QP → ＋MN → －MP → ．结果为０的个数为 （ ）Ａ．１ Ｂ．２ Ｃ．３ Ｄ．４分析 题设条件中多处涉及首尾相接的两个向量求和以及同起点的两个向量相减，对此，我们可以运用向量加减的定义进行合并，当最终形式出现两相反向量之和或相等向量之差时，结果为０．答 Ｄ．点评 本题巩固了向量加减的定义及向量加法的交换律、结合律等基础知识．求解时需将杂乱的向量运算式有序化处理，必要时也可化减为加，减低出错律．注意：AB → = －BA → ，+CB → =AB → ．变题 作图验证 A 1A 2→ ＋A 2A 3→ ＋A 3A 4→ ＋…＋A n －1A n → =A 1A n → （n ≥2，n ∈N ）．例2 如图，在ΔABC 中，D 、E 为边AB的两个三等分点，CA → =3a ，CB → =2b ，求CD → ，CE → ．分析 本题中的已知向量都集中体现在三角形中．为此，可充分利用向量加减法的三角形法则实施求解．如已知CA → 、CB → 可求AB → ，根据AD → 、AE → 、AB → 均为共线向量，故又可求得AD → 、DE → 、．由CA → 、AD → 又可求CD → ，由DE → 、CD → 又可求CE → ．解 AB → =AC → +CB → = －3a +2b ，因D 、E 为AB → 的两个三等分点， 故AD → =31AB → =－a ＋32b =DE → ， CD → =CA → ＋AD → =3a －a ＋32b =2a ＋32b ， CE → =CD → ＋DE → =2a ＋32b －a ＋32b=a ＋34b ． 点评 三角形中两边对应向量已知，可求第三边所对应的向量．值得注意的是，向量的方向不能搞错．当向量运算转化成基底向量的代数式运算时，其运算过程可仿照多项式的加减运算进行．例3 已知A 、B 、C 、P 为平面内四点，求证：A 、B 、C 三点在一条直线上的充要条件是存在一对实数m 、n ，使PC → =mPA → +nPB → ，且m+n=1．分析 A 、B 、C 三点共线的一个充要条件是存在 实数λ，使得AC → =λAB → ．很显然，题设条件中向量表达式并未涉及AC → 、AB → ，对此，我们不妨利用 PC → =PA → ＋AC → 来转化，以便进一步分析求证．证明 充分性，由PC → =mPA → ＋nPB → ， m ＋n=1， 得PA → ＋AC → =mPA → ＋n （PA → ＋AB → ）=（m ＋n ）PA → ＋nAB → =PA → ＋nAB → ，∴AC → =nAB → ．A B D E∴A 、B 、C 三点共线．必要性:由A 、B 、C 三点共线知，存在常数λ，使得AC → =λAB → ，即 AP → +PC → =λ（AP → +PB → ）．PC → =（λ－1）AP → ＋λPB → =（1－λ）PA → ＋λPB → ，m=1－λ，n=λ，m ＋n=1，PC → =mPA → ＋nPB → ．点评 逆向应用向量加法运算法则，使得本题的这种证法比其他证法更简便，值得一提的是，一个向量拆成两个向量的和，一定要强化目标意识．变题 在ΔABC 所在平面上有一点P ，满足PA → ＋PB → ＋PC → =AB → ，试确定点 P 的位置．答：P 在 AC 边上，且 P 为 AC 的一个三等分点（距 A 点较近）例4 （1）若点 O 是三角形ABC 的重心，求证：OA → ＋OB → ＋OC → =0；（2）若 O 为正方形ABCD 的中心，求证：OA → ＋OB → ＋OC → ＋OD → =0；（3）若O 为正五边形ABCDE 的中心，求证：OA → ＋OB → ＋OC → ＋OD → ＋OE → =0．若 O 为正n 边形A 1A 2A 3…A n 的中心，OA 1→ ＋OA 2→ ＋OA 3→ ＋…＋OA n → =0 还成立吗？说明理由．分析 本题四问构成一个题链，条件相似，结论相似，求证方法可望相似．正三角形、正方形性质特殊，我们十分熟悉，求证方法多，不容易发现那一种方更有利于推广，我们选定正五边形来研究．看着结论，联想一个相似的并且已经解决的问题，本课例1的变题A 1A 2→ ＋A 2A 3→ ＋A 3A 4→＋…＋A n －1A n → +A n A 1→ =0 ，这里的向量首尾相接，我们能不能将OA → 、OB → 、OC → 、OD → 、OE → 也转化成首尾相接的形式呢？运用向量相等的定义试试看．解 证（3）以 A 为起点作AB ′→ =OB → ，以 B ′为起点作B ′C ′→ =OC → ，以C ′为起点作C ′D ′→ =OD → ，以D ′为起点作D ′E ′→ =OE → ．∵∠AOB=72º，A BC D EB CD (E)O∴∠OAB ′=108º．同理∠AB ′C ′=∠B ′C ′D ′=∠C ′D ′E ′=108º，故∠D ′E ′A=108º．|OA → |=|AB ′→ |=∣B ′C ′→ |=|C ′D ′→ |=|D ′E ′→ |，故 E ′与 O 重合，OAB ′C ′D ′为正五边形．OA → ＋OB → ＋OC → ＋OD → ＋OE → =OA → ＋AB ′→ ＋B ′C ′→ ＋C ′D ′→ ＋D ′E ′→ =0．正三角形，正方形、正n 边形可类似获证．点评 本题不仅揭示了正多边形的一类共同性质，而且巩固了“以退为进”的数学思想．面对一般的问题，我们经常先考虑其特殊的情况；面对陌生的问题，经常去联想熟悉的模型．注意退是为了进，退到特殊简单情形后，要在求解中悟出一般的规律．如退到正方形情况，发现OA → ＋OB → 与OC → ＋OD → 正好互为相反向量，结论成立．这一方法却不具一般性．【知能集成】1． 基础知识：向量加减的代数形式运算与几何形式运算．2． 基本技能：向量运算中的合二为一与拆一为二．3． 基本思想：向量表达式运算与几何式运算的相互结合思想，联想熟悉的类似的模型，化归转化思想．【训练反馈】1．下列各式正确的是： （ ）A ．∣a －b ∣≤∣a ∣+∣b ∣B ． a +b ∣>∣a ∣+∣b ∣C ．∣a +b ∣>∣a －b ∣D ．∣ a －b ∣=∣a ∣－∣b ∣2．下面式子中不能化简成AD → 的是 （ ）A ．OC → －OA → ＋C D →B ．PB → －DA → －BP →C ．AB → －DC → ＋BC →D ．（AD → －BM → ）＋（BC → －MC → ）3．正方形ABCD 的边长为1，AB → =a ，BC → =b ，AC → =c ，则a ＋b ＋c 、a －b ＋c 、－a －b ＋ c 的摸分别等于 ．4．设a 、b 为已知向量，若3x ＋4y =a ，2x －3y =b ， 则 x = ．y= ．5． 已知 e 1、e 2 不共线，AB → =2e 1＋k e 2，CB → =e 1＋3e 2，C D → =2e 1－e 2，且A 、B 、D 三点在同一条直线上，求实数k ．6．在正六边形ABCDEF 中，O 为中心，若OA → =a ，OE → =b ，用a 、b 表示向量OB → ，OC → ，OD → ，结果分别为 （ ）A ．－b ，－b －a ，－aB ． b ，－a ，b －aC ．－b ，a ，a －bD ．－b ，－a ，a ＋b7． 试用向量方法证明：对角线互相平分的四边形是平行四边形．8．已知P 为△ABO 所在平面内的一点，满足OP →，则P 在 （ ） A ．∠AOB 的平分线所在直线上 B ． 线段AB 的中垂线上C ． AB 边所在的直线上D ． AB 边的中线上．9．设O 是平面正多边形A 1A 2A 3…A n 的中心，P为任意点，求证：PA 1→ ＋PA 2→ ＋PA 3→ ＋…＋PA n → =nPO → ．10．如图设O 为△ABC 内一点，PQ ∥BC ，且PQ → ∶BC → =2∶3， OA → =a ，OB → =b ，OC → =c ， 则 OP → ，OQ → ．11．P 为△ABC 所在平面内一点，PA → ＋PB → ＋PC → =0 ，则P 为△ABC 的 （ ）A ．重心B ．垂心C ． 内心D ．外心 12．在四边形ABCD 中，E 为AD 的中点，F 为BC 的中点．求证：EF → =21（AB → ＋DC → ）．第30课 向量的坐标运算【考点指津】1． 理解平面向量的坐标表示法，知道平面向量和一对有序实数一一对应．2． 掌握平面向量的和、差、实数与向量积的坐标运算，能利用向量的坐标运算解题．3． 掌握平面向量平行的充要条件的坐标表示，并利用它解决向量平行（共线）的有关问题，弄清向量平行和直线平行的区别．BAC O P Q【知识在线】1． 若向量a 的起点坐标为 （－2，1），终点坐标为（2，－1），则向量a 的坐标为2．若O 为坐标原点，向量a =（－3，4），则与a 共线的单位向量为3．已知a =（－1，2），b =（1，－2），则a ＋b 与a －b 的坐标分别为 （ ）A ．（0，0），（－2，4）B ．（0，0），（2，－4）C ．（－2，4），（2，－4）D ．（1，－1），（－3，3）4．若向量a =（x －2，3），与向量b =（1，y ＋2）相等，则 （ ）A. x=I ，y=3， B ． x=3，y=1C ． x=1，y=－5D ． x=5，y=－15．已知A （0，0），B （3，1），C （4，3），D （1，2），M 、N 分别为DC 、AB 的中点．（1） 求证四边形ABCD 为平行四边形；（2） 试判断AM → 、CN → 是否共线？为什么？【讲练平台】例1 已知a =（1，2），b =（－3，2），当k 为何值时，k a +b 与a －3b 平行？分析 已知a 、b 的坐标，可求a －3b 的坐标，k a ＋b 的坐标也可用含k 的表达式表示．运用两向量平行的充要条件x 1y 2－x 2y 1=0可求k 值．解 由已知a =（1，2），b =（－3，2）， 得a －3b =（10，－4）， k a ＋b =（k －3，2k ＋2）．因（k a ＋b ）∥（a －3b ），故10（2k ＋2）＋4（k －3）=0．得k=－31． 点评 坐标形式给出的两个向量，其横坐标之和即为和向量的横坐标；其纵坐标之和即为和向量的纵坐标．实数与向量的积其横、纵坐标分别等于实数与该向量的横、纵坐标的积．向量的平行用坐标形式表达即为一个方程．例2 已知向量a =（21，23），b =（－1，2），c =（2，－4）．求向量d ，使2a ，－b ＋21c 及4（c －a ）与d 四个向量适当平移后，能形成一个顺次首尾相接的封闭向量链．分析 四个向量适当平移后，形成一个顺次首尾相接的封闭向量链，说明这四个向量之和为0．即四个向量的纵横坐标之和均为0．据此列出关于向量d （x ，y ）的方程组，不难求得x 、y ．简解 设向量d 的坐标为（x ，y ），由2a ＋（－b ＋21c ）＋4（c －a ）＋d =0， 可解得d =（－9，23）．点评 数学语言常有多种表达方式，学会转化与变通是求解的关键．本题以几何特征语言形式出现，最终落足点要变式成方程的语言来求解，这一思想方法在求解向量问题时经常用到．例3 已知平面上三点P （2，1），Q （3，－1），R （－1，3）．若点S 与这三点可以为一个平行四边形的四个顶点，求S 的坐标．分析 平行四边形对边对应向量相等或相反，由此可求得S 点的坐标．但由于题设四点构成四边形的四个顶点，那一组边是对边不明显，需要分类讨论．简解 设S 的坐标为（x ，y ）．（1）当PQ → 与RS → 是一组对边时，若PQ → =RS → ，则（3，－1）－（2，1）=（x ＋1，y －3），即 （1，－2）=（x ＋1，y －3），得S 点坐标为（0，1）．若PQ → =SR → ，则S 点坐标为（－2，5）．（2）当PR → 与SQ → 是一组对边时，若PR → =SQ → ，则S 点的坐标为（6，－3）．若PR → =QS → ，则S 点的坐标为（0，1）．（3）当PS → 与RQ → 是一组对边时，若PS → =RQ → ，则S 点的坐标为（6，－3）．若PS → =QR → ，则S 点的坐标为（－2，5）．综上所述，S 点坐标可以为（0，1），（6，－3），（－2，5）．点评 本题求解需运用分类讨论思想．上述解法思路自然、条理清晰，但很显然不是最简方案，如何数形结合，避免重复劳动，读者不妨思考．例4 向量PA → =（k ，12），PB → =（4，5），PC → =（10，k ），当k 为何值时，A 、B 、C 三点共线．分析 三点共线问题前一课已涉及，A 、B 、C 三点共线的充要条件是AB → =λBC → ，本题所不同的是向量用坐标形式给出，对此，我们可以将坐标代入运算．解 AB → =PB → －PA → =（4－k ，－7），BC → = PC → －PB → =（6，k －5）．当A 、B 、C 三点共线时，存在实数λ，使得AB → =λBC → ，将坐标代入，得4－k=6λ，且 －7=λ（k －5），故（4－k ）（k －5）=－42．解得k=11，或k=－2．点评 向量的几何运算与向量的坐标运算，可以从不同角度去求解（证）同一个问题．只不过两套工具各有适用范围，即便两套工具都适用，也可能繁简不一，应用时要注意前瞻性选择．变题 求证：互不重合的三点A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）共线的充要条件是（x 2－x 1）（y 3－y 1）=（x 3－x 1）（y 2－y 1）．证明 必要性（略）．充分性 若（x 2－x 1）（y 3－y 1）=（x 3－x 1）（y 2－y 1），由A 、B 、C 互不重合，得（x 2－x 1）、（y 3－y 1）、（x 3－x 1）、（y 2－y 1）中至少有一个不为零，不妨设x 3－x 1≠0．令x 2－x 1=λ（x 3－x 1），若λ=0，则x 2－x 1=0，此时y 2≠y 1（否则A 、B 重合）．而已知等式不成立，故λ≠0．于是（x 3－x 1）（y 2－y 1）=λ（x 3－x 1）（y 3－y 1）．因x 3－x 1≠0 ，故 （y 2－y 1）=λ（y 3－y 1）．于是（x 2－x 1，y 2－y 1）=λ（x 3－x 1，y 3－y 1），即 AB → =λAC → ，且AC → ≠0 ．又因AB → 与AC → 有相同起点，所以A 、B 、C 三点共线．【知能集成】基础知识：坐标形式的向量的加减运算，实数与向量坐标的积．基本技能：向量平行的充要条件及向量相等的充要条件用坐标形式描述和应用．基本思想：将向量等式转化成方程的思想；对几何图形的分类讨论思想．【训练反馈】1．若a =（2，3），b =（4，y －1），且a ∥b ，则y= （ ）A ．6B ．5C ．7D ． 82．已知点B 的坐标为（m ，n ），AB → 的坐标为（i ，j ），则点A 的坐标为 （ ）A ．（m －i ，n －j ）B ．（i －m ，j －n ）C ．（m ＋i ，n ＋j ）D ．（m ＋n ，i ＋j ）3．若A （－1，－1），B （1，3），C （x ，5）三点共线，则x= ．4．已知a =（5，4），b =（3，2），则与2a －3b 平行的单位向量为5．有下列说法① 已知向量PA → =（x ，y ），则A 点坐标为（x ，y ）；② 位置不同的向量，其坐标有可能相同；③ 已知i =（1，0），j =（0，1），a =（3，4），a =3i －4j ；④ 设a =（m ，n ），b =（p ，q ），则a =b 的充要条件为m=p ，且n=q ．其中正确的说法是 （ ）A ．①③B ．①④C ．②③D ．②④6．下列各向量组中，不能作为表示平面内所有向量的基底的一组是 （ ）A ．a =（－1，2），b =（0，5）B ．a =（1，2），b =（2，1）C ．a =（2，－1）b =（3，4）D ．a =（－2，1），b =（4，－2）7．设a =（－1，2），b =（－1，1），c =（3，－2），用a 、b 作基底，可将向量c 表示为c =p a＋q b ，则 （ ）A ．p=4， q=1B ．p=1， q=－4C ．p=0 ， q=4D ．p=1， q=48．设i =（1，0），j =（0，1），在平行四边形ABCD 中，AC → =4i ＋2j ，BD → =2i ＋6j ，则AB → 的坐标为 ．9．已知3sin β=sin （2α＋β），α≠k π＋2 ，β≠k π，k ∈z ，a =（2，tan （α+β）），b =（1，tan α），求证：a ∥b ．10．已知A （4，0），B （4，4），C （2，6），求AC 与OB 的交点P 的坐标（x ，y ）．11．已知点O （0，0），A （1，2），B （4，5），且OP → =OA → ＋tAB → ．（1） 当t 变化时，点P 是否在一条定直线上运动？（2） 当t 取何值时，点P 在y 轴上？（3） OABP 能否成为平行四边形？若能求出相应的t 值；若不能，请说明理由．第31课 平面向量的数量积【考点指津】1． 掌握平面向量的数量积及其几何意义．2． 了解用平面向量的数量积可以处理有关长度、角度和垂直的问题．3． 掌握向量垂直的条件．【知识在线】1．若∣a ∣=4，∣b ∣=3，a ·b =－6，则a 与b 的夹角等于 （ ）A ．150ºB 120ºC ．60ºD ．30 º2．若a =（－2，1），b =（1，3），则2a 2－a ·b = （ ）A ，15B ．11．C ．9D ．63．已知向量 i =（1，0），j =（0，1），则与向量2i ＋j 垂直的一个向量为 （ ）A ． 2i －jB ． i －2jC ． i ＋jD ． i －j4．已知a =（1，2），b =（1，1），c =b －k a ，且c ⊥a ，则C 点坐标为5．已知∣a ∣=3，∣b ∣=4，且a 与b 夹角为60º，∣k a －2b ∣=13，求k 的值【讲练平台】例1 （1）在直角三角形ABC 中，∠C=90º，AB=5，AC=4，求AB → ·BC →（2）若a =（3，－4），b =（2，1），试求（a －2b ）·（2a ＋3b ）分析 （1）中两向量AB → 、BC → 的模及夹角容易求得，故可用公式a ·b =|a ||b |cos θ求解．（2）中向量a 、b 坐标已知，可求a 2、b 2、a ·b ，也可求a －2b 与2a ＋3b 的坐标，进而用（x 1，y 1）·（x 2，y 2）=x 1x 2＋y 1y 2求解．解（1） 在△ABC 中，∠C=90º，AB=5，AC=4，故BC=3，且cos ∠ABC=53，AB → 与BC → 的夹角θ=π－∠ABC ， ∴AB → ·BC → =－∣AB → ∣∣BC → ∣cos ∠ABC=－5×3×53=－9．（2）解法一 a －2b =（3，－4）－2（2，1）=（－1，－6），2a －3b =2（3，－4）＋3（2，1）=（12，－5），（a －2b ）·（2a ＋3b ）=（－1）×12＋（－6）×（－5）=18．解法二 （a －2b ）·（2a ＋3b ）=2a 2－a ·b －6b 2=2[32＋（－4）2]－[3×2＋（－4）×1]－6（22＋12）=18．点评 向量的数量积有两种计算方法，一是依据模与夹角来计算，二是依据坐标来计算．具体应用时可根据已知条件的特征来选择．值得注意的是，向量的夹角与向量的方向相关，（1）中∠ABC 并非AB → 与BC → 的夹角．从第（2）问的解法二可以看到，向量数量积的运算律，类似于多项式乘法法则，但并不是所有乘法法则都可以推广到向量数量积的运算．如：a ·（b ＋c ）=a ·b ＋b ·c ，而（a ·b ）c ≠a （b ·c ）．例2．已知O 为三角形ABC 所在平面内一点，且满足OA 2+BC 2=OB 2+CA 2，试用向量方法证明AB ⊥OC ．分析 要证AB → ⊥OC → ，即证AB → ·OC → =0，题设中不涉及AB → ，我们用AB → =AO → +OB → 代换，于是只需证AO → ·OC → =BO → ·OC → ．至此，我们可以尝试将已知等式转化成只含有OA → 、OB → 、OC → 的形式．证明 由已知得OA → 2+BC → 2=OB → 2+CA → 2，即OA → 2+（BO → +OC → ）2=OB → 2+（CO → +OA → ）2，整理得AO → ·OC → =BO → ·OC → ，即 OC → ·（BO → +OA → ）=0，故 OC → ·AB → =0．所以 AB → ⊥OC → ．点评 用向量方法证明垂直问题，通常转化为证两个向量的数量积为0．本题已知式与求证式中向量的表达形式不统一，针对差异进行有目标的化归，是求解的关键所在．例3．设OA → =a =（3＋1，3－1），OB → =b =（3，3），试求∠AOB 及ΔAOB 的面积．分析 已知a 、b 可以求|a |、|b |及a ·b ，进而求得∠AOB （即a 与b 的夹角），在求到三角形的两边及夹角后，可用公式：S=21∣a ∣∣b ∣sin θ求面积． 解 设∠AOB=θ，ΔAOB 的面积为S ，由已知得：∣OA → ∣=∣a ∣=22)13()13(-++=22，∣OB → ∣=∣b ∣=23，∴cos θ=b a b a •=()()3222313313⋅-++=22．∴θ=4π． 又S=21∣a ∣∣b ∣sin θ=21·222322••=23， 即∠AOB=4π，ΔAOB 的面积为23． 点评 向量的数量积公式a ·b =∣a ∣∣b ∣cos θ不仅可以用来求数量积，也可以用来求模与夹角．要注意该公式与三角形的面积公式的区别．此外，本题的解题方法可适用于更一般的情况（见变题）．变题 设ΔABC 的面积为S ，AB → =a ，AC → =b ，求证S=21()()22b a b a •-•例4．已知a 与b 都是非零向量，且a +3b 与7a -5b 垂直，a -4b 与7a -2b 垂直，求a 与b 的夹角．分析 要求夹角θ，必需求出cos θ；求cos θ需求出a ·b 与∣a ∣∣b ∣的比值（不一定要求出∣a ∣、∣b ∣的具体值）．由已知的两个向量的垂直关系，可以得到∣a ∣∣b ∣与a ·b 的关系．解 ∵（a +3b ）⊥（7a -5b ），（a -4b ）⊥（7a -2b ），∴ （a +3b ）·（7a -5b ）=0，（a-4b ）·（7a -2b ）=0．即 7a 2+16a ·b -15b 2=0，7a 2-30a ·b +8b 2=0．两式相减，得 b 2=2a ·b ．故 a 2=b 2 ， 即 ∣a ∣=∣b ∣．∴cos θ=b a b a •=21222=b b ． ∴θ=60º ， a 与b 的夹角为60º ．点评 从基本量思想考虑，似乎没有具体的a 与b ，无法求出a 与b 的夹角，其实不然，cos θ是一个a ·b 与∣a ∣∣b ∣的比值，并不需要具体分别求出．类似于本题的条件表明，向量的数量积公式、向量的垂直关系都揭示了一种数量积与模的关系，就此意义而言，它们的本质是一致的相通的，可以相互转化和利用．在本题求解过程中注意，b 2=2a ·b 不能得出b =2a ，同样a 2=b 2也不能得到a =±b ．【知能集成】基础知识：向量数量积的两种计算公式，向量垂直的充要条件．基本技能：求向量数量积、模及向量的夹角，向量垂直问题的论证与求解．基本思想：向量表达式的数量积与多项式乘法进行类比的思想，将线的垂直这一图形特征转化成方程解决的思想．求向量夹角时的设而不求的思想．【训练反馈】1． 已知a =5，a 与b 的夹角的正切值为43，a ·b =12，则b 的模为（ ） A ．4 B ．3 C ．31 D ．512 2．已知a =2，向量a 在单位向量e 方向上的投影为－3，则向量a 与e 向量的夹角为（ ）A ．30ºB ．60ºC ．120ºD ．150º3．已知a =（1，－2），b =（5，8），c =（2，3），则a ·（b ·c ）为 （ ）A ．34B ．（34，－68）C ．－68D ．（－34，68）4．边长为2的正三角形ABC 中，设AB → =c ，BC → =a ，CA → =b ，则a ·b ＋b ·c ＋c ·a 等于（ ）A ． －3B ． 0C ． 1D ． 35．已知a =（1，2），b =（x ，1），当（a ＋2b ）⊥（2a －b ）时，实数x 的值为 ．6．已知m =（－5，3），n =（－1，2），当（λm ＋n ）⊥（2n ＋m ）时，实数λ的值为 ．7．已知|a |=|b |=1，a 与b 夹角为90º，c =2a ＋3b ，d =k a －4b ，且c ⊥d ，则k=8．已知A 、B 、C 、D 是平面上给定的四个点，则AB → ·CD → ＋AC → ·DB → ＋AD → ·BC → = ．9．已知a ＋b =（2，－8），a －b =（－8，16），则a 与b 夹角的余弦值为 ．10．设两向量e 1、e 2满足| e 1|=2，| e 2|=1， e 1、e 2的夹角为60º，若向量2t e 1＋7e 2与向量e 1＋t e 2的夹角为钝角，求实数t 的取值范围．11．设向量a =（cos23º，cos67º），b =（cos68º，cos32º），u =a ＋t b (t ∈R)．（1） 求a ·b ；（2） 求u 的模的最小值．12．设a =（1＋cos α，sin α）， b =（1－cos β，sin β）， c =（1，0）， α∈（0，π），β∈（π，2π），a 与c 的夹角为θ1，b 与c 的夹角为θ2，且θ1－θ2=6π，求sin 4βα-的值．第32课 线段的定比分点、平移【考点指津】1． 掌握线段的定比分点和中点坐标公式，并且熟练运用．2． 掌握平移公式，并能运用平移公式化简函数解析式．3． 理解公式的推导过程，必要时能回到定义去，用向量运算的相关知识，解决定比分点问题和平移问题．【知识在线】1．若P 分AB → 所成的比为43，则A 分BP → 的比为 （ ） A ．73 B ．－73 C ．－37 D ．37 2．设点P 在线段AB 的延长线上，P 分AB → 所成的比为λ，则 （ ）A ．λ＜－1B ．－1＜λ＜0C ．0＜λ＜1D ．λ＞13．按向量a 将点（2，3）平移到（0，1），则按向量a 将点（7，1）平移到点 （ ）A ．（9，－3）B ．（9，3）C ．（5，－1）D ．（－5，－3）4．若函数y=f （1－2x ）的图象，按向量a 平移后，得到函数y=f （－2x ）的图象，则向量a = ．5．设三个向量OA → =（－1，2），OB → =（2，－4），OC → 的终点在同一条直线上（O 为坐标原点）．（1） 若点C 内分AB → 所成的比为23，求C 点坐标； （2） 若点C 外分AB → 所成的比为－23，求C 点坐标． 【讲练平台】例1 已知P （1，1），A （2，3），B （8，－3），且C 、D 顺次为AB 的三等分点（C 靠近A ），求PC → 和PD → 的坐标．分析 已知A 、B 两点坐标，可求AB 的两个三等分点C 、D 的坐标，进而结合已知P 点坐标，可求PC → ，PD → ．解 解法一 由题知，点C 、D 分AB 所成的比分别为λ1=21，λ2=2 ，设C （x ，y ），则()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+-•+==+•+=.12113213,42118212y x 即C （4，1），同理可得D （6，－1）．故PC=（4，1）－（1，1）=（3，0），PD=（6，－1）－（1，1）=（5，－2）．解法二 因A 、B 、C 、D 四点共线，由已知得 31=，AD → =23 AB → ， 故PC → =PA → ＋AC → =（2－1，3－1）＋31（8－2，－3－3）=（3，0）， PD → =PA → ＋AD → =（2－1，3－1）＋23 （8－2，－3－3）=（5，－2）．点评 定比分点公式涉及起点坐标、终点坐标、分点坐标、定比七个量，它们之间固有的联系有两个方程，故已知其中五个量能求其余两个量，若是只考察其中一个方程（如横坐标关系式），只须已知其中三个，可求第四个．对此，我们不仅要考察公式的原形，还需掌握公式的变形．本题的解法二，回归到最基础的向量加减来处理定比分点问题，运算量小，出错率低． 例2 将函数123--=x x y 的图象按向量a 平移后得到函数xk y =的图形，求a 和实数k ． 分析 平移前后的函数表达式已知，可以通过恒等变形，求得整体结构一致，再比较变量x 、y 的变化，确定平移公式，得向量a ，而k 则可通过比较系数法求得．解 212145123+--=--=x x x y 令 x ′ = x －21， y ′=y －21． 原函数解析式变形为y ′=－x '45， ∴ a =（－,21－21）， k=－45． 点评 图形的平移变换，实质是图形上任意一点的变换，求解平移变换问题至关重要的是确定关于点的坐标的平移公式．面对较为复杂的函数表达式，为了画出其图形，并讨论其性质，常采纳平移变换化繁为简．变题 通过平移变换，化简dcx b ax y ++= （ad －bc ≠o ， c ≠o ），并作出图形． 提示：d cx b ax y ++==()c a cd x ad bc c ++-21， 令 ⎪⎩⎪⎨⎧-='+='c a y y c d x x 并记()ad bc c-21=k ≠0， 则原方程化简为x k y '='． 因此，原函数的图象按向量a =⎪⎭⎫ ⎝⎛-c a c d ,平移后得x k y '='的图象，故其图象是以⎪⎭⎫ ⎝⎛-c a c d ,为中心的，以x=c a y c d =-,为渐近线的双曲线． 例3．将函数1372sin 2+⎪⎭⎫ ⎝⎛-=πx y 的图象，按向量a 平移后得到的函数图象关于原点对称．这样的向量是否唯一？若唯一，求出向量a ；若不唯一，求a 模的最小值．分析 正弦函数是周期函数，其图象关于原点对称时，表达式不唯一．就本题而言，平移后的函数解析式可以是y=2sin2x ， 也可以是y=2sin （2x ＋π），y=2sin （2x －π）等等．因此，向量a 不唯一．要求∣a ∣的最小值，首先必需确定平移后函数表达式的一般式，并在此基础上建立关于∣a ∣的目标函数．解 向量a 不唯一．平移后的图象对应解析式可以为y=2sin （2x ＋k π）， k ∈Z 考察原函数表达式1372sin 2+⎪⎭⎫ ⎝⎛-=πx y ， 可令⎪⎩⎪⎨⎧-='-=+'1672y y x k x ππ （k ∈Z ）即 ⎪⎩⎪⎨⎧-='--='1267y y k x x ππ，∴ a =（－267ππk -，－1）， ( k ∈Z)， | a |()221267-+⎪⎭⎫ ⎝⎛--=ππk （k ∈Z ）． ∴ 当k=2 时，∣a ∣取最小值，最小值为3612π+ ．点评 常见向量平移变换应用于三角函数式化简，多数问题思路单一，结论唯一．本题突破常规，开放性的设计，要求解题者具有更深刻的思维能力．例4． 设A （1，1），B （5，5），且P 在直线AB 上，若AB → =λAP → ，AP → =λPB → ，P 点是否可能落在线段AB 的延长线上 ？若能，求出P 点坐标；若不能；说明理由．分析 由AB → =λAP → 知，要使P 落在线段AB 的延长线上，只需λ∈（0，1）．为此，我们设法将两个已知向量等式转化成关于λ的方程，解出λ，检验λ∈（0，1）是否成立．解 AB → =（5，5）－（1，1）=（4，4），设P （x ，y ），则AB → =λAP → =λ2 PB → ．（4，4）=λ2（5－x ，5－y ）=λ（x －1，y －1），⎩⎨⎧=-=-45452222y x λλλλ 且()()⎩⎨⎧-=-=1414y x λλ 依据两个方程组的第一个方程，消去x ，得5λ2－λ（4＋λ）=4，即λ2－λ－1=0，∴ λ=251±． 数形结合知，在AB → =λAP → 时，要P 落在线段AB 的延长线上，则需λ∈（0，1），所求两个λ的值均不符合题意，故P 不可能落在AB 延长线上．【知能集成】基础知识：向量的平移公式，定比分点定义、公式及中点坐标公式．基本技能：求平移公式，求点关于向量平移后的坐标，求函数图象关于向量平移后对应的函数解析式．运用定比分点公式，求端点、分点坐标及定比．基本思想：①回到定义去，回避定比分点公式的繁琐运算．②用基本量思想看定比分点公式．③运用整体分析、比较观点，确定平移公式．【训练反馈】1．点（4，3）关于点（5，－3）的对称点坐标是 （ ）A ．（4，－3）B ．（6，－9）C ．（29，0） D ．（ 12 ，3） 2．点A （0，m ）按向量a 平移后得到点B （m ，0），则向量a 的坐标是 （ ）A ．（m ， m ）B ．（m ， －m ）C ．（－m ， m ）D ．（－m ， －m ）3． 按向量a 可把点（2，0）平移到点（－1，2），则点（－1，2）按向量a 平移后得到的点是（ ）A ．（2，0）B ．（－3，2）C ．（2，4）D ．（－4，4）4．将函数462sin 3+⎪⎭⎫ ⎝⎛--=πx y 的图象，按向量a 平移后得到的图象对应函数y=f （x ）是奇函数，则a 可以是 （ ）A ． （－6π，－4）B ． （－12π，4）C ． （6π，4） D ． （－12π，－4） 5．已知点P （2，3），分P 1P 2所成的比为2，且点P 2（1，2），则点P 1的坐标为（ ）A ．（4，5）B ．（0，1）C ．（3，4）D ．（5，6）6．将函数y=x 2＋mx ＋n 图象的顶点P 按向量a 平移到原点O ，则a = ．7． 函数 的图象按向量a =（2，1）平移后得到函数xy 1=的图象． 8．已知A （2，2），B （－3，4），C （4，－1），则ΔABC 的重心坐标为 ．9．若∣P 1P 2∣=5 cm ，点P 在线段P 1P 2的反向延长线上，且∣P 1P ∣=1 cm ，则P 分P 1P 2所成的比为 ．10． 已知O 为原点，m ∈R 且m ≠0，OA=（m ，2m ），OB=（2，2），求点B 关于直线OA 的对称点C 的坐标．11． 已知关于x 的一次函数y=ax+b 的图象C 按向量p =（1，2）平移后，得到的图象仍然是C ，问这样的一次函数是否唯一？若唯一，求出该函数的解析式；若不唯一，说明这类函数的表达式的共同特征．12．已知A 、B 、C 三点在一条直线上，且OA → －3OB → ＋2OC → =0 ，求点A 分BC → 所成的比λ．第33课 平面向量的应用【考点指津】1． 在阅读、理解具有实际意义的文字材料的基础上，能准确、清晰、有条理地用向量的语言表述问题．2． 能从实际问题中提炼、概括抽象出数学模型．3． 能综合运用所学向量知识及有关数学思想方法，求出数学模型的解．4． 能结合实际意义，正确表述问题的解．5． 能用向量知识简捷地处理其它数学分支相关问题．【知识在线】1．下列各个量：①物体的位移；②汽车的速度；③物体的质量；④某液体的温度．其中能称为向量的有 ．2．已知三个力F 1=（1，3），F 2（－2，1），F 3=（x ，y ），某物体在这三个力的同时作用下保持平衡，则力F 3= ．3．设某人向东走3 km 后，又改变方向向北偏东30º走3 km ，该人行走的路程是 ，他的位移是 ．4．用向量方法证明勾股定理．5．一条东西方向的河流，水流速度为2 km/h ，方向正东．一船从南岸出发，向北岸横渡，船速为4 km/h ，试求船的实际航行速度，并画出图形（角度可用反三角函数表示）．【讲练平台】例1 某一天，一船从南岸出发，向北岸横渡．根据测量，这一天水流速度3km/h ， 方向正东，风向北偏西30º，受风力影响，静水中船的飘行速度大小也为3 km/h ，若要使该船由南向北沿垂直于河岸的方向以2 3 km/h ．的速度横渡，求船本身的速度大小及方向．VV 2 V 1分析 撇开题设情境，提炼出四个速度，即水流速度v 1，风的速度v 2，船本身的速度v 3，船的实际航行速度v ，并且有v 1＋v 2＋v 2=v ，在这一等式中，v 1、v 2、v 已知，v 3可求．略解：设水的速度为v 1 ，风的速度v 2，v 1＋v 2=a ，易求得a 的方向是北偏东 30º，a 的大小为 3 km/h ．设船的实际航行速度v ，方向南向北，大小 2 3 km/h ．．船本身的速度v 3，则a +v 3=v ，即 v 3=v -a ， 数形结合知，v 3方向是北偏西60º，大小为 3 km/h ．．点评 这是一个与“知识在线”第5题相似的问题，熟悉的情境以及简单情况下的解题经验为本题求解奠定了基础．四种速度融为一体，我们采纳分步合成，步步为营的策略．每一次合成只相当于求解了一个简单题．例2 已知O 为ΔABC 所在平面内一点，满足|OA → |2＋| BC → |2=|CA →|2＋|OB →|2=|OC →|2＋|AB →|2．试证明O 是ΔABC 的垂心．分析 已知等式是关于线段长度平方和的等式，OA → 与BC → 、OB →与CA →、OC →与AB → 都不是同一个直角三角形中的线段，用纯平面几何知识证明相当困难．但线段长度平方和即向量模的平方，要证O 是ΔABC 的垂心，只需证得OA → ⊥BC → ，OB →⊥CA →，联想向量的数量积，只需证OA → ·BC → =OB →·CA →=0．|OA → |2＋| BC → |2=|CA →|2＋|OB →|2 ，得a 2＋（c －b ）2=b 2＋（a －c ）2 ， c ·b =a ·c ，即（b －a ）·c =0．OC →·AB →=0， 故 AB →⊥OC →．同理 CA →⊥OB →，BC → ⊥OA → ．故O 是ΔABC 的垂心．点评 向量知识的应用领域很宽泛，中学数学所涉及的平几、立几、解几、函数、方程、数列、不等式等等，都可以与向量综合，求解这类问题的关键在于揭去伪装，合理转化．例3．如图所示，对于同一高度（足够高）的两个定滑轮A 、B ，用一条足够长的绳子跨过它们，并在两端分别挂有质量为m 1和m 2的物体（m 1≠m 2），另在两滑轮中间的一段绳子的O 点处悬挂质量为m 的另一物体，已知m 1∶m 2=OB ∶OA，且系统保持平衡（滑轮半径、绳子质量均忽略不计）．求证：（1） ∠AOB 为定值；（2） 212m m m ＞2． 分析 依据题意，我们可以作出物体的受力图，引用平衡条件可列出方程组，在方程组的变形中，探索∠AOB 的大小，在求出∠AOB 后，再向第2问结论努力．解（1）设两绳子AO 、BO 对物体m 的拉力分别为F 1、F 2，物体m 向下的重力为F ，由系统平衡条件知F 1+F 2+F =0．如图，设∠BAO=α，∠ABO=β，根据平行四边形法则，得F 2cos β+F 1cos （π－α）=0，F 2sin β+F 1sin （π－α）＋F=0．即 m 2cos β－m1 cos α=0 ， ①m 2sin β＋m 1 sin α=m ． ②在ΔAOB 中，由正弦定理，得OB ∶OA= sin α∶sin β，将m 1∶m 2= sin α∶sin β代入①，得sin βcos β= sin αcos α，即sin2β= sin2α．∵m 1≠m 2 ，∴OA ≠OB ． ∴α≠β，2α＋2β=180º．∴α＋β=90º， 即∠AOB=90º．（２）由α＋β=90º，得 cos βcos α＝sin βsin α．将①②平方相加，得m 2=m 12＋m 22 ．由m 2－2m 1m 2=m 12＋m 22－2m 1m 2=（m 1－m 2）2>0 ，得m 2>2m 1m 2． ∴ 212m m m ＞2． 点评 向量在物理中的应用最常见的是力学问题，物体处于平衡状态即所受各力的合力为０，亦即向量之和为零向量，运用三角形法则、平行四边形法则及解斜三角形的基础知识可望得到问题的解．本题所列方程组，是根据物体水平方向、竖直方向所受各力的合力分。

平面向量知识点整理1、概念（1）向量：既有大小，又有方向的量．数量：只有大小，没有方向的量．有向线段的三要素：起点、方向、长度．（2）单位向量：长度等于1个单位的向量．（3）平行向量（共线向量）：方向相同或相反的非零向量．零向量与任一向量平行．提醒：①相等向量一定是共线向量，但共线向量不一定相等；②两个向量平行与两条直线平行是不同的两个概念：两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合；③平行向量无传递性！（因为有零向量 )④三点 A、 B、 C共线AB、AC 共线（4）相等向量：长度相等且方向相同的向量．（5）相反向量：长度相等方向相反的向量。

a 的相反向量是 -a（6）向量表示：几何表示法AB ；字母a表示；坐标表示：a＝ｘｉ＋ｙj＝（ｘ，ｙ）.uuur r uuur的长度叫做向量r r（7）向量的模：设OA a ，则有向线段OA a 的长度或模，记作：| a | .rx2 r 2 rx2 y2。

）（ | a | y2 , a | a |2（8）零向量：长度为0 的向量。

a＝O ｜ a｜＝O.r r r r【例题】 1.下列命题：（ 1）若a b ，则a b 。

（2）两个向量相等的充要条件是uuur uuur它们的起点相同，终点相同。

（3）若AB DC ，则 ABCD 是平行四边形。

（4）若uuur uuur r r r r r r r r r r ABCD 是平行四边形，则 AB DC 。

（5）若 a b,b c ，则 a c 。

（6）若 a // b,b// c ，r r则 a // c 。

其中正确的是_______r r uur r （答：（4）（5））2. 已知 a, b 均为单位向量，它们的夹角为60o，那么 | a 3b | ＝_____（答：13 ）；2、向量加法运算：⑴三角形法则的特点：首尾相连．⑵平行四边形法则的特点：共起点．Crarbr r uuur uuur uuur a b C Cr rrrrr⑶三角形不等式：．⑷运算性质：①交换律： r r rr r r r r r r；a b ba ；②结合律： a bc a bc ③ r r r r r ．a 0 0 a a⑸坐标运算：设 rrx 2 , y 2r rx 1 x 2 , y 1 y 2 ．a x 1, y 1 ， b，则 a b3、向量减法运算：⑴三角形法则的特点：共起点，连终点，方向指向被减向量．⑵坐标运算：设 r r x 2 , y 2 ，则 r r x 1 x 2 , y 1 y 2 ．a x 1, y 1 ，b a b设 、两点的坐标分别为x 1 , y 1 ， x 2 , y 2 ，则 uuurx 1x 2 , y 1y 2 ．【例题】uuur uuur uuuruuur uuur uuur；（ 1） ① AB BC CD ___；② AB AD DCuuur uuur uuuruuur ruuur uuur _____③ ( AB CD ) ( AC BD) （答：① AD ；② CB ；③ 0 ）；uuur r uuur r uuur r r r r（ 2）若正方形 ABCD 的边长为 1， AB a, BC b, AC c ，则 | a b c |＝_____（答： 2 2 ）；（ 3）已知作用在点uur uuruurA(1,1)的三个力 F 1 (3,4), F 2 (2, 5), F 3(3,1) ，则合力uruuruur uurF F 1F 2 F 3 的终点坐标是（答：（9,1））4、向量数乘运算：r ⑴实数r的积是一个向量的运算叫做向量的数乘，记作与向量 aa ．① r r ； a a②当 0 时， r r 的方向相同；a 的方向与 a r当 0 时， r r 的方向相反；当r a 的方向与 a 0 时， a 0 ．⑵运算律：① r r ；②r r r ；③ r r r r aa a a a ab ab ．r x, y ，则 r x, y x, y ．⑶坐标运算：设 a a【例题】（ ）若 （ -3 ， ）， （ ， ），且 MP 1MN1 M -2 N 6 -1 3，则点 P 的坐标为 _______（答： ( 6,7) ）；r rrr35、向量共线定理 ：向量，使a a 0 与b 共线，当且仅当有唯一一个实数 r rr x 1 , y 1r x 2 , y 2r r r r 2r r2。