2017年秋季学期新版冀教版七年级数学上学期2.7、角的和与差同步练习1

2.7角的和差当堂测试1.已知∠α=35°,那么∠α的余角等于( )A.35°B.55°C.65°D.145°解析:因为互为余角的两个角的和为90°,所以∠α的余角=90° - ∠α=90° - 35°=55°.故选B.2.已知射线OA,OB,OC,且OC在∠AOB的内部,下列条件能判定OC是∠AOB的平分线的是( )A.∠AOC=∠BOCB.∠AOB=2∠AOCC.∠BOC=∠AOBD.A,B,C都能解析:因为OC在∠AOB的内部,由角平分线定义可知选项A,B,C都能判定OC是∠AOB的平分线.故选D.3.如图所示,已知∠AOB=110°,∠AOC=∠BOD=70°,则∠COD的度数是 .解析:∠BOC=∠AOB - ∠AOC=110° - 70°=40°,则∠COD=∠BOD - ∠BOC=70° - 40°=30°.故填30°.4.如图所示,∠AOB=35°,∠BOC=50°,∠COD=21°,OE平分∠AOD,求∠BOE的度数.解:因为∠AOB=35°,∠BOC=50°,∠COD=21°,所以∠AOD=35°+50°+21°=106°,因为OE平分∠AOD,所以∠AOE=∠AOD=53°,所以∠BOE=∠AOE - ∠AOB=53° - 35°=18°.2.7 角的和与差课后检测1.如图所示,下面的角中,能与30°角互补的是( )2.如图所示,直线a,b相交于点O,若∠1等于40°,则∠2等于( )A.50°B.60°C.140°D.160°3.如图所示,∠1=∠2,∠3=∠4,则下列结论正确的个数为( )①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.A.4B.3C.2D.14.一个角的补角与它的余角的度数比是3∶1,则这个角是度.5.下面是小马虎解的一道题.题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.解:根据题意可画出图形,如图所示,∠AOC=∠BOA―∠BOC=70°―15°=55°.若你是老师,会判小马虎满分吗?如果会,说明理由;如果不会,请将小马虎的错误指出,并给出你认为正确的解法.6.已知两角的度数之比为2∶1,且这两角之和为直角,则这两个角的大小分别为( )A.70°,20°B.60°,30°C.50°,40°D.55°,35°7.把一张长方形的纸片按如图所示的方式折叠,EM,FM为折痕,折叠后的C'点落在MB'的延长线上,那么∠EMF的度数是 ( )A.85°B.90°C.95°D.100°8.(将一副直角三角尺按如图所示的方式放置,若∠AOD=20°,则∠BOC的大小为( )A.140°B.160°C.170°D.150°9.如图所示,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=∠α,则与∠α的余角度数相等的角是( )A.∠CODB.∠COEC.∠DOAD.∠COA10.如图所示,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=35°,求∠AOD的度数.11.如果∠1和∠2互余,∠1和∠3互补,∠2与∠3的和等于平角的,那么∠1,∠2,∠3的度数分别是( )A.50°,40°,90°B.70°,20°,110°C.75°,15°,105°D.80°,10°,100°12.如图所示,O是直线AB上一点,∠AOE=∠FOD=90°,OB平分∠COD,图中与∠DOE 互余的角有哪些?与∠DOE互补的角有哪些?13.(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;(2)如果(1)中∠AOB=m°,其他条件不变,求∠MON的度数;(3)如果(1)中∠BOC=n°(∠BOC为锐角),其他条件不变,求∠MON的度数.答案与解析1.D(解析:根据补角的定义可知30°角的补角是150°的角,是一个钝角.故选D.)2.C(解析:∠1与∠2的和恰好组成平角,即180°,所以∠2=180° - 40°=140°.)3.C(解析:由题意得AE是∠DAF和∠BAC的平分线,即③⑤正确.故选C.)4.45(解析:设这个角为α,则它的补角为180° - α,余角为90° - α,根据题意得(180° - α)∶(90° - α)=3∶1,解得α=45°.故填45.)5.解:不会.本题还有另一种情况,如图所示,此时∠AOC=∠BOA+∠BOC=70°+15°=85°,所以∠AOC的度数为55°或85°.6.B(解析:设这两个角的度数分别为2x和x,则由题意得2x+x=90°,所以x=30°,2x=60°.)7.B(解析:根据折叠前后相应角度的关系,不难求出∠EMF的度数等于90度.)8.B(解析:因为∠AOD=20°,∠COD=∠AOB=90°,所以∠COA=∠BOD=90° - 20°=70°.所以∠BOC=∠COA+∠AOD+∠BOD=70°+20°+70°=160°.)9.B(解析:因为∠AOB=180°,OD是∠BOC的平分线,OE是∠AOC的平分线,所以∠BOD=∠COD,∠EOC=∠EOA,所以∠EOC+∠COD=90°,所以与∠α的余角度数相等的角是∠EOC,∠EOA.故选B.)10.解:因为∠BOC=∠AOC - ∠AOB=90° - 35°=55°,又OC平分∠BOD,所以∠COD=∠BOC=55°,所以∠AOD=∠AOC+∠COD=90°+55°=145°.11.C(解析:由题意知∠2=90° - ∠1,∠3=180° - ∠1,∠2+∠3=180°×=120°,所以90° - ∠1+180° - ∠1=120°,解得∠1=75°,所以∠2=15°,∠3=105°.)12.解:因为∠AOE=∠FOD=90°,所以∠AOF=∠DOE,∠AOF+∠EOF=90°,∠BOD+∠DOE=90°,∠DOE+∠EOF=90°,因为OB平分∠COD,所以∠BOD=∠BOC,所以与∠DOE互余的角是∠EOF,∠BOD,∠BOC.所以∠EOF=∠BOC,所以∠BOF=∠EOC.因为∠AOF+∠BOF=180°,所以∠DOE+∠BOF=180°,所以与∠DOE互补的角是∠BOF,∠EOC.13.解:(1)因为ON平分∠BOC,所以∠NOC=∠BOC=15°,因为∠AOB=90°,∠BOC=30°,OM平分∠AOC,所以∠MOC=(∠AOB+∠BOC)=60°,所以∠MON=∠MOC - ∠NOC=45°.(2)因为ON平分∠BOC,所以∠NOC=∠BOC=15°.因为OM平分∠AOC,所以∠MOC=(∠AOB+∠BOC)=(m°+30°),所以∠MON=∠MOC - ∠NOC=(m°+30°) - 15°=m°.(3)因为ON平分∠BOC,所以∠NOC=n°,因为OM平分∠AOC,所以∠MOC=(∠AOB+∠BOC)=(90°+n°),所以∠MON=∠MOC - ∠NOC=(90°+n°) - n°=45°.。

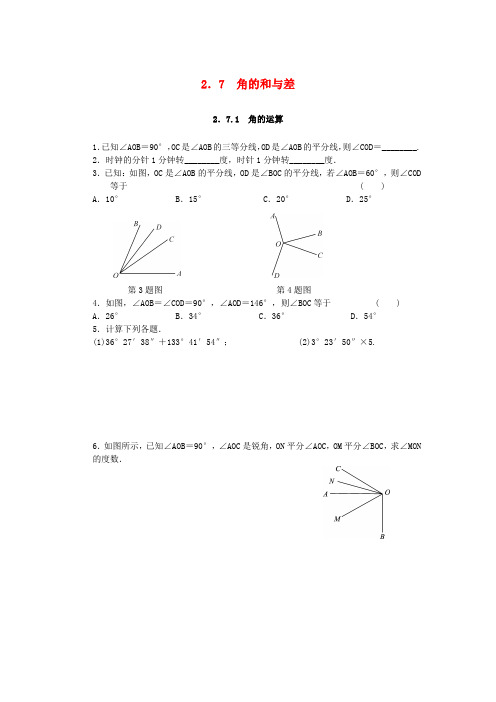
2．7 角的和与差2．7.1 角的运算1．已知∠AOB＝90°，OC是∠AOB的三等分线，OD是∠AOB的平分线，则∠COD＝________. 2．时钟的分针1分钟转________度，时针1分钟转________度．3．已知：如图，OC是∠AOB的平分线，OD是∠BOC的平分线，若∠AOB＝60°，则∠COD 等于 ( ) A．10° B．15° C．20° D．25°第3题图第4题图4．如图，∠AOB＝∠COD＝90°，∠AOD＝146°，则∠BOC等于 ( ) A．26° B．34° C．36° D．54°5．计算下列各题．(1)36°27′38″＋133°41′54″；(2)3°23′50″×5.6．如图所示，已知∠AOB＝90°，∠AOC是锐角，ON平分∠AOC，OM平分∠BOC，求∠MON 的度数．2．7.2 余角和补角1．一个锐角的补角比它的余角大________．2．已知∠1＝20°，∠2＝30°，∠3＝60°，∠4＝150°，则∠2是________的余角，________是∠4的补角．3．若∠α＝39°31′，则∠α的余角∠β＝________，∠α的补角∠γ＝________，∠γ－∠β＝________.4．若∠1＋∠2＝90°，∠3＋∠2＝90°，∠1＝40°，则∠3＝________，依据是____________________．5．一个角等于它的补角的5倍，则这个角的补角的余角等于 ( )A ．30°B ．60°C ．45°D ．50°6．下列说法：(1)互余的两个角一定都是锐角；(2)两个锐角一定互余；(3)互补的两角一定是一锐角和一钝角；(4)一锐角和一钝角一定互补．其中正确的个数是 ( )A ．0B ．1C ．2D ．37．如果从A 看B 的方向是北偏东25°，那么从B 看A 的方向是 ( )A ．南偏东65°B ．南偏西65°C ．南偏东25°D ．南偏西25°8．如图，将长方形ABCD 沿AE 折叠，使D 点落在BC 边上的F 点处，如果∠BAF＝60°，则∠DAE 等于 ( )A ．15°B ．30°C ．45°D ．60°9．一个角与它的余角以及它的补角的和是直角的213倍，求这个角的补角．2．7 角的和与差2．7.1 角的运算1．15° 2.6 0.5 3.B 4.B5．(1)170°9′32″；(2)16°59′10″.6．设∠AON＝∠NOC＝x°，则∠AOC＝2x°，∠BOC＝90°＋2x°，所以∠MON＝∠MOC－∠NOC＝12∠BOC－∠NOC＝12(90°＋2x°)－x°＝45°.2．7.2 余角和补角1．90° 2.∠3∠2 3.50°29′140°29′90°4．40°同角的余角相等5．B 6.B 7.D 8.A 9.120°。

冀教版七年级数学上册：2.7角的和与差同步练习2.7 角的和与差1．下列关于对顶角的语句中，正确的是( ) A ．两条直线相交所成的角B ．有公共顶点并且相等的两个角C ．有公共顶点且方向相反的两个角D ．两条直线相交所成的角，且有一个公共顶点没有公共边2.∠1、∠2互余，可以表示为：(1)∠1+∠2=________；(2)∠1=90-_______或∠2=90-______．3.从乙地看，甲地的方向是西偏南28，那么，从甲地看，乙地的方向是_______．4.30ˊ的补角是_______，3446ˊ23"的余角是______．5.若∠ABC 是∠α与∠β的和，则记作∠ABC=_____．6.∠α、∠β互补，可以表示为∠α+∠β=_______．7.90-3541ˊ=_______；2345ˊ+2415ˊ=_______；1366ˊ-4354ˊ28"=_______． 8.如图，点B 在点A 正北500米处，点C 在点A 的正东方，在点北4.17930ˊ，5513ˊ37"；5.∠α+∠β6.180．7.54 19ˊ；48；92 11ˊ32 "8.(1) 略；(2)1000米9.(1) ∠BON=∠BOM+∠MON，∠BON－∠AON=∠BOM+∠MON－∠AON=(∠BOM－∠AON)+ ∠MON=∠MON+∠MON=2∠MON，所(∠BON－∠AON)；以，∠MON=12(2) ∠AOG+∠BOG=∠AOB+∠BOG+∠BOG=2∠MOB+2∠BOG=2(∠MOB+∠BOG)=2∠MOG，所以，(∠AOG+∠BOG).∠MOG=1210.13011.25。

2.7角的和与差同步测试一、选择题1.如果∠A的补角与∠A的余角互补，那么2∠A是（）A. 锐角B. 直角C. 钝角D. 以上三种都可能2.一副三角板按如图方式摆放，已知∠1=5∠2，则∠1的度数是（）A. 15°B. 18°C. 72°D. 75°3.如图，∠AOC，∠BOD都是直角，∠AOD：∠AOB=3：1，则∠BOC的度数是（）A. 22.5°B. 45°C. 90°D. 135°4.把一副三角板按如图方式的位置摆放，则形成两个角，设分别是∠α，∠β，若∠α=55°，则∠β=（）A. 25°B. 35°C. 45°D. 55°5.下列图形中，∠1与∠2互为补角的是（）A. B. C. D.6.如图，一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置，若∠BCD=30°，下列结论错误的是（）A. ∠ACD=120°B. ∠ACD=∠BCEC. ∠ACE=120°D. ∠ACE﹣∠BCD=120°7.若∠A=34°，则∠A的余角的度数为（）A. 146°B. 54°C. 56°D. 66°8.（2016•工业园区一模）已知∠α和∠β互为余角．若∠α=40°，则∠β等于（）A. 40°B. 50°C. 60°D. 140°9.两个锐角的和（）．A. 必定是锐角;B. 必定是钝角;C. 必定是直角;D. 可能是锐角，可能是直角，也可能是钝角10.如图，已知点O在直线AB上，，则的余角是( )A. B. C. D.二、填空题11.如图，图中小于平角的角共有________ 个，其中能用一个大写字母表示的角是________ ．12.如果∠1+∠2=90°，而∠2与∠3互余，那么∠1与∠3的数量关系是________．13.若∠α比60°角的补角的大35°，则∠α的余角为________°．14.将一副三角板如图放置，若∠AOD=20°，则∠BOC的大小为________．15.已知∠α=40°36′，则∠α的余角为________ ．16.若∠α补角加上30°是∠α余角的3倍，则∠α=________．17.若∠A=66°20′，则∠A的余角等于________18.如图，将一副三角板折叠放在一起，使直角的顶点重合于点O，则∠AOC+∠DOB=________度．三、解答题19.一个锐角的补角等于这个锐角的余角的3倍，求这个锐角？20.已知一个角的补角比这个角的余角的3倍大10°，求这个角的度数．21.如图，AO⊥OC，解答下列问题：①比较∠AOB、∠AOC、∠AOD、∠AOE的大小，并指明其中的锐角、直角、钝角及平角；②写出∠AOB、∠AOC、∠BOC、∠AOE中某些角之间的两个等量关系．22.如图（1）所示，∠AOB、∠COD都是直角．（1）试猜想∠AOD与∠COB在数量上是相等，互余，还是互补的关系．请你用推理的方法说明你的猜想是合理的．（2）当∠COD绕着点O旋转到图（2）所示位置时，你在（1）中的猜想还成立吗？请你证明你的结论．23.如图，将书角斜折过去，使角顶点落在A′处，BC为折痕，∠A′BD=∠DBE，求∠CBD的度数．参考答案一、选择题1.B2.D3.B4.B5.C6.C7.C8.B9.D 10.A二、填空题11.7；∠B，∠C 12.相等13.25 14.160° 15.49°24′ 16.30° 17.23°40′ 18. 180三、解答题19.解：设这个角的度数为x°，则根据题意得：180﹣x=3（90﹣x），解得：x=45，即这个锐角为45°．20.解：设这个角是x，则（180°﹣x）﹣3（90°﹣x）=10°，解得x=50°．故答案为50°21.解：（1）∠AOB＜∠AOC＜∠AOD＜∠AOE，∵AE⊥OC，∴∠AOC=90°，∴∠AOB是锐角，∠AOC是直角，∠AOD是钝角，∠AOE是平角；（2）∠AOB+∠BOC=∠AOC，∠AOB+∠BOC+∠AOC=∠AOE．22.（1）解：∠AOD与∠COB互补．理由如下：∵∠AOB、∠COD都是直角，∴∠AOB=∠COD=90°，∴∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°，∠BOD=∠COD﹣∠COB=90°﹣∠COB，∴∠AOD﹣90°=90°﹣∠COB，∴∠AOD+∠COB=180°，∴∠AOD与∠COB互补（2）解：成立．理由如下：∵∠AOB、∠COD都是直角，∴∠AOB=∠COD=90°，∵∠AOB+∠BOC+∠COD+∠AOD=360°， ∴∠AOD+∠COB=180°，∴∠AOD 与∠COB 互补．23.解：由题意可知，∠ABC=∠A′BC ，∠EBD=∠DBA′， ∴∠CBA′= ∠ABA′，∠A′BD= ∠A′BE ，∴∠CBD=∠CBA′+∠DBA′= （∠A′BA+∠A′BE ）， ∵∠A′BA+∠A′BE=180°，∴∠CBD=90°．。

第2课时互余、互补及其性质知识点 1 互余、互补的概念1．若∠α与∠β互为余角，则∠α＋∠β＝________；若∠α与∠β互为补角，则∠α＋∠β＝________．2．[2017·常德]若一个角为75°，则它的余角的度数为( )A．285° B．105° C．75° D．15°3．若∠A＝34°，则∠A的补角的度数为( )A．56° B．146° C．156° D．166°4．一个角的余角是54°38′，则这个角的补角是________．5．已知∠1与∠2互余，∠2与∠3互补．若∠1＝63°，则∠3＝________．6．如图2－7－17，O是直线AE上的一点，OB是∠AOC的平分线，OD是∠COE的平分线．(1)图中互余的角有哪几对？(2)图中互补的角有哪几对？图2－7－17知识点 2 互余、互补的性质7．(1)若∠1＋∠2＝90°，∠1＋∠3＝90°，则∠2________∠3(填“>”“<”或“＝”)，理由：________________________．(2)若∠1＋∠3＝90°，∠2＋∠4＝90°，且∠1＝∠2，则∠3________∠4(填“>”“<”或“＝”)，理由：________________________．(3)若∠1＋∠2＝180°，∠1＋∠3＝180°，则∠2________∠3(填“>”“<”或“＝”)，理由：________________________．(4)若∠1＋∠3＝180°，∠2＋∠4＝180°，且∠1＝∠2，则∠3________∠4(填“>”“<”或“＝”)，理由：________________________．8．如图2－7－18，OD平分∠BOC，OE平分∠AOC.若∠BOC＝70°，∠AOC＝50°.(1)求出∠AOB及其补角的度数；(2)请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由．图2－7－189．将一副三角尺按如图2－7－19所示的位置摆放，其中∠α与∠β一定互余的是( )图2－7－1910．下列说法正确的是( )A ．互补的两个角一个是锐角，一个是钝角B ．180°的角是补角C ．互余的两个角可能是等角D ．只有锐角有补角11．已知∠α是锐角，∠α与∠β互补，∠α与∠γ互余，则∠β－∠γ的值等于( ) A ．45° B ．60° C ．90° D ．180°12．如果一个角和它的余角的比是1∶3，那么这个角的度数为________．13．已知∠α与∠β互补，且∠α>∠β，试判断∠β与12(∠α－∠β)的数量关系．14.如图2－7－20，将两块直角三角尺的直角顶点C 叠放在一起．(1)若∠DCE ＝35°，求∠ACB 的度数； (2)若∠ACB ＝140°，求∠DCE 的度数；(3)写出∠ACB 与∠DCE 的数量关系，并说明理由．图2－7－2015．如图2－7－21，O为直线AB上的一点，∠AOE为直角，∠DOF＝90°，OB平分∠COD，则图中与∠DOE互余的角有哪些，与∠DOE互补的角有哪些？图2－7－2116．如图2－7－22，∠AOB∶∠BOC∶∠COD＝2∶3∶4，射线OM，ON分别平分∠AOB与∠COD，已知∠MON＝90°，则∠AOB等于( )图2－7－22A．20° B．30° C．40° D．45°17．如图2－7－23①，∠AOB，∠COD都是直角．(1)试猜想，∠AOD和∠BOC在数量上是否存在相等、互余或互补的关系？你能说明你的猜想的正确性吗？(2)当∠COD绕点O旋转到图2－7－23②所示的位置时，(1)中的猜想还成立吗？图2－7－23【详解详析】1．90°180°2．D [解析] 它的余角的度数为90°－75°＝15°.故选D.3．B [解析] ∠A的补角的度数为180°－34°＝146°.故选B.4．144°38′[解析] 根据题意得这个角为90°－54°38′＝35°22′，则这个角的补角为180°－35°22′＝144°38′.5．153° [解析] 因为∠1是∠2的余角，∠3是∠2的补角，所以∠3－∠1＝90°，所以∠3＝90°＋63°＝153°.6．解：(1)∠AOB 与∠DOE ，∠AOB 与∠COD ，∠COD 与∠BOC ，∠BOC 与∠DOE 都是互余的角．(2)∠AOB 与∠BOE ，∠BOC 与∠BOE ，∠AOC 与∠COE ，∠COD 与∠AOD ，∠EOD 与∠AOD 都是互补的角．7．(1)＝ 同角的余角相等 (2)＝ 等角的余角相等 (3)＝ 同角的补角相等 (4)＝ 等角的补角相等8．解：(1)∠AOB ＝∠BOC ＋∠AOC ＝70°＋50°＝120°， 其补角为180°－∠AOB ＝180°－120°＝60°. (2)∠DOC ＝12∠BOC ＝12×70°＝35°，∠AOE ＝12∠AOC ＝12×50°＝25°.∠DOE 与∠AOB 互补．理由：因为∠DOE ＝∠DOC ＋∠COE ＝∠DOC ＋∠AOE ＝35°＋25°＝60°， 所以∠DOE ＋∠AOB ＝60°＋120°＝180°， 故∠DOE 与∠AOB 互补． 9．C 10．C. 11．C 12．[22.5°[解析] 根据题意，知这个角的度数是90°×14＝22.5°.13．解：因为∠α与∠β互补， 所以∠α＋∠β＝180°， 所以∠β＝180°－∠α，所以∠β的余角为90°－(180°－∠α)＝∠α－90°＝∠α－12(∠α＋∠β)＝12∠α－12∠β＝12(∠α－∠β)， 所以∠β＋12(∠α－∠β)＝90°.14．解：(1)因为∠ECB ＝90°，∠DCE ＝35°， 所以∠DCB ＝90°－35°＝55°. 因为∠ACD ＝90°，所以∠ACB ＝∠ACD ＋∠DCB ＝145°.(2)因为∠ACB＝140°，∠ACD＝90°，所以∠DCB＝140°－90°＝50°.因为∠ECB＝90°，所以∠DCE＝90°－50°＝40°.(3)∠ACB＋∠DCE＝180°(或∠ACB与∠DCE互补)．理由：因为∠ECB＝90°，∠ACD＝90°，所以∠ACB＝∠ACD＋∠DCB＝90°＋∠DCB，∠DCE＝∠ECB－∠DCB＝90°－∠DCB，所以∠ACB＋∠DCE＝180°.15．[解析] 本题要根据余角、补角的定义，结合图形认真观察．解：因为∠BOE＝∠AOB－∠AOE＝180°－90°＝90°，所以∠BOD＋∠DOE＝90°，即∠DOE与∠BOD互余．因为OB平分∠COD，所以∠BOC＝∠BOD，所以∠DOE与∠BOC互余．因为∠DOF＝90°，所以∠DOE＋∠EOF＝90°，所以∠DOE与∠EOF互余．即与∠DOE互余的角有∠BOD，∠BOC，∠EOF.因为∠DOE＋∠BOF＝∠DOE＋∠EOF＋∠BOE＝∠DOF＋∠BOE＝180°，所以∠DOE与∠BOF互补．因为∠DOE＋∠COE＝∠DOE＋∠COB＋∠BOE＝∠DOE＋∠BOD＋∠BOE＝∠BOE＋∠BOE＝180°，所以∠DOE与∠COE互补，即与∠DOE互补的角有∠BOF，∠COE.16．B17．解：(1)猜想：∠AOD与∠BOC互补．因为∠AOD＝∠AOB＋∠BOD＝90°＋∠BOD，∠BOD＝90°－∠BOC，所以∠AOD＝90°＋90°－∠BOC，所以∠AOD＋∠BOC＝180°，即∠AOD与∠BOC互补．(2)(1)中的猜想仍然成立．因为∠AOB，∠COD都是直角，所以∠AOB＋∠COD＝180°.又因为∠AOB＋∠BOC＋∠COD＋∠AOD＝ 360°，所以∠AOD＋∠BOC＝180°，所以∠AOD与∠BOC互补．。

2.7第1课时角的和与差及角的平分线知识点1角的和与差1．如图2－7－1，下列式子错误的是()图2－7－1A．∠AOC＝∠AOB＋∠BOCB．∠AOC＝∠AOD－∠CODC．∠AOC＝∠AOB＋∠BOD－∠BOCD．∠AOC＝∠AOD－∠BOD＋∠BOC2．借助常用的三角尺，能画出一些度数的角，下列选项中不能借助三角尺画出角的是()A．15°B．100°C．165°D．135°3．已知∠AOB＝60°，∠BOC＝30°，则∠AOC的度数为()A．90°B．45°或30°C．30°D．90°或30°4．如图2－7－2，已知∠AOC＝90°，直线BD过点O，∠COD＝115°，则∠AOB的度数为________．图2－7－25．如图2－7－3，已知∠AOC ＝∠BOD ＝110°，∠BOC ＝75°，求∠AOD 的度数．图2－7－3知识点 2 角的平分线6．如图2－7－4，已知OC 是∠AOB 的平分线，下列结论不正确的是( )图2－7－4A ．∠AOB ＝∠BOC B ．∠AOC ＝12∠AOBC ．∠AOC ＝∠BOCD ．∠AOB ＝2∠AOC7．如图2－7－5，OC 是∠AOB 的平分线，OD 是∠BOC 的平分线，那么下列各式中正确的是( )图2－7－5A ．∠COD ＝12∠AOB B ．∠AOD ＝23∠AOBC ．∠BOD ＝12∠AOD D ．∠BOC ＝23∠AOD8．如图2－7－6，OC 是∠AOB 的平分线，OD 平分∠AOC ，且∠COD ＝25°，则∠AOB 的度数是( )图2－7－6A ．50°B ．75°C ．100°D ．120°9．如图2－7－7，已知O 是直线CD 上一点，OA 平分∠BOC ，∠AOC ＝35°，求∠BOD 的度数．图2－7－7知识点 3 角度的加减运算10．计算：(1)48°39′＋67°31′； (2)180°－21°17′×5.11．如图2－7－8，已知M 是直线AB 上一点，∠AMC ＝52°48′，∠BMD ＝72°19°，则∠CMD的度数为()图2－7－8A．49°07′B．54°53′C．55°53′D．53°7′12．已知直线AB上有一点O，射线OD和射线OC在AB的同侧，∠AOD＝42°，∠BOC＝34°，则∠AOD与∠BOC的平分线的夹角的度数是()A．142°B．90°C．38°D．以上都不对13．将一张纸按图2－7－9所示的方式折叠，BC，BD为折痕，则∠CBD的度数为()图2－7－9A．80°B．90°C．100°D．110°14．如图2－7－10，已知OE平分∠AOB，OD平分∠BOC，∠AOB＝90°，∠EOD＝70°，则∠BOC的度数为________．图2－7－1015．如图2－7－11，OC是∠AOB的平分线，∠AOD比∠BOD大30°，则∠COD的度数为________．图2－7－1116．如图2－7－12，OB平分∠AOC，∠AOD＝78°.(1)若∠BOC＝20°，求∠COD的度数；(2)若OC是∠AOD的平分线，求∠BOD的度数．图2－7－1217．如图2－7－13，从直线AB上任一点引一条射线OC，已知OD平分∠BOC.若∠EOD＝90°，则OE一定是∠AOC的平分线，请说明理由．图2－7－13 18．已知∠AOB＝80°，∠BOC＝20°，求∠AOC的度数．19．两个角的顶点重合，且有一边重合，另一边互为反向延长线．若这两个角的度数之比为5∶4，则这两个角的度数差是()A．10°B．20°C．30°D．40°20．如图2－7－14，已知同一平面内∠AOB＝90°，∠AOC＝60°.(1)填空：∠BOC＝________°.(2)若OD平分∠BOC，OE平分∠AOC，则∠DOE的度数为________°.(3)在(2)的条件下，如果将题目中“∠AOC＝60°”改成“∠AOC＝2∠α(∠α<45°)”，其他条件不变，你能求出∠DOE的度数吗？若能，请你写出求解过程；若不能，请说明理由．图2－7－14教师详解详析【备课资源】【详解详析】1．90°180°2．C 3.D4．60°150°5．84°[解析] 因为∠α的补角为54°，∠β的余角为48°，所以∠α＝180°－54°＝126°，∠β＝90°－48°＝42°，所以∠α－∠β＝126°－42°＝84°.6．153°[解析] 因为∠1是∠2的余角，∠3是∠2的补角，所以∠3－∠1＝90°，所以∠3＝90°＋63°＝153°.7．解：(1)由题意，得3∠α＋∠α＝180°，解得∠α＝45°.(2)设这个角的度数为x，则它的余角的度数为(90°－x)．由题意，得12x －(90°－x )＝30°，解得x ＝80°.即这个角的度数是80°.8．(1)＝ 同角的余角相等 (2)＝ 等角的余角相等 (3)＝ 同角的补角相等 (4)＝ 等角的补角相等9．解：(1)∠AOB 与∠DOE ，∠AOB 与∠COD ，∠COD 与∠BOC ，∠BOC 与∠DOE 都是互余的角．(2)∠AOB 与∠BOE ，∠BOC 与∠BOE ，∠AOC 与∠COE ，∠COD 与∠AOD ，∠EOD 与∠AOD 都是互补的角．10．C 11.B 12.C13．45° [解析] 设这个角的度数为x ，则90°－x ＋180°－x ＝180°，解得x ＝45°. 14．[解析] 本题要根据余角、补角的定义，结合图形认真观察． 解：因为∠BOE ＝∠AOB －∠AOE ＝180°－90°＝90°， 所以∠BOD ＋∠DOE ＝90°， 即∠DOE 与∠BOD 互余． 因为OB 平分∠COD ， 所以∠BOC ＝∠BOD ， 所以∠DOE 与∠BOC 互余． 因为∠DOF ＝90°， 所以∠DOE ＋∠EOF ＝90°，所以∠DOE 与∠EOF 互余，即与∠DOE 互余的角有∠BOD ，∠BOC ，∠EOF .因为∠DOE ＋∠BOF ＝∠DOE ＋∠EOF ＋∠BOE ＝∠DOF ＋∠BOE ＝180°， 所以∠DOE 与∠BOF 互补．因为∠DOE ＋∠COE ＝∠DOE ＋∠COB ＋∠BOE ＝∠DOE ＋∠BOD ＋∠BOE ＝ ∠BOE ＋∠BOE ＝180°，所以∠DOE 与∠COE 互补，即与∠DOE 互补的角有∠BOF ，∠COE . 15．解：(1)因为直线AB ，CD 相交于点O ，所以∠AOC ＋∠AOD ＝180°，∠BOD ＋∠AOD ＝180°， 所以∠AOC 和∠BOD 分别与∠AOD 互补． 因为OF 平分∠AOE ，所以∠AOF ＝∠EOF . 因为∠DOF ＝90°，所以∠COF ＝∠DOF ＝90°， 所以∠AOC ＝∠DOE ，所以∠DOE 也是∠AOD 的补角， 所以与∠AOD 互补的角有∠AOC ，∠BOD ，∠DOE . (2)因为OF 平分∠AOE ， 所以∠EOF ＝12∠AOE ＝60°.因为∠DOF ＝90°，所以∠DOE ＝∠DOF －∠EOF ＝90°－60°＝30°. 所以∠BOD ＝180°－∠AOE －∠DOE ＝180°－120°－30°＝30°. 16．解：(1)猜想：∠AOD 与∠BOC 互补． 因为∠AOD ＝∠AOB ＋∠BOD ＝90°＋∠BOD ，∠BOD＝90°－∠BOC，所以∠AOD＝90°＋90°－∠BOC，所以∠AOD＋∠BOC＝180°，即∠AOD与∠BOC互补．(2)(1)中的猜想仍然成立．因为∠AOB，∠COD都是直角，所以∠AOB＋∠COD＝180°.又因为∠AOB＋∠BOC＋∠COD＋∠AOD＝360°，所以∠AOD＋∠BOC＝180°，所以∠AOD与∠BOC互补．17．解：(1)∠2是90°的角．理由如下：由折叠可知，∠1＋∠3＝∠2.又因为∠1＋∠2＋∠3＝180°，所以2∠2＝180°，所以∠2＝90°.(2)∠1与∠3互为余角，或∠1＋∠3＝90°.(3)∠1与∠AEC互补，∠3与∠BEF互补，或∠1＋∠AEC＝180°，∠3＋∠BEF＝180°.。

冀教新版七年级上学期《2.7 角的和与差》同步练习卷一．选择题（共33小题）1．已知直线AB，射线OC，OD都在如图所示的量角器上，点O在直线AB上，则下列判断中不正确的是（）A．∠AOC＝56°B．∠AOD＝134°C．∠AOC＜∠COD D．∠BOD与∠BOC互补2．如图，三角板的直角顶点在直线l上，若∠1＝34°，则∠2的度数是（）A．34°B．68°C．56°D．146°3．已知∠α与∠β互补，∠α＝5∠β，则∠α等于（）A．150°B．120°C．90°D．60°4．如图，一副三角板按如图方式摆放，且∠1比∠2大30°，则∠2为（）A．120°B．55°C．60°D．30°5．一个角的补角是它的余角的度数的3倍，则这个角的度数是（）A．45°B．50°C．55°D．60°6．如图，OA⊥OC，OB⊥OD，四位同学观察图形后分别说了自己的观点．甲：∠AOB＝∠COD；乙：∠BOC+∠AOD＝180°；丙：∠AOB+∠COD＝90°；丁：图中小于平角的角有6个．其中观点正确的有（）A．甲、乙、丙B．甲、丙、丁C．乙、丙、丁D．甲、乙、丁7．如图，将一个直角三角形板AOB的顶点O放在直线CD上，若∠AOC＝35°，则∠BOD等于（）A．155°B．145°C．65°D．55°8．若∠α与∠β互为余角，∠β是∠α的2倍，则∠α为（）A．20°B．30°C．40°D．60°9．将一副三角板按如图所示的位置摆放，其中∠α和∠β一定互余的是（）A．B．C．D．10．已知∠α＝140°﹣5m，∠β＝5m﹣50°，∠α，∠β的关系是（）A．∠α＞∠βB．∠α＜∠βC．互余D．互补11．如图，AB、CD相交于O，OE⊥AB，那么下列结论错误的是（）A．∠AOC与∠BOD是对顶角B．∠AOC与∠COE互为余角C．∠BOD与∠COE互为余角D．∠COE与∠BOE互为补角12．已知M、N、P、Q四点的位置如图所示，下列结论中，正确的是（）A．∠NOQ＝42°B．∠NOP＝132°C．∠PON比∠MOQ大D．∠MOQ与∠MOP互补13．如果∠1＝∠2，∠1+∠3＝90°，∠2+∠4＝90°，那么∠3与∠4的关系是（）A．互余B．相等C．互补D．以上都不对14．若∠α+∠θ＝90°，∠β＝∠θ，则∠α与∠β的关系是（）A．∠α与∠β互余B．∠α与∠β互补C．∠α与∠β相等D．∠α大于∠β15．下列图形中，∠1与∠2互为补角的是（）A．B．C．D．16．下列说法错误的是（）A．48°21′36″的余角是41.64°B．点C是线段AB上的点，AB＝10，AC＝6，点D是线段BC的中点，则线段CD＝2C．∠AOC＝60°，经过顶点O引一条射线OD，且∠AOD＝25°，则∠COD ＝85°D．已知线段a，b如图，则尺规作图中，线段AD＝2a﹣b17．若∠A＝64°，则它的余角等于（）A．116°B．26°C．64°D．50°18．已知一个角的补角是这个角的余角的3倍，则这个角的度数为（）A．22.5°B．45°C．60°D．90°19．若∠A的补角加上30°是∠A的余角的5倍，则∠A的度数为（）A．60°B．50°C．40°D．30°20．已知∠1＝40°，则∠1的余角的度数是（）A．40°B．50°C．140°D．150°21．将一副三角板按如图所示位置摆放，其中∠α与∠β一定互余的是（）A．B．C．D．22．下列说法中正确的个数是（）①锐角的补角一定是钝角；②一个角的补角一定大于这个角；③如果两个角是同一个角的补角，那么它们相等；④锐角和钝角互补．A．1B．2C．3D．423．若一个角的补角等于它的余角的3倍，则这个角为（）A．75°B．60°C．45°D．30°24．一个角的度数比它的余角的度数大20°，则这个角的度数是（）A．20°B．35°C．45°D．55°25．若一个角的余角与它补角互补，则这个角是（）A．30°B．45°C．60°D．90°26．如果∠α＝26°，那么∠α余角的补角等于（）A．20°B．70°C．110°D．116°27．一个角的余角和这个角的补角也互为补角，这个角的度数等于（）A．90°B．75°C．45°D．15°28．已知：∠1+∠2＝180°，且∠1＞∠2，那么∠2的余角是（）A．（∠1+∠2）B．∠1C．（∠1﹣∠2）D．不能确定29．已知：∠1+∠2＝180°，且∠1＞∠2，则∠2与（∠1﹣∠2）的关系为（）A．相等B．互补C．互余D．和为45°30．如图，点B，O，D在同一条直线上，∠1＝15°，∠AOC＝90°，则∠2的度数为（）A．15°B．75°C．105°D．165°31．若一个角的余角的两倍与这个角的补角的和210°，这个角的度数为（）A．70°B．60°C．50°D．40°32．如图，在△ABC中，∠C＝90°，点D，E分别在边AC，AB上．若∠B＝∠ADE，则下列结论正确的是（）A．∠A和∠B互为补角B．∠B和∠ADE互为补角C．∠A和∠ADE互为余角D．∠AED和∠DEB互为余角33．一个角的度数比它的余角的度数大20°，则这个角的度数是（）A．35°B．45°C．55°D．65°二．填空题（共13小题）34．若一个角的补角等于它的余角的3倍，则这个角为度．35．一个角的余角的3倍比它的补角的2倍少120°，则这个角的度数为．36．一个角的余角比它的补角的一半还少20°，则这个角为．37．若∠A与∠B互余，∠B与∠C互余，则∠A与∠C的关系是，依据是．38．已知一个角的余角等于这个角的补角的，那这个角是．39．一个角的余角比它的补角的还少20°，则这个角的大小是．40．若∠β＝40°，则∠β的补角等于．41．已知∠AOB＝40°，OC平分∠AOB，则∠AOC的补角等于度．42．一个角的补角的余角等于65°，则这个角等于度．43．30°角的余角是，补角是．44．如图，已知∠AOC＝90°，直线BD过点O，∠COD＝115°15′，则∠AOB ＝．45．如图，∠AOC和∠DOB都是直角，如果∠DOC＝35°，那么∠AOB的度数为．46．一个角的余角比它的补角的少20°，则这个角为．三．解答题（共4小题）47．如图，将两块直角三角板的直角顶点C叠放在一起．（1）若∠DCB＝35°，求∠ACB的度数；（2）若∠ACB＝140°，求∠DCE的度数．48．如图，O为直线DA上一点，OE是∠AOB的平分线，∠FOB＝90°．（1）∠AOF的余角是；（2）∠DOB的补角是；（3）若∠EOF＝20°，求∠AOF的度数．49．已知，如图，AO⊥BC，DO⊥OE．（1）在下面的横线上填上适当的角：∠DOE＝∠+∠；∠BOE＝∠﹣∠；（2）不添加其它条件情况下，请尽可能多地写出图中有关角的等量关系（至少4个）．（3）如果∠COE＝35°，求∠AOD的度数．50．（1）如图①，已知∠AOB＝∠COD＝90°．试写出两个与图①中角（直角除外）有关的结论：（ⅰ）∠＝∠，（ⅱ）∠+∠＝180°；（2）若将图①中∠AOB绕点O旋转到图②的位置，则（1）中的两个结论仍然成立吗？为什么？冀教新版七年级上学期《2.7 角的和与差》2019年同步练习卷参考答案与试题解析一．选择题（共33小题）1．已知直线AB，射线OC，OD都在如图所示的量角器上，点O在直线AB上，则下列判断中不正确的是（）A．∠AOC＝56°B．∠AOD＝134°C．∠AOC＜∠COD D．∠BOD与∠BOC互补【分析】依据图形可对A、B作出判断，然后可求得∠COD的值，从而可对C 作出判断，然后求得∠BOC的度数，最后依据补角的定义可对D作出判断．【解答】解：A、∠AOC＝56°，故A正确，与要求不符；B、∠AOD＝134°，故B正确，与要求不符；C、∠COD＝134°﹣56°＝78°，所以∠AOC＜∠COD，故C正确，与要求不符；D、∠COB＝180°﹣56°＝124°，∠BOD+∠BOC≠180°，故D错误，与要求相符．故选：D．【点评】本题主要考查的是余角和补角的定义、角的度量与计算，求得相关角的度数是解题的关键．2．如图，三角板的直角顶点在直线l上，若∠1＝34°，则∠2的度数是（）A．34°B．68°C．56°D．146°【分析】根据平角定义可得∴∠2＝180°﹣90°﹣∠1，代入数据可得答案．【解答】解：∵∠1＝34°，∴∠2＝180°﹣90°﹣34°＝56°，故选：C．【点评】此题主要考查了余角，关键是掌握平角为180°．3．已知∠α与∠β互补，∠α＝5∠β，则∠α等于（）A．150°B．120°C．90°D．60°【分析】根据补角定义可得∠α+∠β＝180°，再结合条件∠α＝5∠β可得∠β的度数，进而可得∠α的度数．【解答】解：∵∠α与∠β互补，∴∠α+∠β＝180°，∵∠α＝5∠β，∴5∠β+∠β＝180°，∠β＝30°，∴∠α＝150°，故选：A．【点评】此题主要考查了补角，关键是掌握如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．4．如图，一副三角板按如图方式摆放，且∠1比∠2大30°，则∠2为（）A．120°B．55°C．60°D．30°【分析】利用平角定义及已知列出两个方程，求出解即可．【解答】解：根据题意得：∠1+∠2+90°＝180°①，∠1﹣∠2＝30°②，联立①②，解得：∠1＝60°，∠2＝30°，故选：D．【点评】此题考查了余角和补角，熟练掌握各自的定义是解本题的关键．5．一个角的补角是它的余角的度数的3倍，则这个角的度数是（）A．45°B．50°C．55°D．60°【分析】根据补角和余角的定义，利用“一个角的补角是它的余角的度数的3倍”作为相等关系列方程求解即可．【解答】解：设这个角的度数是x，则180°﹣x＝3（90°﹣x），解得x＝45°．所以这个角是45°．故选：A．【点评】本题考查的是余角和补角的定义，如果两个角的和是一个直角，那么称这两个角互为余角．如果两个角的和是一个平角，那么这两个角叫互为补角．其中一个角叫做另一个角的补角．6．如图，OA⊥OC，OB⊥OD，四位同学观察图形后分别说了自己的观点．甲：∠AOB＝∠COD；乙：∠BOC+∠AOD＝180°；丙：∠AOB+∠COD＝90°；丁：图中小于平角的角有6个．其中观点正确的有（）A．甲、乙、丙B．甲、丙、丁C．乙、丙、丁D．甲、乙、丁【分析】根据垂直定义得出∠AOC＝∠BOD＝90°，再逐个进行判断即可．【解答】解：∵OA⊥OC，OB⊥OD，∴∠AOC＝∠BOD＝90°．∴∠AOC﹣∠BOC＝∠BOD﹣∠BOC．∴∠AOB＝∠COD．∴甲同学说的正确；∵∠BOC+∠AOD＝∠AOC+∠COD+∠BOC＝∠AOC+∠BOD＝90°+90°＝180°，∴乙同学说的正确；∵∠AOB+∠BOC＝∠AOB＝90°，∠BOC和∠COD不一定相等，∴丙同学说的错误；∵图中小于平角的角有∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD，共6个，∴丁同学说的正确．故选：D．【点评】本题考查了余角、补角的定义和角的有关推理的应用，能正确进行推理是解此题的关键．7．如图，将一个直角三角形板AOB的顶点O放在直线CD上，若∠AOC＝35°，则∠BOD等于（）A．155°B．145°C．65°D．55°【分析】根据平角定义可得∠AOC+∠BOD＝90°，再根据余角定义进行计算即可．【解答】解：∵∠AOB＝90°，∴∠AOC+∠BOD＝90°，∴∠BOD＝90°﹣35°＝55°，故选：D．【点评】此题主要考查了余角，关键是掌握如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．8．若∠α与∠β互为余角，∠β是∠α的2倍，则∠α为（）A．20°B．30°C．40°D．60°【分析】先用∠α表示出这个角的余角∠β为（90°﹣α），再根据∠β是∠α的2倍列方程求解．【解答】解：根据题意列方程的：90°﹣α＝2α；解得：α＝30°．故选：B．【点评】本题主要考查余角的概念，若两个角的和为90°，则这两个角互余．9．将一副三角板按如图所示的位置摆放，其中∠α和∠β一定互余的是（）A．B．C．D．【分析】根据图形，结合互余的定义判断即可．【解答】解：A、∠α与∠β不互余，故本选项错误；B、∠α与∠β互余，故本选项正确；C、∠α与∠β不互余，故本选项错误；D、∠α与∠β不互余，∠α和∠β互补，故本选项错误；故选：B．【点评】本题考查了对余角和补角的应用，主要考查学生的观察图形的能力和理解能力．10．已知∠α＝140°﹣5m，∠β＝5m﹣50°，∠α，∠β的关系是（）A．∠α＞∠βB．∠α＜∠βC．互余D．互补【分析】根据余角定义：若两个角的和为90°，则这两个角互余；依此即可解答．【解答】解：∵∠α＝140°﹣5m，∠β＝5m﹣50°，140°﹣5m+5m﹣50°＝90°，∴∠α，∠β的关系是互余．故选：C．【点评】本题比较容易，考查互余角的数量关系．互为余角的两个角的和为90°．11．如图，AB、CD相交于O，OE⊥AB，那么下列结论错误的是（）A．∠AOC与∠BOD是对顶角B．∠AOC与∠COE互为余角C．∠BOD与∠COE互为余角D．∠COE与∠BOE互为补角【分析】根据互余两角之和等于90°，互补两角之和等于180°，判断求解即可．【解答】解：A、∵AB、CD相交于O，∴∠AOC与∠BOD是对顶角，本选项正确；B、∵OE⊥AB，∴∠AOE＝90°，∴∠AOC与∠COE互为余角，本选项正确；C、∵∠AOC与∠BOD是对顶角，且∠AOC与∠COE互为余角，∴∠BOD与∠COE互为余角，本选项正确；D、∵∠COE+∠DOE＝180°，∴∠COE与∠DOE互为补角，本选项错误．故选：D．【点评】本题考查了余角和补角的知识，解答本题的关键在于熟练掌握互余两角之和等于90°，互补两角之和等于180°．12．已知M、N、P、Q四点的位置如图所示，下列结论中，正确的是（）A．∠NOQ＝42°B．∠NOP＝132°C．∠PON比∠MOQ大D．∠MOQ与∠MOP互补【分析】根据已知量角器上各点的位置，得出各角的度数，进而得出答案．【解答】解：如图所示：∠NOQ＝138°，故选项A错误；∠NOP＝48°，故选项B错误；如图可得：∠PON＝48°，∠MOQ＝42°，故∠PON比∠MOQ大，故选项C 正确；由以上可得，∠MOQ与∠MOP不互补，故选项D错误．故选：C．【点评】此题主要考查了余角和补角，正确得出各角的度数是解题关键．13．如果∠1＝∠2，∠1+∠3＝90°，∠2+∠4＝90°，那么∠3与∠4的关系是（）A．互余B．相等C．互补D．以上都不对【分析】由角的互余关系和相等关系容易得出结论．【解答】解：∵∠1＝∠2，∠1+∠3＝90°，∠2+∠4＝90°，∴∠3＝∠4；故选：B．【点评】本题考查了互为余角的关系；熟练掌握互余两角的关系是解决问题的关键．14．若∠α+∠θ＝90°，∠β＝∠θ，则∠α与∠β的关系是（）A．∠α与∠β互余B．∠α与∠β互补C．∠α与∠β相等D．∠α大于∠β【分析】根据余角的定义解答即可．【解答】解：∵∠α+∠θ＝90°，∠β＝∠θ，∴∠α+∠β＝90°，∴∠α与∠β互余，故选：A．【点评】主要考查了余角和补角的概念以及运用．互为余角的两角的和为90°，互为补角的两角之和为180°．解此题的关键是能准确的从题意中找出这两个角之间的数量关系，从而判断出两角之间的关系．15．下列图形中，∠1与∠2互为补角的是（）A．B．C．D．【分析】根据补角的概念对各个选项进行判断即可．【解答】解：根据补角的概念可知，C中∠1与∠2互为补角，故选：C．【点评】本题考查的是余角和补角的概念，若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．16．下列说法错误的是（）A．48°21′36″的余角是41.64°B．点C是线段AB上的点，AB＝10，AC＝6，点D是线段BC的中点，则线段CD＝2C．∠AOC＝60°，经过顶点O引一条射线OD，且∠AOD＝25°，则∠COD ＝85°D．已知线段a，b如图，则尺规作图中，线段AD＝2a﹣b【分析】根据余角和补角的概念、度分秒的换算、两点间的距离的计算，角的计算以及基本尺规作图进行判断即可．【解答】解：48°21′36″的余角是41°38′24″，41°38′24″＝41.64°，A说法正确，不合题意；点C是线段AB上的点，AB＝10，AC＝6，则BC＝4，又点D是线段BC的中点，则线段CD＝BC＝2，B说法正确，不合题意；∠AOC＝60°，经过顶点O引一条射线OD，且∠AOD＝25°，则∠COD＝85°或35°，C说法错误，符合题意；根据基本尺规作图的步骤可知，线段AD＝2a﹣b，D说法正确，不合题意；故选：C．【点评】本题考查的是余角和补角的概念、度分秒的换算、两点间的距离的计算，角的计算以及基本尺规作图，正确理解相关的概念和性质以及尺规作图的一般步骤是解题的关键．17．若∠A＝64°，则它的余角等于（）A．116°B．26°C．64°D．50°【分析】根据两个角的和为90°，则这两个角互余计算即可．【解答】解：∵∠A＝64°，∴90°﹣∠A＝26°，∴∠A的余角等于26°，故选：B．【点评】本题考查的是余角和补角的定义，若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．18．已知一个角的补角是这个角的余角的3倍，则这个角的度数为（）A．22.5°B．45°C．60°D．90°【分析】设这个角的度数为x，然后根据补角和余角的定义列出方程，再求解即可．【解答】解：设这个角的度数为x，由题意得，180°﹣x＝3（90°﹣x），解得x＝45°．故选：B．【点评】本题考查了余角和补角，是基础题，熟记概念并准确列出方程是解题的关键．19．若∠A的补角加上30°是∠A的余角的5倍，则∠A的度数为（）A．60°B．50°C．40°D．30°【分析】首先设∠A的度数为x，则∠A的补角是180°﹣x，∠A的余角是90°﹣x，利用∠A的补角加上30°是∠A的余角的5倍得出等式求出答案．【解答】解：设∠A的度数为x，则∠A的补角是180°﹣x，∠A的余角是90°﹣x．根据题意得：180﹣x+30＝5（90﹣x），解得：x＝60．故选：A．【点评】此题主要考查了互补与互余角的关系，正确得出等量关系是解题关键．20．已知∠1＝40°，则∠1的余角的度数是（）A．40°B．50°C．140°D．150°【分析】根据余角的定义作答．【解答】解：∵∠1＝40°，∴∠1的余角的度数＝90°﹣∠1＝50°．故选：B．【点评】此题考查了余角的定义，解决本题的关键是如果两个角的和是90°，那么这两个角互余．21．将一副三角板按如图所示位置摆放，其中∠α与∠β一定互余的是（）A．B．C．D．【分析】根据图形，结合互余的定义判断即可．【解答】解：A、∠α与∠β不互余，故本选项错误；B、∠α与∠β不互余，故本选项错误；C、∠α与∠β互余，故本选项正确；D、∠α与∠β不互余，∠α和∠β互补，故本选项错误；故选：C．【点评】本题考查了对余角和补角的应用，主要考查学生的观察图形的能力和理解能力．22．下列说法中正确的个数是（）①锐角的补角一定是钝角；②一个角的补角一定大于这个角；③如果两个角是同一个角的补角，那么它们相等；④锐角和钝角互补．A．1B．2C．3D．4【分析】首先根据余角与补角的定义，即可作出判断．【解答】解：∵锐角的补角一定是钝角，∴①正确；∵如90°角的补角的度数是90°，∴说一个角的补角一定大于这个角错误，∴②错误；∵如果两个角是同一个角的补角，那么它们相等，∴③正确；∵如∠A＝10°，∠B＝100°，当两角不互补，∴说锐角和钝角互补错误，∴④错误；即正确的有2个，故选：B．【点评】本题考查了补角和余角的定义，以及补角的性质：同角的补角相等，理解定义是关键．23．若一个角的补角等于它的余角的3倍，则这个角为（）A．75°B．60°C．45°D．30°【分析】根据互补的两角之和为180°，互余的两角之和为90°，利用方程思想求解即可．【解答】解：设这个角为x，则余角为90°﹣x，补角为180°﹣x，由题意得，180°﹣x＝3（90°﹣x），解得：x＝45．故选：C．【点评】本题考查了余角和补角的知识，属于基础题，掌握互补的两角之和为180°，互余的两角之和为90°是关键．24．一个角的度数比它的余角的度数大20°，则这个角的度数是（）A．20°B．35°C．45°D．55°【分析】设这个角为x，则它的余角为90°﹣x，根据题意可得出x的值．【解答】解：设这个角为x，则它的余角为90°﹣x，由题意得，x﹣（90°﹣x）＝20°，解得：x＝55°．故选：D．【点评】本题考查了余角和补角的知识，属于基础题，注意掌握互为余角的两角之和为90°．25．若一个角的余角与它补角互补，则这个角是（）A．30°B．45°C．60°D．90°【分析】首先根据余角与补角的定义，设这个角为x°，则它的余角为（90﹣x）°，补角为（180﹣x）°，再根据题中给出的等量关系列方程即可求解．【解答】解：设这个角为x°，则它的余角为（90﹣x）°，补角为（180﹣x）°，根据题意可知，（90﹣x）+（180﹣x）＝180，解得x＝45，故选：B．【点评】此题综合考查余角与补角，属于基础题中较难的题，解答此类题一般先用未知数表示所求角的度数，再根据一个角的余角和补角列出代数式和方程求解．26．如果∠α＝26°，那么∠α余角的补角等于（）A．20°B．70°C．110°D．116°【分析】此题求的是∠α的余角的补角，只要用180°除以它的余角即可得出本题，或者用90°+∠α也可以解出此题．【解答】解：设∠α余角为∠β，∠β的补角为∠γ，则∠β＝90°﹣∠α，∠γ＝180°﹣∠β＝180°﹣（90°﹣∠α＝90°+∠α）＝116°．故选：D．【点评】此题考查的是角的性质，两角互余和为90°，互补和为180°，还考查了换元思想的运用．27．一个角的余角和这个角的补角也互为补角，这个角的度数等于（）A．90°B．75°C．45°D．15°【分析】首先根据余角与补角的定义，设这个角为x°，则它的余角为（90°﹣x），补角为（180°﹣x），再根据题中给出的等量关系列方程即可求解．【解答】解：设这个角的度数为x，则它的余角为（90°﹣x），补角为（180°﹣x），依题意，得（90°﹣x）+（180°﹣x）＝180°解得x＝45°．故选：C．【点评】此题综合考查余角与补角，属于基础题中较难的题，解答此类题一般先用未知数表示所求角的度数，再根据一个角的余角和补角列出方程求解．28．已知：∠1+∠2＝180°，且∠1＞∠2，那么∠2的余角是（）A．（∠1+∠2）B．∠1C．（∠1﹣∠2）D．不能确定【分析】根据题意把∠1+∠2＝180°进行变形，根据余角的概念计算即可．【解答】解：∵∠1+∠2＝180°，∴（∠1+∠2）＝90°，∠2＝180°﹣∠1，∠2的余角是90°﹣（180°﹣∠1）＝∠1﹣90°＝∠1﹣（∠1+∠2）＝（∠1﹣∠2），故选：C．【点评】本题考查的是余角和补角的概念，若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．29．已知：∠1+∠2＝180°，且∠1＞∠2，则∠2与（∠1﹣∠2）的关系为（）A．相等B．互补C．互余D．和为45°【分析】将∠2与（∠1﹣∠2）相加求值，根据余角的定义即可得到∠2与（∠1﹣∠2）的关系．【解答】解：∵∠2+（∠1﹣∠2）＝（∠1+∠2）＝90°，∴∠2与（∠1﹣∠2）的关系是互余．故选：C．【点评】本题考查了互余的定义，知道两个角的和为90°，则这两个角互余是解题的关键．30．如图，点B，O，D在同一条直线上，∠1＝15°，∠AOC＝90°，则∠2的度数为（）A．15°B．75°C．105°D．165°【分析】根据互余的性质求出∠COB的度数，根据互补的概念求出∠2的度数．【解答】解：∵∠1＝15°，∠AOC＝90°，∴∠COB＝75°，∴∠2＝180°﹣∠COB＝105°，故选：C．【点评】本题考查的是余角和补角的概念和性质，掌握若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补是解题的关键．31．若一个角的余角的两倍与这个角的补角的和210°，这个角的度数为（）A．70°B．60°C．50°D．40°【分析】设这个角为x，则这个角的余角为90°﹣x，补角为180°﹣x，然后根据这个角的余角的两倍与这个角的补角的和210°列方程求解即可．【解答】解：设这个角为x，则这个角的余角为90°﹣x，补角为180°﹣x．根据题意得：2（90°﹣x）+180°﹣x＝210°，解得：x＝50°．故选：C．【点评】本题主要考查的是补角和余角的定义，解答本题需要同学们熟记余角和补角的定义，方程思想的应用是解题的关键．32．如图，在△ABC中，∠C＝90°，点D，E分别在边AC，AB上．若∠B＝∠ADE，则下列结论正确的是（）A．∠A和∠B互为补角B．∠B和∠ADE互为补角C．∠A和∠ADE互为余角D．∠AED和∠DEB互为余角【分析】根据余角的定义，即可解答．【解答】解：∵∠C＝90°，∴∠A+∠B＝90°，∵∠B＝∠ADE，∴∠A+∠ADE＝90°，∴∠A和∠ADE互为余角．故选：C．【点评】本题考查了余角和补角，解决本题的关键是熟记余角的定义．33．一个角的度数比它的余角的度数大20°，则这个角的度数是（）A．35°B．45°C．55°D．65°【分析】设这个角为x，则它的余角为90°﹣x，根据题意列出方程可得出x的值．【解答】解：设这个角为x，则它的余角为90°﹣x，由题意得x﹣（90°﹣x）＝20°，解得：x＝55°．故选：C．【点评】本题考查了余角和补角的知识，属于基础题，注意掌握互为余角的两角之和为90°．二．填空题（共13小题）34．若一个角的补角等于它的余角的3倍，则这个角为45度．【分析】根据互补的两角之和为180°，互余的两角之和为90°，利用方程思想求解即可．【解答】解：设这个角为x，则余角为90°﹣x，补角为180°﹣x，由题意得，180°﹣x＝3（90°﹣x），解得：x＝45．故答案为：45；【点评】本题考查了余角和补角的知识，属于基础题，掌握互补的两角之和为180°，互余的两角之和为90°是关键．35．一个角的余角的3倍比它的补角的2倍少120°，则这个角的度数为30°．【分析】若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．结合已知条件列方程求解．【解答】解：设这个角是x°，根据题意，得3（90﹣x）＝2（180﹣x）﹣120，解得x＝30．即这个角的度数为30°．故答案为：30°．【点评】此题考查了余角和补角的知识，属于基础题，解答本题的关键是掌握互余两角之和为90°，互补两角之和为180°．36．一个角的余角比它的补角的一半还少20°，则这个角为40°．【分析】设这个角为x，根据互为余角的两个角的和等于90°表示出它的余角，互为补角的两个角的和等于180°表示出它的补角，然后列出方程求解即可．【解答】解：设这个角为x，则它的余角为90°﹣x，它的补角为180°﹣x，由题意得，90°﹣x＝（180°﹣x）﹣20°，解得x＝40°，所以，这个角为40°．故答案为：40°．【点评】本题考查了余角和补角，熟记概念并列出方程是解题的关键．37．若∠A与∠B互余，∠B与∠C互余，则∠A与∠C的关系是相等，依据是同角的余角相等．【分析】根据∠A与∠B互补，∠B与∠C互余，先把∠A、∠C都用∠B来表示，再进行运算．【解答】解：∵∠A+∠B＝90°∴∠A＝90°﹣∠B又∵∠B+∠C＝90°∴∠C＝90°﹣∠B∴∠A＝∠C．依据是：同角的余角相等．故答案为：相等，同角的余角相等．【点评】本题主要考查余角的知识点，熟记定义是解答本题的关键．38．已知一个角的余角等于这个角的补角的，那这个角是60°．【分析】设这个角是x，根据互余的两个角的和等于90°，互补的两个角的和等于180°表示出它的余角和补角，然后列出方程求解即可．【解答】解：设这个角是x，则它的余角为90°﹣x，补角为180°﹣x，由题意得，90°﹣x＝（180°﹣x），解得x＝60°，即这个角是60°．故答案为：60°．【点评】本题考查了余角和补角，熟记概念并列出方程是解题的关键．39．一个角的余角比它的补角的还少20°，则这个角的大小是75°．【分析】首先根据余角与补角的定义，设这个角为x，则它的余角为（90°﹣x），补角为（180°﹣x），再根据题中给出的等量关系列方程即可求解．【解答】解：设这个角为x，则它的余角为（90°﹣x），补角为（180°﹣x），根据题意可，得90°﹣x＝（180°﹣x）﹣20°，解得x＝75°，故答案为75°．【点评】本题考查了余角与补角的定义，解答此类题一般先用未知数表示所求角的度数，再根据一个角的余角和补角列出代数式和方程求解，难度适中．40．若∠β＝40°，则∠β的补角等于140°．【分析】若两个角的和为180°，则这两个角互补．根据一个角的补角等于180°减去这个角的度数进行计算．【解答】解：∠β的补角＝180°﹣∠β＝180°﹣40°＝140°．故答案为140°．【点评】解答此类题一般根据一个角的补角等于180°减去这个角的度数进行计算．41．已知∠AOB＝40°，OC平分∠AOB，则∠AOC的补角等于160度．【分析】根据角平分线和补角的定义计算．【解答】解：已知∠AOB＝40°，OC平分∠AOB，则∠AOC＝20°∠AOC的补角等于160度．【点评】本题考查余角和补角的定义：如果两个角的和为90°，则这两个角互为余角，如果两个角的和为180°，则这两个角互为补角．42．一个角的补角的余角等于65°，则这个角等于155度．【分析】根据余角、补角的定义计算．【解答】解：一个角的补角的余角等于65°则这个角的补角等于90°﹣65°＝25°故这个角等于155度．故填155．【点评】本题考查补角、余角的定义：如果两个角的和为180°，则这两个角互为补角，如果两个角的和为90°，则这两个角互为余角．43．30°角的余角是60°，补角是150°．【分析】根据互余的两角之和为90°，互补的两角之和为180°，即可得出答案．【解答】解：90°﹣30°＝60°，180°﹣30°＝150°．答：30°的角的余角是60°，补角是150°．故答案为：60°，150°．【点评】本题考查了余角和补角的知识，关键是掌握互余的两角之和为90°，互补的两角之和为180°．44．如图，已知∠AOC＝90°，直线BD过点O，∠COD＝115°15′，则∠AOB ＝25°15′．【分析】由图形可知∠COD+∠COB＝180°，从而可表示出∠COB的度数，然后由∠AOB＝90°﹣∠COB求解即可．【解答】解：∵∠COD+∠COB＝180°，∠COD＝115°15′，∴∠COB＝180°﹣115°15′＝64°45′，∴∠AOB＝90°﹣∠COB＝25°15′．故答案为：25°15′．【点评】考查了余角和补角，余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．解题关键是求出∠COB的度数．45．如图，∠AOC和∠DOB都是直角，如果∠DOC＝35°，那么∠AOB的度数为145°．【分析】先求出∠AOD，再根据∠AOB＝∠AOD+∠BOD计算即可得解．【解答】解：∵∠AOC是直角，∠DOC＝35°，∴∠AOD＝90°﹣∠DOC＝90°﹣35°＝55°，∴∠AOB＝∠AOD+∠BOD＝55°+90°＝145°．故答案为：145°．【点评】本题考查了余角和补角，是基础题，熟记概念并准确识图是解题的关键．46．一个角的余角比它的补角的少20°，则这个角为40°．【分析】设这个角为x，则它的余角为90°﹣x，补角180°﹣x，然后根据题意列方程求解即可．【解答】解：设这个角为x，则它的余角为90°﹣x，补角为180°﹣x．根据题意得：90°﹣x＝．解得：x＝40°．故答案为：40°．【点评】此题考查的是余角和补角的定义，两角互余和为90°，互补和为180°，根据题意列出方程是解题的关键．三．解答题（共4小题）47．如图，将两块直角三角板的直角顶点C叠放在一起．（1）若∠DCB＝35°，求∠ACB的度数；（2）若∠ACB＝140°，求∠DCE的度数．【分析】（1）根据角的和差关系可直接得到∠ACB＝90°+35°＝125°；（2）首先计算出∠BCD的度数，然后再根据∠ABCE＝90°可得∠ECD的度数．【解答】解：（1）∵∠ACD＝90°，∠DCB＝35°，∴∠ACB＝∠ACD+∠DCB＝90°+35°＝125°，（2）∵∠ACB＝140°，∠ACD＝90°，∴∠DCB＝∠ACB﹣∠ACD＝140°﹣90°＝50°，又∵∠ECB＝90°∴∠ECD＝∠ECB﹣∠DCB＝90°﹣50°＝40°．【点评】此题主要考查了余角和补角，关键是理清角之间的和差关系．48．如图，O为直线DA上一点，OE是∠AOB的平分线，∠FOB＝90°．（1）∠AOF的余角是∠BOD；（2）∠DOB的补角是∠AOB；（3）若∠EOF＝20°，求∠AOF的度数．【分析】（1）根据平角定义可得∠AOF+∠BOD＝90°，再根据余角定义可得答案；（2）根据如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角可得答案；（3）首先计算出∠BOE的度数，进而可得∠AOE的度数，再根据角的和差关系可得答案．【解答】解：（1）∵∠BOF＝90°，∴∠AOF+∠BOD＝180°﹣90°＝90°，∴∠AOF的余角是∠BOD，故答案为：∠BOD；（2）∠DOB的补角是∠AOB，故答案为：∠AOB；（3）∵∠EOF＝20°，∠FOB＝90°，∴∠BOE＝70°，∵OE是∠AOB的平分线，∴∠AOE＝∠BOE＝70°，∵∠EOF＝20°，∴∠AOF＝50°．。

冀教版七年级上册数学2.7 角的和与差基础闯关全练知识点一角的和与差1．如图2-7-1所示，下列式子中错误的是( )A.∠AOC= ∠AOB+∠BOCB.∠AOC= ∠AOD-∠CODC.∠AOC= ∠AOB+∠BOD-∠BOCD.∠AOC= ∠AOD-∠BOD+∠BOC2．如图2-7-2，∠AOB=∠COD= 90°，∠BOC= 32°，则∠AOD等于( )A.58°B.158°C.148°D.138°3．把一副三角板按照图2-7-3所示的位置拼在一起，不重叠也没有缝隙，则∠ABC的度数为.4．如图2-7-4所示，A，O，B是同一条直线上的三点，OC，OD，OE是从O点引出的三条射线，且∠1：∠2：∠3：∠4=1：2：3：4．则∠5= °5.计算: (1) 90°-28°12'36"; ( 2) 180°-56°23'48".知识点二角的平分线6．（2019吉林长春德惠期末）如图2-7-5，OC为∠AOB内一条射线，下列条件中不能确定OC平分∠AOB的是( )A. ∠AOC= ∠BOCB.∠AOB=2∠AOCC.∠BOC=21∠AOB D.∠AOC+∠COB= ∠AOB7．（2019湖南张家界桑植期末）如图2-7-6．∠BOA= 90°．OC 平分∠BOA ，OA 平分∠COD ，求∠BOD 的大小，知识点三 互为余角、互为补角的概念及性质8．一个角的余角是54°26'．则这个角的补角是 ．9．如图2-7-7所示，将一副三角板的直角顶点O 重合，证明∠AOD= ∠COB ，并求∠AOC+∠ BOD 的度数.能力提升全练1．如果∠α和∠β互补，且∠α>∠β，那么下列表示∠β的余角的式子中，正确的有( )①90°-∠β；②∠α - 90°；③21（∠α+∠β）；④21（∠α-∠β）． A.4个B.3个C.2个D.1个2．如图2-7-8，OM 是∠AOB 的平分线，OP 是∠MOB 内的一条射线，已知∠AOP 比∠BOP 大30°，则∠MOP= ．3．如图2-7-9，∠AOB=∠DOC= 90°，OE平分∠AOD，反向延长射线OE至F．(1) ∠AOD和∠BOC是否互补？说明理由：(2)射线OF是∠BOC的平分线吗？说明理由．4．如图2-7-10．已知∠AOB= ∠COD=90°，∠BOC= 34°．(1)判断∠BOC与∠AOD之间的数量关系，并说明理由;(2)若OE平分∠AOC，求∠EOC的余角的度数．三年模拟全练一、选择题1．（2018河北石家庄高邑期中，4，★★☆）已知∠α与∠β互补，∠α=5∠β，则∠α等于( )A.150°B.120°C.90°D.60°2．（2019河北沧州献县河城街中学月考，9，★★☆）如图2 -7 - 11，O是直线AB上一点，OD平分∠AOC，∠DOE=90°，则以下结论正确的个数是( )①∠AOD与∠BOE互为余角；②∠AOD=∠COE：③∠BOE=∠COE;④∠DOC与∠DOB互补．A．1B．2C．3D．4二、解答题3．（2018河北唐山乐亭期末，23，★★☆）如图2-7 -12，直线AB与直线CD相交于点O，OE⊥AB，OF平分∠AOC.(1)请写出∠EOC的余角；(2)若∠BOC= 40°，求∠EOF的度数．4．（2019河北唐山滦南期中．25，★★☆）如图2-7-13，直线AB，CD相交于点O，OF平分∠AOE，∠DOF= 90°，垂足为O．(1)写出图中所有与∠AOD互补的角；(2)若∠AOE= 120°，求∠BOD的度数.五年中考全练一、选择题1．（2018广西梧州中考，4，★☆☆）已知∠A= 55°，则它的余角是( )A.25°B.35°C.45°D.55°2．（2018甘肃陇南中考，3，★☆☆）若一个角为65°，则它的补角的度数为( )A.25°B.35°C.115°D.125°二、填空题3．（2018由东日照中考，13，★☆☆）一个角是70°39'，则它的余角的度数是．核心素养全练如图2 -7 - 14，直线AB上有一点O，∠DOB= 90°，∠EOC= 90°．(1)如果∠DOE= 50°，则∠AOC的度数为.(2)直接写出图中相等的锐角，如果∠DOE≠50°，它们还会相等吗？(3)若∠DOE变大，则∠AOC会如何变化？（不必说明理由）答案基础闯关全练1. C 解析：易得A,B,D 中等式成立，C 中,∠AOC= ∠AOB+∠BOD-∠COD ．故选C ．2. C解析：因为∠AOB+ ∠BOC+ ∠COD+ ∠AOD= 360°, ∠AOB=∠COD=90°,∠BOC,=32°,所以∠AOD=360°-90°-32°-90°=148°.3．答案 120°解析 ∠ABC= 30°+90°= 120°.4．答案60解析由A ，O ，B 是同一条直线上的三点，得∠AOB=180°，又由∠1：∠2：∠3=1：2：3，可知∠1= 30°, ∠2= 60°, ∠3=90°，又∠1：∠2：∠3：∠4=1：2：3：4．所以∠4= 120°,所以∠5 =180°-120°= 60°.5．解析(1)原式=89°59'60"- 28°12'36"=61°47 '24".(2)原式=179°59'60"- 56°23 '48"= 123°36'12".6.D解析：A.∠AOC= ∠BOC 能确定OC 平分∠AOB ，故此选项不合题意；B.∠AOB=2∠AOC 能确定OC 平分∠AOB,敞此选项不合题意；C.∠BOC=21∠AOB ，能确定OC 平分∠AOB ，故此选项不合题意；D ．∠AOC+ ∠COB= ∠AOB 不能确定OC 平分∠AOB ，故此选项符合题意．故选D ．7．解析∵∠BOA=90°,OC 平分∠BOA ．∠COA= 45°，又∵OA 平分∠COD,∴∠AOD= ∠COA=45°,∴∠BOD= ∠BOA+∠AOD= 90°+45°=135°.8．答案 144°26'解析∵一个角的余角是54°26'，∴这个角为90°-54°26'=35°34'．∴这个角的补角为180°-35°34'= 144°26'.9．解析①证明：∵∠AOB= ∠DOC=90°,∴∠AOB-∠DOB= ∠DOC-∠DOB.∴ ∠ AOD =∠ BOC.(2)∵∠AOB = ∠ DOC = 900 , ∴∠AOC+ ∠BOD=∠AOB+ ∠ BOC+ ∠ BOD = ∠AOB+ ∠DOC = 90°+90° = 180°.能力提升全练1. B解析：因为90°-∠β+∠β=90°，所以①正确；因为∠α- 90°+∠β= ∠α+∠β-90°= 180°-90°= 90°，所以②正确；因为21(∠α+∠β)+∠β= 21x 180°+∠β= 90°+∠β≠90°，所以③错误；因为21（∠α-∠β）+∠β=21（∠α+∠β）=21×180°= 90°，所以④ 正确，故选B ．2．答案15°解析 因为OM 是∠AOB 的平分线，所以∠AOM= ∠BOM,所以∠AOP- ∠POM=∠BOP+ ∠POM, 所以∠AOP- ∠BOP=2∠POM.因为∠AOP 比∠BOP 大30°,所以2∠POM= 30°，所以MOP= 15°.3．解析(1)互补．理由如下：因为∠AOD+ ∠BOC= 360° -∠ AOB - ∠DOC= 360° - 90° - 90°= 180°,所以∠ AOD 和∠BOC 互补．(2)射线OF 是∠BOC 的平分线，理由如下：因为OE 平分∠ AOD,所以∠AOE=∠DOE ，因为∠COF=180°-∠DOC-∠DOE=90°-∠DOE,∠ BOF= 180°-∠AOB-∠AOE= 90°- ∠AOE.所以∠ COF=∠BOF ，即射线OF 是∠BOC 的平分线．4．解析 (1) ∠BOC+∠AOD= 180°，理由如下：因为∠ AOB= ∠COD= 90°, ∠AOB+ ∠BOC+ ∠COD+ ∠AOD= 360°,所以∠ BOC+ ∠AOD= 360°-∠AOB-∠ COD= 180°.(2)因为∠AOB=90°,∠BOC=34°,所以∠ AOC= ∠AOB+∠BOC=124°,因为OE 平分∠AOC,所以∠EOC= ∠AOE=21∠AOC=62°． 所以∠EOC 的余角的度数为90°-∠EOC=28°，三年模拟全练一、选择题1.A解析： ∵∠α与∠β互补．∴∠α+ ∠β= 180°，∵∠α=5∠β,∴5 ∠β+∠β= 180°，∴∠β= 30°，∴∠α= 150°，故选A.2. C解析： (1)∵∠ DOF,= 90°,∴∠AOD+∠ BOE= 90°,∴∠AOD 与∠BOE 互为余角，故①正确：②∵DD 平分∠ AOC,∴∠AOD=∠COD,∵∠DOC+∠COE= 90°,∴∠AOD+ ∠COE= 90°．故② 错误；③∵ OD 平分∠AOC ．∴∠AOD=∠COD,∵∠DOC+ ∠COE=90°,∠AOD+∠BOE=90°，∴∠CDE=∠BOE,故③正 确；④∵OD 平分∠AOC ，∴∠AOD=∠COD,∵∠AOD+∠DOB = 180°,∴∠DOC+∠ DOB= 180°，故④正确，故选C ．二、解答题3．解析 (1) ∠EOC 的余角有∠BOC 、∠AOD ．(2)∵∠ BOC= 40°,∴∠AOC= 180°-40°= 140°.∵OF 平分∠AOC ．∠FOA=21×140°=70°， ∵EO ⊥AB,∴∠EOA=90°,∴∠EOF=∠EOA-∠FOA=90°-70°=20°.4．解析 (1)∵直线AB ，CD 相交于点O∴∠AOC ，∠BOD 与∠AOD 互补，∵OF 平分∠AOE ，∴∠AOF=∠EOF ．∵∠DOF= 90°.∴∠ COF=∠ DOF= 90°.∴∠DOE=∠AOC.∴∠DOE 也是∠AOD 的补角．∴与∠ AOD 互补的角有∠AOC,∠BOD,∠DOE ．(2)∵OF 分∠AOE,∴∠AOF=21∠AOE=60°, ∵∠ DOF=90°,∴∠BOD= 180°-∠ AOF -∠DOF= 180°-90°-60°=30°.五年中考全练一、选择题1．B解析：∵∠A= 55°．∴它的余角的度数是90°-∠A=90°-55°=35°，故选B.2.C解析：根据互为补角的两个角的度数的和等于180°，得180°-65°= 115°．二、填空题3．答案19°21'解析它的余角的度数是90°-70°39'= 19°21'.核心素养全练解析 (1)∵∠DOB=90°,∴∠AOD=90°,∵∠ DOE= 50°,∠EOC= 90°,∴∠DOC= 40°,∴∠AOC= 90°+40°= 130°故答案为130°.(2) ∠AOE= ∠DOC,∠EOD=∠ COB ，如果∠DOE ≠50°，它们还会相等．理由：∵∠AOD= 90°,∠AOF+∠EOD= 90°.∵∠EOC= 90°.∴∠EOD+∠DOC= 90°,∴∠AOE=∠DOC,∵∠DOB= 90°,∴∠DOC+∠COB= 90°,∴∠EOD= ∠COB.(3)若∠DOE 变大，则∠AOC 变小．∵∠EOC=90°,∴∠DOE+∠DOC=90°.∵∠ DOE 变大．∴∠DOC 变小，∵∠ AOC= ∠AOD+∠DOC=90°+∠DOC ．∴AOC 变小.。