选修4-1高考题精选2

选修4-4 第1节[知能演练]一、选择题1．点M (ρ，θ)关于极点对称的点的坐标为( )A ．(－ρ，－θ)B ．(ρ，π＋θ)C ．(ρ，π－θ)D ．(ρ，－θ)答案：B2．将曲线y ＝12sin3x 变为y ＝sin x 的伸缩变换是( )A.⎩⎪⎨⎪⎧x ＝3x ′y ＝12y ′B.⎩⎪⎨⎪⎧x ′＝3x y ′＝12y C.⎩⎪⎨⎪⎧x ＝3x ′y ＝2y ′D.⎩⎪⎨⎪⎧x ′＝3x y ′＝2y 答案：D3．设点M 的直角坐标为(－1，－3，3)，则它的柱坐标是( )A ．(2，π3，3)B ．(2，2π3，3)C ．(2，4π3，3)D ．(2，5π3，3)解析：ρ＝(－1)2＋(－3)2＝2， tan θ＝3，∴θ＝4π3，z ＝3，∴选C.答案：C4．在极坐标系中，与圆ρ＝4sin θ相切的一条直线方程为( )A ．ρsin θ＝2B ．ρcos θ＝2C ．ρcos θ＝4D ．ρcos θ＝－4解析：圆ρ＝4sin θ的圆心为(2，π2)，半径r ＝2，对于选项A ，方程ρsin θ＝2对应的直线(y ＝2)与圆相交；对于选项B ，方程ρcos θ＝2对应的直线(x ＝2)与圆相切；选项C ，D 对应的直线与圆都相离．答案：B 二、填空题5．已知点M 的极坐标为(6，11π6)，则点M 关于y 轴对称的点的直角坐标为________． 解析：∵点M 的极坐标为(6，11π6)，∴x ＝6cos 11π6＝6cos π6＝6×32＝33，y ＝6sin 11π6＝6sin(－π6)＝－6×12＝－3，∴点M 的直角坐标为(33，－3)，∴点M 关于y 轴对称的点的直角坐标为(－33，－3)． 答案：(－33，－3)6．在极坐标系中，点P (2，3π2)到直线l ：3ρcos θ－4ρsin θ＝3的距离为________．解析：在相应直角坐标系中，P (0，－2)，直线l 方程：3x －4y －3＝0，所以P 到l 的距离：d ＝|3×0－4×(－2)－3|32＋42＝1.答案：1 三、解答题7．说出由曲线y ＝tan x 得到曲线y ＝3tan2x 的变换过程，并求满足其图形变换的伸缩变换．解：y ＝tan x 的纵坐标不变，横坐标缩短为原来的12，得到y ＝tan2x ，再将其纵坐标伸长为原来的3倍，横坐标不变，得到曲线y ＝3tan2x .设y ′＝3tan2x ′，变换为⎩⎪⎨⎪⎧x ′＝λ·x λ>0y ′＝μ·y μ>0，将其代入y ′＝3tan2x ′，得μy ＝3tan2λx与y ＝tan x 比较，可得⎩⎪⎨⎪⎧ μ＝3λ＝12，∴⎩⎪⎨⎪⎧x ′＝12xy ′＝3y.8．从极点O 作直线与另一直线l ：ρcos θ＝4相交于点M ，在OM 上取一点P ，使OM ·OP ＝12.(1)求点P 的轨迹方程；(2)设R 为l 上的任意一点，试求RP 的最小值． 解：(1)设动点P 的坐标为(ρ，θ)， M 的坐标为(ρ0，θ)，则ρρ0＝12，∵ρ0cos θ＝4，∴ρ＝3cos θ即为所求的轨迹方程．(2)由(1)知P 的轨迹是以(32，0)为圆心，半径为32的圆，易得RP 的最小值为1.[高考·模拟·预测]1．极坐标方程ρ＝cos θ化为直角坐标方程为( )A ．(x ＋12)2＋y 2＝14B ．x 2＋(y ＋12)2＝14C ．x 2＋(y －12)2＝14D ．(x －12)2＋y 2＝14解析：由ρ＝cos θ得ρ2＝ρcos θ，∴x 2＋y 2＝x .选D. 答案：D2．在极坐标系中，直线ρsin(θ＋π4)＝2被圆ρ＝4截得的弦长为________．解析：直线ρsin(θ＋π4)＝2可化为x ＋y －22＝0，圆ρ＝4可化为x 2＋y 2＝16，由圆中的弦长公式得2r 2－d 2＝242－(222)2＝4 3.答案：4 33．在极坐标系中，点(1,0)到直线ρ(cos θ＋sin θ)＝2的距离为________．解析：直线ρ(cos θ＋sin θ)＝2可化为x ＋y －2＝0，故点(1,0)到直线距离d ＝|1＋0－2|2＝22.答案：224．两直线ρsin(θ＋π4)＝2008，ρsin(θ－π4)＝2009的位置关系是________．(判断垂直或平行或斜交)解析：两直线方程可化为x ＋y ＝20082，y －x ＝ 20092，故两直线垂直． 答案：垂直5．圆O 1和圆O 2的极坐标方程分别为ρ＝4cos θ，ρ＝－sin θ. (1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程． (2)求经过圆O 1，圆O 2两个交点的直线的直角坐标方程．解：以极点为原点，极轴为x 轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位．(1)x ＝ρcos θ，y ＝ρsin θ，由ρ＝4cos θ得ρ2＝4ρcos θ.所以x 2＋y 2＝4x .即x 2＋y 2－4x ＝0为圆O 1的直角坐标方程． 同理，x 2＋y 2＋y ＝0为圆O 2的直角坐标方程．(2)由⎩⎪⎨⎪⎧x 2＋y 2－4x ＝0，x 2＋y 2＋y ＝0，相减得过交点的直线的直角坐标方程为4x ＋y ＝0.6．求经过极点O (0,0)，A (6，π2)，B (62，9π4)三点的圆的极坐标方程．解：将点的极坐标化为直角坐标，点O ，A ，B 的直角坐标分别为(0,0)，(0,6)，(6,6)，故△OAB 是以OB 为斜边的等腰直角三角形，圆心为(3,3)，半径为32，圆的直角坐标方程为(x －3)2＋(y －3)2＝18，即x 2＋y 2－6x －6y ＝0，将x ＝ρcos θ，y ＝ρsin θ代入上述方程，得ρ2－6ρ(cos θ＋sin θ)＝0，即ρ＝62cos(θ－π4)．。

第2讲 圆周角定理与圆的切线【高考会这样考】考查圆的切线定理和性质定理的应用． 【复习指导】本讲复习时，牢牢抓住圆的切线定理和性质定理，以及圆周角定理和弦切角等有关知识，重点掌握解决问题的基本方法.基础梳理1．圆周角定理(1)圆周角：顶点在圆周上且两边都与圆相交的角． (2)圆周角定理：圆周角的度数等于它所对弧度数的一半． (3)圆周角定理的推论①同弧(或等弧)上的圆周角相等；同圆或等圆中，相等的圆周角所对的弧相等． ②半圆(或直径)所对的圆周角是90°；90°的圆周角所对的弦是直径． 2．圆的切线(1)直线与圆的位置关系直线与圆交点的个数 直线到圆心的距离d 与圆的半径r 的关系 相交 两个 d ＜r 相切 一个 d ＝r 相离无d ＞r(2)切线的性质及判定①切线的性质定理：圆的切线垂直于经过切点的半径． ②切线的判定定理过半径外端且与这条半径垂直的直线是圆的切线． (3)切线长定理从圆外一点引圆的两条切线长相等． 3．弦切角(1)弦切角：顶点在圆上，一边与圆相切，另一边与圆相交的角．(2)弦切角定理及推论①定理：弦切角的度数等于所夹弧的度数的一半．②推论：同弧(或等弧)上的弦切角相等，同弧(或等弧)上的弦切角与圆周角相等．双基自测1．如图所示，△ABC 中，∠C ＝90°，AB ＝10，AC ＝6，以AC 为直径的圆与斜边交于点P ，则BP 长为________．解析 连接CP .由推论2知∠CP A ＝90°，即CP ⊥AB ，由射影定理知，AC 2＝AP ·AB .∴AP ＝3.6，∴BP ＝AB －AP ＝6.4. 答案 6.42．如图所示，AB 、AC 是⊙O 的两条切线，切点分别为B 、C ，D是优弧BC 上的点，已知∠BAC ＝80°， 那么∠BDC ＝________. 解析 连接OB 、OC ，则OB ⊥AB ，OC ⊥AC ，∴∠BOC ＝180°－∠BAC ＝100°，∴∠BDC ＝12∠BOC ＝50°. 答案 50°3．(2011·广州测试(一))如图所示，CD 是圆O 的切线，切点为C ，点A 、B 在圆O 上，BC ＝1，∠BCD ＝30°，则圆O 的面积为________．解析 连接OC ，OB ，依题意得，∠COB ＝2∠CAB ＝2∠BCD ＝60°，又OB ＝OC ， 因此△BOC 是等边三角形，OB ＝OC ＝BC ＝1，即圆O 的半径为1， 所以圆O 的面积为π×12＝π. 答案 π4．(2011·深圳二次调研)如图，直角三角形ABC 中，∠B ＝90°，AB ＝4，以BC 为直径的圆交AC 边于点D ，AD ＝2，则∠C 的大小为________．解析 连接BD ，则有∠ADB ＝90°.在Rt △ABD 中，AB ＝4，AD ＝2，所以∠A ＝60°；在Rt △ABC 中，∠A ＝60°，于是有∠C ＝30°. 答案 30°5．(2011·汕头调研)如图，MN 是圆O 的直径，MN 的延长线与圆O 上过点P 的切线P A 相交于点A ，若∠M ＝30°，AP ＝23，则圆O 的直径为________．解析 连接OP ，因为∠M ＝30°，所以∠AOP ＝60°，因为P A 切圆O 于P ，所以OP ⊥AP ，在Rt △ADO 中，OP ＝AP tan ∠AOP ＝23tan 60°＝2，故圆O 的直径为4.答案 4考向一 圆周角的计算与证明【例1】►(2011·中山模拟)如图，AB 为⊙O 的直径，弦AC 、BD 交于点P ，若AB＝3，CD ＝1，则sin ∠APB ＝________.[审题视点] 连结AD ，BC ，结合正弦定理求解． 解析 连接AD ，BC .因为AB 是圆O 的直径，所以∠ADB ＝∠ACB ＝90°.又∠ACD ＝∠ABD ，所以在△ACD 中，由正弦定理得：CD sin ∠DAC ＝AD sin ∠ACD ＝AD sin ∠ABD ＝AB sin ∠ABD sin ∠ABD ＝AB ＝3，又CD ＝1，所以sin ∠DAC ＝sin ∠DAP ＝13，所以cos ∠DAP ＝23 2.又sin∠APB＝sin (90°＋∠DAP)＝cos∠DAP＝23 2.答案23 2解决本题的关键是寻找∠APB与∠DAP的关系以及AD与AB的关系．【训练1】如图，点A，B，C是圆O上的点，且AB＝4，∠ACB＝30°，则圆O的面积等于________．解析连接AO，OB.因为∠ACB＝30°，所以∠AOB＝60°，△AOB为等边三角形，故圆O的半径r＝OA＝AB＝4，圆O的面积S＝πr2＝16π.答案16π考向二弦切角定理及推论的应用【例2】►如图，梯形ABCD内接于⊙O，AD∥BC，过B引⊙O的切线分别交DA、CA的延长线于E、F.已知BC＝8，CD＝5，AF＝6，则EF的长为________．[审题视点] 先证明△EAB∽△ABC，再由AE∥BC及AB＝CD等条件转化为线段之间的比例关系，从而求解．解析∵BE切⊙O于B，∴∠ABE＝∠ACB.又AD∥BC，∴∠EAB＝∠ABC，∴△EAB∽△ABC，∴BEAC＝ABBC.又AE∥BC，∴EFAF＝BEAC，∴ABBC＝EFAF.又AD∥BC，∴AB＝CD，∴AB＝CD，∴CDBC＝EFAF，∴58＝EF6，∴EF＝308＝154.答案15 4(1)圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系，从而证明三角形全等或相似，可求线段或角的大小．(2)涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直线(或半径)或向弦(弧)两端画圆周角或作弦切角．【训练2】(2010·新课标全国)如图，已知圆上的弧AC＝BD，过C点的圆的切线与BA的延长线交于E点，证明：(1)∠ACE＝∠BCD；(2)BC2＝BE×CD.证明(1)因为AC＝BD，所以∠BCD＝∠ABC.又因为EC与圆相切于点C，故∠ACE＝∠ABC，所以∠ACE＝∠BCD.(2)因为∠ECB＝∠CDB，∠EBC＝∠BCD，所以△BDC∽△ECB，故BCBE＝CDBC，即BC2＝BE×CD.高考中几何证明选讲问题(二)从近两年的新课标高考试题可以看出，圆的切线的有关知识是重点考查对象，并且多以填空题的形式出现．【示例】►(2011·天津卷)如图，已知圆中两条弦AB与CD相交于点F，E是AB 延长线上一点，且DF＝CF＝2，AF∶FB∶BE＝4∶2∶1.若CE与圆相切，则线段CE的长为________．。

A组(供高考题型为填空题的省份使用)1．如图，∠B＝∠D，AE⊥BC，∠ACD＝90°，且AB＝6，AC＝4，AD＝12，则BE＝________.解析∵AC＝4，AD＝12，∠ACD＝90°，∴CD2＝AD2－AC2＝128，∴CD＝8 2.又∵AE⊥BC，∠B＝∠D，∴△ABE∽△ADC，∴ABAD＝BECD，∴BE＝AB·CDAD＝6×8212＝4 2.答案4 22．如图，A，E是半圆周上的两个三等分点，直径BC＝4，AD⊥BC，垂足为D，BE与AD相交于点F，则AF的长为________．解析如图，连接CE，AO，AB.根据A，E是半圆周上的两个三等分点，BC 为直径，可得∠CEB＝90°，∠CBE＝30°，∠AOB＝60°，故△AOB为等边三角形，AD＝3，OD＝BD＝1，∴DF＝3 3，∴AF＝AD－DF＝23 3.答案23 33．如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD＝a2，点E，F分别为线段AB，AD的中点，则EF＝________.解析 连接DE ，由于E 是AB 的中点，故BE ＝a2.又CD ＝a2，AB ∥DC ，CB ⊥AB ， ∴四边形EBCD 是矩形．在Rt △ADE 中，AD ＝a ，F 是AD 的中点，故EF ＝a2. 答案 a 24.如图，已知P A ，PB 是圆O 的切线，A ，B 分别为切点，C 为圆O 上不与A ，B 重合的另一点，若∠ACB ＝120°，则∠APB ＝________.解析 如图，连接OA ，OB ，∠P AO ＝∠PBO ＝90°，∵∠ACB ＝120°，∴∠AOB ＝120°.又P ，A ，O ，B 四点共圆，故∠APB ＝60°. 答案 60°5．如图，点P 在圆O 直径AB 的延长线上，且PB ＝OB ＝2，PC 切圆O 于C 点，CD ⊥AB 于D 点，则CD ＝________.解析 由切割线定理知，C 2＝P A ·PB ，解得PC ＝2 3.连接OC ，又OC ⊥PC ，故CD ＝PC ·OC PO ＝23×24＝ 3. 答案36．如图，点A 、B 、C 都在⊙O 上，过点C 的切线交AB 的延长线于点D ，若AB ＝5，BC ＝3，CD ＝6，则线段AC 的长为________．解析 由切割线定理，得CD 2＝ BD ·AD .因为CD ＝6，AB ＝5，则36＝BD (BD ＋5)， 即BD 2＋5BD －36＝0，即(BD ＋9)(BD －4)＝0，所以BD ＝4.因为∠A ＝∠BCD ，所以△ADC ∽△CDB ，于是AC CB ＝CD BD . 所以AC ＝CD BD ·BC ＝64×3＝92. 答案 927．如图，在△ABC 中，∠C ＝90°，∠A ＝60°，AB ＝20，过C 作△ABC 的外接圆的切线CD ，BD ⊥CD ，BD 与外接圆交于点E ，则DE 的长为______．解析 由题意，得弦切角∠BCD ＝∠A ＝60°，∠ACB ＝∠D ＝90°， ∴△ABC ∽△CBD .∴AB CB ＝AC CD ，CD ＝CB ·AC AB ＝20sin 60°×20cos 60°20＝5 3.又∵CD 与圆相切，∴CD 2＝DE ·DB ，则DE ＝CD 2DB ＝(53)2CB sin 60°＝25×320×sin 60°×sin 60°＝5.答案 58．如图，⊙O 的割线PBA 过圆心O ，弦CD 交P A 于点F ，且△COF ∽△PDF ，若PB ＝OA ＝2，则PF ＝________.解析 由相交弦定理可得BF ·AF ＝DF ·CF ， 由△COF ∽△PDF 可得CF PF ＝OF DF ， 即得DF ·CF ＝PF ·OF .∴BF ·AF ＝PF ·OF ， 即(PF －2)·(6－PF )＝PF ·(4－PF )，解得PF ＝3. 答案 39．如图，四边形ABCD 是圆O 的内接四边形，延长AB 和DC 相交于点P .若PB P A ＝12，PC PD ＝13，则BC AD 的值为________．解析 ∵∠P ＝∠P ，∠PCB ＝∠P AD ， ∴△PCB ∽△P AD .∴PB PD ＝PC P A ＝BC AD . ∵PB P A ＝12，PC PD ＝13，∴BC AD ＝66. 答案 6610.如图，AB 是圆O 的直径，点C 在圆O 上，延长BC 到D 使BC ＝CD ，过C 作圆O 的切线交AD 于E .若AB ＝6，ED ＝2，则BC ＝________.解析 C 为BD 中点，且AC ⊥BC ，故△ABD 为等腰三角形．AB ＝AD ＝6， ∴AE ＝4，DE ＝2，又AE AC ＝ACAD ⇒AC 2＝AE ·AD ＝4×6＝24，AC ＝26，在△ABC 中，BC ＝AB 2－AC 2＝36－24＝2 3. 答案 2 311．如图，已知Rt △ABC 的两条直角边AC ，BC 的长分别为3 cm ，4 cm ，以AC 为直径的圆与AB 交于点D ，则BD ＝________cm.解析 如图，连接DC ，则CD ⊥AB ，Rt △ADC ∽Rt △ACB . 故AD AC ＝AC AB ，即AD 3＝35， AD ＝95(cm)， BD ＝5－95＝165(cm)． 答案 16512．如图所示，直线PB 与圆O 相切于点B ，D 是弦AC 上的点，∠PBA ＝∠DBA .若AD ＝m ，AC ＝n ，则AB ＝________.解析 ∵直线PB 与圆相切于点B ，且∠PBA ＝∠DBA ，∴∠ACB ＝∠ABP ＝∠DBA ，由此可得直线AB 是△BCD 外接圆的切线且B 是切点，则由切割线定理得AB 2＝AD ·AC ＝mn ，即得AB ＝mn . 答案mn13．如图，已知AB 和AC 是圆的两条弦，过点B 作圆的切线与AC 的延长线相交于点D .过点C 作BD 的平行线与圆相交于点E ，与AB 相交于点F ，AF ＝3，FB ＝1，EF ＝32，则线段CD 的长为________．解析 由相交弦定理得AF ·FB ＝EF ·FC ， ∴FC ＝AF ·FBEF ＝2.由△AFC ∽△ABD ， 可知FC BD ＝AF AB ，∴BD ＝FC ·AB AF ＝83. 由切割线定理得DB 2＝DC ·DA ， 又DA ＝4CD ，∴4DC 2＝DB 2＝649，∴DC ＝43. 答案 4314．如图所示，已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且DF ＝CF ＝2，AF ∶FB ∶BE ＝4∶2∶1.若CE 与圆相切，则线段CE 的长为________．解析 设AF ＝4k ，BF ＝2k ，BE ＝k ，由DF ·FC ＝AF ·BF ，得2＝8k 2，即k ＝12.所以AF ＝2，BF ＝1，BE ＝12，AE ＝72.由切割线定理，得CE 2＝BE ·EA ＝12×72＝74，所以CE ＝72. 答案 7215．如图，点D 在⊙O 的弦AB 上移动，AB ＝4，连接OD ，过点D 作OD 的垂线交⊙O 于点C ，则CD 的最大值为________．解析当OD的值最小时，DC最大，易知D为AB的中点时，DB＝DC＝2最大．答案 2B组(供高考题型为解答题的省份使用)1．如图，△ABC的角平分线AD的延长线交它的外接圆于点E.(1)证明：△ABE∽△ADC；(2)若△ABC的面积S＝12AD·AE，求∠BAC的大小．(1)证明由已知条件，可得∠BAE＝∠CAD.因为∠AEB与∠ACB是同弧上的圆周角，所以∠AEB＝∠ACD.故△ABE∽△ADC.(2)解因为△ABE∽△ADC，所以ABAE＝AD AC，即AB·AC＝AD·AE.又S＝12AB·AC sin∠BAC，且S＝12AD·AE，故AB·AC·sin∠BAC＝AD·AE.则sin∠BAC＝1，又∠BAC为三角形内角，所以∠BAC＝90°.2．(2014·辽宁卷)如图，EP交圆于E，C两点，PD切圆于D，G为CE上一点且PG＝PD，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F.(1)求证：AB为圆的直径；(2)若AC＝BD，求证：AB＝ED.证明(1)因为PD＝PG，所以∠PDG＝∠PGD.由于PD为切线，故∠PDA＝∠DBA，又由于∠PGD＝∠EGA，故∠DBA＝∠EGA.所以∠DBA＋∠BAD＝∠EGA＋∠BAD，从而∠BDA＝∠PF A.由于AF⊥EP，所以∠PF A＝90°，于是∠BDA＝90°.故AB是直径．(2)连接BC，DC.由于AB是直径，故∠BDA＝∠ACB＝90°.在Rt△BDA与Rt△ACB中，AB＝BA，AC＝BD，从而Rt△BDA≌Rt△ACB，于是∠DAB＝∠CBA.又因为∠DCB＝∠DAB，所以∠DCB＝∠CBA，故DC∥AB.由于AB⊥EP，所以DC⊥EP，∠DCE为直角．于是ED为直径．由(1)得ED＝AB.3．如图，过圆O外一点M作它的一条切线，切点为A，过A点作直线AP垂直直线OM，垂足为P.(1)证明：OM·OP＝OA2；(2)N为线段AP上一点，直线NB垂直直线ON，且交圆O于B点．过B点的切线交直线ON于K.证明：∠OKM＝90°.证明(1)因为MA是圆O的切线，所以OA⊥AM.又因为AP⊥OM，在Rt△OAM 中，由射影定理知，OA2＝OM·OP.(2)因为BK是圆O的切线，BN⊥OK，同(1)，有OB2＝ON·OK，又OB＝OA，所以OP·OM＝ON·OK，即ONOP＝OMOK.又∠NOP＝∠MOK，所以△ONP∽△OMK，故∠OKM＝∠OPN＝90°.4．如图，已知在△ABC中，AB＝AC，D是△ABC外接圆劣弧上的点(不与点A，C重合)，延长BD至E.(1)求证：AD的延长线平分∠CDE；(2)若∠BAC＝30°，△ABC中BC边上的高为2＋3，求△ABC外接圆的面积．(1)证明如图，设F为AD延长线上一点．∵A、B、C、D四点共圆，∴∠CDF＝∠ABC.又AB＝AC，∴∠ABC＝∠ACB，且∠ADB＝∠ACB，∴∠ADB＝∠CDF.又∠EDF＝∠ADB，故∠EDF＝∠CDF，即AD的延长线平分∠CDE.(2)解设O为外接圆圆心，连接AO交BC于H，则AH⊥BC.连接OC，由题意∠OAC＝∠OCA＝15°，∠ACB＝75°，∴∠OCH＝60°.设圆半径为r，则r＋32r＝2＋3，得r＝2，∴△ABC外接圆的面积为4π.5．如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E.(1)求证：AB2＝DE·BC；(2)若BD＝9，AB＝6，BC＝9，求切线PC的长．(1)证明∵AD∥BC，∴.∴AB＝CD，∠EDC＝∠BCD.又PC与⊙O相切，∴∠ECD＝∠DBC.∴△CDE∽△BCD.∴DCBC＝DEDC.∴CD2＝DE·BC，即AB2＝DE·BC.(2)解由(1)知，DE＝AB2BC＝629＝4，∵AD∥BC，∴△PDE∽△PBC，∴PDPB＝DEBC＝49.又∵PB－PD＝9，∴PD＝365，PB＝815.∴PC2＝PD·PB＝365·815＝54252.∴PC＝545.6.如图，直线AB为圆O的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.(1)证明：DB＝DC；(2)设圆的半径为1，BC＝3，延长CE交AB于点F，求△BCF外接圆的半径．(1)证明如图，连接DE，则∠DCB＝∠DEB，∵DB⊥BE，∴∠DBC＋∠CBE＝90°，∠DEB＋∠EDB＝90°，∴∠DBC＋∠CBE＝∠DEB＋∠EDB，又∠CBE＝∠EBF＝∠EDB，∴∠DBC＝∠DEB＝∠DCB，∴DB＝DC.(2)解由(1)知：∠CBE＝∠EBF＝∠BCE，∴∠BDE＝∠CDE，∴DE是BC的垂直平分线，设交点为H，则BH＝3 2，∴OH＝1－34＝12，∴DH＝3 2，∴tan∠BDE＝3232＝33，∴∠BDE＝30°，∴∠FBE＝∠BDE＝30°，∴∠CBF＋∠BCF＝90°，∴∠BFC＝90°，∴BC是△BCF的外接圆直径．∴△BCF的外接圆半径为3 2.。

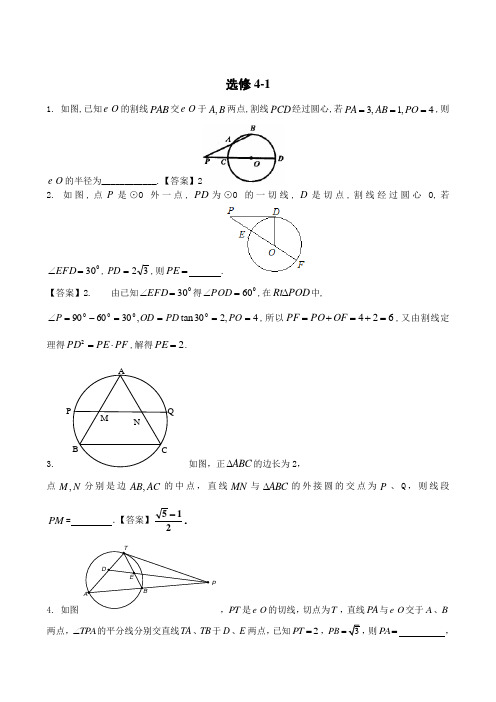
选修4-11. 如图,已知O 的割线PAB 交O 于,A B 两点,割线PCD 经过圆心,若3,1,4PA AB PO ===,则O 的半径为____________.【答案】22. 如图,点P 是⊙O 外一点,PD 为⊙O 的一切线,D 是切点,割线经过圆心O,若030=∠EFD ,32=PD ,则=PE .【答案】2. 由已知030=∠EFD 得060=∠POD ,在POD Rt ∆中,4,230tan ,3060900000====-=∠PO PD OD P ,所以624=+=+=OF PO PF ,又由割线定理得PF PE PD ⋅=2,解得2=PE .3. 如图，正ABC ∆的边长为2，点,M N 分别是边,A B A C 的中点，直线MN 与ABC ∆的外接圆的交点为P 、Q ，则线段PM = ．【答案】215-． 4. 如图P，PT 是O 的切线，切点为T ，直线PA 与O 交于A 、B 两点，TPA ∠的平分线分别交直线TA 、TB 于D、E 两点，已知2PT =，PB =，则PA = ，AP M NBC Q2TE AD = ．5. 如图，直线PC 与圆O 相切于点C ，割线PAB 经过圆心O ，弦CD ⊥AB 于点E ，4PC =，8PB =，则CE =__________.【答案】1256. 如图所示,圆O 上一点C 在直径AB 上的射影为D ，4,8CD BD ==，则圆O 的半径等于____________．【答案】5 7. 已知圆O 的半径为3，从圆O 外一点A 引切线AD 和割线ABC ，圆心O 到AC 的距离为22，3AB =，则切线AD 的长为 _____。

【答案】158.如图，圆O 是ABC ∆的外接圆，过点C 的切线交AB 的延长线于点D ，CD =3AB BC ==。

则BD的长____________，AC 的长____________．【答案】4， 9. 已知AB 是圆O 的直径，EF 切圆O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 长为_______.3210. 如图，过圆O 外一点P 分别作圆的切线和割线交圆于,A B ,《金太阳作业网》编制3 且7PB =，C 是圆上一点使得5BC =，则AB = .【答案】3511. 如图，在⊙O 中，AB 为直径，AD 为弦，过B 点的切线与AD 的延长线交于点C ，且AD=DC ，则sin ∠ACO=_________【答案】1010 12. AB 是圆O 的直径，EF 切圆O 于C ，AD EF ⊥于D ，2AD =，6AB =，则AC的长为 ．【答案】13. 如图，AB 是圆O 的直径，P 在AB 的延长线上，PD 切圆O 于点C .已知圆O 半2OP =，则PC =______；ACD ∠的大小为______.【答案】1,7514. 如图,四边形ABCD 内接于⊙O ,BC 是直径,MN 切⊙O 于A, 25=∠MAB ,则=∠DNA4【答案】115015. 如图，⊙O 的割线PBA 过圆心O ，弦CD 交PA 于点F ，且△COF ∽△PDF ，若PB ＝OA ＝2，则PF ＝________.【答案】316. 如图,在△ABC 中,AB ＝AC,∠C ＝720,⊙O 过A 、B 两点且与BC 相切于点B,与AC 交于点D,连结BD,若BC ＝15-,则AC ＝【答案】217. 如图,AB 是⊙O 的直径,P 是AB 延长线上的一点,过P 作⊙O 的切线,切点为C ,32=PC ,若︒=∠30CAP ,则⊙O 的直径=AB.【答案】418. 如图，四边形ABCD 内接于O ，110BOD ∠=，则BCD ∠=_________．【答案】125 ？O CDB A《金太阳作业网》编制5 19. 如图,圆O 的半径为1,A 、B 、C 是圆周上的三点,满足30ABC ∠=︒,过点A 作圆O 的切线与OC 的延长线交于点P ,则PA =__________.连接OA ,则60AOC ∠=︒,90OAP ∠=︒,因为1OA =,所以PA20. 如图5，半径是O 中，AB 是直径，MN 是过点A 的⊙O 的切线，,AC BD相交于点P ，且030DAN ∠=，2,9CP PA ==，又PD PB >，则线段PD 的长为 .【答案】621. 如图,过点P 的直线与圆O 相交于A,B 两点.若PA=1,AB=2,PO=3,则圆O 的半径等于_______.设PO 交圆O 于C,D,如图,设圆的半径为R,由割线定理知,1(12)(3-)(3),PA PB PC PD r r r ⋅=⋅⨯+=+∴=即P622. 如图所示，圆O 的直径6AB =,C 为圆周上一点，3BC =,过C 作圆的切线l ，则点A 到直线l 的距离AD = .【答案】9223. 如图，从圆O外一点A 引圆的切线AD 和割线ABC ，已知AD =6AC =，圆O 的半径为3，则圆心O 到AC 的距离为．24. 如图4,PT 为圆O 的切线,T 为切点,3ATM π∠=,圆O的面积为2π,则PA = .【答案】2323,22=+==OA PO PA PO OT ，连接.25. 如图,PA 与圆O 相切点A ,PCB 为圆O 的割线,并且不过圆心O , 已知30BPA ∠=,PA =1PC =,则PB = ;圆O 的半径等于 .《金太阳作业网》编制7【答案】12,7.26. 如图圆 O 的割线 PBA 过圆心 O ，弦 CD 交 PA 于点F ，且△COF ∽△PDF ，PB = OA = 2，则PF = 。

⾼考选做题⾼考选做题22. （本⼩题满分10分）选修4-1：⼏何证明选讲如图，AB 是O 的直径，弦BD CA 、的延长线相交于点E 。

EF 垂直BA 的延长线于点F 。

求证：（1）DEA DFA ∠=∠；（2）2AB BE BD AE AC =?-?23. （本⼩题满分10分）选修4-4：坐标系与参数⽅程 1O 和2O 的极坐标⽅程分别为4cos ,4sin ρθρθ==-。

（1）写出1O 和2O 的圆⼼的极坐标；（2）求经过1O 和2O 交点的直线的极坐标⽅程24. （本⼩题满分10分）选修4-5：不等式选讲设函数()|1||2|f x x x =-+-。

（1）画出函数()y f x =的图象；（2）若不等式()()||||||,0,a b a b a f x a a b R ++-≥≠∈、恒成⽴，求实数x 的范围。

22．（选修4—1：⼏何证明选讲）如图，AD 是△ABC 的内⾓平分线，延长AD 交△ABC 的外接圆O 于点E ，过C 、D 、E 三点的圆O 1交AC 的延长线于点F ，连结EF 、DF ．（1）求证：△AEF ∽△FED ；（2）若AD=6，DE=3，求EF 的长． 23．（选修4—4：坐标系与参数⽅程）已知直线l 的参数⽅程,()12,x t t y t =??=+?为参数和圆C 的极坐标⽅程)4πρθ=+．（1）将直线l 的参数⽅程化为普通⽅程，将圆C 的极坐标⽅程化为直⾓坐标⽅程；（2）判断直线l 和圆C 的位置关系． 24．（选修4—5：不等式选讲）已知a 、b 、x 、y 均为正实数，且a 1＞b 1，x ＞y ．求证：a x x +＞by y+ 22．（本⼩题满分10分）选修4—1：⼏何证明选讲如图，AB 是⊙O 的直径，C ，F 是⊙O 上的点，OC 垂直于直径AB ，过F 点作⊙O 的切线交AB 的延长线于D ．连结CF 交AB 于E 点．（I ）求证：2DE DB DA =?；（II ）若⊙O的半径为OB，求EF 的长．AB OC DE已知曲线C 的极坐标⽅程是4cosρθ=．以极点为平⾯直⾓坐标系的原点，极轴为x 轴的正半轴，建⽴平⾯直⾓坐标系，直线l 的参数⽅程是：2x m y ?=+??=（t 是参数）．（I ）将曲线C 的极坐标⽅程和直线l参数⽅程转化为普通⽅程；（II ）若直线l 与曲线C 相交于A 、B 两点，且||AB m 值． 24．（本⼩题满分10分）选修4—5：不等式选讲设函数()|1|||(0)f x x x a a =++->．（I ）作出函数()f x 的图象；（II ）若不等式()5f x ≥的解集为][(,23,)-∞-+∞ ，求a 值．22．（选修4-1⼏何证明选讲）（本⼩题满分10分）如图，圆O 和圆O '相交于A ，B 两点，AC 是圆O '的切线，AD 是圆O 的切线，若BC ＝2，AB ＝4，求BD 的长．23．（选修4-4极坐标与参数⽅程）（本⼩题满分10分）已知直线l 的参数⽅程为+=+=t y t x 232213（t 为参数），曲线C 的参数⽅程为??==θθsin 4cos 4y x （θ为参数）．（1）将曲线C 的参数⽅程化为普通⽅程；（2）若直线l 与曲线C 交于A 、B 两点，求线段AB 的长． 24．（选修4-5不等式选讲）（本⼩题满分10分）设函数()412--+=x x x f ．（1）求不等式()2>x f 的解集；（2）求函数()x f 的最⼩值．22．（本⼩题满分10分）选修4-1：⼏何证明选讲已知：如图，PT 切⊙O 于点T ，PA 交⊙O 于A 、B 两点且与直径CT 交于点D ，CD ＝2，AD ＝3， BD ＝6，求PB 的长。

[课堂练通考点]1．(2013·惠州模拟)如图，P A 切⊙O 于点A ，割线PBC 经过圆心O ，OB＝PB ＝1，OA 绕点O 逆时针旋转60°得到OD ，则PD 的长为________．解析：∵P A 切⊙O 于点A ，B 为PO 的中点，∴∠AOB ＝60°，∴∠POD ＝120°.在△POD 中，由余弦定理，得PD 2＝PO 2＋DO 2－2PO ·DO ·cos ∠POD ＝4＋1－4×(－12)＝7，故PD ＝7.答案：72．(2014·江南十校联考)如图，在圆的内接四边形ABCD 中，∠ABC ＝90°，∠ABD ＝30°，∠BDC ＝45°，AD ＝1，则BC ＝________.解析：连接AC .因为∠ABC ＝90°，所以AC 为圆的直径．又∠ACD ＝∠ABD ＝30°，所以AC ＝2AD ＝2.又∠BAC ＝∠BDC ＝45°，故BC ＝ 2.答案： 23．(2013·广州模拟)如图，已知AB 是⊙O 的一条弦，点P 为AB 上一点，PC ⊥OP ，PC 交⊙O 于C ，若AP ＝4，PB ＝2，则PC 的长是________．解析：如图，延长CP 交⊙O 于点D ，因为PC ⊥OP ，所以P 是弦CD的中点，由相交弦定理知P A ·PB ＝PC 2，即PC 2＝8，故PC ＝2 2.答案：2 24．(2013·新课标卷Ⅰ)如图，直线AB 为圆的切线，切点为B ，点C 在圆上，∠ABC 的角平分线BE 交圆于点E ，DB 垂直BE 交圆于点D .(1)证明：DB ＝DC ；(2)设圆的半径为1，BC ＝3，延长CE 交AB 于点F ，求△BCF 外接圆的半径． 解：(1)证明：如图，连接DE ，交BC 于点G .由弦切角定理得， ∠ABE ＝∠BCE .而∠ABE ＝∠CBE ，故∠CBE ＝∠BCE ，BE ＝CE .又因为DB ⊥BE ，所以DE 为直径，则∠DCE ＝90°，由勾股定理可得DB ＝DC . (2)由(1)知，∠CDE ＝∠BDE ，DB ＝DC ， 故DG 是BC 的中垂线，所以BG ＝32. 设DE 的中点为O ，连接BO ，则∠BOG ＝60°. 从而∠ABE ＝∠BCE ＝∠CBE ＝30°， 所以CF ⊥BF ，故Rt △BCF 外接圆的半径等于32. [课下提升考能]1．如图，四边形ABCD 内接于⊙O ，BC 是直径，MN 与⊙O 相切，切点为A ，∠MAB ＝35°，则∠D ＝________.解析：连接BD ，则∠MAB ＝∠ADB ＝35°，由BC 是直径，知∠BDC ＝90°，所以∠D ＝∠ADB ＋∠BDC ＝125°.答案：125°2．如图，△ABC 内接于⊙O ，∠C ＝30°，AB ＝2，则⊙O 的半径为________．解析：连接AO 并延长交⊙O 于D ，连接BD .∠D ＝∠C ＝30°，在Rt △ABD 中， AD ＝2AB ＝4. ∴半径为2. 答案：23．如图，已知EB 是半圆O 的直径，A 是BE 延长线上一点，AC 切半圆O 于点D ，BC ⊥AC 于点C ，DF ⊥EB 于点F ，若BC ＝6，AC ＝8，则DF ＝________.解析：设圆的半径为r ，AD ＝x ，连接OD ，设OD ⊥AC . 故AD AC ＝OD BC ，即x 8＝r6，故x ＝43r .又由切割线定理 AD 2＝AE ·AB ，即169r 2＝(10－2r )×10，故r ＝154. 由三角形相似，知AD AB ＝DFBC ，则DF ＝3.答案：34．(2014·佛山质检)如图所示，△ABC 内接于圆O ，过点A 的切线交BC 的延长线于点P ，D 为AB 的中点，DP 交AC 于点M ，若BP ＝8，AM ＝4，AC ＝6，则P A ＝________.解析：由题意MC ＝AC －AM ＝6－4＝2.又D 为AB 的中点，∴AD ＝BD .过点C 作CN ∥AB 交PD 于N ，∴AM MC ＝AD CN ＝BD CN ＝BPCP ， ∴8PC ＝42， ∴PC ＝4.∵P A 2＝PC ·PB ＝32， ∴P A ＝4 2. 答案：4 25．(2013·湖南高考)如图，在半径为7的⊙O 中，弦AB ，CD 相交于点P ，P A ＝PB ＝2，PD ＝1，则圆心O 到弦CD 的距离为________．解析：由相交弦定理得AP ·PB ＝DP ·PC ，从而PC ＝AP ·PB DP ＝4，所以DC＝5，所以圆心O 到弦CD 的距离等于(7)2－⎝⎛⎭⎫522＝32.答案：326．(2013·深圳调研)如图，在⊙O 中，直径AB 与弦CD 垂直，垂足为E ，EF ⊥BC ，垂足为F ，若AB ＝6，CF ·CB ＝5，则AE ＝________.解析：设AE ＝x ，则EB ＝6－x ，在Rt △CEB 中，EF ⊥BC ，∴CE 2＝CF ·CB ＝5.又易知CE ＝ED ，由相交弦定理得AE ·EB ＝CE ·ED ＝CE 2＝5，即x (6－x )＝5，得x ＝1.答案：17．如图所示，AB ，CD 是半径为a 的圆O 的两条弦，它们相交于AB的中点P ，PD ＝23a ，∠OAP ＝30°，则CP ＝________.解析：由题意知OP ⊥AB ，且AP ＝32a ， 根据相交弦定理AP 2＝CP ·PD ，CP ＝98a .答案：98a8．(2014·武汉模拟)如图，割线PBC 经过圆心O ，OB ＝PB ＝1，OB绕点O 逆时针旋转120°到OD ，连接PD 交圆O 于点E ，则PE ＝________.解析：在△POD 中，由余弦定理知PD ＝4＋1－4cos 120°＝7，再由PE ·PD ＝PB ·PC ⇒PE ＝377.答案：3779．如图所示，圆O 上一点C 在直径AB 上的射影为D ，CD ＝4，BD ＝8，则圆O 的半径等于________．解析：由射影定理得CD 2＝AD ×BD ，即42＝AD ×8，AD ＝2，圆O 的直径AB ＝AD ＋BD ＝10，故圆O 的半径等于5.答案：510．如图，过点P 作⊙O 的割线P AB 与切线PE ，E 为切点，连接AE ，BE ，∠APE 的平分线分别与AE ，BE 相交于点C ，D ，若∠AEB ＝30°，则∠PCE ＝________.解析：由圆的切割线定理可得PE 2＝PB ·P A ⇒PE PB ＝P A PE，∴△PEB ∽△P AE ，设∠P AE ＝α，则∠PEB ＝α，∠PBE ＝α＋30°，∠APE ＝150°－2α，∴△PCE 中，∠EPC ＝75°－α，∠PEC ＝30°＋α，∴∠PCE ＝75°.答案：75°11．如图，在⊙O 中，弦AB ，CD 相交于点F ，AB ＝10，AF ＝2.若CF ∶DF ＝1∶4，则CF 的长等于________．解析：∵CD ∶DF ＝1∶4， ∴DF ＝4CF ，∵AB ＝10，AF ＝2，∴BF ＝8，∵CF ·DF ＝AF ·BF ，∴CF ·4CF ＝2×8，∴CF ＝2. 答案：212．如图，圆O 的半径为1，A ，B ，C 是圆周上的三点，满足∠ABC ＝30°，过点A 作圆O 的切线与OC 的延长线交于点P ，则P A ＝________.解析：连接OA .∵AP 为⊙O 的切线， ∴OA ⊥AP .又∠ABC ＝30°，∴∠AOC ＝60°.∴在Rt △AOP 中，OA ＝1，P A ＝OA ·tan 60°＝ 3. 答案： 313．如图，PC 与圆O 相切于点C ，直线PO 交圆O 于A ，B 两点，弦CD 垂直AB 于E ，则下面结论中，错误的结论是________．①△BEC ∽△DEA ②∠ACE ＝∠ACP ③DE 2＝OE ·EP ④PC 2＝P A ·AB解析：根据图形逐一判断．因为∠BCE ＝∠DAE ，∠BEC ＝∠DEA ，所以△BEC ∽△DEA ，①正确；由切线的性质及三角形的性质得∠ACE ＝∠CBA ＝∠ACP ，②正确；连接OC ，因为PC 是切线，OC 是半径，所以OC ⊥PC ，且CE ⊥OP ，所以由射影定理可得CE 2＝OE ·EP ，又CE ＝DE ，所以DE 2＝OE ·EP ，③正确；由切割线定理可得PC 2＝P A ·PB ，④错误．答案：④14．如图，已知⊙O 的半径为R ，⊙O ′的半径为r ，两圆⊙O ，⊙O ′内切于点T ，点P 为外圆⊙O 上任意一点，PM 与内圆⊙O ′切于点M .PM ∶PT 为________．解析：作两圆的公切线TQ ，连接OP ，连接PT 交⊙O ′于C ，连接O ′C .设PT 交内圆于C ，则PM 2＝PC ·PT ， 所以PM 2PT 2＝PC ·PT PT 2＝PCPT.由弦切角定理知∠POT ＝2∠PTQ ，∠CO ′T ＝2∠PTQ ， 则∠POT ＝∠CO ′T ，PO ∥CO ′，所以PC PT ＝OO ′OT ＝R －r R ，即PM PT ＝R －rR为定值． 答案：R －rR15．(2013·惠州模拟)如图，已知AD ＝5，DB ＝8，AO ＝310，则圆O 的半径OC 的长为________．解析：取BD 的中点M ，连接OM ，OB ，则OM ⊥BD ，因为BD ＝8，所以DM ＝MB ＝4，AM ＝5＋4＝9，所以OM 2＝AO 2－AM 2＝90－81＝9，所以半径OB ＝OM 2＋BM 2＝9＋16＝25＝5，即OC ＝5.答案：516．(2014·哈师大模拟)如图，圆O 的半径OC 垂直于直径AB ，弦CD 交半径OA 于E ，过D 的切线与BA 的延长线交于M .设圆O 的半径为1，MD ＝3，则CE 的长为________．解析：∵MD 2＝MA ·MB ，∴3＝MA ·(MA ＋2)， ∴MA ＝1.∵在Rt △MDO 中，MO ＝2，MD ＝3，∴∠MOD ＝60°，∴∠COD ＝150°，∴∠ECO ＝15°， CE ＝OC cos ∠ECO ＝1cos 15°＝6－ 2.答案：6－ 217．如图，CD 为△ABC 外接圆的切线，AB 的延长线交直线CD 于点D ，E ，F 分别为弦AB 与弦AC 上的点，且BC ·AE ＝DC ·AF ，B ，E ，F ，C 四点共圆．若DB ＝BE ＝EA ，则过B ，E ，F ，C 四点的圆的面积与△ABC 外接圆面积的比值为________．解析：如图，连接CE ，因为∠CBE ＝90°，所以过B ，E ，F ，C 四点的圆的直径为CE .由DB ＝BE ，有CE ＝DC ，又BC 2＝DB ·BA ＝2DB 2，所以CA 2＝4DB 2＋BC 2＝6DB 2.而DC 2＝DB ·DA ＝3DB 2，故过B ，E ，F ，C 四点的圆的面积与△ABC 外接圆面积的比值为12.答案：12。

截面欣赏 同步练习一、选择题1．如图所示，直线l 1，l 2，l 3，的斜率分别为k 1，k 2，k 3，则 （ ）A ． k 1< k 2< k 3B ． k 3< k 1< k 2C ． k 3< kk 2< k 1D ． k 1< k 3< k 22．点（0，5）到直线y=2x 的距离是（ ）A ．25 B ． 5C ．23 D ．25 3．经过点P （3，2），且倾斜角是直线x-4y+3=0的倾斜角的两倍的直线方程是（ ）A ．8x-15y+6=0B ．x -8y+3=0C ．2x -4y+3=0D ．8x +15y+6=04．方程| x |+| y |=1所表示的图形在直角坐标系中所围成的面积是（ ）A ．2B ．1C ．4D ． 25．过点P （2，3），且在两坐标轴上的截距相等的直线方程是（ ）A ．x +y-5=0或x -y+1=0B ．x -y+1=0C ．3x -2y=0或x +y-5=0D ．x -y+1=0或3x -2y=06．设a 、b 、c 分别是△ABC 中∠A 、∠B 、∠C 所对边的边长，则直线sinA ·x +ay+c=0与bx -sinB ·y+sinC=0的位置关系是（ ）A ．平行B ．重合C ．垂直D ．相交但不垂直7．直线x -y+4=0被圆(x +2)2+(y-2)2=2截得的弦长为（ ）A ． 2B ．22C ．32D ．428．直角坐标系内到两坐标轴距离之差等于1的点的轨迹方程是（ ）A ．| x |-| y |=1B ．x -y=1C ．( | x |-| y | )2=1D ．| x -y |=19．若集合,}1)2(|),{(},16|),{(2222B B A a y x y x B y x y x A =-≤-+=≤+= 且 则a 的取值范围是（ ）A ．1≤aB ．5≥aC ．51≤≤aD ．5≤a10．在约束条件⎪⎩⎪⎨⎧≥-+≤≤0111y x y x 下，目标函数y x z 2+=的最小值和最大值分别是（ ）A ．1，3B ．1，2C ．0，3D ．2，3二、填空题11．如果直线l 与直线x +y-1=0关于y 轴对称，那么直线l 的方程是 ． 12．直线3x +y-23=0截圆x 2+y 2=4，得劣弧所对的圆心角为 ．y xl 2l 1l 3o13．过原点的直线与圆x 2+y 2+4x +3=0相切，若切点在第三象限，则该直线的方程是 ．14．如果直线l 将圆：x 2+y 2-2x -4y=0平分，且不经过第四象限，则l 的斜率的取值范围是 三、解答题15．求经过两点P 1（2，1）和P 2（m ，2）（m ∈R)的直线l 的斜率，并且求出l 的倾斜角α及其取值范围．16．过点P(2,4)作两条互相垂直的直线l １，l ２，若l １交x 轴于A 点，l 2 交y 轴于B 点，求线段AB 的中点M 的轨迹方程．17．已知圆的半径为10，圆心在直线x y 2=上，圆被直线0=-y x 截得的弦长为24，求圆的方程．18．已知常数,0>a 在矩形ABCD 中，AB=4，BC=4a ，O 为AB 的中点，点E 、F 、G分别在BC 、CD 、DA 上移动，且DADGCD CF BC BE ==，P 为GE 与OF 的交点（如图），求P 点的轨迹方程.xyoAB CDE FG P参考答案一．选择题二．填空题11．x - y +1=0 12．3π 13．y=33 x 14． [0，2] 三、解答题15．[解析]：(1)当m=2时，x 1＝x 2＝2，∴直线l 垂直于x 轴，因此直线的斜率不存在，倾斜角α=2π(2)当m ≠2时，直线l 的斜率k=21-m 当m ＞2时，k ＞0． ∴α=arctan 21-m ,α∈（0，2π），当m ＜2时，k ＜0 ∴α＝π＋arctan 21-m ，α∈(2π,π)．16．[解法1]：设点M 的坐标为(x,y),∵M 为线段AB 的中点，∴A 的坐标为(2x,0)，B 的坐标为(0，2y)，∵l １⊥l ２，且l １、l ２过点P(2，4)， ∴PA ⊥PB,k PA ·ｋＰＢ＝－１．而)1(,0224,2204≠--=--=x yk x k AB PA).1(11212≠-=-⋅-∴x y x 整理，得x+2y-5=0(x ≠1)∵当x=1时，A 、B 的坐标分别为(2，0)、(0，4)．∴线段AB 的中点坐标是(1，2)，它满足方程x+2y-5=0，综上所述，点M 的轨迹方程是x+2y-5=0．[解法2]：设M 的坐标为(x,y)，则A 、B 两点的坐标分别 是(2x,0)、(0,2y)，连接PM ，∵l １⊥l ２，∴2｜ＰＭ｜＝｜ＡＢ｜，而｜ＰＭ｜＝22)4()2(-+-y x22)2()2(y x AB += 222244)4()2(2y x y x +=-+-∴ 化简，得x+2y-5=0,为所求轨迹方程． 17．[解析]：设圆心坐标为（m ，2m ）,圆的半径为10，所以圆心到直线x -y=0的距离为2||2||m m =-由半径、弦心距、半径的关系得228102±=∴+=m m∴所求圆的方程为10)4()2(,10)4()2(2222=+++=-+-y x y x18．[解析]：根据题设条件可知，点P(x ，y)的轨迹即直线GE 与直线OF 的交点. 据题意有A （－2，0），B （2，0），C （2，4a ），D （－2，4a ）设)10(≤≤===k k DADC CD CF BC BE ，由此有E （2，4ak ），F （2－4k ，4a ），G （－2，4a －4ak ）. 直线OF 的方程为：0)12(20420040=-+⇒---=--y k ax k x a y ， ① 直线GE 的方程为：02)12()2(2)2()44(4)44(=-+--⇒----=----a y x k a x ak a ak ak a y . ②从①，②消去参数k ，得点P （x ，y ）的轨迹方程是：022222=-+ay y x a ，。

模块综合检测(二)(时间90分钟，满分120分)一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1.如图，AB ∥EM ∥DC ，AE ＝ED ，EF ∥BC ，EF ＝12 cm ，则BC 的长为( )A ．6 cmB ．12 cmC ．18 cmD ．24 cm 解析：选D 根据AE ＝ED ，AB ∥EM ∥DC ，有BM ＝MC .又EF ∥BC ，所以EF ＝MC ，于是EF ＝12BC . 2．在▱ABCD 中，E 是AD 的中点，AC 、BD 交于O ，则与△ABE面积相等的三角形有( )A ．5个B ．6个C ．7个D ．8个解析：选C 利用三角形面积公式，等底等高的两个三角形面积相等，再利用平行四边形的面积为中介，建立面积相等关系．3．在正方形ABCD 中，点E 在AB 边上，且AE ∶EB ＝2∶1，AF ⊥DE 于G ，交BC 于F ，则△AEG 的面积与四边形BEGF 的面积比为( )A ．1∶2B ．1∶4C ．4∶9D ．2∶3解析：选C 易证△ABF ≌△DAE .故知BF ＝AE .因为AE ∶EB ＝2∶1，故可设AE ＝2x ，EB ＝x ，则AB ＝3x ，BF ＝2x .由勾股定理得AF ＝(3x )2＋(2x )2＝13x .易证△AEG ∽△ABF .可得S △AEG ∶S △ABF ＝AE 2∶AF 2＝(2x )2∶(13x )2＝4∶13.可得S △AEG ∶S 四边形BEGF ＝4∶9.4．在梯形ABCD 中，AD ∥BC (其中BC >AD )E 、F 分别是AB 、DC 的中点，连接EF ，且EF 交BD 于G ，交AC 于H ，则GH 等于( )A ．ADB.12(AD ＋BC ) C ．BC D.12(BC －AD ) 解析：选D 结合平行线等分线段定理及梯形中位线定理可解决此问题．5.如图，在梯形ABCD 中，AD ∥BC ，∠BAD ＝135°，以A 为圆心，AB 为半径，作⊙A 交AD 、BC 于E 、F 两点，并交BA 延长线于G ，则BF 的度数是( )A ．45°B ．60°C ．90°D ．135°解析：选C ¼BF的度数等于圆心角∠BAF 的度数． 由题意知∠B ＝45°，所以∠BAF ＝180°－2∠B .6．在△ABC 中，点D 、E 分别在AB 、AC 上，下列条件中，不能判定DE ∥BC 的是( )A ．AD ＝5，AB ＝8，AE ＝10，AC ＝16B ．BD ＝1，AD ＝3，CE ＝2，AE ＝6C ．AB ＝7，BD ＝4，AE ＝4，EC ＝3D ．AB ＝AC ＝9，AD ＝AE ＝8解析：选C 对应线段必须成比例，才能断定DE 和BC 是平行关系，显然C 中的条件不成比例．7.如图，PA 是⊙O 的切线，A 为切点，PC 是⊙O 的割线，且PB＝12BC ，则PA PB 等于( ) A ．2 B.12C. 3 D ．1 解析：选C 利用切割线定理得PA 2＝PB ·PC ＝3PB 2，则PA PB ＝ 3.8．D 、E 、F 是△ABC 的三边中点，设△DEF 的面积为4，△ABC 的周长为9，则△DEF 的周长与△ABC 的面积分别是( )A.92，16 B ．9,4 C.92，8 D.94，16解析：选A 如右图，D 、E 、F 分别为△ABC 三边中点．∴EF 綊12BC ， ∴△AEF ∽△ABC ，且EF BC ＝12. ∴l △DEF l △ABC ＝EF BC ＝12， 又∵l △ABC ＝9，∴l △DEF ＝92.又∵S △DEF S △ABC ＝EF 2BC 2＝14， 又∵S △DEF ＝4，∴S △ABC ＝16.9.如图，已知在△ABC 中，AD ∶DC ＝1∶2，E 为BD 的中点，AE 延长线交BC 于F ，则BF ∶FC 等于( )A ．1∶5B ．1∶4C ．1∶3D ．1∶2解析：选C 过D 作DG 平行于AF ，交BC 于点G ，再根据平行线分线段成比例定理即可解决．10．如图，四边形ABCD 内接于⊙O ，BC 是直径，AD ＝DC ，∠ADB ＝20°，则∠ACB ，∠DBC 分别为( )A ．15°与30°B ．20°与35°C ．20°与40°D ．30°与35°解析：选B ∵∠ADB ＝20°，∴∠ACB ＝∠ADB ＝20°.又∵BC 为⊙O 的直径，∴¼ADC 的度数为180°－40°＝140°. ∵D 为¼AC 的中点， ∴»CD的度数为70°， ∴∠DBC ＝70°2＝35°. 二、填空题(本大题共4小题，每小题5分，共20分．把答案填写在题中的横线上)11.(湖北高考)如图，点D 在⊙O 的弦AB 上移动，AB ＝4，连接OD ，过点D 作OD 的垂线交⊙O 于点C ，则CD 的最大值为________．解析：由题意知CD 2＝OC 2－OD 2，OC 是半径，所以当OD 的值最小时，DC 最大，易知D 为AB 的中点时，DB ＝DC ＝2最大．答案：212．如图，在Rt △ABC 中，∠C ＝90°，以BC 为直径作半圆交AB于D ，过D 作半圆的切线交AC 于E ，若AD ＝2，DB ＝4，则DE ＝________.解析：由切割线定理得：AC 2＝AD ·AB ＝2×6＝12.所以AC ＝2 3.连接CD，可证：EC＝ED，∠A＝∠EDA.所以AE＝ED，所以ED＝AE＝EC＝12AC＝ 3.答案： 313．如图所示，圆O的直径AB＝6，C为圆周上一点，BC＝3，过C作圆的切线l，过A作l的垂线AD，AD分别与直线l、圆交于点D、E，则∠DAC＝________，线段AE的长为________．解析：因为AB为⊙O的直径，所以∠ACB＝90°.又因为AB＝6，BC＝3，所以∠CAB＝30°.又∠DCA＝90°－30°＝60°，而AD⊥DC，所以∠DAC＝30°，即可得出¼AE＝»BC＝»EC.所以AE＝BC＝3.答案：30° 314．如图，△ABC是圆O的内接三角形，PA是圆O的切线，A为切点，PB交AC于点E，交圆O于点D，若PE＝PA，∠ABC＝60°，且PD＝1，BD＝8，则AC＝________.解析：因为PA是圆O的切线，所以∠CAP＝∠ABC＝60°.又PE＝PA，所以△PAE为等边三角形．由切割线定理得PA2＝PD·PB＝1×9＝9，所以PA＝3，所以PA＝PE＝AE＝3，ED＝PE－PD＝3－1＝2，BE＝BD－ED＝8－2＝6.由相交弦定理得AE·EC＝BE·ED.所以EC＝BE·EDAE＝6×23＝4，所以AC＝AE＋EC＝3＋4＝7.答案：7三、解答题(本大题共4个小题，共50分．解答应写出必要的文字说明、证明过程或演算步骤)15．(本小题满分12分)如图，已知在梯形ABCD 中，AD ∥BC ，E 是CD 的中点，EF ∥BC 交AB 于F ，FG ∥BD 交AD 于G .求证：AG ＝DG .证明：∵AD ∥EF ∥BC ，E 是CD 的中点，∴F 是AB 的中点． 又∵FG ∥BD ，∴G 是AD 的中点．∴AG ＝DG .16．(本小题满分12分)(江苏高考)如图，AB 和BC 分别与圆O 相切于点D ，C ，AC 经过圆心O ，且BC ＝2OC .求证：AC ＝2AD .证明：连接OD .因为AB 和BC 分别与圆O 相切于点D ，C ，所以∠ADO ＝∠ACB ＝90°.又因为∠A ＝∠A ，所以Rt △ADO ∽Rt △ACB .所以BC OD ＝AC AD. 又BC ＝2OC ＝2OD ，故AC ＝2AD .17．(本小题满分12分)如图所示，两圆内切于点T ，大圆的弦AB 切小圆于点C .TA ，TB 与小圆分别相交于点E ，F .FE 的延长线交两圆的公切线TP 于点P .求证：(1) »CE＝»CF ； (2)AC ·PF ＝BC ·PT .证明：(1)设小圆的圆心为点O ，连接OC .∵AB 切小圆于点C ，∴OC ⊥AB .∵∠1＝∠3＝∠2，∴EF ∥AB ，∴OC ⊥EF ，∴»CE＝»CF . (2)∵EF ∥AB ，∴AE BF ＝AT BT ＝TE TF. ∵AB 切小圆于点C ，∴AC 2＝AE ·AT ，BC 2＝BF ·BT .∴AC 2BC 2＝AE ·AT BF ·BT ＝TE 2TF 2，AC BC ＝TE TF. ∵PT 是公切线，∴∠PTF ＝90°，∵TF 是⊙O 的直径，∴TE ⊥PF ，△PTF ∽△TEF ，∴PT PF ＝TE TF ，∴AC BC ＝PT PF， ∴AC ·PF ＝BC ·PT .18．(本小题满分14分)如图，在矩形ABCD 中，以A 为圆心，AD为半径的圆交AC ，AB 于M ，E .CE 的延长线交⊙A 于F ，CM ＝2，AB ＝4.(1)求⊙A 的半径；(2)求CE 的长和△AFC 的面积．解：(1)∵四边形ABCD 为矩形，AB ＝4，∴CD ＝4.在Rt △ACD 中，AC 2＝CD 2＋AD 2，∴(2＋AD )2＝42＋AD 2.解得：AD ＝3，即⊙A 的半径为3.(2)过点A 作AG ⊥EF 于点G ，∵BC ＝3，BE ＝AB －AE ＝4－3＝1，∴CE ＝BC 2＋BE 2 ＝32＋12＝10.∵∠ADC ＝90°，∴CD 为⊙A 的切线，∴CE ·CF ＝CD 2，∴CF ＝CD 2CE ＝4210＝8510.又∠B ＝∠AGE ＝90°，∠BEC ＝∠GEA ，∴△BCE ∽△GAE ，∴BC AG ＝CE AE 即3AG ＝103.∴AG ＝91010，∴S △AFC ＝12CF ·AG ＝12×8510×91010＝365.。

《几何证明选讲》习题一考试大纲说明的具体要求：1.了解平行线截割定理，会证直角三角形射影定理.2会证圆周角定理、圆的切线的判定定理及性质定理.3.会证相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理.4.了解平行投影的含义，通过圆柱与平面的位置关系，了解平行投影；会证平面与圆柱面的截线是椭圆(特殊情形是圆).5.了解下面定理：定理在空间中，取直线l为轴，直线l′与l相交于点O，其夹角为α，l′围绕l旋转得到以O为顶点，l′为母线的圆锥面，任取平面π，若它与轴l交角为β(π与l平行，记β＝0)，则：①β＞α，平面π与圆锥的交线为椭圆；②β=α，平面π与圆锥的交线为抛物线；③β<α，平面π与圆锥的交线为双曲线.一、基础知识填空：1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段_________.推论1: 经过三角形一边的中点与另一边平行的直线必______________.推论2: 经过梯形一腰的中点，且与底边平行的直线________________.2.平行线分线段成比例定理：三条平行线截两条直线，所得的________________成比例.推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段___________. 3.相似三角形的性质定理：相似三角形对应高的比、对应中线的比、对应角平分线的比都等于______；相似三角形周长的比、外接圆的直径比、外接圆的周长比都等于_________________；相似三角形面积的比、外接圆的面积比都等于____________________；4. 直角三角形的射影定理：直角三角形斜边上的高是______________________的比例中项；两直角边分别是它们在斜边上_______与_________的比例中项.5.圆周角定理：圆上一条弧所对的圆周角等于它所对的____________的一半.圆心角定理：圆心角的度数等于_______________的度数.推论1：同弧或等弧所对的圆周角_________；同圆或等圆中，相等的圆周角所对的弧_______.推论2：半圆（或直径）所对的圆周角是____；90o的圆周角所对的弦是________. 弦切角定理：弦切角等于它所夹的弧所对的______________. 6.圆内接四边形的性质定理与判定定理：圆的内接四边形的对角______；圆内接四边形的外角等于它的内角的_____.如果一个四边形的对角互补，那么这个四边形的四个顶点______；如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点_________. 7.切线的性质定理：圆的切线垂直于经过切点的__________.推论：经过圆心且垂直于切线的直线必经过_______；经过切点且垂直于切线的直线必经过______.切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的________. 8.相交弦定理:圆内两条相交弦，_____________________的积相等.割线定理:从圆外一点引圆的两条割线，_____________的两条线段长的积相等. 切割线定理:从圆外一点引圆的切线和割线，切线长是__________的比例中项. 切线长定理:从圆外一点引圆的两条切线，它们的切线长____； 圆心和这点的连线平分_____的夹角.二 、经典试题：1.如图所示，在四边形ABCD 中，EF//BC ，FG//AD ，则EF FG+=BC AD．2.在平行四边形ABCD 中，点E 在边AB 上，且AE ：EB=1：2，DE 与AC 交于点F ，若△AEF 的面积为6cm 2，则△ABC 的面积为cm 2．3.如图所示，圆O 上一点C 在直径AB 上的射影为D ，CD=4，BD=8则圆O 的半径等于 ．A BC D E F GBCDE F4.如图所示，从圆O 外一点P 作圆O 的割线PAB 、PCD ，AB 是圆O 的直径， 若PA=4，PC=5，CD=3，则∠CBD= __.5.已知PA 是圆O 的切线，切点为A ，PA=2. AC 是圆O 的直径，PC 与圆O 交于点B ，PB=1， 则圆O 的半径R=_______.6. 如图所示，圆O 的直径AB=6，C 圆周上一点，BC=3，过C过A 作l 的垂线AD ，AD 分别与直线l 、圆交于点 D 、E ，则∠DAC ＝ __，线段AE 的长为 __.三、基础训练：1.如图所示，PC切⊙O 于点C ，割线PAB 经过圆心O ，弦CD ⊥AB 点E ，PC=4，PB=8，则CD=________.2.如图所示，从圆O 外一点A 引圆的切线AD 和割线ABC ，已知AD=AC=6，圆O 的半径为3，则圆心O 到AC 的距 离为________.3.如图所示,圆O 上一点C 在直径AB 上的射影为D ，CD=4，BD=8则圆O 的半径等于 ．4.如图所示，圆O 是△ABC 的外接圆，过点C 的切线交AB 的延长线于点D ，CD=AB=BC=3. 则BD 的长______，AC 的长_______．5. 如图， ⊙O′和⊙O 相交于A 和B ， PQ 切⊙O 于P ， 交⊙O′于Q 和M ，交AB 的延长线于N ， MN=3，NQ=15，则 PN ＝______．6.如图所示, 圆的内接△ABC 的∠C 的平分线CD 延长后交圆于点E ，连接BE ，已知BD=3，CE=7，BC=5，则线段 BE= .7.如图，四边形ABCD 内接于⊙O ，BC 是直径，MN 切⊙O 于A ， ∠MAB=250，则∠D= ___ .8.如图，在△ABC 中，D 是AC 的中点，E 是BD 的中点，AE 交BC于F ，则BF=FC.9.如图：EB 、EC 是⊙O 的两条切线，B 、C 是切点，A 、D 是⊙O 如果∠E ＝460，∠DCF ＝320，则∠A 的度数是 .10. 如图，AB 是圆O 的直径，直线CE 和圆O 相切于点C ，AD ⊥CE 于D ， 若AD=1，∠ABC=300，则圆O 的面积是______.BADCEN CBADEF11.如图，AB 、CD 是圆O 的两条弦，且AB 是线段CD 的中垂线，已知AB=6，CD=52， 则线段AC 的长度为 ．12.已知：如图，在梯形ABCD 中，AD ∥BC ∥EF ， E 是AB 的中点，EF 交BD 于G ，交AC 于H. 若 AD=5，BC=7，则GH=________.13.如图，圆O 上一点C 在直径AB 上的射影为D. AD=2，AC= 52，则AB=____ __,CD=___ __.14.如图，PA 是圆的切线，A 为切点，PBC 是圆的割线，且1PB =BC 2，则PAPB的值是________.15.如图，⊙O 的割线PAB 交⊙O 于A 、B 两点，割线 PCD 经过圆心O ，PE 是⊙O 的切线。