工程力学习题库-弯曲变形

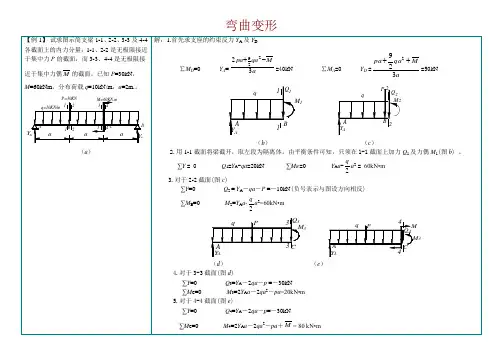
第8章 弯曲变形本章要点【概念】平面弯曲，剪力、弯矩符号规定，纯弯曲，中性轴，曲率，挠度，转角。

剪力、弯矩与荷载集度的关系；弯曲正应力的适用条件；提高梁的弯曲强度的措施；运用叠加法求弯曲变形的前提条件；截面上正应力分布规律、切应力分布规律。

【公式】 1. 弯曲正应力 变形几何关系：yερ=物理关系：Ey σρ=静力关系：0N AF dA σ==⎰，0y AM z dA σ==⎰，2zz AAEI EM y dA y dA σρρ===⎰⎰中性层曲率：1MEIρ=弯曲正应力应力：，My Iσ=，max max z M W σ=弯曲变形的正应力强度条件：[]maxmax zM W σσ=≤ 2. 弯曲切应力矩形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F bh F S S 2323max ==τ工字形梁弯曲切应力：dI S F y z z S ⋅⋅=*)(τ，A F dh F S S ==max τ圆形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F S 34max =τ弯曲切应力强度条件：[]ττ≤max3. 梁的弯曲变形梁的挠曲线近似微分方程：()''EIw M x =-梁的转角方程：1()dwM x dx C dx EIθ==-+⎰ 梁的挠度方程：12()Z M x w dx dx C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰ 练习题一. 单选题1、 建立平面弯曲正应力公式zI My /=σ,需要考虑的关系有（）。

查看答案A 、平衡关系,物理关系，变形几何关系B 、变形几何关系，物理关系，静力关系；C 、变形几何关系，平衡关系，静力关系D 、平衡关系, 物理关系，静力关系；2、 利用积分法求梁的变形，不需要用到下面那类条件（）来确定积分常数。

查看答案A 、平衡条件B 、边界条件C 、连续性条件D 、光滑性条件3、 在图1悬臂梁的AC 段上，各个截面上的（）。

7-2c 梁受力、尺寸、刚度如图所示，求A 处的转角，以及C 、D 截面的挠度。

解：（1）求反力写弯矩方程：)3()(2)(2211x a P x M BCx P x M AB--=-=（2）分段积分''1112)(E I y x P x M AB-=-=''222)3()(EIy x a P x M BC=--=121'14C x P EIy +=222'2)3(2C x a P EIy +--=11131112D x C x P EIy ++=222322)3(6D x C x a P EIy ++-+=（3）边界、连续条件定积分常量00,0111=→==D y x⎪⎪⎪⎩⎪⎪⎪⎨⎧-==-=→⎪⎪⎪⎩⎪⎪⎪⎨⎧+--=+⨯=+⨯+-⨯=⨯+⨯→⎩⎨⎧=====25673)23(2)2(402)23(602)2(1202322221221222313212121Pa D Pa C Pa C C a a P C a P D a C a a P a C a P y y a x x θθ时，(4)该梁的转角方程为⎪⎪⎩⎪⎪⎨⎧∈+--∈-=]3,2[(67)3(2]2,0[(3422221221'a a x Pax a P a x Pa x P EIy该梁的挠曲线方程为⎪⎪⎩⎪⎪⎨⎧∈-+-+∈-=]3,2[(2567)3(6]2,0[(31223223211231a a x Pa x Pax a P a x x Pa x P EIy(5)将横坐标值代入相应的式子可求出EIPay EIPa y EIPaD C A 4,,3332-==-=θ习题7-2c 图 习题7-5图7-5 用叠加法求图示外伸梁C 截面的挠度和转角。

解：（1）将原结构的荷载分解，如图所示。

（2）查表可得各简单载荷作用下的θC 、y C 之值。

并将其叠加，得所求θC 、y C 之值。

第七章 组合变形本章主要讨论建筑工程中常见的组合变形的强度计算问题。

其中斜弯曲、拉（压）与弯曲、偏心拉（压）组合变形的强度计算问题是本章的重点。

第一节 组合变形的概念前面的章节分别研究了杆件在轴向拉（压）、剪切、扭转、平面弯曲基本变形下的强度和刚度计算。

但在工程实际中，结构中一些杆件的受力情况是复杂的，往往同时发生两种或者两种以上的基本变形，这种由两种或两种以上的基本变形组合而成的变形称为组合变形。

例如，图7-1a 所示的烟囱，除自重引起的轴向压缩外，还有水平方向的风力引起的弯曲变形，即同时产生两种基本变形。

又如，图7-1b 所示的备有吊车的厂房柱，作用在立柱上的荷载1F 和2F ,其合力的作用线一般不在立柱轴线上，此时，立柱即发生压缩变形又发生弯曲变形。

再如，图7-1c 所示的曲拐轴，在荷载F 作用下，曲拐AB 段同时发生扭转和弯曲变形。

上述这些杆件的变形，都是结构杆件发生组合变形的工程实例。

图7-1由上一章梁的弯曲可知：外力沿横向作用在梁的纵向对称平面内，梁将发生平面弯曲变形。

那么，外力虽然沿梁的横向（垂直于轴线），但不作用在纵向对称平面内时，梁会发生怎样的变形呢?实验及理论研究得知，此时梁轴线变形后弯成的曲线已不在荷载的作用平面内，即不属于平面弯曲，这种弯曲称为斜弯曲。

若外力不沿梁的横向（斜交于轴线），但力作用仍在纵向对称平面内，梁将发生拉（压）与弯曲组合变形。

若作用外力虽然沿杆件轴向方向，但不与轴线重合，杆件也将发生拉（压）与弯曲组合变形，称为偏心拉（压）。

对发生组合变形的杆件计算应力和变形时，可将荷载进行简化或分解，使简化或分解后得到的静力等效的荷载，每类荷载各自只引起一种基本变形，分别计算，再进行叠加，就得到由原来的荷载所引起的组合变形的应力和变形，这就是组合变形的分析方法和组合变形计算的叠加原理。

这里需要强调的是：叠加原理是在满足小变形和力与位移成线性关系的条件下才适用。

本章将主要讨论斜弯曲、拉压与弯曲、偏心拉伸（压缩）组合变形的强度计算问题。

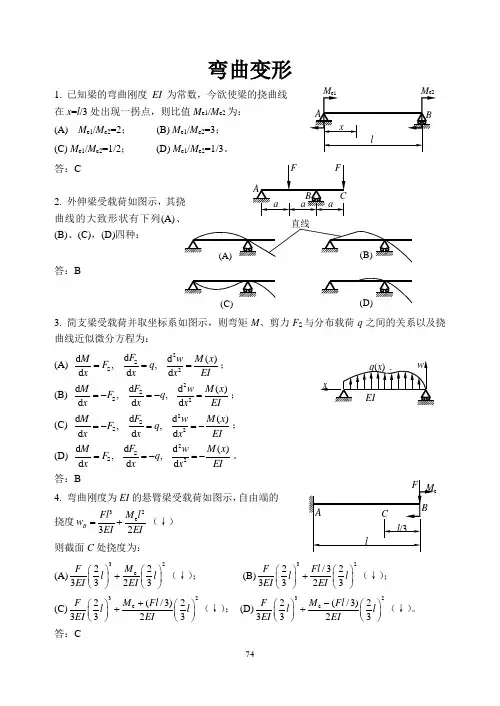
弯曲变形1. 已知梁的弯曲刚度EI为常数，今欲使梁的挠曲线在x=l/3处出现一拐点，则比值M e1/M e2为：(A) M e1/M e2=2；(B) M e1/M e2=3；(C) M e1/M e2=1/2；(D) M e1/M e2=1/3。

答：C2. 外伸梁受载荷如图示，其挠曲线的大致形状有下列(A)、(B)、(C)，(D)四种：答：B3. 简支梁受载荷并取坐标系如图示，则弯矩M、剪力F S与分布载荷q之间的关系以及挠曲线近似微分方程为：(A)2SS2dd d(),,d d dFM w M xF qx x x EI===；(B)2SS2dd d(),,d d dFM w M xF qx x x EI=-=-=；(C)2SS2dd d(),,d d dFM w M xF qx x x EI=-==-；(D)2SS2dd d(),,d d dFM w M xF qx x x EI==-=-。

答：B4. 弯曲刚度为EI的悬臂梁受载荷如图示，自由端的挠度23e32BM lFlwEI EI=+（↓）则截面C处挠度为：(A)32e223323MFl lEI EI⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）；(B)322/323323F Fll lEI EI⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）；(C)32e(/3)223323M FlFl lEI EI+⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）；(D)32e(/3)223323M FlFl lEI EI-⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）。

答：C5. 画出(a)、(b)、(c)三种梁的挠曲线大致形状。

答：6. 试画出图示梁的挠曲线大致形状。

答：7. 正方形截面梁分别按(a)、(b)两种形式放置，则两者间的弯曲刚度关系为下列中的哪一种： (A) (a)＞(b)； (B) (a)＜(b)； (C) (a)=(b)； (D) 不一定。

答：C8. 试写出图示等截面梁的位移边界条件，并定性地画出梁的挠曲线大致形状。

班级：学号：姓名：《工程力学》弯曲变形测试题一、判断题（每小题2分，共20分）1、梁弯曲变形后，最大转角和最大挠度是同一截面。

（×）2、不同材料制成的梁，若截面尺寸和形状完全相同，长度及受力情况也相同，那么这两根梁弯曲变形时，最大挠度值相同。

（×）3、EI是梁的抗弯刚度，提高它的最有效、最合理的方法是改用更好的材料。

（×）4、梁的挠曲线方程随弯矩方程的分段而分段，只要梁不具有中间铰，则梁的挠曲线仍然是一条光滑、连续的曲线。

（√）5、梁弯曲后，梁某点的曲率半径和该点所在横截面位置无关。

（×）6、梁上有两个载荷，梁的变形与两个载荷加载次序无关。

（√ ）7、一般情况下，梁的挠度和转角都要求不超过许用值。

（√ ）8、在铰支座处，挠度和转角均等于零。

（×）9、绘制挠曲线的大致形状，既要根据梁的弯矩图，也要考虑梁的支撑条件。

（√ ）10、弯矩突变的截面转角也有突变。

（×）二、单项选择题（每小题2分，共20分）1、梁的挠度是（B ）。

A. 横截面上任一点沿梁轴方向的位移B. 横截面形心沿垂直梁轴方向的位移C. 横截面形心沿梁轴方向的线位移D. 横截面形心的位移2、在下列关于挠度、转角正负号的概念中，（C）是正确的。

A. 转角的正负号与坐标系有关，挠度的正负号与坐标系无关B. 转角的正负号与坐标系无关，挠度的正负号与坐标系有关C. 转角和挠度的正负号均与坐标系有关D. 转角和挠度的正负号均与坐标系无关3、挠曲线近似微分方程在（D ）条件下成立。

A. 梁的变形属于小变形 B .材料服从胡克定律C. 挠曲线在xoy平面内D. 同时满足A、B、C4、等截面直梁在弯曲变形时，挠曲线的最大曲率发生在（D ）处。

A. 挠度最大B. 转角最大C. 剪力最大D. 弯矩最大5、应用叠加原理求梁横截面的挠度、转角时，需要满足的条件有（C ）A. 梁必须是等截面的B. 梁必须是静定的C. 变形必须是小变形；D. 梁的弯曲必须是平面弯曲6、两简支梁，一根为钢、一根为铜，已知它们的抗弯刚度相同。

弯曲变形基本概念题一、选择题1. 梁的受力情形如下图，该梁变形后的挠曲线如图（）所示(图中挠曲线的虚线部份表示直线，实线部份表示曲线)。

2. 如下图悬臂梁，假设别离采纳两种坐标系，那么由积分法求得的挠度和转角的正负号为（）。

题2图题1图A．两组结果的正负号完全一致B．两组结果的正负号完全相反C．挠度的正负号相反，转角正负号一致D．挠度正负号一致，转角的正负号相反3.已知挠曲线方程y = q0x(l3 - 3lx2 +2 x3)∕(48EI)，如下图，那么两头点的约束可能为以下约束中的（）。

题3图4. 等截面梁如下图，假设用积分法求解梁的转角、挠度，那么以下结论中（）是错误的。

A．该梁应分为AB、BC两段进行积分B．挠度积分表达式中，会显现4个积分常数题4图 题5图 C ．积分常数由边界条件和持续条件来确信D ．边界条件和持续条件表达式为x = 0，y = 0；x = l ，0==右左y y ，0='y 5. 用积分法计算图所示梁的位移，边界条件和持续条件为( )A ．x = 0，y = 0；x = a + l ，y = 0；x = a ，右左y y =，右左y y '=' B ．x = 0，y = 0；x = a + l ，0='y ；x = a ，右左y y =，右左y y '=' C ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y =D ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y '=' 6. 材料相同的悬臂梁I 、Ⅱ，所受荷载及截面尺寸如下图。

关于它们的最大挠度有如下结论，正确的选项是（ ）。

A ． I 梁最大挠度是Ⅱ梁的41倍 B ．I 梁最大挠度是Ⅱ梁的21倍 C ． I 梁最大挠度与Ⅱ梁的相等 D ．I 梁最大挠度是Ⅱ梁的2倍题6图 题7图 7. 如下图等截面梁，用叠加法求得外伸端C 截面的挠度为（ ）。

第八章 直梁弯曲一、填空题1.工程中 发生弯曲 或以 弯曲变形 为主的杆件称为梁。

2.常见梁的力学模型有 简支梁 、 外伸梁 和 悬臂梁 。

3.平面弯曲变形的受力特点是 外力垂直于杆件的轴线，且外力和力偶都作用在梁的纵向对称面内 ；平面弯曲变形的变形特点是 梁的轴线由直线变成了在外力作用面内的一条曲线 ；发生平面弯曲变形的构件特征是 具有一个以上对称面的等截面直梁 。

4.作用在梁上的载荷有 集中力 、 集中力偶 和 分布载荷 。

5.梁弯曲时，横截面上的内力一般包括 剪力 和 弯矩 两个分量，其中对梁的强度影响较大的是 弯矩 。

6.在计算梁的内力时，当梁的长度大于横截面尺寸 五 倍以上时，可将剪力略去不计。

7.梁弯曲时，某一截面上的弯矩，在数值上等于 该截面左侧或右侧梁上各外力对截面形心的力矩 的代数和。

其正负号规定为：当梁弯曲成 凹面向上 时，截面上弯矩为正；当梁弯曲成凸面向上 时，截面上弯矩为负。

8.在集中力偶作用处，弯矩发生突变，突变值等于 集中力偶矩 。

9.横截面上弯矩为 常数 而剪力为 零 的平面弯曲变形称为 纯弯曲变形 。

10.梁纯弯曲变形实验中，横向线仍为直线，且仍与 梁轴线 正交，但两线不再 平行 ，相对倾斜角度θ。

纵向线变为 弧线 ，轴线以上的纵向线缩短，称为 缩短 区，此区梁的宽度 增大 ；轴线以下的纵向线伸长，称为 伸长 区，此区梁的宽度 减小 。

情况与轴向拉伸、压缩时的变形相似。

11.中性层与横截面的交线称为 中性轴 ，变形时梁的 所有横截面 均绕此线相对旋转。

12.在中性层凸出一侧的梁内各点，其正应力均为 正 值，即为 拉 应力。

13.根据弯曲强度条件可以解决 强度校核 、 截面选取 和 确定许可载荷 等三类问题。

14.产生最大正应力的截面又称为 危险截面 ，最大正应力所在的点称为 危险点 。

15.在截面积A 相同的条件下， 抗弯截面系数 越大，则梁的承载能力就越高。

第6章 弯曲变形习题解答6-1 用直接积分法求下列各梁的挠曲线方程和最大挠度。

梁的抗弯刚度EI 为已知。

（a ）解：（1）弯矩方程 0≤ x ≤l+aM (x )=qlx －qx 2/2+q<x-l>2/2-ql 2/2（2）积分 EI θ (x )= qlx 2/2－qx 3/6+q<x-l>3/6-ql 2x /2+CEI ν(x )= qlx 3/6－qx 4/24+q<x-l>4/24-ql 2x 2/4+Cx+D （3）定常数x = 0 θ = 0 → C = 0 x = 0 ν= 0 → D = 0νmax =ν B =)341(84laEI ql +-(↓)（b ）解：（1）支反力 F A = M o / l (↑), F C =－M o / l (↓) （2）弯矩方程 0≤ x ≤ 4l/3M (x )= M o x / l －M o <x-l> / l （3）积分EI θ (x )= M o x 2 / 2l － M o <x-l>2 /2 l +CEI ν(x )= M o x 3 / 6l － M o <x-l>3/6 l +C x+D （4）定常数x = 0 ν= 0 → D = 0x = l ν= 0 → C =－M o l /6νmax =ν B =EIl M o 62(↑)6-2 写出下列各梁的边界条件，并根据弯矩图和支座情况画出挠度曲线的大致形状。

解：x = 0 ν= 0 x = a ν= 0x = l ν= ∆k = M o / lk x = 3a ν= ∆l = Fa /2EA(b) ν(b) (a)x = 0 θ = 0 x = 0 ν= 0 x = 0 ν=0 x = 3a ν= 0x = 0 ν= 0 x = 0 ν= 0 , θ = 0x =2a ν=0 x = 2a ν= 06-3 用叠加法求下列各梁C 截面的挠度和B 截面的转角。

班级： 学号： 姓名：《工程力学》弯曲应力测试题一、判断题（每小题2分，共20分）1、弯曲变形梁，其外力、外力偶作用在梁的纵向对称面内，梁产生对称弯曲。

（ √ ）2、铁路的钢轨制成工字形，只是为了节省材料。

（ × ）3、为了提高梁的强度和刚度，只能通过增加梁的支撑的办法来实现。

（ × ）4、中性轴是中性层与横截面的交线。

（ √ ）5、最大弯矩M max 只可能发生在集中力F 作用处，因此只需校核此截面强度是否满足梁的 强度条件。

（ × ）6、大多数梁只进行弯曲正应力强度校核，而不计算弯曲切应力，这是因为他们横截面上只有正应力存在。

（ × ）7、抗弯截面系数仅与截面形状和尺寸有关，与材料种类无关。

（ √ ）8、矩形截面梁，若其截面高度和宽度都增加一倍，则强度提高到原来的16倍。

（ × ）9、在梁的弯曲正应力公式中，I z 为梁截面对于形心轴的惯性矩。

（ √ ） 10、梁弯曲最合理的截面形状，是在横截面积相同条件下W z 值最大的截面形状。

（ √ ） 二、单项选择题（每小题2分，共20分）1、材料弯曲变形后（ B ）长度不变。

A ．外层 B ．中性层 C ．内层2、梁弯曲时横截面上的最大正应力在（ C ）。

A. 中性轴上B. 对称轴上C. 离中性轴最远处的边缘上3、一圆截面悬臂梁，受力弯曲变形时，若其它条件不变，而直径增加一倍，则其最大正 应力是原来的（ A ）倍。

A.81B. 8C. 2D.214、图示受横力弯曲的简支梁产生纯弯曲变形的梁段是（ D ）A. AC 段B. CD 段C. DB 段D. 不存在 5、由梁弯曲时的平面假设，经变形几何关系分析得到（ C ）A. 中性轴通过截面形心B. 梁只产生平面弯曲；C. y ερ=；D. 1zM EI ρ=6、图示的两铸铁梁，材料相同，承受相同的载荷F 。

当F 增大时，破坏的情况是（ C ）。

一、单选题1、研究梁的变形的目的是（）。

A.进行梁的正应力计算B.进行梁的刚度计算C.进行梁的稳定性计算D.进行梁的剪应力计算正确答案：B2、图示圆截面悬臂梁，若直径d增大1倍(其它条件不变)，则梁的最大正应力、最大挠度分别降至原来的（）。

A.1/2 1/4B.1/4 1/8C.1/8 1/8D.1/8 1/16正确答案：D3、下面关于梁、挠度和转角的讨论中，正确的结论是（）。

A.挠度最大的截面转角为零B.挠度最大的截面转角最大C.转角为零的截面挠度最大D.挠度的一阶导数等于转角正确答案：D4、已知两悬臂梁的抗弯截面刚度EI相同，长度分别为l和2l，在自由端各作用F1和F2，若二者自由端的挠度相等，则F1/F2=（）。

A.2B.4C.6D.8正确答案：D5、梁上弯矩为零处（）。

A.梁的转角一定为零B.梁的挠度一定为零C.挠度一定为零，转角不一定为零D.梁的挠曲线的曲率一定为零正确答案：D6、已知等直梁在某段上的挠曲轴方程w(x)=–Cx4，C为常量，则在该段梁上（）。

A.分布载荷是x的一次函数B.分布载荷是x的二次函数C.无分布载荷作用D.有均匀分布载荷作用正确答案：D7、在等直梁弯曲变形中，挠曲线曲率最大值发生在（）。

A.剪力最大处B.转角最大处C.弯矩最大处D.挠度最大处正确答案：C8、材料相同的（a）悬臂梁和（b）悬臂梁，长度也相同，在自由端各作用2P和P，截面形状分别是b（宽）×2b（高）、b×b。

关于它们的最大挠度正确的是（）。

A.（a）梁最大挠度是（b）梁的1/4倍B.（a）梁最大挠度是（b）梁的1/2倍C.（a）梁最大挠度与（b）梁的相等D.（a）梁最大挠度是（b）梁的2倍正确答案：A9、已知简支梁的EI为常数，在梁的左端和右端分别作用一力偶m1和m2今欲使梁的挠曲线在x=l/3处出现一拐点，则比值m1/m2为（）。

A.2B.3C.1/2D.1/3正确答案：C10、两根梁尺寸，受力和支承情况完全相同，但材料不同，弹性模量分别为E1和E2，且E1=7E2，则两根梁的挠度之比y1/y2为（）。