信号检测与分析答案(苍松教学)

T x 2 (t )dt −2 A
0
Tx(t
0
)sin
(ω
0
t
+θ
)dt
+
A
2
T 0
sin
2
(ω
0
t
+θ
)dt
⎟⎞ ⎠
由于 ∫0Tsin 2 (ω0t
+ θ )dt
=
1 2
∫0T(1 − cos 2(ω0t
+ θ ))dt
=
T 2
，得到
( ) ∫ ∫ f
x A,θ
−1
= Fe N0
T x 2 (t )dt 2 A
ω0
ω0
s(t
)
=
⎪ ⎨
A
⎪
⎪ ⎪⎩
A（1
+
cos
ω0t）
− 2mπ < t ≤ 2mπ
ω0 2mπ
<t
≤
(2ωm0 +1)π
ω0
ω0
试证明时延τ
的无偏估计量的方差为
σ
2 τˆ
≥
3 + 4m
(2E / N0 )ω02
。其中 E 为信号能量。
解：略
9.4 接收信号 x(t) = s(t) + n(t)，s(t)的到达有时延τ ，求时延τ 的无偏估计量τˆ 的最小方差。其中 n(t)
⎤ ⎥⎦
∫ ∫ ∫ ∫ [ ] = 4
N
2 0
T / 2 ∂s(t −τ )
−T / 2 ∂τ
T /2
E
−T / 2
n(t )n(u )
∂s(u −τ ) dudt

信号分析与处理答案第二版HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第二章习题参考解答求下列系统的阶跃响应和冲激响应。

(1)解当激励为时，响应为，即：由于方程简单，可利用迭代法求解：，，…，由此可归纳出的表达式：利用阶跃响应和冲激响应的关系，可以求得阶跃响应：(2)解 (a)求冲激响应，当时，。

特征方程，解得特征根为。

所以：…(2.1.2.1)通过原方程迭代知，，，代入式(2.1.2.1)中得：解得，代入式(2.1.2.1)：…(2.1.2.2)可验证满足式(2.1.2.2)，所以：(b)求阶跃响应通解为特解形式为，，代入原方程有，即完全解为通过原方程迭代之，，由此可得解得，。

所以阶跃响应为：(3)解(4)解当t>0时，原方程变为：。

…(2.1.3.1)…(2.1.3.2)将(2.1.3.1)、式代入原方程，比较两边的系数得：阶跃响应：求下列离散序列的卷积和。

(1)解用表格法求解(2)解用表格法求解(3)和如题图2.2.3所示解用表格法求解(4)解(5)解(6)解参见右图。

当时：当时：当时：当时：当时：(7) ，解参见右图：当时：当时：当时：当时：当时：(8) ，解参见右图当时：当时：当时：当时：(9) ，解(10)，解或写作：求下列连续信号的卷积。

(1) ，解参见右图：当时：当时：当时：当时：当时：当时：(2) 和如图2.3.2所示解当时：当时：当时：当时：当时：(3) ，解(4) ，解(5) ，解参见右图。

当时：当时：当时：当时：(6) ，解(7) ，解(8) ，解(9) ，解试求题图示系统的总冲激响应表达式。

解已知系统的微分方程及初始状态如下，试求系统的零输入响应。

(1) ；解，，(2) ；，解，，，，可定出(3) ；，解，，，可定出某一阶电路如题图所示，电路达到稳定状态后，开关S 于时闭合，试求输出响应。

解由于电容器二端的电压在ｔ＝０时不会发生突变，所以。

“测试信号分析”课程思考题1. 信号分析与信号处理的内容和任务是什么?信号分析就是将一复杂信号分解为若干简单信号分量的叠加,并以这些分量的组成情况去考察信号的特性。

信号处理是指对信号进行某种变换或运算（如滤波、变换、增强、压缩、估计、识别等）。

广义的信号处理可把信号分析也包括在内。

信号处理包括时域和频域的处理，时域处理中最典型的是波形分析。

信号处理另一个重要内容是滤波,将信号中感兴趣的部分（有效信号）提取出来，抑制（削弱或滤波）不感兴趣的部分（干扰或噪声）。

2. 简要说明什么是模拟信号处理系统,什么是数字信号处理系统？系统的输入输出信号都是模拟信号的处理系统，称为模拟信号处理系统.系统的输入输出信号都是数字信号的处理系统，称为数字信号处理系统.3. 离散信号的表示方法是什么？离散信号变量的物理概念是什么？离散时间信号常用序列x(n)来表示，其中n 为整数,表示序号。

序列就是按一定次序排列的一组数，可用函数、数列、图形表示。

离散信号变量代表的是离散的时间，即采集间隔的几倍。

4. 周期序列与非周期序列是如何定义的？试举一周期序列的例子。

具有)()(mN n x n x p p +=形式的序列称为周期序列,其他形式的称为非周期序列。

例如：正弦序列)sin(][ϕ+Ω=n n x （当Ω/2π为非无理数时）5. 根据傅里叶变换性质，当将磁带慢录快放将产生什么样的声音效果?根据傅立叶变换的时间长度变化性质,磁带快放相当于信号在时域中的时间函数压缩了N 倍,则它在频域中的频域函数就扩展N 倍。

因此声音失真.6. 讨论周期为1T 的矩形脉冲信号)(t f T 与它一个周期内的信号)(t f 0的傅里叶变换间的关系.根据时域采样定理说明采样过程中如何减小信号失真。

周期矩形脉冲信号的傅立叶级数的系数等于其单位脉冲信号的傅立叶变换后（w)在1nw w =频率点的值乘以1/1T .连续信号必须是带限信号，采样频率必须大于或等于信号所具有的最高频率的2倍，即hw s w ≥。

3.7 用一个时间常数未0.35S 的一阶装置去测量周期分别为1S 、2S 、5S 的正弦信号，问A （ω）误差为多少？解：τ1 =1S, τ2 =2S, τ3 =5Sω1 =2π/1=2 , ω2 =2π/2= , ω3 =2π/5由式（3.16） A(ω)=1)(12+τω 得幅值比：A 1(ω)=1)1/235.0(12+⨯π =0.413A 2(ω)=1)2/235.0(12+⨯π =0.673A 3(ω)= 1)5/235.0(12+⨯π =0.915误差1 = [1-A 1(ω)]×100%=(1-0.41) ×100% = 58.6%误差2 = [1- A 2(ω)]×100%=（1-0.67）×100% = 32.7%误差3 = [1- A 3(ω)]×100%=(1-0.92) ×100% = 8.5%3.8 求周期信号x(t)=0.5cos10t +0.2cos(100t-45°)通过传递函数为 H(s) = 1005.01+S 的装置后所得到的稳态响应。

解：把原信号分成两个信号：x 1( t ) = 0.5 cos10t , x 2 ( t ) = 0.2cos(100t-45°)ω1= 10S -1, ω2=100S -1由一阶系统的幅频特性 A(ω)=1)(12+τω , 知第一个信号的幅值比 A 1(ω)=1)10005.0(12+⨯ = 0.99875输出幅值A 0=A 1(ω) ×0.5 = 0.99875×0.5 = 0.499第二个信号的幅值比：A 2(ω) =1)100005.0(12+⨯ =0.89443φ1(ω)= -arc tan τω1= -arc tan(10×0.005)= - 2.86° .φ2(ω)= -arc tan τω2= -arc tan(100×0.005)= 26.57°所以，周期信号的稳态响应为：x (t) = 0.499cos(10 t - 2.86°)+0.179cos(100 t - 71.57°)3.9 想用一个一阶系统作100Hz 正弦信号的测量，如要求限制振幅误差在5%以内。

1 −τ
dτ
∫ = 1
π
1
2 −1
2
t
1 dτ +τ
=
−1 π
ln
t t
− +
1
2 1
2
2.
a
(t
)
=
rect
⎛ ⎜⎝
t T
⎞ ⎟⎠
=
⎧⎪⎪1, ⎨ ⎪⎪⎩ 0,
t t
≤T 2
>T 2
A( f ) = T sin c (π fT )
当 ω0 2π
>1 T
即 ω0
>
2π T
时，解析信号和复指数形式信号近似。 ω0 越大越接近。
2⎤ ⎥⎦
=
N0 A2T
=
2 N0 Es
∫ ⎛
⎜ Es = ⎝
T 0
A2 sin2 (ω0t
+θ ) dt
=
A2 2
⎞ ⎟ ⎠
p0 ( y) =
1 2π i2N0Es
exp
⎛ ⎜
−
⎝
y2 2i2 N 0 Es
⎞ ⎟ ⎠
E1
(
y
)
=
E
⎡ ⎢⎣
T
∫0
(
A
sin
(ω0t
+
θ
)
+
n
(
t
)
)
u∗
(
t
)
dt
⎤ ⎥⎦T
tdt
=
0
2
③等效时宽
∫ ∫ δ =
2π 2E
[
∞ t2
−∞
u(t) 2 dt]1/ 2

信号分析与处理答案第二版HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第二章习题参考解答求下列系统的阶跃响应和冲激响应。

(1)解当激励为时，响应为，即：由于方程简单，可利用迭代法求解：，，…，由此可归纳出的表达式：利用阶跃响应和冲激响应的关系，可以求得阶跃响应：(2)解 (a)求冲激响应，当时，。

特征方程，解得特征根为。

所以：…(2.1.2.1)通过原方程迭代知，，，代入式(2.1.2.1)中得：解得，代入式(2.1.2.1)：…(2.1.2.2)可验证满足式(2.1.2.2)，所以：(b)求阶跃响应通解为特解形式为，，代入原方程有，即完全解为通过原方程迭代之，，由此可得解得，。

所以阶跃响应为：(3)解(4)解当t>0时，原方程变为：。

…(2.1.3.1)…(2.1.3.2)将(2.1.3.1)、式代入原方程，比较两边的系数得：阶跃响应：求下列离散序列的卷积和。

(1)解用表格法求解(2)解用表格法求解(3)和如题图2.2.3所示解用表格法求解(4)解(5)解(6)解参见右图。

当时：当时：当时：当时：当时：(7) ，解参见右图：当时：当时：当时：当时：当时：(8) ，解参见右图当时：当时：当时：当时：(9) ，解(10)，解或写作：求下列连续信号的卷积。

(1) ，解参见右图：当时：当时：当时：当时：当时：当时：(2) 和如图2.3.2所示解当时：当时：当时：当时：当时：(3) ，解(4) ，解(5) ，解参见右图。

当时：当时：当时：当时：(6) ，解(7) ，解(8) ，解(9) ，解试求题图示系统的总冲激响应表达式。

解已知系统的微分方程及初始状态如下，试求系统的零输入响应。

(1) ；解，，(2) ；，解，，，，可定出(3) ；，解，，，可定出某一阶电路如题图所示，电路达到稳定状态后，开关S 于时闭合，试求输出响应。

解由于电容器二端的电压在ｔ＝０时不会发生突变，所以。

信号检测期末考试题及答案（注意：以下为示例文章，实际文章内容可能与示例不同）一、选择题1. 在信号检测理论中，常用的两个假设是什么？答案：零假设和备择假设。

2. 什么是误警概率？答案：误警概率是指当零假设成立时，拒绝零假设的概率。

3. 什么是检测概率？答案：检测概率是指当备择假设成立时，正确拒绝零假设的概率。

4. 什么是检测效能？答案：检测效能是指检测系统能够正确检测到信号的能力。

5. 什么是最大似然检测准则？答案：最大似然检测准则是在已知观测信号的条件下，选择使似然函数值最大的假设作为最终决策。

二、填空题1. 当备择假设为H1: X ~ N(1, 1)，零假设为H0: X ~ N(0, 1)时，应该使用的检测准则是________。

答案：N-P检测准则。

2. 假设信号的功率为P1，背景噪声功率为P0，最佳检测准则为最小概率误警准则，则检测阈值应选择为________。

答案：关于噪声功率和信噪比的函数。

3. 当观测信号满足高斯分布时，最佳检测准则为________。

答案：最大似然检测准则。

4. 当信号为常值时，信号出现的概率密度函数为________。

答案：冲激函数。

5. 信号与噪声统计独立且噪声功率已知时，最佳检测准则为________。

答案：能量检测准则。

三、计算题1. 当信噪比为10dB，信号的功率为1W，背景噪声的功率为0.1W 时，计算最佳检测准则的检测门限值。

答案：根据最小概率误警准则公式，检测门限值等于背景噪声功率乘以一个与信噪比和常数有关的函数，根据给定的数值计算得到检测门限值为0.3162。

2. 在一个二元信号检测系统中，假设信号和噪声均服从高斯分布，且功率相等。

当信号出现的概率为0.9时，计算最佳检测准则的检测门限值。

答案：根据最大似然检测准则，将假设信号出现和噪声出现的概率代入似然函数，对似然函数取对数，最后得到检测门限值为0.2553。

四、简答题1. 请简述最小概率误警准则和最大概率检测准则的基本原理。

信号检测期末考试题及答案一、选择题（每题2分，共20分）1. 在信号检测理论中，信号检测的两个主要参数是：A. 信号强度和噪声大小B. 信号频率和信号幅度C. 信号到噪声比和信号的信噪比D. 信号的信噪比和信号的频率带宽2. 信号检测中的ROC曲线表示的是：A. 信号的频率响应曲线B. 信号的幅度响应曲线C. 接收者操作特征曲线D. 信号的时域特性曲线3. 信号检测理论中，d'值表示的是：A. 信号的信噪比B. 信号的幅度C. 信号的频率D. 信号与噪声的区分能力4. 以下哪个不是信号检测理论中常用的指标：A. 灵敏度B. 特异性C. 准确率D. 信噪比5. 信号检测理论中的β错误是指：A. 漏检B. 误报C. 假阳性D. 假阴性...（此处省略剩余选择题）二、简答题（每题10分，共30分）1. 简述信号检测理论中的信号到噪声比（SNR）的概念及其重要性。

2. 解释ROC曲线在信号检测中的应用及其优势。

3. 什么是d'值？它在信号检测中的作用是什么？三、计算题（每题15分，共30分）1. 假设一个信号检测系统接收到的信号强度为10，噪声强度为5，请计算该系统的信号到噪声比（SNR）。

2. 给定一个信号检测系统的ROC曲线数据，计算其d'值和β错误。

四、论述题（每题20分，共20分）1. 论述信号检测理论在实际工程中的应用及其重要性。

答案一、选择题1. D2. C3. D4. D5. A...（此处省略剩余选择题答案）二、简答题1. 信号到噪声比（SNR）是信号检测理论中衡量信号在噪声中可检测性的一个重要参数。

它表示信号强度与背景噪声强度的比值。

高SNR意味着信号更容易被检测和识别，而低SNR则意味着信号可能被噪声淹没，难以检测。

2. ROC曲线是接收者操作特征曲线的简称，它用于描述信号检测系统的性能。

通过绘制不同阈值下系统的正确检测率（真阳性率）与错误检测率（假阳性率）的关系，ROC曲线可以直观地展示系统在不同灵敏度水平下的表现。

第一章信号及其描述（一）填空题1、测试的基本任务是获取有用的信息，而信息总是蕴涵在某些物理量之中，并依靠它们来传输的。

这些物理量就是，其中目前应用最广泛的是电信号。

2、信号的时域描述，以为独立变量；而信号的频域描述，以为独立变量。

3、周期信号的频谱具有三个特 1 Fj*4、靠周期信号包括信号和信号。

5、描述随机信号的时域特征参数有、、o6、对信号的双边谱而言，实频谱（幅频谱）总是对称，虚频谱（相频谱）总是对称。

（二）判断对错题（用。

或X表示）1、各态历经随机过程一定是平稳随机过程。

（）2、信号的时域描述与频域描述包含相同的信息量。

（）3、非周期信号的频谱一定是连续的。

（）4、非周期信号幅频谱与周期信号幅值谱的量纲一样。

（）5、随机信号的频域描述为功率谱。

（）（三）简答和计算题1、求正弦信号x（f） = x Q sin破的绝对均值U ixi和均方根值x rms o2、求正弦信号X。

）= X。

sin（破+ °）的均值从，均方值材；,和概率密度函数p（x）。

3、求指数函数x（.t） = Ae a'（.a>0,t>0）的频谱。

\t\<T4、求被截断的余弦函数x（0 = \ 的傅立叶变换。

[0 \t\>T5、求指数衰减振荡信号xQ） = e~at sin co Q t（a > 0,f Z 0）的频谱。

参考答案第一章信号及其描述（一）1、信号；2、时间（t）,频率（f）； 3、离散性，谐波性，收敛性；4、准周期，瞬态非周期；5、均值均方值，方差b：； 6、偶,奇；(二)1、V； 2, V； 3, X; 4, X; 5、V ；（三）f 2、。

，「13、A4、71X Q COS(仞 +(p)a +网'T sinc((2# + ©o)7j + T sinc((2#-饥)7)；5、—~ ~Q — J —(D Q +第二章测试装置的基本特性（-）填空题1、某一阶系统的频率响应函数为H（jco）= ------ ，输入信号x（0 = sin —,则输出信号2ja）+ l2 yQ）的频率为切=,幅值丫=,相位S =o22、试求传递函数分别为一——和 ~~地--------------- §的两个环节串联后组成的系统的3.5s+ 0.5 妒+i 4旧$ +旧z总灵敏度。

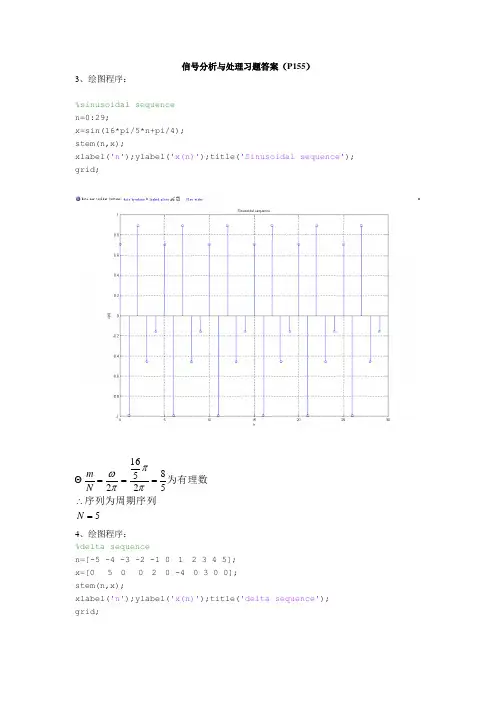
信号分析与处理习题答案（P155）3、绘图程序：%sinusoidal sequence n=0:29;x=sin(16*pi/5*n+pi/4); stem(n,x);xlabel('n');ylabel('x(n)');title('Sinusoidal sequence'); grid;55825162=∴===N N m序列为周期序列为有理数πππω4、绘图程序：%delta sequencen=[-5 -4 -3 -2 -1 0 1 2 3 4 5]; x=[0 5 0 0 2 0 -4 0 3 0 0]; stem(n,x);xlabel('n');ylabel('x(n)');title('delta sequence'); grid;8、根据DTFT 性质， （1）时域尺度变换特性：连续时间傅里叶变换的尺度变换表示为：⎪⎭⎫ ⎝⎛↔a X a at x ω1)( 然而，在离散时间的情况下，若a 不是整数，x[an]就不是一个序列。

另一方面，如果a 是一个整数，例如a=2，那么x[2n]仅包含x[n]的偶数样点。

因此，离散时间中的时域尺度变换与上式有些不同。

令m 为一正整数，则序列的傅里叶变换为⎩⎨⎧≠===km n kmn k x m n x n x m 0][]/[][)(()a b{})(][][][][)()()()(Ω====∑∑∑∞-∞=Ω-∞-∞=Ω-∞-∞=Ω-m X ek x ekm xen xn x F n km j n kmj m n nj m m所以)(0]/[][)(Ω↔⎩⎨⎧≠==m X km n km n m n x n x m⎪⎭⎫⎝⎛Ω↔a X an x )( （3）时域位移：)(][00Ω↔-Ω-X en n x n j)()1()()()2()(22Ω-=Ω-Ω↔--Ω-Ω-X e X eX n x n x j j10.（2）根据P109式3-26)())(()(1)()()(00101000Ω=Ω+=ΩΩ=∑∑-=Ω--=Ωk X qN k X en x Nk X e k X n x N k njk N k njk根据题意，序列x(n)的基本周期为N=8，Ω0=2π/N=π/4 根据欧拉公式，nj nj njnjee een 002121214cos 44Ω-Ω-+=⎪⎪⎭⎫ ⎝⎛+=πππ则x(n)的傅里叶系数为X(1)=1/2，X(-1)= X(-1+8)= X(7)=1/2，其他系数等于0。

4章作业答案(信号和测试)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（4章作业答案(信号和测试)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为4章作业答案(信号和测试)的全部内容。

3—4 有一电阻应变片(见图3—84)，其灵敏度S g ＝2，R ＝120Ω。

设工作时其应变为1000με,问∆R ＝?设将此应变片接成如图所示的电路，试求：1）无应变时电流表示值;2）有应变时电流表示值;3）电流表指示值相对变化量;4）试分析这个变量能否从表中读出？解：根据应变效应表达式g R R S ε∆=得 R =S g R =2100010—6120=0。

241)I 1=1.5/R =1。

5/120=0。

0125A=12.5mA2）I 2=1.5/(R +R )=1。

5/(120+0。

24）0.012475A=12.475mA3）=（I 2-I 1)/I 1100%=0.2％ 4）电流变化量太小，很难从电流表中读出。

如果采用高灵敏度小量程的微安表,则量程不够，无法测量12.5mA 的电流;如果采用毫安表，无法分辨0。

025mA 的电流变化.一般需要电桥来测量，将无应变时的零位电流平衡掉,只取有应变时的微小输出量，并可根据需要采用放大器放大.第四章 信号的调理与记录4-1 以阻值R =120、灵敏度S g =2的电阻丝应变片与阻值为120的固定电阻组成电桥，供桥电压为3V,并假定负载电阻为无穷大，当应变片的应变为2(表示微应变10^(—6）)和2000时，分别求出单臂、双臂电桥的输出电压，并比较两种情况下的灵敏度。

解：这是一个等臂电桥,可以利用等臂电桥和差特性表达式求解。

信号分析与处理课程习题2参考解答-2010（共5篇）第一篇：信号分析与处理课程习题2参考解答-2010P57-101Ω-j52-j5Ω(1)方法1：先时移→F[x(t-5)]=X(Ω)e，后尺度→F[x(2t-5)]=X()eΩt05Ω-j-j1Ω1Ω方法2：P40时移+尺度→F[x(at-t0)]=X()ea→F[x(2t-5)]=X()e2 |a|a221Ω-j(2)方法2：P40时移+尺度→F[x(at-t0)]=X()e|a|aΩt0aΩ→F[x(-t+1)]=X(-Ω)ejΩ(3)P42频域卷积定理→F[x1(t)⋅x2(t)]=X1(Ω)*X2(Ω)2π→F[x(t)⋅cos(t)]=X(Ω)*[πδ(Ω+1)+πδ(Ω-1)]=X(Ω+1)+X(Ω-1)2π22P57-12F[x(t)]=⎰x(t)e-∞∞-jΩtdt=⎰τ-2E(t+)eτ2ττdt+⎰22Eτ8ωττωτ(-t+)e-jΩtdt=2sin2()=Sa2()τ2424ωτP57-13假设矩形脉冲为g(t)=u(t+)-u(t-),其傅里叶变换为G(Ω),则22F[x(t)]=F[E⋅g(t+)-E⋅g(t-)]=E⋅G(Ω)eEΩτ=⋅G(Ω))2j2P57-15ττττjΩτ-E⋅G(Ω)e-jΩτ=E⋅G(Ω)(ejΩτ-e-jΩτ)图a)X(Ω)=|X(Ω)|e-1jΩ⎧AejΩt0,|Ω|<Ω0=⎨|Ω|>Ω0⎩0,→x(t)=F[X(Ω)]=2π⎰Ω0AejΩt0ejΩtdΩ=AΩ0Asin(Ω0(t+t0))=Sa(Ω0(t+t0))π(t+t0)π图b)X(Ω)=|X(Ω)|ejΩ⎧-jπ⎪Ae,-Ω0<Ω<0⎪jπ⎪=⎨Ae2,0<Ω<Ω0⎪0,|Ω|>Ω0⎪⎪⎩→x(t)=F[X(Ω)]=2π-1⎰-Ω0Ae-jπejΩt1dΩ+2π⎰Ω0Ae2ejΩtdΩ=jπA2A2Ω0t(cos(Ω0t-1))=-sin()πtπt2第二篇：高频电子信号第四章习题解答第四章习题解答4-1 为什么低频功率放大器不能工作于丙类？而高频功率放大器则可工作于丙类？分析：本题主要考察两种放大器的信号带宽、导通角和负载等工作参数和工作原理。

2.3 10
已知信号
x(t)
=
sin(t)
×
(u(t)
−
u(t
−
π))，求(1) x1(t)
=
d2 dt2
x(t)
+
x(t);
(2)
x2
(t)
=
∫t
−∞
x(τ )dτ 。
答：(1)
dx(t) dt
=
cos(t) × (u(t) − u(t − π)) + sin(t) × (δ(t) − δ(t − π))
6 第五章
24
6.1 补 1： . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
6.2 补 2： . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1+cos(2t) 2
,
E
= ∞, P
= 1/2.
(4) E = 4/3, P = 0;
(5) E = ∞, P = 1;
(6) E = ∞, P = 1/2.
2 第二章 P. 23
2.1 1
应用∫冲∞激信号的抽样特性，求下列表达式的函数值
(1) f (t − t0) · δ(t)dt = f (−t0) ∫−∞∞
x2(t)
=

1
− cos(t) ∞
, ,
if (t ∈ (0, π]) if (t > π)

1. 如图所示一个理想的低通滤波器其传递函数H(ω)，输入一个零均值、方差为2σ的白噪声（不相关随机变量）序列w(n)。

1) 求解输出序列X (n)的功率谱密度()xxPω并画出其图形；2) 证明X (n)的自相关()xxR m可以表达为：2sin()2()22xxmR mmπσπ=并画出其图形，根据图形说明该滤波器的作用；3) 用两种方式说明22(X)2Eσ=：A.2(X)(0)xxE r=B.21(X)()2xxE P dππωωπ-=⎰解：1）由题意可知，零均值白噪声的功率谱为2()ww wPωσ=，传递函数为()Hω，则，输出序列()X n的功率谱密度()xxPω为：2224,()|()|220,wjxx wP H eωππσωωσ⎧-≤≤⎪==⎨⎪⎩其它其功率谱密度图形如下图所示：2）因为自相关和功率谱密度互为傅里叶逆变换，则：/22/22222/2/22222111()()| 22211()2sin222sin2444422j m j m j m xx xxj m j mwww wwR m P e d e d ejmme e jjm jmmmπππωωωπππππωωωππππππσσπσσσπ----====-==⎰⎰()xxR m图为：由图形可知,该滤波器的波形为：3）根据题意可得：A. 2222sin sin22()(0)222|lim22w mx wx wmmXmm mE rσσπππσπ=→====B. 22222411()()222x wx w E X P d d ππππωσπσωωπ--===⎰⎰2.如图所示，滤波器由下式所述1n n n y x x -=-，其中输入是一个确定性信号n s b n =•(b 是个已知常量)和零均值随机白噪声序列n d 组成，其中噪声方差为2σ，使用叠加原理计算：1）计算输出中信号的成分并绘图；2） 计算噪声功率（即输出中噪声成分的方差）； 3）计算输出中噪声成分的功率谱密度函数并绘图； 4）描述该滤波器的作用并评价其效果。

《信号检测与估计》第九章习题解答9.1 接收信号(((t n t A t x ++=θω0sin ,其中(t n 是高斯白噪声,θ在(π20,均匀分布,现在需求振幅A 的最大似然估计量。

由于θ的先验知识已知,故可先对θ求平均得到(A x f ,试问要求振幅A 的最大似然估计量必须解什么样的方程? 解:接收信号(t x 的似然函数为((([]((((((((⎟⎠⎞⎜⎝⎛+++−−+++−−+−−∫∫∫∫∫===T TT TTdt t A dt t t x A dt t x N dtt A t t Ax t xN dtt A t x N FeFeFeA x f 0002200200022020200sin sin 21sin sin 21sin 1,θωθωθωθωθωθ由于(((∫=+−=∫+TTT dt t dt t 0000222cos 121sin θωθω,得到 ((((020000202sin 21,N TA dt t t x N A dtt x N e eFeA x f T T−+−∫∫=θωθ对θ积分,得到(((((((((θπθπθθθπθωθωπθωπd eeFed e e Fed f A x f A x f dt t t t x N A N T A dt t x N dt t t x N A N T A dt t x N T TTT∫∫∫∫∫∫∫+−−+−−===20cos cos sin sin 22120sin 221 2000000202000020202121,令(ϕωcos cos 00z dt t t x x Tc ==∫,(ϕωsin sin 00z dt t t x x T s ==∫,得到222s cx x z +=,csx x arctg =ϕ (((((⎟⎟⎠⎞⎜⎜⎝⎛====∫∫∫∫∫−+++0020cos 220cos cos sin sin 220cos sin 220 cos cos sin sin 22212121210 000N Az I d ed ed e d eN Azz z N Ax x N Adt t t t x N A c s Tθπθπθπθππϕθπθϕθϕπθθπθωθω 上式中,[](cos exp 21020x I d x =∫πθθπ为零阶修正贝塞尔函数。

答
案
网
(6) x(t ) = cos 2πt × u (t )
jΩ ( n + N )
.c
= e jΩn ，因此有 e jΩn = 1 。
om
da
课后答案网
答案： （1） 是周期信号， T =
（8） 是周期信号， T = 16
kh
3．试判断下列信号是能量信号还是功率信号。 （1） x1 (t ) = Ae
−t
t≥0
（2） x 2 (t ) = A cos(ω 0 t + θ )
解： （1） x1 (t ) = Ae
−t
t≥0
2
T →∞ 0
2 A2 A2 ⎛ 1 ⎞ A −2T lim ( e − 1) = − lim ⎜ = − 1⎟ = 2 T →∞ ⎝ e 2T −2 T →∞ ⎠ 2
∴ x1 (t )为能量信号
kh
=∞
da
= lim [ 2T −
sin 4T sin(2 + 2π )T sin(2 − 2π )T sin 4π T ⎤ + − − 4 2 + 2π 2 − 2π 4 ⎥ ⎦
w
sin(2 − 2π )T sin(2 − 2π )T sin 4π T sin 4π T ⎤ − − − 4 − 4π 4 − 4π 8 8 ⎥ ⎦
A2 1 ⎞ ⎛ 1 lim ⎜ − ⎟=0 2T T →∞ 2 2T ⎠ ⎝ 2Te
aw
T
答
案
网
（3） x3 (t ) = sin 2t + sin 2πt
（4） x 4 (t ) = e sin 2t
w
w
T →∞

一、填空题〔每空1分, 共10分〕1．序列()sin(3/5)x n n π=的周期为 10 。

2．线性时不变系统的性质有交换律、结合律、分配律。

3．因果序列x(n)，在Z →∞时，X(Z)=x(0)。

4．抽样序列的Z 变换与离散傅里叶变换DFT 的关系为k N j e Z π2=。

5．序列x(n)=(1，-2，0，3；n=0，1，2，3), 圆周左移2位得到的序列为{0，3，1，-2; n=0,1,2,3}。

6．设LTI 系统输入为x(n) ，系统单位序列响应为h(n)，那么系统零状态输出()()()y n x n h n =*。

7．对4()()x n R n =的Z 变换为：，其收敛域为： 411,01z z z --->-二、单项选择题〔每题2分, 共20分〕1．δ(n)的Z 变换是B.δ(ωπδ(ωπ2．序列x 1〔n 〕的长度为4，序列x 2〔n 〕的长度为3，那么它们线性卷积的长度是A. 3B. 4C. 6D. 73．LTI 系统，输入x 〔n 〕时，输出y 〔n 〕；输入为3x 〔n-2〕，输出为A. y 〔n-2〕B.3y 〔n-2〕C.3y 〔n 〕D.y 〔n 〕4．下面描述中最适合离散傅立叶变换DFT 的是A.时域为离散序列，频域为连续信号B.时域为离散周期序列，频域也为离散周期序列C.时域为离散无限长序列，频域为连续周期信号D.时域为离散有限长序列，频域也为离散有限长序列5．假设一模拟信号为带限，且对其抽样满足奈奎斯特条件，理想条件下将抽样信号通过 即可完全不失真恢复原信号6．以下哪一个系统是因果系统A.y(n)=x (n+2)B. y(n)= cos(n+1)x (n)C. y(n)=x (2n)D.y(n)=x (- n)7．一个线性时不变离散系统稳定的充要条件是其系统函数的收敛域包括A. 实轴8．序列Z 变换的收敛域为｜z ｜>2，那么该序列为A.有限长序列B.无限长序列C.反因果序列D.因果序列9．假设序列的长度为M ，要能够由频域抽样信号X(k)恢复原序列，而不发生时域混叠现象，那么频域抽样点数N 需满足的条件是A.N≥MB.N≤M C .N≤2M D.N≥2M10．设因果稳定的LTI系统的单位抽样响应h(n)，在n<0时，h(n)=A.0B.∞C. -∞D.1三、判断题〔此题共10个小题，每题1分，共10分〕1．序列的傅立叶变换是频率ω的周期函数，周期是2π。