基于LabVIEW软件的PID自动控制
- 格式:doc
- 大小:1.59 MB
- 文档页数:29


系统PID 校正虚拟实验系统 一、PID 校正原理1、 原理概述在串联校正中,比例控制可提高系统开环增益,减少系统误差,提高系统的控制精度,但会降低系统的相对稳定性,甚至可能造成系统闭环系统不稳定;积分控制可以系统的型别(无差度),有利于提高系统稳态性能,但积分控制增加了一个位于原点的开环极点,使信号产生90度的相位滞后,对系统的稳定不利,故不宜采用单一的积分控制器;微分控制规律能反映输入信号的变化趋势,产生有效的早期修正信号,以增加系统的阻尼程度,从而改善系统的稳定性,但微分控制增加了一个开环零点,使系统的相角裕度提高,因此有助于系统动态性能的改善。
PID 控制器增加了一个位于原点的开环极点和两个位于s 左半平面的开环零点,可提高系统的稳态性能,改善系统的动态性能。
2、原理框图PID 控制器是一种线性控制器,它根据给定值与实际输出值构成控制偏差:对偏差进行比例(P)、积分(I)、微分(D)计算后通过线性组合构成控制量,作用于被控对象,其控制规律为:3、 数学模型的建立PID 控制规律的传递函数为2(1)1()(1)p i di c p d i i K TT s T s G s K T s T s T s++=++=式中p i d K T T 、、分别为,比例系数、积分时间常数、微分时间常数比例环节成比例的反映控制系统的偏差信号,一旦产生偏差,控制器就产生控制作用,来减少偏差。
积分环节主要用于消除静态误差,提高系统的无差度。
积分作用的强弱取决于时间常数i T ,i T 越小,积分作用越强。
微分环节反映偏差信号的变化趋势,在系统中引入一个有效的提前修正信号,来加快系统的动作速度,缩短调节时间。
二、PID 校正虚拟实验系统设计PID 控制器设计的主要任务就是对于用户输入的被控对象,快速地确定比例系数p K 、积分系数i T 和微分系数d T ,使系统满足相应的指标。
1、 Labview 程序设计1) 面板设计启动Labview ,进入仪器编辑环境,建立仪器的面板。

NI DAQ和LabVIEW构造PID控制系统关键词:PID控制;LabVIEW;NI DAQ设备在自动控制中,一个系统的运行要求能够满足给定的性能指标,具有抗干扰能力和稳定性。
对于被控制的对象,其本身的物理结构和工作过程是一定的,在给定信号作用时,对象的输出并不一定能满足系统的性能要求,所以需要加入一个控制器。
控制器与被控对象以闭环的形式构成系统,以帮助整个系统的输出满足给定的性能指标,而控制器运用的控制规律多种多样。
PID(Proportional Integral Derivative比例微分积分)控制是控制工程中技术成熟,应用广泛的一种控制策略,它经过长期工程实践,已形成了一套完整的控制方法和典型的结构。
PID控制PID控制器结构简单、稳定性好、工作可靠、调整方便。
当被控对象的结构和参数不能完全被掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。
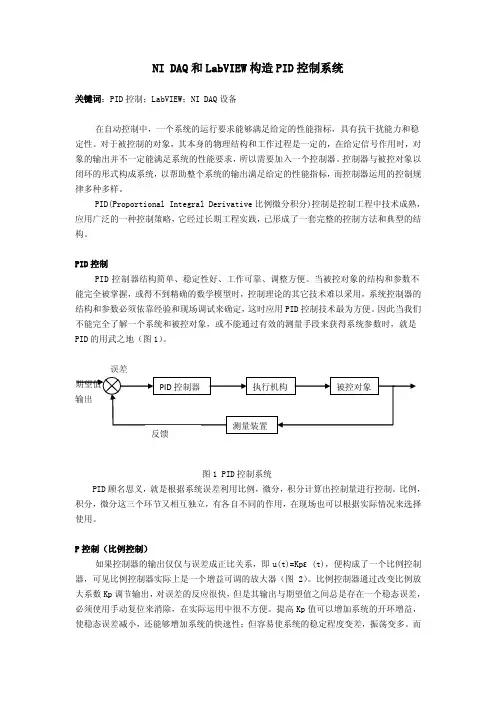
因此当我们不能完全了解一个系统和被控对象,或不能通过有效的测量手段来获得系统参数时,就是PID的用武之地(图1)。
误差图1 PID控制系统PID顾名思义,就是根据系统误差利用比例,微分,积分计算出控制量进行控制。
比例,积分,微分这三个环节又相互独立,有各自不同的作用,在现场也可以根据实际情况来选择使用。
P控制(比例控制)如果控制器的输出仅仅与误差成正比关系,即u(t)=Kpε(t),便构成了一个比例控制器,可见比例控制器实际上是一个增益可调的放大器(图2)。
比例控制器通过改变比例放大系数Kp调节输出,对误差的反应很快,但是其输出与期望值之间总是存在一个稳态误差,必须使用手动复位来消除,在实际运用中很不方便。
提高Kp值可以增加系统的开环增益,使稳态误差减小,还能够增加系统的快速性;但容易使系统的稳定程度变差,振荡变多。
而当Kp值小时,又会使系统动作变得缓慢,所以校正系统很少单独使用P控制。

2011年第21期随着现代控制技术在工业控制领域的发展需要实时现场数据采集,控制,如电厂,钢厂,化工等行业需要的现场,那里的温度数据收集大量生产收集了非常重要的一部分。
在极端不利的条件下,温度测量,往往伴随着影响或高速高温气体,其共同特点是高温度的变化,是短暂的,响应时间,最多到MS 或PS 水平,测量流量巨大的力量是困难的。
目前,最常用的温度采集系统是一个集成的温度传感器和单片机的形式,这种友好的人机界面程序,调试周期长,变化不大方便,所以一个新的测量效率和自动化水平是较高发展趋势的温度控制系统[1]。
Lab view 是美国国家仪器公司开发的一种虚拟仪器平台,开发的一个代码来替换图标的编程语言文本来创建应用程序开发工具。
LabVIEW 的强大,提供了数据收集,分析和储存财富的库函数,包括数据采集器,GPIO ,Rs232/485各种手段,包括所有的标准通信总线功能特点。
设计使用LabVIEW 数据采集系统,可以收集各种模拟信号,但与NI 公司的数据采集板都比较贵,可以在单片机数据采集系统的实际开发。
本文设计了一种基于Labview 的单片机远程温度自动控制系统,并对其系统的组成、实现给出了详细描述。
1.系统硬件设计由计算机系统硬件,单片机,温度测量电路和温度控制电路。
该系统结合在一个电脑,一个强大的图形化编程软件和模块化硬件,灵活和基于计算机的测量和控制解决方案,建立适应建设系统的需要。
使用温度信号的传感器和单片机小系统的温度信号采集,调理和转换,然后再由通过RS -232串行数据传送到计算机,通过计算机和Labview 程序运行的输入数据进行分析处理,并最终由计算机显示的结果。
同时,通过计算机串口采样输入信号,利用Labview 中的PID 控制算法,求出系统输出信号的大小,再由串口将输出信号传输至外部温度控制电路,以实现温度控制。
1.1温度测量电路温度测量电路主要由温度传感器和信号调理部分组成。


LabVIEW中的PID控制器设计与实现PID控制器是一种常用的控制算法,可以实现对控制系统的精确控制。
在LabVIEW中,我们可以利用其强大的功能来设计和实现PID控制器。
一、PID控制器原理简介PID控制器是基于比例(P)、积分(I)和微分(D)三个部分的控制算法。
比例部分根据当前测量值与设定值的偏差来控制输出;积分部分根据时间的累积偏差来控制输出;微分部分根据当前偏差的变化速率来控制输出。
PID控制器的输出是这三个部分的加权和。
二、LabVIEW中PID控制器的设计步骤1. 创建LabVIEW项目并添加控制器模块在LabVIEW中,我们首先需要创建一个新的项目,并在其下创建一个新的VI文件。
然后,在Block Diagram中选择PID控制器组件并将其拖放到界面中。
2. 设置输入和输出在PID控制器的配置界面中,我们需要设定输入和输出的信号类型以及相应的范围。
通常,输入信号为测量值,输出信号为控制量。
3. 配置PID参数在PID控制器配置界面的参数设置中,我们可以设置比例系数、积分时间和微分时间。
这些参数的合理设定对于控制系统的性能至关重要。
4. 编写PID控制器算法在Block Diagram中,我们可以利用LabVIEW的编程功能来实现PID控制器算法。
根据设定好的输入和参数,计算出相应的控制输出。
5. 调试和优化完成PID控制器的编写后,我们需要对其进行调试和优化。
可以利用LabVIEW的调试工具,观察实时数据和算法运行情况,并对PID参数进行适当的调整,以达到系统的最佳控制效果。
三、LabVIEW中PID控制器的实现案例以下是一个实例,展示了如何在LabVIEW中设计和实现PID控制器。
假设我们需要使用PID控制器来控制一个温度系统。
1. 创建LabVIEW项目并添加控制器模块打开LabVIEW软件,创建一个新的项目,并添加一个新的VI文件。
在Block Diagram中选择PID控制器组件并将其拖放到界面中。


#LabVIEW在自动控制原理的应用##简介 LabVIEW 是一种图形化编程环境,被广泛应用于自动控制原理领域。
它将传统的文本编程转化为图形化编程,使得控制系统的设计、调试和维护更加简便和直观。
本文将介绍LabVIEW在自动控制原理中的应用,以及其优势和特点。
##LabVIEW在自动控制原理中的应用LabVIEW在自动控制原理中有着广泛的应用。
它可以用来设计和模拟各种类型的控制系统,包括PID控制、状态空间控制和模糊控制等。
以下是LabVIEW在自动控制原理中的具体应用:1.PID控制LabVIEW可以提供丰富的工具和函数用来实现PID控制器的设计和调节。
通过简单拖拽和连接不同的模块,用户可以轻松地建立PID控制器的结构,并进行参数调整和性能分析。
此外,LabVIEW还可以方便地调节PID控制器的采样时间、输出限幅和反馈算法等。
2.状态空间控制LabVIEW中的状态空间模块可以帮助用户建立和模拟复杂的状态空间控制系统。
用户可以通过拖拽和连接状态空间模块,定义系统的状态方程和输入输出方程,进而进行系统的稳定性分析和性能优化。
3.模糊控制LabVIEW提供了直观的模糊控制设计工具,使得模糊控制器的设计和调节更加简单和直观。
用户可以通过拖拽和连接不同的模糊控制模块,设置模糊控制器的输入输出和规则库,实现对系统的模糊控制。
4.系统建模和仿真LabVIEW中的系统建模和仿真工具可以帮助用户快速建立系统模型,并进行仿真和测试。
用户可以通过拖拽和连接不同的模块,描述系统的结构和动态特性,快速得到系统的响应曲线和频率特性。
##LabVIEW的优势和特点LabVIEW在自动控制原理中具有以下优势和特点:1.图形化编程LabVIEW采用图形化编程方式,使得用户可以通过拖拽和连接模块的方式来实现代码的编写。
这种直观的编程方式可以减轻用户的编程负担,提高编程效率。
2.丰富的库函数和工具LabVIEW提供了丰富的库函数和工具,可以满足不同类型控制系统的设计需求。
应用LabVIEW实现PID控制功能作为虚拟仪器的主流开发语言,图形语言(Graphical Language)在测试系统中得到广泛应用。
优秀的图形语言开发环境使LabVIEW不仅包括了开发虚拟仪器面板的各种对象和进行信号分析的丰富的函数,而且提供了外挂的PID控制工具包,使用户可以将虚拟仪器拓展到自动控制领域。
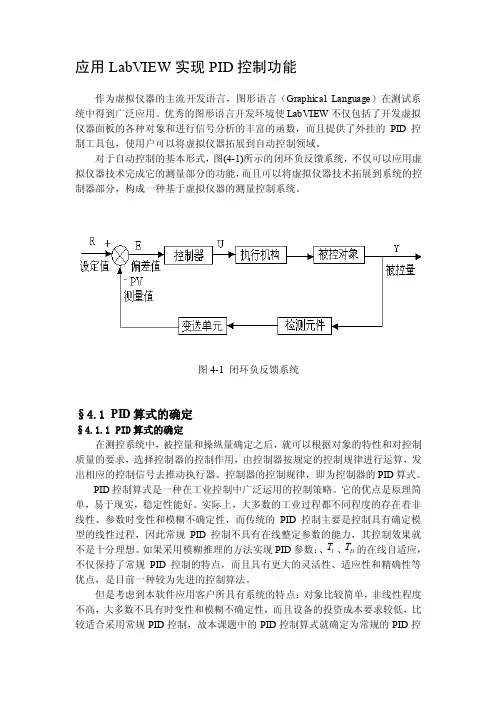
对于自动控制的基本形式,图(4-1)所示的闭环负反馈系统,不仅可以应用虚拟仪器技术完成它的测量部分的功能,而且可以将虚拟仪器技术拓展到系统的控制器部分,构成一种基于虚拟仪器的测量控制系统。
图4-1 闭环负反馈系统§4.1 PID算式的确定§4.1.1 PID算式的确定在测控系统中,被控量和操纵量确定之后,就可以根据对象的特性和对控制质量的要求,选择控制器的控制作用,由控制器按规定的控制规律进行运算,发出相应的控制信号去推动执行器。
控制器的控制规律,即为控制器的PID算式。
PID控制算式是一种在工业控制中广泛运用的控制策略。
它的优点是原理简单,易于现实,稳定性能好。
实际上,大多数的工业过程都不同程度的存在着非线性、参数时变性和模糊不确定性,而传统的PID控制主要是控制具有确定模型的线性过程,因此常规PID控制不具有在线整定参数的能力,其控制效果就不是十分理想。
如果采用模糊推理的方法实现PID参数:、I T、D T的在线自适应,不仅保持了常规PID控制的特点,而且具有更大的灵活性、适应性和精确性等优点,是目前一种较为先进的控制算法。
但是考虑到本软件应用客户所具有系统的特点:对象比较简单,非线性程度不高,大多数不具有时变性和模糊不确定性,而且设备的投资成本要求较低,比较适合采用常规PID控制,故本课题中的PID控制算式就确定为常规的PID控制算式。
§4.1.2数字PID 控制算式PID 控制就是确定一个被控制系统的输出量(Y(t)),驱动过程变量接近设定值,其中被控制的系统参数叫做过程变量(PV —Process V ariable),将被控制的过程变量指定的理想值叫做设定值(R(t))。

【关键字】设计一种基于LABVIEW的PID控制器的设计方法摘要利用虚拟仪器技术,采用LABVIEW图形编程环境,设计了一个PID程序,用于仿真PID控制规律。
PID控制器是一种线性的控制器,具有原理简单、易于整定、使用方便和控制性能较强的优点,它能够对线性控制系统快速准确的确定P、I、D三个参数和阶跃响应曲线。
同时,可以给出控制系统开环或者闭环的阶跃响应。
通过改变P、I、D参数和设定值,观察不同情况下的控制曲线,或在同样参数情况下比较位置型PID与增量型PID的控制效果。
通过对各种控制器作用下,对线性控制对象,阶跃输入的响应曲线分析,从而得到各个阶跃响应特性。
证明该控制器设计正确,实用技术方法可行。
并总结出PID调整Kp,Ki,Kd参数的一般顺序。
该控制器为各个领域的过程控制系统提供了方便,节省了时间,大大的提高了生产效率。
关键词:虚拟仪器;LABVIEW;PID控制Base on LABVIEW for PID controller design methodABSTRACTUsing the technology of virtual instrument, using LABVIEW graphical programming environment, to design a PID program, used to control law simulation PID.PID controller is a linear controller,which has such advantages as simple principles,easy setting,convenient application and strong control performance. It can quickly and exactly define three parameter-P、I、D-for linear control system below three orders,and accurately determine the step response curve of the open loop systems.At the same time,may give the control system split-ring or the closed loop step response.By changing the P, I, D parameters and the set value, observation and control curve under different conditions, the control effect or in the same parameters under the condition of comparative position PID and increment type PID. Through a variety of controller function, linear control object of the order of, response curves of step input, resulting in each step response characteristic. Results show that the controller design is correct, practical and feasible technical method. And summed up the PID Kp, Ki, the general order of Kd parameters.Along with the computer technology, has provided the outstanding solution for the process control and the industrial automation application.Key words:virtual instrument;LABVIEW;PID control目录5 总结................................... 错误!未定义书签。
LabVIEW PID控制器用法一、什么是L a b V I E W P I D控制器L a bV IE W(L ab or at or yV ir tu a lI ns tr um en tE ngi n ee ri ng Wo rk be nch)是一种面向图形化编程环境的系统设计平台,可以用来进行数据采集、仪器控制、信号处理、图像处理和数据分析等。
P ID控制器是一种常用的自动控制算法,用于将系统的实际输出与期望输出进行比较,并根据误差来调整控制量,使系统能够达到期望的控制效果。
二、P I D控制器的基本原理P I D控制器即比例-积分-微分控制器,根据系统的误差、误差累积以及误差变化率来调整控制量。
PI D控制器的基本原理如下:1.比例(P)控制:根据当前的误差值来进行修正,比例放大误差以产生输出。
2.积分(I)控制:根据误差的累积量来进行修正,使系统能够消除静态误差。
3.微分(D)控制:根据误差变化率来进行修正,使系统能够快速响应并减小超调量。
综合上述三个控制方式,PI D控制器能够实现系统的稳定控制和响应速度的平衡。
三、LabVIE W中的PI D控制器在L ab VI EW中,PI D控制器被称为P ID V Is(V ir tu al In st r um en ts,虚拟仪器),是L abV I EW中用于实现P ID控制的函数库。
这些函数库提供了丰富的P ID控制器的模块,包括比例、积分、微分的算法和参数调整等。
1.创建P I D控制器在L ab VI EW中,我们可以使用"PI DC rea t e.vi"来创建PI D控制器。
这个函数需要提供控制器的采样周期、比例增益、积分时间和微分时间等参数,并返回一个PI D控制器对象。
2.配置P I D控制器参数通过"P ID Co nf ig ure.vi"函数,我们可以对已创建的PI D控制器进行参数的配置。
基于LabVIEW的自整定PID控制器设计与分析为进一步提高工业控制效果,本文引入LabVIEW工程开发平台,利用其提供给的友好人机交互界面和较强的数据采集与处理功能对基于继电反馈的PID 控制器展开了详细的设计。
仿真分析结果表明,基于LabVIEW的自整定PID控制器设计能够有效提高工业生产的控制效果,具有良好的使用与推广价值。
标签:工业过程控制;LabVIEW;自整定PID控制器1 继电反馈PID自整定技术分析首先,对PID控制器的基本结构进行分析。
反馈控制系统中,以y和ysp 分别表示系统输出和预先设定值,以e=ysp-y表示控制误差,u表示控制信号[1]。
给出如式1所示的经典PID控制器传递函数:Gc(s)=KP(1++s)(1)其中,KP、和分别表示比例增益、微分时间和积分时间。
需要说明的是,因不同工业控制领域对PID控制器的性能要求具有较大差异,故应对其结构进行针对性改动从而确保达到预期控制效果。
通常情况下,实际应用中的PID控制器大都被进行了微分增益的限幅,由此,其传递函数可改写为如下形式:Gc(s)=KP(1++)(2)其次,给出机电反馈PID的自整定法相关原理。
机电反馈PID自整定法是以非参数模型辨识为依托的自整定法,该方法中,具有机电特性的非线性控制被相应的闭环控制回路所引入,以达到使被控过程产生极限环振荡的目的,同时,以得到的极限环振荡曲线为依据获得相应模型的特征参数,简单说来就是获取模型的振荡周期与临界比例系数Ku和Tu,在此基础上,借助Z-N临界比例度的参数整定表实现具体的PID参数计算。
待整个自整定控制结束后,反馈控制系统将自动切换到PID控制模式。
2 基于LabVIEW PID控制器的设计2.1 PID控制器设计PID控制器设计流程如下:LabVIEW首先变换其采集的被控过程输出量的具体标度,而后,将变换后的标度值与设定值进行比较。
需要说明的是,在自整定开始后,如果输出量超出了期望值,则可将其等效于继电器在关闭状态下输出的电压幅值(以m表示);如果输出量小于期望值,则可将其等效于继电器在导通状态下输出的电压幅值(以M表示。
基于LabVIEW的自动控制系统设计自动控制系统是现代工业生产中不可缺少的重要技术手段,广泛应用于机械制造、化工、石油、电力、交通等领域。
为了提高硬件控制系统的效率和精度,LabVIEW成为了自动控制系统设计的首选开发环境。
本文将介绍基于LabVIEW的自动控制系统设计及其应用。
一、概述LabVIEW(Laboratory Virtual Instrument Engineering Workbench)是一种基于图形化控制编程的软件开发环境,由美国国家仪器公司(National Instruments)开发。
它可以用于设计、控制和测试各种类型的系统。
LabVIEW作为自动控制系统设计的主要开发环境之一,其最重要的功能是通过数据采集、处理和控制算法来实现控制系统的自动化。
二、系统设计流程自动控制系统设计主要分为以下三个步骤:1.系统建模系统建模是自动控制系统设计的第一步。
它通常包括确定系统的物理模型或状态方程、构建传感器模型、以及选择合适的控制器模型。
2.算法设计算法设计是自动控制系统设计的核心部分。
在这个过程中,我们需要根据系统建模结果,选择控制算法来实现系统稳定性的控制。
常用的控制算法包括PID控制、模糊控制、神经网络控制、自适应控制等。
3.实现和调试实现和调试是自动控制系统设计的最后一步,也是最关键的一步。
该步骤中,我们需要在LabVIEW平台上实现控制算法和控制器,并使用硬件平台或仿真平台进行验证和调试。
三、系统实例分析考虑一个简单的自动温度控制系统,该系统由温度传感器、PID控制器和加热元件组成。
在该系统中,温度传感器用于采集与温度相关的数据,并将其传输到PID控制器中,PID控制器根据采集到的数据来计算和控制加热元件的功率,以维持所测温度为设定值。
在LabVIEW中,我们可以使用模块化设计的方式来实现该控制系统。
我们可以将控制器和加热元件分别建模为模块,并使用函数模块来实现PID控制算法。
应用LabVIEW实现PID控制功能作为虚拟仪器的主流开发语言,图形语言(Graphical Language)在测试系统中得到广泛应用。
优秀的图形语言开发环境使LabVIEW不仅包括了开发虚拟仪器面板的各种对象和进行信号分析的丰富的函数,而且提供了外挂的PID控制工具包,使用户可以将虚拟仪器拓展到自动控制领域。
对于自动控制的基本形式,图(4-1)所示的闭环负反馈系统,不仅可以应用虚拟仪器技术完成它的测量部分的功能,而且可以将虚拟仪器技术拓展到系统的控制器部分,构成一种基于虚拟仪器的测量控制系统。
图4-1 闭环负反馈系统§4.1 PID算式的确定§4.1.1 PID算式的确定在测控系统中,被控量和操纵量确定之后,就可以根据对象的特性和对控制质量的要求,选择控制器的控制作用,由控制器按规定的控制规律进行运算,发出相应的控制信号去推动执行器。
控制器的控制规律,即为控制器的PID算式。
PID控制算式是一种在工业控制中广泛运用的控制策略。
它的优点是原理简单,易于现实,稳定性能好。
实际上,大多数的工业过程都不同程度的存在着非线性、参数时变性和模糊不确定性,而传统的PID控制主要是控制具有确定模型的线性过程,因此常规PID控制不具有在线整定参数的能力,其控制效果就不是十分理想。
如果采用模糊推理的方法实现PID参数:、I T、D T的在线自适应,不仅保持了常规PID控制的特点,而且具有更大的灵活性、适应性和精确性等优点,是目前一种较为先进的控制算法。
但是考虑到本软件应用客户所具有系统的特点:对象比较简单,非线性程度不高,大多数不具有时变性和模糊不确定性,而且设备的投资成本要求较低,比较适合采用常规PID控制,故本课题中的PID控制算式就确定为常规的PID控制算式。
§4.1.2数字PID 控制算式PID 控制就是确定一个被控制系统的输出量(Y(t)),驱动过程变量接近设定值,其中被控制的系统参数叫做过程变量(PV —Process Variable),将被控制的过程变量指定的理想值叫做设定值(R(t))。
苏州大学机电工程学院 Soochow University of Mechanical and Electrical Engineering课程设计报告Curriculum design课题名称:基于LabVIEW软件的PID自动控制学院: ********院专业:*********姓名:***学号:****目录一、PID控制原理 (1)1、PID控制介绍 (1)2、PID控制规律 (1)3、PID 控制的性能指标 (3)4、PID 控制器参数整定的分类 (3)5、PID相关控制 (5)6、数字PID (7)二、LabVIEW8.5软件 (9)1、简介 (9)2、特点 (10)3、虚拟仪器 (11)4、应用领域 (12)三、前期练习题目与内容 (14)四、设计内容与要求 (17)1、设计内容 (17)2、设计要求 (17)五、设计方案 (18)1、设计思路 (18)2、程序框图设计 (20)3、控制面板设计 (21)六、最终设计结果及运行情况 (22)1、程序框图 (22)2、控制面板 (22)七、课程设计心得 (25)基于LabVIEW软件的PID自动控制一、PID控制原理1、PID 控制介绍PID 控制是过程控制中广泛应用的一种控制,简单的说就是按偏差的比例(proportional)、积分(Integral)、微分(Derivative)进行的控制。
当今,尽管各种高级控制在不断的完善,但目前在实际生产过程中应用最多的仍是常规PID 控制,其原因是:1) 各种高级控制在应用上还不完善;2) 大多数控制对象使用常规PID 控制即可以满足实际的需要;3) 高级控制难以被企业技术人员掌握。
PID 控制器具有结构简单,参数易于调整等优点。
在长期的工程实践中,人们对PID控制己经积累了丰富的经验。
特别是在那些实际过程控制中,控制对象的精确数学模型难以建立,系统参数又经常发生变化,常采用PID 控制器,并根据经验进行在线整定。
以下将从PID 控制规律、PID 控制的性能指标及PID 控制参数整定三个方面对PID 控制做进一步的介绍。
2、PID 控制规律PID(Proportional,Integral and Differential)控制器是一种基于“过去”,“现在”和“未来”信息估计的简单算法。
常规PID 控制系统原理框图如图3-1 所示,系统主要由PID 控制器和被控对象组成。
作为一种线性控制器,它根据给定值r(t)与实际输出值y(t)构成控制偏差e(t),将偏差按比例、积分、和微分通过线性组合构成控制量u(t),对被控对象进行控制。
控制器的输入输出关系为:式中u(t)是PID 控制器的输出,e(t)是PID 控制器的输入,Kp为比例系数,Ti 为积分时间常数,Td为微分时间常数。
采用PID 控制器的控制系统如图所示。
PID 调节器的传递函数为:比例、积分和微分三个环节的控制是相互关联的,三个参数可以分别调节,也可以只采用其中一种或两种控制规律。
简单的说,PID 控制器各环节的作用如下所述:(1)比例环节:即成比例地反映控制系统的偏差信号e(t),系统偏差一旦产生,调节器立即产生与其成比例的控制作用,以减小偏差。
比例控制反应快,但对某些系统,可能存在稳态误差。
加大比例系数Kp,系统的稳态误差会减小,但稳定性可能变差。
(2)积分环节:积分的控制作用主要用于消除稳态误差,提高系统的无差度。
积分作用的强弱取决于积分时间常数,积分速度越慢,积分作用越弱,反之则越强。
积分环节可能使系统的频带变窄。
积分控制通常与其它控制规律结合,组成PI 控制器或PID 控制器。
(3)微分环节:微分的作用是能反映偏差信号的变化速率,具有预见性,能预见偏差信号的变化趋势,并能在偏差信号的值变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的响应速度,减少超调,减小调节时间。
由于微分反映的是变化率,所以当输入没有变化时,微分环节的输出为零。
微分控制通常与其它控制规律结合,组成PD或者PID 控制器。
为了能更好地理解三个环节具体的设计经验,在这里我们以PI 控制为例加以说明。
实际上,根据我们长期的工作经验及对PID 控制理论的认识,在实际的生产过程中,PI 控制可以满足大多数过程控制的要求。
PI 控制的知识及经验可描述如下:(1)比例主要影响响应速度,Kp愈大,响应愈快,但太大会引起较大的超调和振荡,甚至产生不稳定。
Kp增大则超调增加,上升时间减短;反之,Kp 减小则超调减小,上升时间延长。
(2)积分时间Ti表示由积分作用产生一个比例调节效果的大小。
Ti主要影响静态精度,消除静差。
稳态时,Ti越大,积分速度越慢,消除静差越慢。
反之,Ti 越小,积分速度越快,消除静差越快。
但积分控制作用太强会使静态性能变差。
(3)在偏差较大时,PI 控制器以提高系统动态响应速度为主。
为尽快消除偏差,Kp应取大值,Ti应取小值;在偏差较小时,为继续消除偏差,并防止超调过大而产生振荡,Kp值减小,Ti应取大值;在偏差很小时,以提高静态精度,克服大超调,提高系统稳定性为主,此时Kp值应继续减小,Ti值不变或稍减小。
(4)偏差变化率e(t)的大小反映偏差变化的速率。
e(t)越大,Kp值应越小,Ti 取值也应越小。
反之,e(t)越小,Ti取值也应越大。
3、PID 控制的性能指标衡量一个PID 控制系统性能好坏的指标主要有:上升时间tr、超调量a%、调节时间ts和稳态误差ess。
其中:(1)上升时间tr是指系统实际输出从正常输出的10%上升到正常输出的90%时所需的时间;(2)调节时间ts是指系统实际输出值稳定在正常输出值的5%或2%范围以内时所需的时间;(3)超调量a%是指系统实际输出的最大值与正常值的差与正常值的比值;(4)稳态误差ess是指系统达到稳态时的输出值与正常值差的绝对值与正常值的比值。
这四个参数反映了系统的响应能力和稳定性,通过它们就可以判定一个系统性能的好坏。
4、PID 控制器参数整定的分类PID 控制器广泛地应用于工业过程中,但是PID 控制器的参数整定是一个令人困扰的问题。
一般需要经验丰富的工程技术人员来完成,即耗时又费力,加之实际系统千差万别,又有滞后、非线性等因素,使的PID 参数的整定有一定的难度。
许多实际控制系统无法工作在令人满意的状态,很大一部分是由于控制器的自整定的参数没有达到最优,由此人们提出自整定PID 控制器。
将过程对象的动态性能的确定和PID 控制器参数的计算方法结合起来就可以实现PID 控制器的自整定,自整定的含义是控制器的参数可根据用户的需要自动整定,用户可以通过按动一个按钮或给控制器发送一个命令来启动自整定过程。
PID 控制器参数自动整定过程包括三个部分:一是过程扰动的产生;二是扰动响应的评估;三是控制器参数的计算。
从目前的资料和应用情况来看,根据研究方法,可分为基于频域的PID参数整定方法和基于时域的PID 参数整定方法;按照控制对象的输入和输出个数可分为单变量PID 参数整定方法和多变量PID 参数整定方法;按照控制量的组合形式,可分为常规PID 参数整定方法与智能PID 参数整定方法。
但是总体来说,PID 参数自整定的方法主要归结为:基于模型的PID 参数整定方法;基于规则的PID 参数整定方法和基于在线模式识别PID 参数整定方法。
下面以PID 控制为例,讨论控制参数,即比例系数Kp,积分时间常数Ti 和微分时间常数Td对系统性能的影响,负反馈控制系统如图3-2 所示:(1)比例控制Kp对控制性能的影响1)对动态特性的影响比例控制Kp加大,使系统的动作灵敏速度加快,Kp偏大,振荡次数增多,调节时间加长。
当Kp太大时,系统会趋于不稳定。
若Kp太小,又会使系统的动作缓慢。
2)对稳态特性的影响加大比例控制Kp,在系统稳定的情况下,可以减小稳态误差ess,提高控制精度,但是加大Kp 只是减少ess,却不能完全消除稳态误差。
(2)积分控制Ti对控制性能的影响1)对动态特性的影响积分控制Ti通常使系统的稳定性下降。
Ti太小系统将不稳定。
Ti偏小,振荡次数较多。
Ti太大,对系统性能的影响减少。
当Ti合适时,过渡特性比较理想。
2)对稳态特性的影响积分控制Ti能消除系统的稳态误差,提高控制系统的控制精度。
但是若Ti 太大时,积分作用太弱,以致不能消除稳态误差。
(3)微分控制Td对控制性能的影响微分控制经常与比例控制或积分控制联合作用,构成PD 控制或PID 控制。
微分控制可以改善动态特性,如超调量 a 减少,调节时间ts缩短,允许加大比例控制,是稳态误差减小,提高控制精度。
当Td偏大时,超调量a 较大,调节时间ts较长。
当Td偏小时,超调量a 也较大,调节时间ts也较长。
只有合适时,可以得到比较满意的过渡过程。
5、PID 相关控制PID 控制器的三个组成部分对系统性能有着不同的影响,所以,我们通常需要配合使用来获得最佳的控制效果。
比例、积分、微分控制的不同组合可组成P、PD、PI 和PID 共4 种控制器。
5.1 比例微分控制(PD)若控制器的输出m(t)既与误差信号e(t)成正比,又与误差e(t)的一阶导数成正比,则称这种控制器为比例微分控制器,简称PD 控制器。
采用PD 控制规律的系统称为比例微分控制系统。
PD 控制系统的典型结构如图3-3 所示。
PD 控制器的时域方程为:式中Kp是比例系数;Td微分时间常数。
为讨论方便,令Kp=1,则上式为:易知作为校正装置的比例微分控制器,其传递函数为:PD 控制规律具有鲜明的物理意义。
由于一阶导数表示变化率,故PD 控制中的微分控制分量对于e(t)的变化非常敏感。
误差e(t)一有变动,m(t)值随之变化。
e(t)变化愈剧烈,则m(t)值愈大。
由于比例微分控制器的控制作用m(t)超前于e(t)的变化,说明控制器能够提前行动,及时采取措施对系统作出有效控制,起到了“未雨绸缪”的效果,这就是PD 控制的“提前性”。
另一方面,由于微分控制可以抓住误差e(t)变动的苗头,预测出e(t)的变化趋势,并及时采取措施以控制系统,这就是PD 控制的“预见性”。
“预见性”、“提前性”是微分控制规律的突出优点,它不但能反映误差信号的变化趋势,而且能在误差信号尚未出现之前,就在系统中发出一个有效的早期修正信号,从而有助于系统的稳定性,并抑制过大的超调量[10]。
5.2 比例积分控制(PI)若控制器的输出m(t)既与误差信号e(t)成正比,又与误差信号e(t)对时间的积分成正比,则称这种控制器为比例积分控制器,简称PI 控制器。
采用PI 控制规律的系统称为比例积分控制系统。
PI 控制系统的典型结构如图3-4 所示。
PI 控制器的时域方程为:式中Kp是比例系数;Ti积分时间常数。