电感元件交流电路中电压和电流的关系

理解电路中的电流相位关系与电压相位关系在学习电路的过程中，我们经常会接触到电流相位和电压相位这两个概念。

理解电路中电流和电压的相位关系对于解决电路中的问题非常重要。

在本文中，我们将探讨电流相位和电压相位的概念以及它们之间的关系。

首先，让我们来了解电流相位和电压相位的含义。

在交流电路中，电流和电压的变化都是周期性的。

电流相位指的是电流波形相对于给定的参考点或参考波形所处的位置。

类似地，电压相位是电压波形相对于参考点或参考波形的位置。

在直流电路中，电流和电压都是恒定的，因此相位概念并不适用。

在交流电路中，电流和电压的相位关系是非常重要的。

通常情况下，电流和电压的相位差决定了电路中的功率传输和能量转换。

电流和电压的相位关系可以通过相位角来表示。

相位角是指电流或电压波形相对于参考点的角度位置，通常以弧度为单位。

通过测量电流和电压波形的相位差，我们可以得到相位角的数值。

了解电流和电压的相位关系对于分析和解决电路问题至关重要。

通过观察电流和电压波形的相位差，我们可以确定电路中的电感和电容元件。

例如，当电压波形领先电流波形时，我们可以推断电路中存在电感元件。

相反，如果电压波形滞后于电流波形，则可能存在电容元件。

除了电感和电容元件，电阻元件也会对电流和电压的相位关系产生影响。

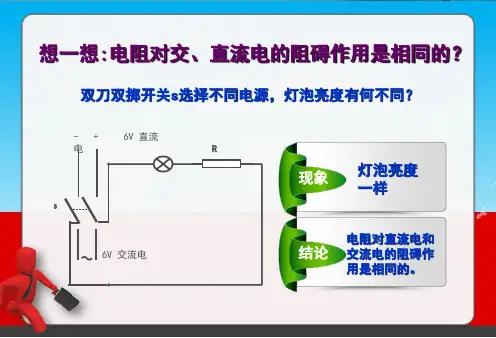
在纯电阻电路中，电流和电压的相位关系是相同的，因为电阻元件不会改变波形的相位。

然而，在电感电路和电容电路中，电流和电压的相位关系将会发生变化。

例如，当电流波形滞后于电压波形时，表示电路中存在电感，而当电流波形领先于电压波形时，说明电路中存在电容。

了解电流相位和电压相位的关系可以帮助我们更好地理解电路中发生的现象。

在分析电路时，我们可以使用相位关系来确定元件的类型和数量，从而解决电路中的问题。

此外，电流相位和电压相位还可以帮助我们设计和优化电路，以实现所需的电路功能。

总结起来，理解电路中的电流相位和电压相位关系对于解决电路问题非常重要。

电流和电压的相位关系可以通过相位角来表示，用于确定电路中存在的元件类型和数量。

3.5 纯电感交流电路同频率
3.5 纯电感交流电路
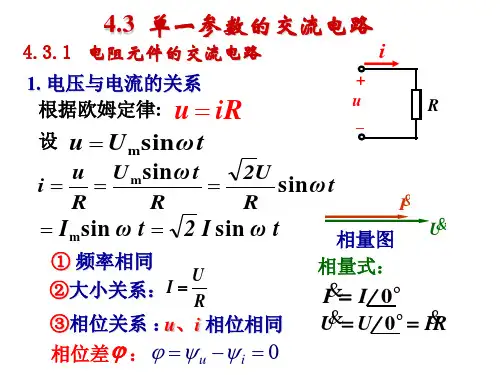
一、电压、电流的关系
2. 波形图：ωt u i
O
u , i U 3. 相量关系：（ψu = ψi ＋90°）
U = j X L I
I
L ＋
u
－i
4. 相量图：
3.5 纯电感交流电路
3.5 纯电感交流电路
二、功率关系
3. 无功功率：Q＝UI= X L I2 单位：var
U2
X L
=
2. 平均功率(有功功率)：P＝0
P=0：电感为储能元件
【例】有一电感器,电阻可忽略不计,电感L = 0.2 H 。

把它接到220 V 工频交流电源上工作，求电感的电流和无功功率？若改接到100 V 的另一交流电源上，测得电流为0.8 A ，此电源的频率是多少？
解:(1) 接到220 V 工频交流电源时
X L =2πf L = 62.8 Ω
U 22062.8
X L I ==A = 3.5 A Q = U I = 220×3.5 var = 770 var
(2) 接到100 V 交流电源时X L 2πL
f ==100 Hz 100U 0.8I X L ==Ω=125 Ω
3.5 纯电感交流电路
总结：
1.电压电流同频率，电压超前于电流90°；
2.电压与电流的关系：
3.平均功率P =0，电感是储能元件。

4.无功功率用来说明电感与其以外电路的能量交换。

U=j X L I。

电路中的交流电压与交流电流在电路中，交流电压和交流电流是两个重要的参数。

交流电压指的是在电路中随时间变化的电压，而交流电流是电路中随时间变化的电流。

交流电压和交流电流的变化规律符合正弦函数，其数学表达式为V(t) = Vm*sin(ωt + φ)和I(t) = Im*sin(ωt + φ)，其中V(t)和I(t)分别表示随时间变化的电压和电流，Vm和Im分别表示电压和电流的最大值，ω表示角频率，φ表示相位。

交流电压和交流电流的变化是由交流电源产生的。

交流电源通过旋转磁场产生交流电压，这种电压随时间变化。

当交流电压进入电路时，电子在正半周期和负半周期中按照不同的方向流动，形成交流电流。

交流电压和交流电流的频率是指单位时间内变化的周期数。

频率的单位是赫兹（Hz），表示每秒钟变化的周期数。

在电力系统中，标准的交流电频率为50赫兹或60赫兹，这意味着电压和电流每秒钟变化50次或60次。

交流电压和交流电流的频率直接影响电路的性能和应用。

在电子设备中，频率会影响电路的幅频特性和相频特性。

幅频特性是指电路中各个频率成分的幅度随频率变化的情况，而相频特性是指电路中各个频率成分的相位随频率变化的情况。

交流电压和交流电流的相位是指电压和电流的相对关系。

当电压达到最大值时，电流是否也达到最大值，以及达到最大值的时间差，都决定了其相位差。

相位差决定了电路中电压和电流的时间关系，对于电路的稳定性和性能有重要影响。

在电路中，交流电压和交流电流通过电阻、电容和电感等元件传输。

在电阻中，交流电流和交流电压的相位相同，大小成比例。

而在电容和电感中，交流电流和交流电压的相位有一定的差异。

电容导致电流超前电压90度，而电感导致电流滞后电压90度。

通过了解交流电压和交流电流的变化规律以及其在电路中的传输特性，我们可以更好地理解电路的工作原理和性能。

在电路设计和故障排除中，对交流电压和交流电流的分析可以帮助我们找出问题的根源并采取相应的措施。

交流电路电压与电流的变化交流电路中的电压和电流是随时间变化的，其变化形式可以用正弦函数表示。

本文将从交流电路的基本概念、电压与电流的变化规律以及交流电路中的重要参数等方面进行介绍。

一、交流电路的基本概念交流电路是指电流方向和大小随时间变化的电路。

与之相对的是直流电路，直流电路中的电流方向和大小保持恒定。

交流电路中，电流和电压都是周期性变化的。

二、交流电路中电压与电流的变化规律1. 正弦波在理想的交流电路中，电压和电流的变化遵循正弦函数规律。

正弦波的图像是一个周期性的波形，可以用数学函数f(t) = A*sin(ωt+φ)来描述，其中A为振幅，ω为角频率，φ为相位差。

2. 相位差相位差表示电压和电流变化的时间差异，也可以理解为波形的起始位置的差异。

相位差的单位是度或弧度。

相位差的变化影响了电路中电压和电流的关系。

3. 幅值幅值是指交流电压或电流的最大值，也就是正弦波的振幅。

幅值通常用Vmax来表示。

4. 频率频率是指单位时间内正弦波完成的周期数，单位是赫兹（Hz）。

频率的倒数称为周期，用T表示。

三、交流电路中的重要参数1. 电阻电阻是交流电路中最基本的参数之一，用于限制电流的流动。

电阻的单位是欧姆（Ω）。

2. 电感电感是交流电路中的另一个重要参数，用于储存电能，并抵抗电流的变化。

电感的单位是亨利（H）。

3. 电容电容是交流电路中的另一个重要参数，用于储存电能，并且能够对电流变化做出快速的响应。

电容的单位是法拉（F）。

4. 交流电阻交流电路中的电阻称为交流电阻，其值与电流的变化有关，通常用复数表示。

四、交流电路中的电压与电流的相位关系交流电路中的电压和电流之间存在相位关系，通过相位差来描述。

当电压和电流的相位差为0时，表示两者完全同相；当相位差为90度时，表示电压和电流是互相垂直的。

五、交流电路中的功率计算在交流电路中，功率的计算需要考虑电压、电流的相位关系。

交流电路中的有功功率和无功功率对于电路的运行状态有重要影响。

交流电路电感电压和电流关系在电路的世界里，电感就像是那个神秘而又聪明的家伙，它在交流电中扮演着不可或缺的角色。

我们今天就来聊聊这个电感和电压、电流之间的那些事儿，让我们一起探寻这个电气界的小秘密吧！1. 电感的基本概念首先，电感是什么呢？简单来说，电感就是一种储存能量的元件。

当电流通过它的时候，电感会在周围形成一个磁场，就像是在空气中偷偷做着它的功课。

你知道吗？这个磁场就像是一位守护神，保护着电流的稳定。

不过，这个守护神也有个脾气，就是它不喜欢电流突然变化，一旦电流一动，它立马就会发出电压反抗。

真是个“拗”脾气的家伙啊！1.1 电压与电流的关系那么，电感中的电压和电流之间有什么样的关系呢？别急，咱们慢慢说。

电感电压和电流之间其实是有一个相位差的。

简单来说，就是电压在电流变化之前出现。

就好比是前面有个“先知”，提前告诉你即将发生的事情。

当电流开始上升，电压就会先“闪亮登场”，你可以想象成电流是个慢半拍的演员，而电压则是那位早到的导演。

1.2 相位差的重要性这个相位差可不是小事，它可是影响整个电路性能的大问题。

为了让电路运行得更加顺畅，电压和电流需要和谐相处。

如果它们之间的相位差过大，电路就会像是跳舞时踩到脚一样，导致能量损失，影响效率。

这时候，电感就像是个调和剂，尽量让电压和电流保持在一个合适的节奏上。

2. 电感的特性接下来，我们来聊聊电感的一些特性。

电感不仅仅是一个简单的元件，它的行为可复杂着呢！首先，我们得知道，电感的自感现象非常有趣。

当电流在电感中变化的时候，它会产生自感电动势，反抗电流的变化。

就像是一个执拗的老头，不管你怎么劝，就是不愿意改变自己的想法。

2.1 储能能力另外，电感还具有很强的储能能力。

当电流通过电感时，能量会存储在它的磁场中。

这种储能就像是把电能存进银行，等到需要的时候再取出来。

不过，电感的“储蓄”可不是无底洞，储存的能量最终还是要通过电流的变化释放出来。

要是你不及时取钱，可能就会面临通货膨胀，哈哈！2.2 阻抗作用还有，电感在交流电路中有个特别的角色，那就是提供阻抗。

电路中的交流电压与电流的频率关系计算方法电路中的交流电压与电流的频率关系是电子工程领域中一个重要而复杂的问题。

要理解这个关系并进行计算，需要一些基础的电路知识和数学工具。

下面将讨论一些常见的计算方法，以帮助读者更好地理解这个问题。

首先，我们要了解电压和电流的频率是如何定义的。

频率是指单位时间内重复发生的周期性事件的次数。

在电路中，我们通常使用赫兹（Hz）作为频率的单位，1赫兹等于每秒一次。

交流电压和电流的频率就是指单位时间内交流电压和电流变化的次数。

在交流电路中，电压和电流可以表示为函数关系的形式，通常使用正弦函数或余弦函数来描述。

这种表示方式是因为正弦函数和余弦函数具有周期性和可重复性的特点，非常适用于描述交流电的变化过程。

为了计算电路中电压和电流的频率关系，我们首先需要知道电路中的频率。

通常，电路的频率可以通过信号源（如发电机或示波器）产生的交流电信号进行测量。

一般情况下，交流电信号的频率是固定的，可以通过设备自身的参数或设置进行调节。

知道了电路的频率后，我们就可以计算电压和电流的频率关系了。

一种常用的计算方法是通过欧姆定律和电感或电容的特性来实现。

对于电阻电路，欧姆定律告诉我们电压和电流之间的关系是线性的，可以用以下公式表示：V = I * R其中，V是电压，I是电流，R是电阻。

此公式可以用于计算任意频率下的电阻电路的电压和电流关系。

对于电感电路和电容电路，我们需要考虑电感和电容对电压和电流的频率特性的影响。

对于电感电路，电感元件会对电流的频率做出响应，并形成电压的相移。

计算电感电路的电压和电流频率关系可以使用以下公式：V = I * jωL其中，V是电压，I是电流，j是虚数单位，ω是角频率，L是电感。

这个公式可以反映电感对电流频率的响应，并给出电压和电流之间的关系。

对于电容电路，电容元件会对电压的频率做出响应，并形成电流的相移。

计算电容电路的电压和电流频率关系可以使用以下公式：V = I / jωC其中，V是电压，I是电流，j是虚数单位，ω是角频率，C是电容。

电路中的电压与电流关系在我们日常生活和现代科技中，电路无处不在。

从简单的手电筒到复杂的计算机系统，都离不开电路的运作。

而理解电路中电压与电流的关系，对于我们掌握电路的工作原理、设计和故障排查至关重要。

首先，让我们来明确一下电压和电流的基本概念。

电压，通俗地说，就是推动电荷流动的“压力”。

就好比水在水管中流动，水压越大，水流就越有力。

在电路中，电压用伏特（V）来度量，它使得电荷能够在电路中移动。

电流呢，则是电荷的定向移动。

想象一下一群有序排队行走的人，这就类似于电流。

电流用安培（A）来衡量，它表示单位时间内通过电路某一横截面的电荷量。

那么，电压和电流之间到底有怎样的关系呢？这就不得不提到欧姆定律。

欧姆定律指出，在一段电路中，通过导体的电流与导体两端的电压成正比，与导体的电阻成反比。

用公式表示就是：I ＝ U ／ R，其中 I 表示电流，U 表示电压，R 表示电阻。

电阻是电路中的一个重要概念。

它可以理解为导体对电流流动的阻碍作用。

不同的材料具有不同的电阻值，比如铜的电阻相对较小，而橡胶的电阻则非常大。

电阻的大小取决于导体的材料、长度、横截面积以及温度等因素。

当我们给一个电阻恒定的电路施加不同的电压时，电流会相应地发生变化。

比如，一个 10 欧姆的电阻，如果施加 5 伏特的电压，根据欧姆定律，电流 I ＝ 5 ／ 10 ＝ 05 安培。

如果将电压提高到 10 伏特，电流就会变成 1 安培。

反过来，如果电路中的电流发生变化，而电阻不变，那么电压也必然会随之改变。

这就像在一个固定粗细的水管中，如果水流变快（电流增大），那么必然是水压增大（电压增大）导致的。

在实际的电路中，电压和电流的关系还会受到其他因素的影响。

比如电源的性质，直流电源和交流电源下，电压和电流的变化规律是不同的。

直流电源提供的电压和电流相对稳定，而交流电源则会周期性地改变电压和电流的大小和方向。

再比如，电路中的元件不仅仅只有电阻，还可能有电容和电感。

论正弦交流纯线性电感电路中 电压、电流和自感电动势的相位关系魏培钦 (2008.06.10)摘要：纯线性电感电路中电压、电流和自感电动势的相位关系早已有结论——电压超前电流90，电流超前自感电动势 90。

可是到目前为至，本人所见的教科书在推导上述结论时都以根本不可能存在的电压、电流、自感电动势的正方向关系为推论的基础，也没有完整清楚地分析电流的变化趋势与自感电动势相位的关系，“虛晃一枪”而过，令学生困惑难已。

本文以电压和电动势方向的规定、法拉第电磁感应定律、楞次定律、基尔霍夫电压定律为基础，既完整分析电流的变化趋势对电压、电流、自感电动势之间相位关系的影响，又以真实的电压、电流、自感电动势的正方向关系建立电压方程，论述纯线性电感电路中电压、电流和自感电动势的相位关系，使学生能更好地理解和掌握纯线性电感电路中电压、电流和自感电动势的相位关系。

一、本人所见的教科书对纯线性电感电路中电压、电流和自感电动势的相位关系的推导过程和存在“问题”图1所示电路中，变化的电流经过电感元件L 时，电感元件L 就产生自感电动势来阻碍电流的变化。

设电路中电阻和电容可忽略不计，L 是线性电感元件，并且电压、电流和自感电动势的正方向如图所示，则：L d die L dt dtΦ=-=- （1—1） 根据基尔霍夫电压定律得：dtdiL e u L L =-= （1—2）设t I i m ωsin =，则：(sin )cos sin(90)sin(90)(13)m L m m m di d I t u LI L tdt dtI L t U t ωωωωωω====+=+-sin(90)sin(90180)sin(90)(14)L L m m m die u LU t dtU t U t ωωω=-=-=-+=+-=--所以，L u 比i 超前90 ，i 比L e 超前90。

显然，上述的推导过程简洁正确，但存在如下令学生费解的“问题”：1．L u 、i 、L e 之间显然不存在着图1所示的正方向关系，由这一根本不存在的电压、电 流、自感电动势之间的正方向关系得出dt di L dt d e L -=Φ-=，并建立方程dtdiL e u L L =-=。

纯电感元件在正弦交流电路中的电压与电流关系
在正弦交流电路中，纯电感元件的电压与电流之间存在一定的关系。

根据电感元件的特性，其电压与电流的关系可以通过以下公式表示：
V = jωLI
其中，V表示电感元件的电压，I表示电感元件的电流，L表示电感元件的电感值，ω表示电路中的角频率。

j是虚数单位，满足j² = -1。

这个公式表明，电压与电流之间存在90度的相位差，且电压与电流之间的关系是线性的，也就是电压与电流成正比。

当电流通过电感元件时，会产生一个由电感元件本身决定的感应电动势，从而引起电压的变化。

需要注意的是，电感元件在交流电路中会引入阻抗，即纯电感元件的阻抗Z可以表示为：
Z = jωL
因此，在交流电路中，纯电感元件的电压和电流之间不仅存在幅值比例关系，还存在相位差。

这个相位差由纯电感元件的阻抗决定，通常为正90度。

电感元件电压电流的相位关系
电感电压电流相位关系：电流总是滞后电压90度，电压超前电流90度。

电感的基本特性是阻碍电流的变化，所以电流总是滞后电压90度。

电容器是一种能储存电荷的容器，电流总是超前电压90度。

当电感元件交流电流过电容器时，电感元件两端的电压相位会滞后电流90度；当流过电感时，电感元件两端的电压相位会超前电流90度。

另外，当交流电流过电阻时，电压和电流是同相位的，即相位差为0。

电感元件两端的电压，除了电感量L以外，与电阻元件R不同，它不是取决于电流i本身，而是取决于电流对时间的变化率。

电流变化愈快，电感两端的电压愈大，反之则愈小。

据此，在稳态情况下，当电流为直流时，电感两端的电压为零；当电流为正弦波时，电感两端的电压也是正弦波，但在相位上要超前电流；当电流为周期性等腰三角形波时，电压为矩形波，如此等等。

总的来说，电感两端的电压波形比电流变化得更快，含有更多的低频成分。

电感器：
电感器是能够把电能转化为磁能而存储起来的元件。

电感器的结构类似于变压器，但只有一个绕组。

电感器具有一定的电感，它只阻碍电流的变化。

如果电感器在没有电流通过的状态下，电路接通时它将试图阻碍电流流过它；如果电感器在有电流通过的状态下，电路断开时它将试图维持电流不变。

电感器又称扼流器、电抗器、动态电抗器。

电感元件电压电流关系公式全文共四篇示例，供读者参考第一篇示例：电感元件是一种广泛应用于电路中的被动元件，它具有存储能量的特性。

电感元件的电压电流关系公式是描述电感元件在电路中电压和电流之间的关系的重要公式，其掌握对于电路工程师和电子爱好者来说至关重要。

电感元件是由螺线管或绕组构成的，当电流通过电感元件时，会在其内部产生一个磁场，这个磁场将存储一部分电能。

根据法拉第定律，变化的磁场将导致感应电动势的产生，从而产生电流。

在直流电路中，电感元件的电流会随时间的变化而变化，根据基尔霍夫电压律，电感元件的电压与其电流之间存在一个关系式：V = L di/dtV表示电感元件的两端电压，L表示电感元件的电感值，di/dt表示电流变化的速率。

这个关系式说明了电感元件的电压取决于电流的变化率，即电感元件对电流变化的反应。

在交流电路中，电感元件对电流的反应更为复杂。

由于交流电压的频率变化很快，电感元件内部的磁场也随之变化，从而产生电感电动势。

在这种情况下，电感元件的电压和电流之间的关系可以表示为：电感元件的电压电流关系公式对于电路设计和分析非常重要。

通过这些公式，我们可以了解电感元件在电路中的作用和特性，进一步优化电路的性能和稳定性。

掌握这些公式也能够帮助我们更好地理解电路中的电磁现象，提高对电磁学的理解。

第二篇示例：电感元件是一种电子元件，它的电压和电流之间存在着一定的关系。

在电路中，电感元件能够产生感应电动势，同时也能储存电磁能量。

了解电感元件的电压和电流关系对于电路设计和分析是非常重要的。

在电路中，当电感元件接通电压时，会产生一个磁场，并且磁场的变化会导致感应电动势的产生。

根据电磁感应定律可以得到感应电动势的公式为：\[ \varepsilon = -L \frac{di}{dt} \]\[ \varepsilon \] 是感应电动势，单位为伏特；L是电感元件的电感，单位为亨利；\[ di/dt \] 是电流i的变化率，单位为安培每秒。

电流随电压的变化规律
电流与电压之间有着密切的关系，可以分为以下几种：
1、直流电流与电压的关系：直流电流在交流电压一定的情况下，会不
断的随电压增大而增大，但一定的电压下电流的变化几乎是匀速的，
直到电压超过电路的额定电压时，电流可能随着电压的上升变得极大。

2、交流电流与电压的关系：交流电流的变化是振荡的，且其变化范围
要远远大于直流电流，交流电路中的电压在某一范围内会使电流近似
于匀速变化，一旦电压超过规定范围，电流就开始振荡，最后电流会
随着电压的升高而变大。

3、有源电路中电流与电压的关系：有源电路中的电压与电流的变化规
律比较复杂，其变化与施加的电压有关，但受有源电路内部参数影响，电流不一定随着施加的电压发生线性变化，往往会随着施加的电压发
生非线性变化。

4、电容电路中电流与电压的关系：电容电路中电流与电压的变化规律
比较复杂，一般情况下电容电路中电流会随着施加的电压迅速增加，
但随着电容内电流的积累，电容电路中的电流会随着施加的电压变化
越来越缓慢，最后得到一个定值。

5、电感电路中电流与电压的关系：电感电路中的电流和电压之间的变化规律基本相反，即电流在施加的电压的达到一定的范围时，其变化要么接近零，要么会随着施加的电压减小而减小，并且最终电感电路中的电流会收敛到一个定值。

电路中的电压电流关系知识点总结在我们日常生活和现代科技中，电路无处不在，从简单的手电筒到复杂的计算机系统，都离不开电路的运作。

而理解电路中电压和电流的关系，是掌握电路知识的关键。

首先，我们来了解一下什么是电压和电流。

电流，简单来说，就是电荷的定向移动。

就好像一群人沿着特定的方向有序地前进。

而电压呢，则是促使电荷定向移动形成电流的原因，它就像一种推动力，驱使电荷在电路中流动。

在一个简单的直流电路中，电压（V）、电流（I）和电阻（R）之间存在着一个非常重要的关系，那就是欧姆定律。

欧姆定律表明：电流等于电压除以电阻，用公式表示就是 I ＝ V ／ R 。

这个公式告诉我们，如果电压增大，在电阻不变的情况下，电流也会增大；反之，如果电阻增大，在电压不变时，电流就会减小。

比如说，我们有一个电路，其中电源提供的电压是 10 伏特，电阻是 5 欧姆，那么根据欧姆定律，通过这个电阻的电流就是 10 ÷ 5 ＝ 2安培。

电阻在电路中起着限制电流的作用。

电阻的大小取决于导体的材料、长度、横截面积以及温度等因素。

一般来说，导体越长、横截面积越小，电阻就越大。

就像一条狭窄又漫长的道路，能够通过的人流（电流）就比较少。

再来说说串联电路中的电压电流关系。

在串联电路中，电流处处相等。

这就好比是一条单行道，不管在哪个位置，通过的车流量（电流）都是一样的。

而总电压等于各个电阻两端的电压之和。

例如，有两个电阻 R1 和 R2 串联在电路中，通过它们的电流都是 I ，电阻 R1 两端的电压是 V1 ＝ I × R1 ，电阻 R2 两端的电压是 V2 ＝ I × R2 ，那么总电压 V 总＝ V1 ＋ V2 ＝ I ×（R1 ＋ R2) 。

接下来是并联电路。

在并联电路中，电压处处相等。

可以想象成几个分支道路都连接到同一个高压水源，每个分支道路的水压（电压）是相同的。

总电流等于各支路电流之和。

比如有两个电阻 R1 和 R2 并联在电路中，它们两端的电压都是 V ，那么通过电阻 R1 的电流是 I1＝ V ／ R1 ，通过电阻 R2 的电流是 I2 ＝ V ／ R2 ，总电流 I 总＝ I1＋ I2 ＝ V ×（1 ／ R1 ＋ 1 ／ R2) 。