当前位置：文档之家 › 第二章基本信息论2_平均互信息量

第二章基本信息论2_平均互信息量

  • 格式：ppt
  • 大小：435.00 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

第二章基本信息论2_平均互信息量

第二章基本信息论2_平均互信息量

m j 1
n i 1
p( xi y j ) lb
p( xi y j ) p( xi ) p( y j )
I ( X ;Y )
m j 1
n i 1
p( xi y j ) lb
p( xi / y j ) p( xi )
p( xi
/
yj)
p( xi y j ) p( y j )
mn j1 i1
p( xi
p(x1) p(1) 1/ 4 p(x2 ) p(0) 3/ 4
信道转移概率p( yj / xi )：
p( y1 / x1) p(1/1) 5/ 6 p( y1 / x2 ) p(1/ 0) 1/ 2
p( y2 / x1) p(0 /1) 1/ 6 p( y2 / x2 ) p(0 / 0) 1/ 2
p(xi y j )I (xi ; y j )
j1 i1
m j 1
n i 1
p( xi y j ) lb
p( xi / y j ) p( xi )
计算步骤：
1）计算联合概率：p(xi y j ) p(xi ) p( y j / xi )
2）计算信宿端概率分布：p( y j ) p(xi ) p( y j / xi )
p( x2
/
y2 )
p(x2 y2 ) /
p( y2 )
3/8 5 / 12
9 10
4）计算互信息量：I
(
xi
;
y
j
)
lb
p(xi / y p( xi )
j
)
I (x1;
y1 )
lb
p(x1 / y1) p( x1 )
lb
5 / 14 1/ 4

第二章 基本信息论

第二章 基本信息论

信息的度量
3.自信息（量） 3.自信息（ 自信息 1)定义自信息量：I(xi)=log1/p(xi)=-logp(xi) 1)定义自信息量：I(xi)=log1/p(xi)=2)含义：描述信源的微观特性，是指消息集中某一消息 2)含义：描述信源的微观特性，是指消息集中某一消息 所含有的信息量。 在xi发生前---描述xi发生的不确定性大小。 发生前---描述xi发生的不确定性大小。 在xi发生后---描述xi所含有的（提供的）信 发生后---描述xi所含有的（提供的）信 息量。 3)采用对数定义的合理性 3)采用对数定义的合理性 对数函数能够同时满足条件，因此定义是合理的。 4)单位: 4)单位: 对数底(>1) 对数底(>1) 单位 2 bit e nat 10 Hart 1 nat=1.44 bit 1 Hart=3.32 bit 5)等概率分布离散信源的平均信息量H(X)=1/q∑logq 5)等概率分布离散信源的平均信息量H(X)=1/q∑logq =logq
信源熵
1. 定义： 定义： 2. 单位：与I(xi)相同。 单位： I(xi)相同。 3．物理意义： 物理意义： 等概率分布情况：一个符号含有的信息量。 非等概率分布情况：一个符号所含有的统计平均信息量， 是对信源宏观特性的描述。 结论： 结论： H(X)表征信源的总体特性----提供的统计平均信息量/ H(X)表征信源的总体特性----提供的统计平均信息量/符号 信源输出前的平均不确定性。 H(X)表征了信源的随机性。 H(X)表征了信源的随机性。
二元联合信源的共熵与条件熵
四．消息的剩余度 1．剩余: 剩余: 由于不等概或相关性使信源熵值减小，欲 输出相同信息量，必须增加位数，此为剩 余。
二元联合信源的共熵与条件熵

信息论第2章(2010)

信息论第2章(2010)

ai 后所获得的信息量。
自信息量的性质：
1）非负性。 2) 单调递减性。 3) 可加性。
I xi ,y j log pxi ,y j
若两个符号x i , y j同时出现，可用联合概率px i , y j 来表示 这时的自信息量为 I y j I xi | y j
例题：二元信源，每个符号发生的概率分别为p(x1)=p，p(x2)=1-p. 试计算信源熵，并画出熵函数H(p)和p的曲线图。
① 等概时（p=0.5)：随机变量具有最大的不确定性
② p=0或1时：随机变量的不确定性消失。
信息熵的物理意义
1）表示了信源输出前，信源的平均不确定性。 2）表示了信源输出后，每个消息或符号所提供的 平均信息量。 3）信息熵反映了变量X的随机性。
平均自信息量H (X ) 表示信源输出消息中的每个符号所含信息量的统计 平均值，其表达式为 q
H ( X ) EI ( xi ) P( xi ) log P( xi )
i 1
式中， E 表示统计平均，
I ( xi ) 表示符号 x i 包含的自信息量。
平均信息量可以表示为：
任何一个物理量的定义都应当符合客观规律和逻辑上 的合理性，信息的度量也不例外。直观经验告诉我们： ① 消息中的信息量与消息发生的概率密切相关：出现消 息出现的可能性越小，则消息携带的信息量就越大。 ② 如果事件发生是必然的（概率为1），则它含有的信息 量应为零。如果一个几乎不可能事件发生了（概率趋 于0），则它含有巨大的信息量。 ③ 如果我们得到不是由一个事件而是由若干个独立事件 构成的消息，那么我们得到的信息量就是若干个独立 事件的信息量的总和。
② 联合信源中平均每个符号对所包含的信息量？

2.2平均互信息量

2.2平均互信息量

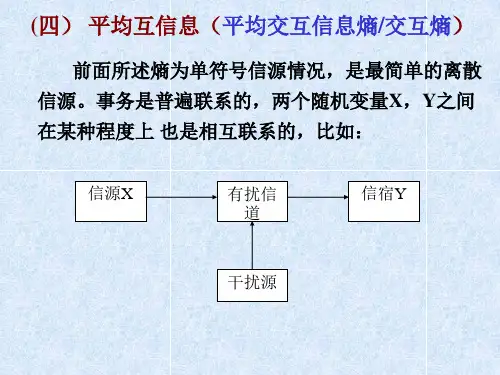
2.2平均互信息量现在来一般地研究平均互信息量。

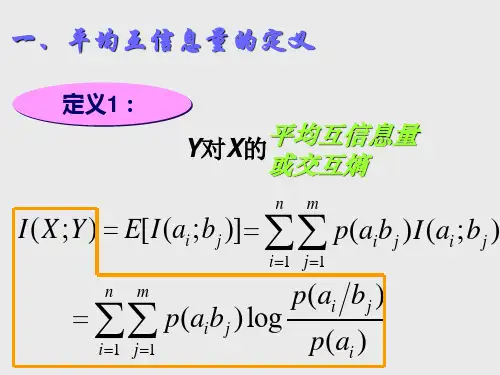
2.2.1平均互信息量的定义定义互信息量在联合概率空间中的统计平均值作为平均互信息量：∑∑===ni mj xi p yj xi p lbxiyj p Y X I 11)()/()();( (2.2.1)考虑到条件概率与联合概率之间的关系式： 容易推出：∑∑===ni mj yj p xi yj p lbxiyj p X Y I 11)()/()();( (2.2.3)2.2.2平均互信息量的物理意义可以从三个不同的角度观察平均互信息。

（1）由式（2.2.3）得： （2）由式（2.2.2）得：（3）由式（2.2.3）得[例 2.2.1]仍以[例 2.1.5]为例，验证式（2.2.4），（2.2.5），（2.2.6）的正确性。

平均互信息的物理意义 （1）Y 对X 的平均互信息)/(log)()/()/()()/(1log)()(1log)()()/(log)();()();(21121121121111j i ni mj j i j i ni mj j i i ni mj j i i j i ni mj j i j i ni mj j i y x p y x p Y X H Y X H X H y x p y x p x p y x p x p y x p y x p y x I y x p Y X I ∑∑∑∑∑∑∑∑∑∑==========-=-=-===其中条件熵：* Y 对X 的平均互信息是对Y 一无所知的情况下，X 的先验不定度与收到Y 后关于X 的后验不定度之差，即收到Y 前、后关于X 的不确定度减少的量。

H(X/Y)表示收到随机变量Y 后，对随机变量X 仍然存在的不确定度，这是Y 关于X 的后验不定度，通常称它为信道疑义度或损失熵(代表了在信道中损失的信息)(2)X 对Y 的平均互信息* X 对Y 的平均互信息是Y 的先验不定度与发出X 后关于Y 的后验不定度之差，即发X 前、后关于Y 的不确定度减少的量。

平均互信息量

平均互信息量
i 1 j 1
n
m
1 p ( xi / y j )
H (X ) H (X /Y)

H(X/Y) —信道疑义度/损失熵。 Y关
于X的后验不确定度。表示收到变量 Y后，对随机变量X仍然存在的不确 定度。代表了在信道中损失的信息。

H(X) —X的先验不确定度/无条件熵。 I(X;Y)—收到Y前、后关于X的不确
举 例

[例2.1.5] 把已知信源 接到图2.1.7所示的信道上， 求在该信道上传输的平均互信息量I(X;Y)，疑义度 H(X/Y)，噪声熵H(Y/X)，联合熵H(XY)。
X x1 , x2 P( X ) 0.5， 0.5
解：(1) 求联合概率
p(xi yj)=p(xi)p(yj/xi) p(x1 y1)=p(x1)p(y1/x1)=0.5×0.98=0.49 p(x1 y2)=p(x1)p(y2/x1)=0.5×0.02=0.01 p(x2 y1)=p(x2)p(y1/x2)=0.5×0.20=0.10 p(x2 y2)=p(x2)p(y2/x2)=0.5×0.98=0.40 (2) 求Y的各消息概率
i 1 j 1
1 2 p( y j )
p( xi y j ) log 2
i 1 j 1
n
m
1 p ( y j / xi )
H (Y ) H (Y / X )


H(Y/X)—噪声熵。表示发出随机变量X 后，对随机变量Y仍然存在的平均不确 定度。如果信道中不存在任何噪声，发 送端和接收端必存在确定的对应关系， 发出X后必能确定对应的Y，而现在不 能完全确定对应的Y，这显然是由信道 噪声所引起的。 I(Y;X) —发出X前、后关于Y的先验不 确定度减少的量。

平均互信息量和各种熵关系

平均互信息量和各种熵关系

p( xi
|
y j ) log
p(xi | y j ) p(xi )
改写为
I(X;
yj
)
X
p( xi
|
y j ) log
p(xi ) p(xi | y j )
令
w
p(xi ) p(xi | y j )
则有 I (X ; y j )
X
p(xi | y j ) log w
利用不等式 ln w w 1; log w ln wlog e
9
HUST Furong WANG--- Information and Coding Theory
平均互信息量的其它定义
平均互信息量I(X;Y)也可定义为
def
I(X;Y)
XY
p(xi y j ) log
p(xi | y j ) p(xi )
def
I(X;Y)
XY
p(xi ) p( y j
平均互信息量I(X;Y)的凸函数性－例题
二元对称信道的X 输入概率空间为
X 0 1
P(X)
p
1 p
0
q
0
1-q
信道的转移概率图为右图所示
求平均互信息量I(X;Y),并画图
1-q
1
q
1
二元对称信道
16
HUST Furong WANG--- Information and Coding Theory
以{Y , P}表示输出离散概率空间
Y
P(Y
)
y1,
p(
y1
),
y2, L p( y2 ),L
, ,
y j , L , ym
p( y j ),L

第二章 信息论基本概念

第二章 信息论基本概念
i 1
一个信源总是包含着多个符号消息，各个符号消息又按概率 空间的先验概率分布，它的不确定度是各个符号的不确定度的数 学期望（即概率加权的统计平均值） 它的熵（平均不确定度）H（X）定义为： H（X）＝ E[I(x)]＝ P(X)I(X) ＝－ P(X)log2P(X) X
X
若信源X中的符号的概率空间简化表示为： X1，X2， „，XN X，PX＝ P1， P2，„， PN 则熵（平均不确定度）H（X）可写成： N H（X）＝－ PilogPi 注意：∵ I(X)为非负， P(X)为非负，且0≤P(X)≤1 ∴ H（X）也为非负
0.8 0.2
其中X1表示摸出的球为红球事件,X2表示摸出的球为白球事件
若告知摸出的是红球，则事件的自信息量为 I(X1)＝－logP(X1)＝－log20.8 bit 若告知摸出的是白球，则事件的自信息量为 I(X2)＝－logP(X2)＝－log20.2 bit 若取回后又放回摸取，如此摸取n此，红球出现的次数nP(X1)， 白球出现的次数为nP(X2)，则总信息量为 I＝nP(X1)I(X1)＋nP(X2)I(X2) 而平均随机摸取一次所获得的信息量为 H（X）＝ 1/n [nP(X1)I(X1)＋nP(X2)I(X2)] ＝－[P(X1)logP(X1)＋P(X2)logP(X2)] 2 ＝－ P(Xi)logP(Xi)
符号xi对联合事件符号yj zk之间的互信息量定义为： I(xi ; yj zk)＝ logP(xi|yj zk)/ P(xi) „„„„*
三. 条件互信息量 含义：在给定zk条件下，xi与yj之间的互信息量
条件互信息量I(xi ; yj|zk)定义为： I(xi ; yj|zk)＝ logP(xi|yj zk)/ P(xi|zk) 从上式，可使*式写成： I(xi ; yj zk)＝ I(xi ; zk) ＋ I(xi ; yj|zk) 推导如下: I(xi ; yj zk)＝ log P(xi|yj zk)/ P(xi)

第二章-信息论基本概念(2)(1)

第二章-信息论基本概念(2)(1)
(四） 平均互信息（平均交互信息熵/交互熵） 四 平均互信息（平均交互信息熵 交互熵） 交互熵
前面所述熵为单符号信源情况， 前面所述熵为单符号信源情况，是最简单的离散 信源。事务是普遍联系的，两个随机变量 ， 之间 信源。事务是普遍联系的，两个随机变量X，Y之间 也是相互联系的，比如： 在某种程度上 也是相互联系的，比如：
1、 离散无记忆信源 扩展信源 、 离散无记忆信源(扩展信源 扩展信源) 概率空间： （1）定义：若单符号离散信源 概率空间： ）定义：若单符号离散信源X概率空间
X a1 , a2 , L , ai , L , aq P( X ) = p(a ), p(a ),L , p(a ),L , p(a ) , ∑ p(ai ) = 1 i 2 i q 1
0( p )
q
X
[例] 二进制对称信道 例
1( p )
q q
q
0
Y
1
H ( X ) = H ( p) = − p log p − p log p
I(X;Y)
H (Y / X ) = H (q) = −q log q − q log q
H (Y ) = H ( pq + pq)
0
1-H(q) 0.5 I(X;Y) H(p) 1 p
5. 数据处理定理 I(X;Z) ≤ I(X;Y) I(X;Z) ≤ I(Y;Z) [意义 信息不增原理 意义] 信息不增原理 原理—— 意义 处理， 每经一次 处理，可能丢失一部分信息 X Y P(Z/;Y) = H(X) – H(X/Y) = H(Y) – H(Y/X) H(XY) = H(X) + H(Y/X) = H(Y) + H(X/Y) I(X;Y) = H(X) + H(Y)－ H(XY) －

平均互信息量

平均互信息量
i 1 j 1
n
m
p(ai b j ) log
i 1 j 1
n
m
p(ai b j ) p(ai )
p(ai b j ) p(b j ) p (ai b j )
I ( X ; Y ) p(ai b j ) log
i 1 j 1 n m
p(ai b j ) p(ai ) p(b j )
3 H ( X ) 0.5 log 0.5 0.5 log 0.5 1(bit
) 符号
) 符号
H (Y ) 0.59 log 0.59 0.41log 0.41 0.98(bit
H (XY )
0.49 log 0.49 0.01log 0.01 0.1log 0.1 0.4 log 0.4
q q
0 1
1
q
p
0.5
当p=0.5 ，
I(X,Y) 最大
当p不变，即固定信源
I(X,Y)
0 1
0.5
0 1 0
0.5
0
0
0.5 1
q
1
1
1 0 1
0
当q=0.5 ， I(X,Y) =0 当q=0或1 ， I(X,Y) 最大
1
I(X;Y)= H（X）-H（X︱Y）
H（X︱Y) = H（X）- I(X;Y)
H（Y）= I(X;Y)+ H（Y︱X）
名称 符号
关系式
图示
I ( X ;Y ) H ( X ) H ( X ) Y 交 I ( X ;Y ) H (Y ) H (Y ) 互 X I (Y ; X ) H ( X ) H (Y ) H ( XY ) 熵 H ( XY ) H ( X ) H (Y ) Y X

西电信息论第二章 平均互信息和熵的关系2011

西电信息论第二章 平均互信息和熵的关系2011

H ( X N ) = NH ( X )
若若符号离散信源的数 学其其为 :
x2 ,..., xi ,.., xn n X x1 , P( X ) = p( x ), p( x ),..., p( x ),..., p( x ), ∑ p( xi ) = 1 1 2 i n i =1 N N 则信源 X的 N次次次信源用 X 来表来 , 该该信源该 n 个个个 (消息消消 )
∑ ∑ P ( a ) P (b
i =1 j =1 r s i
r
s
j
ai ) log ai ) log
P ( b j ai ) P (b j ) P (b j ai )
∑ ∑ P ( a ) P (b
i =1 j =1 i
j
∑ P ( a )P ( b
i =1 i
r
j
ai )
I ( X;Y)
P ={P(ai )}i X
X
Y
H (Y / X ) = H ( XY) − H ( X ) = H (Y ) − I ( X ;Y )
H ( XY ) = H ( X ) + H (Y / X ) = H (Y ) + H ( X / Y ) = H ( X ) + H (Y ) − I ( X ; Y ) = H ( X / Y ) + H (Y / X ) + I ( X ; Y ) I ( X ;Y ) = H ( X ) − H ( X / Y ) = H (Y ) − H (Y / X ) = H ( XY ) − H (Y / X ) − H ( X / Y ) = H ( X ) + H (Y ) − H ( XY )

信息论与编码第二章答案

信息论与编码第二章答案

第二章信息的度量2.1信源在何种分布时，熵值最大？又在何种分布时，熵值最小？答：信源在等概率分布时熵值最大；信源有一个为1，其余为0时熵值最小。

2.2平均互信息量I(X;Y)与信源概率分布q(x)有何关系？与p(y|x)又是什么关系？答：若信道给定，I(X;Y)是q(x)的上凸形函数；若信源给定，I(X;Y)是q(y|x)的下凸形函数。

2.3熵是对信源什么物理量的度量？答：平均信息量2.4设信道输入符号集为{x1,x2,……xk}，则平均每个信道输入符号所能携带的最大信息量是多少？答：kk k xi q xi q X H i log 1log 1)(log )()(2.5根据平均互信息量的链规则，写出I(X;YZ)的表达式。

答：)|;();();(Y Z X I Y X I YZ X I 2.6互信息量I(x;y)有时候取负值，是由于信道存在干扰或噪声的原因，这种说法对吗？答：互信息量)()|(log );(xi q yj xi Q y x I ，若互信息量取负值，即Q(xi|yj)<q(xi)，说明事件yi 的出现告知的是xi 出现的可能性更小了。

从通信角度看，视xi 为发送符号，yi 为接收符号，Q(xi|yj)<q(xi)，说明收到yi 后使发送是否为xi 的不确定性更大，这是由于信道干扰所引起的。

2.7一个马尔可夫信源如图所示，求稳态下各状态的概率分布和信源熵。

答：由图示可知：43)|(41)|(32)|(31)|(41)|(43)|(222111110201s x p s x p s x p s x p s x p s x p 即：43)|(0)|(41)|(31)|(32)|(0)|(0)|(41)|(43)|(222120121110020100s s p s s p s s p s s p s s p s s p s s p s s p s s p 可得：1)()()()(43)(31)()(31)(41)()(41)(43)(210212101200s p s p s p s p s p s p s p s p s p s p s p s p得：114)(113)(114)(210s p s p s p )]|(log )|()|(log )|()[()]|(log )|()|(log )|()[()]|(log )|()|(log )|()[(222220202121211111010100000s s p s s p s s p s s p s p s s p s s p s s p s s p s p s s p s s p s s p s s p s p H 0.25（bit/符号）2.8一个马尔可夫信源，已知：0)2|2(,1)2|1(,31)1|2(,32)1|1(x x p x x p x x p x x p 试画出它的香农线图，并求出信源熵。

信息论第2章(信息量、熵及互信息量)PPT课件

信息论第2章(信息量、熵及互信息量)PPT课件
假设一条电线上串联了8个灯泡x这8个灯泡损坏的可能性是等概率的假设有也只有一个灯泡损坏用万用表去测量获得足够的信息量才能获知和确定哪个灯泡x损坏
信息论基础
The Basis of Information Theory
主题No2：信息量、熵和互信息量
在上一次课中我们提到香农对信息定性的 定义——事物运动状态或存在方式的不确定性 的描述。事实上，香农对信息不仅作了定性描 述，而且还进行了定量分析。
信源发出的消息常常是随机的，具有不确 定性。如果信源中某一消息的不确定性越大， 一旦发生，并为收信者收到，消除的不确定性 就越大，获得的信息也就越大。同时事件发生 的不确定性与事件发生的概率有关，概率越小， 不确定性就越大。
研究通信系统的目的就是要找到信息传输 过程的共同规律，以提高信息传输的可靠性、 有效性、保密性和认证性，以达到信息传输系 统最优化。
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
I(X;Y)是一个用来衡量信道好坏的 非常好的工具。
计算条件熵的例子
例6 设一个二进制对称信道BSC：
其先验概率为p(0)=p(1)=1/2，试计算条 件熵. [解答]由已知条件得：
由条件熵的定义有：
结果表明，虽然每个字符的错误率只有 0.1，可导致整个信宿对信源的平均不确定 性达到了0.469，将近一半。可见通信系统 对信道的要求非常高。

信息论复习提纲

信息论复习提纲

信道传递概率可以用信道矩阵来表示：
x1 x2 P xr
y1 p( y1 | x1 ) p( y | x ) 1 2 p( y1 | xr )
y2 p( y2 | x1 )
p( y2 | x2 ) p( y2 | xr )
ys p( ys | x1 ) 1 p( ys | x2 ) p( ys | xr )
i
第四章：信道及信道容量
二、离散单符号信道及其信道容量
1.离散单符号信道的数学模型（续14）
例3：求二元删除信道的 H ( X )、H (Y )、H ( X | Y )和I ( X ;Y ) 。
已知
1 3 PX 4 4
1 1 2 2 0 P 1 2 0 3 3
3. 后验概率（后向概率）: 贝叶斯公式
p ( xi | y j ) p ( xi y j ) p( y j ) p ( xi ) p ( y j | xi )
p( x ) p( y
i 1 i
r
j
| xi )
（i =1，2，…，r;j =1，2，…，s）
且
p ( xi | y j ) 1
Y y2
ys
i 1, 2,..., r ; j 1, 2,..., s
满足： （1）0≤ p(yj|xi) ≤ 1 (i=1,2,…,r；j=1,2,…,s) （2）
p( y j | xi ) 1
j 1
s
(i=1,2,…,r)
第四章：信道及信道容量
二、离散单符号信道及其信道容量
1.离散单符号信道的数学模型（续2）
r s
第四章：信道及信道容量

信息论第2章 信息的度量

信息论第2章 信息的度量
i 1
4
甲地极端情况: 极端情况1：晴天概率＝1
X 晴 阴 大雨 小雨 P( x) 1 0 0 0 H ( X ) 1 log1 0 log0 0 log0 0 log0
lim log 0 H ( X ) 0(bit / 符号 ) 0 极端情况2：各种天气等概率分布
2.2.1 平均自信息（信息熵）的概念
定义2.3 随机变量X的每一个可能取值的自信息I(xi)的统计平 均值定义为随机变量X的平均自信息量:
H ( X ) E I ( xi ) p( xi ) log p( xi )
i 1 q
这里q为的所有X可能取值的个数。 熵的单位也是与所取的对数底有关，根据所取的对数底 不同，可以是比特 / 符号、奈特 / 符号、哈特莱 / 符号或者 是r进制单位/符号。通常用比特/符号为单位。 一般情况下，信息熵并不等于收信者平均获得的信息量， 收信者不能全部消除信源的平均不确定性，获得的信息量将 小于信息熵。

乙地极端情况:
极端情况1：晴天概率＝1 Y 晴 小雨 P( y ) 1 0 H (Y ) 1 log1 0 log0 0(bit / 符号)
极端情况2：各种天气等概率分布
Y 晴 阴 P ( y ) 1/2 1/2
H ( X ) pi log pi H ( p1 , p2 ,
i 1 q
, pq ) H (p)
熵函数H(P)具有以下性质： 对称性
H ( p1, p2 , , pq ) H ( p2 , p1, , pq )= = H ( pq , p1, , pq1 )
说明熵函数仅与信源的总体统计特性有关。

信息论第二章

信息论第二章
第二章 信息的量度
主要内容： 主要内容： 一、自信息量 平均自信息量（ 二、平均自信息量（熵）及性质 教学要求: 教学要求: 一、了解信息论的基本内容 会自信息量、互信息量、 二、会自信息量、互信息量、平均自 信息量的计算
引言
有效性和可靠性是通信系统中研究的中心问 信息论是在信息可度量基础上， 题，信息论是在信息可度量基础上，研究有效地 和可靠地传递信息的科学。因此，概率论、 和可靠地传递信息的科学。因此，概率论、随机 过程是信息论研究的基础和工具。 过程是信息论研究的基础和工具。
( )
I ( xi y j ) = I ( xi ) + I ( y j )
小结
1、出现概率小的随机事件所包含的不确定性大，也就是它 出现概率小的随机事件所包含的不确定性大， 的自信息量大。出现概率大的随机事件所包含的不确定性小， 的自信息量大。出现概率大的随机事件所包含的不确定性小， 也就是它的自信息量小。在极限情况下，出现概率为1 也就是它的自信息量小。在极限情况下，出现概率为1的随 机事件，其自信息量为零。 机事件，其自信息量为零。 随机事件的不确定性在数量上等于它的自信息量， 2、随机事件的不确定性在数量上等于它的自信息量，两者 单位也相同。 单位也相同。 信宿收到从信道传来的所消息携带的信息量后， 3、信宿收到从信道传来的所消息携带的信息量后，可以全 部或部分消除信宿对信源发出消息的不确定性。特别地， 部或部分消除信宿对信源发出消息的不确定性。特别地，当 信宿收到的信息量等于信源包含的不确定性（即自信息量） 信宿收到的信息量等于信源包含的不确定性（即自信息量） 就可以唯一地确定信源发出的消息。 时，就可以唯一地确定信源发出的消息。 例如：当某随机事件x 出现的概率为P 1/8时 例如：当某随机事件xi出现的概率为P（xi）= 1/8时，它包 含3比特的不确定性；当信宿能收到3比特的信息量，就能唯 比特的不确定性；当信宿能收到3比特的信息量， 一的确定信源发出的是消息x 一的确定信源发出的是消息xi。

信息论基础及应用第2章 信源及其信息的统计度量(2)_2.4~2.7

信息论基础及应用第2章 信源及其信息的统计度量(2)_2.4~2.7

P(x y) P( xy ) log
X ,Y
P(x)
P(y x)
H (Y ) H (Y X ) P(xy)log
X ,Y
P( y)
P(xy)
H ( X ) H (Y ) H ( XY ) P(xy)log
X ,Y
P( x)P( y)
2.4.1 平均互信息
平均互信息的物理含意及其负熵的概念 (1) 式 I(X;Y ) H(X ) H(X Y ) 的物理含意 ◆ I(X;Y) 是信源的原有平均不确定度 H(X) 与仍然保留的平均
数学期望，称为在给定 Z 条件下由 Y 提供的关于 X 的
平均条件互信息（或平均条件互信息量），
定义式为
I ( X ;Y Z ) EX ,Y ,Z [I (x; y z)]
P(x y z)
P(xyz)log
X ,Y ,Z
P(x z)
2.4.2 平均互信息的性质
性质2.31（非负性） I(X;y=bj ) 和 I(X;Y) 是非负的，即
称 H(X | Y) 为信道疑义度（或损失熵）。
2.4.1 平均互信息
平均互信息的物理含意及其负熵的概念 (2) 式 I(X;Y ) H(Y ) H(Y X ) 的物理含意 ◆ I(X;Y)即信道传输的信息量，等于在 H(Y) 中
扣除掉 H(Y | X)后的量值。 ◆H(Y | X) 表示信源发出 X 后，对 Y 依然存在的平均不确定度，
2.4.2 平均互信息的性质
性质2.32（极值性）
H(X ) I ( X ;Y ) H (Y )
性质2.33（互易性、对称性） I(X ;Y ) I(Y ; X )
性质2.34（上凸性） I(X;Y) 是输入信源概率分布 P(x) 的 ∩形凸函数（又称上凸函数）。

第2章 信源熵 第2讲 信源熵(平均自信息量)与 平均互信息量

第2章 信源熵 第2讲 信源熵(平均自信息量)与 平均互信息量
• ① 观察者站在输出端 • I(X;Y) = H(X) – H(X/Y)
• H(X) — X 的先验不确定度。 • H(X/Y) — 疑义度（损失熵）。 表示已知Y 后，对X 仍然存在的不确 定度。代表了在信道中损失的信息。 • I(X;Y) — 已知Y 后关于X 的不确定度 减少的量。从Y 获得的关于X 的平均 信息量。
• 理解：已知 Y 时 X 的不确定度应小于一无所知时 X 的不 确定度。因为已知 Y 后，从 Y 或多或少可以得到一些关 于 X 的信息，从而使 X 的不确定度下降。
余 映 云南大学
19/38
熵的性质
• 证明：
• （利用了极值性）
余 映 云南大学
20/38
熵的性质
• (7) 可加性 H(XY) = H(X)+H(Y/X) H(XY) = H(Y)+H(X/Y)
余 映 云南大学 3/38
信源熵
• 举例
• 一布袋内放100个球，其中80个是黄色的，20个是白色的。 随便摸出一个球，猜测是什么颜色，其概率空间为
– x1：表示摸出的是黄球，x2：表示摸出的是白球
余 映 云南大学
4/38
信源熵与平均自信息量
• 信源熵和平均自信息量两者在数值上是相等的， 但含意并不相同。
余 映 云南大学
24/38
平均互信息量的定义
• 互信息量 I(xi; yj) 在联合概率空间 P(XY) 中的统 计平均值
称为 Y 对 X 的平均互信息量。 • X 对 Y 的平均互信息定义为
余 映 云南大学
25/38
平均互信息量的定义
• 平均互信息的第三种定义
• 平均互信息 I(X;Y) 克服了互信息量 I(xi;yj) 的随机 性，成为一个确定的量。

平均互信息量

平均互信息量

（4）凸函数性
凸函数性： 凸函数性： p 平均互信息量I(X;Y)是信源概率分布 (ai ) 的上凸函数； 的上凸函数； 平均互信息量 是信源概率分布 该性质是研究信道容量的理论基础 平均互信息量I(X;Y)是信道传递概率p (b j / ai ) 的下凸函数。 的下凸函数。 平均互信息量 是信道传递概率 该性质是研究率失真函数的理论基础
H(X/Y)-----信道疑义度 损失熵。Y关于 的后验不确定度。表示收 信道疑义度/损失熵 关于X的后验不确定度 信道疑义度 损失熵。 关于 的后验不确定度。 到变量Y后 对随机变量X仍然存在的不确定度 仍然存在的不确定度。 到变量 后，对随机变量 仍然存在的不确定度。代表了在信道 中 损失的信息 H(X)-----X的先验不确定度 无条件熵 的先验不确定度/无条件熵 I(X;Y)-----收到 前、后关于 的不确定度减少的量。也就是从 获 收到Y前 后关于X的不确定度减少的量 也就是从Y获 的不确定度减少的量。 收到 得的关于 X的平均信息量 的平均信息量
（5）数据处理定理
当消息经过多级处理后， 数据处理定理：当消息经过多级处理后，随着处理 器数目的增多，输入消息与输出消息之间的平均互信息量 器数目的增多，输入消息与输出消息之间的平均互信息量 趋于变小 当对信号、数据或消息进行多级处理时，每处理一次， 当对信号、数据或消息进行多级处理时，每处理一次，就 有可能损失一部分信息，也就是说，数据处理会把信号、 有可能损失一部分信息，也就是说，数据处理会把信号、 数据或消息变成更有用的形式， 数据或消息变成更有用的形式，但是绝不会创造出新的信 息。
y克服了互信息量克服了互信息量的随机性成为一个确定的量因此可以的随机性成为一个确定的量因此可以作为信道中流通信息量的整体测度作为信道中流通信息量的整体测度1观察者站在输出端2观察着站在输入端3观察着站在通信系统总体立场上1观察者站在输出端hxy信道疑义度损失熵

第3讲_信源及其信息量2_平均互信息

第3讲_信源及其信息量2_平均互信息
① 互信息量
举例 某地二月份天气构成的信源为：
x (晴)， x2 (阴)， x3 (雨)， x4 (雪)⎫ ⎡ X ⎤ ⎧ 1 ⎪ ⎪ =⎨ 1 1 1 1 ⎬ ⎢P( X )⎥ ， ， ⎣ ⎦ ⎪ 2， 4 8 8 ⎪ ⎩ ⎭
收到消息 y1：“今天不是晴天” 收到 y1 后：p(x1/y1)=0， p(x2/y1)=1/2， p(x3/y1)=1/4，p(x4/y1)=1/4
2011-3-4
Department of Electronics and Information, NCUT
Song Peng
第10页
2.1.4 平均互信息量
2.1 单 符 号 离 散 信 源
(1) 互信息量和条件互信息量
① 互信息量 互信息量定义：
互信息量：yj 对 xi 的互信息量定义为后验概率与先验概率比 值的对数。
Song Peng
第8页
2.1.4 平均互信息量
2.1 单 符 号 离 散 信 源
(1) 互信息量和条件互信息量
① 互信息量 互信息量定义：
信源 X、信宿 Y 的数学模型为：
x2 , …， xi , …, xn ⎫ ⎡ X ⎤ ⎧ x1 , ⎢ P( X )⎥ = ⎨ p( x ), p( x ), …, p( x ), …, p( x )⎬ ⎣ ⎦ ⎩ 1 i n ⎭ 2 0 ≤ p( xi ) ≤ 1,
Song Peng
第16页
2.1.4 平均互信息量
2.1 单 符 号 离 散 信 源
(1) 互信息量和条件互信息量
① 互信息量
互信息量的三种不同表达式 观察者站在通信系统总体立场上
▼ 通信前：输入随机变量 X 和输出随机变量 Y 之间没有任

信息论第二章信息的度量

信息论第二章信息的度量

I(xi;yj)I(xi)I(xi yj)
log
( xi y j q(xi )
)
（2-6）
称(2-6)式为事件xi和事件yj之间的互信息量。
注：式（2-6）的I(xi ；yj ) 和式（2-3）的I(xiyj )的区别
在于： 前者是事件xi∈X和事件yj∈Y之间的互信息量， 后者是二维空间XY 上元素xi yj 的自信息量。
根据概率互换公式p(xi yj) = p(yj︱xi)q(xi)=φ(xi︱yj)ω(yj) 互信息量I(xi ;yj )有多种表达形式:
I(xi;yj)loq(p x g (ix ) iy (jy )j)I(xi)I(yj)I(xiyj) (2-7)
I(xi;yj)lopg (y(yjjx)i)I(yj)I(yj xi)(2-8)
如底数分别取 2、 e、 10，
则自信息量单位分别为：比特、奈特、哈特
1 na lto2e g 1 .4b 3i3t
1 H a lo r2 1 tg 0 3 .3b 2i2 t
1 bi t0.69 n3 at
1bit0.30H 1art
一个以等概率出现的二进制码元
(0,1)所包含的自信息量为1bit。
第2章 信息的度量
内容提要：
根据香农对于信息的定义，信息是一个系 统不确定性的度量，尤其在通信系统中， 研究的是信息的处理、传输和存储，所以 对于信息的定量计算是非常重要的。本章 主要从通信系统模型入手，研究离散情况 下各种信息的描述方法及定量计算，讨论 它们的性质和相互关系。
2.1 自信息量和互信息量
I(a i)I(bj)
（ 2-4 ）
3.条件自信息量
在已知事件yj条件下,随机事件xi发生的概率为条件概率φ(xi
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
•信宿接受消息Y前后关于X的平均不确定性消除 的程度 •H(X)经信道损失了H(X/Y)后信宿获得的净信息量 •收到消息集合Y后获得关于信源X的平均信息量 •信宿每收到一个消息所获得的平均信息量
2、I (Y ; X )
m j 1
n i 1
p( xi y j ) lb
p( y j / xi ) p( y j )
p( x2
/
y2 )
p(x2 y2 ) /
p( y2 )
3/8 5 / 12
9 10
4）计算互信息量：I
(
xi
;
y
j
)
lb
p(xi / y p( xi )
j
)
I (x1;
y1 )
lb
p(x1 / y1) p( x1 )
lb
5 / 14 1/ 4
lb 10 7
0.515比特/消息
I (x1;
y2 )
lb
m j 1
n i 1
p( xi y j ) lb
p( xi ห้องสมุดไป่ตู้ y j ) p( xi )
n i 1
m j 1
p( xi y j ) lb
1 p(xi )
m j 1
n i 1
p(xi y j ) lb
1 p( xi / y j )
H(X) H(X /Y)
其中：H ( X
/Y)
m j 1
n i 1
m j 1
n i 1
p( xi y j ) lb
1 p( y j )
m j 1
n i 1
p( xi y j ) lb
1 p( y j / xi )
H (Y ) H (Y / X )
其中：H (Y
/X)
m j 1
n i 1
p( xi y j ) lb
1 p( y j / xi )
表示信道输入信号由于信道中的噪声干扰而在信
j1 i1
平均互信息量：
I ( X ;Y ) H ( X ) H ( X /Y ) 0.811 0.744 0.067比特/消息
2）噪声熵：
mn
H (Y / X )
p(xi y j ) lb p( y j / xi ) 0.913比特/消息
j1 i1
平均互信息量：
I ( X ;Y ) H (Y ) H (Y / X ) 0.980 0.913 0.067比特/消息
0.263比特/消息
5）计算平均互信息量：I ( X ;Y ) p(xi y j )I (xi; y j )
ji
I ( X ;Y ) p( x1 y1)I ( x1; y1) p( x1 y2 )I ( x1; y2 )
p( x2 y1)I ( x2; y1) p( x2 y2 )I ( x2; y2 )
1 p( y j )
m j 1
n i 1
p(xi y j ) lb
1 p( xi y j )
H ( X ) H (Y ) H ( XY )
其中：H ( XY )
m j 1
n i 1
p( xi y j ) lb
1 p( xi y j )
为联合熵，表示信源信宿双方通信后整个 系统仍存在的平均不确定度
p(x1)=1/4 x1=1 X空间
5/6 1/2
1/6
y1=1 p(y1) Y空间
p(x2)=3/4 x2=0
1/2
y2=0 p(y2)
分析：已知信源概率分布：p( xi ) 信道转移概率： p( yj / xi )
求平均互信息量：I ( X; Y )
mn
I ( X ;Y ) E[I (xi; y j )]
5 0.515 1 (-1.322) 3 (0.222) 3 0.263
24
24
8
8
0.067比特/消息
因此，信宿收到一个消息后，获得的平均信息量
是0.067比特/消息
思考：1）互信息量有正有负说明什么？ 2）平均互信息量必为正，为什么？
二、平均互信息量的物理意义
1、I ( X ;Y )
•信源发出消息X前后关于信宿Y的平均不确定性的 消除程度
3、I ( X ;Y )
m j 1
n i 1
p( xi y j ) lb
p( xi y j ) p( xi ) p( y j )
n i 1
m j 1
p( xi y j ) lb
1 p(xi )
m j 1
n i 1
p(xi y j ) lb
3）联合熵：
mn
H ( XY )
p( xi y j ) lb p( xi y j ) 1.724比特/消息
j1 i1
平均互信息量：
I ( X ;Y ) H ( X ) H (Y ) H ( XY ) 0.811 0.980 1.724 0.067比特/消息
三、平均互信息量的性质
1、对称性
p(xi y j )I (xi ; y j )
j1 i1
m j 1
n i 1
p( xi y j ) lb
p( xi / y j ) p( xi )
计算步骤：
1）计算联合概率：p(xi y j ) p(xi ) p( y j / xi )
2）计算信宿端概率分布：p( y j ) p(xi ) p( y j / xi )
计算过程：
1）收到yj后，从yj中获得关于xi的非平均信息量
I
( xi
;
y
j
)
lb
p(xi / y p( xi )
j
)
2）收到yj后，从yj中获得关于集合X的平均信息量
I ( X ;
y j
)
EX [I ( xi ; y j )]
n i 1
p( xi
/
y j ) lb
p( xi / y j ) p( xi )
i
3）计算后验概率： p(xi / y j ) p(xi y j ) / p( y j )
4）计算互信息量：I (xi ; 5）计算平均互信息量：
y
j
)
lb
p(xi / y p( xi )
j
)
I ( X ;Y )
p( xi y j )I (xi ; y j )
ji
解：根据题意，信源概率分布：
3）收到集合Y后，从Y中获得关于集合X的平均信 息量
I ( X ;Y )
EY [I ( X ; y j )]
m j 1
n
p( y j )
i 1
p( xi
/
y j ) lb
p( xi / y j ) p( xi )
m j 1
n i 1
p( xi y j ) lb
p( xi / y j ) p( xi )
平均互信息量
I ( X ;Y ) I (Y ; X ) H ( X ) H (Y ) H ( XY )
•信源X的先验平均不确定度+信宿Y的先验平均不
确定度–信源、信宿双方通信后整个系统尚存的后
验平均不确定度
•通信前后关于整个系统平均不确定性消除的程度
[例] 某二元通信系统，它发送1和0的概率分别为： p(1)=1/4，p(0)=3/4，由于信道中有干扰，通信不 能无差错地进行。即有1/6的1在接收端错成0，1/2 的0在接收端错成1。问信宿收到一个消息后，获 得的平均信息量是多少？
j 1
7 lb 7 5 lb 5 0.980比特/消息 12 12 12 12
平均互信息量：
mn
I ( X ;Y )
p( xi y j )I ( xi ; y j ) 0.067比特/消息
j1 i1
1）损失熵：
mn
H ( X /Y )
p( xi y j ) lb p( xi / y j ) 0.744比特/消息
p( xi y j ) lb
1 p( xi / y j )
称为信道疑义度/可疑度（损失熵）
•信宿收到信源发出的消息Y后，对信源X仍存在 的平均不确定度
•通信过程中信息在信道中的损失量
Y对X的平均互信息量
I ( X ;Y ) H ( X ) H ( X /Y )
•信源X的先验平均不确定度–观察到Y后对信源X 尚存的后验平均不确定度
宿端表现的散步范围，称为散布度（噪声熵）
•由于信道噪声的干扰，信源发出消息后无法判断 信宿是否正确收到消息
•信源发出消息X后，对信宿Y仍存在的平均不确 定度
X对Y的平均互信息量
I (Y ; X ) H (Y ) H (Y / X )
•信宿Y的先验平均不确定度–信源发出消息X后对 信宿Y尚存的后验平均不确定度
y
j
) lb
p( xi y j ) p(xi ) p( y
j
)
I (Y ; X )
[例] 某二元通信系统，它发送1和0的概率分别为： p(1)=1/4，p(0)=3/4，由于信道中有干扰，通信不 能无差错地进行。即有1/6的1在接收端错成0，1/2 的0在接收端错成1。问信宿收到一个消息后，获 得的平均信息量是多少？
m j 1
n i 1
p( xi y j ) lb
p( xi y j ) p( xi ) p( y j )
I ( X ;Y )
m j 1
n i 1
p( xi y j ) lb
p( xi / y j ) p( xi )
p( xi
/
yj)
p( xi y j ) p( y j )
mn j1 i1
p( xi
p(x1)=1/4 x1=1 X空间