广西钦州市高新区2020届高三数学12月月考试题文

广西钦州市高新区2016-2017学年高二年级上学期12月份考试理科数学试题(时间：120分钟满分：150分)学校：___________姓名：___________班级：___________考号：___________注意事项：1. 答题前填写好自己的姓名、班级、考号等信息2. 请将答案正确填写在答题卡上一、选择题1. 若直线l 的方向向量为 a =(1,0,2),平面α的法向量为 u =(-2,0,-4),则（）A. l ∥αB. l ⊥αC. l αD. l 与α斜交2. 在正方体ABCD－A 1 B 1 C 1 D 1 中，M、N分别为棱AA 1 和BB 1 的中点，则sin〈，〉的值为( )A．B．C．D．3. 平面α经过三点A(－1,0,1)，B(1,1,2)，C(2，－1,0)，则下列向量中与平面α的法向量不垂直的是( )B．(6，－2，－2)A．( ，－1，－1)C．(4,2,2) D．(－1,1,4)4. 在正三棱柱ABCA 1 B 1 C 1 中，D是AC的中点，AB 1 ⊥BC 1 ，则平面DBC 1 与平面CBC 1所成的角为( )A．30°B．45°C．60°D．90°5. 已知，，，分别是平面，的法向量，则平面，的位置关系式（）A．平行B．垂直C．所成的二面角为锐角D．所成的二面角为钝角6. 已知等差数列的前n项和为，且，则过点和的直线的一个方向向量的坐标可以是（）A．B．(2，4)C．D．（-1，-1）7. 空间直角坐标系中，点与点的距离为，则等于( ) A．B．C．或D．或8. 若，，不共线，对于空间任意一点都有，则，，，四点（）A．不共面B．共面C．共线D．不共线9. 已知向量a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，若a，b，c三个向量共面，则实数λ等于( )A．B．C．D．10. 三棱锥中，两两垂直且相等，点分别是线段和上移动，且满足，，则和所成角余弦值的取值范围是（）A．B．C．D．11. 命题：“对任意”的否定是（）A．存在B．存在C．存在D．对任意12. 下列说法正确的是A．“”是“”的充要条件B．命题“”的否定是“”C．“若都是奇数，则是偶数”的逆否命题是“若不是偶数，则不都是奇数”D．若为假命题,则, 均为假命题二、填空题13. 若双曲线的一条渐近线方程是，则等于▲．14. 在平面直角坐标系xOy中，已知A、B分别是双曲线的左、右焦点，△ABC 的顶点C在双曲线的右支上，则的值是▲15. 设双曲线（，）的离心率为，且它的一条准线与抛物线的准线重合，则此双曲线的渐近线方程为．16. 双曲线的渐近线方程为，则。

2020届高三12月月考数学试卷(理科)说明：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第（1）页至第（3）页，第Ⅱ卷第（4）页至第（6）页。

2、本试卷共150分，考试时间120分钟。

第Ⅰ卷（选择题，共60分）注意事项：1、答第Ⅰ卷前，考生务必将自己的姓名、班级填涂在答题卡上，贴好条形码。

答题卡不要折叠2、每小题选出答案后，用2B 铅笔把答题卡上对应的题目标号涂黑。

答在试卷上无效。

3、考试结束后，监考人员将试卷答题卡收回。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合{}{}2|0|2M x x x N x x =-=＜，＜，则 ( )A ．M N ⋂=∅B ．M N M ⋂=C ．M N M ⋃=D ．M N R =U2． “”是“方程表示双曲线”的 （ )A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件3．正项等差数列{}n a 中的11a ，4027a 是函数()3214433f x x x x =-+-的极值点，则20192log a =( ) A ．2B ．3C ．4D ．54．函数1sin cos (0)y x a x a =+>的图象是由函数25sin 5cos y x x =+的图像向左平移ϕ个单位得到的，则cos ϕ=（ ）A ．35B ．45C 32D 225．新高考方案规定，普通高中学业水平考试分为合格性考试（合格考）和选择性考试（选择考）.其中“选择考”成绩将计入高考总成绩，即“选择考”成绩根据学生考试时的原始卷面分数，由高到低进行排序，评定为A 、B 、C 、D 、E 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍，为了更好地分析该校学生“选择考”的水平情况，统计了该校2016年和2018年“选择考”成绩等级结果，得到如下图表：针对该校“选择考”情况，2018年与2016年比较，下列说法正确的是 （ ）A ．获得A 等级的人数减少了B ．获得B 等级的人数增加了1.5倍C ．获得D 等级的人数减少了一半D ．获得E 等级的人数相同6．设()0sin cos a x x dx π=+⎰，且21nx ax ⎛⎫- ⎪⎝⎭的展开式中只有第4项的二项式系数最大，那么展开式中的所有项的系数之和是 （ ） A ．1 B ．1256 C ．64 D ．1647．直线(1)(2)0()x y R λλλλ+-++=∈恒过定点A ，若点A 在直线20mx ny ++=上，其中0m >，0n >，则21m n+的最小值为 （ ） A ．22B ．4C ．52D ．928．《九章算术》是我国古代的数学巨著，其中《方田》章给出了计算弧田面积所用的经验公式为：弧田面积12=⨯（弦×矢+矢2），弧田（如图阴影部分所示）是由圆弧和弦围成，公式中的“弦”指圆弧所对的弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为23π，矢为2的弧田，按照上述方法计算出其面积是 ( )A ．2+43B ．13+2C ．2+83D ．4+839．执行如图所示的程序框图，则输出n 的值是 （ ）A ．3B ．5C ．7D ．910．已知函数()sin (0)f x x ωω=>，点A ，B 分别为()f x 图像在y 轴右侧的第一个最高点和第一个最低点，O 为坐标原点，若OAB ∆为锐角三角形，则ω的取值范围为（ ）A ．30,2π⎛⎫⎪ ⎪⎝⎭B ．3,22ππ⎛⎫⎪ ⎪⎝⎭C ．0,2π⎛⎫⎪⎝⎭D ．,2π⎛⎫+∞ ⎪⎝⎭11．设函数()f x 在R 上存在导函数'()f x ，x R ∀∈，有3()()f x f x x --=，在(0,)+∞上有22'()30f x x ->，若2(2)()364f m f m m m --≥-+-，则实数m 的取值范围为（ ）A ．[1,1]-B ．(,1]-∞C ．[1,)+∞D ．(,1][1,)-∞-+∞U12．已知函数22,0()(2),0x x x f x f x x ⎧--<=⎨-≥⎩，以下结论正确的是（ ）A ．(3)(2019)3f f -+=-B ．()f x 在区间[]4,5上是增函数C ．若方程() 1f x k x =+恰有3个实根，则11,24k ⎛⎫∈-- ⎪⎝⎭D ．若函数()y f x b =-在(,4)-∞上有6个零点(1,2,3,4,5,6)i x i =，则()61i i i x f x =∑的取值范围是()0,6第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分. 13．已知34a b R a ib i i+=+∈，（，）其中i 为虚数单位，则a bi +=________； 14．已知数列{}n a的首项11a =，且满足11(2)n n n n a a a a n ---=≥，则122320142015a a a a a a +++=L ；15．如图，在矩形ABCD 中，4,2AB AD ==，E 为AB 的中点．将ADE V 沿DE 翻折，得到四棱锥1A DEBC -．设1A C 的中点为M ，在翻折过程中，有下列三个命题：①总有BM ∥平面1A DE ； ②线段BM 的长为定值；③存在某个位置，使DE 与1A C 所成的角为90°． 其中正确的命题是_______．（写出所有正确命题的序号）16．已知双曲线C ：22221(0,0)x y a b a b-=>>的右焦点为F ，左顶点为A ，以F 为圆心，FA 为半径的圆交C 的右支于M ，N 两点，且线段AM 的垂直平分线经过点N ，则C 的离心率为_________.三、解答题：解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分10分）已知函数2()cos 2cos 2()3f x x x x R π⎛⎫=--∈⎪⎝⎭(1)求函数()f x 的单调递增区间；(2)ABC ∆内角,,A B C 的对边分别为,,a b c ，若3()2B f =-，1b =，3c =，且a b >，试求角B 和角C .18．（本小题满分10分）如图，在PBE △中，AB PE ⊥，D 是AE 的中点，C 是线段BE 上的一点，且5AC =，122AB AP AE ===，将PBA ∆沿AB 折起使得二面角P AB E --是直二面角． （l ）求证：CD 平面PAB ；（2）求直线PE 与平面PCD 所成角的正切值．19．（本小题满分10分）2019年3月5日，国务院总理李克强作出的政府工作报告中，提到要“惩戒学术不端，力戒学术不端，力戒浮躁之风”．教育部2014年印发的《学术论文抽检办法》通知中规定：每篇抽检的学术论文送3位同行专家进行评议，3位专家中有2位以上（含3位）专家评议意见为“不合格”的学术论文，将认定为“存在问题学术论文”．有且只有1位专家评议意见为“不合格”的学术论文，将再送另外2位同行专家（不同于前3位专家）进行复评，2位复评专家中有1位以上（含1位）专家评议意见为“不合格”的学术论文，将认定为“存在问题学术论文”．设每篇学术论文被每位专家评议为“不合格”的概率均为()01p p <<，且各篇学术论文是否被评议为“不合格”相互独立．（1）若12p =，求抽检一篇学术论文，被认定为“存在问题学术论文”的概率；（2）现拟定每篇抽检论文不需要复评的评审费用为900元，需要复评的总评审费用1500元；若某次评审抽检论文总数为3000篇，求该次评审费用期望的最大值及对应p 的值．20．（本小题满分10分）在平面直角坐标系xOy中，椭圆G的中心为坐标原点，左焦点为F1（﹣1，0），离心率2e=．（1）求椭圆G 的标准方程；（2）已知直线11l y kx m=+：与椭圆G交于A B，两点，直线2212l y kx m m m=+≠：（）与椭圆G交于C D，两点，且AB CD=，如图所示．①证明：120m m+=；②求四边形ABCD的面积S的最大值．21．（本小题满分10分）已知函数()22,02,0xx xf x xax ax xe⎧-<⎪=⎨+-≥⎪⎩在(),-∞+∞上是增函数．()1求实数a的值；()2若函数()()g x f x kx=-有三个零点，求实数k的取值范围．22．在平面直角坐标系xOy中，曲线C的参数方程为3cos3xyαα=⎧⎪⎨=⎪⎩（α为参数），在以原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为2sin42πρθ⎛⎫-=⎪⎝⎭．（1）求曲线C的普通方程和直线l的直角坐标方程；（2）设点()1,0P-，直线l和曲线C交于,A B两点，求||||PA PB+的值．23．已知函数()()210f x x a x a=++->.（1）当1a =时，求不等式()4f x >的解集；（2）若不等式()42f x x >-对任意的[]3,1x ∈--恒成立，求a 的取值范围.（数学理）1-5 BDCBB 6-10 DDADB 11.B 12 BCD13.5 14. 15. ①② 16. 4 317【解析】（1）233()cos2cos2sin2cos23sin23223f x x x x x xππ⎛⎫⎛⎫=--=-=-⎪ ⎪⎝⎭⎝⎭Q，令222,232k x k k Zπππππ--+∈剟，解得5,1212k x k k Zππππ-+∈剟∴故函数()f x的递增区间为5,()1212k k kππππ⎡⎤-+∈⎢⎥⎣⎦Z.（2）313sin,sin2332Bf B Bππ⎛⎫⎛⎫⎛⎫=-=-∴-=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，20,,,333366B B B Bπππππππ<<∴-<-<∴-=-=Q即，由正弦定理得：13sin sinsin6aA Cπ==，3sin2C∴=，0Cπ<<Q，3Cπ∴=或23π.当3cπ=时，2Aπ=：当23Cπ=时，6Aπ=（不合题意，舍）所以,63B Cππ==.18．如图，在PBE△中，AB PE⊥，D是AE的中点，C是线段BE上的一点，且5AC=，122AB AP AE===，将PBAV沿AB折起使得二面角P AB E--是直二面角．（l）求证：CD平面PAB；（2）求直线PE与平面PCD所成角的正切值．【答案】（1）证明见解析.（2）13.【解析】分析：（1）推导出4,AE AC =是Rt ABE ∆的斜边上的中线，从而C 是BE 的中点，由此能证明//CD 平面PAB ；（2）三棱锥E PAC -的体积为E PAC P ACE V V --=，由此能求出结果．详解：（1）因为122AE =，所以4AE =，又2AB =，AB PE ⊥， 所以22222425BE AB AE =+=+=，又因为152AC BE ==， 所以AC 是Rt ABE n 的斜边BE 上的中线，所以C 是BE 的中点，又因为D 是AE 的中点．所以CD 是ABE n 的中位线，所以CD AB n ， 又因为CD ⊄平面PAB ，AB ⊂平面PAB ，所以CD n 平面PAB ．（2）据题设分析知，AB ，AE ，AP 两两互相垂直，以A 为原点，AB ，AE ，AP 分别为x ，y ，z 轴建立如图所示的空间直角坐标系：因为122AB AP AE ===，且C ，D 分别是BE ，AE 的中点， 所以4AE =，2AD =，所以()040E n n ，()120C n n ，()002P n n ，()020D n n ，所以()042PE =-u u n v n u ，()122PC =-u u n v n u ，()100CD =-u u n vn u ， 设平面PCD 的一个法向量为()n x y z '''=n n ，则00n CD n PC ⎧⋅=⎨⋅=⎩u u u v u u u v ，即0220x x y z ''''-=⎧⎨+-=⎩，所以0x z y =⎧⎨='''⎩，令1y '=，则()011n =n n ，设直线PE 与平面PCD 所成角的大小为θ，则10sin 10PE n PE nθ⋅==⋅u u u v u u u v ． 故直线PE 与平面PCD 所成角的正切值为13．19．2019年3月5日，国务院总理李克强作出的政府工作报告中，提到要“惩戒学术不端，力戒学术不端，力戒浮躁之风”．教育部2014年印发的《学术论文抽检办法》通知中规定：每篇抽检的学术论文送3位同行专家进行评议，3位专家中有2位以上（含3位）专家评议意见为“不合格”的学术论文，将认定为“存在问题学术论文”．有且只有1位专家评议意见为“不合格”的学术论文，将再送另外2位同行专家（不同于前3位专家）进行复评，2位复评专家中有1位以上（含1位）专家评议意见为“不合格”的学术论文，将认定为“存在问题学术论文”．设每篇学术论文被每位专家评议为“不合格”的概率均为()01p p <<，且各篇学术论文是否被评议为“不合格”相互独立．（1）若12p =，求抽检一篇学术论文，被认定为“存在问题学术论文”的概率；（2）现拟定每篇抽检论文不需要复评的评审费用为900元，需要复评的总评审费用1500元；若某次评审抽检论文总数为3000篇，求该次评审费用期望的最大值及对应p 的值．【答案】(1) 2532 (2) 最高费用为350万元．对应13p =．（1）因为一篇学术论文初评被认定为“存在问题学术论文”的概率为()2233331C p p C p -+， 一篇学术论文复评被认定为“存在问题学术论文”的概率为()()2213111C p p p ⎡⎤---⎣⎦， 所以一篇学术论文被认定为“存在 问题学术论文”的概率为()()()()22223313331111f p C p p C p C p p p ⎡⎤=-++---⎣⎦()()()2223313111p p p p p p ⎡⎤=-++---⎣⎦5432312179p p p p =-+-+．∴12p =时，125232f ⎛⎫= ⎪⎝⎭所以抽检一篇的学术论文被认定为“存在问题学术论文”的概率为2532． （2）设每篇学术论文的评审费为X 元，则X 的可能取值为900，1500．()()21315001P X C p p ==-，()()21390011P X C p p ==--，所以()()()()2221133900111500190018001E X C p p C p p p p ⎡⎤=⨯--+⨯-=+-⎣⎦． 令()()21g p p p =-，()0,1p ∈，()()()()()2121311g p p p p p p '=---=--．当10,3p ⎛⎫∈ ⎪⎝⎭时，()0g p '>，()g p 在10,3⎛⎫⎪⎝⎭上单调递增；当1,13p ⎛⎫∈ ⎪⎝⎭时，()0g p '<，()g p 在1,13⎛⎫⎪⎝⎭上单调递减． 所以()g p 的最大值为14327g ⎛⎫= ⎪⎝⎭．所以评审最高费用为44300090018001035027-⎛⎫⨯+⨯⨯= ⎪⎝⎭（万元）．对应13p =．20．在平面直角坐标系xOy 中，椭圆G 的中心为坐标原点，左焦点为F 1（﹣1，0），离心率22e =． （1）求椭圆G 的标准方程；（2）已知直线11l y kx m =+： 与椭圆G 交于 A B ， 两点，直线2212l y kx m m m =+≠：（）与椭圆G 交于C D ， 两点，且AB CD = ，如图所示．①证明：120m m += ；②求四边形ABCD 的面积S 的最大值． （1）设椭圆G 的方程为（a ＞b ＞0）∵左焦点为F 1（﹣1，0），离心率e =．∴c =1，a =，b 2=a 2﹣c 2=1椭圆G 的标准方程为：．（2）设A （x 1，y 1），B （x 2，y 2），C （x 3，y 3），D （x 4，y 4）①证明：由消去y 得（1+2k 2）x 2+4km 1x +2m 12﹣2=0 ，x 1+x 2=，x 1x 2=；|AB |==2；同理|CD |=2，由|AB |=|CD |得2=2，∵m 1≠m 2，∴m 1+m 2=0②四边形ABCD 是平行四边形，设AB ，CD 间的距离d =∵m 1+m 2=0，∴∴s =|AB |×d =2×=.所以当2k 2+1=2m 12时，四边形ABCD 的面积S 的最大值为221．已知函数()22,02,0x x x f x x ax ax x e⎧-<⎪=⎨+-≥⎪⎩在(),-∞+∞上是增函数． ()1求实数a 的值；()2若函数()()g x f x kx =-有三个零点，求实数k 的取值范围．【答案】（1）12a e =；（2）ln211,2e e ⎧⎫⎡⎫⋃-+∞⎨⎬⎪⎢⎩⎭⎣⎭解：()1当0x <时，()2f x x =-是增函数，且()()00f x f <=，故当0x ≥时，()f x 为增函数，即()'0f x ≥恒成立，当0x ≥时，函数的导数()()()211'2221120()x x x xx e xe x f x ax a a x x a e e e --⎛⎫=+-=+-=--≥ ⎪⎝⎭恒成立，当1x ≥时，10x -≤，此时相应120x a e -≤恒成立，即12x a e ≥恒成立，即max 112()x a e e≥=恒成立，当01x ≤<时，10x ->，此时相应120x a e -≥恒成立，即12x a e ≤恒成立，即12a e ≤恒成立， 则12a e =，即12a e=． ()2若0k ≤，则()g x 在R 上是增函数，此时()g x 最多有一个零点，不可能有三个零点，则不满足条件． 故0k >，当0x <时，()2g x x kx =--有一个零点k -，当0x =时，()()0000g f =-=，故0也是故()g x 的一个零点， 故当0x >时， ()g x 有且只有一个零点，即()0g x =有且只有一个解，即202x x x x kx e e e +--=，得22x x x xkx e e e+-=，(0)x >， 则112x x k e e e=+-，在0x >时有且只有一个根， 即y k =与函数()112x x h x e e e=+-，在0x >时有且只有一个交点，()11'2x h x e e=-+，由()'0h x >得1102x e e -+>，即112x e e <得2x e e >，得ln21ln2x e >=+，此时函数递增，由()'0h x <得1102x e e -+<，即112x e e>得2x e e <，得0ln21ln2x e <<=+，此时函数递减，即当1ln2x =+时，函数取得极小值，此时极小值为()1ln211ln211ln22h e e e+++=+- ln211ln2111ln21ln2222222e e e e e e e e e e=++-=++-=⋅， ()110101h e e=+-=-，作出()h x 的图象如图，要使y k =与函数()112x x h x e e e=+-，在0x >时有且只有一个交点， 则ln22k e =或11k e≥-， 即实数k 的取值范围是ln211,2e e ⎧⎫⎡⎫⋃-+∞⎨⎬⎪⎢⎩⎭⎣⎭．22．在平面直角坐标系xOy 中，曲线C 的参数方程为3cos 3x y αα=⎧⎪⎨=⎪⎩（α为参数），在以原点为极点，x 轴正半轴为极轴的极坐标系中，直线l 的极坐标方程为2sin 42πρθ⎛⎫-= ⎪⎝⎭．（1）求曲线C 的普通方程和直线l 的直角坐标方程；（2）设点()1,0P - ，直线l 和曲线C 交于,A B 两点，求||||PA PB +的值．【答案】（1）22193x y +=，10x y -+=；（266（1）因为曲线C 的参数方程为3cos 3x y αα=⎧⎪⎨=⎪⎩（α为参数），所以曲线C 的普通方程为22193x y +=.因为2sin 42πρθ⎛⎫-= ⎪⎝⎭，所以sin cos 1,10x y ρθρθ-=∴-+=. 所以直线l 的直角坐标方程为10x y -+=.（2）由题得点()1,0P -在直线l 上，直线l的参数方程为122x y ⎧=-+⎪⎪⎨⎪=⎪⎩，代入椭圆的方程得2280t -=，所以1212+402t t t t ==-<，所以12|PA|+|PB|=||t t -==. 23．已知函数()()210f x x a x a =++->. （1）当1a =时，求不等式()4f x >的解集；（2）若不等式()42f x x >-对任意的[]3,1x ∈--恒成立，求a 的取值范围.【答案】（1）5|13x x x >⎧⎫<-⎨⎬⎩⎭或；（2）()5,+∞（1）当1a =时，()121f x x x =++-，故()4f x >等价于1314x x ≤-⎧⎨-+>⎩或1134x x -<≤⎧⎨-+>⎩或1314x x >⎧⎨->⎩，解得1x <-或53x >.故不等式()4f x >的解集为5|13x x x >⎧⎫<-⎨⎬⎩⎭或.（2）当[]3,1x ∈--时，由()42f x x >-得22240x a x x ++-+->， 即2x a +>，即2a x >-或2a x <--对任意的[]3,1x ∈--恒成立. 又()max 25x -=，()min 21x --=-，故a 的取值范围为()(),15,-∞-+∞U . 又0a >，所以5a >， 综上，a 的取值范围为()5,+∞.。

广西钦州市钦州港区2016-2017学年高三年级上学期12月份考试理 科 数 学 试 题(时间：120分钟 满分：150分)一、选择题（本大题共12小题，每小题5分，） 1设集合{2,ln }A x =, {,}B x y =若{0}AB =,则y 的值为( )A ．2B ．0C ．eD ．1e2. 已知i 为虚数单位，复数31()1i z i -=+，则z =( ) A. i -B. iC. 1i +D. 1i -+3. “11x x⎧⎫⎨⎬⎩⎭…”是“{} ln 0x x …”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件4．已知直线,a b ，平面,αβ，且a α⊥，b β⊂，则“a b ⊥”是“//αβ”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件5．已知一元二次方程01)1(2=+++++b a x a x 的两个实根为21,x x ，且 1,1021><<x x ，则ab的取值范围是（ ）A ．)21,2(-- B.]21,2(-- C.)21,1(-- D.]21,1(-- 6．函数()sin 6f x x πω⎛⎫=A +⎪⎝⎭（0ω>）的图象与x 轴正半轴交点的横坐标构成一个公差为2π的等差数列，若要得到函数()sin g x x ω=A 的图象，只要将()f x 的图象（ ）个单位 A ．向左平移6π B ．向右平移6πC ．向左平移12π D ．向右平移12π 7．若非零向量,a b 满足a b a b +=-,则a 与b 的夹角为（ ） A.0 B.45 C.90 D.1808.函数sin(2)3y x π=-与2cos(2)3y x π=+的图象关于直线x a =对称，则a 可能是( ) A. 24πB.12π C. 8π D.1124π9.圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为1620π+，则r =( ) （A ）1 （B ）2 （C ）4 （D ）810.已知三个互不重合的平面γβα、、，且c b a ===γβγαβα ,,，给出下列命题：①若c a b a ⊥⊥,，则c b ⊥；②若P b a = ，则P c a = ；③若c a b a ⊥⊥,，则γα⊥；④若b a //，则c a //．其中正确命题个数为（ ） A ．1个B ．2个C ．3个D ．4个11. 已知数列{a n }满足a 1＝1，a n ＋1·a n ＝2n(n ∈N *)，则S 2 017＝( )A ．21 010－1B ．21 010－3C ．3·21 008－1D ．21 009－312. 已知函数()=-xaf x x e 存在单调递减区间，且()=y f x 的图象在0=x 处的切线l 与曲线x y e = 相切，符合情况的切线l ( )A ．有3条B ．有2条C ．有1条D ．有0条二、填空题(本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上) 13. 向量(3,4)在向量(1,2)-上的投影．．为 .14.函数()f x =的最小值为 .15．已知等差数列{}n a 满足：11101a a <-，且它的前n 项和n S 有最大值，则当n S 取到最小正值时，n = ．16．已知数列{}n a 的通项公式为n a n p =-+，数列{}n b 的通项公式为43n n b -=，设nn n n nn na abc b a b ≥⎧=⎨<⎩，在数列{}n c 中，4()n c c n N *>∈,则实数p 的取值范围是 .三、解答题：解答应写出文字说明，证明过程或演算步骤. 17（本小题满分12分）已知函数())cos()sin 244f x x x x ππ=+++． （1）求函数()f x 的单调递增区间； （2）若将()f x 的图象向左平移6π个单位，得到函数()g x 的图象，求函数()g x 在区间[0,]2π上的最大值和最小值． 18. （本小题满分12分）设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈且2514,,a a a 构成等比数列. (1) 证明:2a =(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++<. 19．如图，在四棱锥ABCD S -中，SD ⊥底面ABCD ，ABDC ，AD DC ⊥，1==AD AB ，2==SD DC ，E 为棱SB 上的一点，平面EDC ⊥平面SBC ．（Ⅰ）证明：EB SE 2=；（Ⅱ）求二面角C DE A --的大小．20．已知1m >，直线l ：202m x my --=，椭圆C ：2221x y m +=，12F F 、分别为椭圆C 的左、右焦点．（Ⅰ）当直线l 过右焦点2F 时，求直线l 的方程；（Ⅱ）设直线l 与椭圆C 交于A B ，两点，12AF F ∆，12BF F ∆的重心分别为G H ，．若原点O 在以线段GH 为直径的圆内，求实数m 的取值范围．21．已知函数()()()()22ln ,1212f x a x x g x x x λλ=-=-+--. （1）讨论函数()f x 的单调性；（2）2a =时, 有()()f x g x ≤恒成立, 求整数λ最小值.请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22.（本小题满分10分）选修4—4：坐标系与参数方程．已知1C在直角坐标系下的参数方程为5()1x t y ìïï=ïïïíïïï=-ïïî为参数，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，有曲线2C :θθρsin 4cos 2-=. （Ⅰ）将1C 的方程化为普通方程，并求出2C 的直角坐标方程； （Ⅱ）求曲线1C 和2C 两交点之间的距离.23.（本小题满分10分）选修4—5：不等式选讲． 已知函数()2f x x a a =-+．（Ⅰ）若不等式()6f x ≤的解集为{}23x x -≤≤，求实数a 的值；（Ⅱ）在（Ⅰ）的条件下，若存在实数n 使()()f n m f n ≤--成立，求实数m 的取值范围.参考答案13. -14.215．19 16．(4,7)17. (1) ()2sin 22sin 22f x x x x x π⎛⎫=++=+ ⎪⎝⎭Q 2sin 23x p 骣÷ç=+÷ç÷ç桫 由πππππk x k 223222+≤+≤+-，解得ππππk x k +≤≤+-12125， 所以函数的单调递增区间Z k k k ∈⎥⎦⎤⎢⎣⎡++-,12,125ππππ（2）Q 将()x f 的图象向左平移6π个单位，得到函数()x g 的图象，()⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=∴322sin 2362sin 26ππππx x x f x g2250,,2,2333x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦Q∴当32322ππ=+x 时，23322sin =⎪⎭⎫ ⎝⎛+πx ，()x g 当23322ππ=+x 时，1322sin -=⎪⎭⎫⎝⎛+πx ，()x g 取最小值2-.18．解：(1)当1n =时,22122145,45a a a a =-=+,20n a a >∴=(2)当2n ≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=--()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+ [ ∴当2n ≥时,{}n a 是公差2d =的等差数列.2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =, 由(1)可知,212145=4,1a a a =-∴=21312a a -=-=∴ {}n a 是首项11a =,公差2d =的等差数列. ∴数列{}n a 的通项公式为21n a n =-.(3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦19．（Ⅰ）10x --=；（Ⅱ）()1,2．20．（1）222:=194x y C +，:2100l x y +-=（2）98,55M ⎛⎫ ⎪⎝⎭，min d =21．（1）0,2x ⎛∈ ⎝⎭ 上递增，在,2⎛⎫+∞ ⎪ ⎪⎝⎭递减；（2）2.()0,+∞ 22.解：（1）消参后得1C 为210y x -+=.由2cos 4sin r q q =-得22cos 4sin .r r q rq =-2224.x y x y \+=-2C \的直角坐标方程为22(1)(2)5.x y -++=.…………5分（2）圆心(1,2)-到直线的距离d ==AB \=…………10分23.解：(1)由|2|6x a a -+≤得|2|6,626x a a a x a a -≤--≤-≤-， 即33,32,1a x a a -≤≤∴-== ………5分 （2）由(Ⅰ)知()|21|1,f x x =-+令()()().x f n f n ϕ=+-则124,211()|21||21|24,22124,2n n n n n n n n ϕ⎧-≤-⎪⎪⎪=-+++=-<≤⎨⎪⎪+>⎪⎩∴()n ϕ的最小值为4，故实数m 的取值范围是[4,)+∞．………10分。

广西钦州市高新区2016-2017学年高三年级上学期12月份考试理 科 数 学 试 题(时间：120分钟 满分：150分)一．选择题（本大题共12小题，每小题5分，共60分） 1．已知集合{0,1,2}A =，{1,}B m =，若AB B =，则实数m 的值是（ ）A ．0B ．0或2C ．2D ．0或1或2 2．已知命题p ：“存在[)01,x ∈+∞，使得02(log 3)1x ≥”，则下列说法正确的是（ ）A ．p 是假命题；p ⌝：“任意[1,)x ∈+∞，都有02(log 3)1x <”B ．p 是真命题；p ⌝：“不存在0[1,)x ∈+∞，使得02(log 3)1x <”C ．p 是真命题；p ⌝：“任意[1,)x ∈+∞，都有02(log 3)1x <”D ．p 是假命题；p ⌝：“任意0(,1)x ∈-∞，都有02(log 3)1x <”3．定义运算,,a b ad bc c d=-，若21,2,z i i=，则复数z 对应的点在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限4.已知公差不为0的等差数列{}n a 满足134,,a a a 成等比数列，n S 为数列{}n a 的前n 项和，则3253S S S S --的值为( )A.2-B.3-C.2D.35.“2,0x x a R ∀∈+≥”的否．定形式．．．是( ) A ．2,0x x a R ∀∈+< B ．2,0x x a R ∀∉+≥ C ．2,0x x a R ∃∈+< D ．2,0x x a R ∃∈+≥6.已知函数())220162016log 12016x x f x x x -=++-，则关于x 的不等式()()310f x f x ++>的解集为( )A ．1,4⎛⎫-+∞ ⎪⎝⎭B ．1,4⎛⎫-∞- ⎪⎝⎭C ．()0,+∞D ．(),0-∞7．设变量x ，y 满足约束条件，则z=﹣2x+y 的最小值为（ ）A ． ﹣7B ． ﹣6C ． ﹣1D ． 28．下列函数中在上为减函数的是（ ）A ．y=﹣tanxB ．C ．y=sin2x+cos2xD ．y=2cos 2x ﹣19．已知数列{}n a 是等差数列，1tan 225a =，5113a a =，设n S 为数列{(1)}n n a -的前n 项和，则2015S =（ ）A ．2015B ．2015-C ．3024D ．3022-10．如图，焦点在x 轴上的椭圆22213x y a +=（0a >）的左、右焦点分别为1F ，2F ，P 是椭圆上位于第一象限内的一点，且直线2F P 与y 轴的正半轴交于A 点，1APF ∆的内切圆在边1PF 上的切点为Q ，若1||4F Q =，则该椭圆的离心率为（ ）A ．14 B ．12C ．74D ．13411．N 为圆221x y +=上的一个动点，平面内动点00(,)M x y 满足01y ≥且030OMN ∠= (O 为坐标原点)，则动点M 运动的区域面积为（ ）A.8233π-B.433π233π433π+12．设函数()()()211ln 31f x x g x ax x =+=-+，，若对任意1[0)x ∈+∞，，都存在2x ∈R ，使得()()12f x g x =，则实数a 的最大值为（ ）A ．94 B ．2 C.92D ．4 二．填空题（本大题共4小题，每小题5分， 共20分）13.过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ，且两两夹角都为︒60，若球半径为R ，则弦AB 的长度为____________.（用R 表示）14.某地区为了绿化环境进行大面积植树造林，如右图，在区域{(,)|0,0}x y x y ≥≥内植树，第一颗树在点1(0,1)A ，第二颗树在点1(1,1)B ，第三颗树在点1(1,0)C ，第四颗树在点2(2,0)C ，接着按图中箭头方向每隔一个单位种一颗树，那么（1）第n 颗树所在点的坐标是(10,10)，则n =____________; （2）第2016颗树所在点的坐标是____________．15．已知关于x 的不等式ln 10x ax -+>有且只有一个整数解，则实数a 的取值范围是___________ 16.已知等边三角形ABC 的边长为3,D E 分别,AB AC 为的中点，沿DE 将ABC ∆折成直二面角，则四棱锥A DECB -的外接球的表面积为_________.三．解答题：(本大题共6小题，请写出必要的文字说明和解答过程，共70分) 17．已知函数()sin(4)cos(4)44f x x x ππ=++-.（1）求函数()f x 的最大值；（2）若直线x m =是函数()f x 的对称轴，求实数m 的值.18.已知数列{}n a 满足对任意的*n ∈N ，都有0n a >，且()23331212n n a a a a a a +++=+++．（1）求1a ，2a 的值；（2）求数列{}n a 的通项公式n a ； （3）设数列21n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为nS ，不等式()1log 13n a S a >-对任意的正整数n 恒成立，求C 2C 1B 1 yA 1O实数a 的取值范围．19.（本小题满分12分） 已知数列{}n a 的首项1122,,1,2,3, (31)n n n a a a n a +===+. （1）证明：数列1{1}n a -是等比数列； （2）求数列{}nna 的前n 项和n S ．19. （本小题满分12分）如图，四棱锥S —ABCD 的底面是正方形，SD ⊥平面ABCD ，SD=2a ，2AD a =点E 是SD 上的点，且(02)DE a λλ=<≤（Ⅰ）求证：对任意的(0,2]λ∈，都有AC BE ⊥ （Ⅱ）设二面角C —AE —D 的大小为θ，直线BE 与平面ABCD 所成的角为ϕ，若tan tan 1θϕ=，求λ的值.21. （本小题满分12分） 设函数()1xf x e -=-.(Ⅰ)证明:当x ＞-1时,()1xf x x ≥+; (Ⅱ)设当0x ≥时,()1xf x ax ≤+,求a 的取值范围. 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．在直角坐标系中，圆1C ：22x y +＝经过伸缩变换'3'2x xy y=⎧⎨=⎩后得到曲线2C ．以坐标原点为极点，x 轴的正半轴为极轴，并在两种坐标系中取相同的单位长度， 建立极坐标系，直线的极坐标方程为ρθθ10sin 2cos =+·（1）求曲线2C 的直角坐标方程及直线的直角坐标方程；（2）在2C 上求一点M ，使点M 到直线的距离最小，并求出最小距离． 23．已知函数()a x x f -=（Ⅰ）若()m x f ≤的解集为[]5,1-，求实数m a ,的值；（Ⅱ）当2=a 且20<≤t 时，解关于x 的不等式()()2+≥+x f t x f参考答案1．B2.C3.B 4.C5.C 6.A7. A 8.B 9.D10.D11.A12.A 13.R a 362= 14. （1）110；（2）(8,44)15、1ln 2[,1)2+ 16、52π17．（1）最大值是2；（2）416k m ππ=+()k ∈Z ． 18．（Ⅰ）证明见解析；（Ⅱ）120︒．19. （1）∵121n n n a a a +=+，∴111111222n n n n a a a a ++==+⋅，11111(1)2n na a +-=-， 又123a =，∴11112a -=，数列1{1}n a -是以为12首项，12为公比的等比数列． （2）由（Ⅰ）知1111111222n n n a -+-=⋅=，即1112n n a =+，∴2n n n nn a =+． 设23123222n T =+++ (2)n n+， ① 则23112222n T =++ (1122)nn n n+-++，②由①-②得2111222n T =++ (111)11(1)1122112222212n n n n n n n n n +++-+-=-=---，∴11222n n nnT -=--．∴ 又123+++…(1)2n n n ++=． 数列{}n n a 的前n 项和 22(1)4222222n n nn n n n n n S +++++=-+== 20. （Ⅰ）证法1：如图1，连接BE 、BD ，由地面ABCD 是正方形可得AC ⊥BD 。

广西钦州市高新区高三数学12月月考试题文数 学 试 题(时间：120分钟 满分：150分)一、选择题（本大题共12小题，每小题5分，共60） 1.已知集合{}1,0,1,2A =-，{}2|log (1)0B x x =+>，则A B =（ ）A ．{}0,1,2B ．(0,2]C ．{}1,2D ．[1,2]2.已知复数z 满足3z i i ⋅=-，则z =（ ） A ．1 B ． 3 C ．10 D ．103.已知等差数列}{n a 的前n 项和为n S ，若36-=a ，216=S ，则5a 等于（ ） A ．3- B ．1- C ．1 D ．44.下列函数中，图象的一部分如右图所示的是（ ） （A ）sin 6y x π⎛⎫=+⎪⎝⎭（B ）sin 26y x π⎛⎫=-⎪⎝⎭（C ）cos 43y x π⎛⎫=-⎪⎝⎭（D ）cos 26y x π⎛⎫=-⎪⎝⎭5.已知等比数列{n a }的前n 项和12-=n n S ，则++2221a a …2n a +等于（ ）A ．2)12(-nB ．)12(31-nC ．14-nD ．)14(31-n6．若两个非零向量，满足|+|=|﹣|=2||，则向量+与﹣的夹角是（ ） A ．B ．C ．D ．7．设变量x ，y 满足约束条件，则z=﹣2x+y 的最小值为（ ）A ． ﹣7B ． ﹣6C ． ﹣1D ． 28、把函数sin()6y x π=+图象上各点的横坐标缩小到原来的12（纵坐标不变），再将图象向右平移3π个单位，那么所得图象的一条对称轴为（ ） A.2x π=-B.4x π=-C.8x π=D.4x π=9、某四棱锥的三视图如图所示（单位：cm),则该四棱锥的表面积是 A ．2)7313(cm + B ．2)3412(cm + C ．2)7318(cm + D ．2(93235)cm ++10、已知△ABC 是边长为1的等边三角形，点D 、E 分别是边AB 、BC 的中点，连接DE 并延长到点F ，使得EF DE 2=，则=⋅BC AF A ．85- B ．81 C ．41 D ．81111.已知非零向量,a b 的夹角为60，且满足22a b -=，则a b ⋅的最大值为（ ） A ．21B ．1C ．2D ．3 12.已知点B A M ，，，)01(是椭圆1422=+y x 上的动点，且0MA MB ⋅=，则MA BA ⋅的取值范围是（ ）.A.⎥⎦⎤⎢⎣⎡132，B. ⎥⎦⎤⎢⎣⎡932， C. []91， D.⎥⎦⎤⎢⎣⎡336， 二、 填空题（本大题共4小题，每小题5分，共20分）13.221,4()log ,4x x f x x x ⎧-≤=⎨>⎩，则((3))f f =_________________14．设F 为抛物线2:4C y x =的焦点，曲线ky x=（0k >）与抛物线C 交于点P ，PF ⊥x 轴，则k =_________15．正三角形ABC 的边长为2，将它沿高AD 翻折，使点B 与点C 间的距离为，此时四面体ABCD外接球表面积为______． 16 ．过双曲线=1（a ＞0，b ＞0）的左焦点F （﹣c ，0）作圆x 2+y 2=a 2的切线，切点为E ，延长FE 交抛物线y 2=4cx 于点P ，O 为原点，若，则双曲线的离心率为 ．三、解答题：本大题共6小题，选作题10分，其它每题12分，共70分。

2020年广西壮族自治区钦州市新洲中学高三数学文联考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 设，则（）A. B.C. D.参考答案：B【分析】利用单调性，通过取中间值，即可得到.再不等式的性质，以及对数的运算，即可得到.再通过作差法，即可得到，从而得到的大小比较.【详解】因为，所以，因为，而，所以，即可得，因为，所以，所以，故选B.【点睛】本题主要考查了比较大小的问题，涉及到单调性的运用、对数运算公式以及不等式的性质应用，属于中档题.对于比较大小问题，常用的方法有：（1）作差法，通过两式作差、化简，然后与进行比较，从而确定大小关系；（2）作商法，通过两式作商、化简（注意分母不能为零），然后与进行比较，从而确定大小关系；（3）取中间值法，通过取特殊的中间值（一般取等），分别比较两式与中间值的大小关系，再利用不等式的传递性即可得到两式的大小关系；（4）构造函数法，通过构造函数，使得两式均为该函数的函数值，然后利用该函数的单调性以及对应自变量的大小关系，从而得到两式的大小关系. 2. 已知，为的导函数，则的图象是参考答案：A试题分析：函数，，，故为奇函数，故函数图象关于原点对称，排除，，故不对，答案为A．考点：函数图象的判断．3. 设z=1﹣i（i是虚数单位），若复数在复平面内对应的向量为，则向量的模是（）A．1 B．C．D．2参考答案：B【考点】复数求模．【分析】利用复数的除法的运算法则化简复数，然后求解向量的模．【解答】解：z=1﹣i（i是虚数单位），复数===1﹣i．向量的模： =．故选：B．【点评】本题考查复数的代数形式混合运算，复数的模的求法，考查计算能力．4. 函数（ω＞0，）的部分图象如图所示，则φ的值为（）A．B．C．D．参考答案：B【考点】HK：由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由题意可得T，利用周期公式可求ω=2π，由于点（，0）在函数图象上，可得：0=cos （2π×+φ），由余弦函数的图象和性质结合范围，即可计算得解．【解答】解：由题意可得： =﹣=，∴T=1=，解得ω=2π，∴f（x）=cos（2πx+φ），∵点（，0）在函数图象上，可得：0=cos（2π×+φ），∴2π×+φ=kπ+，k∈Z，解得φ=kπ+，k∈Z，∵，∴当k=0时，φ=．故选：B．5. 已知命题，命题，则下列说法正确的是 ( )A．是的充要条件 B．是的充分不必要条件C．是的必要不充分条件 D．是的既不充分也不必要条件参考答案：B6. 已知函数则（）A． B．2 C．4 D．11参考答案：C7. 如图，A，B是半径为2的圆周上的定点，P为圆周上的动点，是锐角，大小为β.图中阴影区域的面积的最大值为A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ参考答案：B【分析】阴影部分的面积S=S△PAB+ S1- S△OAB.其中S1、S△OAB的值为定值.当且仅当S△PAB取最大值时阴影部分的面积S取最大值.【详解】观察图象可知，当P为弧AB的中点时，阴影部分的面积S取最大值，此时∠BOP =∠AOP =π-β, 面积S 最大值为βr 2+S △POB + S △POA =4β+|OP ||OB |s in （π-β）+|OP ||OA |Sin（π-β）=4β+2Sinβ+2Sinβ=4β+4 Sinβ，故选B .8. 已知全集为,集合,,则( )A.B.C.D.参考答案：D9. 已知集合，，则A ∩B =（ ）A. [－2,4]B. [1,+∞)C. (0,4]D. [－2,+∞)参考答案：C 【分析】 算出集合后可求.【详解】，，故，故选C. 【点睛】本题考查集合的交集，属于基础题，解题时注意对数不等式的等价转化. 10. 设，则“”是“为偶函数”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件参考答案：A 略二、 填空题:本大题共7小题,每小题4分,共28分11. 曲线上的点到直线x 十y+1=0的距离的最小值为_________.参考答案：略12. 在△ABC 中，边角，过作，且，则.参考答案：略13. 若锐角满足，则__________________.参考答案：略14. 若在区间[ 0, 1] 上存在实数x 使2x （3 x+a ）<1成立, 则a 的取值范围是 。

广西钦州市高新区2016-2017学年高三年级上学期12月份考试理 科 数 学 试 题(时间：120分钟 满分：150分)一．选择题（本大题共12小题，每小题5分，共60分） 1．已知集合{0,1,2}A =，{1,}B m =，若AB B =，则实数m 的值是（ ）A ．0B ．0或2C ．2D ．0或1或2 2．已知命题p ：“存在[)01,x ∈+∞，使得02(log 3)1x ≥”，则下列说法正确的是（ ）A ．p 是假命题；p ⌝：“任意[1,)x ∈+∞，都有02(log 3)1x <”B ．p 是真命题；p ⌝：“不存在0[1,)x ∈+∞，使得02(log 3)1x <”C ．p 是真命题；p ⌝：“任意[1,)x ∈+∞，都有02(log 3)1x <”D ．p 是假命题；p ⌝：“任意0(,1)x ∈-∞，都有02(log 3)1x <”3．定义运算,,a b ad bc c d=-，若21,2,z i i=，则复数z 对应的点在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限4.已知公差不为0的等差数列{}n a 满足134,,a a a 成等比数列，n S 为数列{}n a 的前n 项和，则3253S S S S --的值为( )A.2-B.3-C.2D.35.“2,0x x a R ∀∈+≥”的否．定形式．．．是( ) A ．2,0x x a R ∀∈+< B ．2,0x x a R ∀∉+≥ C ．2,0x x a R ∃∈+< D ．2,0x x a R ∃∈+≥6.已知函数())20162016log 2016x x f x x -=+-，则关于x 的不等式()()310f x f x ++>的解集为( )A ．1,4⎛⎫-+∞ ⎪⎝⎭B ．1,4⎛⎫-∞- ⎪⎝⎭C ．()0,+∞D ．(),0-∞7．设变量x ，y 满足约束条件，则z=﹣2x+y 的最小值为（ ）A ． ﹣7B ． ﹣6C ． ﹣1D ． 28．下列函数中在上为减函数的是（ ）A ．y=﹣tanxB ．C ．y=sin2x+cos2xD ．y=2cos 2x ﹣19．已知数列{}n a 是等差数列，1tan 225a =，5113a a =，设n S 为数列{(1)}n n a -的前n 项和，则2015S =（ ）A ．2015B ．2015-C ．3024D ．3022-10．如图，焦点在x 轴上的椭圆22213x y a +=（0a >）的左、右焦点分别为1F ，2F ，P 是椭圆上位于第一象限内的一点，且直线2F P 与y 轴的正半轴交于A 点，1APF ∆的内切圆在边1PF 上的切点为Q ，若1||4F Q =，则该椭圆的离心率为（ ）A ．14 B ．12C D ．11．N 为圆221x y +=上的一个动点，平面内动点00(,)M x y 满足01y ≥且030OMN ∠= (O 为坐标原点)，则动点M 运动的区域面积为（ ）A.83π-B.43π23π43π+12．设函数()()()21ln 31f x g x ax x ==-+，，若对任意1[0)x ∈+∞，，都存在2x ∈R ，使得()()12f x g x =，则实数a 的最大值为（ ）A ．94 B ．2 C.92D ．4 二．填空题（本大题共4小题，每小题5分， 共20分）13.过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ，且两两夹角都为︒60，若球半径为R ，则弦AB 的长度为____________.（用R 表示）14.某地区为了绿化环境进行大面积植树造林，如右图，在区域{(,)|0,0}x y x y ≥≥内植树，第一颗树在点1(0,1)A ，第二颗树在点1(1,1)B ，第三颗树在点1(1,0)C ，第四颗树在点2(2,0)C ，接着按图中箭头方向每隔一个单位种一颗树，那么（1）第n 颗树所在点的坐标是(10,10)，则n =____________; （2）第2016颗树所在点的坐标是____________．15．已知关于x 的不等式ln 10x ax -+>有且只有一个整数解，则实数a 的取值范围是___________ 16.已知等边三角形ABC的边长为,D E 分别,AB AC 为的中点，沿DE 将ABC ∆折成直二面角，则四棱锥A DECB -的外接球的表面积为_________.三．解答题：(本大题共6小题，请写出必要的文字说明和解答过程，共70分) 17．已知函数()sin(4)cos(4)44f x x x ππ=++-.（1）求函数()f x 的最大值；（2）若直线x m =是函数()f x 的对称轴，求实数m 的值.18.已知数列{}n a 满足对任意的*n ∈N ，都有0n a >，且()23331212n n a a a a a a +++=+++．（1）求1a ，2a 的值；（2）求数列{}n a 的通项公式n a ； （3）设数列21n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为nS ，不等式()1log 13n a S a >-对任意的正整数n 恒成立，求C 2C 1B 1 yA 1O实数a 的取值范围．19.（本小题满分12分） 已知数列{}n a 的首项1122,,1,2,3, (31)n n n a a a n a +===+. （1）证明：数列1{1}n a -是等比数列； （2）求数列{}nna 的前n 项和n S ．19. （本小题满分12分）如图，四棱锥S —ABCD 的底面是正方形，SD ⊥平面ABCD ，SD=2a，AD =点E 是SD 上的点，且(02)DE a λλ=<≤（Ⅰ）求证：对任意的(0,2]λ∈，都有AC BE ⊥ （Ⅱ）设二面角C —AE —D 的大小为θ，直线BE 与平面ABCD 所成的角为ϕ，若t a n t a n 1θϕ=g ，求λ的值.21. （本小题满分12分） 设函数()1xf x e -=-.(Ⅰ)证明:当x ＞-1时,()1xf x x ≥+; (Ⅱ)设当0x ≥时,()1xf x ax ≤+,求a 的取值范围. 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．在直角坐标系中，圆1C ：22x y +＝经过伸缩变换'3'2x xy y=⎧⎨=⎩后得到曲线2C ．以坐标原点为极点，x 轴的正半轴为极轴，并在两种坐标系中取相同的单位长度， 建立极坐标系，直线的极坐标方程为ρθθ10sin 2cos =+·（1）求曲线2C 的直角坐标方程及直线的直角坐标方程；（2）在2C 上求一点M ，使点M 到直线的距离最小，并求出最小距离． 23．已知函数()a x x f -=（Ⅰ）若()m x f ≤的解集为[]5,1-，求实数m a ,的值；（Ⅱ）当2=a 且20<≤t 时，解关于x 的不等式()()2+≥+x f t x f参考答案1．B2.C3.B 4.C5.C 6.A7. A 8.B 9.D10.D11.A12.A 13.R a 362= 14. （1）110；（2）(8,44)15、1ln 2[,1)2+ 16、52π17．（1）最大值是2；（2）416k m ππ=+()k ∈Z ． 18．（Ⅰ）证明见解析；（Ⅱ）120︒．19. （1）∵121n n n a a a +=+，∴ 111111222n n n n a a a a ++==+⋅，\11111(1)2n n a a +-=-， 又123a =，∴11112a -=，数列1{1}n a -是以为12首项，12为公比的等比数列． （2）由（Ⅰ）知1111111222n n n a -+-=⋅=，即1112n n a =+，∴2n n n nn a =+． 设23123222n T =+++ (2)n n+， ① 则23112222n T =++ (1122)nn n n+-++，②由①-②得2111222n T =++ (111)11(1)1122112222212n n n n n n n n n +++-+-=-=---，∴11222n n nnT -=--．∴ 又123+++ (1)2n n n ++=． 数列{}n n a 的前n 项和 22(1)4222222n n nn n n n n n S +++++=-+== 20. （Ⅰ）证法1：如图1，连接BE 、BD ，由地面ABCD 是正方形可得AC ⊥BD 。

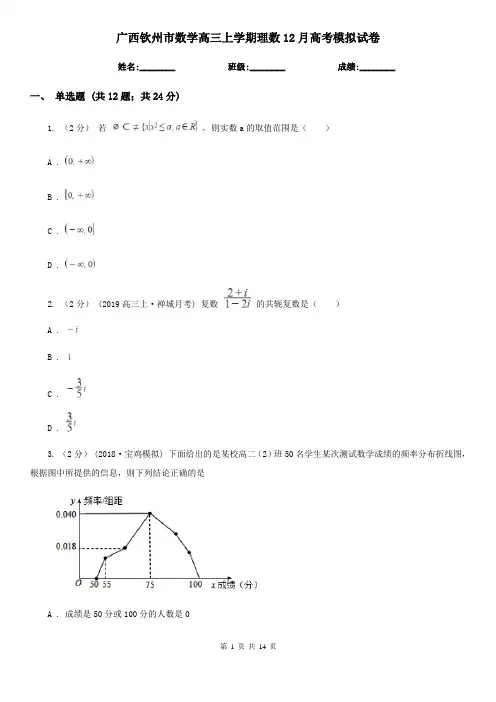
广西钦州市数学高三上学期理数12月高考模拟试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）若，则实数a的取值范围是（）A .B .C .D .2. （2分） (2019高三上·禅城月考) 复数的共轭复数是（）A .B . ｉC .D .3. （2分）(2018·宝鸡模拟) 下面给出的是某校高二（2）班50名学生某次测试数学成绩的频率分布折线图，根据图中所提供的信息，则下列结论正确的是A . 成绩是50分或100分的人数是0B . 成绩为75分的人数为20C . 成绩为60分的频率为0.18D . 成绩落在60—80分的人数为294. （2分）已知二项式的展开式中第4项为常数项，则中项的系数为（）A . -19B . 19C . 20D . -205. （2分） (2018高一下·长阳期末) 在等差数列中，若是数列的前项和，则的值为（）A . 48B . 54C . 60D . 666. （2分）在三棱锥P-ABC中，PA,PB,PC两两垂直，且PA=3，PB=2，PC=1，设M是底面△ABC内一点，定义，其中m,n,p分别是三棱锥M-ABC，三棱锥M-PBC，三棱锥M-PCA的体积，若，且，则正实数a的最小值为（）A . 1B . 2C .D . 47. （2分）奇函数、偶函数的图象分别如图1、2所示，方程，的实根个数分别为a、b，则a+b等于（）A . 14B . 10C . 7D . 38. （2分）(2017·安庆模拟) 在如图的程序框图中，任意输入一次x（0≤x≤1）与y（0≤y≤1），则能输出“恭喜中奖！”的概率为（）A .B .C .D .9. （2分） (2019高二上·阜阳月考) 已知点是抛物线上的一动点，为抛物线的焦点，是圆：上一动点，则的最小值为（）A . 3B . 4C . 5D . 610. （2分） (2017高二上·集宁期末) 过P（﹣4，1）的直线l与双曲线仅有一个公共点，则这样的直线l有（）条．A . 1B . 2C . 3D . 411. （2分）能够把圆的周长和面积同时分为相等的两部分的函数称为圆的“和谐函数”,下列函数不是圆的“和谐函数”的是（）A .B .C .D .12. （2分） (2019高一上·沈阳月考) 已知奇函数的定义域为，且对任意正实数，恒有﹥0 ，则一定有（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） f（x）=x+ （x＜1）的最大值为________．14. （1分）(2018高三上·龙泉驿月考) 已知为数列的前项和，且，若，，给定四个命题① ；② ；③ ；④ .则上述四个命题中真命题的序号为________.15. （1分） (2020高三上·潮州期末) 函数在处取得最大值，则 ________16. （1分）已知正三棱柱底面边长为，高为，圆是等边三角形的内切圆，点是圆上任意一点，则三棱锥的外接球的表面积为________．三、解答题 (共7题；共65分)17. （10分）已知有穷数列{an}，{bn}对任意的正整数n∈N*都有a1bn+a2bn﹣1+a3bn﹣2+…+an﹣1b2+anb1=2n+1﹣n﹣2．（1）若{an}是等差数列，且首项和公差相等，求证：{bn}是等比数列．（2）若{an}是等差数列，且{bn}是等比数列，求证：anbn=n•2n﹣1 ．18. （10分）某家电专卖店试销A，B，C三种新型空调，销售情况记录如表：第一周第二周第三周第四周第五周A型数量（台）101015A4A5B型数量（台）101213B4B5C型数量（台）15812C4C5（Ⅰ）为跟踪调查空调的使用情况，根据销售记录，从该家电专卖店前三周售出的所有空调中随机抽取一台，求抽到的空调“是B型空调或是第一周售出空调”的概率；（Ⅱ）为跟踪调查空调的使用情况，根据销售记录，从该家电专卖店第二周和第三周售出的空调中分别随机抽取一台，求抽取的两台空调中A型空调台数X的分布列和数学期望．19. （15分）(2017·赣州模拟) 如图，五面体ABCDE中，四边形ABDE是菱形，△ABC是边长为2的正三角形，∠DBA=60°，．（1）证明：DC⊥AB；（2）若点C在平面ABDE内的射影H，求CH与平面BCD所成的角的正弦值．20. （10分） (2019高二上·成都期中) 已知动点满足： .（1）求动点的轨迹的方程；（2）设过点的直线与曲线交于两点，点关于轴的对称点为（点与点不重合），证明：直线恒过定点，并求该定点的坐标.21. （5分）(2020·天津模拟) 已知函数，函数，其中，是的一个极值点，且 .（1）讨论的单调性（2）求实数和a的值（3）证明22. （10分） (2019高三上·牡丹江月考) 在直角坐标系中，曲线的参数方程为（为参数）．坐标原点为极点，轴的正半轴为极轴，取相同长度单位建立极坐标系，直线的极坐标方程为．（1）求曲线的普通方程和极坐标方程；（2）设射线与曲线交于点，与直线交于点，求线段的长．23. （5分） (2016高二上·临沂期中) 制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损分别为30%和10%．投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共65分)17-1、18-1、19-1、19-2、20-1、20-2、21-1、21-2、21-3、22-1、22-2、23-1、。

【关键字】数学广西钦州市钦州港区2016-2017学年高三年级上学期12月份考试数学试题(时间：120分钟满分：150分)一．选择题（本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.设集合，，若，则（）A. B. C. D.2．若奇函数f（x）的定义域为R，则有（）A．f（x）＞f（-x）C．f（x）≤f（-x）C．f（x）·f（-x）≤0D．f（x）·f（-x）＞03．若a,b是异面直线，且a∥平面，那么b与平面的位置关系是（）A．b∥B．b与相交C．b D．以上三种情况都有可能4．“”是“直线与直线平行”的（）条件。

A．充分但不必要B．必要但不充分C．充分D．既不充分也不必要5.设直线与平面相交但不笔直，则下列命题错误的是（）A．在平面内存在直线与直线平行B．在平面内存在直线与直线笔直C．在平面内存在直线与直线相交D．在平面内存在直线与直线异面6、已知x, y满足不等式组，则的最大值为A．8 B．．12 D．147、要计算的结果，下面程序框图中的判断框内可以填（）A．B．C．D．8.如图，周长为1的圆的圆心在轴上，顶点，一动点从开始逆时针绕圆运动一周，记走过的弧长，直线与轴交于点，则函数的图像大致为（）9.《九章算术》中，将底面是直角形的直三棱柱称之为“堑堵” ，已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”的侧面积为（）.A. 2B.C. D.10. 已知满足，若不等式恒成立，则实数的取值范围是( ).A. B. C. D.11．已知点P为函数f（x）=lnx的图象上任意一点，点Q为圆[x﹣（e+）]2+y2=1任意一点，则线段PQ的长度的最小值为（）A．B．C．D．e+﹣112．已知f（x）=x（1+lnx），若k∈Z，且k（x﹣2）＜f（x）对任意x＞2恒成立，则k的最大值为（）A．3 B. 4 C．5 D．6二．填空题：13、曲线在点处的切线方程为____________14、定义在上的函数满足，.现有以下三种叙述：①是函数的一个周期；②的图象关于直线对称；③是偶函数.其中正确的是_____15．已知数列满足对任意的，都有，又，则____________.16．已知关于的不等式有且只有一个整数解，则实数的取值范围是___________三．解答题（本大题共6小题,满分70分，解答应写出文字说明，证明过程或演算步骤.）17．已知数列的首项，前项和为，且．（1）设，求数列的通项公式；（2）求数列的前项和．18、已知函数的最大值为2.(1)求函数在上的单调递减区间;(2)△ABC中,,角A、B、C所对的边分别是a、b、c,且C=60,c=3,求△ABC的面积.19．在如图所示的四棱锥中，，，．（1）在棱上确定一点，使得∥平面，保留作图痕迹，并证明你的结论。

广西钦州市高新区2016-2017学年高三年级上学期12月份考试理 科 数 学 试 题(时间：120分钟 满分：150分)一．选择题（本大题共12小题，每小题5分，共60分） 1．已知集合{0,1,2}A =，{1,}B m =，若AB B =，则实数m 的值是（）A ．0B ．0或2C ．2D ．0或1或2 2．已知命题p ：“存在[)01,x ∈+∞，使得02(log 3)1x ≥”，则下列说法正确的是（）A ．p 是假命题；p ⌝：“任意[1,)x ∈+∞，都有02(log 3)1x <”B ．p 是真命题；p ⌝：“不存在0[1,)x ∈+∞，使得02(log 3)1x <”C ．p 是真命题；p ⌝：“任意[1,)x ∈+∞，都有02(log 3)1x <”D ．p 是假命题；p ⌝：“任意0(,1)x ∈-∞，都有02(log 3)1x <”3．定义运算,,a b ad bc c d=-，若21,2,z i i=，则复数z 对应的点在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限4.已知公差不为0的等差数列{}n a 满足134,,a a a 成等比数列，n S 为数列{}n a 的前n 项和，则3253S S S S --的值为( )A.2-B.3-C.2D.35.“2,0x x a R ∀∈+≥”的否．定形式．．．是( ) A ．2,0x x a R ∀∈+< B ．2,0x x a R ∀∉+≥ C ．2,0x x a R ∃∈+< D ．2,0x x a R ∃∈+≥6.已知函数())20162016log 2016x x f x x -=+-，则关于x 的不等式()()310f x f x ++>的解集为( )A ．1,4⎛⎫-+∞ ⎪⎝⎭B ．1,4⎛⎫-∞- ⎪⎝⎭C ．()0,+∞D ．(),0-∞7．设变量x ，y 满足约束条件，则z=﹣2x+y 的最小值为（ ）A ． ﹣7B ． ﹣6C ． ﹣1D ． 28．下列函数中在上为减函数的是（ ）A ．y=﹣tanxB ．C ．y=sin2x+cos2xD ．y=2cos 2x ﹣19．已知数列{}n a 是等差数列，1tan 225a =，5113a a =，设n S 为数列{(1)}n n a -的前n 项和，则2015S =（）A ．2015B ．2015-C ．3024D ．3022-10．如图，焦点在x 轴上的椭圆22213x y a +=（0a >）的左、右焦点分别为1F ，2F ，P 是椭圆上位于第一象限内的一点，且直线2F P 与y 轴的正半轴交于A 点，1APF ∆的内切圆在边1PF 上的切点为Q ，若1||4F Q =，则该椭圆的离心率为（）A ．14 B ．12C D ．11．N 为圆221x y +=上的一个动点，平面内动点00(,)M x y 满足01y ≥且030OMN ∠= (O 为坐标原点)，则动点M 运动的区域面积为（）A.83π-B.43π23π43π+12．设函数()()()21ln 31f x g x ax x ==-+，，若对任意1[0)x ∈+∞，，都存在2x ∈R ，使得()()12f x g x =，则实数a 的最大值为（）A ．94 B ．2 C.92D ．4 二．填空题（本大题共4小题，每小题5分，共20分）13.过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ，且两两夹角都为︒60，若球半径为R ，则弦AB 的长度为____________.（用R 表示）14.某地区为了绿化环境进行大面积植树造林，如右图，在区域{(,)|0,0}x y x y ≥≥内植树，第一颗树在点1(0,1)A ，第二颗树在点1(1,1)B ，第三颗树在点1(1,0)C ，第四颗树在点2(2,0)C ，接着按图中箭头方向每隔一个单位种一颗树，那么（1）第n 颗树所在点的坐标是(10,10)，则n =____________; （2）第2016颗树所在点的坐标是____________．15．已知关于x 的不等式ln 10x ax -+>有且只有一个整数解，则实数a 的取值范围是___________ 16.已知等边三角形ABC的边长为,D E 分别,AB AC 为的中点，沿DE 将ABC ∆折成直二面角，则四棱锥A DECB -的外接球的表面积为_________.三．解答题：(本大题共6小题，请写出必要的文字说明和解答过程，共70分) 17．已知函数()sin(4)cos(4)44f x x x ππ=++-.（1）求函数()f x 的最大值；（2）若直线x m =是函数()f x 的对称轴，求实数m 的值.18.已知数列{}n a 满足对任意的*n ∈N ，都有0n a >，且()23331212n n a a a a a a +++=+++．（1）求1a ，2a 的值；（2）求数列{}n a 的通项公式n a ； （3）设数列21n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为nS ，不等式()1log 13n a S a >-对任意的正整数n 恒成立，求实C 2C 1B 1 yA 1O数a 的取值范围．19.（本小题满分12分） 已知数列{}n a 的首项1122,,1,2,3, (31)n n n a a a n a +===+. （1）证明：数列1{1}n a -是等比数列； （2）求数列{}nna 的前n 项和n S ．19. （本小题满分12分）如图，四棱锥S —ABCD 的底面是正方形，SD ⊥平面ABCD ，SD=2a，AD =点E 是SD 上的点，且(02)DE a λλ=<≤（Ⅰ）求证：对任意的(0,2]λ∈，都有AC BE ⊥ （Ⅱ）设二面角C —AE —D 的大小为θ，直线BE 与平面ABCD 所成的角为ϕ，若t a n t a n 1θϕ=g ，求λ的值.21. （本小题满分12分） 设函数()1xf x e -=-.(Ⅰ)证明:当x ＞-1时,()1xf x x ≥+; (Ⅱ)设当0x ≥时,()1xf x ax ≤+,求a 的取值范围. 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．在直角坐标系中，圆1C ：22x y +＝经过伸缩变换'3'2x xy y=⎧⎨=⎩后得到曲线2C ．以坐标原点为极点，x 轴的正半轴为极轴，并在两种坐标系中取相同的单位长度， 建立极坐标系，直线的极坐标方程为ρθθ10sin 2cos =+·（1）求曲线2C 的直角坐标方程及直线的直角坐标方程；（2）在2C 上求一点M ，使点M 到直线的距离最小，并求出最小距离． 23．已知函数()a x x f -=（Ⅰ）若()m x f ≤的解集为[]5,1-，求实数m a ,的值；（Ⅱ）当2=a 且20<≤t 时，解关于x 的不等式()()2+≥+x f t x f参考答案1．B2.C3.B 4.C5.C 6.A7. A 8.B 9.D10.D11.A12.A 13.R a 362=14.（1）110；（2）(8,44)15、1ln 2[,1)2+16、52π17．（1）最大值是2；（2）416k m ππ=+()k ∈Z ． 18．（Ⅰ）证明见解析；（Ⅱ）120︒．19. （1）∵121n n n a a a +=+，∴111111222n n n n a a a a ++==+⋅，\11111(1)2n na a +-=-， 又123a =，∴11112a -=，数列1{1}n a -是以为12首项，12为公比的等比数列． （2）由（Ⅰ）知1111111222n n n a -+-=⋅=，即1112n n a =+，∴2n n n nn a =+． 设23123222n T =+++ (2)n n+， ①则23112222n T =++ (1122)nn n n+-++，②由①-②得2111222n T =++ (111)11(1)1122112222212n n n n n n n n n +++-+-=-=---，∴11222n n nnT -=--． ∴ 又123+++ (1)2n n n ++=． 数列{}n n a 的前n 项和 22(1)4222222n n nn n n n n n S +++++=-+== 20.（Ⅰ）证法1：如图1，连接BE 、BD ，由地面ABCD 是正方形可得AC ⊥BD 。

广西钦州市钦州港经济技术开发区中学2022届高三班级12月份考试数学文科试卷 （考试用时：120分 全卷满分：150分 ） 留意事项：1. 答卷前，考生务必得将自己的姓名，座位号和准考证号填写在答题卡上。

2. 回答选择题时，每小题选出答案后，用2B 铅笔把答题卷上对应题目的答案标号涂黑，如需改动，用橡皮擦洁净后，再选涂其他答案标号，在试题卷上作答无效。

3. 回答主观题时，将答案写在答题卡上对应位置，写在本试卷上无效。

4. 考试结束后，将答题卡交回。

第Ι卷（选择题部分，共60分）一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1.已知等比数列，则1"0"a >是2017"0"a >的A.充分不必要条件B. 必要不充分条件C. 充要条件D.既不充分也不必要条件2.复数20165(1)i z i =-的共轭复数在复平面上对应的点位于（ ）A.第一象限B.其次象限C.第三象限D.第四象限3．“4a <-”是“函数()3f x ax =+在区间[-1，1]上存在零点”的（ ）SX021001 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．函数)32sin(π-=x y 在区间[-ππ,2]上的简图是（ ）5. 已知0,0>>b a ，若不等式ba m ba313+≥+恒成立，则m 的最大值为A.9B.12 C.18 D.246.函数()sin()(0,||)2f x x πωϕωϕ=+><的图像如图所示，为了得到函数cos()6y x πω=+的图像，只需将()y f x =的图像（ ）A.向右平移3π个单位长度 B.向左平移3π个单位长度 C.向右平移6π个单位长度 D.向左平移6π个单位长度 7. 把函数)6sin(π+=x y 图象上各点的横坐标缩短到原来的21倍（纵坐标不变），再将图象向右平移3π个单位，那么所得图象的一条对称轴方程为 ( ) A ．2π-=x B ．4π-=x C ．8π=x D ．4π=x8. 已知函数⎩⎨⎧>+≤+=-0,log 0,12)(3x ax x x x f x ，若a f f 4))1((>-，则实数a 的取值范围为（ ）A. ），（51-∞ B. ），（0-∞ C. ），（1-∞ D. ），（∞+19. 已知非零向量,a b 满足||b 4||a =，且(2)a a b ⊥+，则a b 与的夹角为A.3π B.2π C.32πD.56π10.已知双曲线2213y x -=上存在两点M,N 关于直线y x m =+对称，且MN 的中点在抛物线29y x =上，则实数m 的值为（ ）A.4B.-4C.0或4D.0或-411. 已知,a b 为两条不同的直线，,αβ为两个不同的平面，且a α⊥，b β⊥，则下列命题中的假命题是（ ）A ．若a ∥b ，则α∥βB ．若αβ⊥，则a b ⊥C ．若,a b 相交，则,αβ相交D ．若,αβ相交，则,a b 相交1 -12π-3π-6ππB1-1 2π-3π-6ππA 1-12π-6π-3ππC1-11 2π-6π-3ππD12．已知函数)(x f 是定义在R 上的奇函数，且在区间),0[∞+上单调递增，若)1(2|)1(ln )(ln |f x f x f >-，则x 的取值范围是（ ）A.)1,e ∞-（ B. ),∞+e （ C. ),1e e （ D. )1,0e（),∞+⋃e （ 本卷包括必考题和选考题两部分。