径向基(RBF)神经网络的介绍及其案例实现

rbf神经网络原理RBF神经网络原理。

RBF神经网络是一种基于径向基函数的神经网络模型，它具有良好的非线性逼近能力和较快的学习速度，在模式识别、函数逼近、时间序列预测等领域有着广泛的应用。

本文将介绍RBF神经网络的原理及其在实际应用中的一些特点。

首先，RBF神经网络由三层结构组成，输入层、隐含层和输出层。

输入层接收外部输入信号，并将其传递给隐含层；隐含层使用径向基函数对输入信号进行非线性映射；输出层对隐含层的输出进行加权求和，并经过激活函数得到最终的输出结果。

整个网络的学习过程包括初始化、前向传播、误差反向传播和参数更新等步骤。

其次，RBF神经网络的核心在于径向基函数的选择。

常用的径向基函数包括高斯函数、多孔径函数等，它们具有局部化、非线性化的特点，能够更好地拟合复杂的非线性关系。

在实际应用中，选择适当的径向基函数对网络的性能有着重要影响，需要根据具体问题进行调整和优化。

另外，RBF神经网络的学习算法通常采用最小均方误差或梯度下降等方法，通过不断调整网络参数来最小化目标函数。

与传统的BP神经网络相比，RBF神经网络在学习速度和全局最优解的搜索能力上有一定优势，但也存在着局部最优解、过拟合等问题，需要结合具体问题进行调整和改进。

此外，RBF神经网络在模式识别、函数逼近、时间序列预测等领域有着广泛的应用。

例如，在模式识别中，RBF神经网络能够处理非线性可分问题，并且对噪声具有一定的鲁棒性；在函数逼近中，RBF神经网络能够较好地拟合复杂的非线性函数关系；在时间序列预测中，RBF神经网络能够捕捉数据的非线性动态特性，有着较好的预测效果。

综上所述，RBF神经网络是一种基于径向基函数的神经网络模型，具有良好的非线性逼近能力和较快的学习速度，在模式识别、函数逼近、时间序列预测等领域有着广泛的应用前景。

然而，在实际应用中，还需要进一步研究和改进其学习算法、径向基函数的选择以及网络结构的优化，以提高网络的性能和稳定性。

径向基神经网络RBF介绍径向基神经网络（Radial Basis Function Neural Network，以下简称RBF神经网络）是一种人工神经网络模型。

它以径向基函数为激活函数，具有快速学习速度和较高的逼近能力，被广泛应用于函数逼近、模式识别、时间序列预测等领域。

下面将详细介绍RBF神经网络的基本原理、结构和学习算法。

1.基本原理：RBF神经网络由输入层、隐藏层和输出层组成。

输入层接收外部输入数据，隐藏层由一组径向基函数组成，输出层计算输出值。

其基本原理是通过适当的权值与径向基函数的线性组合，将输入空间映射到高维特征空间，并在该空间中进行线性回归或分类。

RBF神经网络的关键在于选择合适的径向基函数和隐藏层节点的中心点。

2.网络结构：隐藏层是RBF神经网络的核心，它由一组径向基函数组成。

每个径向基函数具有一个中心点和一个半径。

典型的径向基函数有高斯函数和多项式函数。

高斯函数的形式为：φ(x) = exp(-β*，x-c，^2)其中，β为控制函数衰减速度的参数，c为径向基函数的中心点，x为输入向量。

隐藏层的输出由输入向量与每个径向基函数的权值进行加权求和后经过激活函数得到。

输出层通常采用线性激活函数，用于输出预测值。

3.学习算法：RBF神经网络的学习算法包括两个步骤：网络初始化和权值训练。

网络初始化时需要确定隐藏层节点的中心点和半径。

常用的方法有K-means 聚类和最大极大算法。

权值训练阶段的目标是通过输入样本和对应的目标值来调整权值，使得网络的输出尽可能接近目标值。

常用的方法有最小均方误差算法（Least Mean Square，LMS）和最小二乘法。

最小均方误差算法通过梯度下降法修改权值，使网络输出的均方误差最小化。

最小二乘法则通过求解线性方程组得到最优权值。

在训练过程中，需要进行误差反向传播，根据输出误差调整权值。

4.特点与应用：RBF神经网络具有以下特点：-输入输出非线性映射能力强，可以逼近复杂的非线性函数关系；-学习速度较快，只需通过非线性映射学习输出函数，避免了反向传播算法的迭代计算；-具有较好的泛化能力，对噪声和异常数据有一定的鲁棒性。

神经网络控制(RBF)神经网络控制（RBF）是一种基于径向基函数（RBF）的神经网络，用于控制系统，其主要功能是通过对输入信号进行处理来实现对系统输出的控制。

通过神经网络控制，控制器可以学习系统的动态行为和非线性模型，从而使得控制器能够自适应地进行调整和优化，实现对系统的精确控制。

RBF 网络通常由三层组成：输入层、隐藏层和输出层。

输入层接受系统的输入信号，并将其传递到隐藏层，隐藏层对输入数据进行处理并输出中间层的值，其中每个中间层神经元都使用一个基函数来转换输入数据。

最后，输出层根据隐藏层输出以及学习过程中的权重调整，计算并输出最终的控制信号。

RBF 网络的核心是数据集，该数据集由训练数据和测试数据组成。

在训练过程中，通过输入训练数据来调整网络参数和权重。

训练过程分为两个阶段，第一阶段是特征选择，该阶段通过数据挖掘技术来确定最优的基函数数量和位置，并为每个基函数分配一个合适的权重。

第二阶段是更新参数，该阶段通过反向传播算法来更新网络参数和权重，以优化网络的性能和控制精度。

RBF 网络控制的优点在于其对非线性控制问题具有优秀的适应性和泛化性能。

另外，RBF 网络还具有强大的学习和自适应调整能力，能够学习并预测系统的动态行为，同时还可以自动调整参数以提高控制性能。

此外，RBF 网络控制器的结构简单、易于实现，并且具有快速的响应速度，可以满足实时控制应用的要求。

然而，RBF 网络控制也存在一些局限性。

首先，RBF 网络需要大量的训练数据来确定最佳的基函数数量和位置。

此外，由于网络参数和权重的计算量较大，实时性较低，可能存在延迟等问题。

同时，选择合适的基函数以及与其相应的权重也是一项挑战，这需要在控制问题中进行深入的技术和经验探索。

总体而言，RBF 网络控制是一种非常有效的控制方法，可以在广泛的控制问题中使用。

其结构简单，性能稳定，具有很强的适应性和泛化性能，可以实现实时控制，为复杂工业控制问题的解决提供了一个重要的解决方案。

MATLAB 神经⽹络（7）RBF ⽹络的回归——⾮线性函数回归的实现7.1 案例背景7.1.1 RBF 神经⽹络概述径向基函数是多维空间插值的传统技术，RBF 神经⽹络属于前向神经⽹络类型，⽹络的结构与多层前向⽹络类似，是⼀种三层的前向⽹络。

第⼀层为输⼊层，由信号源结点组成；第⼆层为隐藏层，隐藏层节点数视所描述问题的需要⽽定，隐藏层中神经元的变换函数即径向基函数是对中⼼点径向对称且衰减的⾮负⾮线性函数，该函数是局部响应函数，⽽以前的前向⽹络变换函数都是全局响应的函数；第三层为输出层，它对输⼊模式作出响应。

RBF ⽹络的基本思想是：⽤RBF 作为隐单元的“基”构成隐藏层空间，隐含层对输⼊⽮量进⾏变换，将低维的模式输⼊数据变换到⾼维空间内，使得在低维空间内的线性不可分的问题在⾼维空间内线性可分。

RBF 神经⽹络结构简单、训练简洁⽽且学习收敛速度快，能够逼近任意⾮线性函数，因此已被⼴泛应⽤于时间序列分析、模式识别、⾮线性控制和图形处理等领域。

7.1.2 RBF 神经⽹络结构模型径向基神经⽹络的节点激活函数采⽤径向基函数，通常定义为空间任⼀点到某⼀中⼼之间的欧式距离的单调函数。

径向基神经⽹络的激活函数是以输⼊向量和权值向盘之间的距离||dist ||作为⾃变量的。

径向基神经⽹络的激活函数的⼀般表达式为R (||dist ||)=e −||dist ||2随着权值和输⼊向量之间距离的减少，⽹络输出是递增的，当输⼊向量和权值向量⼀致时，神经元输出为1。

图中的b 为阔值，⽤于调整神经元的灵敏度。

利⽤径向基神经元和线性神经元可以建⽴⼴义回归神经⽹络，此种神经⽹络适⽤于函数逼近⽅⾯的应⽤；径向基神经元和竞争神经元可以建⽴概率神经⽹络，此种神经⽹络适⽤于解决分类问题。

RBF 神经⽹络中，输⼊层仅仅起到传输信号的作⽤，与前⾯所讲述的神经⽹络相⽐较，输⼊层和隐含层之间可以看作连接权值为1的连接，输出层和隐含层所完成的任务是不同的，因⽽它们的学习策略也不相同。

RBF神经网络概述1 RBF神经网络的基本原理2 RBF神经网络的网络结构3 RBF神经网络的优点1 RBF神经网络的基本原理人工神经网络以其独特的信息处理能力在许多领域得到了成功的应用。

它不仅具有强大的非线性映射能力，而且具有自适应、自学习和容错性等，能够从大量的历史数据中进行聚类和学习，进而找到某些行为变化的规律。

径向基函数(RBF)神经网络是一种新颖有效的前馈式神经网络，它具有最佳逼近和全局最优的性能，同时训练方法快速易行，不存在局部最优问题，这些优点使得RBF网络在非线性时间序列预测中得到了广泛的应用。

1985年，Powell提出了多变量插值的径向基函数(Radial-Basis Function, RBF)方法。

1988年，Broomhead和Lowe首先将RBF应用于神经网络设计，构成了径向基函数神经网络，即RBF神经网络。

用径向基函数(RBF)作为隐单元的“基”构成隐含层空间，对输入矢量进行一次变换，将低维的模式输入数据变换到高维空间内，通过对隐单元输出的加权求和得到输出，这就是RBF网络的基本思想。

2 RBF神经网络的网络结构RBF网络是一种三层前向网络：第一层为输入层，由信号源节点组成。

第二层为隐含层，隐单元的变换函数是一种局部分布的非负非线性函数，他对中心点径向对称且衰减。

隐含层的单元数由所描述问题的需要确定。

第三层为输出层，网络的输出是隐单元输出的线性加权。

RBF网络的输入空间到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间的变换是线性。

不失一般性，假定输出层只有一个隐单元，令网络的训练样本对为，其中为训练样本的输入，为训练样本的期望输出，对应的实际输出为;基函数为第个隐单元的输出为基函数的中心;为第个隐单元与输出单元之间的权值。

单输出的RBF网络的拓扑图如图1所示:图1RBF网络的拓扑图当网络输入训练样本时，网络的实际输出为:(1)通常使用的RBF有：高斯函数、多二次函数(multiquadric function)、逆多二次函数、薄板样条函数等。

径向基函数（RBF）神经⽹络RBF⽹络能够逼近任意的⾮线性函数，可以处理系统内的难以解析的规律性，具有良好的泛化能⼒，并有很快的学习收敛速度，已成功应⽤于⾮线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。

简单说明⼀下为什么RBF⽹络学习收敛得⽐较快。

当⽹络的⼀个或多个可调参数（权值或阈值）对任何⼀个输出都有影响时，这样的⽹络称为全局逼近⽹络。

由于对于每次输⼊，⽹络上的每⼀个权值都要调整，从⽽导致全局逼近⽹络的学习速度很慢。

BP⽹络就是⼀个典型的例⼦。

如果对于输⼊空间的某个局部区域只有少数⼏个连接权值影响输出，则该⽹络称为局部逼近⽹络。

常见的局部逼近⽹络有RBF⽹络、⼩脑模型（CMAC）⽹络、B样条⽹络等。

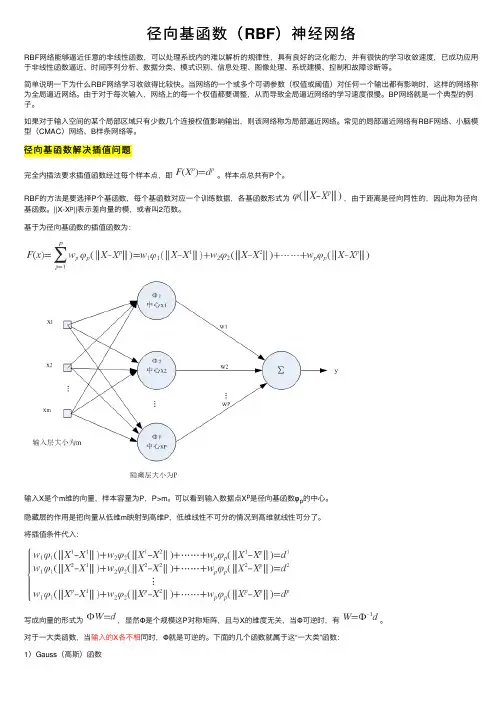
径向基函数解决插值问题完全内插法要求插值函数经过每个样本点，即。

样本点总共有P个。

RBF的⽅法是要选择P个基函数，每个基函数对应⼀个训练数据，各基函数形式为，由于距离是径向同性的，因此称为径向基函数。

||X-X p||表⽰差向量的模，或者叫2范数。

基于为径向基函数的插值函数为：输⼊X是个m维的向量，样本容量为P，P>m。

可以看到输⼊数据点X p是径向基函数φp的中⼼。

隐藏层的作⽤是把向量从低维m映射到⾼维P，低维线性不可分的情况到⾼维就线性可分了。

将插值条件代⼊：写成向量的形式为，显然Φ是个规模这P对称矩阵，且与X的维度⽆关，当Φ可逆时，有。

对于⼀⼤类函数，当输⼊的X各不相同时，Φ就是可逆的。

下⾯的⼏个函数就属于这“⼀⼤类”函数：1）Gauss（⾼斯）函数2）Reflected Sigmoidal（反常S型）函数3）Inverse multiquadrics（拟多⼆次）函数σ称为径向基函数的扩展常数，它反应了函数图像的宽度，σ越⼩，宽度越窄，函数越具有选择性。

完全内插存在⼀些问题：1）插值曲⾯必须经过所有样本点，当样本中包含噪声时，神经⽹络将拟合出⼀个错误的曲⾯，从⽽使泛化能⼒下降。

RBF（径向基）神经⽹络 只要模型是⼀层⼀层的，并使⽤AD/BP算法，就能称作 BP神经⽹络。

RBF 神经⽹络是其中⼀个特例。

本⽂主要包括以下内容：什么是径向基函数RBF神经⽹络RBF神经⽹络的学习问题RBF神经⽹络与BP神经⽹络的区别RBF神经⽹络与SVM的区别为什么⾼斯核函数就是映射到⾼维区间前馈⽹络、递归⽹络和反馈⽹络完全内插法⼀、什么是径向基函数 1985年，Powell提出了多变量插值的径向基函数（RBF）⽅法。

径向基函数是⼀个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意⼀点c的距离，c点称为中⼼点，也就是Φ（x，c）=Φ(‖x-c‖)。

任意⼀个满⾜Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数，标准的⼀般使⽤欧⽒距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。

最常⽤的径向基函数是⾼斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中x_c为核函数中⼼,σ为函数的宽度参数 , 控制了函数的径向作⽤范围。

⼆、RBF神经⽹络 RBF神将⽹络是⼀种三层神经⽹络，其包括输⼊层、隐层、输出层。

从输⼊空间到隐层空间的变换是⾮线性的，⽽从隐层空间到输出层空间变换是线性的。

流图如下： RBF⽹络的基本思想是：⽤RBF作为隐单元的“基”构成隐含层空间，这样就可以将输⼊⽮量直接映射到隐空间，⽽不需要通过权连接。

当RBF的中⼼点确定以后，这种映射关系也就确定了。

⽽隐含层空间到输出空间的映射是线性的，即⽹络的输出是隐单元输出的线性加权和，此处的权即为⽹络可调参数。

其中，隐含层的作⽤是把向量从低维度的p映射到⾼维度的h，这样低维度线性不可分的情况到⾼维度就可以变得线性可分了，主要就是核函数的思想。

这样，⽹络由输⼊到输出的映射是⾮线性的，⽽⽹络输出对可调参数⽽⾔却⼜是线性的。

⽹络的权就可由线性⽅程组直接解出，从⽽⼤⼤加快学习速度并避免局部极⼩问题。

径向基（RBF）神经⽹络python实现 1from numpy import array, append, vstack, transpose, reshape, \2 dot, true_divide, mean, exp, sqrt, log, \3 loadtxt, savetxt, zeros, frombuffer4from numpy.linalg import norm, lstsq5from multiprocessing import Process, Array6from random import sample7from time import time8from sys import stdout9from ctypes import c_double10from h5py import File111213def metrics(a, b):14return norm(a - b)151617def gaussian (x, mu, sigma):18return exp(- metrics(mu, x)**2 / (2 * sigma**2))192021def multiQuadric (x, mu, sigma):22return pow(metrics(mu,x)**2 + sigma**2, 0.5)232425def invMultiQuadric (x, mu, sigma):26return pow(metrics(mu,x)**2 + sigma**2, -0.5)272829def plateSpine (x,mu):30 r = metrics(mu,x)31return (r**2) * log(r)323334class Rbf:35def__init__(self, prefix = 'rbf', workers = 4, extra_neurons = 0, from_files = None):36 self.prefix = prefix37 self.workers = workers38 self.extra_neurons = extra_neurons3940# Import partial model41if from_files is not None:42 w_handle = self.w_handle = File(from_files['w'], 'r')43 mu_handle = self.mu_handle = File(from_files['mu'], 'r')44 sigma_handle = self.sigma_handle = File(from_files['sigma'], 'r')4546 self.w = w_handle['w']47 self.mu = mu_handle['mu']48 self.sigmas = sigma_handle['sigmas']4950 self.neurons = self.sigmas.shape[0]5152def _calculate_error(self, y):53 self.error = mean(abs(self.os - y))54 self.relative_error = true_divide(self.error, mean(y))5556def _generate_mu(self, x):57 n = self.n58 extra_neurons = self.extra_neurons5960# TODO: Make reusable61 mu_clusters = loadtxt('clusters100.txt', delimiter='\t')6263 mu_indices = sample(range(n), extra_neurons)64 mu_new = x[mu_indices, :]65 mu = vstack((mu_clusters, mu_new))6667return mu6869def _calculate_sigmas(self):70 neurons = self.neurons71 mu = self.mu7273 sigmas = zeros((neurons, ))74for i in xrange(neurons):75 dists = [0 for _ in xrange(neurons)]76for j in xrange(neurons):77if i != j:78 dists[j] = metrics(mu[i], mu[j])79 sigmas[i] = mean(dists)* 280# max(dists) / sqrt(neurons * 2))81return sigmas8283def _calculate_phi(self, x):84 C = self.workers85 neurons = self.neurons86 mu = self.mu87 sigmas = self.sigmas88 phi = self.phi = None89 n = self.n909192def heavy_lifting(c, phi):93 s = jobs[c][1] - jobs[c][0]94for k, i in enumerate(xrange(jobs[c][0], jobs[c][1])):95for j in xrange(neurons):96# phi[i, j] = metrics(x[i,:], mu[j])**3)97# phi[i, j] = plateSpine(x[i,:], mu[j]))98# phi[i, j] = invMultiQuadric(x[i,:], mu[j], sigmas[j]))99 phi[i, j] = multiQuadric(x[i,:], mu[j], sigmas[j])100# phi[i, j] = gaussian(x[i,:], mu[j], sigmas[j]))101if k % 1000 == 0:102 percent = true_divide(k, s)*100103print(c, ': {:2.2f}%'.format(percent))104print(c, ': Done')105106# distributing the work between 4 workers107 shared_array = Array(c_double, n * neurons)108 phi = frombuffer(shared_array.get_obj())109 phi = phi.reshape((n, neurons))110111 jobs = []112 workers = []113114 p = n / C115 m = n % C116for c in range(C):117 jobs.append((c*p, (c+1)*p + (m if c == C-1 else 0)))118 worker = Process(target = heavy_lifting, args = (c, phi))119 workers.append(worker)120 worker.start()121122for worker in workers:123 worker.join()124125return phi126127def _do_algebra(self, y):128 phi = self.phi129130 w = lstsq(phi, y)[0]131 os = dot(w, transpose(phi))132return w, os133# Saving to HDF5134 os_h5 = os_handle.create_dataset('os', data = os)135136def train(self, x, y):137 self.n = x.shape[0]138139## Initialize HDF5 caches140 prefix = self.prefix141 postfix = str(self.n) + '-' + str(self.extra_neurons) + '.hdf5'142 name_template = prefix + '-{}-' + postfix143 phi_handle = self.phi_handle = File(name_template.format('phi'), 'w')144 os_handle = self.w_handle = File(name_template.format('os'), 'w')145 w_handle = self.w_handle = File(name_template.format('w'), 'w')146 mu_handle = self.mu_handle = File(name_template.format('mu'), 'w')147 sigma_handle = self.sigma_handle = File(name_template.format('sigma'), 'w') 148149## Mu generation150 mu = self.mu = self._generate_mu(x)151 self.neurons = mu.shape[0]152print('({} neurons)'.format(self.neurons))153# Save to HDF5154 mu_h5 = mu_handle.create_dataset('mu', data = mu)155156## Sigma calculation157print('Calculating Sigma...')158 sigmas = self.sigmas = self._calculate_sigmas()159# Save to HDF5160 sigmas_h5 = sigma_handle.create_dataset('sigmas', data = sigmas)161print('Done')162163## Phi calculation164print('Calculating Phi...')165 phi = self.phi = self._calculate_phi(x)166print('Done')167# Saving to HDF5168print('Serializing...')169 phi_h5 = phi_handle.create_dataset('phi', data = phi)170del phi171 self.phi = phi_h5172print('Done')173174## Algebra175print('Doing final algebra...')176 w, os = self.w, _ = self._do_algebra(y)177# Saving to HDF5178 w_h5 = w_handle.create_dataset('w', data = w)179 os_h5 = os_handle.create_dataset('os', data = os)180181## Calculate error182 self._calculate_error(y)183print('Done')184185def predict(self, test_data):186 mu = self.mu = self.mu.value187 sigmas = self.sigmas = self.sigmas.value188 w = self.w = self.w.value189190print('Calculating phi for test data...')191 phi = self._calculate_phi(test_data)192 os = dot(w, transpose(phi))193 savetxt('iok3834.txt', os, delimiter='\n')194return os195196 @property197def summary(self):198return'\n'.join( \199 ['-----------------',200'Training set size: {}'.format(self.n),201'Hidden layer size: {}'.format(self.neurons),202'-----------------',203'Absolute error : {:02.2f}'.format(self.error),204'Relative error : {:02.2f}%'.format(self.relative_error * 100)]) 205206207def predict(test_data):208 mu = File('rbf-mu-212243-2400.hdf5', 'r')['mu'].value209 sigmas = File('rbf-sigma-212243-2400.hdf5', 'r')['sigmas'].value 210 w = File('rbf-w-212243-2400.hdf5', 'r')['w'].value211212 n = test_data.shape[0]213 neur = mu.shape[0]214215 mu = transpose(mu)216 mu.reshape((n, neur))217218 phi = zeros((n, neur))219for i in range(n):220for j in range(neur):221 phi[i, j] = multiQuadric(test_data[i,:], mu[j], sigmas[j])222223 os = dot(w, transpose(phi))224 savetxt('iok3834.txt', os, delimiter='\n')225return os。

RBF网络原理及应用RBF（Radial Basis Function）网络是一种基于radial基函数的前向神经网络，它是一种具有局部适应性和全局逼近能力的非线性模型。

其原理和应用如下：1.原理：RBF网络由输入层、隐藏层和输出层组成。

隐藏层的每一个神经元使用具有特定中心和宽度参数的radial基函数作为激活函数。

输入信号通过输入层传递到隐藏层，隐藏层的神经元计算输入信号与其对应的中心的距离，并将距离作为输入信号传递给输出层。

输出层的神经元根据权重和输入信号计算输出值。

整个网络通过不断调整隐藏层的参数和输出层的权重来进行训练，以实现模型的优化。

2.应用：-回归分析：RBF网络可以用于函数逼近问题，通过学习输入值与输出值之间的函数关系，实现对未知输入的预测。

例如，可以用RBF网络建模销售数据，根据历史数据预测未来销售情况。

-控制系统：RBF网络可以用于建立非线性的控制模型。

通过学习输入与输出之间的非线性映射，可以根据输入信号来控制输出信号，实现控制系统对复杂非线性过程的控制。

-时间序列预测：RBF网络可以用于预测时间序列数据，如股票价格、气温变化等。

通过学习历史数据的模式，可以对未来的趋势和变化进行预测。

3.RBF网络的优势：-具有局部适应性：每个隐藏神经元只对输入空间的一部分进行响应，具有局部适应性，更适合处理复杂非线性问题。

-具有全局逼近能力：通过增加足够多的隐藏神经元，RBF网络可以以任意精度逼近任何连续函数，具有较强的全局逼近能力。

-训练简单：RBF网络的训练相对简单，可以使用基于梯度下降法的误差反向传播算法进行训练。

-鲁棒性高：RBF网络对噪声和输入变化具有较好的鲁棒性，在一定程度上可以处理输入数据中的不确定性。

总结起来，RBF网络是一种基于radial基函数的前向神经网络，具有局部适应性、全局逼近能力以及鲁棒性高等优点。

它在模式识别、回归分析、控制系统、时间序列预测等领域有广泛应用，并且可以通过简单的训练方法进行优化。

径向基神经网络的介绍及其案例实现径向基（RBF）神经网络是一种常用的人工神经网络模型，它以径向基函数作为激活函数来进行模式分类和回归任务。

该网络在模式识别、函数逼近、数据挖掘等领域都具有良好的性能，并且具有较好的泛化能力。

引言：径向基（RBF）神经网络最早是由Broomhead和Lowe于1988年引入的，它是一种前馈式神经网络。

RBF神经网络的主要思想是以输入向量与一组高斯函数的基函数作为输入层，然后再通过隐藏层进行特征映射，最后通过输出层进行模式分类或回归。

1.RBF神经网络的结构：RBF神经网络包括输入层、隐藏层和输出层三层。

输入层负责接收输入向量，隐藏层负责特征映射，输出层负责输出结果。

输入层：输入层接收具有所要分类或回归的特征的数据，通常使用欧几里德距离计算输入层的神经元与输入向量之间的距离。

隐藏层：隐藏层是RBF神经网络的核心部分，它通过一组径向基函数来进行特征映射。

隐藏层的神经元数量通常和训练样本数量相同，每个神经元负责响应一个数据样本。

输出层：输出层根据隐藏层的输出结果进行模式分类或回归预测，并输出网络的最终结果。

2.RBF神经网络的训练：RBF神经网络的训练主要包括两个步骤：聚类和权值调整。

聚类：首先通过K-means等聚类算法将训练样本划分为若干个类别，每个类别对应一个隐藏层神经元。

这样可以将输入空间划分为若干个区域，每个区域中只有一个样本。

权值调整：通过最小化残差误差或最小化目标函数来优化隐藏层和输出层的权值。

常用的优化算法有最小二乘法、梯度下降法等。

3.RBF神经网络的案例实现：案例1：手写数字识别案例2：股票市场预测RBF神经网络也可以应用于股票市场的预测。

该案例中，RBF神经网络接收一组与股票相关的指标作为输入，通过隐藏层的特征映射将指标转化为更有意义的特征表示，最后通过输出层进行未来股价的回归预测。

该系统的训练样本为历史股票数据以及与之对应的未来股价。

结论：径向基（RBF）神经网络是一种应用广泛且效果良好的人工神经网络模型。

径向基函数神经网络模型及其在预测系统中的应用概述：径向基函数神经网络(Radial Basis Function Neural Network, RBFNN)是一种基于神经网络的非线性模型，具有广泛的应用领域。

在预测系统中，RBFNN能够准确预测未知输入与输出之间的关系，从而为预测问题的解决提供了有效的方法。

一、径向基函数神经网络模型的基本原理1.1 RBFNN的结构径向基函数神经网络由输入层、隐含层和输出层构成。

输入层接受原始数据，隐含层通过径向基函数对输入数据进行转换，输出层将转换后的数据映射到期望的输出。

1.2 径向基函数的选择径向基函数的选择对RBFNN的性能有重要影响。

常用的径向基函数有高斯函数、多项式函数和细分函数等。

根据问题的需求和特点选择合适的径向基函数，以提高模型的预测能力。

1.3 模型的训练与优化通过使用已知输入与输出的训练数据，结合误差反向传播算法，可以对RBFNN的参数进行学习和优化。

训练的目标是使得模型的输出与实际输出之间的误差最小化，从而提高预测的准确性。

二、径向基函数神经网络模型在预测系统中的应用2.1 股票市场预测股票市场价格的预测一直是金融领域的研究热点。

RBFNN通过学习历史价格与因素的关系，能够预测未来的股票价格走势。

通过准确的预测，投资者可以做出更明智的决策，提高投资回报率。

2.2 污染物浓度预测环境污染是当今社会面临的严重问题之一。

RBFNN可以利用区域内的环境数据，如气象数据、监测数据等，预测出某个时刻某地区的污染物浓度。

这有助于预警系统的建立，提前采取措施避免污染的扩散。

2.3 交通流量预测交通流量的预测在城市交通管理中具有重要意义。

通过收集历史交通流量和相关影响因素的数据，RBFNN能够准确预测未来某个时间段某条道路的交通流量。

这有助于交通规划和拥堵疏导的决策。

2.4 预测市场需求在制造业和零售业等领域，准确预测市场的需求对企业决策具有重要影响。

RBFNN可以通过学习历史销售数据和市场因素的关系，预测未来某段时间内产品的需求量。