径向基函数

径向基函数核
径向基函数核是一种常用的核函数，可以用于支持向量机等机器学习算法中。

其原理是将样本数据通过一个基函数映射到高维空间中，然后在高维空间中进行分类或回归等任务。

常用的径向基函数包括高斯核、拉普拉斯核和指数核等。

径向基函数核的优势在于可以处理非线性数据，并且能够保证模型在训练集和测试集上的泛化能力。

在使用径向基函数核时，需要调节参数，例如高斯核的带宽参数和拉普拉斯核的参数等。

通常可以通过交叉验证等方法来选择最优的参数。

- 1 -。

支持向量回归模型,径向基函数1.引言1.1 概述概述支持向量回归模型是一种机器学习算法，用于解决回归问题。

它基于支持向量机（Support Vector Machine，简称SVM）算法发展而来，相比于传统的回归模型，支持向量回归模型具有更强的鲁棒性和泛化能力。

支持向量回归模型的核心思想是通过在训练数据中找到能够最好地拟合数据的超平面，以预测目标变量的值。

与传统的回归模型不同，支持向量回归模型不仅考虑样本点的位置关系，还引入了一个叫做“支持向量”的概念。

支持向量是在模型训练过程中起关键作用的样本点，它们离超平面的距离最近，决定了超平面的位置和形状。

径向基函数是支持向量回归模型中常用的核函数。

径向基函数通过将原始特征映射到高维空间，使得原本线性不可分的数据在新的空间中变得线性可分。

在支持向量回归模型中，径向基函数可以用于构建非线性的映射关系，从而提高模型的预测能力。

本文将围绕支持向量回归模型和径向基函数展开讨论。

首先，我们将详细介绍支持向量回归模型的原理和算法。

然后，我们将探讨径向基函数的概念和应用场景。

接下来，我们将设计实验来验证支持向量回归模型在不同数据集上的表现，并对实验结果进行分析。

最后，我们将对本文进行总结，并展望支持向量回归模型和径向基函数在未来的研究和应用中的潜力。

通过本文的阅读，读者将对支持向量回归模型和径向基函数有更深入的了解，并能够将其应用于实际问题中。

支持向量回归模型的引入和径向基函数的使用为解决回归问题提供了一种新的思路和方法，对于提高预测精度和模型的鲁棒性具有重要意义。

1.2文章结构文章结构部分可以描述整篇文章的组织和章节安排，使读者能够清楚地了解文章的框架和内容概要。

在本篇文章中，主要分为以下几个章节：1. 引言：- 1.1 概述：简要介绍支持向量回归模型和径向基函数的背景和概念。

- 1.2 文章结构：对整篇文章的章节和内容进行概述，让读者知道接下来会涉及到哪些内容。

- 1.3 目的：明确本文的研究目的和动机。

径向基函数(rbf)
径向基函数（radial basis function，简称RBF）是一类基于距
离的函数，在机器学习和统计模型中被广泛使用。

它们的主要方法是
将观测数据空间映射到一个高维特征空间，然后在特征空间中选择一
个合适的核函数，以此来建立模型。

RBF函数主要有三种类型：高斯函数、多次项函数和反函数。

其中高斯函数是RBF中最常见的一种，它可以有效地表示各种距离之间的
相似度，具有很好的非线性特性。

RBF在机器学习领域中的应用非常广泛，尤其是在监督学习算法中。

其中最经典的应用是径向基函数神经网络（radial basis function neural network，简称RBFNN），它是一种三层前向式神经网络，由输入层、隐含层和输出层组成。

RBFNN的隐含层是一组集中的RBF节点，用于对输入数据进行特征提取和非线性映射，而输出层则是一个线性
模型。

RBFS的主要优点是可以处理非线性问题，能够在高维特征空间中
实现有效的决策边界，具有很好的鲁棒性和泛化能力。

此外，RBF也可
以作为一种优秀的插值和拟合方法，用于函数逼近、信号处理和图像处理等领域。

然而，在实际应用中，RBF也存在一些问题。

首先，RBF无法处理参数多样性的问题，需要通过选择合适的核函数和调整参数来解决。

其次，RBF的计算复杂度较高，需要对大量数据进行处理，会导致处理速度慢。

此外，RBF也容易陷入局部极小值和过拟合等问题，需要通过一系列的优化方法来解决。

在未来的研究中，RBF可以通过结合其他机器学习算法和深度学习技术来进一步优化和完善，以实现更高效和准确的模型训练和预测。

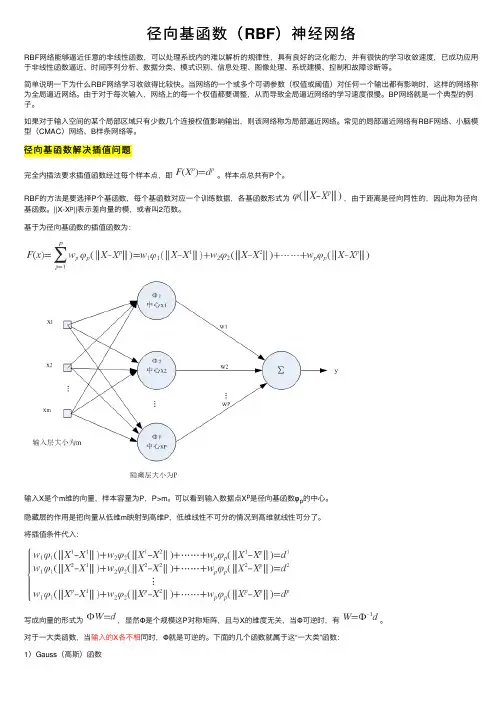
径向基函数（RBF）神经⽹络RBF⽹络能够逼近任意的⾮线性函数，可以处理系统内的难以解析的规律性，具有良好的泛化能⼒，并有很快的学习收敛速度，已成功应⽤于⾮线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。

简单说明⼀下为什么RBF⽹络学习收敛得⽐较快。

当⽹络的⼀个或多个可调参数（权值或阈值）对任何⼀个输出都有影响时，这样的⽹络称为全局逼近⽹络。

由于对于每次输⼊，⽹络上的每⼀个权值都要调整，从⽽导致全局逼近⽹络的学习速度很慢。

BP⽹络就是⼀个典型的例⼦。

如果对于输⼊空间的某个局部区域只有少数⼏个连接权值影响输出，则该⽹络称为局部逼近⽹络。

常见的局部逼近⽹络有RBF⽹络、⼩脑模型（CMAC）⽹络、B样条⽹络等。

径向基函数解决插值问题完全内插法要求插值函数经过每个样本点，即。

样本点总共有P个。

RBF的⽅法是要选择P个基函数，每个基函数对应⼀个训练数据，各基函数形式为，由于距离是径向同性的，因此称为径向基函数。

||X-X p||表⽰差向量的模，或者叫2范数。

基于为径向基函数的插值函数为：输⼊X是个m维的向量，样本容量为P，P>m。

可以看到输⼊数据点X p是径向基函数φp的中⼼。

隐藏层的作⽤是把向量从低维m映射到⾼维P，低维线性不可分的情况到⾼维就线性可分了。

将插值条件代⼊：写成向量的形式为，显然Φ是个规模这P对称矩阵，且与X的维度⽆关，当Φ可逆时，有。

对于⼀⼤类函数，当输⼊的X各不相同时，Φ就是可逆的。

下⾯的⼏个函数就属于这“⼀⼤类”函数：1）Gauss（⾼斯）函数2）Reflected Sigmoidal（反常S型）函数3）Inverse multiquadrics（拟多⼆次）函数σ称为径向基函数的扩展常数，它反应了函数图像的宽度，σ越⼩，宽度越窄，函数越具有选择性。

完全内插存在⼀些问题：1）插值曲⾯必须经过所有样本点，当样本中包含噪声时，神经⽹络将拟合出⼀个错误的曲⾯，从⽽使泛化能⼒下降。

径向基函数回归应用较多的径向基函数有： Odds、 Accumulated standard deviation、 eLeave、 Accumulated t-test、 Avogadro等。

其中Odds算法应用最广，为文献[2]——[5]所采用，本文将对Odds进行改进，采用最小二乘法（ MINOR）构建自由度矩阵，并利用经验证明其有效性和可靠性。

本文采用城市规划作为应用实例，实证分析了MINOR回归模型的拟合程度及可靠性。

对于多个城市进行多种不同类型规划的仿真实验，对比分析了改进后的MINOR回归模型。

实验结果表明，改进后的MINOR 模型可以克服Odds算法容易受到多重共线性和异方差影响的缺陷，提高了解释效果和拟合程度，是一种值得推广应用的径向基函数算法。

径向基回归能够在不同的分布上有着优良的准确性，在建立标准化的尺度参数或采用非尺度参数描述空间结构时更显示出它的优越性。

径向基回归具有许多优点：能将数据与空间结构联系起来；在测定空间结构中的每一维时都能很好地逼近待估计的非线性变量的统计特征；对初值敏感性不大，尤其适用于离散点数据的拟合；这种统计方法有能力估计整个规划区域内的平均值，而不必估计每一处的标准偏差。

因此，对规划数据进行解释是十分有效的。

可以用来估计位置偏好和规划密度函数。

本文首先利用对成本回归分析法对规划区域进行估计，并依此建立非尺度距离，最后建立改进后的非尺度距离和权重，并引入可观察标度变量，根据实际数据的仿真实验，证明了改进后的非尺度距离和权重在多种不同分布上的有效性和可靠性。

为了充分利用计算机资源，本文引入最小二乘法，并对改进后的非尺度距离和权重进行多元回归分析。

实验结果表明，多元回归分析的结果基本满足了多项式要求，从而充分说明了本文提出的径向基函数回归方法的有效性。

为了充分发挥本文提出的新的非尺度距离在距离回归中的作用，本文运用结构矩阵对改进后的非尺度距离进行了多元回归分析，进一步增强了径向基函数回归模型在处理分布上存在异方差或多重共线性问题时的优势。

径向基函数径向基函数是一种常用的函数类型，通常用于数学计算、信号处理、图像处理及机器学习等领域。

它们的主要特点是具有局部特性和无限可微性，因此能够适应多种复杂数据的建模需求。

下面，我们来逐步阐述径向基函数的相关概念和应用。

第一步：径向基函数的定义径向基函数（Radial Basis Function，简称RBF）是以某一点为中心，以此点到其他所有数据点的距离为核心的一类函数。

常见的径向基函数有高斯径向基函数、多孔径向基函数等。

高斯径向基函数的公式为：φ(r) = e^(-r^2/2σ^2)其中r为点到中心点的距离。

第二步：径向基函数的应用径向基函数在多个领域有着广泛的应用。

以下是其中几个领域的应用举例：1. 信号处理：在信号处理中，径向基函数可以用于特征提取和去噪处理。

例如，将信号分解为多个径向基函数的线性组合，可以提取出信号中的有用信息。

2. 图像处理：在图像处理中，径向基函数可以用于图像配准、图像分割和图像重建等方面。

例如，将图像中的每个像素点看作一个数据点，使用多个径向基函数将图像进行拟合，可以得到更清晰的图像信息。

3. 机器学习：在机器学习中，径向基函数可以用于分类、聚类和回归等方面。

例如，在支持向量机中，径向基函数可以用于定义支持向量的核函数，以实现非线性分类。

第三步：径向基函数的优点与其他函数类型相比，径向基函数具有以下优点：1. 局部特性：径向基函数在计算权重时只使用局部数据点，可以适应非线性和复杂的数据分布。

2. 无限可微性：径向基函数是无限可微的函数类型，可以在数据中心点处获得连续可导的导函数，因此可大幅降低过拟合的可能性。

3. 灵活性：径向基函数可以使用不同的核参数，如高斯核、多孔核等，以适应不同数据类型和建模需求。

总之，径向基函数在多个领域有着广泛的应用，并且具有许多优点。

不过，在使用径向基函数时也需要注意其参数的选择和模型调参，以获得更好的建模效果。

高斯径向基高斯径向基函数（Gaussian radial basis function，简称RBF）是一种非线性函数，广泛应用于模式识别、数据挖掘、函数逼近、非线性优化等领域。

它的数学形式为：$$\varphi(\textbf{x}) =\exp\left(-\frac{\|\textbf{x}-\textbf{c}\|^2}{2\sigma^2}\right)$$其中，$\textbf{x}$是输入向量，$\textbf{c}$是中心向量，$\sigma$是控制函数值下降速度的参数。

RBF函数的值随着$\textbf{x}$与$\textbf{c}$之间的距离逐渐增大而逐渐减小，呈现出高斯分布的形态。

RBF函数可以看作是一组基函数，通过构造不同的中心向量和参数值，可以得到不同的基函数。

对于一个输入向量$\textbf{x}$，其可以表示为一组RBF基函数的线性组合：$$y(\textbf{x}) = \sum_{i=1}^{M} w_i\varphi(\textbf{x}-\textbf{c}_i)$$其中，$M$为基函数的个数，$w_i$为基函数的系数。

RBF网络可以看作是由一个隐藏层和一个输出层组成的神经网络。

隐藏层的单元函数为RBF函数，输出层的单元函数为线性函数。

在训练过程中，通过调整基函数的参数和系数来优化网络的性能。

RBF网络具有以下优点：1. 非线性逼近能力强。

由于RBF函数具有非线性特性，因此可以用来拟合非线性函数。

2. 收敛速度快。

由于RBF网络只有一个隐藏层，因此训练速度较快。

3. 模型具有较好的泛化能力。

由于RBF网络具有较少的参数，因此可以避免过拟合的问题。

4. 构建简单。

相比于其他神经网络，RBF网络的构建过程较为简单，不需要进行复杂的参数调整。

RBF网络的应用范围广泛，主要包括以下几个方面：1. 模式识别。

RBF网络常常用于图像处理、语音识别、手写字符识别等方面。

2. 数据挖掘。

matlab径向基函数Matlab中的径向基函数（RBF）是一种非常有用的数学工具，它在机器学习、数据挖掘和模式识别等领域中被广泛应用。

本文将详细介绍Matlab中径向基函数的定义、原理、实现以及应用。

一、定义径向基函数是一种基于距离的函数，可以将一个点映射到一个高维空间。

在Matlab中，常见的径向基函数包括高斯函数、多项式函数、细胞函数等等。

高斯函数最常用，定义如下：$$\phi_j(x)=exp(-\frac{\parallel x-x_j\parallel^2}{2\sigma_j^2})$$$x$是数据点，$x_j$是高斯函数的中心点，$\sigma_j$是高斯函数的带宽。

根据高斯函数的定义，带宽越小，函数在中心点处的值就越大，函数在中心点附近的值也会更大，但是随着距离的增加，函数值会急剧下降；带宽越大，函数在中心点处的值就越小，函数在中心点附近的值也会更小，但是随着距离的增加，函数值会缓慢下降。

二、原理径向基函数的原理是基于距离的概念，即同类样本之间的距离相对较小，而不同类样本之间的距离相对较大。

在分类或聚类任务中，将样本点映射到高维空间，利用高斯函数或其他径向基函数完成对样本点的聚类或分类。

三、实现在Matlab中，实现径向基函数可以采用以下步骤：1.读取数据集可以采用读取csv文件、Excel文件等方式获取数据集。

在本文中，我们使用Matlab自带的鸢尾花数据集（Iris）进行演示。

2.选择使用的径向基函数本文采用高斯函数，即：$$\phi_j(x)=exp(-\frac{\parallel x-x_j\parallel^2}{2\sigma_j^2})$$3.计算高斯函数参数可以采用层次聚类（hierarchical clustering）、K-means聚类等方法，计算高斯函数的中心点和带宽。

4.计算径向基函数矩阵根据高斯函数的定义，可以根据数据集、高斯函数中心点和带宽计算径向基函数矩阵，具体方法如下：```matlabfunction Gaussian_RBF_Matrix =Gaussian_RBF(dataPoints,numberOfCenters,Gaussian_RBF_Radii)randomIndexs = randperm(size(dataPoints,1));dataPoints = dataPoints(randomIndexs,:); %shuffle datapointscenters = datasample(dataPoints,numberOfCenters); % selects numberOfCenters number of centers at randomdistances = pdist2(dataPoints,centers);Gaussian_RBF_Matrix = exp(-((distances./Gaussian_RBF_Radii).^2));end````dataPoints`是数据集，`numberOfCenters`是高斯函数中心点的数量，`Gaussian_RBF_Radii`是高斯函数的带宽。

高斯核函数的特点高斯核函数是一种常用的核函数，也被称为径向基函数（Radial Basis Function，简称RBF）。

其主要特点是通过计算样本点与中心点之间的距离来度量样本之间的相似性，从而对样本进行非线性映射，使得在高维空间中的样本更易于线性分割。

在机器学习中，核函数是支持向量机（Support Vector Machine，简称SVM）等算法中的关键组成部分。

这些算法一般基于线性模型，但很多实际问题难以通过线性模型进行有效的分类或回归。

为了解决这个问题，可以通过核函数将样本映射到更高维的特征空间中，在该特征空间中进行线性分割。

高斯核函数是一种常见的核函数，其具有以下特点。

1. 高斯核函数是一个非线性函数，可以将原始数据映射到高维空间中，使得原本线性不可分的样本在新的空间中呈现出线性可分的特性。

这是因为高斯核函数对样本之间的相似性进行度量，相似的样本在新的特征空间中会更加接近，从而更容易被线性分割。

2. 高斯核函数具有一定的平滑性，可以在一定程度上处理噪声和异常值。

由于高斯核函数将样本映射到高维空间中，相似的样本会更加接近，而不相似的样本则会分散开来。

这种分散效果可以一定程度上降低噪声和异常值对分类结果的影响。

3. 高斯核函数的形状呈现出钟形曲线，中心扩展下的描述正是指随着中心点的移动，高斯核函数的曲线也会相应扩展或压缩。

当中心点接近某个样本时，该样本对分类结果的影响会更大；而当中心点远离样本时，该样本对分类结果的影响会减小。

这种中心扩展的特性使得高斯核函数能够自适应地调整对不同样本的关注程度，更好地拟合数据。

4. 高斯核函数具有参数调节的灵活性。

高斯核函数的形状由一个参数σ决定，该参数控制了高斯曲线的宽度。

当σ较小时，高斯核函数的曲线较窄，对样本的影响范围较小；当σ较大时，高斯核函数的曲线较宽，对样本的影响范围较大。

通过调节σ的取值，可以灵活地控制高斯核函数的形状，以适应不同的数据分布和分类需求。

高斯径向基函数rbf一、引言高斯径向基函数（Radial Basis Function，简称RBF）是一种常用的非线性函数，广泛应用于机器学习、数据挖掘等领域。

本文将详细介绍高斯径向基函数的定义、特点、应用及其实现过程。

二、高斯径向基函数的定义高斯径向基函数是一种以距离为自变量的非线性函数，其公式如下：$$\phi(\mathbf{x},\mathbf{c})=e^{-\gamma \|\mathbf{x}-\mathbf{c}\|^2}$$其中，$\mathbf{x}$表示输入样本点，$\mathbf{c}$表示中心点或参考点，$\gamma$为高斯核函数的带宽参数。

当$\gamma$越大时，高斯核函数的作用范围越小；当$\gamma$越小时，高斯核函数的作用范围越大。

三、高斯径向基函数的特点1. 非线性：高斯径向基函数是一种非线性函数，在处理非线性问题时具有很好的表达能力。

2. 局部化：高斯径向基函数在中心点附近有较大的值，而在远离中心点时逐渐减小至零。

因此，在处理局部问题时具有很好的适应能力。

3. 具有平滑性：高斯径向基函数具有平滑性，可以减少噪声的影响。

4. 可解释性差：高斯径向基函数的参数难以解释，因此在实际应用中需要通过交叉验证等方法来确定参数值。

四、高斯径向基函数的应用1. 支持向量机（Support Vector Machine，简称SVM）中的核函数：SVM是一种常用的分类器，在训练过程中需要选择合适的核函数。

高斯径向基函数是常用的核函数之一。

2. 数据聚类：高斯径向基函数可以用于数据聚类，通过将数据点映射到高维空间中，使得相似的数据点在空间中距离较近。

3. 函数拟合：高斯径向基函数可以用于非线性函数拟合，通过将输入变量映射到高维空间中，使得模型能够更好地适应非线性问题。

五、高斯径向基函数的实现过程以下是一个简单的Python实现示例：```pythonimport numpy as npdef rbf_kernel(x, c, gamma):"""高斯径向基函数:param x: 输入样本点:param c: 中心点或参考点:param gamma: 高斯核带宽参数:return: 核矩阵"""n_samples = x.shape[0]n_centers = c.shape[0]kernel_matrix = np.zeros((n_samples, n_centers))for i in range(n_samples):for j in range(n_centers):kernel_matrix[i, j] = np.exp(-gamma * np.linalg.norm(x[i]- c[j]) ** 2)return kernel_matrix```该函数接受三个参数：输入样本点$x$、中心点或参考点$c$、高斯核带宽参数$\gamma$。

径向基函数网络算法在分类问题中的应用随着计算机技术的不断发展和深入，人工智能技术越来越受到人们的重视和关注。

其中，机器学习算法作为人工智能的一个重要分支，其应用广泛。

在很多分类问题中，径向基函数网络算法作为一种常用的机器学习算法，其性能表现优异，得到了广泛的应用。

一、径向基函数网络算法简介径向基函数网络算法（Radial Basis Function Network，简称RBFN）是一种人工神经网络算法。

它的核心思想是将高维空间中的数据映射到低维空间中，通过对映射后的数据进行分类来解决分类问题。

RBFN算法的基本结构包括输入层、隐藏层和输出层。

其中，隐藏层是一个非线性的映射函数，它利用径向基函数将输入数据从高维转化到低维，同时隐藏层的神经元数量也是一个关键参数，它的大小会直接影响分类器的性能。

当数据映射到低维空间后，就可以使用输出层的线性分类器来对数据进行分类。

二、径向基函数网络算法的优点1.非线性逼近能力强径向基函数网络算法通过使用非线性映射函数实现了非线性变换，使得它具有很好的逼近复杂函数的能力。

因此，它在解决高维复杂问题方面比其他线性分类器具有更好的性能。

2.分类速度快与其他机器学习算法相比，径向基函数网络算法在分类时的速度较快。

这是因为它在训练时能够快速地找到合适的分类器，从而大大缩短了分类时间。

3.容易并行化处理随着计算机硬件和软件的不断发展，多核处理器的应用越来越普遍。

对于很多大规模数据处理的应用，径向基函数网络算法能够被很好地并行化处理。

这使得它在分布式计算环境下的并行计算有着很好的应用前景。

三、径向基函数网络算法在分类问题中的应用实例1.手写数字识别手写数字识别是图像处理中一个经典的问题，很多机器学习算法都会应用于此类问题中。

在手写数字识别中，数据的特征维度很高，而且数据本身也很复杂。

径向基函数网络算法可以有效地解决这类问题，在很多实验中表现出了良好的分类效果。

2.互联网安全领域在互联网安全领域，径向基函数网络算法被广泛用于恶意代码检测、垃圾邮件过滤等问题中。

⾼斯核函数（径向基函数）Consider the polynomial kernel of degree 2 defined by, k(x, y) = (x Ty)2 where x, y \in \mathbb{R}^2 and x = (x_1, x_2), y = (y_1, y_2). Thereby, the kernel function can be written as,k(x, y) = (x_1y_1 + x_2y_2)^2= x_{1}2y_{1}2 + 2x_1x_2y_1y_2 + x_{2}2y_{2}2.Now, let us try to come up with a feature map \Phi such that the kernel function can be written as k(x, y) = \Phi(x)^T\Phi(y).Consider the following feature map, \Phi(x) = (x_1^2, \sqrt{2}x_1x_2, x_2^2). Basically, this feature map is mapping the points in\mathbb{R}^2 to points in \mathbb{R}^3. Also, notice that, \Phi(x)^T\Phi(y) = x_12y_12 + 2x_1x_2y_1y_2 + x_22y_22 which is essentially our kernel function.This means that our kernel function is actually computing the inner/dot product of points in \mathbb{R}^3. That is, it is implicitly mapping our points from \mathbb{R}^2 to \mathbb{R}^3.Exercise Question : If your points are in \mathbb{R}^n, a polynomial kernel of degree 2 will map implicitly map it to some vector space F. What is the dimension of this vector space F? Hint: Everything I did above is a clue.Now, coming to RBF.Let us consider the RBF kernel again for points in \mathbb{R}^2. Then, the kernel can be written ask(x, y) = \exp(-|x - y|^2)= \exp(- (x_1 - y_1)^2 - (x_2 - y_2)^2)= \exp(- x_1^2 + 2x_1y_1 - y_1^2 - x_2^2 + 2x_2y_2 - y_2^2)= \exp(-|x|^2) \exp(-|y|^2) \exp(2x^Ty)(assuming gamma = 1). Using the taylor series you can write this as,k(x, y) = \exp(-|x|^2) \exp(-|y|^2) \sum_{n = 0}^{\infty} \frac{(2x Ty)n}{n!}Now, if we were to come up with a feature map \Phi just like we did for the polynomial kernel, you would realize that the feature map would map every point in our \mathbb{R}^2 to an infinite vector. Thus, RBF implicitly maps every point to an infinite dimensional space.。