lingo结果分析及灵敏性分析

[数学软件及应用(Lingo)实验报告范文]lingo实验报告范文心得2022~2022学年第二学期短学期《数学软件及应用(Lingo)》实验报告班级数学131班姓名张金库学号成绩实验名称奶制品的生产与销售方案的制定完成日期：2022年9月3日实验名称：奶制品的生产与销售方案的制定二、实验目的及任务了解并掌握LINGO的使用方法、功能与应用；学会利用LINGO去解决实际中的优化问题。

三、实验内容问题一奶制品加工厂用牛奶生产，两种奶制品，1桶牛奶可以在甲类设备上用12h加工成3kg，或者在乙类设备上用8h加工成4kg。

根据市场的需求，生产,全部能售出，且每千克获利24元，每千克获利16元。

现在现在加工场每天能的到50桶牛奶的供给，每天正式工人总的劳动时间为480h，并且甲类设备每天至多能加工100kg，乙类设备的加工能力没有限制。

为增加工厂的利益，开发奶制品的深加工技术：用2h和3元加工费，可将1kg加工成0.8kg高级奶制品，也可将1kg加工成0.75kg高级奶制品，每千克能获利44元，每千克能获利32元。

试为该工厂制订一个生产销售方案，使每天的净利润最大，并讨论以下问题：假设投资30元可以增加供给1桶牛奶，投资3元可以增加1h的劳动时间，应否做这些投资？假设每天投资150，可以赚回多少？每千克高级奶制品，的获利经常有10%的波动，对制订的生产销售方案有无影响？假设每千克获利下降10%，方案应该变化吗？假设公司已经签订了每天销售10kg的合同并且必须满足，该合同对公司的利润有什么影响？问题分析要求制定生产销售方案，决策变量可以先取作每天用多少桶牛奶生产，，再添上用多少千克加工，用多少千克加工，但是问题要分析，的获利对生产销售方案的影响，所以决策变量取作，，，每天的销售量更为方便。

目标函数是工厂每天的净利润——，，，的获利之和扣除深加工费用。

根本模型决策变量：设每天销售kg，kg，kg，kg，用kg加工，用kg加工。

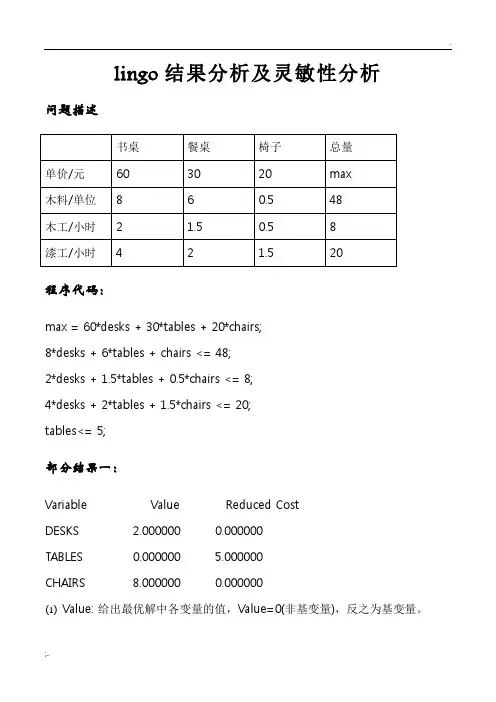
lingo结果分析及灵敏性分析问题描述程序代码：max = 60*desks + 30*tables + 20*chairs;8*desks + 6*tables + chairs <= 48;2*desks + 1.5*tables + 0.5*chairs <= 8;4*desks + 2*tables + 1.5*chairs <= 20;tables<= 5;部分结果一：Variable Value Reduced CostDESKS 2.000000 0.000000TABLES 0.000000 5.000000CHAIRS 8.000000 0.000000⑴Value:给出最优解中各变量的值，Value=0(非基变量)，反之为基变量。

⑵Reduced Cost：表示当非基变量有微小变动时, 目标函数的变化率。

本例中：变量tables 对应的reduced cost 值为5，表示当非基变量tables 的值从0 变为1 时（此时假定其他非基变量保持不变,但为了满足约束条件，基变量显然会发生变化），最优的目标函数值= 280 - 5 = 275。

部分结果二：Row Slack or Surplus Dual Price1 280.0000 1.0000002 24.00000 0.0000003 0.000000 10.000004 0.000000 10.000005 5.000000 0.000000⑴“Slack or Surplus”――松驰变量。

⑵“Dual Price”――对偶价格表示当对应约束有微小变动时, 目标函数的变化率。

若其数值为p，表示对应约束中不等式右端项若增加1个单位，目标函数将增加p个单位（max 型问题）。

⑶如果在最优解处约束正好取等号（紧约束，也称为有效约束或起作用约束），对偶价格值才可能不是0。

本例中：第3、4 行是紧约束，对应的对偶价格值为10，表示当紧约束4) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 20 变为4) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 21 时，目标函数值= 280 +10 = 290。

LINGO结果窗⼝内容解读与灵敏度分析1.结果窗⼝内容解读1. ⽬标函数值:Global option solution found.表⽰求出了全局最优解;Objective value表⽰最优⽬标值，Total solver iretion表⽰求解时共⽤了⼏次迭代2. 决策变量:Value给出最优解中各变量的值3. 变量的判别数：Reduced Cost表⽰最优单纯形表中判别数所在的⾏的变量的系数，表⽰当变量有微⼩变化时，⽬标函数的变化率。

其中基变量的reduced cost值应为零。

对于基变量相应的reduced cost值表⽰这个变量增加⼀个单位时⽬标函数值减少的量(max型问题)4. 紧约束与松约束：slack or Surplus给出松弛或剩余变量的值,其值为零的对应约束为"紧约束"，表⽰在最优解下该项资源已经⽤完；其值为⾮零的对应约束为"松约束"，表⽰在最优解下该项资源还有剩余5. 对偶价格(经济学:影⼦价格)：DUAl PRICE(对偶价格)表⽰当对应约束有微⼩变动时⽬标函数的变化率。

输出结果中对应每⼀个"紧约束"有⼀个对偶价格。

若其数值为怕，则表⽰对应约束不等式右端项正好增加⼀个单位，⽬标函数将增加P个单位(max)模型。

显然，如果在最优解处约束条件正好取等号(也就是"紧约束"，也称为有效约束或起作⽤约束)，对偶价格值才可能不是0.6. 变量框(Variables):Total表⽰当前模型的全部变量数，Nonlinear显⽰其中的⾮线性变量数，Integers显⽰其中的整数变量数。

⾮线性变量是指它⾄少处于某⼀个约束条件中的⾮线性关系中。

7. 约束(Constains)框：Total表⽰当前模型扩展后的全部约束个数，Nonlinear显⽰其中的⾮线性约束个数。

⾮线性约束是该约束⾄少有⼀个⾮线性变量。

如果⼀个约束中的所有变量都是定值，那么该约束就以定值不等式表⽰，该约束的真假由变量的具体值决定，仍计⼊约束总数中。

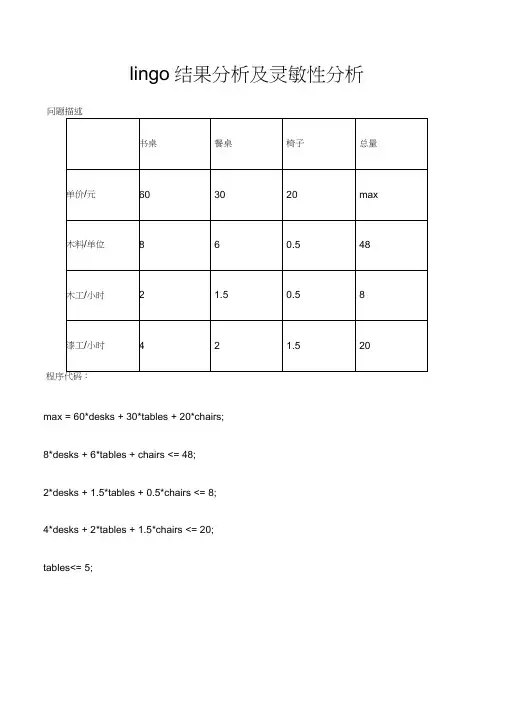
lingo结果分析及灵敏性分析问题描述程序代码：max = 60*desks + 30*tables + 20*chairs;8*desks + 6*tables + chairs <= 48;2*desks + 1.5*tables + 0.5*chairs <= 8;4*desks + 2*tables + 1.5*chairs <= 20;tables<= 5;部分结果一：Variable Value Reduced CostDESKS 2.000000 0.000000TABLES 0.000000 5.000000CHAIRS 8.000000 0.000000⑴ Value: 给出最优解中各变量的值，Value=0（非基变量），反之为基变量。

⑵ Reduced Cost ：表示当非基变量有微小变动时, 目标函数的变化率。

本例中：变量tables 对应的reduced cost 值为5 ，表示当非基变量tables 的值从0 变为1 时（此时假定其他非基变量保持不变, 但为了满足约束条件，基变量显然会发生变化），最优的目标函数值= 280 - 5 = 275 。

部分结果二：Row Slack or Surplus Dual Price1 280.0000 1.0000002 24.00000 0.0000003 0.000000 10.000004 0.000000 10.000005 5.000000 0.000000⑴ “ Slack or Surplus 松驰变量。

⑵ “Dual Price ” ―― 对偶价格表示当对应约束有微小变动时, 目标函数的变化率。

若其数值为p ，表示对应约束中不等式右端项若增加1 个单位，目标函数将增加p 个单位（max 型问题）。

⑶ 如果在最优解处约束正好取等号（紧约束，也称为有效约束或起作用约束），对偶价格值才可能不是0 。

lingo实验报告Lingo实验报告引言：在当今全球化的时代，语言的学习和掌握对于个人和社会的发展起着至关重要的作用。

为了更好地理解和应用语言，人们不断探索和研究各种学习方法和工具。

本实验报告将介绍一种被广泛使用的语言学习应用程序——Lingo，并通过实验结果分析其效果和优势。

一、Lingo的背景和特点Lingo是一款基于智能手机的语言学习应用程序，它提供了多种语言学习功能和资源，旨在帮助用户提高语言能力。

与传统的语言学习方法相比，Lingo具有以下几个突出特点：1. 多样化的学习资源：Lingo提供了丰富的学习资源，包括词汇、语法、听力、口语和阅读等方面的练习材料。

用户可以根据自己的需求和兴趣选择不同的学习内容，以提高自己的语言技能。

2. 个性化学习计划：Lingo根据用户的语言水平和学习目标，为每个用户制定个性化的学习计划。

通过分析用户的学习进度和反馈，Lingo能够自动调整学习内容和难度，使学习过程更加高效和有针对性。

3. 互动学习体验：Lingo提供了各种互动学习方式，如语音识别和对话模拟等。

用户可以通过与应用程序进行对话和互动，提高自己的口语表达能力和听力理解能力。

二、实验设计和方法为了评估Lingo的效果和优势，我们进行了一项实验。

实验对象为一群初学者级别的英语学习者，他们被随机分为两组，一组使用Lingo进行语言学习，另一组使用传统的教材和课堂学习。

在实验期间，我们对两组学习者进行了多次测试，包括词汇测试、语法测试和听力测试等。

同时，我们还收集了学习者的学习反馈和满意度调查数据，以了解他们对Lingo的使用体验和效果评价。

三、实验结果分析通过对实验数据的分析，我们得出以下结论：1. 学习成绩提升：与传统学习方法相比，使用Lingo进行语言学习的学习者在词汇、语法和听力等方面的成绩有明显提升。

这表明Lingo在帮助学习者提高语言能力方面具有一定的优势。

2. 学习动力增强：使用Lingo的学习者普遍表现出更高的学习动力和积极性。

Lingo简单⼊门，以及对线性规划做敏感性分析设置Lingo中⽤!表⽰注释，注释结束⽤;表⽰，lingo不区分⼤⼩写，运⾏时会⾃动统⼀装换成⼤写编程步骤：1.推算出正确的模型2.确定描述集，定义集合3.确定变量4.正确写出每个式⼦常⽤函数（lingo每个函数都必须⽤@强调）：!max, min⽤于⽤于定义⽬标函数@bin(x)表⽰x为0或1@gin(x)表⽰x是整数@free(x)表⽰x为任意实数，因为变量默认为⾮负实数，所以必须⽤这个函数解除这种限制@bnd(1, x, u)表⽰x为[1, u]之间的实数如表⽰x在（-5,5)之间的整数，@free(x),@gin(x),@bnd(-5, x, 5)编程⽅法：1.不使⽤集合语⾔--解决⼩规模问题（笨⽅法编程）例如解下⾯这个线性规划问题max = 72 * x1 + 64 * x2;x1 + x2 < 50;12 * x1 + 8 * x2 < 480;3 * x1 < 100;x1, x2 >= 0;model:max = 72 * x1 + 64 * x2;[milk] x1 + x2 < 50; !milk是约束条件的别名，⽅便在结果窗⼝中查看相关信息;[time] 12 * x1 + 8 * x2 < 480; !time也是别名;[cpct] 3 * x1 < 100; !cpct也是别名;end运⾏结果（会弹出两个窗⼝,只需关⼼下⾯这个窗⼝，另⼀个不⽤管）2.使⽤集合语⾔--解决⼤规模问题sets: !定义集合;S/1..6/: a, b, d; !S集合下标范围是1到6，a b d这三个变量⽤到了这个集合;T/1..2/: e, x, y;U(S, T): c; !双索引的集合，c⽤到了这个集合;endsets !结束集合的定义;data: !定义已知变量,也就是为每个已知变量赋值;a =1.258.750.55.7537.25;b =1.250.754.7556.57.75;d =3547611;x =52;y =17;e =2020;enddata !结束数据的写⼊;!⽬标⽅程;min=@sum(T(j):@sum(S(i):c(i, j) *@sqrt((x(j) - a(i))^2+ (y(j) - b(i))^2)));!约束条件;@for(S(i):@sum(T(j):c(i, j)) = d(i)); !i属于S集合范围，j属于T集合范围，这个约束条件的意思是在j⽅向上对Cij求和== d(i);@for(T(j):@sum(S(i):c(i, j)) <= e(j));(建议1.25倍速）对线性规划做敏感性分析设置(这⾥⽤第⼀个题⽬做样例）点击lingo -> option -> general solver -> Dura Computations -> Price& ranges -> apply -> save --> ok 点击lingo -> range。

2014~2015学年第二学期短学期《数学软件及应用(Lingo)》实验报告班级数学131班姓名张金库学号成绩实验名称奶制品的生产与销售计划的制定完成日期：2015年9月3日一、实验名称：奶制品的生产与销售计划的制定二、实验目的及任务1.了解并掌握LINGO 的使用方法、功能与应用；2.学会利用LINGO 去解决实际中的优化问题。

三、实验内容问题 一奶制品加工厂用牛奶生产1A ，2A 两种奶制品，1桶牛奶可以在甲类设备上用12h 加工成3kg 1A ，或者在乙类设备上用8h 加工成4kg 2A 。

根据市场的需求，生产1A ,2A 全部能售出，且每千克1A 获利24元，每千克2A 获利16元。

现在现在加工场每天能的到50桶牛奶的供应，每天正式工人总的劳动时间为480h ，并且甲类设备每天至多能加工100kg 1A ，乙类设备的加工能力没有限制。

为增加工厂的利益，开发奶制品的深加工技术：用2h 和3元加工费，可将1kg 1A 加工成高级奶制品1B ，也可将1kg 2A 加工成高级奶制品2B ，每千克1B 能获利44元，每千克2B 能获利32元。

试为该工厂制订一个生产销售计划，使每天的净利润最大，并讨论以下问题：（1）若投资30元可以增加供应1桶牛奶，投资3元可以增加1h 的劳动时间，应否做这些投资若每天投资150，可以赚回多少（2）每千克高级奶制品1B ，2B 的获利经常有10%的波动，对制订的生产销售计划有无影响若每千克1B 获利下降10%，计划应该变化吗（3）若公司已经签订了每天销售10kg 1A 的合同并且必须满足，该合同对公司的利润有什么影响问题分析 要求制定生产销售计划，决策变量可以先取作每天用多少桶牛奶生产1A ，2A ，再添上用多少千克1A 加工1B ，用多少千克2A 加工2B ，但是问题要分析1B ，2B 的获利对生产销售计划的影响，所以决策变量取作1A ，2A ，1B ，2B 每天的销售量更为方便。

l i n g o结果分析及灵敏性分析精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-lingo结果分析及灵敏性分析问题描述程序代码：max = 60*desks + 30*tables + 20*chairs;8*desks + 6*tables + chairs <= 48;2*desks + 1.5*tables + 0.5*chairs <= 8;4*desks + 2*tables + 1.5*chairs <= 20;tables<= 5;部分结果一：Variable Value Reduced CostDESKS 2.000000 0.000000TABLES 0.000000 5.000000CHAIRS 8.000000 0.000000⑴Value: 给出最优解中各变量的值，Value=0(非基变量)，反之为基变量。

⑵Reduced Cost：表示当非基变量有微小变动时, 目标函数的变化率。

本例中：变量 tables 对应的 reduced cost 值为 5，表示当非基变量 tables 的值从0 变为 1 时（此时假定其他非基变量保持不变,但为了满足约束条件，基变量显然会发生变化），最优的目标函数值 = 280 - 5 = 275。

部分结果二：Row Slack or Surplus Dual Price1 280.0000 1.0000002 24.00000 0.0000003 0.000000 10.000004 0.000000 10.000005 5.000000 0.000000⑴“Slack or Surplus”――松驰变量。

⑵“Dual Price”――对偶价格表示当对应约束有微小变动时, 目标函数的变化率。

若其数值为 p，表示对应约束中不等式右端项若增加 1个单位，目标函数将增加 p个单位（max 型问题）。

一个很好的运算结果分析莫版！！！例5.1某家具公司制造书桌、餐桌和椅子，所用的资源有三种：木料、木工和漆工。

生产数据如下表所示：每个书桌每个餐桌每个椅子现有资源总数木料8单位6单位1单位48单位漆工4单位2单位 1.5单位20单位木工2单位 1.5单位0.5单位8单位成品单价60单位30单位20单位若要求桌子的生产量不超过5件，如何安排三种产品的生产可使利润最大？用DESKS、TABLES和CHAIRS分别表示三种产品的生产量，建立LP模型。

[OBJ] max=60*desks+30*tables+20*chairs;[ml] 8*desks+6*tables+chairs<=48;[qg] 4*desks+2*tables+1.5*chairs<=20;[mg] 2*desks+1.5*tables+.5*chairs<=8;[zz] tables<=5;Global optimal solution found at iteration: 0Objective value: 280.0000Variable Value Reduced CostDESKS 2.000000 0.000000TABLES 0.000000 5.000000CHAIRS 8.000000 0.000000Row Slack or Surplus Dual PriceOBJ 280.0000 1.000000ML 24.00000 0.000000QG 0.000000 10.00000MG 0.000000 10.00000ZZ 5.000000 0.000000“Global optimal solution found at iteration: 3”表示3次迭代后得到全局最优解。

“Objective value: 280.0000”表示最优目标值为280。

“Value”给出最优解中各变量的值：造2个书桌（desks）“Reduced Cost”列出最优单纯形表中判别数所在行的变量的系数，表示当变量有微小变动时, 目标函数的变化率。

线性规划问题及灵敏度分析在LINGO软件中的实现一、问题的提出：某公司饲养实验用的动物以出售给动物研究所，已知这些动物的生长对饲料中3种营养成分（蛋白质、矿物质和维生素）特别敏感，每个动物每周至少需要蛋白质60g，矿物质3g，维生素8mg，该公司能买到5种不同的饲料，每种饲料1kg所含各种营养成分和成本如下表所示，如果每个小动物每周食用饲料不超过52kg，才能满足动物生长需要。

A1A2A3A4A5营养最低要 求蛋白质(g)0.3210.6 1.860矿物质(g)0.10.050.020.20.053维生素(mg)0.050.10.020.20.088成本（元/ kg）0.20.70.40.30.5问题：1．求使得总成本最低的饲料配方？2．如果另一个动物研究对蛋白质的营养要求变为59单位，但是要求动物的价格比现在的价格便宜0.3元，问该养殖所值不值得接受？3．由于市场因素的影响，X2的价格降为0.6元每千克，问是否要改变饲料配方？二、建立线性规划数学模型解答：（1）设需要饲料A1, A2, A3, A4分别为X1, X2, X3, X4kg，则建立线性规划数学模型如下：目标函数：MinS=0.2X1+0.7X2+0.4X3+0.3X4+0.5X5约束条件：0.3X1+2X2+X3+0.6X4+1.8X5>=600.1X1+0.05X2+0.02X3+0.2X4+0.05X5>=3005X1+0.1X2+0.02X3+0.2X4+0.08X5>=8X1+X2+X3+X4+X5<=52X1, X2, X3, X4, X5>=0三、在LINGO软件中的求解在LINGO中输入下面的命令：Model：Min=0.2*x1+0.7*x2+0.4*x3+0.3*x4+0.5*x5;0.3*x1+2*x2+x3+0.6*x4+1.8*x5>60;0.1*x1+0.05*x2+0.02*x3+0.2*x4+0.05*x5>3;0.05*x1+0.1*x2+0.02*x3+0.2*x4+0.08*x5>8;x1+x2+x3+x4+x5<52;end操作：选菜单Lingo|Solve(或按Ctrl+S),或用鼠标点击“求解”按纽，如果模型有语法错误，则弹出一个标题为“LINGO Error Message”(错误信息)的窗口，指出在哪一行有怎样的错误，每一种错误都有一个编号（具体含义可查阅相关文献或LINGO的Help）.改正错误以后再求解，如果语法通过，LINGO用内部所带的求解程序求出模型的解，然后弹出一个标题为“LINGO Solver Status”（求解状态）的窗口，其内容为变量个数、约束条件个数、优化状态、耗费内存、所花时间等信息，点击Close关闭窗口，屏幕上出现标题为“Solution Report”（解的报告）的信息窗口，显示优化计算（线性规划中换基迭代）的步数、优化后的目标函数值、列出各变量的计算结果.输出结果如下:Global optimal solution found at iteration: 4Objective value: 22.40000Variable Value Reduced CostX1 0.000000 0.7000000X2 12.00000 0.000000X3 0.000000 0.6166667X4 30.00000 0.000000X5 10.00000 0.000000Row Slack or Surplus Dual Price1 22.40000 -1.0000002 0.000000 -0.58333333 4.100000 0.0000004 0.000000 -4.1666675 0.000000 0.8833333四、结果分析：(一) 一般分析1.因此,每周每个动物的配料为饲料A2、A4、A5分别为12、30和10kg，合计为52KG，可使得饲养成本达到最小，最小成本为22.4元；2. “Reduced Cost”表示当变量有微小变动时, 目标函数的变化率。

【精品】LINGO软件灵敏度分析LINGO是一种非常实用的数学建模软件，可用于线性规划、非线性规划、整数规划、混合整数规划、二次规划、非线性二次规划、全局优化、动态规划等方面。

在LINGO中，灵敏度分析可以帮助用户更好地理解线性规划问题的解，并探究约束、变量、最优值等因素的变化对于优化结果的影响。

下面将详细介绍LINGO软件的灵敏度分析功能。

一、约束灵敏度分析在LINGO中，可以通过在“呼出”窗口中选择“求解”菜单，再选中“灵敏度分析”，来进行约束灵敏度分析。

当我们需要对某一约束条件进行灵敏度分析时，可以在“PSens”一栏中选中要进行分析的约束条件，并选择需要分析的灵敏度类型：1. 左侧界（Lower Bound）灵敏度分析：在该约束条件的左侧界上下浮动，观察最优解随着左侧界的变化而产生的变化情况。

进行变量灵敏度分析时，LINGO会输出一个名为“Variable Sensitivity”的窗口，其中包含了与所选中变量相关的数据，如灵敏度系数、上/下限边界、最小可行解等。

另外，该窗口还提供了一个“Graph”选项卡，可以展示出灵敏度分析的图表，帮助用户更直观地理解灵敏度的变化情况。

在LINGO中，最优解灵敏度分析可以探究最优解随着目标函数系数的变化而产生的变化情况。

用户可以在“呼出”窗口中选择“求解”菜单，再选中“灵敏度分析”，然后在“Objective Sensitivity”选项卡中选中需要进行分析的目标函数变量。

总之，LINGO软件的灵敏度分析功能可以在优化过程中帮助用户更好地了解问题的解，探究约束、变量、目标函数系数等因素对应问题的影响，帮助用户优化模型，从而达到更好的优化效果。

lingo 软件求解线性规划及灵敏度分析注：以目标函数最大化为例进行讨论，对求最小的问题，有类似的分析方法！所有程序运行环境为lingo10。

一、用lingo 软件求解线性规划例1：max 23..43103512,0z x y s t x y x y x y =++≤+≤≥在模型窗口输入：model: max=2*x+3*y; 4*x+3*y<=10; 3*x+5*y<12;! the optimal value is :7.454545 ; End 如图所示：运行结果如下（点击 工具栏上的‘solve ’或点击菜单‘lingo ’下的‘solve ’即可）：Global optimal solution found.Objective value: 7.454545（最优解函数值） Total solver iterations: 2（迭代次数）Variable （最优解） Value Reduced Cost X 1.272727 0.000000 Y 1.636364 0.000000Row Slack or Surplus Dual Price 1 7.454545 1.000000 2 0.000000 0.9090909E-01 3 0.000000 0.5454545例2：12123124125max 54..390280450z x x s t x x x x x x x x x x =+++=++=++=≥ 在模型窗口输入：model:max=5*x1+4*x2; x1+3*x2+x3=90; 2*x1+x2+x4=80; x1+x2+x5=45; end运行（solve ）结果如下：Global optimal solution found.Objective value: 215.0000 Total solver iterations: 3Variable Value Reduced Cost X1 35.00000 0.000000 X2 10.00000 0.000000 X3 25.00000 0.000000 X4 0.000000 1.000000 X5 0.000000 3.000000Row Slack or Surplus Dual Price 1 215.0000 1.000000 2 0.000000 0.000000 3 0.000000 1.000000 4 0.000000 3.000000例323123234235min 2..223120z x x s t x x x x x x x x x x =-+-+=-+=-+=≥ 在模型窗口输入：model:min=-x2+2*x3; x1-2*x2+x3=2; x2-3*x3+x4=1; x2-x3+x5=2; end运行结果如下：Global optimal solution found.Objective value: -1.500000 Total solver iterations: 2Variable Value Reduced Cost X2 2.500000 0.000000 X3 0.5000000 0.000000 X1 6.500000 0.000000 X4 0.000000 0.5000000 X5 0.000000 0.5000000Row Slack or Surplus Dual Price 1 -1.500000 -1.000000 2 0.000000 0.000000 3 0.000000 0.5000000 4 0.000000 0.5000000例4：min ..124x y z s t x y x z +++≤+= 在模型窗口输入：model :min =@abs (x)+@abs (y)+@abs (z); x+y<1; 2*x+z=4; @free (x); @free (y); @free (z);End求解器状态如下：（可看出是非线性模型！）运行结果为：Linearization components added:Constraints: 12Variables: 12Integers: 3Global optimal solution found.Objective value: 3.000000Extended solver steps: 0Total solver iterations: 4Variable Value Reduced Cost X 2.000000 0.000000Y -1.000000 0.000000 Z 0.000000 0.000000Row Slack or Surplus Dual Price1 3.000000 -1.0000002 0.000000 1.0000003 0.000000 -1.000000二、用lingo软件进行灵敏度分析实例例5：max 603020864842 1.5202 1.50.585,,0S x y z x y z x y z x y z y x y z =++++≤++≤++≤≤≥在模型窗口输入： Lingo 模型：model:max=60*x+30*y+20*z; 8*x+6*y+z<48; 4*x+2*y+1.5*z<20; 2*x+1.5*y+0.5*z<8; y<5; end（一）求解报告（solution report ）通过菜单Lingo →Solve 可以得到求解报告（solution report ）如下：Global optimal solution found at iteration: 0 Objective value: 280.0000Variable Value Reduced Cost X 2.000000 0.000000 Y 0.000000 5.000000 Z 8.000000 0.000000Row Slack or Surplus Dual Price 1 280.0000 1.000000 2 24.00000 0.000000 3 0.000000 10.00000 4 0.000000 10.00000 5 5.000000 0.000000分析Value,Reduced Cost ，Slack or Surplus ，Dual Price 的意义如下： 1、最优解和基变量的确定Value 所在列给出了问题的最优解。