灵敏度分析,计算软件

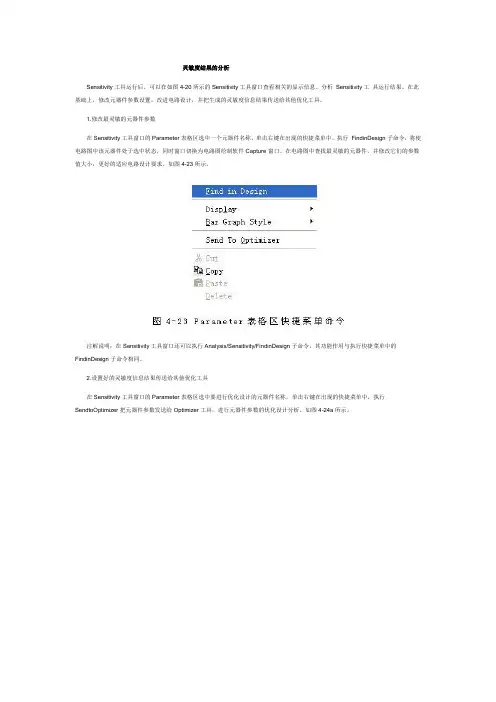
灵敏度结果的分析Sensitivity工具运行后，可以在如图4-20所示的Sensitivity工具窗口查看相关的显示信息。

分析Sensitivity工具运行结果。

在此基础上，修改元器件参数设置，改进电路设计，并把生成的灵敏度信息结果传送给其他优化工具。

1.修改最灵敏的元器件参数在Sensitivity工具窗口的Parameter表格区选中一个元器件名称，单击右键在出现的快捷菜单中，执行FindinDesign子命令，将使电路图中该元器件处于选中状态，同时窗口切换为电路图绘制软件Capture窗口。

在电路图中查找最灵敏的元器件，并修改它们的参数值大小，更好的适应电路设计要求。

如图4-23所示。

注解说明：在Sensitivity工具窗口还可以执行Analysis/Sensitivity/FindinDesign子命令，其功能作用与执行快捷菜单中的FindinDesign子命令相同。

2.设置好的灵敏度信息结果传送给其他优化工具在Sensitivity工具窗口的Parameter表格区选中要进行优化设计的元器件名称，单击右键在出现的快捷菜单中，执行SendtoOptimizer把元器件参数发送给Optimizer工具，进行元器件参数的优化设计分析。

如图4-24a所示。

同样,在Sensitivity工具窗口的Specification表格区选中要进行优化设计的电路特性函数名称，单击右键在出现的快捷菜单中，执行Sendto子命令把元器件参数发送给Optimizer/MonteCarlo工具。

如图4-24b所示。

若要查看灵敏度原始数据只要按如图4-25所示，在灵敏度分析窗口按下如图4-22所示命令即可调出Sensitivity分析结果清单。

调出的原始数据如图4-26所示，图中显示最后第18次运行结果。

4.7本章小结本章在介绍灵敏度分析基本概念（定义、重要性等）的基础上重点介绍了如何使用Sensitivity工具对电路进行灵敏度分析。

AHP灵敏度分析1. 简介层次分析法（Analytic Hierarchy Process，AHP）是一种多标准决策分析方法，用于对复杂问题进行系统化的分析和决策。

AHP具有结构化、直观和灵活等特点，广泛应用于各个领域，如工程管理、经济学、环境科学等。

在进行决策分析时，灵敏度分析是 AHP 中重要的一部分，用于评估决策结果对输入参数变化的敏感性。

2. AHP 简要回顾在 AHP 中，决策问题被组织成层次结构，包括目标层、准则层和方案层。

目标层是最高层，表示要达到的总体目标；准则层是目标的分解层次，包含影响目标实现的关键准则；方案层是准则层的子层次，表示可供选择的方案。

AHP 使用一种两两比较的方法来判断每个层次结构中的元素（目标、准则和方案）之间的相对重要性。

比较结果通过建立判断矩阵表示，矩阵的每个元素代表两个元素之间的相对权重。

通过计算每个层次结构的权重，可以确定最终决策的最佳选择。

但是，由于AHP 是基于主观判断的方法，输入参数的变化可能会对结果产生影响。

因此，需要进行灵敏度分析来评估决策结果对参数变化的敏感性。

3. AHP 灵敏度分析方法AHP 灵敏度分析主要通过以下几个步骤进行：3.1 确定输入参数的范围在进行灵敏度分析前，需要确定哪些输入参数会产生变化，并确定它们的取值范围。

可以通过专家意见、历史数据或试验结果等来确定参数的范围。

3.2 设计实验方案根据参数的范围，设计一组实验方案来评估参数变化对决策结果的影响。

实验方案可以通过正交试验设计等方法来确定。

3.3 运行实验根据设计的实验方案，运行实验并记录结果。

可以使用 AHP 方法对每组实验结果进行权重计算，得到不同参数取值下的最佳选择。

3.4 分析实验结果根据实验结果，分析不同参数取值下的决策结果变化情况。

可以比较最佳选择的权重变化，评估参数对结果的影响程度。

还可以使用灵敏度指标来度量参数变化对结果的影响程度。

4. AHP 灵敏度分析的意义AHP 灵敏度分析可以帮助决策者评估决策结果的可靠性和稳定性。

基于应面法ANSYS灵敏度分析肖禧成（东南大学机械工程学院,120176）摘要:基于响应面法的ANSYS灵敏度分析是一种可靠有效的分析方法,本文详细阐述了ANSYS中基于响应面法的灵敏度分析基本原理,为基于ANSYS的结构灵敏度分析提供参考;应用ANSYS对一个流固耦合模型中固体接触面内应力受冷、热水流体温度的影响进行了灵敏度分析,并寻求一组最佳参数值，使当冷、热水入口的速度、温度在一定范围内变化的情况下，使中心块的内应力最小。

并通过对计算结果的分析，验证了基于响应面法ANSYS灵敏度分析的高效性和可靠性。

关键词:灵敏度分析;响应面法;流固耦合;ANSYSAbstract: The sensitivity analysis( SA) based on response surface method in ANSYS is a reliable and effective method, the basic SA theory based on response surface method in ANSYS is presented in detail, which can be a reference of structural SA using ANSYS. A Fluid-solid coupling model is analyzed by using ANSYS, and the sensitivity values of intra-stress on the contract surfaces of the solid responses to different velocity and temperature of the inlet and outlet are calculated, which can be used to compute a fittest parameter making the intra-stress minimum. The analysis of the calculated results verifies the reliability and effectiveness of SA based on experimental data.Key words: sensitivity analysis (SA);response surface methods; Fluid-solid coupling; ANSYS目录1. 响应面法 (2)2. ANSYS灵敏度分析的基本原理 (4)2.1 ANSYS概率设计系统（PDS） (4)2.2 基于Spearman秩相关系数【9】的ANSYS灵敏度分析 (5)3. 流场腔内固定块的应力场的灵敏度分析 (5)3.1 ANSYS CFX分析 (5)3.2 求解壁面应力灵敏度 (11)4. 结论 (17)参考文献 (18)1. 响应面法响应面方法是进行灵敏度分析的一种有效方法，其思想是通过一系列确定性试验拟合一个响应面来模拟真实极限状态曲面．假设Z 与系统随机参量12[,,,]r Q Q Q Q =的关系可用式(1)描述，通过随机抽样法得到随机参量的N 个样本值，对这N 个样本值数值计算得到系统响应的一组样本值12(,,,)s z z z 利用最小二乘法得到该系统函数；用该响应面方程代替有限元模型进行失效模式分析，在结构响应Z 未知的情况下，用响应面函数代替结构的真实响应，将大大节约计算时间【1】．011ˆRRRi i ij i ji i j iZ a a Q a Q Q ====++∑∑∑ (1) 式中0,,(1,,;,,)i ij a a a i R j i R ==为待定系数，共1(1)/2n n n +++个．采用矩阵法对每个随机变量取三个水平点，按照某种法则得出中心所在点和边中点作为样本值点．图1.1表示三变量 123(,,)Q Q Q 样本值点。

灵敏度分析与全局敏感度分析比较研究论文素材在数学建模、系统分析、风险评估等领域中，灵敏度分析和全局敏感度分析是两个常用的方法。

本文将对这两种分析方法进行比较研究，探讨其优缺点及适用场景，为相关领域的研究者提供参考。

一、灵敏度分析灵敏度分析是一种用来评估模型中参数对输出结果的影响程度的方法。

它通过改变模型中的一个或多个参数，并观察模型输出结果的变化，来衡量参数对结果的敏感程度。

灵敏度分析可分为局部敏感度分析和全局敏感度分析两种方法，下面将重点介绍局部敏感度分析。

1. 局部敏感度分析局部敏感度分析是在给定某一特定点上，对各个参数的灵敏度进行分析。

它的核心思想是通过改变参数的值，并观察输出结果的变化，来判断参数对结果的影响程度。

常用的方法包括参数敏感度指标、敏感度曲线等。

2. 局部敏感度分析的优点和适用场景局部敏感度分析的优点是计算简单、易于理解，并且适用于大多数情况下。

它可以帮助研究者了解模型中各个参数对结果的影响程度，进行参数的优化和调整。

适用场景包括模型初步建立阶段、局部问题分析以及参数敏感度分析等。

二、全局敏感度分析全局敏感度分析是在整个参数空间范围内，对各个参数的灵敏度进行分析。

与局部敏感度分析不同的是，全局敏感度分析考虑了参数之间的相互作用和不确定性，能够更全面地评估参数对模型输出结果的影响。

1. 全局敏感度分析方法全局敏感度分析方法包括元胞自动机方法、Monte Carlo方法、Sobol分析等。

其中，Sobol分析是一种较为常用的方法，可用于评估参数对输出的主效应和交互效应。

2. 全局敏感度分析的优点和适用场景全局敏感度分析的优点是能够综合考虑参数之间的相互作用，更全面地评估参数对输出结果的影响。

它可以帮助研究者了解参数之间的关联性，提高模型的可信度。

适用于参数空间较大、参数之间相互关联较强的情况下。

三、灵敏度分析与全局敏感度分析的比较灵敏度分析和全局敏感度分析都可以评估参数对输出结果的影响程度，但在方法、计算复杂度和适用场景上存在差异。

灵敏度分析仪操作流程操作流程：1. 准备工作在进行灵敏度分析之前，需要准备以下工作：- 确定要分析的系统或模型，例如物理系统、金融模型等。

- 确定系统或模型的输入变量，即对系统或模型输入有影响的变量。

- 确定系统或模型的输出指标，即对系统或模型输出结果的关注点。

- 确定灵敏度分析的方法，例如全局灵敏度分析、局部灵敏度分析等。

2. 收集数据根据所选的灵敏度分析方法，收集系统或模型所需的数据。

数据可以通过实验、测量、模拟等方式获取。

确保数据的准确性和可靠性。

3. 定义变量范围对于每个输入变量，定义其可能的取值范围。

可以根据实际情况、专家意见或历史数据进行定义。

确保变量范围的全面性和合理性。

4. 设计实验根据变量范围和所选的灵敏度分析方法，设计实验来评估不同输入变量对输出指标的影响程度。

实验设计可以是全因素设计、部分因素设计、随机抽样设计等。

5. 运行实验根据实验设计，逐个设置输入变量的值，并运行系统或模型得到对应的输出结果。

保持其他变量不变，只改变待分析的变量。

记录并保存实验数据。

6. 计算灵敏度指标根据实验数据，计算灵敏度指标来评估各个输入变量对输出指标的贡献程度。

常用的灵敏度指标包括主效应指标、总效应指标、局部效应指标等。

7. 分析结果根据计算得到的灵敏度指标，对系统或模型的输入变量进行排序，确定其对输出指标的重要性。

可以利用图表、可视化工具等方式呈现分析结果，以便更好地理解和解释。

8. 结论与应用根据灵敏度分析的结果，得出结论并提出相应的应用建议。

根据对不同输入变量的重要性排序，优化系统或模型的设计、参数设置或决策制定。

9. 结束和总结总结整个灵敏度分析的过程和结果。

对实验数据、计算方法、分析结果进行审查和验证，确保分析的准确性和可信度。

对于不足之处，提出改进的建议。

通过以上操作流程，可以对系统或模型的输入变量进行灵敏度分析，了解其对输出指标的影响程度，从而提供决策支持和优化方案。

灵敏度分析仪的应用范围广泛，可以用于工程设计、金融风险评估、环境影响评估等领域。

题目如何利用EXC E L求解线性规划问题及其灵敏度分析第 8 组姓名学号乐俊松 090960125孙然 090960122徐正超 090960121崔凯 090960120王炜垚 090960118蔡淼 090960117南京航空航天大学（贸易经济）系2011年（5）月（3）日摘要线性规划是运筹学的重要组成部分，在工业、军事、经济计划等领域有着广泛的应用，但其手工求解方法的计算步骤繁琐复杂。

本文以实际生产计划投资组合最优化问题为例详细介绍了Excel软件的”规划求解”和“solvertable”功能辅助求解线性规划模型的具体步骤，并对其进行了灵敏度分析。

目录引言 (4)软件的使用步骤 (4)结果分析 (9)结论与展望 (10)参考文献 (11)1. 引言对于整个运筹学来说，线性规划(Linear Programming)是形成最早、最成熟的一个分支，是优化理论最基础的部分，也是运筹学最核心的内容之一。

它是应用分析、量化的方法，在一定的约束条件下，对管理系统中的有限资源进行统筹规划，为决策者提供最优方案，以便产生最大的经济和社会效益。

因此，将线性规划方法用于企业的产、销、研等过程成为了现代科学管理的重要手段之一。

[1] Excel中的线性规划求解和solvertable功能并不作为命令直接显示在菜单中，因此，使用前需首先加载该模块。

具体操作过程为：在Excel的菜单栏中选择“工具／加载宏”，然后在弹出的对话框中选择“规划求解”和“solvertable”，并用鼠标左键单击“确定”。

加载成功后，在菜单栏中选择“工具／规划求解”，便会弹出“规划求解参数”对话框。

在开始求解之前，需先在对话框中设置好各种参数，包括目标单元格、问题类型(求最大值还是最小值)、可变单元格以及约束条件等。

2 软件的使用步骤“规划求解”可以解决数学、财务、金融、经济、统计等诸多实际问题，在此我们只举一个简单的应用实例，说明其具体的操作方法。

分析灵敏度和功能灵敏度灵敏度和功能灵敏度是两个涉及到系统或设备性能评估的重要指标。

本文将详细介绍灵敏度和功能灵敏度的定义、应用领域、计算方法以及其在实际中的意义。

一、灵敏度的定义与应用领域灵敏度是指系统或设备输出对输入的变化的响应程度。

在控制论和系统理论中，灵敏度是系统响应对输入参数改变的敏感程度的定量化描述。

在工程领域，灵敏度常用于衡量系统或设备对外部环境变化的响应能力。

例如，在自动驾驶系统中，灵敏度可以用来评估车辆对于各种路况的适应能力，以及对不同驾驶指令的响应程度。

另外，灵敏度也被广泛应用于电子、光学、机械等领域中的传感器设计和控制系统优化等方面。

二、灵敏度的计算方法灵敏度的计算方法通常涉及到导数的概念。

灵敏度可以通过计算输出变化与输入变化之间的比率来衡量。

具体而言，灵敏度可以通过以下公式计算得到：Sensitivity = (Output Change) / (Input Change)其中，输出变化和输入变化分别表示系统或设备响应的输出和输入的变化量。

灵敏度的计算结果通常为一个无量纲数值，并可以用百分比或分贝等单位进行表示。

三、功能灵敏度的定义与应用领域功能灵敏度是指系统或设备在输入参数变化时，所提供的功能性能的变化程度。

功能灵敏度与灵敏度不同的是，它更关注于系统功能的变化，而不仅仅是输出与输入之间的关系。

在软件开发和软件测试领域，功能灵敏度常用于评估软件系统在不同输入条件下的功能完整性和可靠性。

通过对功能灵敏度的分析，可以确定系统在不同输入条件下的正确性和适应性，从而帮助开发人员优化软件设计和解决问题。

四、功能灵敏度的计算方法功能灵敏度的计算方法与灵敏度类似，也常使用变化量的比率来衡量。

具体而言，功能灵敏度可以通过以下公式计算得到：Functional Sensitivity = (Functional Change) / (Input Change)其中，功能变化表示系统功能的变化量，输入变化表示系统输入的变化量。

【精品】LINGO软件灵敏度分析LINGO是一种非常实用的数学建模软件，可用于线性规划、非线性规划、整数规划、混合整数规划、二次规划、非线性二次规划、全局优化、动态规划等方面。

在LINGO中，灵敏度分析可以帮助用户更好地理解线性规划问题的解，并探究约束、变量、最优值等因素的变化对于优化结果的影响。

下面将详细介绍LINGO软件的灵敏度分析功能。

一、约束灵敏度分析在LINGO中，可以通过在“呼出”窗口中选择“求解”菜单，再选中“灵敏度分析”，来进行约束灵敏度分析。

当我们需要对某一约束条件进行灵敏度分析时，可以在“PSens”一栏中选中要进行分析的约束条件，并选择需要分析的灵敏度类型：1. 左侧界（Lower Bound）灵敏度分析：在该约束条件的左侧界上下浮动，观察最优解随着左侧界的变化而产生的变化情况。

进行变量灵敏度分析时，LINGO会输出一个名为“Variable Sensitivity”的窗口，其中包含了与所选中变量相关的数据，如灵敏度系数、上/下限边界、最小可行解等。

另外，该窗口还提供了一个“Graph”选项卡，可以展示出灵敏度分析的图表，帮助用户更直观地理解灵敏度的变化情况。

在LINGO中，最优解灵敏度分析可以探究最优解随着目标函数系数的变化而产生的变化情况。

用户可以在“呼出”窗口中选择“求解”菜单，再选中“灵敏度分析”，然后在“Objective Sensitivity”选项卡中选中需要进行分析的目标函数变量。

总之，LINGO软件的灵敏度分析功能可以在优化过程中帮助用户更好地了解问题的解，探究约束、变量、目标函数系数等因素对应问题的影响，帮助用户优化模型，从而达到更好的优化效果。

灵敏度分析教程
（一）建立模型
利用CATIA软件在曲面设计模块建立线条模型
由点建立线
（注意：要逐点连接）
保存格式为STP格式。

二、分析
（1）打开ANSYS软件在第一个的分析拉出静力学项目
（2）导入几何模型并设置模型材料（这里我选择默认材料）
（3）模型处理
然后点击更新
效果图
（4）在Concept中的Cross Section中给予线体截面
（5）定义管件厚度
（6）回到首页进入model界面进行网格划分和分析
（7）网格划分，鼠标在mesh右键，选择到sizing，然后再定义网格尺寸
进行网格求解
进行载荷，约束施加
（三）建立各个参数的连接（1）管件大小
（2）质量
（3）应力
设置实验次数与最优解的个数
21。

. . . ... ..2011——2012学年第二学期合肥学院数理系实验报告课程名称：运筹学实验项目：线性规划的灵敏度分析实验类别：综合性□设计性□验证性□√专业班级： 09级数学与应用数学（1）班姓名：王秀秀学号： 0907021006 实验地点： 9#503实验时间： 2012-4-25 指导教师：管梅成绩：一.实验目的熟悉LINDO软件的灵敏度分析功能；二.实验内容1、求解线性规划。

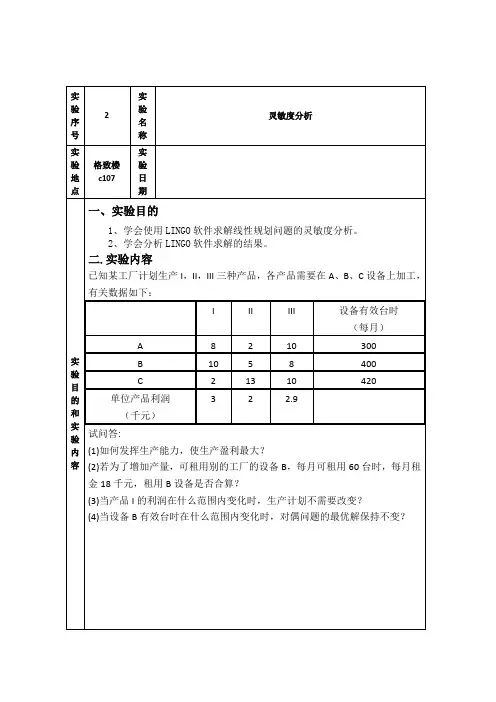
12121212max z x2x2x5x12 s.t.x2x8x,x0=++≥⎧⎪+≤⎨⎪≥⎩并对价值系数、右端常量进行灵敏度分析2、已知某工厂计划生产I，II，III三种产品，各产品需要在A、B、C设备上加工，有关数据如下：试问答:(1)如何发挥生产能力，使生产盈利最大？(2)若为了增加产量，可租用别工厂设备B，每月可租用60台时，租金1.8万元，租用B设备是否合算？(3)若另有二种新产品IV 、V ，其中新产品IV 需用设备A 为12台时、B 为5台时、C 为10台时，单位产品盈利2.1千元；新产品V 需用设备A 为4台时、B 为4台时、C 为12台时，单位产品盈利1.87千元。

如A 、B 、C 的设备台时不增加，这两种新产品投产在经济上是否划算？ (4)对产品工艺重新进行设计，改进结构。

改进后生产每件产品I 需用设备A 为9台时、设备B 为12台时、设备C 为4台时，单位产品盈利4.5千元，这时对原计划有何影响？ 三. 模型建立 1、数学模型为12121212max z x 2x 2x 5x 12s.t.x 2x 8x ,x 0=++≥⎧⎪+≤⎨⎪≥⎩ 2、设分别生产I ，II ，III 三种产品1x ，2x ，3x 件， （1）数学模型为：123122123123123123max z 3x 2x 2.9x 8x 2x 10x 30010x 5x 8x 400s.t.2x 13x 10x 420x x x 0x ,x x =++++≤⎧⎪++≤⎪⎪++≤⎨⎪≥⎪⎪⎩，，，，为整数（2）数学模型为：123122123123123123max z 3x 2x 2.9x 188x 2x 10x 30010x 5x 8x 460s.t.2x 13x 10x 420x x x 0x ,x x =++-++≤⎧⎪++≤⎪⎪++≤⎨⎪≥⎪⎪⎩，，，，为整数（3）设分别生产I ，II ，III 、IV 、V 的件数为1x ，2x ，3x ，4x ，5x 数学模型为：123451224512345123451234512345max z 3x 2x 2.9x 2.1x 1.87x 8x 2x 10x 12x 4x 30010x 5x 8x 5x 4x 400s.t.2x 13x 10x 10x 12x 420x x x x x 0x ,x x x x =++++++++≤⎧⎪++++≤⎪⎪++++≤⎨⎪≥⎪⎪⎩，，，，，，，，为整数（4）设分别生产I ，II ，III 三种产品1x ，2x ，3x 件， 数学模型为：123122123123123123max z 4.5x 2x 2.9x 9x 2x 10x 30012x 5x 8x 400s.t.4x 13x 10x 420x x x 0x ,x x =++++≤⎧⎪++≤⎪⎪++≤⎨⎪≥⎪⎪⎩，，，，为整数四. 模型求解（含经调试后正确的源程序） 1、求解：model:max=x1+2*x2; 2*x1+5*x2>=12; x1+2*x2<=8; end结果显示：2、求解：（1）model:max=3*x1+2*x2+2.9*x3; 8*x1+2*x2+10*x3<=300; 10*x1+5*x2+8*x3<=400; 2*x1+13*x2+10*x3<=420; gin(x1);gin(x2);gin(x3);end结果显示：（2）model:max=3*x1+2*x2+2.9*x3-18; 8*x1+2*x2+10*x3<=300;10*x1+5*x2+8*x3<=460;2*x1+13*x2+10*x3<=420; gin(x1);gin(x2);gin(x3);end结果显示：（3）model:max=3*x1+2*x2+2.9*x3+2.1*x4+1.87*x5; 8*x1+2*x2+10*x3+12*x4+4*x5<=300;10*x1+5*x2+8*x3+5*x4+4*x5<=400;2*x1+13*x2+10*x3+10*x4+12*x5<=420; gin(x1);gin(x2);gin(x3);gin(x4);gin(x5);End结果显示：（4）model:max=4.5*x1+2*x2+2.9*x3;9*x1+2*x2+10*x3<=300;12*x1+5*x2+8*x3<=400;4*x1+13*x2+10*x3<=420;gin(x1);gin(x2);gin(x3);End结果显示：五．结果分析第一题该线性规划问题的最优解为：X*=(0,4)，最优值为：z*=8 c1＝1c1在（0, +∞）内原最优解不变，但最优值是要变的c2＝2c2在（-∞,0）内原最优解不变，但最优值是要变的b1=12b1在（8, +∞）内原最优基不变，但最优解和最优值是要变的b2=6b2在（-∞，3.2）内原最优基不变，但最优解和最优值是要变的第二题(1)最优解：x1=24;x2=24;x3=5 最优值max=134.5;(2)最优解： x1=31;x2=26;x3=0 最优值max=127;所以租用B设备不合算(3)最优解： x1=26;x2=19;x3=1;x4=1;x5=8 最优值max=135.96;所以增加新产品投产在经济上是划算的(4)最优解： x1=22;x2=24;x3=2 最优值max=152.8;改进后生产利益增大了。

估算和评估报告中的不确定性和灵敏度分析随着社会的发展和科技的进步，估算和评估报告在各个领域中扮演着重要的角色。

无论是在工程项目、金融投资还是环境评估等领域，准确评估和估算结果的不确定性是至关重要的。

为了满足这一要求，不确定性和灵敏度分析成为了估算和评估报告中不可或缺的步骤。

不确定性分析是指对估算和评估结果中的不确定性进行量化和评估的过程。

在进行任何估算或评估之前，我们必须认识到估算结果的不确定性来源于很多方面，如数据的缺乏、模型中的误差以及人为因素等。

因此，通过不确定性分析，我们可以确定估算结果的可能范围，提供给决策者一个更加全面的信息。

在不确定性分析中，我们可以采用不同的方法进行估算结果的量化。

最常用的方法包括参数分布法、蒙特卡洛模拟和贝叶斯方法等。

参数分布法是通过对估算参数进行概率分布的设定，利用概率统计的方法得出估算结果的概率分布。

蒙特卡洛模拟是通过对不确定参数进行随机抽样，并进行大量的迭代计算，得出估算结果的分布。

贝叶斯方法则是结合先验知识和观测数据，通过贝叶斯公式计算后验概率，得出估算结果的概率分布。

一旦完成了不确定性分析，下一步就是进行灵敏度分析。

灵敏度分析是研究估算参数变化对估算结果的影响程度的过程。

通过灵敏度分析，我们可以确定影响估算结果的关键因素，进而优化估算模型和提高估算准确性。

在进行灵敏度分析时，我们可以使用不同的方法，如单参数灵敏度分析、全局灵敏度分析和局部灵敏度分析等。

单参数灵敏度分析是通过将单个参数进行变化，观察估算结果的变化程度，来确定参数对估算结果的影响程度。

全局灵敏度分析则是通过研究所有参数的变化对估算结果的影响程度，得出参数的重要性排序。

局部灵敏度分析则是对特定参数进行变化，并观察估算结果的变化程度。

不确定性和灵敏度分析在估算和评估报告中的作用不可忽视。

首先，不确定性分析能够提供准确的估算结果的范围，使决策者能够更加全面地评估风险和不确定性。

其次，灵敏度分析能够帮助决策者确定关键因素，并进行针对性的修正和优化。