2021届高考数学二轮复习核心热点突破-专题二第1讲 等差数列与等比数列
- 格式:doc
- 大小:452.50 KB
- 文档页数:18


专题8 等差数列与等比数列1.等差数列必记结论 (1)若项数为偶数2n,则S 2n =n(a 1+a 2n )=n(a n +a n+1);S 偶-S 奇=nd; 错误!未找到引用源。
=错误!未找到引用源。
. (2)若项数为奇数2n-1,则S 2n-1=(2n-1)a n ; S 奇-S 偶=a n ;错误!未找到引用源。
=错误!未找到引用源。
. 2.等比数列必记结论 (1)a k ,a k+m ,a k+2m ,…仍是等比数列,公比为q m (k,m ∈N *). (2)若数列{a n }的项数为2n,则错误!未找到引用考向一 等差数列基本量的计算 【典例】 (2020·全国Ⅱ卷)记S n 为等差数列错误!未找到引用源。
的前n 项和.若a 1=-2,a 2+a 6=2①,则错误!未找到引用源。
=________.① 根据基本量列方程② 前n 项和公式求解考向二 等比数列基本量的计算 【典例】(2020·全国Ⅰ卷)设{a n }是等比数列,且a 1+a 2+a 3=1,a 2+a 3+a 4=2,则a 6+a 7+a 8=( ) A.12B.24C.30D.321.在公比为错误!未找到引用源。
的等比数列错误!未找到引用源。
中,若sin 错误!未找到引用源。
=错误!未找到引用源。
,则cos 错误!未找到引用源。
的值是A.-错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
2.数列{a n}中,a1=2,a2=1,则错误!未找到引用源。
+错误!未找到引用源。
=错误!未找到引用源。
(n∈N*),则a10等于( )A.-5B.-错误!未找到引用源。
C.5D.错误!未找到引用源。
3.若数列{x n}满足lg x n+1=1+lg x n(n∈N+),且x1+x2+x3+…+x100=100,则lg(x101+x102+…+x200)的值为A.102B.101C.100D.994.我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )A.相邻两个节气晷长减少或增加的量为一尺B.春分和秋分两个节气的晷长相同C.立冬的晷长为一丈五寸D.立春的晷长比立秋的晷长短5.数列错误!未找到引用源。

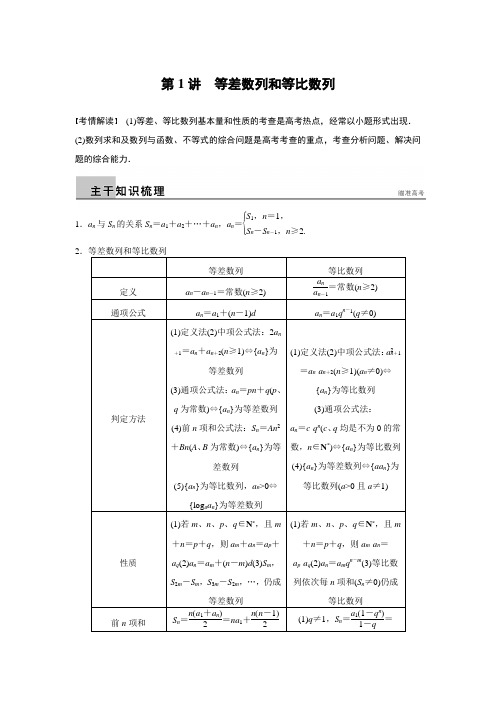



数列专题2第1讲 等差数列与等比数列等差、等比数列的基本运算 授课提示:对应学生用书第21页考情调研考向分析以考查等差、等比数列的通项、前n 项和的运算为主,在高考中既可以以选择、填空的形式进行考查,也可以以解答题的形式进行考查.解答题往往与等差(比)数列、数列求和、不等式等问题综合考查.1.等差(比)数列中a 1、n 、d (q )、a n 、S n 量的计算.2.等差、等比数列的交汇运算.1.(2019·开封模拟)设S n 为等差数列{a n }的前n 项和,若3S 3=S 2+S 4,a 5=-10,则a 1=( )A .-3B .-2C .2D .3解析:由题得⎩⎪⎨⎪⎧9a 1+9d =6a 1+7da 1+4d =-10,∴a 1=2,d =-3.故选C.答案:C2.(2019·攀枝花模拟)已知等差数列{a n }的公差为3,且a 1+a 3=8,则数列{a n }的前4项的和S 4的值为( )A .10B .16C .22D .35解析:∵等差数列{a n }的公差为3,且a 1+a 3=8, ∴2a 1+2×3=8, ∴a 1=1,∴S 4=4×1+4×32×3=22,故选C.答案:C3.(2019·晋城模拟)设正项等比数列{a n}的前n项和为S n,若S2=5,S4=85,则公比q =( )A.5 B.4C.3 D.2解析:因为S2=5,S4=85,S4-S2=80,所以⎩⎪⎨⎪⎧a1+a2=5a3+a4=80,两个方程左右两边分别相除,得q2=16,因为数列是正项等比数列,所以q=4,故选B.答案:B4.(2019·九江模拟)已知等差数列{a n}的前n项和为S n,若2a5-a2=2,则S15=( ) A.28 B.30C.56 D.60解析:设等差数列{a n}公差为d,由2a5-a2=2得2(a1+4d)-(a1+d)=a1+7d=2,∴a8=2,∴S15=15a8=15×2=30.故选B.答案:B[题后悟通]等差(比)数列基本运算的解题思路(1)设基本量:首项a1和公差d(公比q).(2)列、解方程(组):把条件转化为关于a1和d(或q)的方程(组),然后求解,注意整体计算,以减少运算量.等差、等比数列的判定与证明授课提示:对应学生用书第22页考情调研考向分析等差、等比数列的证明是考查的热点.在高考中主要以解答题的形式进行考查.解答题往往与等差(比)数列、数列求和、不等式等问题综合考查.1.定义法.2.等差(比)中项法.[题组练透]1.已知数列{a n }的前n 项和为S n ,且S n =2a n -3n (n ∈N *). (1)求a 1,a 2,a 3的值;(2)设b n =a n +3,证明数列{b n }为等比数列,并求通项公式a n . 解析:(1)因为数列{a n }的前n 项和为S n ,且S n =2a n -3n (n ∈N *). 所以n =1时,由a 1=S 1=2a 1-3×1,解得a 1=3,n =2时,由S 2=2a 2-3×2,得a 2=9, n =3时,由S 3=2a 3-3×3,得a 3=21.(2)证明:因为S n =2a n -3n , 所以S n +1=2a n +1-3(n +1), 两式相减,得a n +1=2a n +3,由b n =a n +3得b n +1=a n +1+3=2a n +6=2(a n +3), 所以b n +1=2b n (n ∈N *),且b 1=6,所以数列{b n }是以6为首项,2为公比的等比数列, 所以b n =6×2n -1,所以a n =b n -3=6×2n -1-3=3(2n-1).2.数列{a n }满足a 1=6,a n +1=6a n -9a n(n ∈N *).(1)求证:数列⎩⎨⎧⎭⎬⎫1a n -3是等差数列; (2)求数列{}lg a n 的前999项和.解析:(1)证明:数列{a n }满足:a 1=6,a n +1=6a n -9a n(n ∈N *),1a n +1-3=16a n -9a n-3=a n -3+33a n -3=13+1a n -3,所以,1a n +1-3-1a n -3=13,即数列⎩⎨⎧⎭⎬⎫1a n -3是以1a 1-3=13为首项,13为公差的等差数列.(2)由(1)得1a n -3=13+13(n -1), 解得:a n =3n +1n, 所以,lg a n =lg3n +1n=lg 3+lg(n +1)-lg n , 于是,T n =[lg 3+lg 2-lg 1]+[lg 3+lg 3-lg 2]+…+[lg 3+lg(n +1)-lg n ]=n lg 3+lg(n+1),当n=999时,T999=999lg 3+lg 1 000=3+999lg 3.[题后悟通]数列{a n}是等差数列或等比数列的证明方法(1)证明数列{a n}是等差数列的两种基本方法①利用定义,证明a n+1-a n(n∈N*)为一常数.②利用等差中项,即证明2a n=a n-1+a n+1(n≥2).(2)证明{a n}是等比数列的两种基本方法①利用定义,证明a n+1a n(n∈N*)为一常数.②利用等比中项,即证明a2n=a n-1a n+1(n≥2).等差、等比数列的性质授课提示:对应学生用书第23页考情调研考向分析以考查等差、等比数列的性质为主,在高考中既可以以选择题、填空题的形式进行考查,也可以以解答题的形式进行考查.解答题往往与等差(比)数列、数列求和、不等式等问题综合考查.1.等差、等比数列项的性质.2.等差、等比数列和的性质.[题组练透]1.在等差数列{a n}中,a2与a4是方程x2-4x+3=0的两根,则a1+a2+a3+a4+a5=( ) A.6 B.8C.10 D.12解析:∵a2与a4是方程x2-4x+3=0的两根,∴a2+a4=4=a1+a5=2a3,则a1+a2+a3+a4+a5=10.故选C.答案:C2.已知等差数列{a n}的前n项和为S n,S7=21,则a4=( )A .0B . 2C .3D .6解析:因为{a n }是等差数列,所以S 7=7a 1+a 72=21⇒a 1+a 7=6⇒2a 4=6⇒a 4=3,故选C.答案:C3.在正项等比数列{a n }中,a 1a 5+2a 3a 7+a 5a 9=16,且a 5与a 9的等差中项为4,则{a n }的公比是( )A .1B .2 C.22D. 2解析:由题意,正项等比数列{a n }中,a 1a 5+2a 3a 7+a 5a 9=16,可得a 23+2a 3a 7+a 27=(a 3+a 7)2=16,即a 3+a 7=4,a 5与a 9的等差中项为4,即a 5+a 9=8,设公比为q ,则q 2(a 3+a 7)=4q 2=8, 则q =2(负的舍去),故选D. 答案:D4.设等差数列{a n }的前n 项和为S n 若S 3=9,S 6=27,则S 9=( ) A .45 B .54 C .72D .81解析:因为{a n }为等差数列,所以S 3,S 6-S 3,S 9-S 6为等差数列,所以2(S 6-S 3)=S 3+S 9-S 6即36=9+S 9-27,所以S 9=54,故选B.答案:B[题后悟通]等差、等比数列性质问题的求解策略 抓 关 系 抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解用 性 质 数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的性质解题。

2021年高考数学二轮复习第一讲等差数列与等比数列一、选择题1.已知等差数列{an}中,前n项和为Sn,若a3+a9=6,则S11=( ) A.12 B.33 C.66 D.99解析:∵{an}为等差数列且a3+a9=6,∴a6+a6=a3+a9=6.∴a6=3.∴S11=a1+a112×11=a6+a62×11=11a6=11×3=33.答案:B2.在等比数列{an}中,若a1+a2=20,a3+a4=40,则数列{an}的前6项和S6=( ) A.120 B.140 C.160 D.180解析:∵{an}为等比数列,∴a1+a2,a3+a4,a5+a6为等比数列.∴(a3+a4)2=(a1+a2)(a5+a6).即a5+a6=(a3+a4)2a1+a2=40220=80.∴S6=a1+a2+a3+a4+a5+a6=20+40+80=140.答案:B3.已知数列{an}的前n项和Sn=n2-2n-1,则a3+a17=( ) A.15 B.17 C.34 D.398解析:∵Sn=n2-2n-1,∴a1=S1=12-2-1=-2.当n≥2时,an=Sn-Sn-1=n2-2n-1-[(n-1)2-2(n-1)-1]=n 2-(n -1)2+2(n -1)-2n -1+1=n 2-n 2+2n -1+2n -2-2n=2n -3.∴an =⎩⎪⎨⎪⎧-2,n =1,2n -3,n ≥2. ∴a 3+a 17=(2×3-3)+(2×17-3)=3+31=34.答案:C4.(xx·陕西卷)原命题为“若an +an +12<an ,n ∈N +,则{an }为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )A .真,真,真B .假,假,真C .真,真,假D .假,假,假解析:由an +an +12<an ⇒an +1<an ⇒{an }为递减数列,所以原命题为真命题;逆命题:若{an }为递减数列,则an +an +12<an ,n ∈N +;若{an }为递减数列,则an +1<an ,即an +an +12<an ,所以逆命题为真; 否命题:若an +an +12≥an ,n ∈N +,则{an }不为递减数列;由an +an +12≥an ⇒an ≤an +1⇒{an }不为递减数列,所以否命题为真;因为逆否命题的真假为原命题的真假相同,所以逆否命题也为真命题.故选A.答案:A5.某棵果树前n 年的总产量Sn 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为( )A .5B .7C .9D .11解析:由图可知6,7,8,9这几年增长最快,超过平均值,所以应该加入m =9,因此选C.答案:C二、填空题6. (xx·江西卷)在等差数列{an }中,a 1=7,公差为d ,前n 项和为Sn ,当且仅当n =8时Sn 取最大值,则d 的取值范围是________.解析:由题意得:a 8>0,a 9<0,所以7+7d >0,7+8d <0,即-1<d <-78. 答案:⎝⎛⎭⎪⎫-1,-787.设公比为q (q >0)的等比数列{an }的前n 项和为Sn .若S 2=3a 2+2,S 4=3a 4+2,则q =________________________________________________________________________.解析:将S 2=3a 2+2,S 4=3a 4+2两个式子全部转化成用a 1,q 表示的式子, 即⎩⎪⎨⎪⎧a 1+a 1q =3a 1q +2,a 1+a 1q +a 1q 2+a 1q 3=3a 1q 3+2,两式作差得:a 1q 2+a 1q 3=3a 1q (q 2-1),即:2q 2-q -3=0,解得q =32或q =-1(舍去). 答案:328.(xx·广东卷)等比数列{an }的各项均为正数,且a 1a 5=4,则log2a 1+log2a 2+log2a 3+log2a 4+log2a 5=__________.解析:由题意知a 1a 5=a 23=4,且数列{an }的各项均为正数,所以a 3=2,∴a 1a 2a 3a 4a 5=(a 1a 5)·(a 2a 4)·a 3=(a 23)2·a 3=a 53=25,∴log2a 1+log2a 2+log2a 3+log2a 4+log2a 5=log2(a 1a 2a 3a 4a 5)=log225=5. 答案:5三、解答题9.已知数列{an }满足,a 1=1,a 2=2,an +2 =an +an +12,n ∈N*.(1)令bn =an +1-an ,证明:{bn }是等比数列;(2)求{an }的通项公式.(1)证明:b 1=a 2-a 1=1,当n ≥2时,b n =a n +1-a n =an -1+an 2-a n =-12(a n -a n -1)=-12b n -1, 所以{bn }是以1为首项,-12为公比的等比数列. (2)解析:由(1)知b n =a n +1-a n =⎝ ⎛⎭⎪⎫-12n -1, 当n ≥2时,a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1) =1+1+⎝ ⎛⎭⎪⎫-12+…+⎝ ⎛⎭⎪⎫-12n -2=1+1-⎝ ⎛⎭⎪⎫-12n -11-⎝ ⎛⎭⎪⎫-12=1+23⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-12n -1 =53-23⎝ ⎛⎭⎪⎫-12n -1, 当n =1时,53-23⎝ ⎛⎭⎪⎫-121-1=1=a 1. 所以a n =53-23⎝ ⎛⎭⎪⎫-12n -1(n ∈N *).10.(xx·广东卷)设各项均为正数的数列{an }的前n 项和为S n ,满足4S n =a 2n +1-4n -1,n ∈N*,且a 2,a 5,a 14构成等比数列.(1) 证明:a 2=4a 1+5;(2) 求数列{an }的通项公式;(3) 证明:对一切正整数n ,有1a 1a 2+1a 2a 3+…+1anan +1<12.(1)证明:当n =1时,4a 1=a 22-5,a 22=4a 1+5,∵a n>0,∴a2=4a1+5.(2)解析:当n≥2时,4S n-1=a2n-4(n-1)-1,4a n=4Sn-4Sn-1=a2n+1-a2n-4 ,a2n+1=a2n+4a n+4=(a n+2)2,∵a n>0,∴a n+1=a n+2,所以当n≥2时,{a n}是公差d=2的等差数列.因为a2,a5,a14构成等比数列,所以a25=a2·a14,(a2+6)2=a2·(a2+24),解得a2=3,由(1)可知,4a1=a22-5=4,∴a1=1,因为a2-a1=3-1=2,所以{an}是首项为1,公差d=2的等差数列.所以数列{an}的通项公式为a n=2n-1.(3)证明:1a1a2+1a2a3+…+1anan+1=11×3+13×5+15×7+…+1(2n-1)(2n+1)=12×[⎝⎛⎭⎪⎫1-13+⎝⎛⎭⎪⎫13-15+⎝⎛⎭⎪⎫15-17+…+⎝⎛⎭⎪⎫12n-1-12n+1]=12×⎝⎛⎭⎪⎫1-12n+1<12.2 h35671 8B57 譗2986774AB 璫U21830 5546 商 35756 8BAC 讬c$39774 9B5E 魞26295 66B7 暷。




专题二 数列 第1讲 等差数列与等比数列第一课 等差、等比数列基本运算和性质一:前测回顾1.已知{a n }是等差数列,若2a 7-a 5-3=0,则a 9=________.2.已知{a n }是等差数列,S n 是其前n 项和.若a 1+a 22=-3,S 5=10,则a 9的值是________.3.已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=________.4.已知数列{a n }是等比数列,S n 为其前n 项和,若a 1+a 2+a 3=4,a 4+a 5+a 6=8,则S 12=________.5.若等差数列{a n }满足a 7+a 8+a 9>0,a 7+a 10<0,则当n =________时,{a n }的前n 项和最大.二:方法联想1.基本量运算 2.性质的应用3.等差数列S n 的最值问题 三:热点训练热点一 等差、等比数列的基本运算1.数列{a n }中,a 1=2,a m +n =a m a n .若a k +1+a k +2+…+a k +10=215-25,则k =( ) A.2B.3C.4D.52.若等比数列{a n }的前n 项和为S n ,已知a 2a 5=3a 3,且a 4与9a 7的等差中项为2,则S 5=( ) A.1123B.112C.12127D.1213.设{a n }是等差数列,a 1=-10,且a 2+10,a 3+8,a 4+6成等比数列. ①求{a n }的通项公式;②记{a n }的前n 项和为S n ,求S n 的最小值.4.已知{a n }是公差不为零的等差数列,a 4=26,且a 1,a 2,a 7成等比数列.①求数列{a n }的通项公式;②设b n =(-1)n +1a n ,数列{b n }的前n 项和为T n ,求T 511.热点二 等差(比)数列的性质1.在数列{a n }中,2a n +1=a n +a n +2,且a n ≠0.若a n -1-a 2n +a n +1=0(n ≥2),且S 2n -1=38,则n =( ) A.38 B.20 C.10 D.92.已知正项等比数列{a n }的前n 项和为S n ,且S 8-2S 4=5,则a 9+a 10+a 11+a 12的最小值为( ) A.25B.20C.15D.103.在各项均为正数的等差数列{}n a 中,n S 为其前n 项和,7S =14,则2614t a a =+的最小值为( ) A .9B .94C .52D .24.在等差数列{}n a 中,0223276=+-a a a 数列{}n b 是等比数列,且77a b =,则()268log b b =( )A .1B .2C .4D .85.数列{}n a 满足13n n a a ++=且2469a a a =++,则()6579log a a a ++的值是( ) A .-2 B .12-C .2D .126.设等差数列{}n a 的前n 项和n S ,且1310670,0,0a a a a a >+><,则满足0n S >的最大自然数n 的值为( ) A .6 B .7 C .12D .137.已知数列{a n }的各项都为正数,对任意的m ,n ∈N *,a m ·a n =a m +n 恒成立,且a 3·a 5+a 4=72,则log 2a 1+log 2a 2+…+log 2a 7=________.8.设等比数列{a n }的前n 项和为S n ,若S m -1=5,S m =-11,S m +1=21,则m 等于________. 9.在等差数列{a n }中,a 1=-2 015,其前n 项和为S n ,若S 1212-S 1010=2,则2021s 的值为________. 10.设等比数列{a n }满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为________.专题二 数列 第1讲 等差数列与等比数列第二课 等差、等比数列基本运算和性质一、前测回顾1.函数y =x 2(x >0)的图象在点(a k ,a 2k )处的切线与x 轴交点的横坐标为a k +1,k 为正整数,a 1=16,则a 1+a 3+a 5=________.2.已知数列{a n }的前n 项和S n =an 2+bn +c (a ,b ,c ∈R ),则“c =0”是“{a n }是等差数列”的______条件.3.已知1a ,1b ,1c 成等差数列,求证:b +c a ,c +a b ,a +b c 也成等差数列. 4.已知a n +1= 2a n a n +2,a 1=2 ,求证:数列{1a n }的等差数列.5.数列{a n }前n 项和为S n ,若a n +S n =n ,令b n =a n -1,求证:数列{b n }是等比数列.二、方法联想1.等差、等比数列的证明2.等差、等比数列的判断三、热点专练1.已知数列{a n }中,a 1=2,且a 2n +1a n =4(a n +1-a n )(n ∈N *),则其前9项和S 9=________.2.已知数列{a n }中a 1=23,a n +1=3a n 2a n +1(n ∈N *),求证:⎩⎨⎧⎭⎬⎫1a n -1是等比数列,并求出{a n }的通项公式.3.已知数列{a n },{b n }满足a 1=3,a n b n =2,b n +1=a n (b n -21+a n ),n ∈N *,证明数列{1b n }是等差数列,并求数列{b n }的通项公式.4.已知数列{a n }的前n 项和S n =1+λa n ,其中λ≠0,证明{a n }是等比数列,并求其通项公式.5 已知数列{a n }是等比数列(q ≠-1),S n 是其前n 项的和,求证:S k ,S 2k -S k ,S 3k -S 2k 仍成等比数列.6 .设数列{ a n }的前n 项和为S n ,n ∈N *.已知a 1=1,a 2=32,a 3=54,且当n ≥2时,4S n +2+5S n =8S n+1+S n -1.(1)求a 4的值;(2)证明:{a n +1-12a n }为等比数列.7.已知数列{a n }的前n 项和为S n ,a 1=1,a n >0,S 2n =a 2n +1-λS n +1,其中λ为常数.(1)证明:S n +1=2S n +λ;(2)是否存在实数λ,使得数列{a n }为等比数列?若存在,求出λ;若不存在,请说明理由.8.已知数列{a n }的前n 项和为S n ,且2S n =3a n -3n +1+3(n ∈N *).(1)设b n =a n3n ,求证:数列{b n }为等差数列,并求出数列{a n }的通项公式; (2)设c n =a n n -a n3n ,T n =c 1+c 2+c 3+…+c n ,求T n .9.从①前n 项和S n =n 2+p (p ∈R );②a n =a n +1-3;③a 6=11且2a n +1=a n +a n +2这三个条件中任选一个,填至横线上,并完成解答.在数列{a n }中,a 1=1,________,其中n ∈N *. (1)求数列{a n }的通项公式;(2)若a 1,a n ,a m 成等比数列,其中m ,n ∈N *,且m >n >1,求m 的最小值. (注:如果选择多个条件分别解答,按第一个解答计分)10.已知{a n }是公比为q 的无穷等比数列,其前n 项和为S n ,满足a 3=12,________.是否存在正整数k ,使得S k >2 020?若存在,求k 的最小值;若不存在,说明理由.从①q =2,②q =12,③q =-2这三个条件中任选一个,补充在上面横线处并作答. (注:如果选择多个条件分别解答,按第一个解答计分)专题二 数列 解析 第1讲 等差数列与等比数列高考定位1.等差、等比数列基本运算和性质的考查是高考热点,经常以选择题、填空题的形式出现;2.数列的通项也是高考热点,常在解答题中的第(1)问出现,难度中档以下.第一课 等差、等比数列基本运算和性质一:前测回顾1.已知{a n }是等差数列,若2a 7-a 5-3=0,则a 9=________. 答案:3.解析:方法一:设公差为d ,则2(a 1+6d )-(a 1+4d )-3=0,即a 1+8d =3,所以a 9=3.方法二:由等差数列的性质得a 5+a 9=2a 7,所以(a 5+a 9)-a 5-3=0,即a 9=3.2.已知{a n }是等差数列,S n 是其前n 项和.若a 1+a 22=-3,S 5=10,则a 9的值是________.答案:20.解析:设等差数列{a n }公差为d ,由题意可得:⎩⎪⎨⎪⎧a 1+(a 1+d )2=-3,5a 1+5×42d =10,解得⎩⎪⎨⎪⎧a 1=-4,d =3, 则a 9=a 1+8d =-4+8×3=20.3.已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=________. 答案:-7.解析:设数列{a n }的公比为q ,由⎩⎪⎨⎪⎧ a 4+a 7=2,a 5·a 6=a 4·a 7=-8得⎩⎪⎨⎪⎧ a 4=4,a 7=-2或⎩⎪⎨⎪⎧a 4=-2,a 7=4,所以⎩⎪⎨⎪⎧a 1=-8,q 3=-12或⎩⎪⎨⎪⎧ a 1=1,q 3=-2,所以⎩⎪⎨⎪⎧ a 1=-8,a 10=1或⎩⎪⎨⎪⎧a 1=1,a 10=-8,所以a 1+a 10=-7.4.已知数列{a n }是等比数列,S n 为其前n 项和,若a 1+a 2+a 3=4,a 4+a 5+a 6=8,则S 12=________.答案:60.解析:方法一:设等比数列{a n }公比为q ,由题意可得q ≠1,则由⎩⎨⎧ a 1(1-q 3)1-q =4,a 1(1-q 6)1-q =4+8 ,得⎩⎪⎨⎪⎧a 11-q =-4,q 3=2,所以S 12=a 1 (1-q 12)1-q =60.方法二:由等比数列的性质可知,数列S 3,S 6-S 3,S 9-S 6,S 12-S 9是等比数列,即数列4,8,S 9-S 6,S 12-S 9是等比数列,所以S 9-S 6=16,S 12-S 9=32,所以S 12=(S 12-S 9)+(S 9-S 6)+(S 6-S 3)+S 3=32+16+8+4=60.5.若等差数列{a n }满足a 7+a 8+a 9>0,a 7+a 10<0,则当n =________时,{a n }的前n 项和最大. 答案:8.解析:根据题意知a 7+a 8+a 9=3a 8>0,即a 8>0.又a 8+a 9=a 7+a 10<0,所以a 9<0,所以当n =8时,{a n }的前n 项和最大.二:方法联想1.基本量运算等差数列的通项公式及前n 项和公式,共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了用方程的思想解决问题.求解涉及等差、等比数列的运算问题时,通常会抓住a 1、d (或q ),列出方程、不等式或方程组求解,这样做的好处是思路简洁,目标明确,但有时运算量比较大.为了减少运算量,我们要掌握一些运算技巧,例如“设而不求,整体代入”.2.性质的应用用好等差、等比数列的性质也能减少运算量:方法(1)在等差数列{a n }中,若m +n =p +q 则a m +a n =a p +a q .特别若m +n =2p ,则a m +a n =2a p . 在等比数列{a n }中,若m +n =p +q 则a m a n =a p a q .特别若m +n =2p ,则a m a n =a p 2. (2) 在等差数列{a n }中,由S n =n (a 1+a n )2得,若n 为奇数,则S 2n -1=(2n -1)a n . 方法 在等差数列{a n }中,S n ,S 2n -S n ,S 3n -S 2n 成等差数列.在等比数列{a n }中,一般情况下S n ,S 2n -S n ,S 3n -S 2n 成等比数列.3.等差数列S n 的最值问题方法 在等差数列{ a n }中S n 的最值问题:方法1:(1)当a 1>0,d <0时,满足⎩⎨⎧a m ≥0,a m +1≤0的项数m 使得S m 取最大值. (2)当a 1<0,d >0时,满足⎩⎨⎧a m ≤0,a m +1≥0的项数m 使得S m 取最小值,方法2:由S n 的解析式,结合二次函数图象分析. 三:热点训练热点一 等差、等比数列的基本运算1.数列{a n }中,a 1=2,a m +n =a m a n .若a k +1+a k +2+…+a k +10=215-25,则k =( ) A.2B.3C.4D.5解析 ∵a 1=2,a m +n =a m a n ,令m =1,则a n +1=a 1a n =2a n , ∴{a n }是以a 1=2为首项,2为公比的等比数列,∴a n =2×2n -1=2n . 又∵a k +1+a k +2+…+a k +10=215-25,∴2k +1(1-210)1-2=215-25,即2k +1(210-1)=25(210-1),∴2k +1=25,∴k +1=5,∴k =4. 答案 C2.若等比数列{a n }的前n 项和为S n ,已知a 2a 5=3a 3,且a 4与9a 7的等差中项为2,则S 5=( ) A.1123B.112C.12127D.121解析:设等比数列{a n }的公比为q ,由已知得a 2a 5=a 3a 4=3a 3,因为a 3≠0,所以a 4=3,即a 1q 3=3 ①.因为a 4与9a 7的等差中项为2,所以a 4+9a 7=a 4(1+9q 3)=4 ②, 联立①②解得q =13,a 1=81.所以S 5=81×⎣⎡⎦⎤1-⎝⎛⎭⎫1351-13=121.答案 D3.设{a n }是等差数列,a 1=-10,且a 2+10,a 3+8,a 4+6成等比数列. ①求{a n }的通项公式;②记{a n }的前n 项和为S n ,求S n 的最小值. 解 ①设{a n }的公差为d .因为a 1=-10,所以a 2=-10+d ,a 3=-10+2d ,a 4=-10+3d . 因为a 2+10,a 3+8,a 4+6成等比数列,所以(a 3+8)2=(a 2+10)(a 4+6). 所以(-2+2d )2=d (-4+3d ).解得d =2.所以a n =a 1+(n -1)d =2n -12. ②法一 由①知,a n =2n -12.则当n ≥7时,a n >0;当n =6时,a n =0;当n <6时,a n <0; 所以S n 的最小值为S 5=S 6=-30.法二 由①知,S n =n 2(a 1+a n )=n (n -11)=⎝⎛⎭⎫n -1122-1214,又n ∈N *,∴当n =5或n =6时,S n 的最小值S 5=S 6=-30.4.已知{a n }是公差不为零的等差数列,a 4=26,且a 1,a 2,a 7成等比数列.①求数列{a n }的通项公式;②设b n =(-1)n +1a n ,数列{b n }的前n 项和为T n ,求T 511.(2)解 ①设数列{a n }的公差为d ,d ≠0.∵a 1,a 2,a 7成等比数列,∴a 22=a 1a 7,即(a 1+d )2=a 1(a 1+6d ),则d 2=4a 1d .又d ≠0,∴d =4a 1,①由于a 4=a 1+3d =26,②联立①②,得⎩⎪⎨⎪⎧d =4a 1,a 1+3d =26,解得⎩⎪⎨⎪⎧a 1=2,d =8,∴a n =2+8(n -1)=8n -6. ②∵b n =(-1)n +1a n =(-1)n +1(8n -6).∴T 511=b 1+b 2+…+b 511=2-10+18-26+…+4 066-4 074+4 082 =(2-10)+(18-26)+…+(4 066-4 074)+4 082=-8×255+4 082=2 042.热点二 等差(比)数列的性质1.在数列{a n }中,2a n +1=a n +a n +2,且a n ≠0.若a n -1-a 2n +a n +1=0(n ≥2),且S 2n -1=38,则n =( )A.38B.20C.10D.9【详解】在数列{a n }中,因为2a n +1=a n +a n +2,所以a n +2-a n +1=a n +1-a n ,所以数列{a n }为等差数列.由a n -1-a 2n +a n +1=0(n ≥2),得2a n -a 2n =0,又a n ≠0,解得a n =2.又S 2n -1=38,即(2n -1)(a 1+a 2n -1)2=(2n -1)a n =38, 即(2n -1)×2=38,解得n =10.2.已知正项等比数列{a n }的前n 项和为S n ,且S 8-2S 4=5,则a 9+a 10+a 11+a 12的最小值为( ) A.25B.20C.15D.10【详解】在正项等比数列{a n }中,S n >0.因为S 8-2S 4=5,则S 8-S 4=5+S 4, 易知S 4,S 8-S 4,S 12-S 8是等比数列,所以(S 8-S 4)2=S 4·(S 12-S 8), 所以a 9+a 10+a 11+a 12=S 12-S 8=(S 4+5)2S 4=25S 4+S 4+10≥225S 4·S 4+10=20(当且仅当S 4=5时取等号).故a 9+a 10+a 11+a 12的最小值为20.3.在各项均为正数的等差数列{}n a 中,n S 为其前n 项和,7S =14,则2614t a a =+的最小值为( ) A .9B .94C .52D .2【答案】B【详解】由题意172677()7()1422a a a a S ++===,∴264a a +=, ∴26262614114()()4t a a a a a a =+=++62264119(5)(5444a a a a =++≥+=,当且仅当62264a a a a =,即622a a =时等号成立.故选:B . 4.在等差数列{}n a 中,0223276=+-a a a 数列{}n b 是等比数列,且77a b =,则()268log b b =( )A .1B .2C .4D .8【答案】C【解析】根据等差数列的性质得:7682a a a +=,0223276=+-a a a 变为:2774a a =, 解得74a =,70a =(舍去),所以774b a ==,则268716b b b ==.所以()2682log log 164b b ==故选C .5.数列{}n a 满足13n n a a ++=且2469a a a =++,则()6579log a a a ++的值是( ) A .-2 B .12- C .2 D .12【答案】C【解析】由13n n a a ++=,可知数列{}n a 是公差为3的等差数列, 因为246439a a a =a =++,所以43a =,所以7433912a a +d ==+=()()6579676log log 3log 362a a a =a ++==.故选C.6.设等差数列{}n a 的前n 项和n S ,且1310670,0,0a a a a a >+><,则满足0n S >的最大自然数n 的值为( ) A .6 B .7 C .12D .13【答案】C【解析】由3100a a +>,利用等差数列的性质可得:310670a a a a +=+>,又67a a <0,1a >0, ∴6a >0,7a <0.∴()()()1121131267137121360,13022a a a a S a a S a ++==+>==<,则满足S n >0的最大自然数n 的值为12.故选C.【点睛】求解等差数列问题时,要多多使用等差数列的性质,如{}n a 为等差数列,若m n p q +=+,则m n p q a a a a +=+.由此得:1()2n n n a a S +=, 当21n k =-为奇数时,21(21)2(21)2kk k k a S k a --==-, 当2n k =为偶数时,1212()()2k k k k k k a a S k a a +++==+. 7.已知数列{a n }的各项都为正数,对任意的m ,n ∈N *,a m ·a n =a m +n 恒成立,且a 3·a 5+a 4=72,则log 2a 1+log 2a 2+…+log 2a 7=________.【详解】因为对任意的m ,n ∈N *,a m ·a n =a m +n 恒成立,令m =1,则a 1·a n =a 1+n 对任意的n ∈N *恒成立,∴数列{a n }为等比数列,公比为a 1,由等比数列的性质有a 3a 5=a 24,因为a 3·a 5+a 4=72,则a 24+a 4=72,∵a 4>0,∴a 4=8,∴log 2a 1+log 2a 2+…+log 2a 7=log 2(a 1·a 2·…·a 7)=log 2a 74=log 287=21.8.设等比数列{a n }的前n 项和为S n ,若S m -1=5,S m =-11,S m +1=21,则m 等于________. 答案:5.9..在等差数列{a n }中,a 1=-2 015,其前n 项和为S n ,若S 1212-S 1010=2,则2021s 的值为________. 答案:-2021.解析:根据等差数列的性质,得数列⎭⎬⎫⎩⎨⎧n s n 也是等差数列,由已知可得S 11=a 1=-2 015,由S 1212-S 1010=2=2d ,得公差d =1.20212021-=s10..设等比数列{a n }满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为________. 答案:64.解析:设等比数列{a n }的公比为q ,则由a 1+a 3=10,a 2+a 4=q (a 1+a 3)=5,知q =12.又a 1+a 1q 2=10,所以a 1=8.故a 1a 2…a n =a n 1q 1+2+…+(n -1)=23n·⎝⎛⎭⎫12(n -1)n 2=23n -n 22+n 2=2-n 22+72n .记t =-n 22+7n 2=-12(n 2-7n )=-12⎝⎛⎭⎫n -722+498,结合n ∈N *可知n =3或4时,t 有最大值6.又y =2t 为增函数,从而a 1a 2…a n 的最大值为26=64.第二课 等差、等比数列基本运算和性质一、前测回顾1.函数y =x 2(x >0)的图象在点(a k ,a 2k )处的切线与x 轴交点的横坐标为a k +1,k 为正整数,a 1=16,则a 1+a 3+a 5=________.答案:21.解析:在点(a k ,a 2k )处的切线方程为:y -a 2k =2a k (x -a k ),当y =0时,解得x =a k 2,所以a k +1=a k2,故{a n }是a 1=16,q =12的等比数列,即a n =16×⎝⎛⎭⎫12n -1,所以a 1+a 3+a 5=16+4+1=21. 2.已知数列{a n }的前n 项和S n =an 2+bn +c (a ,b ,c ∈R ),则“c =0”是“{a n }是等差数列”的______条件. 答案:充要.解析:a 1=a +b +c ,a 2=S 2-a 1=3a +b ,a 3=S 3-S 2=5a +b ,若{a n }是等差数列,则2a 2=a 1+a 3,解得c =0,所以“c =0”是“{a n }是等差数列”的必要条件;当c =0时,S n =an 2+bn ,当n =1时,a 1=a +b ;当n ≥2时,a n =S n -S n -1=2an +b -a ,显然当n =1时也满足上式,所以a n =2an +b -a (n ∈N *),进而可得a n -a n -1=2a (n ∈N *),所以{a n }是等差数列,所以“c =0”是“{a n }是等差数列”的充分条件; 综上可知,“c =0”是“{a n }是等差数列”的充要条件.3.已知1a ,1b ,1c 成等差数列,求证:b +c a ,c +a b ,a +b c 也成等差数列.解:由已知得b (a +c )=2ac ,所以b +c a +a +b c =b (a +c )+a 2+c 2ac =2ac +a 2+c 2ac=2(a +c )b , 所以b +c a ,c +a b ,a +bc 也成等差数列.4.已知a n +1= 2a n a n +2,a 1=2 ,求证:数列{1a n }的等差数列.解:由已知,a 1=2,故a n ≠0,所以1 a n +1=a n +22a n =1 a n +12,所以1 a n +1-1 a n =12,所以数列{1a n }是等差数列.5.数列{a n }前n 项和为S n ,若a n +S n =n ,令b n =a n -1,求证:数列{b n }是等比数列. 解:由a n +S n =n ,得n ≥2时,a n -1+S n -1=n -1,两式相减得2a n -a n -1=1, 即2b n =b n -1.从而有b n b n -1=12(常数),所以数列{b n }是等比数列.二、方法联想1.等差、等比数列的证明 方法 证明数列是等差数列:方法1 定义法,即当n ∈N *时,a n +1-a n 为同一常数. 方法2 中项公式法,即当n ∈N*时,2a n +1=a n +a n +2均成立.说明:得到2a n +1=a n +a n +2后,最好改写为a n +1-a n =a n -a n -1=…=a 2-a 1,回到定义. 方法 证明数列是等比数列:方法1 定义法,即当n ∈N *时,a n +1a n 为同一常数.方法2 中项公式法,即当n ∈N *时,a n +12=a n a n +2均成立,且数列{a n }没有0. 说明:得到2a n +1=a n +a n +2后,最好改写为a n +1a n =a n a n -1=…=a 2a 1,回到定义.2.等差、等比数列的判断判断数列是等差数列方法1 定义法,即当n ≥1且n ∈N*时,a n +1-a n 为同一常数. 方法2 中项公式法,即当n ≥1且n ∈N *时,2a n +1=a n +a n +2均成立. 方法3 特殊值法,如前3项成等差,再证明其对任意n ∈N *成等差数列. 方法4 通项为一次形式,即a n =an +b .方法5 前n 项和为不含常数项的二次形式,即S n =an 2+bn . 方法6 若数列{a n }为等比数列,则{log a a n }为等差数列. 注意 方法4、5、6只能做为判断,作为解答题需要证明. 判断数列不是等差数列方法 通常用特殊值法,如取连续3项验证不成等差数列. 判断数列是等比数列方法1 定义法,即当n ∈N *时,a n +1a n 为同一常数.方法2 中项公式法,即当n ∈N *时, a n +12=a n a n +2均成立.方法3 特殊值法,如前3项成等比,再证明其对任意n ∈N *成等比数列. 方法4 通项公式为指数幂形式,即a n =aq n . 方法5 若数列{a n }为等差数列,则{a an }为等比数列. 注意 方法4、5只能做为判断,作为解答题需要证明. 判断数列不是等比数列方法 通常用特殊值法,如取连续3项验证不成等比数列.三、热点专练1.已知数列{a n }中,a 1=2,且a 2n +1a n =4(a n +1-a n )(n ∈N *),则其前9项和S 9=________. (由定义判定等比数列) 答案:1 022.解析:由已知,得a 2n +1=4a n a n +1-4a 2n ,即a 2n +1-4a n a n +1+4a 2n =(a n +1-2a n )2=0,所以a n +1=2a n ,又因为a 1=2,所以数列{a n }是首项为2,公比为2的等比数列,故S 9=2×(1-29)1-2=210-2=1 022.2.已知数列{a n }中a 1=23,a n +1=3a n 2a n +1(n ∈N *),求证:⎩⎨⎧⎭⎬⎫1a n -1是等比数列,并求出{a n }的通项公式.(根据定义证明等比数列)解:由题意a n ≠0,a n ≠1,记b n =1a n -1,则b n +1b n =1a n +1-11a n -1=2a n +13a n -11a n -1=2a n +1-3a n 3-3a n =1-a n 3(1-a n )=13,又b 1=1a 1-1=32-1=12,所以⎩⎨⎧⎭⎬⎫1a n -1是首项为12,公比为13的等比数列.所以1a n -1=12×⎝⎛⎭⎫13n -1,即a n =2×3n -11+2×3n -1.所以数列{a n }的通项公式为a n =2×3n -11+2×3n -1. 3.已知数列{a n },{b n }满足a 1=3,a n b n =2,b n +1=a n (b n -21+a n ),n ∈N *,证明数列{1b n }是等差数列,并求数列{b n }的通项公式. (根据定义证明等差数列)解:因为a n b n =2,所以a n =2b n ,则b n +1=a n b n -2a n1+a n =2-4b n1+2b n=2-4b n +2=2b n b n +2,所以1b n +1-1b n =12.又a 1=3,所以b 1=23.故1b n 是首项为32,公差为12的等差数列,即1b n =32+(n -1)×12=n +22,所以b n =2n +2. 4.已知数列{a n }的前n 项和S n =1+λa n ,其中λ≠0,证明{a n }是等比数列,并求其通项公式. (由S n 与a n 关系,结合定义证明等比数列)解:由题意得a 1=S 1=1+λa 1,故λ≠1,a 1=11-λ,a 1≠0.由S n =1+λa n ,S n +1=1+λa n +1, 得a n +1=λa n +1-λa n ,即a n +1(λ-1)=λa n ,由a 1≠0,λ≠0得a n ≠0, 所以a n +1a n =λλ-1.因此{a n }是首项为11-λ,公比为λλ-1的等比数列,于是a n =11-λ⎝⎛⎭⎫λλ-1n -1.5 已知数列{a n }是等比数列(q ≠-1),S n 是其前n 项的和,求证:S k ,S 2k -S k ,S 3k -S 2k 仍成等比数列. 解:方法一:(1)当q =1时,结论显然成立;(2)当q ≠1时, S k =a 1(1-q k )1-q ,S 2k =a 1(1-q 2k )1-q ,S 3k =a 1(1-q 3k )1-q . S 2k -S k =a 1(1-q 2k )1-q -a 1(1-q k )1-q =a 1q k (1-q k )1-q . S 3k -S 2k =a 1(1-q 3k )1-q -a 1(1-q 2k )1-q =a 1q 2k (1-q k )1-q .所以(S 2k -S k )2=a 21q 2k (1-q k )2(1-q )2S k ·(S 3k -S 2k )=a 1(1-q k )1-q ·a 1q 2k (1-q k )1-q =a 12q 2k (1-q k )2(1-q )2. 所以(S 2k -S k )2=S k ·(S 3k -S 2k ), 又因为q ≠-1,所以S k ,S 2k -S k ,S 3k -S 2k 中没有零, 所以S 2k -S k S k =S 3k -S 2kS 2k -S k ,所以S k ,S 2k -S k ,S 3k -S 2k 成等比数列. 方法二:S 2k -S k =(a 1+a 2+a 3+…a 2k )-(a 1+a 2+a 3+…a k )=a k +1+a k +2+a k +3+…a 2k =q k (a 1+a 2+a 3+…a k )=q k S k ≠0. 同理,S 3k -S 2k =a 2k +1+a 2k +2+a 2k +3+…a 3k = q 2k S k ≠0. 所以(S 2k -S k )2=S k ·(S 3k -S 2k ),下同方法一.6 .设数列{ a n }的前n 项和为S n ,n ∈N *.已知a 1=1,a 2=32,a 3=54,且当n ≥2时,4S n +2+5S n =8S n+1+S n -1.(1)求a 4的值;(2)证明:{a n +1-12a n }为等比数列. 解:(1)当n =2时,4S 4+5S 2=8S 3+S 1,即4×(1+32+54+a 4)+5×(1+32)=8×(1+32+54)+1,解得a 4=78. (2)由4S n +2+5S n =8S n +1+S n -1 (n ≥2), 得4S n +2-4S n +1+S n -S n -1=4S n +1-4S n (n ≥2), 即4a n +2+a n =4a n +1 (n ≥2).∵4a 3+a 1=4×54+1=6=4a 2,∴4a n +2+a n =4a n +1,∴a n +2-12a n +1a n +1-12a n =4a n +2-2a n +14a n +1-2a n =4a n +1-a n -2a n +14a n +1-2a n =2a n +1-a n 2(2a n +1-a n )=12 ∴数列{a n +1-12a n }是以a 2-12a 1=1为首项,12为公比的等比数列.7.已知数列{a n }的前n 项和为S n ,a 1=1,a n >0,S 2n =a 2n +1-λS n +1,其中λ为常数.(1)证明:S n +1=2S n +λ;(2)是否存在实数λ,使得数列{a n }为等比数列?若存在,求出λ;若不存在,请说明理由.(1)证明 ∵a n +1=S n +1-S n ,S 2n =a 2n +1-λS n +1,∴S 2n =(S n +1-S n )2-λS n +1,则S n +1(S n +1-2S n -λ)=0.∵a n >0,知S n +1>0,∴S n +1-2S n -λ=0,故S n +1=2S n +λ. (2)解 由(1)知,S n +1=2S n +λ,当n ≥2时,S n =2S n -1+λ,两式相减,a n +1=2a n (n ≥2,n ∈N *), 所以数列{a n }从第二项起成等比数列,且公比q =2.又S 2=2S 1+λ,即a 2+a 1=2a 1+λ,∴a 2=a 1+λ=1+λ>0,得λ>-1.因此a n =⎩⎪⎨⎪⎧1,n =1,(λ+1)·2n -2,n ≥2. 若数列{a n }是等比数列,则a 2=1+λ=2a 1=2. ∴λ=1,经验证得λ=1时,数列{a n }是等比数列.探究提高 1.判定等差(比)数列的主要方法:(1)定义法:对于任意n ≥1,n ∈N *,验证a n +1-a n ⎝⎛⎭⎫或a n +1a n 为与正整数n 无关的一常数;(2)中项公式法.2.a n +1a n =q 和a 2n =a n -1a n +1(n ≥2)都是数列{a n }为等比数列的必要不充分条件,判定时还要看各项是否为零.8.已知数列{a n }的前n 项和为S n ,且2S n =3a n -3n +1+3(n ∈N *).(1)设b n =a n3n ,求证:数列{b n }为等差数列,并求出数列{a n }的通项公式;(2)设c n =a n n -a n3n ,T n =c 1+c 2+c 3+…+c n ,求T n . (1)证明 由已知2S n =3a n -3n +1+3(n ∈N *),① n ≥2时,2S n -1=3a n -1-3n +3,②①-②得:2a n =3a n -3a n -1-2·3n ⇒a n =3a n -1+2·3n , 故a n 3n =a n -13n -1+2,则b n -b n -1=2(n ≥2).又n =1时,2a 1=3a 1-9+3,解得a 1=6,则b 1=a 13=2.故数列{b n }是以2为首项,2为公差的等差数列,∴b n =2+2(n -1)=2n ⇒a n =2n ·3n . (2)解 由(1),得c n =2·3n -2nT n =2(3+32+33+…+3n )-2(1+2+…+n )=2·3(1-3n )1-3-2·(1+n )n2=3n +1-n 2-n -3. 等差、等比数列的综合问题9.从①前n 项和S n =n 2+p (p ∈R );②a n =a n +1-3;③a 6=11且2a n +1=a n +a n +2这三个条件中任选一个,填至横线上,并完成解答.在数列{a n }中,a 1=1,________,其中n ∈N *. (1)求数列{a n }的通项公式;(2)若a 1,a n ,a m 成等比数列,其中m ,n ∈N *,且m >n >1,求m 的最小值. (注:如果选择多个条件分别解答,按第一个解答计分) 解 选择①:(1)当n =1时,由S 1=a 1=1,得p =0.当n ≥2时,由题意,得S n -1=(n -1)2,所以a n =S n -S n -1=2n -1(n ≥2). 经检验,a 1=1符合上式,所以a n =2n -1(n ∈N *) (2)由a 1,a n ,a m 成等比数列,得a 2n =a 1a m ,即(2n -1)2=1×(2m -1).化简,得m =2n 2-2n +1=2⎝⎛⎭⎫n -122+12.因为m ,n 是大于1的正整数,且m >n ,所以当n =2时,m 有最小值5. 选择②:(1)因为a n =a n +1-3,所以a n +1-a n =3,所以数列{a n }是公差d =3的等差数列, 所以a n =a 1+(n -1)d =3n -2(n ∈N *).(2)由a 1,a n ,a m 成等比数列,得a 2n =a 1a m ,即(3n -2)2=1×(3m -2).化简,得m =3n 2-4n +2=3⎝⎛⎭⎫n -232+23.因为m ,n 是大于1的正整数,且m >n ,所以当n =2时,m 取到最小值6. 选择③:(1)因为2a n +1=a n +a n +2,所以数列{a n }是等差数列.设数列{a n }的公差为d . 因为a 1=1,a 6=a 1+5d =11,所以d =2.所以a n =a 1+(n -1)d =2n -1(n ∈N *) . (2)因为a 1,a n ,a m 成等比数列,所以a 2n =a 1a m ,即(2n -1)2=1×(2m -1).化简,得m =2n 2-2n +1=2⎝⎛⎭⎫n -122+12.因为m ,n 是大于1的正整数,且m >n , 所以当n =2时,m 有最小值5.10.已知{a n }是公比为q 的无穷等比数列,其前n 项和为S n ,满足a 3=12,________.是否存在正整数k ,使得S k >2 020?若存在,求k 的最小值;若不存在,说明理由.从①q =2,②q =12,③q =-2这三个条件中任选一个,补充在上面横线处并作答. (注:如果选择多个条件分别解答,按第一个解答计分) 解 选择①:存在满足条件的正整数k .求解过程如下:因为a 3=12,所以a 1=a 3q 2=3.所以S n =3(1-2n )1-2=3(2n -1).令S k >2 020,则2k>2 0233.因为29<2 0233<210,所以使S k >2 020的正整数k 的最小值为10.选择②:不存在满足条件的正整数k .理由如下:因为a 3=12,所以a 1=a 3q 2=48.所以S n =48×⎝⎛⎭⎫1-12n 1-12=96⎝⎛⎭⎫1-12n .因为S n <96<2 020,所以不存在满足条件的正整数k .选择③:存在满足条件的正整数k .求解过程如下:因为a 3=12,所以a 1=a 3q 2=3. 所以S n =3×[1-(-2)n ]1-(-2)=1-(-2)n .令S k >2 020,则1-(-2)k >2 020, 整理得(-2)k <-2 019.当k 为偶数时,原不等式无解.当k 为奇数时,原不等式等价于2k >2 019.所以使S k >2 020的正整数k 的最小值为11.。