北京模考前 -谢元坤 2

2023北京昌平初三二模语文2023.05本试卷共8页，共100分。

考试时长150分钟。

考生务必将答案填涂或书写在答题卡上，在试卷上作答无效。

考试结束后，将答题卡交回。

一、基础·运用（共15分）为了给初中三年的青春时光留下永久的纪念，你所在的学习小组准备制作一本青春纪念册。

请你对其中的文字内容进行核对、修改。

第一部分卷首语夏风轻起，芳草萋萋，三年时光弹指一挥；朝霞灿烂，岁月如歌，我们迎来了毕业季。

美丽校园载．青春年华，三载．情谊．当永世珍藏。

这段校园生活，将化作轻轻的风，飞扬的梦，难忘的歌，常伴你我。

1.请你用正楷字书写“岁月如歌”四个字作为纪念册封面上的标题。

（1分）2.请你判断文段中加点字读音，恰当的一项是（2分）A.载．青春zài 三载． zǎi 情谊． yìB.载．青春zài 三载．zài 情谊． yíC.载．青春zǎi 三载．zài 情谊．yìD.载．青春zǎi 三载．zǎi 情谊． yí第二部分友情·难忘青春的潮水澎湃着我们的热情，翻卷着我们的梦想。

同窗三年，情谊难忘：挥洒汗水的篮球联赛，场上激烈比拼，场下欢呼雀跃．．．．；思想交锋的辩论场．．．．；激动人心的歌咏比赛，赛前紧张排练，赛时精彩纷程上，台上唇枪舌剑．．．．．．．．……在这段纯真岁月，我们共同抒写了许多青春的故事。

故事里有苦有甜，有泪有笑，有奋进也有徘徊，有成功也有失败。

青春的故事是美好的，更是难忘的。

望同学们别后常忆今朝，愿同学们此去繁花似锦，归来仍是少年。

3.检查文段，你发现了一处书写错误。

下列选项中说法正确的一项是（2分）A.因为表达的是“高兴得像鸟儿一样跳跃起来”的意思，所以“欢呼雀跃”中有错字。

B.因为表达的是“美好事物纷纷在眼前展现”的意思，所以“精彩纷程”中有错字。

C.因为表达的是“争辩激烈，言辞锋利”的意思，所以“唇枪舌剑”中有错字。

二次函数（对称性、增减性）一、对称性、增减性1、（2021.北京26题）在平面直角坐标系xOy 中，点(1，m )和点(3，n )在抛物线()20y ax bx a =+>上.(1)若m =3，n =15，求该抛物线的对称轴；(2)已知点123()()()124y y y -，，，，，在该抛物线上，若mn <0，比较123y y y ，，，的大小，并说明理由【答案】（1）1x =-;（2）213y y y <<解析：二次函数综合，考察点和对称轴的位置判断函数值的大小. ①当m <0,n >0时，由二次函数恒过（0，0）点知此时抛物线开口向下，a <0,与a >0矛盾；②当m >0,n <0时，对称轴为13,22x <<故351357(1),2,4.222222x x x <--<<-<<-< ∴()214x x x -<--<- ∵0a > ∴213y y y <<2、（2020.北京26题）在平面直角坐标系xOy 中，()11,M x y ，()22,N x y 为抛物线()20y ax bx c a =++>上任意两点，其中12x x <．（1）若抛物线的对称轴为=1x ，当1x ，2x 为何值时，12y y c ==；（2）设抛物线的对称轴为=x t ．若对于123x x +>．都有12y y <，求t 的取值范围．【解析】：(1)当12y y c ==时∴令y c =时，代入()20y ax bx c a =++>()20c ax bx c a ∴=++> ()0x ax b ∴=+120,b x x a ∴==-1,22bx b a a=-==-又对称轴即 222ax a-∴=-= (2)作点M 关于x t =的对称点,M 设点M ()31,x y132x x t ∴+= 1212,3y y x x <+>1232,2x x t t t ∴+>≤≤即23,注：此时，是可以取等值的，一定要特别注意。

一、基础·运用（共12分）2023年4月15日，经过改造复建的北京工人体育场正式启用。

学校组织大家到那里开展研学活动。

活动结束后，你们小组合作完成了一篇研学日志。

第一部分时代经典1959年竣工的北京工人体育场，是当时全国最大的综合性体育场。

作为北京的一处标致性建筑，它与一街之隔的工人体育馆一起，被北京市民亲切地称为“工体”。

它是首都工人阶级向新中国成立十周年的献礼工程，也是第一届北京十大建筑之一。

一座北京工人体育场，半部新中国体育史。

从第一届全运会到第四届全运会，从1990年第十一届亚洲运动会到2004年亚洲杯足球赛、2008年奥运会的部分比赛……北京工人体育场鉴证了新中国体育事业的蓬勃发举行；再后来，国内一些重要的文艺演出、庆祝活动也都衷情于这里。

“工体”两个字，也从一个具体的地名，慢慢成为北京人心中的文化圣地。

1．检查文段，你发现了多处书写错误。

下列选项中说法不正确的一项是(2分)A．因为工人体育场是能表现行业精髓的代表性作品，所以“经典”应写作“精典”。

B．作为十大建筑之一，工人体育场是北京的一张名片，所以“标致”应写作“标志”。

C．工人体育场经历了新中国体育事业发展强大的过程，所以“鉴证”应写作“见证”。

D．因为人们喜爱在工体举办重要的文艺演出、庆祝活动，所以“衷情”应写作“钟情”。

2．为使语意连贯，你准备在文段横线处填入一句承上启下的话。

下列最恰当的一项是（2分）A．因为它是为举行体育赛事而建，所以它的作用不止于此。

B．虽然它是为举行体育赛事而建，但是它的作用不止于此。

C. 因为它是新中国成立十周年的献礼工程，所以它的作用不止于此。

D．虽然它是新中国成立十周年的献礼工程，但是它的作用不止于此。

第二部分你好，新工体青灰色清水混凝土外立面，传承了老工体庄重典雅的建筑风格；宏大的罩棚仿佛倒扣的“钢铁巨碗”，重现足球场饱满沉稳的身型；6.8万张“国槐绿”座椅相连，给人强烈的视觉冲击；世界顶级的专业草坪，静待球员回归【甲】历时两年半，这座阔别许久的城市地标盛装回归！新工体遵循“①”的原则:保持椭圆形造型、外立面形式和比例、特色元素三个不变；进入到工体内部，则是焕然一新的现代感——世界一流的声光电设施、对标世界杯球场的屏幕呈现……改造后的新工体完成了“历史风貌留存保护”和“功能体验提质升级”的双重任务，成为国内首批、北京首座国际标准专业足球场。

2024年北京中考语文第二次模拟考试一、基础·运用（共13分）为了传承汉字文化，我校初一年级将开展“畅游汉字王国”的主题活动。

年级将要布展一面文化墙，请你参与各板块的筹备工作，完成下面小题。

第一板块：谈“心”“心”字是一个象形字，中间是心脏，外部的一圈儿则是心包络。

后经引申，“心”还用来表示思虑。

于是古人用心来代指大脑，创造了很多心字底和竖心旁的字，来表示与心理活动有关的事情。

比如，常说的“思想”，西方人认为取决于头脑，而我们的先人则认为其来源于“心”。

意志源于心，感恩源于心，sǒng yǒng也源于心；憧的观念。

憬源于心，愉悦源于心，慷慨也源于心，所以，中国人自古以来就有心主神志．．．．1．同学们给“心”字的不同书体制作标签，下列判断正确的一项是（）（2分）【甲】【乙】【丙】【丁】A．【甲】行书【乙】篆书【丙】隶书【丁】楷书B．【甲】行书【乙】篆书【丙】楷书【丁】隶书C．【甲】篆书【乙】行书【丙】楷书【丁】隶书D．【甲】篆书【乙】行书【丙】隶书【丁】楷书2．请根据文中的拼音，将所对应的汉字依次工整地书写下来。

（1分）3．有同学对“心主神志”不甚理解，请你结合语段内容，用简洁的语言进行解释。

（2分）第二板块：说“中”“中”，是一个顶级汉字。

为什么这样说呢？一方面，商朝人把自己居住的地域看作是被周围国家围绕的世界中心，故在殷墟出土的甲骨上，多有“立中”的字眼，它【甲】体现了华夏人对世界的最早看法。

另一方面，甲骨文的“中”字像极了一面随风飘扬的旗帜。

战时，旗帜就掌握在王者的手中。

因此，“中”是权力的象征，权威的中心。

“中”，有两个读音。

这是为什么呢？那应该从它的【乙】笔画讲起。

汉代许慎在《说文解字》中说：“中，内也。

从‘口’。

‘丨’，上下通。

”清代文字音韵训话学家段玉裁则认为“口”像靶子，“丨”像箭。

箭射到靶子上，即为“命中”。

所以，“命中”的“中”，读音应为①。

至于“中”的另一读音，《澄衷蒙学堂字课图说》中讲，“中”字的“口”像四方的样子，“丨”表示在中间位置。

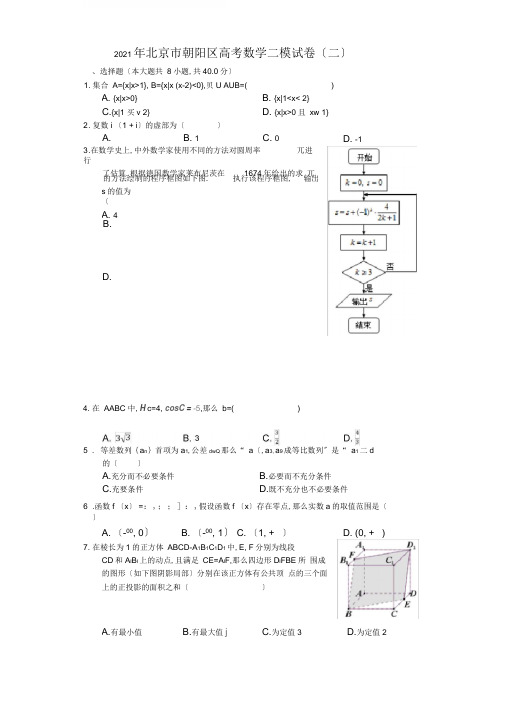
A. 〔-00, 0〕B. 〔-00, 1〕C. 〔1, +°°〕7. 在棱长为1的正方体 ABCD-A 1B 1C 1D 1中,E, F 分别为线段CD 和A I B I 上的动点,且满足 CE=A I F,那么四边形D I FBE 所 围成的图形〔如下图阴影局部〕分别在该正方体有公共顶 点的三个面上的正投影的面积之和〔〕D. (0, +°°)A.有最小值B.有最大值jC.为定值35 . 等差数列｛a n ｝首项为a 1,公差dwQ 那么“ a 〔,a 3, a 9成等比数列〞是“ a 1二d的〔〕A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件6 .函数f 〔x 〕 =：,；；］：,假设函数f 〔x 〕存在零点,那么实数a 的取值范围是〔 〕2021年北京市朝阳区高考数学二模试卷〔二〕 、选择题〔本大题共 8小题,共40.0分〕1. 集合 A={x|x>1}, B={x|x (x-2)<0},贝U AUB=( ) A. {x|x>0} B. {x|1<x< 2} C.{x|1 买v 2} D. {x|x>0且 xw 1} 2 . 复数i 〔1 + i 〕的虚部为〔 〕 A. B. 1 C. 0 3 .在数学史上,中外数学家使用不同的方法对圆周率 兀进行 了估算.根据德国数学家莱布尼茨在 1674年给出的求 兀D. -1的方法绘制的程序框图如下图. 执行该程序框图, s 的值为〔 A. 4 B. D.输出 4. 在 AABC 中,H c=4, cosC = -5,那么 b=()D.为定值28 . 在同一平面内, A 为动点,B, C 为定点,且/BAC4, 二A 却？于口,BC=1, P为BC 中点•过点p 作pQ gC 交AC 所在直线于Q ,那么;Q 在;c 方向上投影的最大值 二、填空题(本大题共 6小题,共30.0分)9 . a=log 3e, b=ln3, c=log 32,贝U a, b, c 中最小的是 .10 .点M (1, 2)在抛物线 C: y 2=2px (p>0)上,那么点M 到抛物线C 焦点的距 离是.I x - votO.* ( i = 1 + 2r,11 .圆心；｛y = 1十(.为参数)上的点P 到直线| y = —1 + (t 为参数)的距离 最小值是. f 工之L12 .实数x, y 满足 ¥=#,能说明“假设z=x+y 的最大值为4,那么x=1, y=3〞为假 [x 4- y < 4.命题的一组(x, y)值是.13 .由数字1, 2, 3, 4, 5, 6组成没有重复数字的三位数,偶数共有 个,其中 个位数字比十位数字大的偶数共有 个. 14 .如图,在平面直角坐标系xOy 中,点 O (0, 0) , M (-4, 0) , N (4, 0),P (0, -2) , Q (0, 2) , H (4, 2).线段OM 上的动点A 满足;力一%时(''(必‘))； 线段HN 上的动点B 满足j 二"N 直线PA 与直线QB 交于点L,设直线PA 的斜 ntf ni\ 7率记为k,直线QB 的斜率记为k',那么k?k'的值为;当入变化时,动点L 一定 在 (填“圆、椭圆、双曲线、抛物线〞之中的一个)上.三、解做题(本大题共 6小题,共80.0分) 15 .函数 fix) = 2sinxcosx + 入瓦,".一超.(I )求函数f (x)的最小正周期；(n )当某E [一彳,同时,求证：/(X )之一十B.C.是(某电视台举行文艺比赛, 并通过网络比照赛进行直播. 比16.赛现场有5名专家评委给每位参赛选手评分, 场外观众可以通过网络给每位参赛选手评分. 每位选手的最终得分由专家评分和观众评分确定.某选手参与比赛后,现场专家评分情况如表；场外有数万名观众参与评分,将评分根据[7, 8) , [8, 9) , [9, 10]分组,绘成频率分布直方图如图：专家A B C D E评分9.69.59.68.99.7(I )求a的值,并用频率估计概率,估计某场外观众评分不小于9的概率；(n)从5名专家中随机选取3人,X表示评分不小于9分的人数；从场外观众中随机选取3人,用频率估计概率, Y表示评分不小于9分的人数；试求 E (X)与E (Y)的值；(出)考虑以下两种方案来确定该选手的最终得分：方案一：用所有专家与观众的评分的平均数匚作为该选手的最终得分.r 4方案二：分别计算专家评分的平均数;和观众评分的平均数；,用以士作为该选手最终得分.请直接写出f与',的大小关系.频率在三^柱ABC-A i B i C i中,底面ABC是正三角形,侧棱AAUB面17.ABC. D, E分别是边BC, AC的中点,线段BC i与B i C交于点G,且AB=4, 叫=2k.(I )求证：EG//平面AB i D；(n)求证：BC i"面AB i D；(m )求二面角A-B i C-B的余弦值.18.函数f (x) = (2ax2+4x) lnx-ax2-4x (aCR,且a*O) (I )求曲线y=f(x)在点(1, f (1))处的切线方程;(n )假设函数f (x)的极小值为试求a的值.19 .椭圆C: 4 + y Z= l (a>1)的离心率为坐.(I )求椭圆C的方程；(n)设直线l过点M (1, 0)且与椭圆C相交于A, B两点.过点A作直线x=3 的垂线,垂足为D .证实直线BD过x轴上的定点.20 .对于由有限个自然数组成的集合A,定义集合S (A) ={a+b|aCA, bCA},记集合S(A)的元素个数为d (S (A)).定义变换T,变换T将集合A变换为集合T (A) =AUS (A).(I )假设A={0 , 1, 2},求S (A) , T (A);(n)假设集合A有n个元素,证实：" d (S (A) ) =2n-1〞的充要条件是“集合A 中的所有元素能组成公差不为.的等差数列〞；(出)假设A?{1 , 2, 3, 4, 5, 6, 7, 8}且{1 , 2, 3,…,25, 26}? T (T (A)), 求元素个数最少的集合 A.1 .答案：A解析：解：根据不等式的解法,易得 B={x|0vx 匚< 2},均召-2? 4 5 .又有 A={ x|x> 1},那么 AUB={x|x>0}. 应选：A.根据不等式的解法,B={x[0vx<2},然后根据并集的定义“由所有属于集合 A 或属于集合B 的元素所组成的集合叫做并集〞进行求解即可. 此题考查并集的运算,注意结合数轴来求解,属于容易题.2 .答案：B 解析：解：.i (1 + i) =-1 + i,. i (1 + i)的虚部为1. 应选：B.直接利用复数代数形式的乘除运算化简得答案.此题考查复数代数形式的乘除运算,考查复数的根本概念,是根底题.3 .答案：C 解析：解：第一次,s=4, k=1, k>3否,第二次, 乂辐,k =2 ,k4否, 第二次,s= |+?=m ,k=3, k>3是, 程序终止,输出s=* 应选：C.根据程序框图进行模拟运算即可. 此题主要考查程序框图的识别和判断, 根据条件进行模拟运算是解决此题的关键.比拟根底.4 .答案：B 解析：【分析】由利用同角三角函数根本关系式可求 值. 此题主要考查了同角三角函数根本关系式, 础题. 【解答】解：*c=4, CORC =(, sinC=dl-co5i 々巧,,由正弦定理 岛可得：解得：b=3. 应选：B.答案与解析sinC 的值,根据正弦定理即可计算得解b 的正弦定理在解三角形中的综合应用,属于基5 .答案：C 解析：【分析】此题考查等差、等比数列的定义以及判断,涉及充分必要的定义与判断,属于根底题. 根据题意,设数列｛a n ｝的公差为d,从充分性与必要性的角度分析“ a i, a 3, a 9成等比 数列〞和“ a i =d 〞的关系,综合即可得答案. 【解答】解：根据题意,设数列｛a n ｝的公差为d,假设 a i, a 3, a 9成等比数列,那么〔a 3〕2=a i 39,即〔a i +2d 〕 2=a i • 〔a i +8d 〕,变形可得：a i =d,那么“a i, a 3, a 9成等比数列〞是“ a i =d 〞的充分条件；假设 a i =d,贝U a 3=a i +2d=3d, a 9=a i +8d=9d,贝U 有〔a 3〕2=a i a 9,贝U " a i, a 3, a 9成等比数 列〞是“ a i =d 〞的必要条件；综合可得：“ a i, a 3, a 9成等比数列〞是“ a i =d 〞的充要条件； 应选：C.6 .答案：D 解析：解：函数f 〔x 〕=：上管,函数的图象如图：函数f 〔x 〕存在零点,那么实数 a 的取值范围是： 〔.,+°°〕. 应选：D.画出函数的图象,利用数形结合推出 a 的范围即可.此题考查分段函数的应用,函数的零点的判断, 考查数形结合以及计算水平.7 .答案：DD'B'E f解后面解：依题意,设四边形D I FBE的四个顶点在后面,上面,左面的投影点分别为D', F', B', E',那么四边形D I FBE在上面,后面,左面的投影分别如上图.所以在后面的投影的面积为S后=1 M=1 ,在上面的投影面积S±=D'E' 1=DEX1 = DE,在左面的投影面积S左=B'E' 1=CEX1=CE,所以四边形D1FBE所围成的图形〔如下图阴影局部〕分别在该正方体有公共顶点的三个面上的正投影的面积之和S=S 后+S 上+S 左=1 + DE+CE=1 + CD=2.应选：D.分别在后,上,左三个平面得到该四边形的投影,求其面积和即可.此题考查了正方体中四边形的投影问题,考查空间想象水平.属于中档题.8 .答案：C 解析：解：建立如下图的平面直角坐标系,那么〔4, 0〕, C4,0〕, P〔0,0〕,设 A 〔x, y〕,那么xv 0,设直线AB, AC的斜率分别为k b k2, 由到角公式得：G an J化简彳导:x2+ (y-,)=；,口次那么x*:,那么」苧叔V0,由;在；方向上投影的几何意义可得:.在；方向上投影为DP|二|x|, 那么H、方向上投影的最大值是降应选：C.先建系,再由到角公式得：=常二tan,化简得：x2+ (y<)=：,那么x29［那么-;今v 0,再由二在M方向上投影的几何意义可得解・此题考查了到角公式及平面向量数量积的运算,属中档题.9 .答案：c 解析：解：b=ln3>1,又2V ev 3,所以10g32V log3ev 1,即cv a< b,故a, b, c中最小的是 c.故答案为：c由对数值大小的比拟得：b=1n3>1,又2V e<3,所以10g32v1og3ev 1,即cvavb,得解.此题考查了对数值大小的比拟,属简单题.10 .答案：2解析：解：由点M (1, 2)在抛物线C: y2=2px (p>0)上,可得4=2p, p=2,抛物线C： y2=4x,焦点坐标F (1, 0),那么点M到抛物线C焦点的距离是：2,故答案为：2.由题意可知：点的坐标代入抛物线方程,求出p=2,求得焦点F (1, 0),利用直线的两点式,即可求点M到抛物线C焦点的距离.此题考查抛物线的标准方程及简单几何性质,直线的两点式方程,考查计算水平,属于根底题. 11 .答案：睥1 解析：解：由ly = 1+ 就月.得x2+(y-1)2=1,由,ly =一1 + t 得x-2y-3=0 ,,一,、一■ 一I r , r、 _ ■ - . |0"2~ 3| J-1圆心〔0, 1〕到直线x+2y+1=0的距离d=:=、后,所以所求距离的最小值为-1故答案为：.^5-1.化成直角坐标方程后用点到直线的距离,再减去半径. 此题考查了参数方程化成普通方程,属中档题.12 .答案:〔2, 2〕r x>l,解析：解：实数x, y 满足y 皂币 的可行域 以及x+y=4的直线方程如图：能说明"假设z=x+y 的最大值为4,那么x=1,y=3〞 为假命题的一组〔x, y 〕值是〔2, 2〕. 故答案为：〔2, 2〕.画出约束条件的可行域,目标函数取得最大值 的直线,然后求解即可.此题考查线性规划的简单应用,画出可行域是 解题的关键.13 .答案：60 36解析：解：根据题意, 对于第一空：分 2步分析：①要求是没有重复数字的三位偶数,其个位是 ②在剩下的5个数字中任选2个,安排在前 那么有3X20=60个符合题意的三位偶数； 对于第二空：分 3种情况讨论：①,当其个位为2时,十位数字只能是 的三位数；②,当其个位为4时,十位数字可以是 个符合题意的三位数；③,当其个位为6时,十位数字可以是5 >4=20个符合题意的三位数；那么有4+12+20=36个符合题意的三位数; 故答案为：60, 36.对于第一空：分 2步分析：①分析可得要求三位偶数的个位有 3种情况,②在剩下的 5个数字中任选2个,安排在前2个数位,由分步计数原理计算可得答案；对于第二空：按个位数字分 3种情况讨论,分别求出每种情况下的三位数的数目,由加 法原理计算可得答案.此题考查排列、组合的应用,涉及分步、分类计数原理的应用,属于根底题.解析：解：叫；「A (-4 入,0),又 P (0, -2) , .*=*$； r 二厂 _ ___ . , 2(-2) / . . , L HRB (4,2-2 k= 4^0- =-2, kk =,设 L (x, y),那么 k=\ k =^, .kk1 = 1?；〞=；, 1 / = = X,即彳-适=1 .2、4或6,有3种情况, 2个数位,有 A 52=20种情况,1,百位数字有4种情况,此时有4个符合题意 1、2、3,百位数字有4种情况,此时有 3>4=121、2、3、4、5,百位数字有4种情况,此时有14.答案：； 双曲线故答案为：:,彳先=1 .根据向量关系得到 A, B 的坐标,再根据斜率公式可得 kk'=;设P (x, y),根据斜 I 率公式可得P 点轨迹方程.此题考查了圆锥曲线的轨迹问题,属中档题. 15 .答案：解：(I) J ⑺="Ehwhh + 笈 3gA -木, =#i 也 2M + \3cosZx, =・ 证实：(II)由于第中, 即归+沁一,1, 所以f (x)在上单调递增. 当 2# + ；=—；时, J Q即工:一;,时, /.%山=一"手所以当X E 时,f W > 75.解析：(I)首先利用三角函数关系式的恒等变换, 把函数的关系式变形成正弦型函数,进一步求出函数的最小正周期.(n )利用函数的关系式,进一步利用函数的定义域求出函数的值域.此题考查的知识要点：三角函数关系式的变换,正弦函数的性质的应用,主要考察学生 的运算水平和转换水平,属于根底题型.16 .答案：解：(I)由图知a=0.3,某场外观众评分不小于 9的概率是1. (n ) X 的可能取值为 2, 3. P (X=2)所以X 的分布列为： X233 dP 弱3J 12 所以 E (X ) =2乂-+3XG = M .J0*J 1由题意可知,T 〜巩工］,所以E (Y)所以f (x)的最小正周期 2ltT=V =n3 / 、端 2W ； P (X =3)= np=|(m)* * * = 2 ^ x0 + 0x4 + 0x 2.= 0BC i DA'-=OxO + 〔-2〕x4+2\Nx2u2 = OBC 1 叫'所以 BC i ±DA, BCUDB i.又由于DA ADB I =D,所以BC i,平面AB i D. ............................ 〔 9分〕 (出)解：显然平面 B i CB 的一个法向量为“ =(I, 0, 0)'=0, L *呼n 8-诙平片灯=0,付1 4尸窗％ ; 0, 【电/ 4叼如ririA.设二面角A-BiC-B 的平面角为0,由图可知此二面角为锐二面角,解析：(I)证实EG/AB i.然后利用直线与平面平行的判定定理证实 EG/印面AB i D.(n )取B iC i 的中点D i,连接DD i,建立空间直角坐标系 D-xyz,通过向量的数量积证实BC i IDA, BCODB i,然后证实BC i 」平面AB i D.(出)求出平面 B i CB 的一个法向量,平面 AB i C 的一个法向量,设二面角 A-B i C-B 的平面角为0,利用空间向量的数量积求解二面角的余弦函数值即可. 此题考查直线与平面垂直以及平行的判定定理的应用, 二面角的平面角的求法,考查计算水平.解析：此题考查了离散型随机变量的期望和方差,属中档题.(I )由图知a=0.3,某场外观众评分不小于 9的概率是:(n )计算概率可得分布列和期望;(m)专家评分的平均分高于观众评分的平均分,17.答案：(本小题总分值14分)(I)证实：由于E 为AC 中点,G 为B i C 中点.所以EG/AB 1. 又由于EG?平面AB i D, AB i ?平面AB i D, 所以EG/狂面AB i D. .................... ( 4分) (II )证实：取BiCi 的中点Di,连接DDi.显然DA, DC, DD i 两两互相垂直,如图,建立空间直角坐 标系D-xyz,那么 D (0,0,0),42、, 0, 0),B (0,-2,0),fl 1(O 1 -2, 2j),2. 2^2), B R G, 1, 0), C (0, 2, 0). 所以又由于 设平面AB i C 的一个法向量为:叼=〔x, y, z 〕,又；=(一2屈 2,.) ni L, ■ =〔.,4, -西设x=i ,贝U y =/1,上二亚,那么:a,隹两.'III所以COSfi =而・. 〔 I4 分〕但专家人数远小于观众人数, 故小于.18 .答案：(本小题总分值13分)解：(I )函数 f (x) = (2ax 2+4x) lnx-ax 2-4x (aCR,且 aw .. 由题意可知 f' (x) =4 (ax+1) lnx, xC (0, +°°).f' (1) =0, f (1) =-a-4, .•曲线y=f (x)在点(1, f (1))处的切线方程为 y=-a-4. ....... ( 3分) (n )①当av-1时,x 变化时f (x) , f (x)变化情况如下表：x ◎ 4 Tf-l 1)1 (1, +°°) f (x) -0 +0 -f (x)极小值极大值此时晨一：)②当a=-1时,f' (x) wo 在(0, +oo )上恒成立,所以f (x)在(0, +°°)单调递减. 此时f (x)无极小值,故不成立.③当-1<av .时,x 变化时f' (x) , f (x)变化情况如下表： x (0, 1) 1 J 1A+ 8)f (x) -0 + 0 -f (x)极小值/极大值解得u = -2 +避或a = -2—?3. 由于-1vav0,所以 u =④当a>0时,x 变化时f' (x) , f (x)变化情况如下表: x (0, 1) 1 (1, +°°) f (x)-+f (x)极小值解得a =—2 +小或H =一2-$3 ,故不成立. 综上所述,二-2 +祠. ............ . (13分)解析：(I )由题意可知 f (x) =4 (ax+1) lnx, xC (0, +0°) , f' (1) =0, f (1) =-a-4, 由此能求出曲线 y=f (x)在点(1, f (1))处的切线方程.(n )当av-1时,求出f]-3 =1 +力M-口)=；,解得口 = -^>-1 ,不成立；②当a=-1 f (x)在(0, +8)单调递减.f (x)无极小值;由题意可得一以一4=：,求出4=\信-2；当a>0时,极小值f (1) =-a-4.由此能求出a 的值.此题考查切线方程的求法,考查实数值的求法,考查导数性质、函数的单调性、最值等 根底知识,考查运算求解水平,考查化归与转化思想,是中档题.= 119 .答案：(I )解：由题意可得[〞 —3 解得a=J , b=1 ,\a 2 = b 2 + c 2时,f (x) w 师(0, +oo)上恒成立, 当-1vav0 时,极小值 f (1) =-a-4,所以椭圆C 的方程为；+y 2=i.(n )直线BD 恒过x 轴上的定点 N (2, 0).证实如下 (1)当直线l 斜率不存在时,直线l 的方程为x=1, 不妨设 A (1,乎),B (1, ¥), D (3,悟)此时,直线BD 的方程为：y ((x-2),所以直线BD 过点(2, 0)(2)当直线l 的斜率存在时,设 A (xi, yi) , B (x2, y2),直线AB 为y=k (x-1), D (3, yi).解析：(I )由题意列关于a, b, c 的方程组,求解可得 a, b, c 的值,那么椭圆方程可 求；(n)当直线AB 的斜率不存在时,直线 BD 过点(2, 0).当直线AB 的斜率存在时, 设直线AB 为y=k (x-i),联立方程组,消去 y 整理得：(i+3k 2) x 2-6k 2x+3k 2-3=0,利 用韦达定理、直线方程,结合条件求出直线BD 过x 轴上的定点.此题考查椭圆方程求法,考查考查两直线的交点是否为定点的判断与求法,考查椭圆、 韦达定理、根的判别式、直线方程、弦长公式等根底知识,考查推理论证水平、运算求 解水平,考查化归与转化思想、函数与方程思想,是中档题.20 .答案：解：(I )假设集合 A={0 , i, 2},那么 S (A) =T (A) ={0 , i, 2, 3, 4} •….(3 分)(n )令 A={Xi, x2,…xn}.不妨设 xi 〈x2<e y xn. 充分性：设{xk}是公差为d (dWQ)的等差数列. 贝U x i +x j =x i + (i-i) d+x i + (j-i) d=2x i + (i+j-2) d (iW, j 而)且2M+jwm.所以x i +x j 共有2n-i 个不同的值.即 d (S (A) ) =2n-i. 必要性：假设 d (S (A) ) =2n-i . 由于 2x i 〈x i +x i+i v 2x i+i, ( i=i, 2,…,n-i).所以 S (A)中有 2n-i 个不同的元素：2x i, 2x 2 ,…,2x n, x i + x 2, x 2+x 3,…,x n-i +x n. 任意x i +x j (iw, j 切)的值都与上述某一项相等.又 x i +x i+i v x i +x i+2V x i+i + x i+2, 且 x i + x i+i V 2x i+i V x i+i +x i+2 , i=i , 2 , …,n-2 . 所以X i +x i+2=2x i+i ,所以{x k }是等差数列,且公差不为 0.….(8分)(出)首先证实：iCA.假设i?A, A 中的元素均大于i,从而i?S (A), 因此 i?T (A) , i?S (T (A)),故 i?T (T (A)),与{i , 2, 3,…,25, 26} ?T (T (A))矛盾,因此i CA. 设A 的元素个数为n, S (A)的元素个数至多为C ： + n,从而T (A),的元素个数至多为 C -+n+n=,f^m. * 2假设n=2,那么T (A)元素个数至多为5,从而T (T (A))的元素个数至多为亨=20, 而T (T (A))中元素至少为 26,因此n>3假设 A 有三个元素,设 A={1 , a2, a 3},且 1va 2〈a3W8,那么 1, 2, a2, a 2+1, a 3, a 3+1, 2a 2, a 2+a 3, 2a 3C T (A),, = «一1) x 2+ 所以 x i +x 2= :(1+3k 2) x 2-6k 2x+3k 2-3=0.直线 北BD: y-y i = 所以由于(x-3),令 y=0,得 x-3=故直线BD 过点(2,0). 综上所述,直线 BD 恒过x 轴上的定点(2, 0)从而1, 2, 3, 47(T (A) ) .假设a2>5, T (T (A))中比4大的最小数为32,那么5?T (T (A)),与题意矛盾,故a2<5.集合T (T (A)).中最大数为4a3,由于26CT (T (A)),故4a3> 26从而a3>7, (i)假设A={1 , a2, 7},且a2<5.此时1, 2, a2, a2+1, 7, 8, 2a2, 7+a2, 14b (A), 那么有8+14=22, 2X14=28CT (T (A)),在22 与28之间可能的数为14+2a2, 21+a2. 此时23, 24, 25, 26不能全在T (T (A)).中,不满足题意. (ii)假设A={1 , 32, 8},且32<5 此时1, 2 , 32 , 32+1, 8 , 9 , 232 , 8+ 32, 16CT (A), 那么有16+9=25 CT (T (A)),假设26 CT (T (A)),那么16+232=26 或16+ (8+32)=26, 解得32=5或32=2 .当A={1 , 2, 8}时,15, 21, 23?T (T (A)).,不满足题意.当A={1 , 2, 8}时,T (T (A) ) ={1 , 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 29, 32},满足题意.故元素个数最少的集合A为{1, 5, 8} ....................... ... ( 13分)解析：(I)根据定义直接进行计算即可(n)根据充分条件和必要条件的一结合等差数列的性质进行证实(m )首先证实：1 CA,然后根据条件分别判断A中元素情况即可得到结论.此题主要考查集合元素性质以及充分条件和必要条件的应用, 综合性强,难度比拟大.不太好理解.。

2025届北京市西城区北京师范大学第二附属中学高三冲刺模拟物理试卷注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、单项选择题：本题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、如图所示空间中存在沿水平方向的匀强磁场，磁感应强度大小为0B ，将长度为2L 的通电直导线由中点O 处弯成折线，夹角为60°，现在导线中通有恒定电流I 。

如果在空间另外施加一磁感应强度大小为0B 的匀强磁场，且使导线MO 、NO 所受的安培力相等，则下列说法正确的是（ ）A ．磁场的方向斜向左下方与水平方向成60°角，MO 受到的安培力的大小为0B IL B ．磁场方向竖直向上，MO 受到的安培力的大小为02B ILC ．磁场方向竖直向下，MO 受到的安培力的大小为02B ILD ．磁场方向斜向右上方与水平方向成60°角，MO 03B IL 2、关于天然放射现象，下列说法正确的是（ ）A ．放出的各种射线中，α粒子动能最大，因此贯穿其他物质的本领最强B ．原子的核外具有较高能量的电子离开原子时，表现为放射出β粒子C ．原子核发生衰变后生成的新核辐射出γ射线D ．原子核内的核子有一半发生衰变时，所需的时间就是半衰期 3、伽利略通过斜面理想实验得出了（ ） A ．力是维持物体运动的原因 B ．物体的加速度与外力成正比 C ．物体运动不需要力来维持D ．力是克服物体惯性的原因4、下列四幅图的有关说法中正确的是（ ）A ．图（l ）若将电源极性反接，电路中一定没有光电流产生B ．图(2)卢瑟福通过α粒子散射实验提出了原子核的构成C ．图(3)一群氢原子处于n =5的激发态跃迁到n =1的基态最多能辐射6种不同频率的光子D ．图(4)原子核D 、E 结合成F 时会有质量亏损，要释放能量5、篮球运动深受同学们喜爱。

北京市人大附中2024年高三第二学期三模全真演练物理试题（基础必刷）学校：_______ 班级：__________姓名：_______ 考号：__________（满分：100分时间：75分钟）总分栏题号一二三四五六七总分得分评卷人得分一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的） (共8题)第(1)题如图甲所示为一个超声波加湿器，如图乙所示为其内部湿度监测装置的简化电路图。

已知电源电压为，定值电阻的阻值为，电流表的量程为，电压表的量程为，湿敏电阻R的阻值随湿度变化的关系图像如图丙所示，其阻值最大为（图中未画出）。

则在电路安全工作的前提下，下列说法正确的是（ ）A．湿敏电阻R的电流最小值为B．定值电阻R0的电功率范围为C．电路消耗的总功率最大值为D．此装置能监测的湿度范围为第(2)题一些星球由于某种原因而发生收缩，假设某星球的直径缩小到原来的四分之一。

若收缩时质量与自转周期均不变，与收缩前相比，则（ ）A．该星球的密度增大到原来的16倍B．该星球表面的重力加速度增大到原来的16倍C．该星球的第一宇宙速度增大到原来的16倍D．该星球的同步卫星到星球中心的距离增大到原来的16倍第(3)题钠的放射性同位素经过一次衰变后产生稳定的镁（）。

已知的半衰期为15h，将一个放射强度为每秒次的溶液样本注射到某病人血液中，45h后从该病人体内抽取6mL的血液，测得其放射强度为每秒5次。

下列说法正确的是（）A．该衰变过程为衰变B．进入到血液后半衰期变长C．45h后样本放射强度变为原来的D．该病人体内血液的总体积约为4.8L第(4)题物理关系式不仅反映了物理量之间的关系，也确定了单位之间的关系。

如关系式，既反映了电流、电荷量和时间之间的关系，也确定了A（安）与C（库）和s（秒）的比值等效。

现有物理量单位m（米）、s（秒）、N（牛）、C（库）、A（安）、V（伏）、Ω（欧），由它们组合成的单位不与磁感应强度单位T（特斯拉）等效的是（ ）A．B．C．D．第(5)题如图，两个质量都为m的球A、B用轻绳连接，A球套在水平细杆上（球孔比杆的直径略大），对B球施加水平风力作用，结果A球与B球相对静止一起向右做匀速运动，此时细绳与竖直方向的夹角为θ。

2024届高三第二次教学质量检测（二模）语文试题（附参考答案）（考试时间：150分钟满分：150分）注意事项：1.答卷前,务必将自己的姓名和座位号填写在答题卡和试卷上。

2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动,务必擦净后再选涂其它答案标号。

回答非选择题时,将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后,将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）现代文阅读I（本题共5小题,18分）阅读下面的文字,完成1~5题。

材料一：古希腊以来的许多唯物主义者,他们思考的问题不是物本身,而是对物的阐释。

从泰勒斯的水、赫拉克利特的火到德谟克利特的原子,他们都在言说物的存在本质在于其物质上的构成。

这是一种最为朴素的对物的理解与阐释,仿佛在我们弄清楚了物的构成物质之后,便可以很清晰地理解物以及物的本质。

一把铁锤之所以是物,是因为它是由铁原子构成的；一个电脑之所以是物,是因为它是由电脑的硬件物质构成的;一个数字空间中的怪物,我们无法说这个数字怪物是由某种有机化合物组成的,但仍然可以将这个怪物看成是一个电子脉冲或比特。

这种对物的理解方式,可以被认为是向下还原。

海德格尔则以一个古希腊陶壶为例,提出了自己的理解：壶之所以为壶,不在于壶壁和壶底,而在于居于其中的虚空。

这句话很容易让我们联想到《道德经》中的“埏埴以为器,当其无,有器之用”。

不过,海德格尔关注的并不仅仅是壶中虚无的物质形态,而且是我们如何在观念中架构了壶这个物体。

也就是说,人将壶之物纳入人类本身的生存机制之中,当我们使用壶来装水、酒等物时,壶才向我们呈现为一个壶。

壹的物性,并不在于它如何呈现出自己物质材料的构成,而在于它是一种可以在人的生存机制中找到使用位置的物品。

这种对物的理解方式,可以被认为是向上还原。

无论是向下还原还是向上还原,都是把人当作主体,而把物当作外在于人的客体。

在数字空间中,情况却完全不同。

2022~2023学年北京市东城区高三（第二次）模拟考试物理试卷1. 卢瑟福提出原子核式结构模型是为了解释( )A. 粒子散射实验B. 核聚变反应C. 天然放射现象D. 核裂变反应2. 下列说法正确的是( )A. 液体分子的无规则运动称为布朗运动B. 分子间距离减小时，分子间的作用力也减小C. 物体从外界吸收热量，其内能不一定增加D. 物体温度升高，每个分子热运动的动能均增大3. 汽车以的速度在马路上匀速行驶，驾驶员发现正前方20m处有障碍物，立即刹车，汽车恰好停在障碍物前。

已知驾驶员反应时间为，汽车运动的图像如图所示。

在刹车过程中，汽车的加速度大小为( )A. B. C. D.4. 下列说法正确的是( )A. 在空气中，可见光和超声波传播速度相同B. 电磁波和机械波都需要介质才能传播C. 无线电波和紫外线都可以发生偏振现象D. 红外线的波长比X射线的波长短5. 某光源发出的光由不同波长的光组成。

不同波长的光的强度表示光的强弱如图所示。

使金属恰好发生光电效应的光的波长，称为极限波长。

表中为一些金属的极限波长。

用该光源照射表中金属表面，则( )材料铂钨钠极限波长196274542A. 只有钠表面有电子逸出B. 只有铂表面有电子逸出C. 钨、铂表面均有电子逸出D. 铂、钨、钠表面均有电子逸出6. 如图所示，质量为m的木箱在大小为F的水平外力作用下，沿倾角为的斜面匀速向上运动。

已知重力加速度为g，不计空气阻力。

下列说法正确的是( )A.木箱所受合力大小为B. 斜面对木箱的支持力大小为C.斜面对木箱的摩擦力大小为D. 斜面对木箱作用力的合力大小为7. 图示为一颗人造地球卫星发射过程的简化示意图。

卫星先进入圆轨道1做匀速圆周运动，再经椭圆轨道2，最终进入圆轨道3做匀速圆周运动。

轨道2分别与轨道1、轨道3相切于P、Q两点。

下列说法正确的是( )A. 卫星在轨道1上运行时，向心力始终不改变B. 卫星在轨道1的运行周期大于其在轨道3的运行周期C. 卫星在轨道2上从P点运动到Q点的过程中，速度越来越大D. 不论在轨道2运行还是在轨道3运行，卫星在Q点的加速度都相同8. 如图甲所示，轻弹簧的一端固定，另一端连接一个有孔的小球球下固定有笔头，小球套在光滑的杆上，沿水平方向做简谐运动。