高中数学 2.2.1线面平行教案 苏教版必修2

a
b
树人学校2021-2021学年第二学期高一数学导学案
直线与平面的位置关系—直线与平面平行
【教学目标】1掌握直线与平面的三种位置关系； ２．掌握直线和平面平行的判定与性质定理；
3应用直线和平面平行的判定和性质定理证明线线平行和线面平行等
有关问题．
【教学重难点】直线和平面平行的判定和性质定理
【新课讲授】
1直线与平面的位置关系：
2直线与平面平行的判定定理：
自然语言： 图形语言：
符号语言：
【例题分析】
例1 分别是三棱锥的侧棱的中点，求证：平面
变1：如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点求证:AB
变2：如图，正方体中，是对角线,的中点
求证：直线平面
【拓展迁移】
1.假设分别是△ACD 和△ABC的重心，你能找出三棱锥的
四个面中与平行的平面吗？
2.如图，三棱柱中，是的中点，
判断与平面的位置关系，并证明你的结论【总结提炼】。

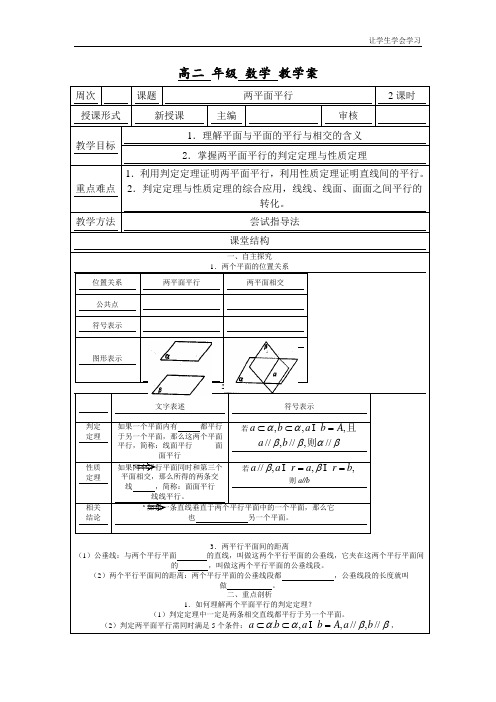
高二 年级 数学 教学案周次课题两平面平行2课时 授课形式 新授课主编审核教学目标1．理解平面与平面的平行与相交的含义 2．掌握两平面平行的判定定理与性质定理重点难点 1．利用判定定理证明两平面平行，利用性质定理证明直线间的平行。

2．判定定理与性质定理的综合应用，线线、线面、面面之间平行的转化。

教学方法尝试指导法 课堂结构一、自主探究1．两个平面的位置关系位置关系 两平面平行两平面相交公共点 符号表示图形表示2．两个平面平行文字表述符号表示判定 定理如果一个平面内有 都平行于另一个平面，那么这两个平面平行，简称：线面平行 面面平行 若且,,,A b a b a=⊂⊂I αα βαββ//,//,//则b a性质 定理如果两个平行平面同时和第三个平面相交，那么所得的两条交线 ，简称：面面平行线线平行。

若,,,//b r a r a a ==I I ββ则a//b相关 结论 如果一条直线垂直于两个平行平面中的一个平面，那么它也 另一个平面。

3．两平行平面间的距离（1）公垂线：与两个平行平面 的直线，叫做这两个平行平面的公垂线，它夹在这两个平行平面间的 ，叫做这两个平行平面的公垂线段。

（2）两个平行平面间的距离：两个平行平面的公垂线段都 ，公垂线段的长度就叫做 。

二、重点剖析1．如何理解两个平面平行的判定定理？（1）判定定理中一定是两条相交直线都平行于另一个平面。

（2）判定两平面平行需同时满足5个条件：ββαα//,//,,.b a A b a b a=⊂⊂I ，（3）定理将平面与平面平行的问题转化成了直线与平面平行的问题。

2．如何理解面面平行的性质定理？ （1）面面平行的性质定理的条件有三个： ①βα//；②a r =I α；③b r =I β三个条件缺一不可。

（2）定理的实质是由面面平行得线线平行，其应用过程是构造与两个平行平面都相交的一个平面，由其结论可知定理可用来证明线线平行。

（3）面面平行的性质定理的推证过程应用了平行线的定义。

教学目标
一、知识与技能
1、通过直观感知、操作确认，理解直线与平面平行的判定定理并能进行简单应用
2、进一步培养学生观察、发现问题的能力和空间想像能力
二、过程与方法
1、启发式。

以实物（教室等）为媒体，启发、诱思学生逐步经历定理的直观感知过程。

2、指导学生进行合情推理。

对于立体几何的学习，学生已初步入门，让学生自己主动地去获取知识、发
现问题、教师予以指导，帮助学生合情推理、澄清概念、加深认识、正确运用。

三、情感态度与价值观
1、让学生亲身经历数学研究的过程，体验创造的激情，享受成功的喜悦，感受数学的魅力。

2、在培养学生逻辑思维能力的同时，养成学生办事认真仔细的习惯及合情推理的探究精神
教学的重点与难点：
教学重点：通过直观感知、操作确认，归纳出直线和平面平行的判定及其应用。

教学难点：直线和平面平行的判定定理的探索过程及其应用。

教学过程设计：。

高中数学必修2《直线和平面平行的判定》说课稿一、教材内容分析教材内容的地位和作用：直线与平面平行的判定是江苏版普通高中课程标准实验教科书《数学》必修2第一章第二节第三部分内容；它在第一章线与线、线与面、面与面的知识结构中起着承上启下的作用，也是今后学习共面向量的基础。

在此之前，学生已学习了空间两直线的位置关系,这为过渡到本节的学习起着铺垫作用。

本节的主要内容有直线和平面的三种位置关系和直线与平面平行的判定两部分。

平行关系是全章的主要内容之一，而直线与平面平行的判定是平行关系的初步。

因此，在立体几何中，占据重要的地位。

作为一名数学老师,不仅要传授给学生数学知识,更重要的是传授给学生数学思想、数学意识，因此本节课在教学中让学生首先借助长方体模型和演示实验，直接认识和理解直线和平面平行的理由和条件。

学生在应用观察、猜想等手段探索研究判定定理时，能获得视觉上的愉悦，增强探求的好奇心，激发出潜在的创造力，形成创新意识。

教学重点、难点因为新课标教材重视展现知识发生和发展的过程，因此本节教学重点是两个过程的教学：（1）直线和平面的三种位置关系的发现过程；（2）直线和平面平行关系的判定的形成过程。

通过直观类比、探究发现、观察实验来突出重点。

由于新课标对判定定理的证明没有要求，而要求学生直接通过直观感知、操作确认，认识和理解判定定理；并能运用定理证明一些空间位置关系的简单命题。

因此我把难点定为直线和平面平行的判定定理理解及应用，通过分组讨论、设计练习循序渐进等教学手段来突破难点二、教学目标根据上述教材内容分析，并结合学生的认知水平和思维特点，我将教学目标分为三部分进行说明：1、知识与技能目标（1）通过直观感知、操作确认归纳出直线与平面的三种位置关系；（2）掌握直线和平面平行的判定定理；（3）能较灵活运用判定定理解决有关问题。

2、过程与方法目标（1）通过学生观察实物，培养学生抽象概括能力；（2）通过学生对图形的分析，培养学生空间想象能力3、情感态度与价值观目标（1）通过教学使学生认识到研究直线和平面的位置关系以及直线与平面平行是实际生产的需要，充分体现了理论来源于实践并应用于实践，充分体现了理论联系实际的原则；（2）在师生对数学图形分析的过程中，培养学生积极进行数学交流、乐于探索创新的科学精神。

2.2.1直线与平面平行的判定2.2.2平面与平面平行的判定一、课标解读1、通过直观感知——观察——操作确认的认识方法理解并掌握直线与平面平行的判定定理，掌握直线与平面平行的画法并能准确使用数学符号语言、文字语言表述判定定理2、理解并掌握两平面平行的判定定理，让学生通过观察实物及模型，得出两平面平行的判定3、培养学生观察、探究、发现的能力和空间想象能力、逻辑思维能力4、让学生在观察、探究、发现中学习，在自主合作、交流中学习，体验学习的乐趣，增强自信心，树立积极的学习态度，提高学习的自我效能感二、自学导引问题1：如果你手里拿着一支笔（看作一条直线），如何保证笔与桌面平行呢？有哪些方法？直线和平面平行的判定定理符号表示问题2：空间两个不同平面的位置关系有哪几种情况？问题3：两个平面平行的基本特征是什么？有什么简单办法判定两个平面平行呢？平面与平面平行的判定定理三、合作探究1.根据定义，判定平面与平面平行的关键是什么？2.若一个平面内的所有直线都与另一个平面平行，那么这两个平面的位置关系怎样？若一个平面内有一条直线与另一个平面有公共点，那么这两个平面的位置关系又会怎样呢？3.三角板的一条边所在直线与桌面平行，这个三角板所在平面与桌面平行吗？4.三角板的两条边所在直线分别与桌面平行，三角板所在平面与桌面平行吗？四、典例精析例1 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,M是线段EF的中点,求证:AM∥平面BDE.变式训练1 三棱柱111C B A ABC -中,E 为1AC 中点,F 为1CB 的中点.求证:EF ∥平面ABC例2 如图所示,在正方体1111D C B A ABCD -中.求证:平面11D AB ∥平面BD C 1变式训练2 在正方体1111D C B A ABCD -中,P N M ,,分别是11111,,D C C B C C 的中点,求证:平面MNP ∥平面BD A 1例3 如图所示,B 为ACD ∆所在平面外的一点,G N M ,,分别为BCD ABC ∆∆,的重心.(1) 求证:平面MNG ∥平面ACD(2) 求AD G MNG S S ∆∆:变式训练3 如图所示,a ∥α,αα∈D C B A ,,的另一侧的点，是,线段AC AB ,,AD 分别交α于G F E ,,,若5,4,4===AF CF BD ,则=EG ＿＿＿＿＿＿五、自主反馈1、判断下列说法是否正确？(1) 如果一条直线不在平面内，则这条直线就与平面平行 ( )(2) 若一条直线a 和一个平面内的一条直线b 平行，则直线a 和这个平面平行( )(3) 若平面α外一直线a 与内α一直线b 平行，则a 与 α 平行 ( )2.判断下列命题是否正确，正确的说明理由，错误的举例说明： （1）已知平面α，β和直线m ，n ，若α⊂m ,α⊂n ,β//m ,β//n ,则βα//；（2）一个平面α内两条不平行的直线都是平行与另一个平面β，则βα//.3.平面α与平面β平行的条件可以是（ ）（A ）α内有无穷多条直线都与β平行（B ）直线α//a ，β//a ，且直线a 不在α内，也不在β内（C ）直线α⊂a ，直线β⊂b ，且β//a ，α//b（D ）α内的任何直线都与β平行4.如图，长方体1111ABCD A BC D -中，(1)与AB 平行的平面是 (2)与1AA 平行的平面是(3)与AD 平行的平面是5.如图,正方体ABCD-A 1B 1C 1D 1中，M ，N ，E ，F 分别是棱A 1B 1，A 1D 1，B 1C 1，C 1D 1的中点.求证：平面AMN //平面EFDB .答案2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定例1 证明：OE O BD AC 连接设,=是矩形的中点，分别为ACEF EF AC M O ,, OE AM AOEM //∴∴是平行四边形，四边形 BDE AM BDE OE 平面平面⊄⊂,BDE AM 平面//∴例2 证明：设11111,O C A D B O AC BD == 为平行四边形四边形由1111,//B BDD DD BB ∴= BD C D B D B BD 11111//,//平面∴∴AO O C AO O C AO O C 111111//四边形，，且又∴= BD C AO OC AO 1111//,//平面为平行四边形，∴∴ BD C D AB 111//平面平面∴例3 证明：（1）连接BG BN BM ,,H F P CD AD AC ,,,,于并延长交的重心分别为BCD ABD ABC G N M ∆∆∆,,,, 则有2===GH BGNF BNMP BM连接PF MN PH FH PF //,,,有ACD MN ACD PF 平面，平面又⊄⊂ACD MG ACD MN 平面同理平面//,//∴ACD MNG M MN MG 平面平面//,∴=(2)9:1:=∆∆AD C MNG S S变式训练1. 略2.证明：连接11D B111111//,,D B PN C B C D N P ∴的中点分别是 BD PN BD D B //,//11∴又BD A BD BD A PN 11,⊂⊄平面BD A MN BD A PN 11//,//平面同理平面∴BD A PMN N PN MN 1//,平面平面又∴= 3.920自主反馈答案1.（1）错 （2）错 （3）对2.（1）错误 （2）正确3.D4.略5.略。

直线与平面平行的判定与性质教学设计【课题】直线与平面平行的判定与性质【授课教师】顾伟业【授课类型】复习课一、教材分析：1、本节课内容安排在空间几何体的根本知识和空间点、直线、平面之间的位置关系之后，是学生对空间点、线、面的位置关系形成直观感知的根底上学习的，有了一定的构建知识根底。

直线与平面平行的判定定理是对空间点、线、面位置关系的进一步理性认识，同时也为之后的平面与平面平行的判定及性质起到奠基、铺垫作用。

二、教学目标：〔一〕知识目标1．掌握由线线平行到线面平行证法2．理解直线和平面平行的判定定理与性质定理并能简单应用．〔二〕能力目标1．理解并掌握直线和平面平行．3．能运用直线和平面的判定定理，把线面平行转化为线线平行．〔三〕情感目标1．体验获取知识的成功感受，激发学生研究的积极性和对数学的情感。

2．在问题的讨论和探究过程中年，培养学生严谨的治学态度和良好的思维习惯。

三、教学重点和难点：重点：直线和平面平行的判定定理与性质定理。

难点：直线和平面平行的判定定理与性质定理的应用。

四、教学过程设计1．先让学生回忆直线与平面平行的判定定理文字语言，并能根据图形语言说出符号语言。

由线面平行的判定定理可知，要想证得线面平行，必须在平面内找到一条线与其平行，然后由线线平行转化得到线面平行，那么你是如何得到线线平行的呢？然后让学生完成引例和例1并总结引例：如图，四棱锥是上取一点G，过G和A于GH,求证：AN五、归纳小结：先由学生口头总结，然后教师归纳总结〔由多媒体幻灯片展示〕：师：下面请同学们回忆一下，这节课学习的主要内容？1〕直线与平面平行的判定定理与性质定理2〕定理运用的关键是找〔作〕面内的线与面外的线平行，途径有：取中点利用平行四边形或三角形中位线性质、相似比的性质等。

3〕应用定理证明线面平行时要注意三个条件缺一不可，其中最容易漏了条件师：用到了哪些数学思想方法：转化的思想方法, 化归的思想方法。

直线与平面平行的判定【教学目标】1．理解并掌握直线与平面平行的判定定理；2．进一步培养学生观察、发现的能力和空间想象能力；【重点难点】重点：直线与平面平行的判定定理及应用。

难点：直线与平面平行的判定定理及应用。

【教学设想】【教学过程】备注一、复习回顾，引入课题1、复习：（提问）直线与平面的位置关系有哪些？分别用符号语言和图形语言来表示？（用课件展示图形，请学生根据图形用符号语言进行描述）(请学生演板)2、引入：在直线与平面的位置关系中，平行是一种非常重要的关系，它是空间线面位置关系的一种基本形态。

不仅应用较多，也是学习面面平行的基础，那么怎样判定直线与平面平行呢？(首先我们想到的是定义法，利用定义证明——即证明直线与平面没有公共点，但是直线是无限延伸的，平面是无限延展，如何保证直线与平面没有公共点呢？直接利用定义证明不方便，今天我们在定义的基础上来探讨判定直线与平面平行的方法，引出课题)二、观察实例，归纳结论设计三个活动活动1.观察1：生活中，我们注意到门扇的两边是平行的. 当门扇绕着一边转动时，观察门扇转动的一边l 与门框所在平面的位置关系如何？结论：平行活动2. 观察2：若将一本书平放在桌面上，封面的两边是平行的，翻动书的封面，观察封面边缘所在直线AB与桌面所在的平面具有怎样的位置关系？结论：平行活动3. 观察3：下面我们一起来做个游戏，拿两支笔（看成两条直线）使它们平行，一支不动，另一支沿一条直线平移得一平面，观察直线（不动的笔）与平面的位置关系。

结论：平行或直线在平面内（注意这种情况易忽略）（在三个实例的基础上，引导学生归纳结论）结论：如图，设直线b在平面α内，直线a在平面α外，在什么条件下直线a与平面α平行？结论：当a∥b，直线a与平面α平行（如果这个结论成立，我们就可以用线与线的平行关系来证明线与面的平行关系，下面我们一起来探索结论的证明方法。

三、推理论证，得到定理（为了减少证明的难度，证明过程分解成以下环节）思考1：如果平面α外的直线a与平面α内的一条直线b平行(1)直线a与直线b共面吗？若共面，则它们确定的平面与平面α位置关系(2) 直线a与平面α的位置关系有哪些？直线a与平面α能相交吗？5` 10`结论：（1）由于a∥b，故直线a与直线b确定一个平面β，且α∩β=b（2）由于a⊄α，故直线a与平面α相交或平行，所以不相交就平行（直接证明平行不方便，转换思路，我们只要能够否定直线与平面相交，不就肯定了直线与平面平行了吗？），（下一个问题：如何否定呢？我们常用反证法，假设直线与平面相交，推出矛盾，从而否定假设，肯定结论，这种方法叫做反证法）思考2：如果直线a与平面α相交，交点的位置能确定吗？由此你能得到什么结论？结论：如果直线a与平面α相交，交点就一定在直线b上，这与已知a∥b矛盾这是因为α∩β=b，（告诉学生，这种推理的方法叫做反证法）思考3：通过上述分析，我们可以得到判定直线与平面平行的一个定理，你能用文字语言表述出该定理的内容吗？（请学生根据探究的过程，自己归纳总结,教师适当的修正）定理: 若平面外一条直线与平面内的一条直线平行，则该直线与此平面平行.思考4：上述定理通常称为直线与平面平行的判定定理，该定理用符号语言可怎样表述？（大屏幕上给出图形，请学生结合图形用符号语言描述）思考5：直线与平面平行的判定定理的证明？证明：假设直线a与平面α有公共点P则点P∈b或点P∈b若点P∈b，则a∩b＝P，这与a∥b矛盾.若点P∈b，又b⊂α，a∩α＝P由于与平面相交的直线和这个平面内不过交点的直线是异面直线∴a、b异面，这与a∥b也矛盾综上所述，假设错误，故a∥α.（注：这种证明数学问题的方法叫做反证法，要求学生看懂即可，不要求学生自己证明）思考6：直线与平面平行的判定定理可简述“线线平行，则线面平行”，在实际应用中它有何理论作用？结论：把直线与平面的平行关系转化为直线与直线的平行关系，（师：这体现了我们解决立体几何问题的基本思想——空间问题平面化）定理的注解：注1：判定定理是证明直线与平面平行的重要方法；注2：能够运用定理的条件是要满足：面外、面内和平行注3：运用定理的关键是找平行线；找平行线又经常会用到三角形中位线定理或平行四边形的性质定理等证明线线平行的定理.四、应用定理，解决问题（典型例题）例1.在空间四边形ABCD中，E，F分别是AB，AD的中点，求证：EF//平面BCD.处理方法：由教师分析思路，学生在笔记本上整理过程，并用语言叙述（注意提醒学生应用定理的注意事项）15` 20` 25` 30`。

高中数学必修2《直线、平面平行的判定及其性质》教案一、知识与技能：1、理解并掌握直线与平面平行的性质定理;2、引导学生探究线面平行的问题可以转化为线线平行的问题，从而能够通过化归解决有关问题，进一步体会数学转化的思想。

二、过程与方法：通过直观观察、猜想研究线面平行的性质定理，培养学生的自主学习能力，发展学生的合情推理能力及逻辑论证能力。

三、情感、态度与价值观：培养学生主动探究知识、合作交流的意识，在体验数学转化过程中激发学生的学习兴趣，从而培养学生勤于动脑和动手的良好品质。

2重点难点教学重点:线与面平行的性质定理及其应用。

教学难点:线与面的性质定理的应用。

3教学过程3.1 第一学时教学活动活动1【导入】问题引入一、问题引入木工小刘在处理如图所示的一块木料，已知木料的棱BC∥平面A C .现在小刘要经过平面A C 内一点P和棱BC将木料锯开，却不知如何画线，你能帮助他解决这个问题吗?预设：(1)过P作一条直线平行于B C(2)过P作一条直线平行与BC。

(问题引入的目的在于激起学生对于这堂课的兴趣，带着问题学习目的性更强，效果也会更好。

)活动2【讲授】新课讲授二、知识回顾判定一条直线与一个平面平行的方法：1、定义法：直线与平面没有公共点。

2、判定定理法：平面外一条直线与平面内的一条直线平行，则该直线与此平面平行。

(线线平行线面平行)三、知识探究(一)思考一：如果直线a与平面平行，那么直线a与平面内的直线有哪些位置关系?答：平行或异面。

思考2：若直线a与平面平行，那么在平面内与直线a平行的直线有多少条?这些直线的位置关系如何?答：无数条;平行。

思考3：如果直线a与平面平行，经过直线a的平面与平面相交于直线b，那么直线a、b的位置关系如何?为什么?答：平行;因为a∥，所以a与没有公共点，则a与b没有公共点，又a与b在同一平面内，所以a与b平行。

思考4：综上分析，在直线a与平面平行的条件下我们可以得到什么结论?答：如果一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行.(四个思考题的目的在于引导学生探究直线与平面平行的性质定理。