气体动理论2-2
- 格式:ppt
- 大小:1.66 MB
- 文档页数:67


理想气体的分子动理论气体分子的运动与理想气体定律理想气体的分子动理论与气体分子的运动气体是一种物质的形态,也是我们生活中经常接触到的物质。
了解气体分子的运动和理论,能够帮助我们更好地理解气体的性质和行为。
本文将介绍理想气体的分子动理论,并探讨气体分子在空间中的运动方式以及与理想气体定律的关系。
一、理想气体的分子动理论理想气体的分子动理论是描述气体分子运动行为的理论模型。
根据分子动理论,气体分子是以高速无规则的方式在空间中运动的。
以下是气体分子的运动特征:1. 气体分子运动无规则性:气体分子在空间中以高速运动,并且没有固定的运动轨迹。
分子之间相互碰撞,这种碰撞是弹性碰撞,没有能量的损失。
2. 气体分子间的相互作用力可忽略不计:气体分子之间的相互作用力非常微弱,可以忽略不计。
这个假设的前提是气体分子之间的距离相对较远,而且气体分子体积相对较小。
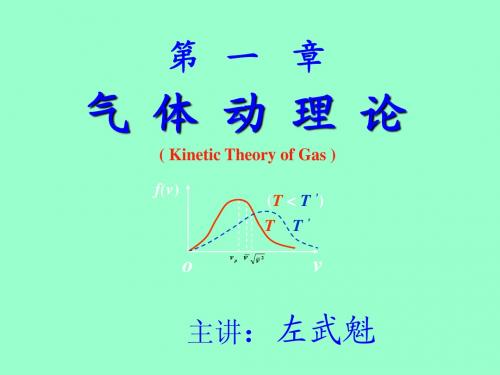
3. 气体分子的速度服从麦克斯韦速度分布定律:根据麦克斯韦速度分布定律,气体分子的速度符合高斯分布(也称为正态分布),其中大多数分子具有平均速度,速度分布呈现钟形曲线。
二、气体分子的运动方式理想气体分子的运动方式可以通过分子运动学理论进行研究。
以下是气体分子的运动方式:1. 直线运动:气体分子在空间中以直线的方式运动。
当碰撞到容器壁或其他分子时,会发生反弹,继续直线运动。
2. 碰撞运动:由于气体分子之间的无规则运动,分子之间会发生碰撞现象。
这种碰撞是弹性碰撞,即碰撞后没有能量损失。
3. 自由平均路径:气体分子在碰撞之间的平均路径称为自由平均路径。
自由平均路径受气体分子的浓度和温度的影响。
三、气体分子的运动与理想气体定律的关系理想气体定律是描述理想气体状态的数学表达式,包括波义耳定律、查理定律和盖-吕萨克定律。
这些定律可以通过气体分子的运动来解释。
1. 波义耳定律:波义耳定律描述了气体压强与温度之间的关系。
根据理论分析,当气体分子碰撞容器壁时会产生压力,而压强与温度成正比。

第四章⽓体动理论总结第四章⽓体动理论单个分⼦的运动具有⽆序性布朗运动⼤量分⼦的运动具有规律性伽尔顿板热平衡定律(热⼒学第零定律)实验表明:若 A 与C 热平衡 B 与C 热平衡则 A 与B 热平衡意义:互为热平衡的物体必然存在⼀个相同的特征--- 它们的温度相同定义温度:处于同⼀热平衡态下的热⼒学系统所具有的共同的宏观性质,称为温度。
⼀切处于同⼀热平衡态的系统有相同的温度。
理想⽓体状态⽅程: 形式1:mol M PV =RT =νRTM形式2:222111T V p T V p =形式3: nkT P =n ----分⼦数密度(单位体积中的分⼦数) k = R/NA = 1.38*10 –23 J/K----玻⽿兹曼常数在通常的压强与温度下,各种实际⽓体都服从理想⽓体状态⽅程。
§4-2 ⽓体动理论的压强公式VNV N n ==d d 1)分⼦按位置的分布是均匀的2)分⼦各⽅向运动概率均等、速度各种平均值相等kj i iz iy ix iv v v v ++=分⼦运动速度单个分⼦碰撞器壁的作⽤⼒是不连续的、偶然的、不均匀的。
从总的效果上来看,⼀个持续的平均作⽤⼒。
2213212()323p nmvp n mv n ω===v----摩尔数R--普适⽓体恒量描述⽓体状态三个物理量: P,V T 压强公式122ω=mv理想⽓体的压强公式揭⽰了宏观量与微观量统计平均值之间的关系,说明压强具有统计意义;压强公式指出:有两个途径可以增加压强 1)增加分⼦数密度n 即增加碰壁的个数2)增加分⼦运动的平均平动能即增加每次碰壁的强度思考题:对于⼀定量的⽓体来说,当温度不变时,⽓体的压强随体积的减⼩⽽增⼤(玻意⽿定律);当体积不变时,压强随温度的升⾼⽽增⼤(查理定律)。
从宏观来看,这两种变化同样使压强增⼤,从微观(分⼦运动)来看,它们有什么区别?对⼀定量的⽓体,在温度不变时,体积减⼩使单位体积内的分⼦数增多,则单位时间内与器壁碰撞的分⼦数增多,器壁所受的平均冲⼒增⼤,因⽽压强增⼤。

气体动理论公式总结气体动理论是研究气体分子在微观层面上的运动规律的一门学科。
它主要研究气体分子的速度、能量、碰撞等方面的性质。
气体动理论公式是描述气体分子运动规律的数学表达式,可以用来计算气体分子的平均速度、平均能量等参数。
下面将总结一些常见的气体动理论公式。
1. 理想气体状态方程理想气体状态方程描述了理想气体在一定温度、压力和体积下的状态关系。
它的数学表达式为:PV = nRT其中,P为气体的压力,V为气体的体积,n为气体的摩尔数,R为气体常数,T为气体的温度。
2. 平均动能公式平均动能公式描述了气体分子的平均动能与温度之间的关系。
它的数学表达式为:K = (3/2)kT其中,K为气体分子的平均动能,k为玻尔兹曼常数,T为气体的温度。
3. 动量-速度关系动量-速度关系描述了气体分子的动量与速度之间的关系。
它的数学表达式为:p = mv其中,p为气体分子的动量,m为气体分子的质量,v为气体分子的速度。
4. 均方根速度公式均方根速度公式描述了气体分子的速度分布规律。
它的数学表达式为:v = √(3kT/m)其中,v为气体分子的均方根速度,k为玻尔兹曼常数,T为气体的温度,m为气体分子的质量。
5. 平均自由程公式平均自由程公式描述了气体分子在运动过程中与其他分子或壁面碰撞的平均距离。
它的数学表达式为:λ = (1/√2πd^2n)其中,λ为气体分子的平均自由程,d为气体分子的直径,n 为气体分子的密度。
6. 分子碰撞频率公式分子碰撞频率公式描述了气体分子碰撞的频率与气体分子数密度之间的关系。
它的数学表达式为:Z = 4πn(d^2)v其中,Z为气体分子的碰撞频率,n为气体分子的数密度,d 为气体分子的直径,v为气体分子的速度。
以上是一些常见的气体动理论公式总结,它们可以用来描述气体分子的运动规律和性质。
利用这些公式,我们可以进行气体的热力学计算和分析,深入理解气体的特性和行为。
同时,这些公式也为相关实验提供了理论基础,促进了气体动理论的发展。