工程力学工力题解
- 格式:doc
- 大小:692.00 KB
- 文档页数:16


4图 5-305-4图示插销拉杆,插销孔处横截面尺寸 大应力。
解:1)求轴力F N = F N =80kN2)求最大应力b=50mm ,h=20mm ,H=60mm, F=80kN,试求拉杆的最___U ____________ —一到—轴 向 拉 伸 与 压 缩5-1已知F i =20kN , F 2= 8kN , F 3=10kN ,用截面法求图示杆件指定截面的轴力。
解:用简便方法求截面轴力a ) :F NI = F i -F 2=20-8=12kN图 5-28aF N2= -F 2=-8kNb ): F NI = F 2=8kNF N 2= F 2-F i =8-20=-12kNF N3= F 2 - F i + F 3=8-20+10=-2kN5-2图示杆件,求各段内截面的轴力,并画出轴力图。
解:用简便方法求截面轴力a ):F NAB =10kNF NBC =10-40= -30kN.…40kN+B _ _ CL —i」图5-29a命j 10kN----- ge-30kNb ): F NAB =-5kNF NBc =-5+15=10kN F NCD =-5+15-6=4kN加A/图 5-29b10kN㊉ L 4kN-5kN 5-3题5-2a 图中杆件较细段 A 1=200mm 2 面的应力。
解:画轴力图 较粗段 A 2=300 mm 2,E=200GPa , l=100mm,求各段截 F NAB 10 103 AB 50MPaABA 1 200F NBC30 103BC100MPaA 2 300、z 、、 40khl些理 -------------- 7 a _ _匸 J ------- -i[图 5-29a' 10kN |£A-30kNmax4图 5-30F NF N80 103iaxb(H h) 50 (60 20)40MPa170所以,d=20mm5-5 图示油缸盖与缸体采用 6个内径d=10mm 的螺栓联接,已知油缸内径 D=200mm ,油压p=2MPa,若螺栓材料的许用应力[c ]=170MPa ,试校核螺栓的强度。


工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交 NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
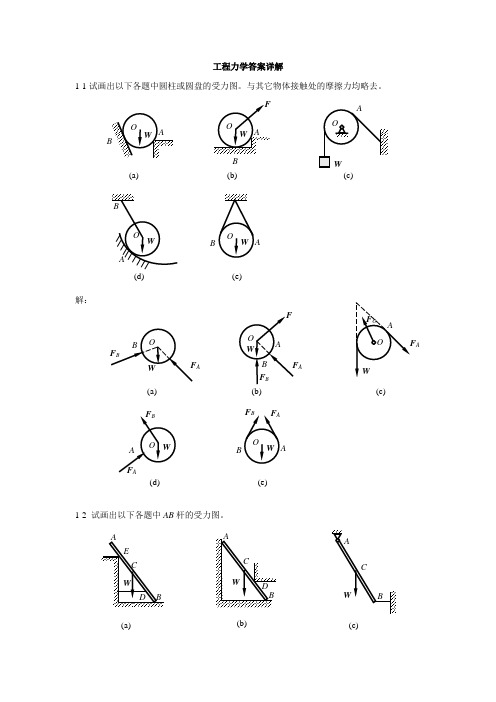
工程力学答案详解1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e) A(a)(b) A(c)A(d)A(e)(c)(a)(b)解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d) D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D BF1-5 试画出以下各题中指定物体的受力图。
(a) 结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d) 杠杆AB,切刀CEF及整体;(e) 秤杆AB,秤盘架BCD及整体。
解:(a)(b)(c)(d)ATF BAF(b)(e)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。

工程力学试题及答案一、填空题1。
物体的平衡是指物体相对于地面__________或作________运动的状态2。
平面汇交力系平衡的必要与充分条件是:_____。
该力系中各力构成的力多边形____ 3.一物块重600N,放在不光滑的平面上,摩擦系数f=0。
3,在左侧有一推力150N,物块有向右滑动的趋势F max=__________,所以此物块处于静止状态,而其F=__________。
4。
刚体在作平动过程中,其上各点的__________相同,每一瞬时,各点具有__________的速度和加速度。
5。
AB杆质量为m,长为L,曲柄O1A、O2B质量不计,且O1A=O2B=R,O1O2=L,当φ=60°时,O1A杆绕O1轴转动,角速度ω为常量,则该瞬时AB杆应加的惯性力大小为__________,方向为__________6。
使材料丧失正常工作能力的应力称为极限应力.工程上一般把__________作为塑性材料的极限应力;对于脆性材料,则把________作为极限应力。
7。
__________面称为主平面。
主平面上的正应力称为______________.8。
当圆环匀速转动时,环内的动应力只与材料的密度ρ和_____________有关,而与__________无关。
二、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内.每小题3分,共18分)1.某简支梁AB受载荷如图所示,现分别用R A、R B表示支座A、B处的约束反力,则它们的关系为( )。
A。
R A〈R BB.R A>R BC.R A=R BD.无法比较2。
材料不同的两物块A和B叠放在水平面上,已知物块A重0.5kN,物块B重0。
2kN,物块A、B间的摩擦系数f1=0。
25,物块B与地面间的摩擦系数f2=0.2,拉动B物块所需要的最小力为()A。
0.14kNB。
0.265kNC。
0.213kND.0。
【最新整理,下载后即可编辑】1-1、已知:F1=2000N,F2=150N,F3=200N,F4=100N,各力的方向如图1-1所示。
试求各力在x、y轴上的投影。
解题提示计算方法:F x= + F cosαF y= + F sinα注意:力的投影为代数量;式中:F x、F y的“+”的选取由力F的指向来确定;α为力F与x轴所夹的锐角。
图1-1 1-2、铆接薄钢板在孔A、B、C、D处受四个力作用,孔间尺寸如图1-2所示。
已知:F1=50N,F2=100N,F3=150N,F4=220N,求此汇交力系的合力。
解题提示——计算方法。
一、解析法F=F1x+F2x+……+F n x=∑F xR xF=F1y+F2y+……+F ny=∑F yR yF= √ F R x2+ F R y2Rtanα=∣F R y/ F R x∣二、几何法按力多边形法则作力多边形,从图1-2 图中量得F R的大小和方向。
1-3、求图1-3所示各种情况下力F对点O的力矩。
图1-3解题提示——计算方法。
①按力矩的定义计算M O(F)= + Fd②按合力矩定理计算M O(F)= M O(F x)+M O(F y)1-4、求图1-4所示两种情况下G与F对转心A之矩。
解题提示此题按合力矩定理计算各力矩较方便、简捷。
以图1-4a为例:力F、G至A点的距离不易确定,如按力矩的定义计算力矩图1-4既繁琐,又容易出错。
若将力F、G分别沿矩形两边长方向分解,则各分力的力臂不需计算、一目了然,只需计算各分力的大小,即可按合力矩定理计算出各力的力矩。
M A(F)= -F cosαb- F sinαaM A(G)= -G cosαa/2 - G sinαb/21-5、如图1-5所示,矩形钢板的边长为a=4m,b=2m,作用力偶M(F,F′)。
当F=F′=200N时,才能使钢板转动。
试考虑选择加力的位置与方向才能使所费力为最小而达到使钢板转一角度的目的,并求出此最小力的值。
第一章静力学基本概念与物体的受力分析下列习题中,未画出重力的各物体的自重不计,所有接触面均为光滑接触。
1.1试画出下列各物体(不包括销钉与支座)的受力图。
解:如图1.2画出下列各物体系统中各物体(不包括销钉与支座)以及物体系统整体受力图。
解:如图F B F Ax A---- M\—2>C 談F N F CFAyBF B (a) FAx J' CF B• %(b)x-7丫AFaFC(d)(C)(e) (f)(g)(h)OAF12 ◎F F(i)1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成,如题 1.3图所示。
在定滑轮上吊有重为W的物体H。
试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。
解:如图1.4题1.4图示齿轮传动系统,O i为主动轮,旋转方向如图所示。
试分别画出两齿轮的受力图。
解: Bxo2y1.5结构如题1.5图所示,试画出各个部分的受力图。
解:第二章汇交力系2.1在刚体的A点作用有四个平面汇交力。
其中F i = 2kN , F2=3kN , F3=lkN , F4=2.5kN , 方向如题2.1图所示。
用解析法求该力系的合成结果。
F1 = 1kN , F2=2kN , F3=|.5kN。
求该力系解F RX=' X = F J COS300 F4 COS450 - F2 COS600 - F3 COS450 = 1.29KN F R y 八丫=F1 sin300 -F4cos450 F2 sin600 - F3 cos450 = 2.54KNF R - F RX F Ry =2.85KN(F R,X)二arctan^ =63.0702.2题2.2图所示固定环受三条绳的作用,已知的合成结果。
解:2.2图示可简化为如右图所示F R^ \ X -F2 F3COS60° =2.75KNF Ry 二'丫二F i —F s Sin600= —0.3KNF R— F RX F Ry =2.77KNF3FRy 0W(F R ,X)二 arctan6.2F Rx2.3力系如题2.3图所示。
工程力学真题答案及解析工程力学是一门研究物体在力的作用下的运动和变形规律的学科。
对于学习和理解工程力学的学生来说,经常会遇到一些难题,在考试前期准备阶段,真题的练习和分析是非常重要的。
在本文中,我们将提供一些工程力学真题的答案和解析,希望可以帮助大家更好地理解和掌握这门学科。
一、静力学题目1. 一根长度为L的均匀竖直悬臂梁,两端分别用一质量为m1和m2的物体挂在上面,求解这两个物体的重力分别是多少。
答:根据静力学的原理,悬臂梁保持平衡的条件是所有外力合力为零。
由此可得:m1g+m2g=0,解得m1=-m2。
解析:这道题考察了学生对静力学平衡条件的理解和应用能力。
通过将问题转化成方程,并按照力平衡的原理进行计算,可以得到正确的答案。
二、杆的弯曲题目2. 一根弹性模量为E、截面积为A的均匀杆,两端分别固定在两个支点上,长度为L。
当杆由平衡状态开始受到一个外力F垂直作用在杆的端点上,求解杆的变形量ΔL。
答:根据杨氏弹性模量的定义E=σ/ε,可以得到杆的变形量ΔL=F*L/(AE)。
解析:这道题考察了学生对于杨氏弹性模量和杆的弯曲变形的理解和计算能力。
通过运用弹性模量的定义,可以得到正确的计算式子。
三、悬链线题目3. 一根质量为m的均匀链条悬挂在两个支点上,支点之间的距离为L。
当链条的一段长度为x时,求解该段链条的重力和张力。
答:当链条的一段长度为x时,该段链条的重力为mgx/L,张力为mg(1-x/L)。
解析:这道题考察了学生对悬链线的分析和计算能力。
通过将链条的每一段作为一个小块,可以得到正确的表达式。
四、力矩题目4. 在一个平衡状态的物体上,有多个力作用在不同点上。
求解物体的平衡条件和力矩的平衡方程。
答:物体的平衡条件是合力和合力矩均为零。
力矩的平衡方程是ΣM=0。
解析:这道题考察了学生对平衡条件和力矩的理解和应用能力。
通过让学生了解和运用平衡条件和力矩平衡方程,可以解决该问题。
通过以上的真题答案和解析,我们可以看到,工程力学是一门需要理解和应用的学科。
第五章 轴向拉伸与压缩5-1 已知F 1=20kN ,F 2= 8kN ,F 3=10kN ,用截面法求图示杆件指定截面的轴力。
解:用简便方法求截面轴力 a ): F N1= F 1-F 2=20-8=12kNF N2= -F 2=-8kN b ):F N1= F 2=8kNF N2= F 2 -F 1=8-20=-12kN F N3= F 2 -F 1+ F 3=8-20+10=-2kN5-2 图示杆件,求各段内截面的轴力,并画出轴力图。
解:用简便方法求截面轴力 a ): F NAB =10kNF NBC =10-40= -30kNb ):F NAB =-5kNF NBC =-5+15=10kN F NCD =-5+15-6=4kN5-3 题5-2a 图中杆件较细段A 1=200mm 2,较粗段A 2=300 mm 2,E =200GPa ,l =100mm,求各段截面的应力。
解:画轴力图MPa 50200101031=⨯==A F NAB AB σMPa 100300103032=⨯==A F NBC BCσ5-4 图示插销拉杆,插销孔处横截面尺寸b =50mm ,h =20mm ,H =60mm,F =80kN,试求拉杆的最大应力。
解:1)求轴力 F N = F N =80kN 2)求最大应力MPa 40)2060(501080)(3max max =-⨯⨯=-==h H b F A F N N σ图5-28a图5-28b图5-29a 10kN-30kN图5-29b 10kN-5kN 4kN图5-29a10kN-30kN图5-305-5 图示油缸盖与缸体采用6个内径d =10mm 的螺栓联接,已知油缸内径D =200mm ,油压p =2MPa,若螺栓材料的许用应力[σ]=170MPa ,试校核螺栓的强度。
解:1)求轴力F N = F =p πD 2/4=2×π×2002/4=20π×103N=20πkN 2)强度计算MPa 3.1334/1061020623max=⨯⨯⨯==ππσA F N <[σ] 螺栓强度满足。
5-6 图示钢拉杆受轴向载荷F =128kN ,材料的许用应力[σ]=160MPa ,横截面为矩形,其中h =2b ,试设计拉杆的截面尺寸b 、h 。
解:1)求轴力F N = F = 40πkN 2)强度计算由正应力强度准则][22max σσ≤==bFA F N N 得 mm 20160210128][23=⨯⨯=≥σN F b 所以 b =20mm, h =40mm5-7 图示桁架,AB 、AC 杆铰接于A 点,在A 点悬吊重物G =17πkN ,两杆材料相同,[σ]=170MPa ,试设计两杆的直径。
解:1)取A 点画受力图求杆件轴力∑F x =0: F AC cos30︒-F AB cos30︒ =0 F AC =F AB ∑F y =0: F AC sin30︒-F AB sin30︒-G =0F AC =F AB =G =17π kN 2)强度计算由正应力强度准则σmax =AF N≤[σ]得 A =42d π≥][N σFd ≥17010174][43⨯⨯⨯=ππσπNF =20mm所以,d =20mm图5-31图5-32yF AB 120︒ F ACxG图5-335-8 图示支架,AB 杆为钢杆,横截面A 1= 300mm 2,许用应力[σ1]=160MPa ;BC 杆为木杆,横截面A 2=200×102mm 2,许用应力[σ2]=5MPa ,试确定支架的许可载荷[G ]。
解:1)取A 点画受力图求杆件轴力 ∑F y =0: F BC sin60︒-G =0 F BC =G 332 ∑F x =0: F BA – F BC cos60︒ =0F BA = 21F BC =G 33 2)强度计算对AB 杆,由正应力强度准则σmax =][33111BA σ≤=A GA F 得 kN 1.83N 101.833001603][3311=⨯=⨯⨯=≤A G σ对BC 杆,由正应力强度准则σmax =][332222BC σ≤=A GA F 得 kN 6.86N 106.86210200532][33222=⨯=⨯⨯⨯=≤A G σ所以 [G ]=83.1kN5-9 在圆截面拉杆上铣出一槽如图示,已知杆径d =20mm ,[σ]=120MPa ,确定该拉杆的许可载荷[F ]。
(提示:铣槽的横截面面积近似地按矩形计算。
)解:1)求杆件轴力F N = F 2)强度计算由正应力强度准则σ =][m inm in σ≤=A FA F N 得 kN 7.25N 107.25420)1(120)44(][][322min=⨯=⨯-⨯=⨯-⨯=≤ππσσd d d A F所以 [F ]=25.7kN5-10 题5-2a 图中杆件较细段A 1=200mm 2,较粗段A 2=300 mm 2,E =200GPa ,l =100mm,求杆件的变形。
图5-34F BA B60︒ F BC G图5-28b解: 1)画轴力图求截面内力F N1=10kN F N1=-30kN 2)求杆件的变形∆l =22N 11N EA l F EA l F ⋅+⋅=)(22N 11A F A F E l N + =)30010302001010(10200100333⨯-+⨯⨯ =-2.5×10-2mm= -0.025mm5-11 图示拉杆横截面b =20mm, h =40mm, l =0.5m ,E =200GPa,测得其轴向线应变 ε=3.0×10-4,计算拉杆横截面的应力和杆件的变形。
解:1)求截面应力σ =E ·ε =200×103×3.0×10-4=60MPa2)求杆端外力F =σ·A =60×20×40=48×103N=48kN 3)求杆件变形∆l =ε·l =3×10-4×0.5×103=1.5×10-1mm=0.15mm5-12 图示结构中,杆1为钢质杆,A 1= 400mm 2,E =200GPa ;杆2为铜质杆,A 2= 800mm 2E =100GPa ;横杆AB 的变形和自重忽略不计。
求 (1)载荷作用在何处,才能使AB 杆保持水平? (2)若F =30KN 时,求两拉杆截面的应力。
解:1)画横杆AB 受力图列平衡方程求F 力作用点x ∑M c (F )=0: -F N1·x + F N2(l - x )=0 F N1·x =F N2(l - x ) AB 保持水平, 即杆1与杆2的变形相等∆ l 1=20010200105.123N11111N ⨯⨯⨯⨯=⋅F A E l F =∆ l 2=40010100100.123N22222N ⨯⨯⨯⨯=⋅F A E l F 得:1.5F N1=F N2代入上式 F N1·x =1.5F N1(l - x ) x =52353⨯=l =1.2m 2)已知F =30kN,求杆件截面应力F N1 F F N2xA C Bl图5-28b图5-29a 10kN-30kN图5-36∑F y =0: F N1 + F N2-F =0 将1.5F N1 =F N2代入得 F N1 =305252⨯=F =12kN F N2 =305353⨯=F =18kN σ1 =400101231N1⨯=A F =30MPa σ2 =800101832N2⨯=A F =22.5MPa5-13 某钢的拉伸试件,直径d =10mm ,标距l 0=50mm 。
在试验的比例阶段测得拉力增量ΔF =9KN 、对应伸长量Δ(Δl )=0.028mm,屈服点时拉力F S =17kN,拉断前最大拉力F b =32kN,拉断后量得标距l 1=62mm 、断口处直径d 1=6.9mm ,试计算该钢的E 、σS、σb、δ和Ψ值。
解:E =23321010284501094//⨯⨯⨯⨯⨯⨯=⋅⋅⋅⋅==-ππεσd Δl l ΔF l Δl A ΔF =204.6×103MPa=204.6GPa σs =4/10101723⨯⨯=πA F s =216.5MPa σ b =4/10103223⨯⨯=πA F b =407.4MPaδ =%505062%1-=-l l l =24% ψ=%109.610%444%22222121-=-=-d d d AA A πππ=52.4%5-14 图示钢制链环的直径d =20mm ,材料的比例极限σp =180MPa 、屈服点σs =240MPa 、抗拉强度σb =400MPa ,若选用安全系数n =2,链环承受的最大载荷F =40kN ,试校核链环的强度。
解:1)求许用应力MPa 1202240][===nsσσ 2) 用截面法求轴力F N = F/2=40/2=20kN 3)强度计算][MPa 7.634/20102023maxσπσ<=⨯⨯==A F N 链环强度满足。
5-15飞机操纵系统的钢拉索,长l =3m ,承受拉力F =24kN ,钢索的E =200GPa,[σ]=120MPa ,若要使钢索的伸长量不超过2mm ,问钢索的截面面积至少应有多大?解:1)按强度准则设计图5-38由正应力强度准则][max σσ≤==A FA F N 得 23mm 2001201024][=⨯=≥σFA 2)按变形条件设计由变形条件][N l EAFl EA l F l ∆∆≤==得 2333mm 1802102001031024][=⨯⨯⨯⨯⨯=≥l E Fl A ∆ 所以,钢索的截面面积A =200mm 25-16 图示等截面钢杆AB ,已知其横截面面积A =2×103mm 2,在杆轴线C 处作用F =120kN 的轴向力,试求杆件各段横截面上的应力。
解:已知l 1=200mm , l 2=400mm1)画AB 杆的受力图列平衡方程∑F y =0: -F A -F B + F =0 F A +F B = F2)由变形协调方程∆ l 1=EA l F A 1⋅=∆ l 2=EAlF B 2⋅得F A l 1= F B l 2代入上式则 F A (1+21l l )= F kN 801204.02.04.0212=⨯+=+=F l l l F A kN 401204.02.02.0211=⨯+=+=F l l l F B 3)求各段横截面应力MPa 40102108033=⨯⨯==A F A ACσ MPa 20102104033=⨯⨯==A F B BC σ 5-17 图示木制短柱的四角用四个40×40×4的等边角钢加固,已知角钢的[σ1]=160MPa ,E 1=200GPa ;木材的[σ2]=12MPa ,E 2=10GPa 。